Model Development for the Viral Kcv Potassium Channel

Abstract

A computational model for the open state of the short viral Kcv potassium channel was created and tested based on homology modeling and extensive molecular-dynamics simulation in a membrane environment. Particular attention was paid to the structure of the highly flexible N-terminal region and to the protonation state of membrane-exposed lysine residues. Data from various experimental sources, NMR spectroscopy, and electrophysiology, as well as results from three-dimensional reference interaction site model integral equation theory were taken into account to select the most reasonable model among possible variants. The final model exhibits spontaneous ion transitions across the complete pore, with and without application of an external field. The nonequilibrium transport events could be induced reproducibly without abnormally large driving potential and without the need to place ions artificially at certain key positions along the transition path. The transport mechanism through the filter region corresponds to the classic view of single-file motion, which in our case is coupled to frequent exchange of ions between the innermost filter position and the cavity.

Introduction

Kcv, a viral channel from Paramecium bursaria chlorella virus (PBCV-1), represents the shortest functional potassium channel, with only 94 amino acids (aas) per monomer known to date (1,2). The topology of Kcv comprises two transmembrane domains (TM1/TM2), the signature sequence TXXTXGFGD, the N-terminal “slide” (s-)helix, a short pore (p-)helix, and two loops linking TM1 with the p-helix and TM2 with the filter, respectively. Electrophysiological studies have shown that Kcv shares many functional characteristics with longer channels, such as sensitivity to K⁺ channel blockers and voltage-dependent gating. Kcv is therefore an ideal model system for studying structure-function relationships to understand basic transport mechanisms.

From a microscopic perspective, the availability of an atomistic Kcv channel model for use in molecular dynamics (MD) simulation studies would be highly desirable. Most MD simulations carried out on channels to date have been based on x-ray structures (3–7), although numerous examples are documented in the literature, including studies in which homology models were successfully used for simulation (8–12), and theoretical studies (13–15). Computational approaches to determine Kcv function suffer from two problems: 1), the Kcv crystal structure has not yet been determined; and 2), Kcv has a low sequence identity (∼10% compared to channels with available structure). Therefore, we recently developed the hypothesis of “functional analogy” between channels (16). According to this hypothesis, the functional principle of conserved regions, such as the filter signature TXXTXGFGD (17), is extended to other pivotal sequence components, whereas other sequence regions are poorly conserved (18). In a previous study (16) we used KirBac1.1 as “functional analog” to Kcv because a functionally important kink-forming proline is found in both cases that marks the transition between the TM1 segment and the s-helix. Furthermore, the N-terminal s-helix contains a comparable pattern of charged residues. Since successive truncation of the Kcv N-terminus leads to a loss of function when a positive residue is cut off, we constructed a KirBac1.1-Kcv chimera model (“KB-Kcv”), truncated and mutated in analogy to Kcv, and studied it by using extensive MD simulations and a number of what we believe are novel analysis techniques. The consequences of the mutations as measured by electrophysiology correlate quite well with the properties of analogous KB-Kcv mutants.

To test the functional analogy hypothesis, we proceeded in this work to use a complementary approach: the construction of an appropriate Kcv homology model. Because of the low sequence identity with other channels, fully automated procedures are not likely to work well. Since sequence alignment has to take into account pivotal positions as discussed above, we used the KirBac1.1 structure (19) as a template. We considered all available structural experimental data—in this case, from an NMR study of the isolated and synthetically generated N-terminus, a 16-residue peptide in aqueous solution. The corresponding conformation was merged with the homology model for the rest, and results were compared with a purely helical model of the N-terminus.

A further complication for model construction concerns a possibly charged lysine residue at position 29 that is most likely located in a membrane-exposed helix segment. Charged side chains play an important role in K⁺ channel function (for example, see Schulte and Fakler (20)). Although our Lys²⁹ positioning may be a modeling artifact, the presence of a titratable residue in a membrane environment cannot be ruled out. For instance, recent studies have shown that varying protonation states of titratable residues in a membrane environment have a large impact on the structure of both the membrane and the protein (21,22). The membrane-spanning S4 helix of other K⁺ channels, which is a suspected voltage sensor, contains four or more titratable residues carrying possibly positive charges (23). Furthermore, the free-energy penalty to include a lysine residue in the center of a hydrophobic segment is as low as 2.6 kcal mol⁻¹ (24), and simulation studies show that the hydrogen-bonded network of water and lipid phosphates around a charged side-chain has a stabilizing effect (21). On the other hand, one can rationalize a deprotonated lysine state by recognizing that the pK_a of a lysine residue in bulk water is 8.95, whereas pK_a shifts of up to −7 units in various environments have been reported (25,26). Although conceptual problems with pK_a calculations are not yet fully resolved (27,28), recent computational work demonstrated that the pK_a of arginine shifts to ∼7 near the center of a lipid bilayer (29). Thus arginine can remain protonated in highly hydrophobic environments. In contrast, lysine deprotonation becomes likely the deeper it penetrates a bilayer (30).

Because of the uncertainty of the lysine state when it is part of a protein embedded in a membrane, we focused on functional analysis of a number of possible variants based on simulations. We tested both the Lys²⁹ protonation state and the N-terminus conformation (NMR versus helical homology structure) by extensive MD simulations of four models, termed Kcv-HOM-K29_deprot, Kcv-HOM-K29_prot, Kcv-NMR-K29_deprot, and Kcv-NMR-K29_prot. As we shall see, the results and particularly the stability analysis along the lines of Holyoake et al. (31) suggest that the model with helical N-terminal and deprotonated Lys²⁹ (Kcv-HOM-K29_deprot) shows all the signatures of a functional, “open-state” channel pore. This choice of the appropriate model is further supported by sterical and three-dimensional reference interaction site model (3D-RISM) integral equation theory (32,33) analyses applied to structures obtained by a simulated annealing protocol, similar to our previously described methodology (16). Furthermore, experimental evidence for the Lys²⁹ protonation state and location in a helix is found in electrophysiological results for a number of Lys²⁹ mutants. As a final quality check, it is ultimately shown that the Kcv-HOM-K29_deprot model exhibits reproducible single-file potassium ion transitions spontaneously in an equilibrium simulation, as well as with the application of external voltage in nonequilibrium situations.

Materials and Methods

Sequence alignment and structure prediction

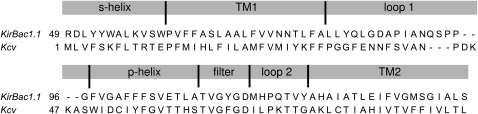
Since automatic multiple alignment with ClustalX (34) of Kcv with sequences of channels with known x-ray structure and a set of related sequences identified by PSI-BLAST (35) yielded no reasonable results, we proceeded by analyzing the structural properties manually. Information about the secondary structure was obtained from the structural prediction programs PROF (36), TMPRED/TMBASE (37), and TMHMM (38). Kcv consists of the pore unit only. Alignment is therefore based on the identification of the s-helix, TM1, loop 1, p-helix, filter, loop 2, TM2, and a cytosolic domain (CD). There are only 26 aas downstream from the signaling sequence (the selectivity filter, residues 63–68), which is just enough to comprise a TM helix and a linker. Although there is no way to determine the length of a loop ab initio, the minimal length of a TM helix seems to be as short as 10 aas, e.g., residue 193–203 of a chloride channel (Protein Data Bank (PDB) code 1KPL) or residue 77–87 of an aquaporin (PDB code 1H6I). We assigned the C-terminal residues 76–94 to TM2, and residues 69–75 to loop 2. The p-helix on the opposite side of the filter has to be attached to the filter, hence position 62 marks one end of the p-helix. Its length is ∼12 aas, which means that residues 50–62 probably form the p-helix. The N-terminal residues include TM1, and an additional s-helix may be present. Proline is known to destroy helical symmetry, and the presence of such a residue within a TM domain is unlikely. Proline at similar positions in MthK (39) and KirBac1.1 (19) also marks the start of the cytosolic terminus of TM1. We assigned residues 1–13 to the s-helix because it is likely that Pro¹³ in Kcv causes the same effect; residues 14–32 were assigned to TM1 with the typical length of 18 aas. The remaining residues 33–49 form loop 1, which links TM1 and the p-helix. All of these assignments were in agreement with the results from prediction programs. In summary, we made the following assignments: s-helix: 1–13, TM1: 14–32, loop 1: 33–49; p-helix: 50–62, filter: 63–68, loop 2: 69–75; and TM2: 76–94. The absence of a CD is in agreement with the results from the structural prediction programs. The alignment of Kcv with KirBac1.1 is shown in Fig. 1. Regions 1–45 (s-helix/TM1/loop 1), 46–72 (loop 1/p-helix/filter/loop 2), and 73–94 (loop 2/TM2) were aligned with ClustalX (34) independently, and the filter was aligned manually. On both sides of KirBac1.1 the termini were truncated by the number of residues that exceeded the length of the Kcv sequence. The aligned regions were merged and artificial gaps were removed.

Figure 1.

Alignment of Kcv with respect to KirBac1.1, used as input for 3D modeling.

NMR spectroscopy

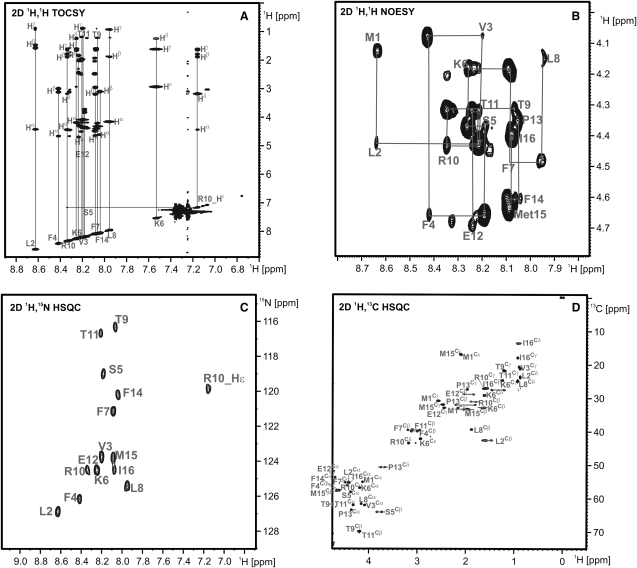
NMR spectra were recorded at 300 K on a Bruker (Rheinstetten, Germany) 600 MHz spectrometer equipped with a triple resonance probe with xyz gradients. The data were processed with TopSpin 1.3 (Bruker) and analyzed using SPARKY 3.1 (40). The peptide NH₂-MLVFSKFLTRTEPFMI-COOH was dissolved in 0.5 mL of H₂O-D₂O (9:1) to obtain a peptide concentration of 2 mM. A complete set of homonuclear NMR experiments were recorded with 2D correlation spectroscopy (COSY), 2D total correlation spectroscopy (TOCSY), and 2D nuclear Overhauser effect spectroscopy (NOESY) (41–43). In all homonuclear 2D experiments, the solvent signal was suppressed using excitation sculpting (44) with a selective 180° pulse length of 4.6 ms to minimize saturation of H^α-protons. All experiments were acquired with a sweep width of 7800 Hz, 512 complex points in the indirect t₁ dimension, an acquisition time of 260 ms, a relaxation delay of 2 s, and 16 scans per t₁ increment. Sign discrimination in the indirect dimension was achieved using the States-TPPI method (45). The bandwidth of the proton pulse was 33 kHz. The mixing time was set to 80 ms for the TOCSY (bandwidth of 10 kHz) and 300 ms for the NOESY. ¹H, ¹⁵N-HSQC, and ¹H, ¹³C-HSQC spectra at natural abundance were recorded using 256 and 64 scans per t₁ increment, respectively. In the ¹H, ¹⁵N-HSQC spectra, the solvent signal was suppressed using the WATERGATE (46) sequence, whereas in the ¹H, ¹³C-HSQC spectra, gradient coherence selection was applied. The total measurement time of all experiments was 54 h. Spectra are shown in Fig. 2 (more details are provided in the Supporting Material).

Figure 2.

NMR spectra recorded on the 16mer peptide at a temperature of 300 K at 600 MHz. (A) Assigned NH/aliphatic region in the 2D TOCSY with a mixing time of 80 ms. (B) Sequential resonance assignment walk in 2D NOESY with a mixing time of 300 ms. (C and D) Nitrogen and carbon HSQCs of the peptide with annotated resonance assignment.

Structure calculations

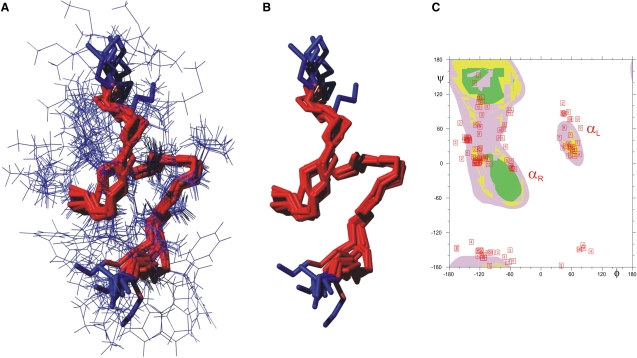
Structure calculations based on the NMR NOE data were performed with CNX 2002 (47). The protein allhdg force field 4 (48) was used. In total, 100 structures were calculated using 102 distance restraints. For the structure calculations, a two-stage simulated annealing (SA) protocol was applied using torsion angle dynamics (TAD). The high-temperature stage consisted of 1000 steps at 50,000 K. This was followed by a cooling stage, 1000 steps to 0 K, and a final minimization of 2000 steps. The force constant for the NOE restraints was set to 150 kcal mol⁻¹Å⁻² during the SA protocol and 75 kcal mol⁻¹Å⁻² during the minimization. The final nine lowest-energy structures were further analyzed with PROCHECK (49). The results are depicted in Fig. 3.

Figure 3.

(A and B) Overlay of the nine lowest-energy structures out of 100 calculated structures. (B) Only the backbone is shown. The RMSD value for all heavy atoms is ∼2 Å and 0.8 Å for the backbone atoms. (C) Ramachandran statistics for the nine lowest-energy structures.

3D modeling

An initial model for Kcv based on the tetrameric form of the KirBac1.1 (PDB-Code: 1P7B) x-ray template structure was created by MODELLER (50). Harmonic restraints were applied to the filter region as well as to the ions to prevent distortion of this sensitive region. To validate the resulting ensemble of 100 configurations, we calculated the energy, DOPE score, and the DOPE plot (51) with MODELLER, and pseudo-pair energies for all Cα-Cα pairs with PROSA II (52). PROCHECK (49) was used to evaluate the stereochemistry, e.g., by calculating Ramachandran plots (53). We chose the structure that performed best with respect to its energetic and geometric features after performing a number of simulated annealing refinement runs for further processing. The value of the dihedral angle formed by Arg¹⁰-Cα, Arg¹⁰-C, Thr¹¹-N, and Thr¹¹-Cα in the model was 179.5°, leading to an Arg¹⁰ side-chain orientation hidden from the solvent. Energetic optimization using SYBYL (54) with respect to this torsion angle under the constraint of Arg¹⁰ solvent exposure yielded a value of 0° with similar energy. Missing protons were added using the academic version of CHARMM V31b1 (55) and optimized with an adopted basis Newton-Raphson minimizer for 2000 steps. The resulting geometry has a helical N-terminus and forms the basis for the models Kcv-HOM-K29_deprot and Kcv-HOM-K29_prot. For the models Kcv-NMR-K29_deprot and Kcv-NMR-K29_prot the structure of the synthetic N-terminal peptide MLVFSKFLTRTEPFMI (see Fig. 3) as determined by NMR spectroscopy was merged with the original homology model by superposition of corresponding atom coordinates. MODELLER was used as described above to create and optimize the chimera model composed of the NMR-derived N-terminus and KirBac1.1-based remaining residues. In all models, Lys²⁹ was found to be membrane-exposed. This is a direct consequence of choosing Pro¹³ as the pivotal residue marking the transition between the TM helix and N-terminus. Any other Lys²⁹ orientation would have required the introduction of a gap between Pro¹³ and TM1, which is highly unlikely.

MD simulations

The simulation procedures closely followed the steps used for KB-Kcv simulations performed previously by our group (16) and others (56,57). Briefly, the systems were constructed using CHARMM V31b1 with the CHARMM22 potential function for proteins (58), CHARMM27 for phospholipids (59), and ion parameters from the Roux lab (60). All titratable residues (except for Lys²⁹; see discussion above) were kept at their standard protonation state. This is reasonable for similarly critical Lys⁷² and Lys⁷⁷, which turned out to be buried in the protein, not membrane-exposed. The total charge was +8 for the protonated models and +4 for the deprotonated models. In the latter potential function, we used CHARMM22's methylamine parameters for the lysine amino group. Simulation runs were performed with NAMD2.5/2.6 (61). Kcv-HOM-K29_deprot was taken as the basis, translated with respect to its center of mass (located in the cavity); all other models were superimposed onto the filter coordinates. The structures were embedded in dimyristoylphosphatidylcholine (DMPC) membranes and KCl/TIP3P water phases of ∼100 mM as in our previous work (16). The systems comprised 64 lipid molecules on the intracellular and 54 on the extracellular side, corresponding to a cross-sectional area of 59 Ų per DMPC molecule (57). Two K⁺ ions on filter binding sites S1 and S3 (in the terminology defined by Berneche and Roux (3)) were kept while two water molecules on S0 and S2 in the filter were created. The final ion number was 19 K⁺ throughout and 27/23 Cl⁻ for the protonated/deprotonated variants, respectively. The total number of atoms was 48707/48571/48617/48886, including 9559/9511/9529/9616 water molecules for Kcv-HOM-K29_deprot/Kcv-HOM-K29_prot/Kcv-NMR-K29_deprot/Kcv-NMR-K29_prot, respectively. The initial dimensions of the orthorhombic simulation box were 92 Å along the z axis and 72 Å in the xy plane.

Pressure was kept constant at 1 atm by the Langevin piston algorithm (62,63) with an oscillation period of 200 fs and damping constant of 100 fs. A Langevin thermostat that kept the temperature constant at 330 K was coupled to the system (coupling constant: 5 ps⁻¹). Hydrogen-heavy atom distances were constrained using the SHAKE algorithm (64), allowing for an integration time step of 2 fs. A smooth cutoff over a distance of 10–12 Å was used to truncate the Lennard-Jones interactions. Electrostatic interactions were treated by the particle mesh Ewald algorithm (65) with a grid resolution of ∼1 Å. Initially, simulations with harmonic restraints on the protein and the membrane were performed to allow smooth relaxation of the system. These restraints were gradually lifted. Strong restraints (Force constant 10 kcal mol⁻¹ Å⁻²) were applied to the filter residues (TVGFGD), including the K⁺ ions and water molecules in the filter, to preserve the filter configuration, followed by a very short restraint-free NpT run of 20 ps at the end of the construction phase to allow the filter region to accommodate. The filter restraints were again applied for the initial 30 ns simulation time and removed afterward. The total simulation time was 90.8 ns/74.4 ns/92.64 ns/43.32 ns for the Kcv-HOM-K29_deprot/Kcv-HOM-K29_prot/Kcv-NMR-K29_deprot/Kcv-NMR-K29_prot systems, respectively. Two additional independent nonequilibrium simulations (Kcv-HOM-K29_deprot-E1 and Kcv-HOM-K29_deprot-E2) were performed by restarting the Kcv-HOM-K29_deprot trajectory after removing the constraints and applying a constant external electric field along the z axis corresponding to +100 mV over a time of 12 ns. Two further independent nonequilibrium simulations with +100 mV external potential over 10 ns were conducted with the protonated homology model, Kcv-HOM-K29_prot-E3 and Kcv-HOM-K29_prot-E4, starting with the last frame of the simulation with a flexible filter.

Structural, thermodynamic, and dynamical evaluations

Standard techniques for evaluating simulation results, such as computing the root mean-square (RMS) fluctuations (RMSF)/thermal B factors and RMS deviations (RMSD) of the structures from the initial state, were used to characterize the stability of the simulations. RMSD time-series calculations were carried out with the RMSDTT v1.9.2.2 plugin (66) for VMD v1.8.3 (67) for constrained and unconstrained runs, for all Cα atoms, and further dissected into contributions from the s-helix only. For a stability analysis to check and compare the homology model's quality along the lines of Holyoake et al. (31), we calculated stability measures between structures at 0 and 28 ns of the rigid filter runs (the static RMSD between these two snapshots and the α-helicity loss, as determined by the STRIDE algorithm (68) for the complete protein, and for TM1 and TM2 separately).

Further analysis is possible with symmetrized average structures. We previously outlined a procedure for extracting such geometries from very long trajectories by a simulated annealing approach with CHARMM V31b1 in the field of average distance restraints (16). We followed this strategy for the rigid filter runs in this work using the following protocol: heavy atom pairs within a cutoff of 11 Å, all charged residues (including the C- and N-termini), and all Cα-Cα pair distances were averaged over the final 20 ns of the constrained trajectories. Force constants for harmonic restraints were set to 15/10/10/10 kcal mol⁻¹ Å⁻² for Cα-Cα pairs, 1/1/1/3 kcal mol⁻¹ Å⁻² for all charged residue pairs, and 0.10/0.15/0.10/0.10 kcal mol⁻¹ Å⁻² for all others in the Kcv-HOM-K29_deprot/Kcv-HOM-K29_prot/Kcv-NMR-K29_deprot/Kcv-NMR-K29_prot systems, respectively, all weighted by the inverse fluctuations. The values were maximized for each system separately with respect to stable annealing runs. The initial temperature was 750 K and the annealing window interval was 200 fs. Symmetrization was applied after each window as described previously (16).

The pore diameters of the symmetric average structures were calculated by HOLE (69). Ramachandran plot analysis has been done with PROCHECK (49). We furthermore applied 3D-RISM integral equation theory to these structures to elucidate potassium and chloride ion distributions and the influence of the protonation state on these quantities. Again, the procedure closely followed the one outlined previously (16). The solvent susceptibility was computed from the dielectrically consistent 1D-RISM equations (70,71) on a logarithmically spaced grid of 512 points ranging from 5.98·10⁻³ Å to 164.02 Å using a variant of the modified inversion of iterative subspace (MDIIS) method (72). The temperature was set to 298.15 K, a 1 M electrolyte concentration corresponding to number densities of 0.032367 Å⁻³ for water and 0.000602 Å⁻³ for KCl (73) was used. The dielectric constant of the solvent was set to 68.5. The 3D-RISM equations were solved within a fourth-order partially expanded closure approximation, which is a generalization of the (first-order) partially linearized Kovalenko-Hirata closure (74), on a cubic grid of 128³ points with a 0.6 Å spacing by the MDIIS technique (72). Long-range electrostatics were treated by Ewald summation (74), taking into account conducting boundary conditions. Artifacts caused by the net charge of the solute were corrected by a renormalization technique (75). Density distributions were integrated within the radius given by HOLE along the central channel axis, yielding a local concentration profile by dividing the number of particles within a slice of the grid by the associated slice volume.

Mutagenesis and transfection of mammalian cell lines

The Kcv gene was cloned into the BgIII and EcoRI sites of the pEGFP-N2 eukaryotic expression vector (Clontech, Palo Alto, CA) in frame with the downstream enhanced green fluorescent protein (EGFP) gene by deleting the Kcv stop codon. Point mutations K29A, K29L, K29R, K29S, K29V, K29W, and K29H were created by the QuickChange method (Stratagene, La Jolla, CA) and validated by sequencing. HEK293 cells were transfected with Kcv::EGFP and the Kcv mutants. Control cells were transfected with the empty plasmid (pEGFP-N2). The liposomal transfection reagent metafectene (Biontex Laboratories, Munich, Germany) was used to transiently transfect HEK293 cells.

Electrophysiology

After transfection, the cells were incubated at 37°C in 5% CO₂ for 1–2 d. The cells were dispersed by trypsin, plated at a low density on 35 mm culture dishes, and allowed to settle overnight. Single cells were patch-clamped in the whole-cell configuration according to standard methods (76) using an EPC-9 patch-clamp amplifier (HEKA, Lambrecht, Germany). Data were gathered and analyzed with Pulse software (HEKA). The bathing solution consisted of 100 mM KCl, 1.8 mM CaCl₂, 1 mM MgCl₂, and 5 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES, pH 7.4). Osmolarity was kept constant at 300 mOsmol with choline-Cl. The pipette solution contained 130 mM D-potassium-gluconic acid, 10 mM NaCl, 5 mM HEPES, 0.1 mM guanosine triphosphate (Na salt), 0.1 μM CaCl₂, 2 mM MgCl₂, 5 mM phosphocreatine, and 2 mM adenosine triphosphate (Na salt, pH 7.4).

Results and Discussion

General model features

A number of structural and topological features for our homology models, even before they were relaxed by simulations, are in agreement with x-ray structures published for other channels: 1), Both the characteristic topology of a K⁺ channel and the filter geometry are preserved. Furthermore, since there is no bundle crossing of the TM2 helices, these models satisfy a proposed condition for an open-state model (77). 2), The TM domains are equipped mainly with hydrophobic residues, whereas the solvent-exposed loops and s-helices are mainly hydrophilic. 3), The cavity is lined mainly by hydrophobic amino acids originating from TM2 (Phe⁸⁸, Phe⁸⁹, Leu⁹², and Leu⁹⁴). In particular, the presence of one (for KcsA (78), KirBac1.1 (19), KvAP (79), and MthK (39)) or more phenylalanine residues (for NaK (80)) exposed to the cavity are typical features of K⁺ channels. The overall hydrophobic cavity lining maximizes the interaction of potassium ions with water because there is hardly competition from the protein surface (81).

Model quality assessment from equilibrium simulation phenomenology

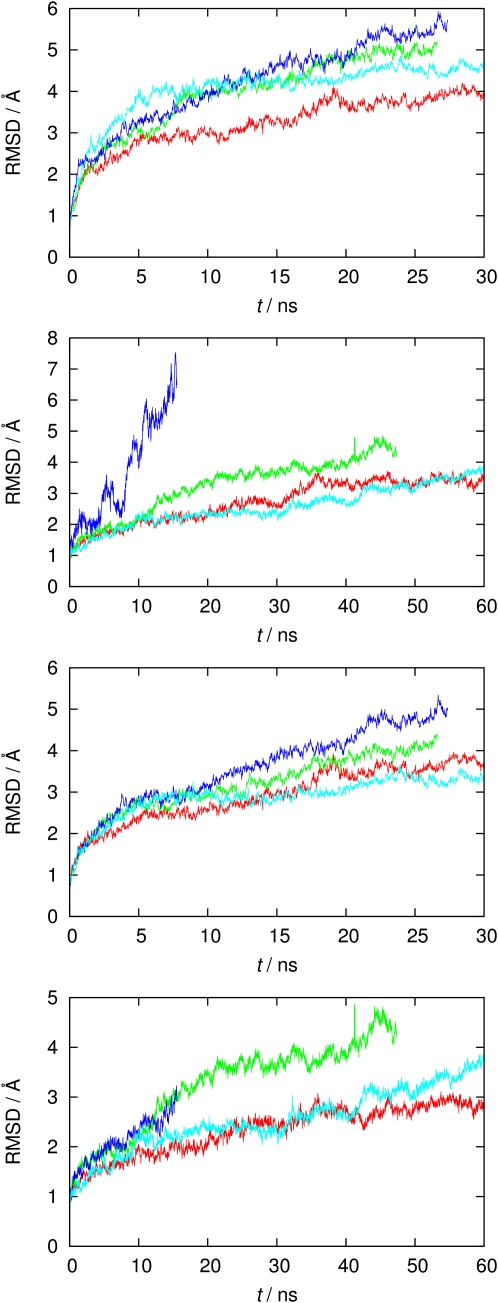
The total energy, volume, density profiles, etc. all indicate a stationary state that was reached after a few nanoseconds. As shown for the RMSD time series in Fig. 4, all simulations with rigid filter restraints appear to be stable, since the largest part of the structural drift occurred within 3 ns. Releasing the filter restraints led, as anticipated (5,16,82), to further structural drift. Large RMSD drifts, particularly observed for Kcv-NMR-K29_prot, are located mainly in the highly flexible s-helices, as evidenced in the two lower panels of Fig. 4. Notice that the protonated models (blue and green curves) show significantly less stability, particularly after release of filter restraints, as compared to deprotonated systems (red and cyan curves). This is the first indication that deprotonated Lys²⁹ appears to be associated with a more stable protein structure and a functional pore state.

Figure 4.

Cα RMSD time series of the four variants (red: Kcv-HOM-K29_deprot; green: Kcv-HOM-K29_prot; cyan: Kcv-NMR-K29_deprot; blue: Kcv-NMR-K29_prot). From top to bottom: computed for all residues from rigid filter runs, subsequent fully flexible runs (time was reset to zero), computed for non-s-helix residues from rigid filter, and from fully flexible runs.

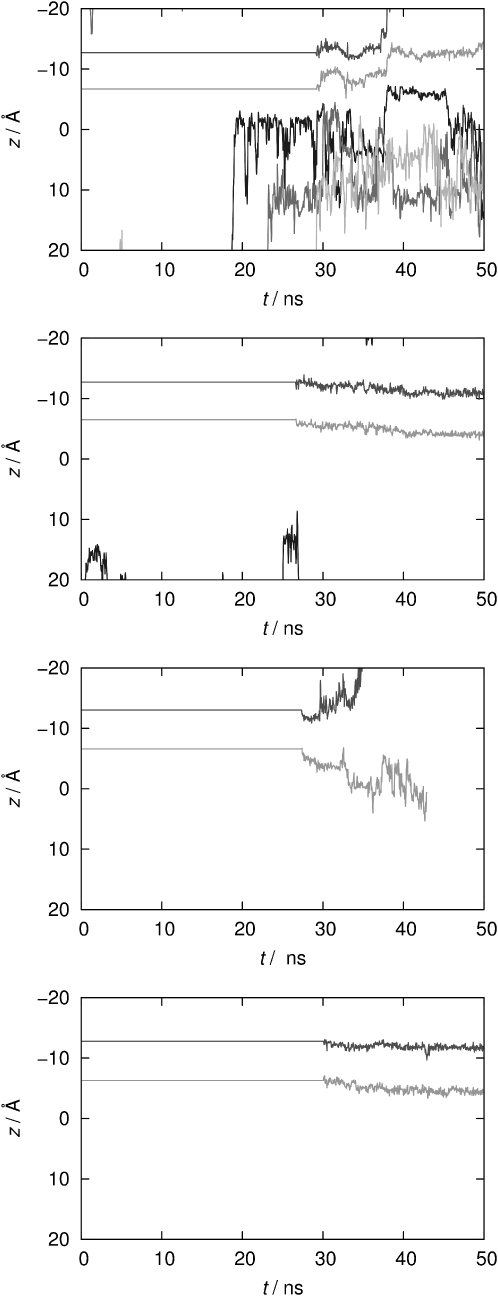
More evidence for the functional deprotonated state is found by visualization of K⁺ ion transition events, shown in Fig. 5. Apparently, only the Kcv-HOM-K29_deprot model (top panel) is capable of continuous ion transport; even in an equilibrium situation, spontaneous single-file ion motion is observed after 38–39 ns (we will come back to this point later). The trajectory shows that a K⁺ ion is rapidly shifted to a position near the filter as soon as it passes the intracellular mouth, as expected from the hydrophobic cavity lining. The cavity is populated on average by 2–3 ions, in line with results found for KB-Kcv wild-type in our earlier work (16). The other models, including all NMR variants, appear to rest in an inactive state. Not a single ion passage through the inner mouth is observed, even after very long simulation times.

Figure 5.

z coordinates (measured along the channel axis, intracellular mouth is located around z = 10 Å) of potassium ions over simulation time, from top to bottom: Kcv-HOM-K29_deprot, Kcv-HOM-K29_prot, Kcv-NMR-K29_deprot, Kcv-NMR-K29_prot. Only K⁺ ions that rested for more than 200 ps near the protein atoms are shown. Different shades of gray are used to distinguish ions.

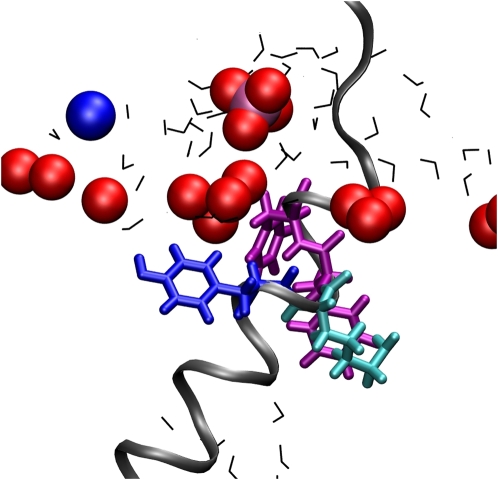
Kcv-HOM-K29_deprot also appears to be a reasonable model from an analysis of specific residue locations. It has been proposed that amphipathic aromatic side chains (such as tryptophane and tyrosine) that are associated with the membrane-water interface should be located at the end of a TM domain (see Nyholm et al. (83)). Indeed, Trp⁵⁰ is located at the extracellular side, and the polar hydroxyl group of Tyr²⁸ is in permanent contact with the lipid heads even though it is buried in the bilayer, as shown in Fig. 6 for Kcv-HOM-K29_deprot. The absence of tryptophane and tyrosine at the intracellular site is consistent with the structure of MthK (39). Furthermore, a typical salt bridge pattern is observed that resembles the situation found for our KB-Kcv model (16) and also for NaK (80): Lys⁶ and Arg¹⁰ both form salt bridges with the C-terminus (taking the role of Lys⁹ in KB-Kcv).

Figure 6.

Snapshot from the Kcv-HOM-K29_deprot simulation showing the conformation of residues 28–31 (YKFF) in a single TM1. Only water and lipid atoms (N: blue; P: magenta; O: red) within a radius of 10 Å of the residues are shown. Blue sticks: Tyr²⁸; cyan sticks: Lys²⁹; magenta sticks: Phe³⁰ and Phe³¹; gray ribbons: Kcv backbone; black lines: water.

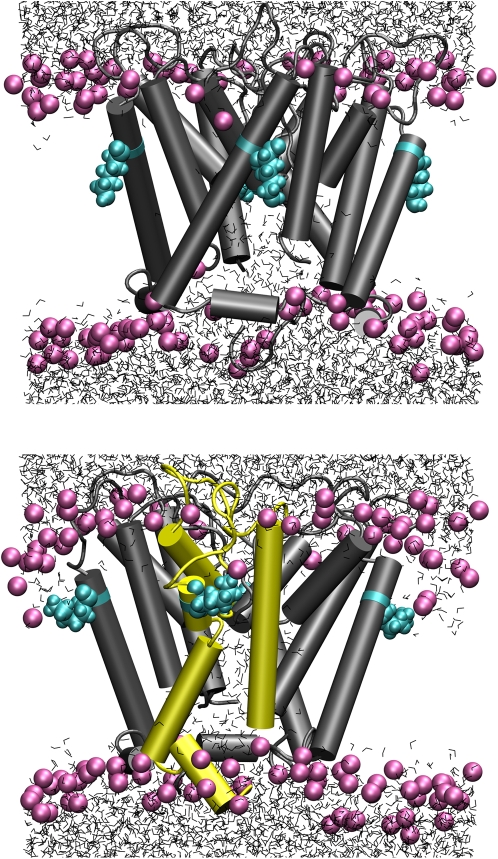
The effect of protonation of Lys²⁹ becomes clearer from snapshots of the Kcv-HOM simulations, depicted in Fig. 7. In the deprotonated state the Lys²⁹ side chain is oriented toward the center of the lipid bilayer. Lipid headgroups are barely affected; water hardly penetrates the membrane. The presence of deprotonated lysine near the bilayer center is compatible with recent computational results (30). The situation changes dramatically upon protonation: Lys²⁹ “snorkels” (84,85) toward the extracellular side, and the membrane thins out due to lipid heads getting dragged into the bilayer. This allows a significant number of water molecules to solvate the polar Lys²⁹ residue. Additionally, the helical structure of the TM helix gets distorted. These observations, consistent with recent simulations (22), explain the lower stability of protonated versus deprotonated models.

Figure 7.

Snapshots at t = 39 ns (i.e., 9 ns after filter constraints were removed), Kcv-HOM-K29_deprot (top) and Kcv-HOM-K29_prot (bottom). For lipids only P atoms are shown (magenta); Lys²⁹: cyan; water: gray tubes; cylinders: α-helices as recognized by STRIDE (yellow tubes in bottom figure denote regions with the largest helix loss).

There seems to be a delicate cooperation between Lys²⁹ and its neighbors, as is also seen in Fig. 6. Hydrophobic residues Phe³⁰ and Phe³¹ are located behind Lys²⁹, and tend to interact with the hydrophobic part of the bilayer. On the other hand, Tyr²⁸ and Lys²⁹ penetrate similarly deep into the membrane. Tyrosine as an amphipathic aromatic residue is proposed to be located at the end of a TM (83). Although this is not the case in our model, the polar group of Tyr²⁸ always stays in contact with the polar environment: an H-bond between the hydroxyl group of Tyr²⁸ and an acceptor site either from water or from lipid headgroups was continuously observed. The position and orientation of Tyr²⁸ are not likely to be modeling artifacts, since tyrosine is observed at equivalent positions in the x-ray structures of KvAP (79) and MthK (39).

Table 1 summarizes the stability issues in terms of α-helicity loss and static RMSD between certain snapshot structures. Both quantities are lower for deprotonated as compared to protonated models. Kcv-HOM-K29_deprot is the only model with no helicity loss in both TM segments. NMR models are inferior to pure homology models, as evidenced by the substantial total and TM-specific α-helicity losses. In summary, the analyses described so far all indicate that only Kcv-HOM-K29_deprot represents a functional and reasonable Kcv model.

Table 1.

Validation of various Kcv models^∗

	Favored (%)	RMSD/Å	α-Helicity loss (%)
			Total	TM1	TM2
Kcv-HOM-K29deprot	100.0	4.48	−3.81	−5.00	−13.84
Kcv-HOM-K29prot	98.8	5.50	−1.90	8.33	−12.31
Kcv-NMR-K29deprot	97.6	5.42	7.59	6.56	1.21
Kcv-NMR-K29prot	98.8	6.28	9.96	8.19	13.25
Kcv-HOM-K29deprot-E1	—	4.92	−7.14	−5.00	−16.93
Kcv-HOM-K29deprot-E2	—	4.32	0.00	−5.00	−13.84

^∗Percentage of residues in favored regions as obtained from Ramachandran analysis of the symmetrized average structures; Cα RMSD values and relative α-helicity loss between snapshot structures as obtained from homology modeling and after 18/10 ns of the fully flexible equilibrium/nonequilibrium simulations. Negative values for α-helicity loss indicate an actual gain in helix stability.

Analysis of symmetrized average structures

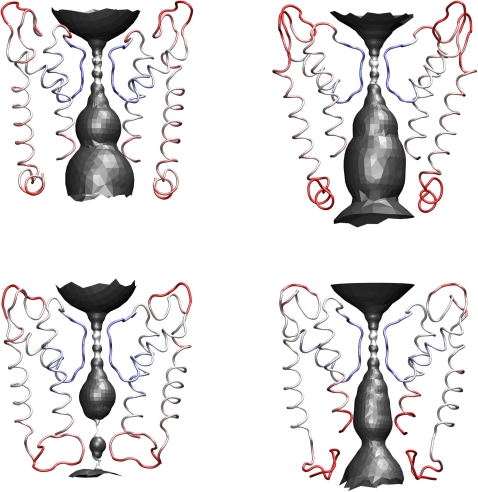
Fig. 8 shows the structures of the four models as obtained from the symmetrizing annealing procedure, along with the accessible volume from HOLE analysis and color-coded local B factors averaged over the final 4.5 ns of the rigid filter simulations. The intracellular mouth is formed by the s-helix, rather than by TM2, which is too short to exhibit bundle crossing of these segments (cf. Jiang et al. (77)), in line with our earlier results (16). However, caution is advised because the limited homology between Kcv and the template (KirBac1.1) in this region could lead to a very different orientation of the s-helix without the bundle crossing present in KirBac1.1. Furthermore, we cannot immediately expect an isolated 13-mer peptide studied by NMR in solution to represent its structure in the tetramer, where clearly additional interactions (including forces from the membrane) are involved. It is therefore not surprising that the s-helices of full homology and NMR models are markedly different: helical structure is conserved in the former class, whereas in the latter the “untangled” character of the isolated peptide (cf. Fig. 3) is still observed, despite the inherently large flexibility measured via thermal B factors. Another difference concerns the intracellular mouth: the mouths of the NMR models are narrower than those of the homology models. Particularly in the case of Kcv-NMR-K29_deprot, this static view suggests that the mouth presents a substantial sterical barrier for ions. In contrast, the intracellular mouths of both pure homology models are wide open. On the other hand, we find confirmation for our previous finding that an open mouth does not necessarily imply permeability (16).

Figure 8.

HOLE analysis and backbone atomic B factors (blue: <10 Ų; red: >20 Ų) mapped onto symmetrized average structures. Kcv-HOM-K29_deprot (top left), Kcv-HOM-K29_prot (top right), Kcv-NMR-K29_deprot (bottom left), Kcv-NMR-K29_prot (bottom right).

The open/closed character of the inner mouth can be verified directly by monitoring the trajectory, and does not represent an artifact from the averaging procedure. The helicity loss in the NMR model cases, summarized in Table 1, can also be determined visually for the symmetrized structures. It therefore appears likely that the NMR model structures should be discarded as long as functional pore states must be maintained. This does not rule out the possibility that the NMR geometry of the N-terminus plays another role in Kcv transport mechanisms.

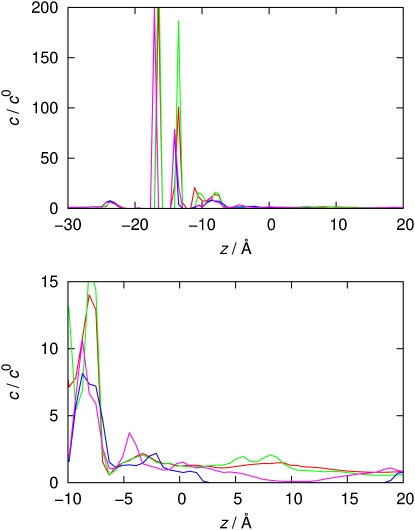
The purely sterical picture, however, is not entirely satisfactory. More insight is gained by analyzing the density distributions as obtained from 3D-RISM theory. Results for concentration profiles are depicted in Fig. 9. The filter is found around z = −15 Å, and the mouth at approximately z = 10–12 Å. The concentration profiles clearly show almost complete depletion of K⁺ ions for the NMR models near the mouth. This corresponds to high barriers for ion transport, whereas the homology models do not show significant barriers in this region. Despite the sterical possibility of allowing ion transport in the case of Kcv-NMR-K29_prot, the mouth lining is unfavorable for K⁺, in line with the dynamical results shown in Fig. 5. The NMR models can therefore consistently be characterized as closed/nonconductive or dysfunctional. The situation with Kcv-HOM-K29_prot, however, is less clear since the integral equation results would allow ion passage. This contradicts the helix instability arising upon protonation (Fig. 7) and the dynamic data shown in Fig. 5. Remarkably, the 3D-RISM profiles show a substantial stabilization of the K⁺ ions residing in the filter upon protonation of Lys²⁹, which is counterintuitive. The dynamical behavior of the ions in the filter region shown in Fig. 5 supports this result (protonated species are depicted in the second and fourth panels).

Figure 9.

K⁺ concentration profiles along the pore axis from 3D-RISM theory for symmetrized average structures in c⁰ = 1 M KCl solution: Kcv-HOM-K29_deprot (red), Kcv-HOM-K29_prot (green), Kcv-NMR-K29_deprot (blue), Kcv-NMR-K29_prot (cyan). Top: View along the entire system. Bottom: Enlarged cavity and mouth region.

It is possible that we did not observe ions entering the cavity in simulations of Kcv-HOM-K29_prot (although they come close; see Fig. 5) simply because more equilibration time would have been necessary. Given the large simulation time for Kcv-HOM-K29_prot, however, there must be other reasons for the apparent mouth barrier that cannot be deduced from static averages alone. Fig. 8 (top) shows that the s-helices are considerably more flexible for the protonated as compared to the deprotonated model. This means that transient fluctuations could lead to temporary constrictions with greater probability for Kcv-HOM-K29_prot than for Kcv-HOM-K29_deprot. Restricted flexibility in the mouth region could therefore be an important feature of a conducting channel state. Furthermore, Fig. 5 suggests that rapid ion exchange between cavity and bulk is coupled with filter flexibility and cation translocation through that region. Experimental evidence for such long-distance interactions was previously found for Kcv (86), but more work is required to clarify the situation. Static and dynamical considerations support the choice of Kcv-HOM-K29_deprot as the most promising model for a functional, conducting channel.

Electrophysiology

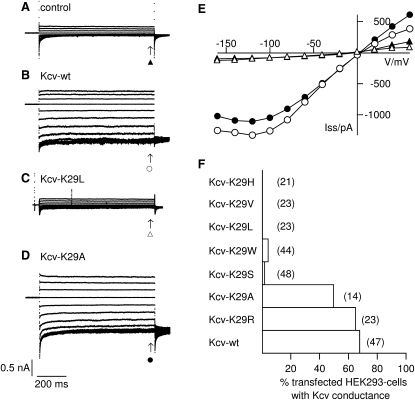
Fig. 10 shows results from electrophysiological studies on various Lys²⁹ mutants to provide more insight into the protonation state of the active system. The current responses and the corresponding I/V relations obtained in nontransfected HEK²⁹³ cells and cells transfected with Kcv-wt are in agreement with previous measurements (2). It is characteristic of Kcv currents in HEK²⁹³ cells that the ratio of slope conductance at negative voltages (−20 mV to −60 mV) versus conductance at positive voltages (0 to +60 mV) was always greater than one; in control, nontransfected cells this ratio was significantly smaller than one (2). With this criterion we find that ∼65% of all cells expressing the Kcv-wt gene reveal a visible Kcv-type current. Also, more than 50% of cells expressing Kcv-K29A and Kcv-K29R are found to exhibit the same kind of Kcv-type current (Fig. 10, D–F). With a lower frequency, we also observe the same type of current in cells expressing either the mutant K29S or K29W (Fig. 10, F). As far as the other mutants (K29L, K29V, and K29H) are concerned, no current response with the aforementioned criterion is observed. Thus, the channels are either inactive or too small, or they were not sorted properly to the plasma membrane. The results of these experiments show that the channel does not tolerate every amino acid in this position. But the fact that the mutation of Lys²⁹ into the nonpolar residue alanine (and other nonpolar amino acids) does not affect the phenotype of the Kcv conductance suggests that Lys²⁹ in the wild-type and Arg²⁹ in the K29R mutant are not charged, or that protonation has no apparent influence. The fact that arginine can replace lysine at position 29 may be an indication that the amino group indeed plays a genuine role, but it is still very likely that arginine is deprotonated as well. Since alanine is a helix-forming residue, positioning of Lys²⁹ in a TM segment of our model is now experimentally well founded.

Figure 10.

Current responses of HEK293 cells transfected with GFP: control (A), Kcv-wt (B), Kcv-K29L (C), and Kcv-K29A (D) to standard voltage protocol from holding voltage (0 mV) to test voltages between +60 mV and −160 mV. (E) Steady-state I/V relations of currents in A–D; symbols cross-reference with symbols in A–D. (F) Percentage of transfected HEK293 cells with Kcv conductance, for Kcv-wt and mutants; the number of recordings is indicated in brackets.

Thus, there is still no conclusive evidence as to the choice of the protonation state in the Kcv model. In light of the experimental data, however, it is obviously not important to give a definitive answer, and we are therefore allowed to choose a model based on pragmatic arguments. Taken together, the computational and experimental quantities analyzed up to this point strongly favor the full homology model with deprotonated Lys²⁹, Kcv-HOM-K29_deprot, as the most promising candidate for an active Kcv pore state.

Single-file event analysis

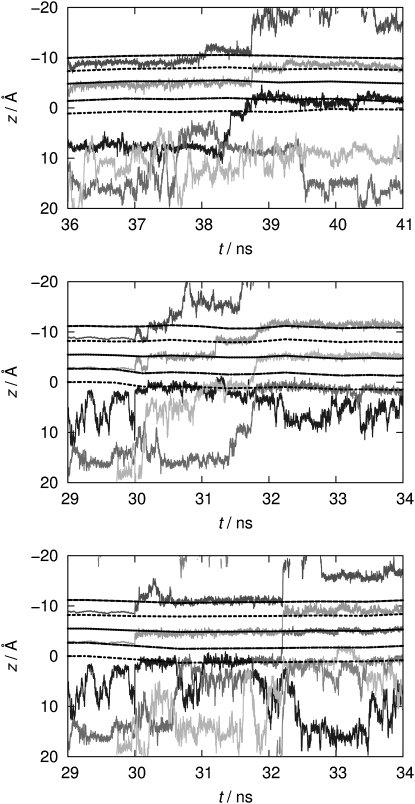
We find that K⁺ ions translocate in single-file fashion for both equilibrium and nonequilibrium trajectories of Kcv-HOM-K29_deprot, as illustrated in Fig. 11. Such a classical single-file motion is in agreement with earlier work (3,6,12,87). This behavior serves as the ultimate quality check for the model, since it is, to the best of our knowledge, the first time that such a mechanism has been found for a homology model of a potassium channel. Even more interesting is the observation that ion transport through the filter is accompanied by concerted transitions from the bulk solution into the cavity. Therefore, this represents the first documented case of spontaneous ion transport through the entire pore without artificially large external fields and specific ion placements to induce the transport mechanism (6). In the nonequilibrium cases, the bulk/mouth-to-cavity and filter transitions even appear to occur in a concerted fashion.

Figure 11.

z coordinates (measured along the channel axis) of potassium ions over 6 ns simulation time for flexible filter runs of Kcv-HOM-K29_deprot, from top to bottom: without external field (enlarged view of top panel of Fig. 5), simulations E1 and E2 with constant external field corresponding to +100 mV voltage. Dashed/dotted lines show the positions of binding sites S0–S4 (from top to bottom). The positions were defined as the geometric center of the oxygen rings of two adjacent filter residues (62–67). Different shades of gray are used to distinguish ions.

In the equilibrium case (top panel of Fig. 5), a K⁺ ion enters the cavity after ∼19 ns of rigid-filter simulation time. A second K⁺ ion gets trapped near the intracellular mouth after ∼23 ns. Immediately after the filter restraints are lifted, the ion at position S3 moves to position S2. Simultaneously, a third K⁺ ion stays near the intracellular mouth; <1 ns later, the second ion enters the cavity. For another 9 ns, these three ions randomly exchange their positions. A coordinated three-K⁺ transition occurs at 38.4 ns (top panel of Fig. 11), comprising the first K⁺ ion that has entered the cavity as well as both ions in the filter. The transition event starts with one cavity ion moving to S4, and, at the same time, the ion at S1 moving to S0. For a short period (∼200 ps), the S0/S2/S4 configuration is formed, which has been proposed to be an energetically favored (87–89) though rapid intermediate state (6,12). Then the ion at S4 moves to S3, the ion at S0 leaves the filter, and the ion at S2 is shifted to S1 simultaneously, restoring the initial S1/S3 configuration.

A similar mechanism is observed for the two nonequililbrium trajectories, Kcv-HOM-K29_deprot-E1/E2, although filter transitions occur much sooner (after ∼2 ns) and with different ion configurations as compared to the equilibrium case. Furthermore, the S0/S2/S4 configuration is longer-lived; these binding sites are always occupied right before conductance occurs (bottom panels of Fig. 11). This is in agreement with filter-restrained simulations of Kv1.2 (6). In detail, in the first run (E1) the same S0/S2/S4 configuration as observed in the equilibrium trajectory is formed before the transition event; ∼1 ns after the S0 ion dissolves into the bulk, the S2 ion moves to S1. Another 0.5 ns later, it moves to S0 while the S4 ion jumps to S2 and an ion from the cavity occupies S4. Again, the S0/S2/S4 configuration is restored. In the second run (E2), the S0/S2/S4 positions are also occupied immediately after the restraints are removed. During the next 2 ns, two different cavity ions occupy S4 by exchanging their position twice. In contrast to the other runs, the following four events occur almost simultaneously: the S0 ion dissolves into the bulk, S2 ion moves to S1, S4 ion jumps to S2, and another ion from the cavity occupies S4. The single-file event in the second nonequilibrium trajectory is provided as Movie S1.

The ion dynamics in the other two nonequilibrium simulations of the protonated homology model (Kcv-HOM-K29_prot-E3/E4) are markedly different (Fig. S1). In both cases, the outermost ion is pulled out of the filter after quite some time. Nothing else happens in one of the simulations, and no ion enters the cavity. In the other simulation, the second filter ion moves to the first ion's former position. After that event, a K⁺ ion moves from the bulk directly to a filter position, and later the outermost ion again leaves the filter. There is no indication of a concerted single-file motion involving three ions for these protonated models. The translocations appear to be enforced and entirely controlled by the external field.

Concluding Remarks

All our computational and experimental analyses of the initial model and the simulation results point to the pure homology model with deprotonated Lys²⁹, Kcv-HOM-K29_deprot, as the most reasonable choice for a simulation system with an open, functional Kcv pore state. It is reasonable because it combines superior stability with the ability to conduct K⁺ ions. We have shown that Kcv-HOM-K29_deprot reproduces all discussed features in agreement with experimental (2,81,83,88) and theoretical (3,5,6,22,89) data. For designing an appropriate model, static structural analysis alone would not be sufficient, and substantial simulation effort is essential. In our case, the ultimate model validation step was the simulation under mild nonequilibrium conditions. Single-file ion transport events that were also observed in the absence of an external field could be reproducibly induced by application of a field. In the presence of the field, single-file events appeared to be coupled in a concerted manner to ion transitions near the inner mouth.

Regardless of the structure of the N-terminus, taken from NMR spectroscopy or from homology modeling, protonation of Lys²⁹ has a negative impact on stability and functionality, although it cannot be ruled out that the protonated full homology model might be functional after a much longer equilibration time. The data suggest, however, that the protonation state of specific amino acids can apparently contribute to the probability of ion transition events and therefore may be important for channel function. On the other hand, the NMR-based model with deprotonated Lys²⁹ is similarly stable, though inactive or closed. It is therefore tempting to speculate that one or both features—the protonation state and the N-terminal structure—may be involved in channel gating. The dynamic coupling between ion transitions from the bulk into the cavity and from the filter into the bulk, which could be facilitated by restricting flexibility in the mouth region upon deprotonation of Lys²⁹, is particularly interesting. This point requires further scrutiny. In our simulation systems, all four lysine residues were treated equivalently, although in reality all possible permutations of local protonation states could exist in a dynamic equilibrium and modulate the pore function gradually. Analogously, from our earlier simulations of KirBac1.1-Kcv chimeras, we have inferred a possible role of the N-terminus for gating.

From a practical perspective and regardless of persisting uncertainties, Kcv-HOM-K29_deprot appears to be an ideal model case for studying ion transitions in K⁺ channels under conditions that are close to physiological ones or are directly accessible in an experimental setup. This model will therefore serve as a suitable basis for future in silico structure-function studies.

Supporting Material

A figure, two tables, and a movie are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(08)00065-9.