Charge Separation, Stabilization, and Protein Relaxation in Photosystem II Core Particles with Closed Reaction Center

Abstract

The fluorescence kinetics of cyanobacterial photosystem II (PSII) core particles with closed reaction centers (RCs) were studied with picosecond resolution. The data are modeled in terms of electron transfer (ET) and associated protein conformational relaxation processes, resolving four different radical pair (RP) states. The target analyses reveal the importance of protein relaxation steps in the ET chain for the functioning of PSII. We also tested previously published data on cyanobacterial PSII with open RCs using models that involved protein relaxation steps as suggested by our data on closed RCs. The rationale for this reanalysis is that at least one short-lived component could not be described in the previous simpler models. This new analysis supports the involvement of a protein relaxation step for open RCs as well. In this model the rate of ET from reduced pheophytin to the primary quinone Q_A is determined to be 4.1 ns⁻¹. The rate of initial charge separation is slowed down substantially from ∼170 ns⁻¹ in PSII with open RCs to 56 ns⁻¹ upon reduction of Q_A. However, the free-energy drop of the first RP is not changed substantially between the two RC redox states. The currently assumed mechanistic model, assuming the same early RP intermediates in both states of RC, is inconsistent with the presented energetics of the RPs. Additionally, a comparison between PSII with closed RCs in isolated cores and in intact cells reveals slightly different relaxation kinetics, with a ∼3.7 ns component present only in isolated cores.

Introduction

Photosystem II (PSII) is one of the photosystems of oxygenic photosynthetic organisms that is responsible for oxygen evolution (1,2). Its structure was recently determined at a relatively high resolution, down to 3 Å (3,4). In cyanobacteria, PSII captures light energy by a small core antenna consisting of the CP43 and CP47 antenna subunits, which is consequently transferred to the reaction center (RC) pigments, where it triggers the charge separation (CS) process and secondary electron transfer (ET) steps. The ET chain consists of chlorophyll (Chl) P_D1, accessory Chl (Chl_accD1), pheophytin (Pheo_D1), and plastoquinones A (Q_A) and B (Q_B). After double reduction and succeeding protonation of Q_B, quinone B is released to the plastoquinole pool and new plastoquinone enters the Q_B cavity. On the donor side, water is oxidized to molecular oxygen by the manganese cluster (Mn₄Ca) driven by highly oxidizing P_D1⁺ via tyrosine (Tyr_z)—for recent reviews see (5–7).

In contrast to earlier mechanistic models that assumed P_D1 as the primary electron donor and Pheo_D1 as the primary acceptor, it was recently shown that for intact PSII cores with open RCs (Q_A oxidized) (8), as well as for isolated D1-D2-cyt_b559-RCs that do not contain Q_A (8,9), the primary electron donor is Chl_accD1 and the primary acceptor is Pheo_D1 at physiological temperatures. Only in the second ET step is P_D1⁺ formed by oxidation from Chl_accD1. It was previously shown by Prokhorenko and Holzwarth (10) that for isolated RCs at low temperature the primary electron donor is Chl_accD1, and this was recently confirmed by transient absorption spectroscopy on PSII RC mutants (11). The same rate constants for the primary ET steps were found for isolated RCs and open PSII cores (8). Although Groot et al. (9) and Holzwarth et al. (8) proposed the same ET mechanism for RCs, the rate constants for primary CS differed by a factor of more than 5 in their models.

The kinetics of PSII with closed RCs (Q_A reduced) in isolated cores, Berthold Babcock Yocum preparation particles, and intact organisms (e.g., green algae) has been studied by a number of authors (12–14). One of the most pronounced effects of closing the RC in PSII is an increase in the yield of fluorescence by a factor of 4–6, and a corresponding lengthening of the average fluorescence lifetime (13,15). This effect has been explained in the “exciton-radical pair equilibrium” (ERPE) model (16) by electrostatic repulsion of the charge on Q_A and the corresponding negative charge on Pheo_D1. As a consequence, the energy of the primary RP (at that time assumed to be P⁺Pheo⁻) would be raised above the energy of the equilibrated excited state [Ant-P680]^∗, resulting in a decrease of the primary CS rate and a concomitant increase of the charge recombination rate (17). Gibasiewicz et al. (18) performed time-resolved photovoltage measurements on destacked PSII membranes and came to similar conclusions. They found, however, a larger influence of Q_A⁻ on the charge recombination rate than on the primary CS rate, in contrast to Schatz et al. (17). The long lifetimes for PSII with closed RCs found in a large variety of studies varied from 1 to 7 ns (15,17,19–21). Even longer lifetimes (≥10 ns with large amplitudes) are found when the primary quinone Q_A is double-reduced (21,22).

Although studies on the primary events in PSII were initiated over 20 years ago, there is still no agreement on the character of the energy and ET kinetics (for a more detailed discussion of the current knowledge on this topic, see previous reviews (5,7)). Schatz et al. (16) developed the ERPE model representing exciton trapping, CS, charge recombination, and charge stabilization processes. The key point of this model is a trap-limited kinetics, implying rapid energy equilibration between antenna and RC Chls and a much slower CS step. The main idea of the ERPE model was confirmed by a number of experiments (8,13,23), which resulted in the common value of the intrinsic CS rate of about (5–6 ps)⁻¹. Of interest, for a CP47-D1/D2 preparation, Andrizhiyevskaya et al. (24) reported an intermediate kinetics just between the trap- and the diffusion-limited cases, whereas other authors proposed a diffusion-limited kinetics for intact PSII cores (25,26).

All photosystems consist of pigments and other cofactors embedded in a protein matrix. As a consequence the rates of the energy transfer and ET reactions depend critically on the pigment-protein interactions. Time-dependent radical pair (RP) relaxation has been studied in detail for bacterial RCs (27–30) (see also Renger and Holzwarth (7) for a review). For bacterial RCs the rates of charge recombination from P⁺Q_B⁻ and P⁺Q_A⁻ are strongly dependent on multiple turnover processes and/or dark/light adaptation (31–36), proving the involvement of protein conformational changes. These processes have been discussed in terms of nonequilibrium self-organization of proteins in ET reactions (32). For PSII, a dynamical RP relaxation has been demonstrated for isolated D1-D2-cyt_b559 RCs (8,37–39), which therefore may also be expected for intact PSII cores. The current work reports a picosecond fluorescence study on cyanobacterial intact PSII core complexes with closed RCs. We address the following questions: 1), what are the rates of the ET steps; 2), what is the nature of the RPs in PSII with reduced Q_A; and 3), most importantly, which role does protein relaxation play in CS and stabilization of the RPs. In this work we focus exclusively on the ET steps, and therefore the experimental data are analyzed in terms of models with three or four RPs that reflect both ET processes and protein relaxation steps. (Note that recently published theoretical calculations by Raszewski et al. (69) suggest that the bottleneck for the decay of PSII excited states is energy transfer from the antennae system to the RC. Experimental data (8) are in conflict with the slow energy transfer hypothesis. If the energy transfer were indeed slow, this would have some influence on the primary charge separation rate determined in our model for open RCs. For closed RCs the influence would be negligible anyway due to the slowing down of ET. Overall, the issue of the exact energy transfer rate is thus of minor importance at best for the work presented here. We will deal with this issue in a separate work.)

Materials and Methods

Sample preparation

Time-resolved fluorescence measurements were conducted on PSII core complexes from Thermosynechococcus elongatus with an active oxygen-evolving complex as described earlier (23). Samples with closed RCs were measured under oxygen-free conditions by adding an oxygen-scavenging system (65 μg/mL glucoseoxidase, 65 μg/mL catalase, and 8 mM glucose). Buffer components were as follows: 20 mM 2[N-morpholino]ethanesulfonic acid (MES; pH 6.5) containing 10 mM MgCl₂, 10 mM CaCl₂, 0.5 M mannitol, and 0.03% n-dodecyl-β-D-maltoside (β-DM). Since 60–70% of the particles contain a Q_B molecule, 3-(3,4-dichlorophenyl)-1,1-dimethylurea (DCMU) plus weak light irradiation was used to ensure complete removal of Q_B from its binding pocket (40,41) and to reliably reduce Q_A while at the same time avoiding double reduction of Q_A (22). Two different concentrations of DCMU were tested (20 μM and 100 μM), but no influence on the kinetics was observed under these conditions. The results presented in this work were obtained with 20 μM DCMU unless mentioned otherwise. During measurements, Q_A was kept in the reduced state by illumination of the rotation cuvette with an orange light-emitting diode (LED; λ = 630 nm, intensity of 3 μE/m²s), just before entering the measuring laser beam. This LED intensity corresponds to less than four photons absorbed per PSII particle per second. To clarify the origin of the long lifetime component, pH-dependent measurements were carried out in the pH range from 5.5 to 8.5. For that purpose, three different buffers were used: MES (pH 5.5, 6.0, 6.5), HEPES (pH 7.0, 7.5, 8.0), and Tricine (pH 8.5).

Additional measurements were performed on intact cells of T. elongatus to clarify the origin of the longer (nanoseconds) lifetimes. The cultures were grown in a rotary shaker in BG-11 medium, bubbled with CO₂-enriched air (5%), and illuminated with white light (40 μE/m²s intensity). For time-resolved fluorescence experiments, the cells were centrifuged for 4 min at room temperature (4000 g) and afterward resuspended in fresh medium BG-11 to a concentration corresponding to optical density = 0.26/cm at 675 nm. The sample was slowly pumped through a flow cuvette with 1 mm path length. To achieve prereduction of Q_A, 20 μM of DCMU was used together with additional background light (LED, λ = 630 nm, 500 μE/m² s) for a short time (1–2 s) just before the sample entered the cuvette.

Experimental technique

Measurements were performed using the single photon timing technique as described previously (23,42). For PSII particles, a particularly important part of the experimental setup is the rotating cuvette (∼10 cm diameter), which moved sideways with 66 Hz and was rotated at 4000 rpm. Together with low excitation intensity, this ensures that multiple excitations of the PSII particles by the same laser pulse and by subsequent laser pulses are avoided. The estimated probability of a PSII particle being excited during the passage through the laser beam is ≤10⁻². All measurements were carried out at room temperature.

To check the stability of the sample, steady-state fluorescence spectra were collected before and after each lifetime experiment.

Time-resolved fluorescence kinetics data analyses

The time-resolved fluorescence data were first analyzed by global lifetime analysis. Advanced kinetic modeling was subsequently performed by global target analysis (43,44). Several alternative compartmental models were tested on the data and the results were judged by the χ² values, the residuals plots, and the shape of the species-associated (emission) spectra (SAES). The excitation vectors used in this study were determined from calculations based on the absorption spectra of isolated CP43, CP47, and PSII D1-D2-cyt_b559 RCs (45).

Results

PSII core complexes with closed RC

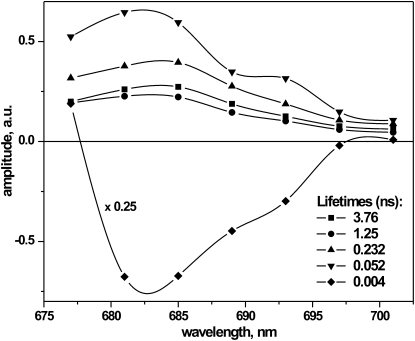
PSII cores were excited at the blue side of the Q_y absorption band of the antenna Chls (at 663 nm) and fluorescence was detected in the range of 677–701 nm, with a step size of 4 nm. Global analysis resulted in decay-associated spectra (DAS), representing a set of lifetimes and their associated amplitudes (Fig. 1). The fluorescence decays required five exponentials for a good fit, with lifetimes of 4 ps, 52 ps, 232 ps, 1.25 ns, and ∼3.75 ns. The shortest lifetime shows a large negative amplitude over the whole detection range. It represents an energy transfer process, i.e., energy transfer between the two core antennae subunits CP43 and CP47 and the RC. The largest positive amplitude is associated with a 52 ps lifetime component, whereas the longer lifetimes have about half that amplitude.

Figure 1.

DAS of cyanobacterial PSII with closed RC (upon 100 μM DCMU treatment) resulting from global analysis calculations.

Target modeling

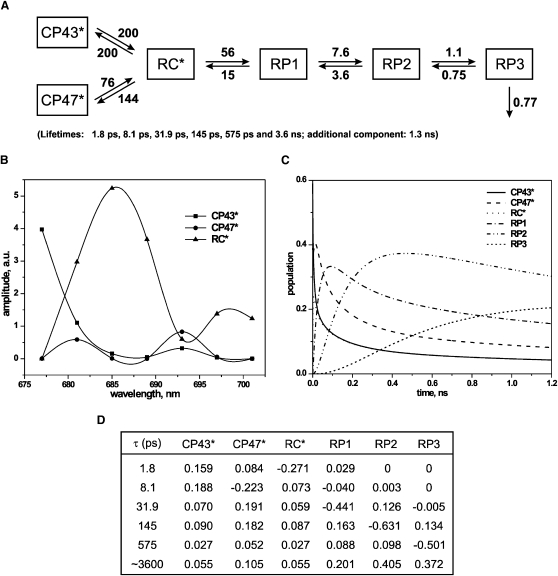
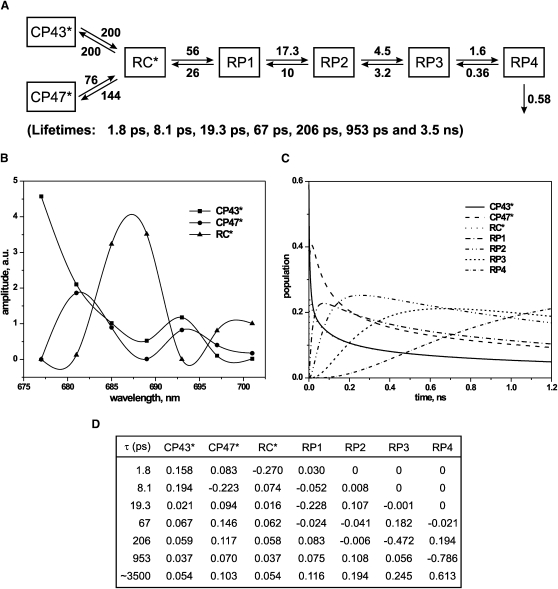
To explore various kinetic models and determine the rates of processes, compartment modeling was applied to the data. A number of different models were tested, all of which incorporated three excited states (corresponding to CP43^∗, CP47^∗, and RC^∗) (23). Some models included only two RPs and no, one, or two additional lifetime components not connected to the kinetic scheme. Other models comprised three or four RPs with one or no additional component required for a good fit. The aim of the modeling was to arrive at a consistent model capable of describing all major lifetime components found in global lifetime analysis (Fig. 1). Different starting values for rate constants were applied and the final models were subjected to an extensive error search of the parameters. The acceptance or rejection of a model was based on the fit parameters (χ² value and residuals) and the spectral shape of the SAES. This time-consuming but necessary procedure of probing the solution space resulted in the two final models shown in Figs. 2 and 3. The simplest kinetic scheme that fulfils the above-mentioned conditions involves six compartments (Fig. 2 A): three excited states (antennae CP43^∗, CP47^∗, and RC^∗), three RPs (RP1, RP2, and RP3), and one additional component. The three SAES (Fig. 2 B) describe the excited-state compartments, whereas the SAES of RPs are zero by definition since RPs do not emit fluorescence. The figure also shows the compartment population dynamics (Fig. 2 C). The best solution found in the target modeling procedure results in a set of six lifetimes: 1.8 ps, 8.1 ps, 31.9 ps, 145 ps, 575 ps, and 3.6 ns. The additional component of 1.3 ns shows a contribution to the fluorescence signal with a relative amplitude of ∼20%, ∼13% relative yield, and a spectrum very similar to that of the long-lived component of the model. Thus, in an additional model (Fig. 3, A–D) it was tested whether the remaining additional component could also be incorporated into a consistent model in a sequential scheme because there was a priori no reason to assume a large heterogeneity of the sample to which this additional component (20% amplitude) should be ascribed. This incorporation was indeed possible with an equally good fit quality. The enlarged model results in the following lifetimes: 1.8 ps, 8.1 ps, 19.3 ps, 67 ps, 206 ps, 953 ps, and 3.5 ns. These lifetimes differ slightly from the lifetimes obtained from global analysis (Fig. 1). The differences result from the experimental errors and the much more severe constraints used in the target modeling compared to the global analysis.

Figure 2.

Results of target analyses of the fluorescence decay of dimeric PSII core particles in the closed form upon excitation at 663 nm; kinetic model with three RPs. (A) Kinetic scheme (all rates are given in ns⁻¹); rates corresponding to energy transfer processes are characterized by errors of 15% and ET rates of ∼10%. (B) SAES associated with the kinetic model presented in A. (C) Population dynamics of the kinetic model compartments. (D) Weighted eigenvectors representing amplitudes of compartments of the kinetic model shown in A; excitation vector used in the analyses: 0.59 (CP43^∗), 0.39 (CP47^∗), and 0.03 (RC^∗).

Figure 3.

Results of target analyses of the fluorescence decay of dimeric PSII core particles in the closed form upon excitation at 663 nm; kinetic model with four RPs. (A) Kinetic scheme (all rates are given in ns⁻¹); rates corresponding to energy transfer processes are characterized by errors of 15% and ET rates of ∼10%. (B) SAES associated with the kinetic model presented in A. (C) Population dynamics of the kinetic model compartments. (D) Weighted eigenvectors representing amplitudes of compartments of the kinetic model shown in A; excitation vector used in the analyses: 0.59 (CP43^∗), 0.39 (CP47^∗), and 0.03 (RC^∗).

Influence of pH

The long-lifetime components were tested for their dependence on the pH of the medium. However, global and target modeling performed on these data did not reveal any correlation between buffer pH and the average lifetime of fluorescence (∼850 ps) or the relative yield of the long-lifetime components.

PSII core complexes with open RC—target modeling

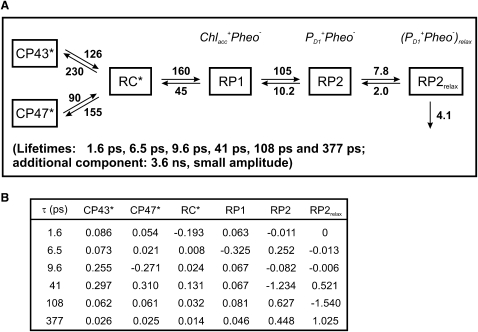
Time-resolved fluorescence decay data on PSII core complexes with open RCs (Q_A oxidized) were analyzed in a previous study in terms of target modeling (23). The model presented in that work represents the minimal scheme that describes the CS and energy transfer processes and their corresponding rates. One lifetime component could not be incorporated into the model and remained unassigned. The authors speculated about the possibility of a protein relaxation step to explain that additional component. Therefore, we reanalyzed the same data in the framework of an extended model that includes an additional RP, which would represent a protein relaxation step. The current kinetic model (Fig. 4 A) thus involves three excited states (CP43^∗, CP47^∗, and RC^∗) and three RPs (RP1, RP2, and RP2_relax). In addition, a very small amplitude component of a 3.6 ns lifetime is present, reflecting PSII with closed centers (23).

Figure 4.

(A) Extended kinetic model for cyanobacterial PSII in open state; assignment of RPs is shown. (B) Weighted eigenvectors representing amplitudes of compartments of the kinetic model for open PSII particles; excitation vector: 0.9 (CP43^∗), 0.1 (CP47^∗).

Intact cells—global and target modeling

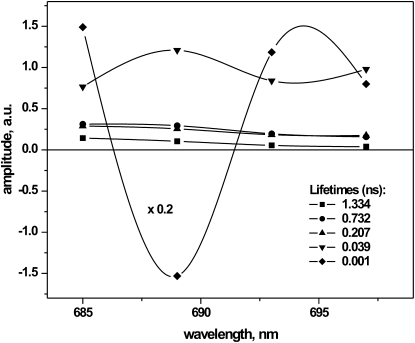
Intact cells of T. elongatus were excited at 675 nm to avoid excitation of the allophycocyanin antenna present in the cyanobacterial light-harvesting complexes. The fluorescence was detected in the range of 685–697 nm. Global analysis resulted in the set of five lifetimes and corresponding DAS shown in Fig. 5. The shortest lifetime component (1 ps), with characteristic negative/positive features, indicates an energy transfer process. The second-shortest lifetime (39 ps) does not exhibit the spectral shape typical of PSII since it shows high amplitude in the red tail of the spectrum. It is thus assigned mainly to PSI. Three longer lifetimes ranging between 200 ps and 1.4 ns can be attributed to PSII, again because of their spectral shape. It is noteworthy that no component with a lifetime > 1.4 ns could be detected. However, we cannot exclude the possibility that due to the intact cells forming a much bigger system, the energy transfer from PSII to other complexes present in the cells might shorten the observed lifetimes.

Figure 5.

DAS resulting from global analysis of the fluorescence decay of intact cyanobacterial cells in the closed form; the amplitude of the shortest lifetime was divided five times for better understanding and presentation of other components.

Discussion

Closed RC—target modeling

Fig. 2, A–D, illustrates the results of the target modeling on our data in the form of the kinetic scheme and rates (Fig. 2 A), SAES (Fig. 2 B), population dynamics (Fig. 2 C), and eigenvector matrix (Fig. 2 D). The CS process is described with the 56 ns⁻¹ rate constant, which is ∼4 times larger than the charge recombination rate. The ratio of forward and backward rates (k_for and k_back, respectively) between RP1 and RP2 is ∼2 times smaller (7.6 ns⁻¹/3.6 ns⁻¹ = 2.1), whereas the k_for/k_back ratio of the last resolved step reaches only ∼1.5. The kinetic scheme allows the matrix of the so-called weighted eigenvectors to be constructed. This matrix allows a particular lifetime to be associated with a particular reaction step. A negative value of the matrix element describes the rise of the population of a particular compartment, whereas a positive value describes its decay (for details see Müller et al. (46)). Thus, the two shortest lifetimes in Fig. 2 A are attributed to the energy transfer and equilibration between excited states of antennae and RC, with 1.8 ps representing the main contribution to the rise of the RC^∗ state population. The apparent CS and consequently the first RP formation are characterized by the 31.9 ps lifetime and to a very small extent also by the 8 ps lifetime. The first charge stabilization occurs with 145 ps lifetime, whereas RP3 is formed with a 575 ps lifetime and decays with more than 3.5 ns. The ∼1.3 ns lifetime component is not included in the model. Target analysis resulted in the SAES presented in Fig. 2 B and the plot in Fig. 2 C, which shows the time course of the relative populations.

Since there is no a priori reason to not assign the relatively large amplitude of the ∼1.3 ns lifetime to intact PSII particles, we also tested an extended model that contains one additional RP. The results of these fits are given in Fig. 3, A–D. A comparison of the SAES in Figs. 2 B and 3 B shows no major differences in the excited-state emission spectra between both models, with RC^∗ peaking around 686–687 nm. The early processes have the same meaning, and lifetimes very similar to those in the simpler model are obtained. However, the extended model associates the CS step with the 19.3 ps lifetime, and the first charge stabilization with the 67 ps lifetime, whereas the formation of RP3 and RP4 is almost exclusively related to the 205 ps and 953 ps lifetimes, respectively. The last RP decays with 3.6 ns lifetime, i.e., in a manner quite similar to the simpler kinetic scheme. In essence, the 31.9 ps component is resolved into two components in the extended model.

PSII with open RC—target modeling revisited

The kinetic modeling for open PSII cores presented previously by Miloslavina et al. (23) included two RPs and two unconnected components of 111 ps and 2.3 ns. The latter is due to a small amount of closed RCs. There are two possible explanations for the 111 ps lifetime. The first one considers the possibility of a heterogeneous nature of the ET from Pheo to Q_A, whereas an alternative explanation assumes a protein conformational response to the charges flowing through the RC, i.e., an RP relaxation process. The latter case is well documented for bacterial RCs and isolated PSII RCs (8,27–30,37–39). The transient absorption measurements on the same particles (8) did not show any changes in the transient spectra on the 100 ps timescale. Such changes would be expected if at least one of the chromophores involved in the RP states changed its redox state. However, the data (8) show a rather wide range of a lifetime distribution, ranging from ∼100 ps to nearly 300 ps. Thus the most reasonable assignment of the ∼110 ps component is a protein relaxation step that does not involve a change in the redox state of any of the cofactors. Thus the RPs in Fig. 4 A are assigned, in analogy with a previous study (8), as follows: RP1 = Chl_accD1⁺Pheo_D1⁻, RP2 = P_D1⁺Pheo_D1⁻, and RP2_relax = (P_D1⁺Pheo_D1⁻)_relax. The two latter RPs reflect the same redox state but differ in their energy and the conformation of the surrounding protein.

The eigenvector matrix corresponding to the kinetic scheme presented in Fig. 4 A can be found in Fig. 4 B. In this model the energy transfer between antennae and the RC is described by the lifetimes of 1.6 ps and 9.6 ps, while the main part of the apparent CS process occurs with the 6.5 ps lifetime. This is essentially the same as for the previously published simpler model. The RP2 redox state is populated with the 41 ps lifetime. RP2 then relaxes to RP2_relax by protein relaxation with the 108 ps lifetime component as a response to the charges moving along the cofactor chain. The state RP2_relax is depopulated with the 380 ps lifetime, reflecting the apparent ET from Pheo_D1⁻ to Q_A. Its rate constant is 4.1 ns⁻¹, resulting in an effective transfer lifetime of ∼245 ps. As suggested in our previous article (23), extension of the model does not affect the kinetics of the Q_A reduction.

In the model presented here, the total trapping time τ_{tot trap} = 72 ps, whereas in the simpler scheme the trapping was τ_{tot trap} = 65 ps, with 9 ps energy transfer and 56 ps CS times. Therefore, the contribution of the CS process to the overall trapping kinetics remains dominant, whereas the energy delivery to the RC is extremely fast and hardly contributes to τ_{tot trap}. Thus the model remains trap-limited, as previously assigned on the basis of the simpler model (8,23). Closure of the RCs slows down CS and thus also does not change the type of kinetics. Somewhat different energy transfer rates were found for particles with open RCs (23) and closed RCs (this work). These differences (which, however do not change to any significant extent the excited-state equilibration between the antenna and RC) are explained by two factors. Measurements on open RCs were made without a polarizer in the emission beam, and thus the early kinetics may be somewhat distorted. This was done to ensure that the RCs were kept open, since the strong reduction of fluorescence intensity by the polarizer would be unacceptable. This problem does not arise with closed RCs, where the fluorescence intensity is much higher, and thus it was possible to use the polarizer. Second, for the modeling of the closed RCs (vide supra), we used an excitation vector that correctly reflects the relative absorptions of CP43, CP47, and the RC. This was not the case for the previous modeling of the open RCs and was a matter of concern.

Energetics and CS mechanism in closed RCs

From the rate constants of forward and backward transfer, one can calculate the free-energy differences ΔG between the excited RC^∗ state and the RPs. Fig. 6 shows the results for both open (left) and closed (middle and right) RCs. Both graphs corresponding to the models with three RPs illustrate a similar drop in the free energy, i.e., 32–33 meV, for the first ET step, regardless of the redox state of Q_A. The overall drop in free energy is smaller for closed RCs than for open RCs, in agreement with earlier findings (17,18). However, great care must be taken when comparing the free-energy drops found here for the individual steps with previous data. It had been argued that the electrostatic interaction between reduced Q_A in closed RCs and the formed Pheo_D1⁻ would greatly increase the free energy of the first RP (17,18). Furthermore, the free-energy data derived from the photovoltage measurements of Gibasiewicz et al. (18) combine the free energies of the actual redox processes on the one hand and the protein relaxation steps on the other hand, unlike the fluorescence kinetics data. Since the earlier measurements were obtained (17), an additional RP has been resolved for PSII cores with open RCs (8). However, this RP also involves a reduced Pheo_D1 and thus would be also expected to show a substantial rise in the free energy versus the same state with open RC. This is, however, not the case with our data (Fig. 6). For the simpler model (Fig. 2), the free-energy drop of the first RP is about the same as for open RCs, whereas for the extended model (Fig. 3) that drop is only slightly smaller. Ishikita et al. (47) predicted from theoretical calculations an increase in the free energy of ∼90 meV in closed RCs due to the electrostatic repulsions between reduced Q_A and Pheo_D1⁻. Our data for the free energy of the first RP in closed RCs do not at all reflect such a drastic effect. The only possible way to reconcile these data is the hypothesis that Pheo_D1 is not reduced in the RPs in closed RCs and a different redox state is formed. We cannot get any direct information on the redox nature of an RP from fluorescence measurements. However, recent experimental data on RC triplet formation and quenching in PSII with closed RCs strongly suggest that different early RPs are formed in PSII with closed RCs (48). If Pheo_D1 is indeed not reduced and a different RP that does not involve Pheo_D1 is formed in closed RCs, then we also do not expect a large increase in the free energy of the first RP in closed RCs. This could also explain the large decrease in the CS rate of ∼3 times in closed RCs versus open RCs in our data. If the first ET step were to form the same RP in open and closed RCs, then the drop in the CS rate would also have to be associated with a decrease in the free-energy difference for this step. Thus we tentatively conclude that the RP(s) formed in open and closed RCs involve different redox cofactors. Vassiliev et al. also found, based on a model that included protein dynamics, a decrease in free energy for the CS step in PSII with both open and closed RCs. However, in contrast to our findings, the ΔG values reported in their work differ for both preparations. Additionally, the authors showed the overall free-energy drop in PSII with reduced Q_A to be on the order of 160 meV, a factor of 2 greater than reported here. This, however, may be explained with the differences in the method used to close RCs. Vassiliev et al. (19) used hydroxylamine treatment, which inhibits the oxygen-evolving complex, whereas in our experiments the oxygen-evolving complex was fully functional. Gibasiewicz et al. (18) concluded that the closing of the RC mainly causes an increase in the charge recombination rate, but very little change in the CS rate. This is not in agreement with our data. However, the discrepancy is easily explained by the fact that Gibasiewicz et al. (18) did not resolve the first ET step in their measurements.

Figure 6.

Schematic representation of the free-energy differences ΔG between different compartments of kinetic models found for dimeric PSII core particles in both open (left) and closed (right) states. For the latter preparation, both models presented in the text are shown (model with three RPs, middle; model with four RPs, right). RC^∗ stands for RC excited state and constitutes the reference state for the free-energy calculations.

Protein dynamics

All of the models of kinetics in PSII particles with open and closed RCs presented above required more than two RP states for a satisfactory fit. For PSII with open RCs, two different redox states of the RC were resolved that occur before the reduction of Q_A (8). We cannot by fluorescence characterize the redox nature of a RP even if it gives rise to charge recombination fluorescence. However, it is quite unlikely that for PSII with closed RC there should be more than two RPs reflecting different redox states. This implies that one or more of the RPs resolved in the fluorescence kinetics should be interpreted as RPs formed by protein relaxation steps but reflecting the same redox state. Protein relaxation steps lower the free energy of the RPs. Also, the rates of fast ET steps can be very sensitive to protein dynamics and conformation (28,49,50). Such protein relaxation is well known for bacterial RCs (27,29,49,51,52) and isolated PSII RCs (37–39,53–55). Protein dynamic processes span a huge range of time, from picoseconds to hours (32,56–58). It is generally not easy to measure the free energy of the states involved in protein relaxation. However, photosynthetic RCs in general and PSII in particular provide an especially favorable case because they show charge recombination fluorescence from the relaxing RP states (17,19,27,51). Of importance, in such measurements the excited state of the RC, from which all the observed fluorescence derives, functions as an energetic reference state whose energy is essentially independent of protein relaxation.

In the light of the above considerations, we will tentatively assume for the following discussion that for closed RCs the first two resolved RPs (RP1 and RP2) reflect different redox states formed by ET, whereas the following two RPs (RP3 and RP4 in Fig. 3) reflect protein-relaxed RPs without involving an ET process, i.e., the same redox states of the cofactors are involved. For open RCs (Fig. 4), the comparison with the transient absorption data (8) also indicates that the third RP resolved in the present fluorescence analysis (designated as RP2_relax) must reflect a protein-relaxed RP. It is clear that the actual ET processes leading to RP formation also involve protein relaxation. However, the two processes occur concomitantly on the same timescale and cannot be separated in that case.

For PSII with open RCs, the first resolved protein relaxation step occurs with a lifetime of 108 ps and involves a free-energy relaxation of −35 meV (Fig. 6). Presumably, further protein relaxation steps would follow. However, for open RCs the ET to Q_A prevents that process. For closed RCs, two protein relaxation steps are resolved. They occur with ∼200 ps and 950 ps lifetimes, and involve free-energy relaxation of ∼−9 meV and ∼−38 meV, respectively. The relationship is clear: given more time, the free energy can relax more. In comparison to closed RCs, the −35 meV drop with the short lifetime of 108 ps in open RCs is quite interesting. Presumably, the very fast initial ET steps in that case occur with relatively little protein relaxation. Thus a larger drop in free energy by protein relaxation occurs after CS. It follows from these data that CS in PSII would be overall much less efficient if protein relaxation did not occur, as discussed in a recent review (7).

Origin of the long-lifetime component

Although it is well known that the fluorescence yield and average lifetime of PSII increase upon closure of the RCs (14,15,16), a phenomenon that forms the basis of all fluorescence induction measurements (59–64), we detected an unusually large (up to 10-fold) increase in the fluorescence yield upon closure of the RCs (see Fig. S1 in the Supporting Material). This is also reflected in the increase of the average fluorescence lifetime τ_av, which changes from 0.09 ns to 0.87 ns for PSII with open and closed RCs, respectively. Fluorescence yield and lifetime increases of a factor of 5–7 are more common, in particular for PSII in intact thylakoids or BBY particles. This large increase in fluorescence yield is associated with the long-lived (∼3.7 ns) component in our data. Of interest, we found no lifetime of ∼11 ns as reported by Schlodder and Brettel (14), or ∼7 ns as found by Vasiliev et al. (19). Such long-lived components are believed to arise from double reduction of Q_A due to the use of dithionite or hydroxylamine and strong light irradiation (21,22). We thus intentionally avoided such methods for closing the RCs and applied the milder and more clearly defined method of using DCMU to block Q_A to Q_B ET. The longest lifetime under our conditions was 3–4 ns, as found in both global and target analyses. We thus performed various experiments to better identify the origin of this long-lived component. We studied, for example, the possible dependence of the ET processes on pH in the range from 5.5 to 8.5. However, we did not find any significant dependence of the ET rates or lifetimes on pH. In addition, the relative amplitude and relative yields of the long-lived components did not change. For all pH conditions applied in the experiment, the long lifetime is characterized by a relative yield of ∼70–80% and relative amplitude varying from 17% to 21%. We have to conclude that the 3.6 ns lifetime cannot be associated with the changes in the protonation state of the protein. Other experimental conditions, such as different DCMU concentrations or different intensities of the background light, also did not give rise to any substantial changes in the amplitudes or lifetimes of the long-lived (∼3.4 ns) component. Of interest, no substantial 3–4 ns component was detected in the fluorescence of intact leaves from higher plants either (unpublished results). We thus performed measurements on intact cells of T. elongatus with closed RCs. Of significant interest, global analysis of these fluorescence decays did not reveal any lifetime longer than 1.5 ns. The shortest lifetime (1–2 ps) exhibits an energy transfer behavior (positive/negative amplitude), whereas the remaining ones display only positive amplitudes. The three longest lifetimes (1.3 ns, 732 ps, and 207 ps) clearly describe the PSII part of the system, whereas the 39 ps component must be attributed in large part to PSI, based on the strongly red-shifted spectrum.

It is known (65,66) that P680⁺ can be reduced at low temperatures by the carotenoid present in the RC or at higher temperatures by Chl_Z (peripheral Chl). The oxidation of Car by P680⁺ in isolated D1-D2-cytb559 RCs takes place at a low rate of ∼1/ms. The electron donation to P680⁺ and subsequent oxidation of Car⁺ by cyt_b559 or Chl_z constitutes the so-called cyclic electron flow. However, these processes were proposed on the basis of experiments on Mn-depleted PSII particles or D1-D2-cyt_b559 preparations, whereas our PSII core particles are highly active in oxygen evolution. We thus believe that such effects can be ruled out. A more likely explanation for the presence of the ∼3.5 ns fluorescence lifetime component may be related to an alteration of the electron donation from tyrosine (Tyr_D) to P680⁺ under our experimental conditions. Under normal physiological conditions, reduced Tyr_D will be oxidized upon the onset of light. The tyrosyl radical (Tyr_D^•) is stable for hours, and although it does not take part directly in the redox activity of PSII, it has been proposed to facilitate the reduction of P680⁺ by Tyr_Z (67). It has also been proposed that the Tyr_D^• radical is involved in the recombination reaction of P⁺Q_A⁻ under certain conditions (68). A different charge on a cofactor of the RC not involved in primary ET could well provide a possible explanation for the differences between isolated PSII particles and the in vivo system. A likely candidate would be Tyr_D, whose different redox states could easily influence the lifetimes of RP relaxation of PSII with closed RC. Such an influence could be exerted, for example, by a modification of the energetics of the RPs due to an electrostatic interaction of the primary or secondary RP with a charge on another cofactor not directly involved in the ET reaction(s). An alternative possibility that cannot be excluded, however, is that the surrounding of the PSII particle (i.e., native membrane versus detergent) influences the protein relaxation dynamics of the RC in the closed state. These points deserve further investigation.

Conclusions

Time-resolved fluorescence experiments reveal the interplay between fast photosynthetic CS processes and the relaxation of the protein environment. We have shown in this work that such processes can be successfully incorporated into the description of the kinetics of PSII with open RCs. PSII particles with reduced Q_A show similar behavior, with up to two resolved relaxed RPs. Of interest, the free-energy drop for the first RP is similar to that for open RCs. This is inconsistent with the expected substantial drop of the redox potential of Pheo_D1, predicted to be −90 meV in theoretical calculations, upon reduction of Q_A. We thus hypothesize that reduced Pheo_D1 is not formed in the RC with reduced Q_A. Instead, some other redox state must be present. We have shown that the long-lifetime component found in the PSII cores with closed RCs does not depend on the pH of the medium, the concentration of herbicide inhibitor used, or the background light intensity. On the other hand, it is not present in the fluorescence signal from intact cells with closed PSII RCs. The reason for this is unclear. It may suggest changes in the protein state (oxidation/reduction) or protonation of a component that is near the ET cofactors but does not participate directly in the RP formation. Such changes may cause modifications in the free-energy landscape of the RPs.

Supporting Material

A figure is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(08)00044-1.