Abstract
We study the folding of small proteins inside confining potentials. Proteins are described using an effective potential model that contains the Ramachandran angles as degrees of freedom and does not need any a priori information about the native state. Hydrogen bonds, dipole-dipole-, and hydrophobic interactions are taken explicitly into account. An interesting feature displayed by this potential is the presence of metastable intermediates between the unfolded and native states. We consider different types of confining potentials to describe proteins folding inside cages with repulsive or attractive walls. Using the Wang-Landau algorithm, we determine the density of states and analyze in detail the thermodynamical properties of the confined proteins for different sizes of the cages. We show that confinement dramatically reduces the phase space available to the protein and that the presence of intermediate states can be controlled by varying the properties of the confining potential. Cages with strongly attractive walls destabilize the intermediate states and lead to a two-state folding into a configuration that is less stable than the native structure. However, cages with slightly attractive walls enhance the stability of native structure and induce a folding process, which occurs through intermediate configurations.
Introduction
Protein folding is one of the most intensively studied and still unsolved problems in biology. Many diseases such as Alzheimer and Parkinson are believed to be caused by the misfolding and aggregation of certain proteins (1–3). Although in the last years several aspects related to the Levinthal's paradox have been clarified with the help of lattice models and other approaches (4–7), many questions regarding details of the folding and misfolding mechanisms still remain open.
In this article, we focus on the problem of protein folding assisted by Chaperones, which is one of the mechanisms present in nature to avoid aggregation and misfolding. Chaperones are molecules in the form of a cage inside which proteins fold correctly. Recently, some progress has been achieved in the understanding of the folding of proteins inside chaperones. These studies have shown that stability and folding kinetics are strongly correlated with the geometry and the degree of confinement inside the cage (8–13). However, many details of the folding under confinement still remain uncovered.
In this work, we focus on the folding of the peptide V3-loop, Protein Data Bank ID 1NJ0, and analyze it under two kinds of time-independent confining potentials. The first potential simulates a cage being composed by rigid walls, while the second potential describes a cage with an attractive inner surface. The influence of both potentials is reflected in the thermodynamical properties, which we calculate using the Wang-Landau algorithm (14,15).
As one of the main results of this work, we obtain that the folding process of V3-loop occurs through metastable intermediate states (16), and that the presence of those states can be controlled by the confining potential.
For the description of the protein, we use a force field that does not depend on the previous knowledge of the native structure and is also able to describe folding of proteins into both helices and β-sheets with the same set of parameters (17). In addition to this improvement, two new features not reported previously are included: 1), the dipole-dipole interaction between the CO-NH pairs lying on the amide plane; and 2), the local hydrophobic interaction between neighboring residues, which takes into account the hydrophobic and hydrophilic properties of the side chains. The sequence of the amino acids is the only input of the force field.
The article is organized as follows. In Theory, we describe the model used and the Monte Carlo method applied to calculate the thermodynamical properties of the protein. In Results and Discussion, we present our results and make a careful analysis of our simulations and finally, we present a summary.
Theory
The model
The structure of the protein is simulated using the reduced off-lattice model developed in Chen et al. (17). The amino acids are represented by means of backbones. Each backbone contains the atoms N, Cα, C′, O, and H. The residues are modeled as spherical beads, R, attached to the Cα values. The only remaining degrees of freedom are the Ramachandran angles ψ and ϕ. The values for the bond lengths and angles are given in Solomons and Fryhle (18).
The force field containing all relevant interactions in the protein is given by
| (1) |
where ESteric represents a hard-core interparticle-potential to avoid unphysical contacts, EHB accounts for the hydrogen bonding, and EDD describes the dipole-dipole interactions. EMJ is a distance-dependent version of the Miyazawa-Jerningan (MJ) matrix (19), which describes the interactions between residues. ELocalHP accounts for local hydrophobic effects. The role of the presence of water molecules is taken into account by the terms EMJ and ELocalHP. It is important to point out that EMJ partially includes the effect of water polarization (20). The values of the parameters of this potential are given in the original work by Chen et al. (17).
In addition to EProtein we add a term to simulate the confinement of the protein within the cage. This is accomplished in the present work by using two different kinds of spherically symmetric potentials depending on a radius Rc, which is a measure of the size of the cage. In a first approach, we use an external potential V1(r) which allows the protein to fold freely for distances r smaller than Rc, but has a strongly repulsive part for larger distances, simulating the presence of the walls of the cage. The potential V1(r) reads (11)
| (2) |
where denotes the position of each residue.
Since V1(r) might represent a too-simple description of the confining potential of a chaperon, we also investigate the effect of an external potential V2(r) simulating attractive walls (21), which reads
| (3) |
The physical meaning of the different parameters in Eq. 3 can be described as follows. A uniform distribution of beads spreads out on the surface of the cage with a number density 1/σ2. The parameter ɛ is used to simulate the degree of attraction of the inner surface of the cage. A wall with a purely attractive lining has a value of ɛ = 1 whereas a purely repulsive lining has a value ɛ = 0. In Eq. 3, we set ɛh = 1.25 kcal/mol and σ = 3.8 Å. The external potential V1(r) has the only effect of confining the protein inside the cage whereas the external potential V2(r) interacts with the protein by slightly reducing its energy as ɛ increases. As a consequence, the residues tend to be far apart of each other in the region close to the walls of the cage.
Simulations
Various methods based on Monte Carlo (MC) simulations have been proposed to compute the thermodynamical properties of finite systems. They include, for instance, multicanonical simulations (22) and simulated annealing (23). In this work we use the Wang-Landau algorithm (14), also including a recent improvement introduced by Pereyra et al. (15). One of the main advantages of Wang-Landau simulations is that they allow us to obtain directly the density of states (DOS) of the system, which is, of course, independent of the simulation temperature. Once the DOS is known, one can obtain all the thermodynamical properties of the system at any temperature. Within this framework, the transition probability between two conformations before and after a MC trial move, X1 and X2 respectively, is calculated as
| (4) |
where g(X) is the DOS of the system and X is a generalized coordinate, which in our case is represented by a vector with two entries X = (E, Q), being E the configurational energy and Q the end-to-end distance of the protein structure. Note that Q can be interpreted as an order parameter for the folding (unfolding) transition.
The original scheme developed by Wang and Landau (14) can be briefly described as follows: one sets the initial function g(X) together with an auxiliary histogram H(X) to be equal to 1. Then, each time the bin X is visited, one updates the histogram H(X) and modifies g(X) as , with f = e = 2.718281…. This procedure is continued until a flat histogram (with a certain significance, i.e., 80%) is obtained. At this step, the histogram H(X) is reset and the factor f is reduced. The usual way to perform this reduction is by taking . Convergence is achieved when a value for fi+1 close enough to 1 is obtained. The last step must be compatible with the desired accuracy, for example f = exp(10−7).
We use the modified Wang-Landau approach proposed in Berlardinelli and Pereyra (15), which has been shown to speed up simulations and to partially avoid the problem of saturation error. According to the new scheme, one does not need to wait until the histogram H(X) is flat, but it is enough to require that all the entries of H(X) are visited. Then H(X) = 0 is reset, and is updated.
Following Berlardinelli and Pereyra (15), we employ a second histogram H2(X) which is never reset during the whole simulation and define the Monte Carlo time-step as t = j/N, with N being the number of points in the energy axis and j the number of trial moves performed. If fi+1 ≤ t−1 then fi+1 = f(t) = t−1, and from this point on, f(t) is updated at each Monte Carlo time step. H(X) is not used during the rest of the calculation. Convergence is achieved when f(t) < ffinal. In the present simulations we used ffinal = exp(10−7). Finally, the thermodynamical properties of the system such as the free energy F(T), internal energy U(T), entropy S(T), and specific heat C(T) can be calculated from g(X). For the specific case treated in this work, where X = (E, Q), the corresponding definitions read as
| (5) |
| (6) |
| (7) |
| (8) |
where β = 1/kBT and kB is the Boltzmann constant. The free energy landscape as a function of E and Q can be computed as
| (9) |
and
| (10) |
Results and Discussion
We focused our attention on a peptide composed of 16 amino acids with PDB code 1NJ0 to study the folding mediated by confining potentials. This peptide conforms to the V3-loop of the exterior membrane glycoprotein of the Human Immunodeficiency Virus type 1.
To explore the relevant part of the phase space of the protein we have chosen an energy window between −132.0 kcal/mol and −30 kcal/mol and the end-to-end distance Q ranging from 5 Å to 50 Å. This region is enough to cover both the highly ordered structures (present at T ∼ 0) and the fully disordered random coils (stable for T ∼ ∞). The MC search was generated by changing each pair of Ramachandran angles ψi and ϕi at each MC step using cutoffs with values |Δψc| ≤ 40° and |Δϕc| ≤ 40°. To reach ffinal = exp(10−7), 8 × 109 trial moves were necessary.
We first analyze the properties of the peptide without confinement (bulk case). The obtained ground-state structure of the V3-loop is depicted in Fig. 1. It consists of a β-sheet structure with energy ∼−132.0 Kcal/mol and an end-to-end distance of ∼5.5 Å.
Figure 1.

Ground-state structure (β-sheet) of the peptide 1NJ0 (Eg ∼ −132.0).
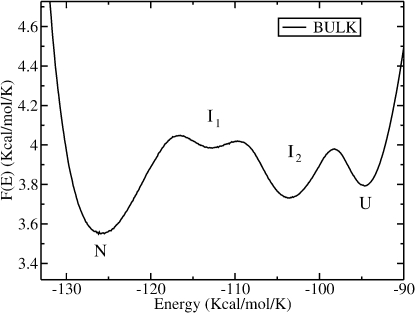
A new feature described by our force field is the presence of intermediate structures between the native (N) and the unfolded (U) states as shown in Fig. 2 (16). We obtain two intermediate states in the free energy profile F(E) at the transition temperature. The intermediates, denoted as I1 and I2 in the figure, appear as local minima of F(E) versus E. To analyze the nature of the intermediate states we have split the energetic and entropic parts of the free energy. Results indicate that the intermediates are mainly stabilized by their energy, but that there is a nonnegligible entropic contribution.
Figure 2.
Free energy as a function of the configurational energy E for the bulk (Rc → ∞) showing the presence of the native (N), the intermediate (I1, I2), and the unfolded (U) states.
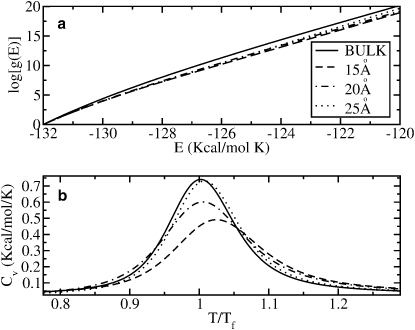
The next problem to be addressed is the influence of confinement on the free energy landscapes and folding behavior of the V3-loop. For this purpose, we calculated first the DOS and the specific heat of the protein assuming the rigid-wall confining potential V1(r) described above. We considered different cage-diameters (Rc = 15 Å, 20 Å, and 25 Å). In Fig. 3 a, we show influence of V1(r) on the behavior of the DOS. Note that, due to confinement, log [g(E)] considerably decreases at high energies compared to the bulk case (Rc → ∞). For energies close to the ground state, log [g(E)] does not exhibit any noticeable change because the protein is almost folded. Since its gyration radius in the ground state is Rg ∼ 13 Å, barriers of radii equal or larger than 15 Å do not affect folded structures. This result is consistent with the intuitive picture that cages, for instance chaperones, restrict the otherwise huge phase space for high energies, making the number of available structures, and consequently the entropy, considerably smaller than in absence of a cage. The effect of confinement can be also observed in the specific heat of the V3-loop, which we show in Fig. 3 b. Here, we plot the specific heat for different values of the cage radius (15 Å, 20 Å, 25 Å) and for the bulk case (Rc → ∞) as a function of T/T0f, where T0f = 321 K is the transition (unfolding) temperature in absence of a cage. The effect of the rigid-wall potential V1(r) is to increase the transition temperature (see Table 1) and to make the curve of the specific heat broader as the radius of the cage decreases. A broader curve means that there are more structures with energies close to the native state than in the bulk-case, where only the native state is the most important compact structure. For radii larger than 25 Å, the transition temperatures are equal to T0f within the statistical error of our simulations. We conclude that the protein is more stable as the radius of the cage decreases. This results are in agreement with Rathore et al. (11), in which Monte Carlo simulations were used, and with Takagi et al. (9) and Lu et al. (21), where Langevin simulations were performed. It is important to mention, however, that in those cited simulations a simplified Gō-type force field was used. Thirumalai et al. (24) made a considerable improvement to the force field by introducing the effect of the nonnative interactions. However, important interactions such as dipole-dipole and hydrogen bonds were not taken into account. The presence of intermediates was not reported either in those studies.
Figure 3.
(a) Logarithm of the density of states (DOS) g(E) of the protein inside the confining potential V1(r) and for different values of Rc (15 Å, 20 Å, 25 Å) as well as for the bulk case. One notices the remarkable decrease of the DOS for decreasing Rc. (b) Specific heat for the bulk case and for confining potentials with radii 15 Å, 20 Å, and 25 Å. Tf = 321 K is the transition temperature in the bulk case. Tf increases as the radius Rc decreases. The confining potential in panels a and b is purely repulsive.
Table 1.
Transition temperatures Tf for different values of the radius Rc of the potential V1(r) (see main text)
| Temperature (K) | Radius (Å) |
|---|---|
| 329.2 | 15 |
| 323.4 | 20 |
| 323.2 | 25 |
| 321.0 | ∞ |
Note that Tf decreases for increasing Rc.
The main goal of this article is the study of the influence of confinement on the potential landscape and, consequently, on the stability of the native and intermediate states. Note that the intermediates can be better characterized by analyzing the free energy F as a function of both the energy E and the order parameter Q. In Fig. 4 a, we show the contour plot of F(E, Q) for the bulk case. Clearly, the two intermediate structures, which we denote as I1 and I2, can be identified as local minima of F(E, Q). It is important to point out that the values of the end-to-end distance Q in the intermediates I1 and I2 are larger than in the native structure, but smaller than in the unfolded state. Fig. 3 a shows the importance of choosing the adequate order parameters to plot the free energy.
Figure 4.
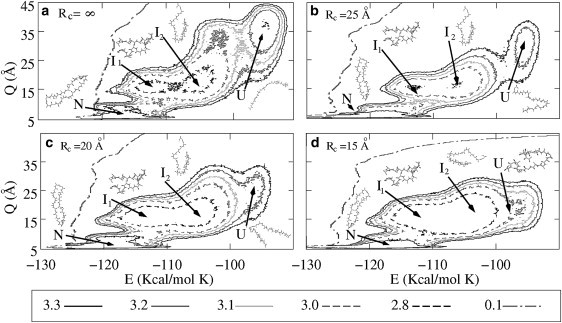
Contour plots of the free energy landscape F(E, Q) as a function of the configurational energy E and the end-to-end distance Q for a purely repulsive confining potential. Plots a–d correspond to the bulk case and cages of radius 15 Å, 20 Å, and 25 Å, respectively. The unfolded states are strongly affected when the size of the cage decreases. The native state and the intermediates are only slightly modified. The contour lines represent the free energy difference with respect to the native state and are given in Kcal/mol K.
To study the effect of a cage with purely repulsive walls (potential V1(r)) we have determined F(E, Q) for different values of the cage-radius Rc. In Fig. 4, b–d, we show the corresponding contour plots for Rc = 25 Å, Rc = 20 Å, and Rc = 15 Å, respectively. The different minima of F(E, Q) are shown together with representative snapshots of the corresponding structures. The main effect of the cage of Rc = 25 Å is to restrict the size of the unfolded states (U), which is reflected in a shift of the local U-minimum to a smaller value of Q (see Fig. 4 b). Further decrease of Rc leads to a stronger reduction of the size of the unfolded states. For example, for Rc = 15 Å the local U-minimum is situated at Q ∼20 Å, i.e., which means that the end-to-end distance of the unfolded states has been halved in value with respect to the bulk case. This can also be observed by the change in the form of the unfolded structures shown in the figure. Interestingly, there is also a small shift of the U-minimum to lower energies for decreasing Rc. This is simply because strong spatial confinement necessarily leads to the formation of contacts which were not present in the bulk. The shift of the U-minimum to lower energies also explains the reduction of the DOS upon confinement shown in Fig. 3 a.
In contrast to the unfolded states, the native structure is practically not affected by confinement, at least up to Rc = 15 Å, and the position of the N-minimum remains almost unchanged (see Fig. 4).
Different and interesting features are observed in the behavior of the intermediate states I1 and I2 upon repulsive confinement. In the bulk, the minima corresponding to the intermediates are well defined and separated by a potential barrier. Although both the position of the minima and the structure of the intermediates remain unchanged when the radius of the cage is reduced, the depth of the energy minima and the potential barrier between them decrease. Already for Rc = 20 Å, both minima start to merge and form an extended and shallow minimum. This effect is even stronger for Rc = 15 Å. Note that this happens when the radius of the confining potential becomes comparable to the end-to-end distance of the intermediate states in the bulk.
Now, we report on the influence of hydrophobic effects in the inner surface of the cage. Attractive cage-walls were considered by using the confining potential V2(r) (Eq. 3) with radius Rc = 30 Å. The degree of attraction is described by the coefficient ɛ. A completely attractive cage-wall is obtained when ɛ = 1.0, whereas ɛ = 0.0 corresponds to a completely repulsive or neutral inner surface of the cage. The effect of ɛ can be visualized in the following way: as ɛ increases from 0 to 1, the walls of the cage tend to attract the residues because of the relative minimum generated by the potential V2(r). The deepest minimum of V2(r, ɛ) is reached when ɛ = 1.0 and corresponds to Vmin2 ∼5 Kcal/mol. This energy is comparable to the energy required to break one hydrogen bond, ΔEHB ∼ 4.8 Kcal/mol. Therefore, for ɛ ∼ 1.0 the potential is able to destroy the structure of the protein (denaturation).
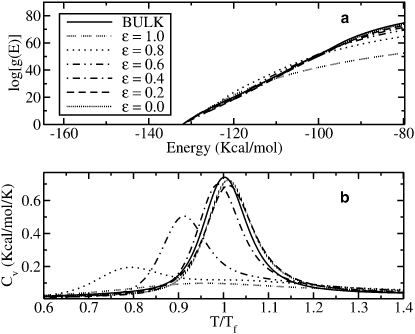
The influence of the confining potential V2(r) on the DOS of the protein is shown in Fig. 5 a, where different degrees of attraction and the bulk case are considered. Two clear features can be distinguished. First, the DOS at energies close to the native state increases for increasing ɛ. This means that the potential landscape is changed near the global minimum. Furthermore, for large energies one can clearly observe a dramatic reduction of g(E) by up to ∼13 orders of magnitude as ɛ goes from 0 to 1. However, this remarkable reduction of the phase space in this case does not help the protein to fold correctly but forces it to acquire a denatured conformation. This effect occurs because the peptide decreases its energy by placing some of the residues close to the border of the cage. Then, the number of accessible states at those energies decreases and residues are no longer allowed to be far apart from the border, since it would cost much energy. As a consequence, the peptide sticks to the wall of the cage.
Figure 5.
(a) Logarithm of the DOS g(E) for different degrees of hydrophobicity (ɛ = 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0) and for the bulk case. Notice the abrupt decay of g(E) by ∼13 orders of magnitude as ɛ goes from 0.0 to 1.0. For high values of ɛ, the protein tends to be in the unfolded state. (b) Specific heat of the protein for different values of ɛ, 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0, compared to the bulk case. Tf = 321 K is the transition temperature for the bulk. Notice how Tf and the peak of the specific heat decrease as ɛ goes from 0 (purely repulsive wall) to 1 (strongly attractive wall).
The influence of the potential V2(r) on the specific heat C(T) is shown in Fig. 5 b. As ɛ increases, the curve C(T) becomes broader. The transition temperatures for different values of ɛ and for the bulk case are presented in Table 2. Interestingly, for ɛ = 0–0.4 we obtain an increase of the transition temperature compared to the bulk case. The range 0.3 ≤ ɛ ≤ 0.4 seems to be the optimal one regarding stability. For that range of ɛ, the protein is more stable than in the absence of a cage. For higher values of ɛ, the transition temperatures become lower. For ɛ = 1.0, the curve of the specific heat is extremely broad and attenuated, reflecting the fact that the protein is almost denatured.
Table 2.
Transition temperatures Tf for the confining potential V2(r) (see main text) for different degrees of hydrophobicity, ɛ = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0, and for the bulk case
| Temperature (K) | Radius (Å) |
|---|---|
| 321.0 | Bulk |
| 324.2 | ɛ = 0.0 |
| 324.1 | ɛ = 0.2 |
| 314.5 | ɛ = 0.4 |
| 292.1 | ɛ = 0.6 |
| 253.5 | ɛ = 0.8 |
| — | ɛ = 1.0 |
Notice that in general Tf decreases as ɛ increases. For ɛ = 1.0 it is not possible to define Tf because the specific heat is almost completely attenuated.
One of the main results of this article is illustrated in Fig. 6, where we show the contour plots the free energy F(E, Q) for different values of ɛ. The radius of the cage is equal to 30 Å in all cases.
Figure 6.
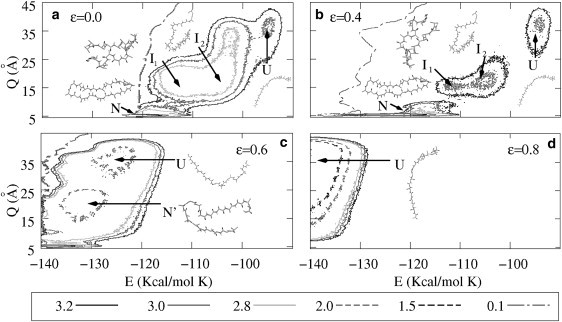
Contour plots of the free energy landscape F(E, Q) for a cage with attractive inner surface. Different degrees of hydrophobicity are displayed in plots a–d, corresponding to ɛ = 0.0, ɛ = 0.4, ɛ = 0.6, and ɛ = 0.8, respectively. The native and the intermediates states are slightly modified for 0.0 < ɛ < 0.4 but for larger values of ɛ the intermediate states disappear and the native structure is deformed. As a consequence, F(E, Q) represents a two-states landscape. The contour lines represent the free energy difference with respect to the native state and are given in Kcal/mol K.
For ɛ = 0 (Fig. 6 a), the presence of the native state (N), the intermediates (I1 and I2), and the unfolded states (U) can be clearly observed. The increase of ɛ leads to an effective increase of the confinement, and also to the presence of shallower minima for the intermediate states. For ɛ = 0.4 (Fig. 6 b), the global minimum and the three local minima can still be distinguished. However, the intermediates become almost unstable and the energy landscape has practically only two well-defined minima. A further increase of ɛ completely changes the energy landscape. For ɛ = 0.6 (Fig. 6 c), the native state and the intermediates I1 and I2 are no longer present. Instead, a new intermediate state N′ appears, which has more native contacts than I1 and I2, but less than N, and exhibits a much lower value of energy E. By looking at the structure corresponding to the minimum denoted by N′ it is clear that is very similar to N, but not completely folded. We interpret that the N′ state is a slight deformation of the native state produced by the presence of attractive wall. Note that also the U-minimum is shifted to much lower energies. This clearly indicates that the protein sticks to the wall of the cage. The net effect is that the potential landscape shows for this value of ɛ a two-state situation. Finally, for ɛ = 0.8 (Fig. 6 d), only the unfolded states are present.
Jewett et al. (13) showed that, for a particular protein, one metastable state might exist in the presence of a weakly hydrophobic barrier. In this work and for the peptide V3-loop we obtain a different result, namely, that the protein shows a folding behavior through intermediates in the bulk, but an attractive barrier with an optimum degree of hydrophobicity can lead to weakening the intermediate states and inducing a quasi two-state folding process.
Summarizing, we have studied the folding of the peptide 1NJ0 under different kinds of confining potentials. We used a force field which is independent on the native structure and includes relevant interactions such as the dipole-dipole and hydrogen bonds. We demonstrated the presence of intermediate states not reported before. These intermediates are strongly affected by the confining potentials.
Acknowledgments
P.O. thanks the Deutscher Akademischer Austausch Dienst for the financial support for his PhD.
References
- 1.Etienne M., Aucoin J., Fu Y., McCarley R., Hammer R. Stoichiometric inhibition of amyloid-protein aggregation with peptides containing alternating a,a, disubstituted amino acids. J. Am. Chem. Soc. 2006;128:3522–3523. doi: 10.1021/ja0600678. [DOI] [PubMed] [Google Scholar]
- 2.Kelly J. The alternative conformations of amyloidogenic proteins and their multi-step assembly pathways. Curr. Opin. Struct. Biol. 1998;8:101–106. doi: 10.1016/s0959-440x(98)80016-x. [DOI] [PubMed] [Google Scholar]
- 3.Lynn D., Meredith S. Review: Model peptides and the physicochemical approach to β-amyloids. J. Struct. Biol. 2000;130:153–173. doi: 10.1006/jsbi.2000.4287. [DOI] [PubMed] [Google Scholar]
- 4.Skolnick J., Kolinski A. Simulations of the folding of a globular protein. Science. 1990;250:1121–1125. doi: 10.1126/science.250.4984.1121. [DOI] [PubMed] [Google Scholar]
- 5.Abkevich V., Gutin A., Shakhnovich E. Specific nucleus as the transition state for protein folding: evidence from the lattice model. Biochemistry. 1994;33:10026–10036. doi: 10.1021/bi00199a029. [DOI] [PubMed] [Google Scholar]
- 6.Duan Y., Wang L., Kollman P. The early stage of folding of villin headpiece subdomain observed in a 200-nanosecond fully solvated molecular dynamics simulation. Proc. Natl. Acad. Sci. USA. 1998;95:9897–9902. doi: 10.1073/pnas.95.17.9897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Guo Z., Thirumalai D. Kinetics and thermodynamics of folding of ADE novodesigned four-helix bundle protein. Proc. Natl. Acad. Sci. USA. 1998;263:9897–9902. [Google Scholar]
- 8.Fang F., Szleifer L. Controlled release of proteins from polymer-modified surfaces. Proc. Natl. Acad. Sci. USA. 2006;103:5769–5774. doi: 10.1073/pnas.0509688103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Takagi F., Koga N., Takada S. How protein thermodynamics and folding mechanisms are altered by the chaperonin cage: molecular simulations review. Proc. Natl. Acad. Sci. USA. 2003;100:11367–11372. doi: 10.1073/pnas.1831920100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Thirumalai D., Klimov D., Lorimer G. Caging helps proteins fold. Proc. Natl. Acad. Sci. USA. 2003;100:11195–11197. doi: 10.1073/pnas.2035072100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rathore N., Knotts T., Pablo J. Confinement effects on the thermodynamics of protein folding: Monte Carlo simulations. Biophys. J. 2005;90:1767–1773. doi: 10.1529/biophysj.105.071076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Netto A., Silva C., Caparica A. Wang-Landau sampling in three-dimensional polymers. Braz. J. Phys. 2006;36:619–622. [Google Scholar]
- 13.Jewett A., Baumketner A., Shea J. Accelerated folding in the weak hydrophobic environment of a chaperonin cavity: creation of an alternate fast folding pathway. Proc. Natl. Acad. Sci. USA. 2004;101:13192–13197. doi: 10.1073/pnas.0400720101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang F., Landau D. Efficient, multiple-range random walk algorithm to calculate the density of states. Phys. Rev. Lett. 2001;86:2050–2053. doi: 10.1103/PhysRevLett.86.2050. [DOI] [PubMed] [Google Scholar]
- 15.Belardinelli R.E., Pereyra V.D. Fast algorithm to calculate density of states. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007;75:046701–046705. doi: 10.1103/PhysRevE.75.046701. [DOI] [PubMed] [Google Scholar]
- 16.Schnabel S., Bachmann M., Janke W. Two-state folding, folding through intermediates, and metastability in a minimalistic hydrophobic-polar model for proteins. Phys. Rev. Lett. 2007;98:048103. doi: 10.1103/PhysRevLett.98.048103. [DOI] [PubMed] [Google Scholar]
- 17.Chen N.-Y., Su Z.-Y., Mou C.-Y. Effective potentials for folding proteins. Phys. Rev. Lett. 2006;96:078103–078107. doi: 10.1103/PhysRevLett.96.078103. [DOI] [PubMed] [Google Scholar]
- 18.Solomons G., Fryhle C. 7th Ed. John Wiley & Sons; Oxford: 2000. Organic Chemistry. [Google Scholar]
- 19.Miyazawa S., Jerningan R. Residue potentials with a favorable contact pair term and an unfavorable high packing density term, for simulation and threading. J. Mol. Biol. 1996;256:623–644. doi: 10.1006/jmbi.1996.0114. [DOI] [PubMed] [Google Scholar]
- 20.Wang Z., Lee H. Origin of the native driving force for protein folding. Phys. Rev. Lett. 2000;84:574–577. doi: 10.1103/PhysRevLett.84.574. [DOI] [PubMed] [Google Scholar]
- 21.Lu D., Lu Z., Wu J. Structural transitions of confined model proteins: molecular dynamics simulation and experimental validation. Biophys. J. 2006;90:3224–3238. doi: 10.1529/biophysj.105.071761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Berg B., Neuhaus T. Multicanonical algorithms for first order phase transitions. Phys. Lett. B. 1991;267:249–253. doi: 10.1103/PhysRevLett.68.9. [DOI] [PubMed] [Google Scholar]
- 23.Kirkpatrick S., Gelat C., Vecci M. Optimization by simulated annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 24.Thirumalai D., Klimov D., Lorimer G. Nanopore-protein interactions dramatically alter stability and yield of the native state in restricted spaces. J. Mol. Biol. 2006;357:632–643. doi: 10.1016/j.jmb.2005.12.048. [DOI] [PubMed] [Google Scholar]