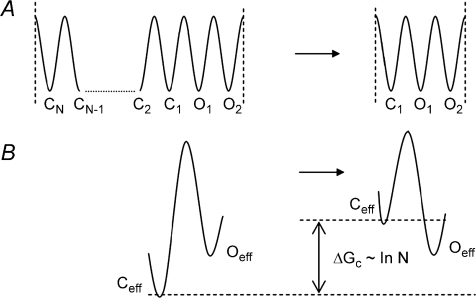
Figure 5. A simplified model of gating energy profile transformations leading to extreme Φ values.

The left energy profile in A represents ligand unbound states of the CFTR channel with N closed states and 2 open states available. It relates to the pore structure only and is assumed to be independent of the influence of unliganded NBDs. For simplicity all open (O_i) and closed (C_i) structural substates of the CFTR channel are shown as states of equal energies with identical energy barriers between them. This energy profile will result in equilibrium constant K=k_o/k_c=τ_o/τ_c= 2/N and ΔG∼ logK∼ log(2/N). The probability of the open state P_o=K/(1 +K) = 2/(2 +N) could be very low for the unbound CFTR if N≫ 2. We assume that a set of N available closed state structural configurations could be dramatically reduced to not less than 1 as a result of interaction of ligand bound NBDs with the channel structure. All open states as well as the rest of available closed states remain invariant. For simplicity we left only a single closed state configuration available after interaction of ligand bound NBDs with the channel structure and the invariant set of 2 open state configurations. The energy profile in A with a single closed state and the same set of 2 open states is a result of such an interaction and will lead to ΔG∼ logK∼ log2. The overall ΔΔG for the gating process is proportional to log N and P_o will increase. The arrest in the closed states is available after ligand dissociation only when the multiplicity of closed states resets and no additional coupling is required. Of course, the real energy profile is much more complex and we have used a simplified version to demonstrate the basic idea and distinctive properties of the mechanism suggested. The transitions to C₁ are still available in the open state on the right side of Fig. 5A and could be recorded as a brief intraburst closing if the experimental set-up has sufficient time resolution. The effective two state energy diagram available from single channel recording after strong low pass filtration is shown in B. The Φ value for the process of closed states reduction is 1 and does not impose restrictions on the backward process.