Computer-aided detection of pulmonary embolism in computed tomographic pulmonary angiography (CTPA): Performance evaluation with independent data sets

Abstract

The authors are developing a computer-aided detection system for pulmonary emboli (PE) in computed tomographic pulmonary angiography (CTPA) scans. The pulmonary vessel tree is extracted using a 3D expectation-maximization segmentation method based on the analysis of eigenvalues of Hessian matrices at multiple scales. A parallel multiprescreening method is applied to the segmented vessels to identify volume of interests (VOIs) that contained suspicious PE. A linear discriminant analysis (LDA) classifier with feature selection is designed to reduce false positives (FPs). Features that characterize the contrast, gray level, and size of PE are extracted as input predictor variables to the LDA classifier. With the IRB approval, 59 CTPA PE cases were collected retrospectively from the patient files (UM cases). With access permission, 69 CTPA PE cases were randomly selected from the data set of the prospective investigation of pulmonary embolism diagnosis (PIOPED) II clinical trial. Extensive lung parenchymal or pleural diseases were present in 22∕59 UM and 26∕69 PIOPED cases. Experienced thoracic radiologists manually marked 595 and 800 PE as the reference standards in the UM and PIOPED data sets, respectively. PE occlusion of arteries ranged from 5% to 100%, with PE located from the main pulmonary artery to the subsegmental artery levels. Of the 595 PE identified in the UM cases, 245 and 350 PE were located in the subsegmental arteries and the more proximal arteries, respectively. The detection performance was assessed by free response ROC (FROC) analysis. The FROC analysis indicated that the PE detection system could achieve an overall sensitivity of 80% at 18.9 FPs∕case for the PIOPED cases when the LDA classifier was trained with the UM cases. The test sensitivity with the UM cases was 80% at 22.6 FPs∕cases when the LDA classifier was trained with the PIOPED cases. The detection performance depended on the arterial level where the PE was located and on the percentage of occlusion. The sensitivity was lower for PE in the subsegmental arteries than in more proximal arteries and was lower for PE with less than 20% occlusion. The results indicate that the PE detection system achieves high sensitivity for PE detection on independent CTPA scans for both the PIOPED and UM data sets and demonstrate the potential that the automated PE detection approach can be generalized to unknown cases.

INTRODUCTION

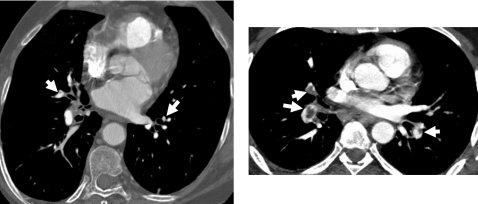
Pulmonary emboli (PE) partially or completely occlude pulmonary arteries after thrombi that usually form in the veins of the lower extremities or pelvis embolize into the pulmonary arteries. PE is a common condition and a leading cause of deaths in hospitalized patients. Prompt diagnosis and treatment of PE greatly influences patient outcome.^{1, 2} The majority of studies performed to date have shown that computed tomographic pulmonary angiography (CTPA) is the best choice for the evaluation of suspected PE, with excellent accuracy for PE in the main, lobar, and segmental pulmonary artery levels^{3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18} but lesser accuracy for PE in the subsegmental arteries.^{12, 15, 19, 20} The reported sensitivity ranges from 53% to 100% and specificity from 75% to 100%,^{3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18} depending on patient cohorts, imaging parameters, and CT scanner generation. The recent prospective multicenter clinical trial, prospective investigation of pulmonary embolism diagnosis (PIOPED) II,¹⁸ reported an overall sensitivity of 83% with a specificity of 96% and positive predictive values of 97%, 68%, and 25% for PE in main or lobar, segmental, and subsegmental arteries, respectively. The large variation in sensitivity and specificity is due not only to the difficulty of PE diagnosis in small subsegmental arteries but may also be due to subtle PE with small percentages of arterial occlusion. Although there are differing views about the clinical significance of small peripheral PE in the absence of central emboli, small PE may produce significant morbidity in patients with underlying cardiopulmonary disease^{21, 22} and may indicate a risk for recurrence of more significant PE among stable patients. In addition, it is important to estimate the total burden of pulmonary vascular clots in patients with acute PE to determine proper therapy and improve patient outcome.^{23, 24, 25, 26, 27, 28} Therefore, before a definitive study indicates otherwise, accurate detection of PE at all arterial levels may provide useful information for diagnosis and treatment.²⁹ Figure 1 shows examples of PE visualized on CTPA images.

Figure 1.

Examples of PE visualized on CTPA images. The PE identified by radiologists were marked by white arrows.

Thin-section multidetector computed tomography (MDCT) pulmonary angiography examinations for suspected PE routinely produce approximately 500–600 axial images of the thorax.³⁰ Radiologists have to visually track the pulmonary arteries down to the sixth-order branches. False negatives (FNs) are not uncommon because of the complexity of the images and the large number of arteries to be tracked in each case. Computer-aided detection (CAD) techniques may be a viable approach for assisting radiologists in the demanding task of PE detection and reducing the chance of missing PE.^{30, 31}

Automated detection of PE on CT images is a challenging area of computer vision application. This area has not attracted the interest of the CAD community until recently. Our recent review article indicated that the few studies performed to date are very preliminary using relatively small data sets.³² These previous studies have also suggested that the characteristics of PE, such as PE size, percentage of arterial occlusion, and the size of the involved arteries, as well as the presence of other pulmonary diseases, and CT image quality should be taken into consideration when evaluating the performance of a CAD PE system. Before a common data set is available, comparison among the performance of different systems will be difficult.

Although very few studies have been conducted to evaluate the value of CAD as a second reader in PE detection, studies^{33, 34, 35, 36} to date indicate that CAD is useful in improving the performance for PE diagnosis and can help radiologists as a second reader. For example, Engelke et al.³⁶ assessed the performance of a CAD system by a commercial company and its effects as a second reader on the detection of PE by two experienced and two inexperienced chest radiologists. A total of 1116 PE was identified in the CTPA scans of 56 patients through an independent consensus panel of two experienced radiologists who had knowledge on the results of the study readers and the results of CAD. Despite the low sensitivity of the CAD system (sensitivity of 30.7 at 4.1 FPs∕patient), the sensitivities of radiologists with CAD increased to a range of 83%–96%, from 77% to 93% without CAD. The overall performance in terms of the area A_z under the receiver operating characteristic (ROC) curve of individual radiologists also increased with CAD, and the improvement for the inexperienced radiologists was statistically significant (p=0.041).

We are developing computer vision techniques for the automated detection of PE on CTPA images.^{37, 38} In this study, we developed a prototype system for PE detection using multiscale vessel segmentation and vessel tree construction, parallel multiprescreening method for suspicious PE detection, and linear discriminant analysis (LDA) classifier for false positive (FP) reduction. The performance of our method was evaluated on two relatively large independent data sets to demonstrate the feasibility of our methods in PE detection and the robustness of our method in independent cases.

MATERIALS AND METHODS

Materials

With the approval of our Institutional Review Board (IRB), we collected 59 inpatient CTPA PE-positive cases retrospectively from the patient files at the University of Michigan (UM). The images were acquired with GE multidetector CT scanners, 120–140 kVp, 300–600 mA s, reconstructed at 1.25 mm slice thickness. Of the 59 cases, 16, 3, 34, and 6 cases were acquired with a 4-, 8-, 16-, and 64-slice CT scanner, respectively. Twenty-two of the 59 cases had extensive lung parenchymal and∕or pleural disease. With access permission, 69 CTPA PE-positive cases were randomly selected from the data set collected in PIOPED II trial, a multicenter, prospective trial supported by the National Institutes of Health and the National Heart, Lung, and Blood Institute. This study was designed to assess the validity of contrast enhanced spiral CT in the diagnosis of acute PE. According to the latest report presented,^{18, 39} PIOPED II study recruited 1090 patients that satisfied their protocol entry criteria. All patients were examined with helical CTPA and CT venography and a composite reference standard that included ventilation∕perfusion lung scan and ultrasound of the lower extremities. CTPA examinations were obtained on MDCT scanners of 4, 8, and 16 detector rows, at 1–1.25 mm collimation and reconstruction interval. All diagnostic tests except venous ultrasonography were interpreted based on the agreement of two certified central readers not at the patient’s clinical center. Additional readers were used until agreement of two was obtained. Central readers were blinded to clinical information and results of other imaging tests. The central CT readers recorded which arteries contained PE and were incorporated into the reference standard. The PIOPED II study reported about 23% PE prevalence among 824 patients with a reference diagnosis and a completed CT study.¹⁸ Of the 69 PIOPED PE-positive cases selected for this study, 59, 7, and 1 cases were acquired with GE 4-, 8-, and 16-slice CT scanner, respectively. Two cases were acquired with Siemens 4-slice CT scanner. The images were acquired at 120–140 kVp and 170–400 mA s. Of the 69 cases, 26 also had extensive lung parenchymal or pleural diseases.

For the UM cases, PE locations were marked by three experienced thoracic radiologists on a computer graphical user interface (GUI) developed in our laboratory. The PE locations in the PIOPED cases were also marked by our radiologists with reference to the documented diagnosis in the PIOPED study. The GUI has functions allowing the radiologist to cine-page through the CT slices, scroll in and out of individual arteries, adjust window setting, and zoom to improve visualization. The radiologists marked the PE location in every artery where it was present. For a contiguous volume of PE that occluded more than one level of the arteries, and branches of arteries at the same level, the radiologists virtually split the single PE volume by marking the PE segment in each branch as a separate PE. For each PE, radiologists marked the approximate location of its center and the starting and ending slices of the PE segment with a cursor, identified the anatomical level of the artery (trunk, main, lobar, segmental, and subsegmental), measured the diameter of the artery with an electronic ruler, and visually estimated the percentage of PE occlusion in the artery. To generate a volume of the PE, we developed a semiautomatic computer tool to segment the PE voxels within the radiologist-marked PE volume of interest (VOI) using a supervised region growing method.^{40, 41, 42, 43}

Radiologists manually marked 595 and 800 PE in the UM and PIOPED data sets, respectively. Table 1 shows the distributions of PE identified in the two data sets according to their major artery location and the percentage of arterial occlusion. These marked locations were used as the reference standard for algorithm development and evaluation. The PE occlusion in the data sets ranged from 5% to 100%. Of the 595 PE identified in UM cases, 245 (41%) and 350 (59%) PE were located in subsegmental arteries and the more proximal arteries, respectively. Of the 800 PE identified in the PIOPED cases, 282 (35%) and 518 (65%) PE were located in the subsegmental and more proximal arteries, respectively.

Table 1.

Reference standard PE identified by radiologists by artery level and percent arterial occlusion.

Data set	Percent occlusion	Proximal PE No. (%)	Subsegmental PE No. (%)	All PE
59 UM cases	⩽20%	52 (8.7%)	33 (5.6%)	85 (14.3)
	20%–80%	170 (28.6%)	94 (15.8%)	264 (44.4%)
	⩾80%	128 (21.5%)	118 (19.8%)	246 (41.3%)
	All occlusion	350 (58.8%)	245 (41.2%)	595
69 PIOPED cases	⩽20%	53 (6.7%)	33 (4.1%)	86 (10.8%)
	20%–80%	279 (34.9%)	153 (19.1%)	432 (54.0%)
	⩾80%	186 (23.3%)	96 (12.0%)	282 (35.3%)
	All occlusion	518 (64.8%)	282 (35.2%)	800

Methods

Pulmonary vessel tree segmentation

Because PE only occurs inside the pulmonary arteries, automatic and accurate segmentation of the pulmonary vessels in 3D CTPA images is an essential step for a PE CAD system. We developed an automatic multiscale enhancement and segmentation method to construct pulmonary artery tree. Details of the method was described elsewhere.³⁸ Briefly, all CT scans were interpolated to have isotropic voxels before processing for PE detection. The lung region was first extracted by applying expectation-maximization (EM) segmentation method to the volume of the scan. A morphological “closing” operation was then used to fill in the gaps along the boundary of the segmented lung region and “holes” inside the lung regions. The vascular structures in the lung volume were enhanced by 3D multiscale filtering and analysis of the eigenvalues of Hessian matrices using a vessel enhancement response function specially designed to enhance pulmonary vascular structures including the vessel bifurcations and to suppress nonvessel structures such as the lymphoid tissues surrounding the arteries. At each scale, the CT volume was convolved with a 3D Gaussian filter and the Hessian matrix was calculated at each voxel. A VOI containing the response function value at each voxel was defined. In this VOI, voxels with a high response indicated an enhanced vessel whose size matched the given filter scale. An EM estimation was then applied to the VOI to segment the vessels by extracting the high response voxels at each scale. Finally, the vessel tree was constructed using a hierarchical integration scheme to combine the segmented vessels at all scales and retain their size information.³⁸ The centerline of the constructed vessel tree was extracted based on the morphological “hit-and-miss” transform.⁴⁴ A 3D morphological hit-and-miss transform with a structuring element of 3×3×3 cross was successively applied to the segmented vessel volume to remove the voxels from the vessel boundary until no more voxel could be removed. The points along the centerline can be expressed in term of the hit-and-miss transform as

$$\text{Center}\text{Point}(I,J)=I-\left[\text{hit}\text{-}\text{and}\text{-}\text{miss}(I,J)\right],$$ (1)

where I is the set of voxels of the segmented vessel, J is the morphological structuring element, and the subtraction is a logical subtraction.

Parallel multiprescreening of suspicious PE

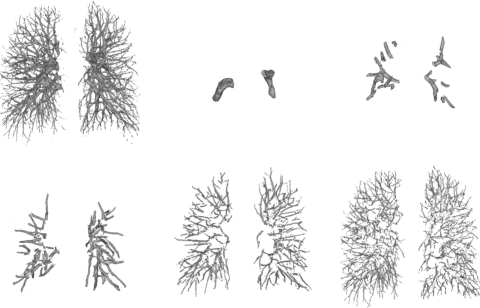
PE can exist anywhere within the arteries, from the main pulmonary artery to the subsegmental arteries and smaller, over which the radius of the arteries may change from over 10 mm to less than 2 mm. The percentage of observable PE occlusion on the CT images ranges widely from 100% to 5%. It is difficult to use one single method to effectively detect all PE because of the large variations in the characteristics of the PE in the patient population. We developed a multiprescreening scheme to identify VOI that contained suspicious PE.^{45, 46} In this study, two independent prescreening methods were developed to search for suspicious PE locally and globally in parallel in the constructed pulmonary arterial tree. The scale information on the vessels was simultaneously recorded and each voxel of a vessel was labeled by the scale value when the vessel tree was reconstructed using our multiscale segmentation and integration methods.³⁸ The labeled scale of each voxel therefore provided the approximate local vessel size information from which the size of the search region was estimated, for example, the cubic VOI along the segmented vessels for local search (method 1 described below), and the vessel tree stratified to different scale ranges for multiscale global search (method 2 described below). The suspicious objects detected by each prescreening method were added to a candidate pool subjected to subsequent false positive reduction. For overlapped objects resulted from the two prescreening methods, only the largest object would be chosen as candidate.

Method 1: Local search for the transition regions containing both normal and PE occluded vessel. This prescreening method is based on the properties of partial or complete filling defects within the lumen of the contrast-enhanced pulmonary arteries. The partial filling defect is often manifested as an area with lower CT values located at the marginal or intravascular central region that is surrounded by a variable amount of contrast material that exhibits higher CT values. Complete filling defect often results in an entire arterial section having low CT values. We developed an EM segmentation based prescreening method to search for the regions containing partial filling defect and the transition regions between normal arterial section and section of complete filling defect in a local region as follows. After vessel segmentation and reconstruction, a local cubic VOI was formed to enclose several slices of a single branch of the vessel tree. The VOI was centered at a given point along the vessel centerline extracted based on the morphological hit-and-miss transform. The size of the cubic VOI was determined by the labeled scale information on the vessel region, as described above. The local search method was based on the assumption that there were two classes of voxels in the local region: One class belonged to the contrast-filled vessel and the other PE and∕or lymphoid tissues. A 3D adaptive EM segmentation was applied to the segmented vessel within the VOI to separate the two classes of voxels. With the assumption as a priori knowledge, two Gaussians with equal variances were evenly placed across the gray-level histogram of the local voxels as the initial estimates. After several iterations, the EM algorithm found the optimally fitted Gaussians to the histogram. If there was no PE or lymphoid tissue in the local volume, the two Gaussian distributions on the histogram might overlap and merge. The EM segmentation would therefore only output one class of voxels: The contrast-filled vessel regions. Otherwise, the EM would output two classes: Region of suspicious PE and∕or lymphoid tissue and the vessel. The CT values of lymphoid tissue is similar to those of PE so that they cannot be separated in EM segmentation. The PE candidates will be further analyzed in the feature classification step to reduce the FPs such as lymphoid tissue. The VOI would be moved by centering the VOI at each point along the centerline, with its size adapted to each local vessel region, until the entire vessel was screened by the EM segmentation.

Method 2: Multiscale adaptive thresholding for global search in the vessel tree. Because of the assumption that there were two classes in the local volume when using EM analysis, the local search method could only detect the suspicious PE regions in the local volume that contained both normal and abnormal vessel segments. However, a significant PE can occlude an artery by a large percentage, for example, >80%, and extend further beyond the local volume. A local volume at the transition region may contain only very few contrast-filled voxels. The EM segmentation of the local search method may output one class of voxels which will be labeled as normal vessel. The PE of large occlusion thus may be missed by the local search method. We developed a global search method to overcome the above limitation. Because the contrast flows from the central toward the peripheral and smaller arteries, the CT values have different ranges at different arterial levels. For example, the CT values in small arteries may be lower than those in larger arteries; thus, the CT value of PE occluded larger artery may be close to those of normal small arteries. To detect the PE at different levels of arteries, we developed an adaptive multiscale detection method⁴⁵ to search for PE in vessels of different sizes. Because the vessel tree was reconstructed using our multiscale segmentation and integration methods,³⁸ each voxel of a segmented vessel was labeled by the scale information. The vessels were stratified to different range of scales, as illustrated in Fig. 2. Note that the vessels were not stratified at every single scale, the vessel voxels labeled by a specified range of scales were grouped into one stratified vessel structure. PE prescreening was performed separately in each stratified vessel structure using an EM segmentation to identify suspicious PE objects. Assume that there were two classes of voxels in the stratified vessel structure: Voxels in contrast-filled vessel region and voxels of PE and∕or lymphoid tissue region. If there is no soft tissue or PE, then EM analysis will find one Gaussian distribution. Otherwise, EM algorithm will output two separate Gaussian distributions: Contrast-filled vessel region and PE and∕or lymphoid tissue region.

Figure 2.

Vessel tree stratification. The computer constructed vessel (top-left) was stratified to multiple levels in terms of the scales (approximately related to the vessel sizes) derived from our vessel segmentation and integration method. The diameters of vessels were stratified from large to small (as shown above from left to right, top to bottom).

False positive reduction to determine the true PE

Our previous studies of CAD for breast and lung cancer indicated that linear or nonlinear combination of a number of features can be very effective in reducing FPs.^{47, 48, 49, 50} In this study, we investigated the feasibility of training a LDA classifier with stepwise feature selection to remove the prescreened objects that were substantially different from the true PE and generalizing the trained classifier to a relatively large independent test data set. The details of the implementation of LDA classifier with stepwise feature selection method for CAD applications can be found in our previous studies.^{51, 52}

Briefly, LDA is a well established technique^{53, 54} to find the linear combination of features which best separate two or more classes of data. For a two-class problem, the linear discriminant function is formulated as a weighted sum of a set of selected features as input predictor variables,

$$D=a_0+\sum _{i-1}^n{a}_i{X}_i,$$ (2)

where n is the number of selected feature variables, X_i are the values of the feature variables and a_i are coefficients (or weights) estimated from the input data during training such that the separation between the distributions of the discriminant scores D of the two classes is a maximum. To select the best set of features as input variables.^{51, 52, 55} We used a stepwise procedure to identify the useful features from the available input feature pool using a forward inclusion and backward removal process. The significance of the change in a feature selection criterion, which was chosen to be the Wilks’ lambda (ratio of the within-class sum of squares to the total sum of squares of the two-class distributions), when a new feature is entered or when an included feature is removed is determined based on F statistics.

For each suspicious PE object detected in the prescreening step above, nine features were extracted. The accurate identification of a true PE is based on the depiction of partial or complete filling defect within the lumen of the contrast-enhanced pulmonary arteries. We designed the following nine features to describe the filling defects for a detected suspicious PE object.

(f₁) Average CT value of the detected object (AvgO):

$$\mathrm{AvgO}=\frac{{\sum }_i^{n}x\left(i\right)}{n},$$ (3)

where x(i), i=1,…,n, represents the CT value of voxel i and n is the number of voxels in the object.

(f₂) Dominant CT value of the detected object (DIO):

$$\mathrm{DIO}=\underset{x}{\arg \max }H\left(x\right),$$ (4)

where H(x) is the histogram of CT values of the detected object and x is the CT value. DIO is the largest CT value of the histogram H(x).

(f₃), (f₄) Maximum (MaxScale) and mean (MeanScale) scales of the voxels of the detected object:

$$\mathrm{MaxScale}=\underset{i}{\overset{n}{\max }}\left[S\left(i\right)\right],$$ (5)

$$\mathrm{MeanScale}=\frac{{\sum }_i^{n}S\left(i\right)}{n},$$ (6)

where S(i) is the scale value of the ith voxel of the object. The voxels were labeled when the arterial tree was reconstructed using our multiscale segmentation and integration methods.³⁸

(f₅) Number of slices that enclose the detected object (NumSlice).

(f₆) Volume of the detected object (VolO).

(f₇), (f₈), (f₉) Three features that describe the difference in CT values between the detected object and the surrounding vessel (ID₁) and the nonvessel background (ID₂ and ID₃) are extracted as follows. Let S(i) be the labeled scale value of voxel i in the segmented vessel tree and h(x) represents the CT value histogram of voxels for which their labeled scale value S(i) are MaxScale−2⩽S(i)⩽MaxScale, the feature ID₁ is defined as

$${\mathrm{ID}}_1=\frac{\arg {\max }_{x}h\left(x\right)}{\mathrm{DIO}},$$ (7)

where DIO is the feature f₂ dominant intensity of the detected object.

For a detected object O, a morphological dilation with a structuring element that has a diameter of about the equivalent radius of the object is used to enlarge the object to about two times that of the original object O so that the surrounding nonvessel background of object O is enclosed. Let AvgIn denote the average CT value of the voxels of object O and AvgOut the average CT value of the voxels in the nonvessel background surrounding object O (outside the object O but inside the enlarged object EO), the features ID₂ and ID₃ are defined as

$${\mathrm{ID}}_2=\mathrm{AvgIn}∕\mathrm{AvgOut},$$ (8)

$${\mathrm{ID}}_3={\left(\mathrm{AvgIn}\right)}^2∕\mathrm{AvgOut}.$$ (9)

Performance evaluation

We used an overlap criterion to determine whether a detected object was true positive (TP) or FP. A computer-detected object was scored as TP when it overlapped with a reference standard PE by greater than a threshold T. The overlap ratio was defined as Jaccard coefficient (or Jaccard index),⁵⁶

$$\text{Overlap}=\frac{\mathrm{VolO}\cap \mathrm{VolR}}{\mathrm{VolO}\cup \mathrm{VolR}},$$ (10)

where VolO is the volume of the detected object and VolR is the volume of the reference standard. The threshold was chosen to be 10% in this study. The sensitivity was evaluated relative to the individual PE after virtual splitting described above (Sec. 2A). The performance of the LDA classifier was evaluated by ROC analysis. The detection performance was assessed by free response ROC (FROC) analysis.

RESULTS

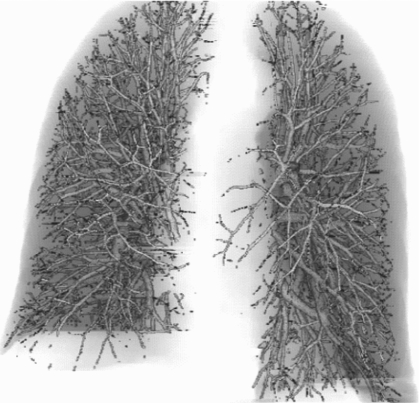
Figure 3 shows an example of a computer constructed vessel tree. The accuracy of vessel extraction was evaluated in our previous study³⁸ which demonstrated that vessel segmentation using our method can extract the pulmonary vessels accurately and the performance is not degraded by PE occlusion to the vessels. Two independent data sets including 59 UM and 69 PIOPED CTPA PE cases were used for the performance evaluation of our method in PE detection. A LDA classifier with stepwise feature selection was trained with the 59 UM cases, and the performance of the trained classifier was evaluated on the 69 PIOPED cases and vice versa.

Figure 3.

An example of a computer constructed pulmonary vessel tree within the segmented lung regions.

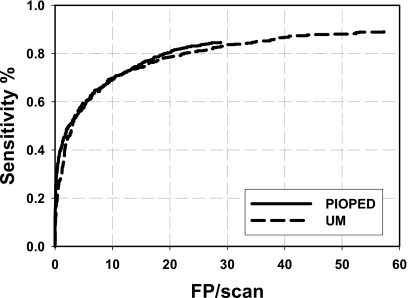
Table 2 shows the A_z values for the training and test sets, standard deviations, and the number of features selected when the LDA classifier was trained with the UM or the PIOPED cases. Figure 4 shows the test FROC curves for the independent data sets when the classifier was trained with UM cases and PIOPED cases, respectively. These curves represent the performance of our PE detection system for all PE with a range of 5%–100% occlusion and for all CTPA examinations in each data set including those with extensive parenchymal or pleural disease. The FROC analysis indicated that the overall performance of our PE detection system could achieve a test sensitivity of 80% at 18.9 FPs∕case for the PIOPED cases when the LDA classifier was trained with the UM cases. The test sensitivity with the UM cases was 80% at 22.6 FPs∕cases when the LDA classifier was trained with the PIOPED cases.

Table 2.

A_z value of training and test sets and the corresponding SD, the number of features selected as the input to LDA classifiers when trained with UM and PIOPED cases, respectively.

Data set	Training Az	SD of training Az	Test Az	SD of test Az	No. of selected features
Train in PIOPED cases, test on UM cases	0.855	0.009	0.877	0.008	5f1,f3,f4,f5,f7
Train in UM cases, test on PIOPED cases	0.881	0.008	0.851	0.009	6f1,f3,f4,f5,f8,f9

Figure 4.

The test FROC curves for PIOPED and UM cases, when the LDA classifier was trained with UM cases and PIOPED cases, respectively.

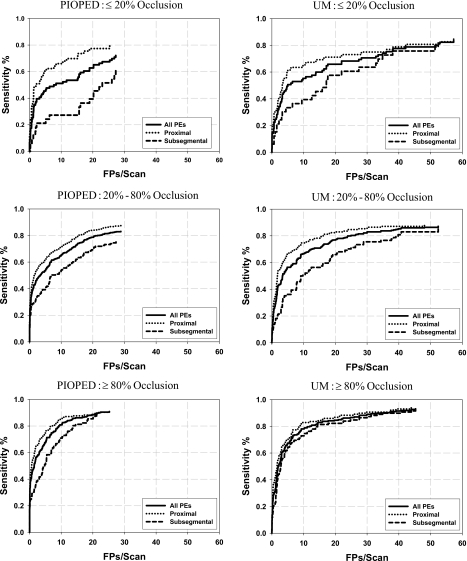
The detection performance depended on the arterial level where the PE was located and on the percentage of occlusion. Figure 5 shows the test FROC curves stratified for PE located at two arterial levels (subsegmental arteries and proximal arteries) with different percentage of occlusion (⩽20, 20%–80%, and ⩾80%). As expected, the FROC curves indicated that the sensitivity was lower for PE in the subsegmental arteries than those in the more proximal arteries and was lower for PE with less percent occlusion. Figures 6a, 6b, 6c, 6d, 6e show examples of computer-detected true positive PE with different occlusion to the arteries, false positives, and false negative (missed) PE.

Figure 5.

The test FROC curves stratified for PE located at two arterial levels (subsegmental arteries and proximal arteries) and with different percentages of occlusion (⩽20%, 20%–80% and ⩾80%). The left and right columns are test results for the PIOPED and UM cases, respectively.

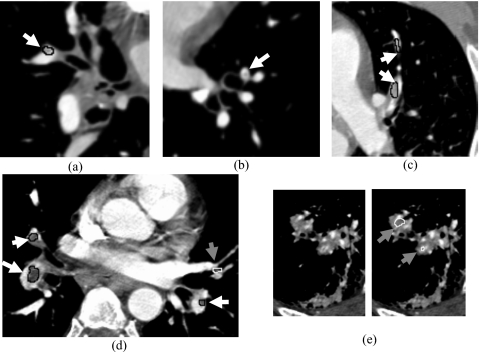
Figure 6.

Examples of the computer detected PE with different occlusions, FP and FN PE. A true-positive PE was enclosed by a black contour and marked by a white arrow, a false-positive was enclosed by a white contour and marked by a gray arrow, and a false-negative was marked by a white arrow without contour. Image (a) a TP subsegmental PE with 30% occlusion, (b) an FN subsegmental PE with 15% occlusion, (c) two TP PE with 90% occlusion which were splitted from the segmental (lower) to the subsegmental level (upper). (d) Three TP PE were detected, three lobar PE (top-left, bottom-left and bottom-right) with 95%, 60% and 40% occlusion, respectively. The FP in (d) was caused by partial volume effect between a lobar and a subsegmental artery. The two FPs in (e) were caused by extensive lung pleural disease.

DISCUSSION

Although the development of CAD systems for PE detection in CTPA is still at an early stage,³² recent studies^{33, 34, 35, 57} indicated that CAD is useful in improving the performance for PE diagnosis and can help radiologists as a second opinion. Automated detection of PE in CTPA scans is challenging. The difficulty of computerized PE detection is not only because of the large volume of data but also because of the complexity of the images and the partial volume effect, motion, or other imaging conditions. The performance of a CAD system also depends strongly on the characteristics of the PE such as their size, percentage of arterial occlusion by PE, and the diameter of the artery involved. To develop a CAD system, one of the most challenging tasks is to collect a sufficiently large data set for training and testing the computer algorithms. The collected cases should be representative of patient population and the reference truth of the lesion should be well defined. For the clinical CTPA PE cases, there is no equivalent to biopsy-proven “ground truth” as to whether PE are present or absent in a given artery. In our study, experienced thoracic radiologists provided the reference standard for PE by manually marking PE locations and providing the relevant information such as the size of the PE, percentage of the PE arterial occlusion, and the anatomic level of the artery occluded. Because a PE can extend to multiple branches down to multiple levels of artery, to evaluate the performance of our CAD system at different levels of the arteries, our radiologists virtually split a single volume of PE into volumes according to the branching of the artery by marking the PE segment in each branch as a separate PE. The sensitivity of a CAD algorithm for individual PE in a case can be treated, in a way, as the collective evaluation of the sensitivity of PE of different degrees of occlusion and conspicuity that may occur in many PE cases. Therefore, in the developmental process of a CAD system, it is useful to evaluate the sensitivity for detection of individual PE. This will also increase the number of individual PE for training the CAD system far beyond the number of CTPA cases available because many cases have multiple PE. The splitting of PE volume allows us to evaluate the performance of the CAD system at different arterial levels. However, it will also reduce the apparent sensitivity of the CAD system because a nonsplit PE extending from large to small arteries can be counted as a TP if any part of the PE is detected, whereas the same PE split into different arterial branches may generate several FNs if the split PE in the small arteries are missed. Nevertheless, before a large data set of PE cases that contains a sufficiently large number of single PE located at different levels of the pulmonary tree can be collected, the PE splitting method may be a good alternative to estimate detection performance at different arterial levels and to alleviate the problem of a limited data set.

As we discussed in Sec. 1, the PIOPED II cases were collected prospectively from multiple centers with a well-defined composite reference standard for PE diagnosis. It may be the best available data set to date for the evaluation of a CAD system. However, the written description of the “gold standard” established by the PIOPED readers is not specific in terms of individual PE locations, and many of the PE characteristics that are useful for CAD system performance evaluation, such as the size of the PE, percentage of arterial occlusion, the likelihood of being a true PE and conspicuity, were not collected in the PIOPED trial. To utilize the PIOPED cases in our study, our radiologists followed the PIOPED case reports and marked the PE locations on the CTPA scan using the same protocol of marking PE in UM cases. Since the UM data set does not have as rigorous reference standard as the PIOPED II data set, it is useful to compare the PE detection system performance in the UM set to that in the PIOPED II set as a reference. The result indicates that the performance in the UM data set does not appear to be overly optimistic relative to that in the PIOPED II data set.

Our two independent data sets were acquired with different (4-, 8-, 16-, and 64-slice) CT scanners. Of the 59 UM cases, 16, 3, 34, and 6 cases were acquired with 4-, 8-, 16-, and 64-slice CT scanners, respectively. Of the 69 PIOPED cases, 61, 7, and 1 cases were acquired with 4-, 8-, and 16-slice CT scanners, respectively. To evaluate the effects of different CT scanners on PE detection using our CAD system, an ROC analysis was used to assess the LDA classifier performance for differentiating TPs and FPs when the classifier was trained with the 69 PIOPED cases and tested on the 59 UM cases. The test A_z values were 0.898±0.014, 0.899±0.027, 0.863±0.012, and 0.898±0.029 for the 59 UM cases acquired with 4-, 8-, 16-, and 64-slice CT scanners, respectively. The differences in A_z did not achieve statistical significance (p>0.05). Note that although the numbers of cases with different CT scanners are small, the numbers of TPs and FPs were quite large for individual set (138 TPs and 926 FPs in the 16 4-slice cases, 40 TPs and 192 FPs in the 3 8-slice cases, 315 TPs and 1993 FPs in the 34 16-slice cases, 36 TPs and 331 FPs in the 6 64-slice cases, respectively). The study indicated that our CAD system is reasonably robust for CTPA scans acquired with different CT scanners.

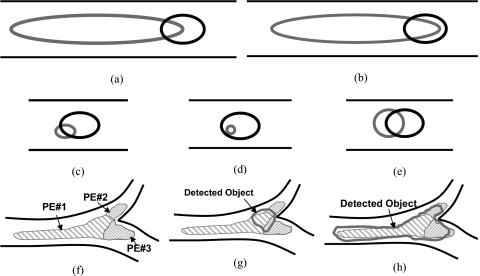
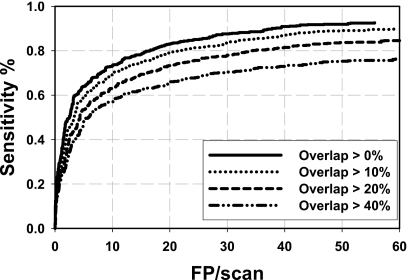
The methods for the determination of ground truth or the criteria for establishing reference standard for the training and testing samples, as well as the methods for scoring the true lesions and FPs, affect the apparent performance of the CAD system. The criterion that the detected object intersects with a reference standard, without a threshold, was used for scoring a true PE (TP) in most reported studies,^{33, 34, 35} while other studies^{36, 58} did not mention the scoring method. In our study, we also used an overlap criterion to determine whether a detected object was TP or FP. But a detected object could only be scored as TP when it overlapped with a reference standard by greater than a threshold T instead of intersecting with any voxel of the reference standard. Using the union of the detected object volume and the reference standard PE volume and imposing an overlap threshold can avoid scoring a detected object as a TP when its size is too large or too small compared to the size of the reference standard. Figure 7 illustrates examples of situations of overlap between a detected object and a reference standard. Using our TP scoring criterion, if the overlap threshold was set to a certain value, for example, 10% as in this study, although there was a large overlap compared to the region of either the reference standard [(a) and (b)] or the detected object [(c) and (d)], the detected object in (a)–(d) was still scored as FP. Only the object in (e) could be scored as a TP. However, if the criterion was set to be any intersection between the detected object and the reference standard (equivalent to a threshold of >0%), which was commonly used in reported studies,^{33, 34, 35} all objects (a)–(e) would be counted as TP. In an extreme case, for example, if the entire vessel was segmented as a detected object, any PE in the vessel would be counted as TP, resulting in overly optimistic estimate of sensitivity for algorithms that tended to mark long sections of vessels as detected objects. Figure 8 shows the dependence of the test FROC curves for the UM cases on the overlap thresholds when the LDA classifier was trained with the PIOPED cases. The FROC curves indicated that the best performance was achieved using an overlap threshold of T>0%. The performance increased when the overlap threshold decreased.

Figure 7.

Illustration of different situations of overlapping between a computer detected object (gray) and reference standards (dark (a)–(e), or gray with hatched (f)–(h)) located in a segmented vessel (two parallel lines in dark).

Figure 8.

Dependence of test FROC curves for UM cases on the overlap thresholds to score detected objects as TP or FP when the LDA classifier was trained with the PIOPED cases.

Because the task of PE detection is to alert radiologists to the locations suspected of having PE, the CAD mark indicating a detected PE location should be close to the true PE. However, the CAD mark location depends on the accurate volume segmentation of the detected PE. If the CAD mark was placed at the center of the detected object, for an elongated object as shown in Figs. 7a, 7b, the CAD mark would be too far from the true PE. Furthermore, in our study, for a contiguous volume of PE that occluded more than one level of the arteries and branches of arteries at the same level, the radiologists virtually split the single PE volume by marking the PE segment in each branch as a separate PE. Figure 7f shows an example of a contiguous PE split into three pieces. A detected object had overlap with all three PE in Figs. 7g, 7h. However, the detected object in (g) would not be scored as a TP if its overlap with all three PE was less than the threshold. Although the object in (h) has large overlap with PE No. 1 and could be scored as TP, PE No. 2 and PE No. 3 would be missed due to overlap below the threshold, resulting in a decrease in the overall sensitivity. In the current study, we chose an overlap threshold of 10% to determine whether a detected object was a TP or FP. This may be somewhat arbitrary but no standardization of scoring method has been established to date. The determination of reference standard, scoring methods and criterion, and the methods for presentation of the CAD marks to radiologists is a very important issue for CAD development, comparison, and implementation in clinical practice and warrants further investigations in future studies.

In our parallel multiprescreening scheme for suspicious PE detection, two independent prescreening methods were used. Our previous studies^{37, 59, 60} used a local search method (the first prescreening method in the current study) to detect the transition regions containing both normal and PE occluded artery segments. Due to partial volume effect, the changes in CT values between the normal and the occluded segments of the artery may not be significant enough so that the transition region was difficult to detect. For an elongated PE that extended to more than one branch level of arteries, only one end of the PE would show a transition in the CT values from a normal to an occluded region (or vice versa) because our radiologists virtually split the PE in different branches as separate PE for our reference standard. The other end of the PE would be directly connected to another PE at the branching point and there would be no transition region. The split PE were more difficult to detect, especially when they had a large occlusion (⩾80%) to an artery due to the single and short transition region. For a PE with less occlusion (<80%) to an artery, the PE surrounded by contrast material may present better CT value transition. This observation is supported by results from our previous studies that the sensitivity of detecting elongated PE with larger occlusion (>80% occlusion) was substantially lower than that of the PE (20%–80% occlusion) with less occlusion. The second prescreening method in our current study was specifically designed to employ global CT value information for the detection of PE that occluded an artery with a large percentage and long extension. The basic idea of this prescreening method is to apply EM segmentation to vessel structures stratified in terms of vessel sizes, which generally are also related to vessel levels. At a similar level, since the CT values of normal arteries and unoccluded segments of the arteries are comparable, they can be distinguished from PE by EM analysis of the gray-level histogram. The FROC results shown in Fig. 5 demonstrated that the computer can identify the PE accurately with our new multiscreening method even when PE occluded an artery larger than 80%.

In our early preliminary studies,⁴⁵ a rule-based classifier was trained to identify true PE using CT values, gradient, and size features extracted from the 2D slices and the 3D volume. The results tested on 44 CTPA UM cases indicated that, at an average of 33 and 24 FPs∕case, with sensitivities of PE detection method of 81% and 78%, respectively, for PE in proximal arteries, and 79% and 73%, respectively, for PE in the subsegmental arteries. A disadvantage of a rule-based classifier is that it is difficult to combine and weigh even a moderate number of features. In this study, a trained LDA classifier with feature selection is used for FP reduction. To demonstrate the feasibility of whether a LDA classifier can be trained to reduce FPs for computerized PE detection application, we extracted nine features for each suspicious object detected in the prescreening step. Unlike the lesions such as nodule and breast mass exhibiting a round or compact shape, PE can elongate to multiple arterial level without consistent shapes. We therefore did not include shape features for the classification. Using stepwise feature selection, six and five features were selected from the nine features when a LDA classifier was trained with the UM and PIOPED cases, respectively. Four of the selected features for the two data sets were the same. This indicated that the features are reasonably stable and the test results demonstrated the robustness of the classifier such that it can be generalized to independent data set containing relatively large case samples. Compared to our previous study using 44 PE cases that were part of our 69 UM cases, the test performance of our current system using the LDA classifier was improved to a sensitivity of 80% at 18.9 and 22.5 FPs∕scan for the PIOPED and UM sets, respectively, for all PE with a range of 5%–100% occlusion. This indicated that the new features and the LDA classifier have the potential to improve the overall accuracy of the CAD system. Our study also revealed that, as shown in Fig. 5, it is more challenging to detect subtle PE with small occlusion (⩽20%) to an artery, especially for those located in small arteries. Many FPs detected by our method are due to partial volume effects or additional lung diseases as shown in the example of Figs. 6d, 6e. Furthermore, our current vessel segmentation technique does not distinguish arteries and veins. Many FPs are detected in the pulmonary veins that have lower CT values, similar to those of PE occluded arteries. These FPs can be reduced substantially if the pulmonary veins can be differentiated from the arteries. Compared to reported studies in literature,^{33, 34, 35, 36, 58} our current CAD system has higher number of FPs than some^{33, 34, 35, 58} but lower than the other³⁶ studies at similar sensitivity levels. Since the detection accuracy depends strongly on factors such as the characteristics of the PE and the case samples, the reference standard, the scoring method and criteria, and whether the reported performance is obtained from independent testing, it may not be meaningful to compare directly the results from different studies. Further development of our computer vision techniques is underway to improve its sensitivity and reduce FP detection.

CONCLUSION

Our PE detection system that uses multiscale vessel segmentation technique, parallel multiprescreening method, and LDA classifier for FP reduction achieves high sensitivity for PE detection on independent CTPA scans. This study demonstrates the potential that our automated PE detection approach can be generalized to unknown cases. Further study is underway to improve the detection sensitivity for subtle PE (⩽20% occlusion) and to reduce the FPs. A fully developed CAD system is expected to provide a useful aid for PE detection in CTPA. Further evaluation in a data set of normal CTPA examinations is needed to evaluate the specificity of the CAD system at the patient level.