Modelling the kinetics of hepatitis C virus RNA decline over 4 weeks of treatment with pegylated interferon α-2b

SUMMARY

Viral kinetic models for hepatitis C virus (HCV) have generally assumed that the effectiveness of therapy in blocking virion production, ε, is constant. However, with pegylated interferon α-2b (PEG-IFN) given weekly, there are significant changes in drug concentration between doses that may lead to changes in drug effectiveness and viral rebounds towards the end of the dosing interval. Here we investigate the effects of using a model that assumes a constant effectiveness for studies involving PEG-IFN. We simulated PEG-IFN treatment in a population of 294 computer simulated ‘patients’, each characterized by a different set of pharmacokinetic and pharmacodynamic parameters. We then sampled the simulated treatment data over 4 weeks with a schedule similar to that used in viral kinetic studies, and fitted a viral kinetic model assuming constant drug effectiveness, the CE model, to that data. Although the CE model was able to fit to the data well in most cases, the parameter estimates obtained scattered widely both above and below the true values. Thus, this model is less useful to analyse HCV RNA data during therapy with PEG-IFN than with standard IFN given daily. With PEG-IFN accurate estimation of viral dynamic parameters necessitates concomitant measurements of serum viral load and drug concentration.

INTRODUCTION

The analysis of hepatitis C virus (HCV) RNA kinetic data after the initiation of antiviral therapy is frequently done using a simple model, developed by Neumann et al. [1]. The model was developed and tested against data obtained with daily dosing of standard interferon (IFN). Now that the standard of care involves the use of pegylated forms of IFN (PEG-IFN) plus ribavirin, one needs to examine whether the Neumann et al. model is still the appropriate model to use. The concern, which we raised in recent papers [2–4], is that with PEG-IFN α2b viral load rebounds are frequently observed toward the end of the weekly dosing interval [5,6]. This observation calls into question the assumption of the Neumann et al. model – that the effect of drug therapy can be summarized by single constant parameter, ε, the drug efficacy or effectiveness in blocking virion production. Previously [3], we showed that the Neumann et al. [1] model, which we called the constant effectiveness or CE model, when used to analyse HCV RNA data taken frequently for a week after a single dose of pegylated IFN α2b can lead to systematic errors in the estimation of the average drug effectiveness and of the infected cell loss rate. Here, we analyse a more realistic case of data collected over 4 weeks at a sampling rate characteristic of many clinical studies. Because a viral load decline should be more apparent when 4 weeks of data are analysed, we speculated that a more accurate estimate of the infected cell loss rate, δ, might be obtained than when only 1 week worth of data was used. However, we find the average effectiveness and the infected cell loss rate are either underestimated or overestimated depending on the pharmacokinetics (PK) and pharmacodynamics (PD) parameters characterizing each patient.

MODEL AND METHODS

The details of the model and method are similar to Shudo et al. [3]. Briefly (see also Fig. 1), we used the viral kinetic model of Powers et al. [4] and Talal et al. [2], in which PEG-IFN effectiveness depends on the time-varying drug concentration to generate artificial data sets of HCV RNA changes. The PK and PD parameters used to create these data sets are based on estimates by Talal et al. [2]. We generated a total of 294 data sets for different PK/PD parameters (see Table 1 in [3]). We then assumed no knowledge of drug concentration or variation in effectiveness, and fitted the simulated HCV RNA datasets to the CE model as in [3].

Fig. 1.

Surrogate viral load data generated assuming PEG-IFNα2b was given on days 0, 7, 14, 21 and 28 and HCV RNA was sampled at day 0, 1, 2, 3, 4, 7, 14, 21 and 28. Closed circles represent the surrogate data obtained by numerical simulation of the PK/PD model [2,4]. Solid lines in the top row show the viral kinetics predicted by the CE model [1] with the best-fit parameters. Here, the assumed detection limit of the HCV RNA assay is 50 IU/mL (dashed lines). The dotted and solid lines in bottom row are the actual effectiveness and the estimated effectiveness by the CE model, respectively. The parameters used to generate the surrogate data in the figures are: (a) k_a = 2/day, EC₅₀ = 0.1 µg/L, k_e = 0.2/day, n = 1, (b) k_a = 7/day, EC₅₀ = 0.6 µ/L, k_e = 0.7/day, n = 1, (c) k_a = 7/day, EC₅₀ = 0.4 µg/L, k_e = 0.2/day, n = 3 and (d) k_a = 0.19/day, EC₅₀ = 0.6 µg/L, k_e = 0.2/day, n = 3, respectively. The viral clearance rate, c, was fixed at 9.9/day. The estimated values of δ (δ̂), average of estimated effectiveness (ɛ̂ _a) and the average of actual effectiveness (ε_a) for the four panels were

Panels	(a)	(b)	(c)	(d)
δ/(day)	0.30	0.15	0.26	0.57
ɛ̂a	0.88	0.41	0.88	0.36
εa	0.88	0.24	0.83	0.58

Using the simulated data from day 0 to 2 8 as if it were real clinical data, we estimated parameters by performing nonlinear least squares fitting of the CE model to each patient's data. The parameter c was fixed to the value 9.9/day estimated in [2], since there was insufficient data during the first 2 days of therapy to estimate it accurately. We assumed that HCV RNA was measured at days 0, 1, 2, 3, 4, 7, 14, 21 and 28 after the initiation of therapy, which is typical of the frequency of measurements made in viral kinetic studies [5–9].

The data analysis method used here is slightly different from that used in our previous study [3], in that a lower limit of detection for HCV RNA (50 IU/mL) was assumed. When the viral load in the simulated data was less than this limit, the value was replaced by 50 IU/mL. In addition, if the viral load reached this limit at t = t_m and did not rebound, data points after t_m were excluded during data fitting. If only four data points were available due to this exclusion (2/294 cases), we estimated δ and ε, keeping the initial viral load (V₀) and the pharmacological delay (t₀) fixed at 5 × 10⁶ IU/mL and 0 days, respectively. If only three data points were available (2/294 cases), we estimated ε by the first-phase decay formula of the CE model (V(t) ≈ V₀(1 − ε + ε e^−c(t-t₀))) with V₀ and t₀ fixed, and δ ignored. However, in the remaining 290/294 cases, at least five data points were available and we estimated the parameters δ, ε, V₀ and t₀.

RESULTS

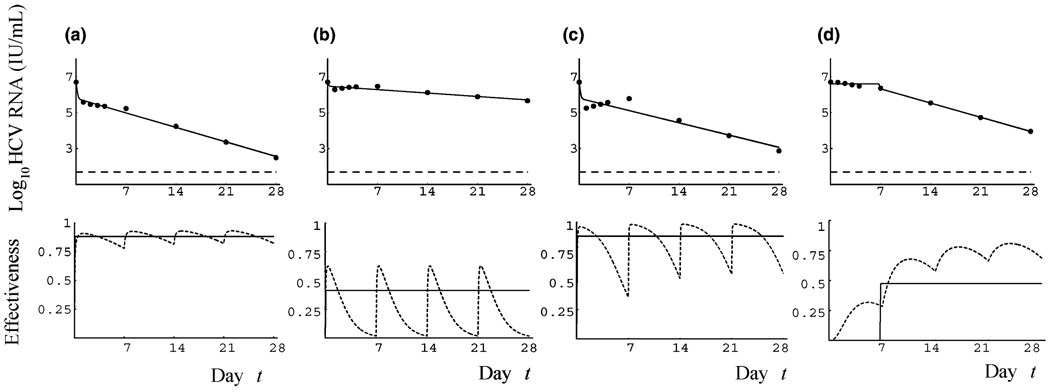
We generated by numerical simulation surrogate viral load data sets and then fitted the CE model to this data. Figure 1 shows some examples of the viral load profiles obtained over the course of 4 weeks. The drug effectiveness used to generate the simulated data fluctuates between doses, as shown in the bottom panels. Nonetheless, as shown in Fig. 1a, it is possible for the viral load profile to look biphasic, because of the infrequent sampling. In particular, this is the case if the effectiveness is maintained at a reasonably high level during the entire 4 weeks.

In Fig. 1a, the PEG-IFN effectiveness fluctuates between 0.78 and 0.93. On the other hand, if the drug effectiveness used to generate the surrogate data only reaches moderate levels, e.g. 0.63, and then decreases to a low (≍0) level, HCV RNA declines slowly and the viral profile is that of a null responder (Fig. 1b). Figure 1c illustrates a case where the effectiveness reaches a high level (0.98) but then decreases to a moderate level (0.36), due to rapid drug elimination. In this case, we observe a viral rebound at the end of the first week of therapy followed by a typical second phase decline. Because of weekly sampling after day 7, the subsequent end of the week rebounds are not observed. Figure 1c shows the fit of the CE model to the data, but one could also easily envision fitting a triphasic decline model [10–12] to the data, since there is little net decline in HCV RNA between days-2 and 14. In fact, slight increases in HCV RNA during the shoulder or flat second phase of triphasic declines are noticeable in some patient data that has been fit with a triphasic model (see Fig. 2 in Hermann et al. [12] and Fig. 3 in Dahari et al. [11]). These increases could be due to loss of drug effectiveness as in the simulated data shown here. Some patients have slow drug absorption and elimination. In this case, illustrated in Fig. 1d, the drug concentration and hence effectiveness increases gradually with time on therapy. When this occurs, HCV RNA initially decays very slowly and fitting such data with the CE model yields an estimated pharmacokinetic delay t₀ that is large, followed by a slow HCV RNA decay (Fig. 1d). Here no distinct first phase is apparent. A number of HIV/HCV coinfected patients studied by Torriani et al. [10] exhibited long delays (e.g. 13.6 days in patient S6) followed by a monophasic HCV RNA decay that thus resemble the kinetic pattern shown in Fig 1d.

Relationship between actual effectiveness and estimated effectiveness

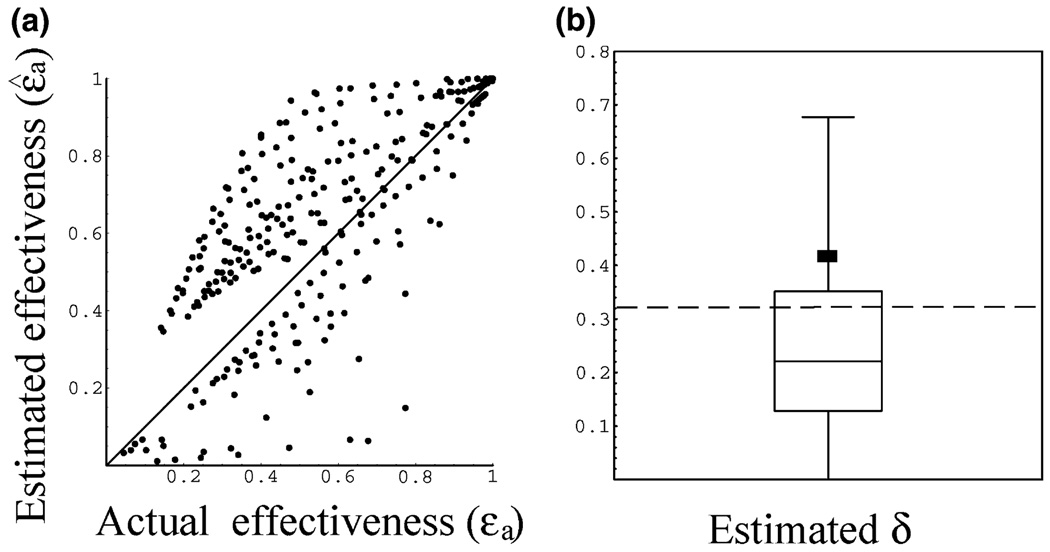
In the surrogate data, the drug effectiveness varies with time. We thus calculated its average, ε_a, over the entire 4 weeks, and compared it to the average of the estimated effectiveness, ɛ̂_a = ɛ̂ (28 − t₀)/28, where the estimated effectiveness, ɛ̂, is obtained by fitting the CE model to the surrogate data. Figure 2a shows the relationship between the actual average effectiveness and the estimated average effectiveness. The estimates scatter both above and below the true average effectiveness, and can give rise to large inaccuracies. For example, when the actual average effectiveness is 0.6, one can obtain estimates that vary between 0.52 and 0.97. Conversely, when the estimate is 0.6, the actual average effective may vary between 0.25 and 0.75. To access the overall error of the estimates we calculated the relative root mean squared (RMS) error, i.e. $\sqrt{\frac{1}{294}{\displaystyle {\sum }_{\mathrm{i}=1}^{294}{[({\widehat{\epsilon }}_{a\mathrm{i}}-{\epsilon }_{a\mathrm{i}})/{\epsilon }_{a\mathrm{i}}]}^2}}$, where for each simulated patient we calculated the relative difference between the estimated and actual average effectiveness. For the data in Figure 2a this error was 57%.

Fig. 2.

(a) The estimated average effectiveness ɛ̂_a, obtained by fitting the CE model to the surrogate data, plotted against the actual effectiveness used to generate the data ε_a. (b) Estimates of the infected cell loss rate, δ̂, obtained using the CE model. The dashed line indicates the true value of δ (0.32/day). The horizontal line within the box denotes the median (δ = 0.22/day), while the lines at the bottom and top of the box show the 25 and 75% quartiles, respectively. Whiskers outside the box show the 10 and 90% percentiles. The square indicates the estimated average (δ = 0.42/day).

Estimate of the infected cell loss rate

When we generated the surrogate data sets, we fixed the value of the virion clearance rate c at 9.9/day, and the infected cell loss rate δ at 0.32/day, the average values estimated by Talal et al. [2]. To estimate the parameters of the CE model, we fixed c to 9.9/day [2], although when we fixed c to a different value (e.g. 6.2/day [1]), the results were not altered qualitatively. The value of δ estimated from fitting the CE model to the surrogate data is denoted δ̂. The distribution of estimated values for δ̂ is shown in Fig. 2b as a box plot. The estimation of δ was inaccurate: 7.02/day (max), 0.0/day (min), 0.42/day (average) and 0.22/day (median) while the true value of δ was 0.32/day.

DISCUSSION

We have previously shown that estimates of viral kinetic parameters obtained using the constant effectiveness model to fit HCV RNA data obtained during the first week of PEG-IFNa2b therapy can be unreliable, even when frequent sampling is available. Here we analysed the effect of collecting data over a longer time frame (4 weeks), and used a sampling scheme similar to those used in viral kinetic studies [5–9]. In the simulated data analysed in this paper, viral loads decline to a low level toward the end of therapy (28 days) with repeated rebounds between doses. However, because of the infrequent sampling, the viral load rebound within this period was not obvious in the HCV RNA data (Fig. 1a). Therefore, the HCV viral load appeared to decrease monotonically, and this apparent monotonic decrease allowed us to estimate δ in a majority of cases, which was not possible before with data only from the first week [3]. Although most of the values for δ, obtained by nonlinear least-squares fitting of the model to the data, tended to be to an underestimate of the true value, the estimated mean infected cell loss rate, δ, was actually an overestimate (estimated mean 0.42/day vs a true value of 0.32/day). This discrepancy was due to the large variation in estimated values (Fig. 2b). In addition, the estimate for the average effectiveness of PEG-IFN was also inaccurate and the relative RMS error was 57%.

Talal et al. [2] and Powers et al. [4] estimated viral kinetic parameters for patients treated with PEG-IFNα2b by using pharmacokinetic data as well as HCV RNA. Their model, which incorporated both PK and PD can describe the HCV RNA rebound seen in some patients towards the end of the dosing interval when drug concentrations are low, while the CE model cannot. However, unless frequent measurements of plasma drug levels are available, their detailed approach cannot be implemented, and simpler models are needed. In clinical research, it is common to only assay HCV RNA. Therefore, the CE model, which is independent of pharmacokinetic data, is easily implemented for the estimation of viral kinetics parameters [8,9]. However, here we showed that the use of the CE model, with its constant effectiveness, leads to inaccurate estimations of the infected cell loss rate and the average PEG-IFN effectiveness. One way to achieve more accurate parameter values is to measure the serum concentrations of both HCV RNA and PEG-IFN as was done by Talal et al. [2] and Powers et al. [4]. This approach has also recently been applied to the study of PEG-IFN α-2b treatment of HBV [13].

Abbreviations

HCV

hepatitis C virus

PEG-IFN

pegylated interferon α-2b