Abstract
Objective
The current study re-examined the Project MATCH (Matching Alcoholism Treatments to Client Heterogeneity) hypothesis that individuals with high network support for drinking would have the best treatment outcomes if they were assigned to twelve-step facilitation (TSF).
Method
Drinking consequences, as measured by the Drinking Inventory of Consequences, was the primary outcome measure. Growth mixture models with multiple groups were used to estimate the drinking consequence trajectories of 952 outpatients during the 12 months following treatment for each of the three Project MATCH treatment conditions. Growth factors within latent trajectory classes were regressed on network support for drinking to assess whether treatment condition moderated the relationship between network support for drinking and drinking consequences over time.
Results
Three latent classes were identified, representing low (n = 154, 16.2%), medium (n = 400, 42%), and high (n = 398, 41.8%) levels of drinking consequences. Classes did not differ across treatment groups. Greater network support for drinking predicted more drinking consequences over time but only for clients assigned to cognitive-behavioral therapy and motivational enhancement therapy, not TSF.
Conclusions
This study provides further support for one of the original Project MATCH matching hypotheses: Clients with social networks supportive of drinking had better outcomes immediately after treatment if they were assigned to TSF. Because the original Project MATCH studies found this matching effect only at the 3-year follow-up, these results add validity to the network support for drinking matching effect. The study also provides additional evidence that accounting for heterogeneity in alcohol treatment outcomes is important for accurately estimating treatment effectiveness.
Network support for drinking has been defined as the extent to which an individual’s social network is supportive of the individual’s drinking behavior (Clifford and Longabaugh, 1991). This construct can be differentiated from general social support, which is often a protective factor for many addictive disorders (Beattie and Longabaugh, 1997; Rice and Longabaugh, 1996). On the other hand, network support for drinking has been consistently shown to predict negative drinking outcomes for treatment-seeking clients (Havassy et al., 1991; Longabaugh et al., 1993, 1998, 2001). Given this prognostic effect, Longabaugh et al. (1995) proposed that for clients with social networks supportive of drinking, receiving a treatment with the goal of either decreasing support for drinking or increasing support for abstinence will be effective in improving subsequent drinking outcomes.
The results from more than 30 previous alcoholism matching studies have made client-treatment matching an exciting clinical research interest (Donovan and Mattson, 1994; Longabaugh et al., 1994; Mattson et al., 1994), and these empirical data were the basis for the multisite, randomized clinical trial of alcohol treatment matching known as Matching Alcoholism Treatments to Client Heterogeneity (Project MATCH; Project MATCH Research Group, 1993). The trial recruited 1,726 participants with alcohol-use disorders and randomly assigned them to three individually delivered treatments: (1) cognitive-behavioral therapy (CBT; Kadden et al., 1992), (2) motivational enhancement therapy (MET; Miller et al., 1992), and (3) twelve-step facilitation (TSF; Nowinski et al., 1992). A comprehensive report of the rationale, protocol, results, and implications of Project MATCH can be found in “Treatment Matching in Alcoholism” (Babor and Del Boca, 2003).
In Project MATCH, TSF was a relationship-based intervention designed to decrease a client’s social support for drinking while increasing a client’s social support for abstinence through reliance on Alcoholics Anonymous (AA) fellowship as the foundation for recovery and sobriety (Nowinski and Baker, 1992). In short, the goal of TSF was to enhance the clients’ experience of AA fellowship and expose them to a network of people who have a goal of sobriety and who support one another in achieving this goal. In contrast, CBT therapists focused on interactions among clients’ thoughts, feelings, and behaviors, and attempted to increase clients’ abstinence self-efficacy (Kadden et al., 1992), and MET therapists encouraged clients to use personal motivation to stop drinking by pointing out discrepancies between current behavior and future goals (Miller et al., 1992). AA fellowship was not an important aim in either CBT or MET. The Project MATCH Research Group (1993) hypothesized that for individuals with social networks supportive of drinking, matching them to TSF, instead of CBT or MET, would appreciably improve treatment outcomes.
Using data from 952 outpatients in Project MATCH, Longabaugh et al. (1998) found support for this matching hypothesis but not during the expected time frame. Higher intake network support for drinking predicted greater drinking frequency and quantity at the 3-year follow-up for clients assigned to CBT and MET but not for those assigned to TSF. This was evidence to suggest that if a client had social networks that were supportive of his or her drinking, then matching this client to TSF, as opposed to CBT or MET, would buffer the negative effects of network support for drinking and thereby enhance treatment outcome in the long run.
In Project MATCH, 16 main contrasts were hypothesized involving 10 client characteristics. The only characteristic that showed a significant matching effect was network support for drinking. In addition, 2 out of 17 secondary contrasts were found to be significant: (1) outpatients high in anger had better posttreatment outcomes if they were matched to MET instead of CBT, and (2) aftercare patients high in alcohol dependence had better posttreatment outcomes if they were matched to TSF instead of CBT or MET. Despite the seemingly positive matching effect of the network support for drinking variable, there were many lingering questions. One criticism of Longabaugh et al.’s (1998) study was the apparent “disappearance” of the matching effect during the 12 months following treatment. Longabaugh et al. noted that, “During the initial 1-year post-treatment period, network support for drinking did not show significant matching effects on the primary dependent variables. Thus, the validity of this matching effect emerging at 3 years must be questioned. Is it a spurious finding?” (p. 1,328). Second, the analyses conducted in Project MATCH have been called into question because the researchers relied on the general linear model and ignored the heterogeneity of posttreatment alcohol use (Witkiewitz et al., 2007). In response to several criticisms, the Project MATCH Research Group recognized that, “Perhaps if we had examined the data in another way, the results might have been different” (Project MATCH Research Group, 1999, p. 69). Third, Project MATCH focused specifically on the frequency and quantity of alcohol use as treatment outcomes (Glaser, 1999), but it may be more meaningful to examine other dimensions, such as quality of life (Drummond, 1999) and drinking-related consequences (San, 1999). Longabaugh et al. (2001) stated, “Our interest in alcohol treatment is in reducing or eliminating the negative consequences of drinking rather than ending drinking itself. Thus, the negative consequences from drinking should be the primary measure of outcome” (p. 323). Although drinking consequences were examined as treatment outcomes in Babor and Del Boca (2003), the relationship between network support for drinking and drinking consequences was not looked at. With this in mind, examining drinking consequences, rather than percentage days abstinent or drinks per drinking day, may provide a better measure for evaluating the network support for drinking matching effect.
These limitations served as the impetus for the current study, as we attempted to answer three essential questions: (1) Does greater network support for drinking predict more subsequent drinking consequences? (2) For clients with greater network support for drinking, does assignment to TSF buffer the negative effects on drinking consequences? (3) Can this matching effect be found during the 12-month follow-up period if we analyze the data in “another way”? In other words, will the matching effect be even more robust using a methodology that takes into account the nonlinearity and heterogeneity in alcohol treatment outcomes immediately following treatment?
To address these three questions, the first goal of the current study was to characterize the trajectory of drinking consequences over time. Drawing from research on finite mixture modeling (Everitt and Hand, 1981), Muthén and Shedden (1999) introduced growth mixture modeling (GMM), with the purpose of grouping individuals with similar growth factors into the same class. Essentially GMM estimates continuous latent growth factors (i.e., intercept, slope, and nonlinear slope) as indicators of a categorical latent variable. The categorical latent variable defines the multiple latent “classes” (often thought of as subpopulations), each with its own estimates of growth factors that represent the mean intercept and slope for all the individuals grouped into that class. Recently a number of GMMs have been applied to characterize heterogeneity in longitudinal drinking outcomes and identify covariates (Chassin et al., 2002; Greenbaum et al., 2005; Jackson and Sher, 2005; Witkiewitz et al., 2007).
As an extension to GMM, the current study used a growth mixture model with multiple groups (GMM-MG; Muthén and Muthén, 2004). As the name suggests, a GMM-MG incorporates in a single model all the features of a GMM and allows for the regression of growth factors on covariates to vary across different groups for which membership is known (i.e., assignment to different treatments). Thus a GMM-MG allows for an efficient test of the extent to which a relationship between a covariate (e.g., network support for drinking) and growth factor (e.g., slope of drinking consequences) is moderated by treatment assignment.
Method
Participants
Project MATCH consisted of two independent arms of investigation, referred to as “outpatient” and “aftercare” studies. A total of 1,726 clients (952 outpatients, 774 after-care) were recruited from nine clinical research sites across the United States. In the outpatient arm, participants were recruited from the community or outpatient treatment centers. In the aftercare arm, participants were recruited from intensive day hospital or inpatient treatment centers. For the current study, only the outpatients were included in the analyses because prior findings relevant to the current study’s goals pertain only to the outpatient sample. Inclusion criteria were (1) current Diagnostic and Statistical Manual of Mental Disorders, Third Edition, Revised (DSM-III-R; American Psychiatric Association, 1994), diagnosis of alcohol abuse or dependence; (2) active drinking within the 3 months before intake; (3) alcohol as the principal drug of problematic use; (4) minimum age of 18 years; and (5) minimum sixth grade reading level. Exclusion criteria were (1) current DSM-III-R diagnosis of sedative, stimulant, or opiate dependence; (2) any intravenous drug use within the 6 months before intake; (3) danger to self or others; (4) probation requirements that might interfere with participation; (5) residential instability; (6) no emergency contact; (7) acute psychosis; (8) severe organic impairment; and (9) involvement in alternative treatment for drinking problems, with the exception of self-help groups such as AA. Table 1 provides the demographic characteristics of the 952 outpatients, as well as the means and standard deviations for the variables analyzed in the current study. In addition, 95% of participants met criteria for alcohol dependence, and 46% of men and 39% of women reported illicit drug use.
Table 1.
Outpatient demographic characteristics
| Variable | Men | Women |
|---|---|---|
| N 688 | 264 | |
| Age, mean (SD) | 38.7 (10.5) | 39.3 (11.2) |
| Ethnicity, % | ||
| White | 81 | 78 |
| Black | 4 | 9 |
| Hispanic | 13 | 10 |
| Other | 2 | 3 |
| Years of education, mean (SD) | 13.4 (2.2) | 13.6 (2.1) |
| Relationship status, % | ||
| Single | 38 | 29 |
| Couple | 62 | 71 |
| Employment status, % | ||
| Employed | 56 | 38 |
| Not employed | 44 | 62 |
| Prior alcohol treatment, % | ||
| Yes | 48 | 39 |
| No | 52 | 61 |
| Dependence symptoms, mean (SD) | 5.8 (1.9) | 5.6 (1.9) |
| DrInC total scores | ||
| DrInC score baseline, mean (SD) | 46.25 (22.01) | 44.52 (20.50) |
| DrInC score 3 months, mean (SD) | 32.85 (25.14) | 32.97 (22.73) |
| DrInC score 6 months, mean (SD) | 27.61 (23.09) | 30.47 (22.85) |
| DrInC score 9 months, mean (SD) | 28.07 (23.12) | 27.30 (21.44) |
| DrInC score 12 months, mean (SD) | 25.00 (23.46) | 27.33 (20.45) |
| DrInC score 15 months, mean (SD) | 27.72 (22.28) | 28.94 (23.93) |
| Network support for drinking score, mean (SD) | 0.05 (0.47) | 0.01 (0.47) |
Note: DrInC = Drinker Inventory of Consequences.
Design
On meeting the inclusion and exclusion criteria, participants were given an intake diagnostic evaluation that consisted of (1) a brief demographic history; (2) the alcohol, drug, and psychotic screen sections of the Structured Clinical Interview for DSM-III-R (Spitzer and Williams, 1988); (3) estimates of alcohol consumption via the Form 90 (Miller, 1996); (4) the legal, psychiatric, and family history sections of the Addiction Severity Index (McLellan et al., 1992); and (5) a psychological evaluation for the purpose of identifying mood disorders, sociopathy, and social support. After providing informed consent and completing intake assessments, participants were then randomized to one of three treatments: (1) CBT (Kadden et al., 1992), (2) MET (Miller et al., 1992), or (3) TSF (Nowinski et al., 1992). The therapy protocol for each treatment is described in detailed manuals (Kadden et al., 1992; Miller et al., 1992; Nowinski et al., 1992). Treatments (i.e., 12 sessions for CBT and TSF clients and 4 sessions for MET clients) lasted for 3 months and were delivered as individual therapy. In addition to the intake assessment, follow-up assessments were conducted at 3 (end of treatment), 6, 9, 12, and 15 months after the first therapy session. A comprehensive list of all follow-up assessments can be found in previous Project MATCH publications (Project MATCH Research Group, 1993, 1997). Only measures relevant to the current study are described below.
Measures
Drinking consequences
The Drinker Inventory of Consequences-Recent (DrInC; Miller et al., 1995) was used to assess consequences experienced as a result of drinking in the last 3 months. The reliability of DrInC in the current study was acceptable (Cronbach’s α = .91). The DrInC is a self-administered 50-item questionnaire designed to measure the adverse consequences of drinking in five areas: (1) impulse control (e.g., driving under the influence; 12 items), (2) physical (e.g., hangovers; 8 items), (3) intrapersonal (e.g., feeling guilty; 8 items), (4) interpersonal (e.g., relationship problems; 10 items), and (5) social responsibility (e.g., absenteeism; 7 items). The DrInC asks the respondent to report on a 4-point Likert-type scale (0 = never, 3 = daily) how frequently they have experienced each of the 45 drinking consequences within the last 3 months. The five scales were summed to provide a total DrInC score at each assessment period. Higher scores indicate more consequences. DrInC scores were obtained every 3 months in the 15-month study period.
Network support for drinking
The Important People and Activities (IPA; Clifford and Longabaugh, 1991) instrument was used to assess network support for drinking at intake. The IPA is a structured interview consisting of three main sections. First, a client’s social network and the characteristics of each network member are obtained. Second, the four most important network members are identified and additional information is collected on these four individuals. Last, questions are asked about important activities in which the client is engaged.
The network support for drinking variable used in Project MATCH is an overall sum of 11 indexes based on the first two sections of the IPA (Longabaugh et al., 1998), with adequate psychometric properties (Shrout-Fleiss intraclass and product moment correlations = .80 and .95, respectively). Indexes 1–3 measure client investment in their social network. Indexes 4–8 measure network drinking behavior. Indexes 9–11 measure the reactions of the most important network members to the client’s drinking. Each index was standardized to have a mean of 0 and SD of 1 and summed to yield an overall measure of network support for drinking (Longabaugh et al., 2001). Higher scores on the overall sum indicate greater network support for drinking.
Data analyses
The program Mplus version 4.1 (Muthén and Muthén, 2004) was used to estimate all models. Mplus uses the expectation maximization (EM) algorithm (Allison, 2002) to obtain maximum likelihood estimation with robust standard errors (MLR), a widely accepted approach to handling data that are missing at random (Little and Rubin, 2002; Muthén and Shedden, 1999). MLR generates the most likely parameters, given the variances and covariances of the observed data.
To begin to describe the steps of the analyses, it is useful to consider a traditional latent growth model (LGM) first, because it represents a special case of a GMM in which only one class is estimated (Muthén, 2004). Total DrInC scores at Months 3, 6, 9, 12, and 15 were used as the observed indicators in the growth model. Next, three latent growth factors were estimated: (1) intercept (i.e., drinking consequences during treatment), (2) linear slope (i.e., linear rate of change after treatment), and (3) quadratic slope (i.e., nonlinear rate of change after treatment). Individuals were allowed to vary in intercepts and linear slopes, so that these growth factors can be regressed on covariates. Variance of the quadratic slope, however, was fixed at zero for the models to converge. We estimated models with one to four classes and the relative fit of these models was assessed using three widely cited methods: (1) Bayesian information criterion (BIC; Schwarz, 1978), (2) the Lo-Mendell-Rubin likelihood ratio test (LMR; Lo et al., 2001), and (3) entropy (Ramaswamy et al., 1993).
The BIC assesses relative model fit based on a function of the log-likelihood value that rewards models with more explanatory power (i.e., fits the observed data better) but also exacts a penalty for having more parameters in the model. A smaller BIC value corresponds to a better model with a higher log-likelihood value and fewer parameters (Muthén, 2004). The LMR tests the extent to which adding one more class would improve model fit. A significant chi-square value (p < .05) indicates that the specified model fits the observed data better than a model with one less class. The entropy statistic is an overall estimate of each individual’s class membership probability. Entropy values can range from 0.0 to 1.0, with higher values indicating better classification. Taken together, the best fitting model would generate a lower BIC, a significant LMR p value, and higher entropy.
After estimating a model with the optimal number of classes, the next step was to simultaneously regress the growth factors (i.e., intercept and slope) on network support for drinking, while controlling for other covariates: (1) baseline drinking consequences, (2) baseline drinks per drinking day, and (3) missing data at each point. To test for the Network Support for Drinking × Treatment interaction, we added an interaction term by multiplying a binary treatment variable (0 = CBT and MET, 1 = TSF) with network support for drinking, which was centered at the mean (Aiken and West, 1991). Growth factors were regressed on this interaction term to test for the significance of a treatment moderation effect. For model identification purposes, the slope variance for the low class was constrained to zero because it was nonsignificant, and when the low class slope variance was allowed to be freely estimated, a negative estimate was derived (variance = −0.10, SD = 0.09, p = .23). Slope variances for the medium class (variance = 4.20, SD = 1.40, p < .01) and high class (variance = 12.73, SD = 4.87, p < .01) were significantly greater than zero, and therefore the regression of DrInC slope on the Network Support for Drinking × Treatment interaction was estimated only for these classes. Finally, to probe the relationship between network support for drinking and drinking consequences, we allowed the regression parameters of growth factors on network support for drinking to vary across the three treatment groups. This is one of the major advantages of using a GMM-MG. Essentially we tested the extent to which the relationships between network support for drinking and drinking consequences over time were different for individuals assigned to CBT, MET, and TSF in one encompassing model.
Missing data
There were large percentages of missing data across the 15-month follow-up, ranging from 19% missing at baseline to 47% missing at the 12-month follow-up. Missing data analyses using binary logistic regression with a dummy-coded DrInC missingness variable for each point revealed that DrInC classes were related to missingness at Month 9. Individuals classified into the high class were twice as likely to have missing data at Month 9 (odds ratio = 2.03, p < .01) compared with those in the low class. Hence the regression of DrInC class on missingness at Month 9 was included in all models described below. Missing DrInC scores at every other time point did not influence class membership.
Results
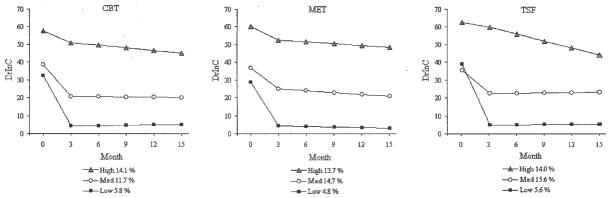
The relative model fit indexes for models with one to four classes are provided in Table 2. By comparing BICs for the one-class versus the two-, three-, and four-class models, it is clear that a multiple-class solution was superior (i.e., fits the observed data better). Furthermore, by examining the LMR p values, it is apparent that a two-class model fit significantly better than a one-class model and a three-class model fit significantly better than a two-class model. Estimating a fourth class, however, did not add improvement relative to the three-class model. In addition, by comparing both the entropy and BIC indexes, the three-class model seemed to strike the best balance between power and parsimony and was therefore selected as the best-fitting model. Figure 1 shows the estimated trajectories of the three-class model for each treatment group. Month 0 represents baseline drinking consequences. The three classes were defined as (1) low (n = 154, 16.2%), the greatest reduction in drinking consequences during treatment and no change over time after treatment; (2) medium (n = 400, 42%), a moderate reduction during treatment and no change over time after treatment; and (3) high (n = 398, 41.8%), the least reduction during treatment but a consistent decrease over time after treatment. Individuals assigned to CBT, MET, and TSF did not differ in terms of their trajectories. This suggests that all three treatments worked equally well in terms of being able to reduce the clients’ drinking consequences.
Table 2.
Relative model fit indexes for one- to four-class growth mixture models
| Model | Parameters | Log-likelihood | Entropya | BICb | LMR p valuec |
|---|---|---|---|---|---|
| One class | 21 | −20,864 | – | 41,873 | – |
| Two class | 26 | −12,689 | .57 | 25,552 | .0039 |
| Three class | 30 | −9,294 | .76 | 18,780 | .0004 |
| Four class | 37 | −9,270 | .73 | 18,782 | .1373 |
Notes: Covariates were included in model estimations.
Entropy = average classification precision; higher values indicate better classification of individuals into distinct classes;
BIC = Bayesian Information Criterion; lower values indicate better fit;
LMR p value = Lo-Mendell-Rubin p value; indicates significance in model fit improvement by estimating one more class.
Figure 1.
Estimated trajectories for the three-class model as a function of treatment (n = 952). DrInC = Drinker Inventory of Consequences; CBT = cognitive-behavioral therapy; MET = motivational enhancement therapy; TSF = twelve-step facilitation.
Individuals in higher classes had more baseline drinks per drinking day (low = 10.3, medium = 12.7, high = 16.1) (F = 63.15, 2/949 df, p < .01) and more baseline drinking consequences (see Figure 1). Examining baseline correlations, we find that higher DrInC scores were correlated with more drinks per drinking day (r = .24, p < .01). Higher baseline DrInC scores also predicted a higher DrInC slope (β = .24, p < .05; r2 = .09). Consistent with our hypothesis, higher network support for drinking predicted a higher DrInC slope (β = .27, p < .01; r2 = .11). However, this main effect is qualified by a significant interaction because treatment assignment moderated the relationship between DrInC slope and network support for drinking (see below). No other covariates, including missingness at any time point, were significantly related to the intercept or slope.
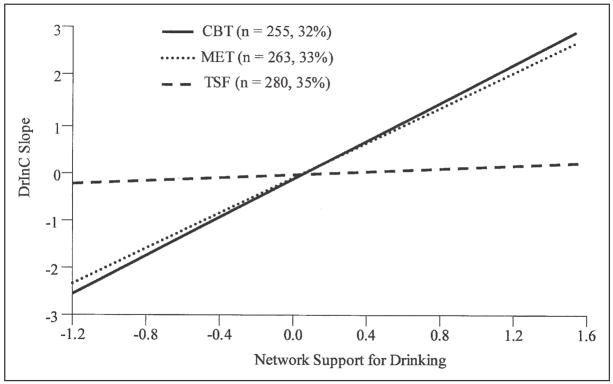
Consistent with our hypothesis, we found strong evidence for a matching effect. The regression of DrInC slope on the Network Support for Drinking × Treatment interaction term was significant (β = −.41, p < .01; r2 = .14), thus suggesting evidence for the existence of a treatment moderation effect. As shown in Figure 2, there is a disordinal interaction for Network Support for Drinking × Treatment Group within the medium and high DrInC classes. Individuals assigned to CBT and MET had higher DrInC slopes as network support for drinking increased (CBT: β = .43, p < .01; r2 = .29; MET: β = .40, p < .01; r2 = .27), whereas individuals with high network support for drinking who were assigned to TSF did not experience increased drinking consequences (β = −.12, p = .62; r2 = .01). Thus, among those individuals in the medium and high DrInC classes, higher network support for drinking predicted more drinking consequences over time immediately after treatment for clients assigned to CBT and MET. For clients assigned to TSF, however, higher network support for drinking was not associated with more drinking consequences among those individuals in the medium and high DrInC classes.
Figure 2.
Regression lines between network support for drinking and Drinker Inventory of Consequences (DrInC) slope as a function of treatment (N = 798; 154 individuals classified into the low class were excluded owing to nonpositive definite slope variance). CBT = cognitive-behavioral therapy; MET = motivational enhancement therapy; TSF = twelve-step facilitation.
Discussion
A number of studies have shown that treatment-seeking individuals with social networks supportive of their drinking behavior tend to have poorer drinking outcomes than those with social networks unsupportive of their drinking behavior (Havassy et al., 1991; Longabaugh et al., 1993, 1998). Our study adds further support to this literature. Consistent with the findings of prior studies, we found that individuals with higher network support for drinking experienced more drinking consequences over time after treatment than those with less network support for drinking. However, this undesirable relationship is dependent on what type of alcohol treatment one receives. Longabaugh et al. (1995) indicated that, for clients with social networks supportive of drinking, receiving a treatment with the goal of decreasing support for drinking or increasing support for abstinence will be effective in improving subsequent alcohol treatment outcomes. The results of the current study provide further empirical evidence for client-treatment matching.
We found that for clients with social networks supportive of drinking, their posttreatment drinking outcomes were significantly better if they were matched to TSF instead of CBT or MET. For those mismatched to CBT or MET, higher network support for drinking was associated with greater accumulation of drinking consequences throughout the 12 months immediately after treatment. Clients assigned to TSF, however, did not show this negative prognostic effect. This finding adds to the generalizability of the matching effect found by Project MATCH researchers 9 years ago (Longabaugh et al., 1998). They found that TSF clients (compared with CBT and MET clients) with social networks supportive of drinking drank less after treatment, whereas we found that these clients also experienced fewer drinking consequences. In addition, they found that this buffering effect emerged at a discrete time 3 years after treatment ended, whereas we found that this buffering effect was present continuously throughout the 12 months immediately after treatment.
Unlike the previous study, we evaluated a model of drinking consequences that allowed for individual heterogeneity during the 15-month study period of Project MATCH. A three-class growth mixture model provided the best fit to the data. The “low” class was characterized by individuals who had the most improvement during treatment, and their change in drinking consequences remained constant after treatment. Individuals in the “medium” class began treatment with more drinking consequences than those in the low class, but their posttreatment trajectories did not differ from those in the low class. Last, individuals in the “high” class improved the least during treatment, but their drinking consequences continued to decrease after treatment as the year progressed. If an LGM was used instead, as was the case in the original Project MATCH studies, then all 952 individuals would be grouped into one class and differences in individual trajectories would not have been discerned. In addition, the combination of findings that most people were not in the low class (83.8%) and that network support for drinking had no relationship with DrInC slope in the low class suggests that the impact of network support for drinking may be particularly relevant when individuals with alcohol problems experience a considerable amount of drinking consequences. That is, individuals at the low end of drinking consequences do not appear to be vulnerable to the undesirable effects of network support for drinking.
Limitations and future directions
Two limitations of the current study should be addressed. First, using growth mixture modeling to extract latent trajectory classes is hotly debated (see Bauer and Curran [2003] and the series of commentaries in the same issue of Psychological Methods). Growth mixture models have primarily been used for two purposes: (1) to identify qualitatively distinct classes of individuals in the population (Muthén, 2004; Nagin and Tremblay, 1999) and (2) to approximate complex distributions with a small number of simpler component distributions (Bauer and Curran, 2003; Jedidi et al., 1997). In the current study, we took the latter approach. Thus we do not attempt to make any claim that the low, medium, and high classes represent true subpopulations of individuals. As described by Bauer and Curran (2003), one should be cautious in the interpretation of these classes, particularly when evaluating predictors of class membership.
Second, although the matching effect for drinking consequences was found during the 12 months after treatment, we did not test for the mechanism by which TSF buffered individuals with networks supportive of drinking. Several studies have suggested that AA involvement partially mediates the relationship between network support for drinking (Tonigan et al., 1996) and subsequent drinking outcomes (Humphreys et al., 1994; Longabaugh et al., 1998, 2001). That is, individuals assigned to TSF have greater subsequent AA involvement compared with those assigned to CBT or MET, and it is the AA involvement that leads to better drinking outcomes by buffering the negative effects of social networks supportive of drinking. Involvement in AA fellowship exposes a person to a network of people who have a goal of sobriety and who support one another in achieving this goal (Nowinski and Baker, 1992). Future studies could examine the causal chain model in greater detail: (1) network support for drinking predicts more drinking consequences, (2) this negative effect is moderated by treatment, (3) TSF increases AA involvement, and (4) AA mediates the relationship between network support for drinking and drinking consequences. Results from the current study support the first two steps, and the third step is supported by Longabaugh et al.’s (1998) study. In addition, future studies could examine the possibility of using the IPA as a screening measure to determine whether an individual is best suited for TSF versus alternative treatments.
Conclusions
Despite these limitations, the current study adds both analytical and clinical importance to the field of addictive behaviors. Analytically, the results provide a more thorough understanding of the heterogeneity in drinking consequences during and after treatment. Specifically, using a growth mixture model with multiple groups, we were able to better discern individual trajectories by approximating heterogeneity with multiple latent classes, test for unique covariate effects, and examine treatment group differences, all in one encompassing model. Clinically, the network support for drinking matching effect suggests that, if an alcohol-dependent individual has family and friends that support his or her drinking behavior, then the person would likely experience more drinking consequences over time immediately after treatment as a result of this “prodrinking” social environment. Based on the results from the current study, however, participating in TSF might buffer the undesirable effect that network support for drinking has on subsequent drinking consequences. In the larger context, the current study adds empirical validity to the notion and importance of client-treatment matching.
Footnotes
This research was supported by National Institute on Alcohol Abuse and Alcoholism grant R03 AA016322-01 awarded to principal investigator Katie Witkiewitz. The study was completed as a master’s thesis in the clinical psychology program by Johnny Wu at the University of Illinois at Chicago, supervised by Katie Witkiewitz. The research protocol met the criteria for exemption, as defined in the U.S. Department of Health (protocol number: 2007-0099).
References
- Aiken LS, West SG. Multiple Regression: Testing and Interpreting Interactions. Thousand Oaks, CA: Sage; 1991. [Google Scholar]
- Allison PD. Missing Data. Thousand Oaks, CA: Sage; 2002. [Google Scholar]
- American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders (DSM-IV) Washington, DC: 1994. [Google Scholar]
- Babor TF, Del Boca FK, editors. Treatment Matching in Alcoholism. New York: Cambridge Univ. Press; 2003. [Google Scholar]
- Bauer DJ, Curran PJ. Distributional assumptions of growth mixture models: Implications for overextraction of latent trajectory classes. Psychol Meth. 2003;8:338–363. doi: 10.1037/1082-989X.8.3.338. [DOI] [PubMed] [Google Scholar]
- Beattie MC, Longabaugh R. Interpersonal factors and post-treatment drinking and subjective wellbeing. Addiction. 1997;92:1507–1521. [PubMed] [Google Scholar]
- Chassin L, Pitts SC, Prost J. Binge drinking trajectories from adolescence to emerging adulthood in a high-risk sample: Predictors and substance abuse outcomes. J Cons Clin Psychol. 2002;70:67–78. [PubMed] [Google Scholar]
- Clifford PR, Longabaugh R. Manual for the Administration of the Important People and Activities Instrument. Richard Longabaugh, Brown University, Center for Alcohol and Addiction Studies; 800 Butler Drive, Providence, RI, 02906: 1991. [Google Scholar]
- Donovan DM, Mattson ME. Alcoholism treatment matching research: Methodological and clinical issues. J Stud Alcohol. 1994;(12):4–14. [PubMed] [Google Scholar]
- Drummond DC. Treatment research in the wake of Project MATCH. Addiction. 1999;94:39–42. [PubMed] [Google Scholar]
- Everitt BS, Hand DJ. Finite Mixture Distributions. New York: Chapman and Hall; 1981. [Google Scholar]
- Glaser FB. The unsinkable Project MATCH. Addiction. 1999;94:34–36. [PubMed] [Google Scholar]
- Greenbaum PE, Del Boca FK, Darkes J, Wang CP, Goldman MS. Variation in the drinking trajectories of freshmen college students. J Cons Clin Psychol. 2005;73:229–238. doi: 10.1037/0022-006X.73.2.229. [DOI] [PubMed] [Google Scholar]
- Havassy BE, Hall SM, Wasserman DA. Social support and relapse: Commonalities among alcoholics, opiate users, and cigarette smokers. Addict Behav. 1991;16:235–246. doi: 10.1016/0306-4603(91)90016-b. [DOI] [PubMed] [Google Scholar]
- Humphreys K, Finney JW, Moos RH. Applying a stress and coping framework to research on mutual help organizations. J Commun Psychol. 1994;22:312–327. [Google Scholar]
- Jackson KM, Sher KJ. Similarities and differences of longitudinal phenotypes across alternate indices of alcohol involvement: A methodologic comparison of trajectory approaches. Psychol Addict Behav. 2005;19:339–351. doi: 10.1037/0893-164X.19.4.339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jedidi K, Jagpal HS, DeSarbo WS. Finite-mixture structural equation models for response-based segmentation and unobserved heterogeneity. Market Sci. 1997;16:39–59. [Google Scholar]
- Kadden R, Carroll K, Donovan D, Cooney N, Monti P, Abrams D, Litt M, Hester R. NIAAA Project MATCH Monograph Series, Vol. 3, DHHS Publication No. (ADM) Washington: Government Printing Office; 1992. Cognitive-Behavioral Copings Skills Therapy Manual: A Clinical Research Guide for Therapists Treating Individuals with Alcohol Abuse and Dependence; pp. 92–1895. [Google Scholar]
- Little RJA, Rubin DB. Statistical Analysis with Missing Data. 2. Hoboken, NJ: John Wiley & Sons; 2002. [Google Scholar]
- Lo Y, Mendell NR, Rubin DB. Testing the number of components in a normal mixture. Biometrika. 2001;88:767–778. [Google Scholar]
- Longabaugh R, Beattie M, Noel N, Stout R, Malloy P. The effect of social investment on treatment outcome. J Stud Alcohol. 1993;54:465–478. doi: 10.15288/jsa.1993.54.465. [DOI] [PubMed] [Google Scholar]
- Longabaugh R, Wirtz PW, Beattie MC, Noel N, Stout R. Matching treatment focus to patient social investment and support: 18-month follow-up results. J Cons Clin Psychol. 1995;63:296–307. doi: 10.1037//0022-006x.63.2.296. [DOI] [PubMed] [Google Scholar]
- Longabaugh R, Wirtz PW, DiClemente CC, Litt M. Issues in the development of client-treatment matching hypotheses. J Stud Alcohol. 1994;(12):46–59. doi: 10.15288/jsas.1994.s12.46. [DOI] [PubMed] [Google Scholar]
- Longabaugh R, Wirtz PW, Zweben A, Stout RL. Network support for drinking, Alcoholics Anonymous and long-term matching effects. Addiction. 1998;93:1313–1333. doi: 10.1046/j.1360-0443.1998.93913133.x. [DOI] [PubMed] [Google Scholar]
- Longabaugh R, Wirtz PW, Zweben A, Stout R. Network support for drinking. Project MATCH Hypotheses: Results and Causal Chain Analyses. In: Longabaugh R, Wirtz PW, editors. NIAAA Project MATCH Monograph Series, Vol. 8, NIH Publication No. 01–4238. Washington: Government Printing Office; 2001. pp. 260–275. [Google Scholar]
- McLellan AT, Kushner H, Metzger D, Peters R, Smith I, Grissom GP, Pettinati H, Argeriou M. The fifth edition of the Addiction Severity Index. J Subst Abuse Treat. 1992;9:199–213. doi: 10.1016/0740-5472(92)90062-s. [DOI] [PubMed] [Google Scholar]
- Mattson ME, Allen JP, Longabaugh R, Nickless CJ, Connors GJ, Kadden RM. A chronological review of empirical studies matching alcoholic clients to treatment. J Stud Alcohol. 1994;(12):16–29. doi: 10.15288/jsas.1994.s12.16. [DOI] [PubMed] [Google Scholar]
- Miller WR. NIAAA Project MATCH Monograph Series, Vol. 5, NIH Publication No. 96–4004. Bethesda, MD: National Institute on Alcohol Abuse and Alcoholism; 1996. Form 90: A Structured Assessment Interview for Drinking and Related Behaviors: Test Manual. [Google Scholar]
- Miller WR, Tonigan JS, Longabaugh R. NIAAA Project MATCH Monograph Series, Vol. 4, NIH Publication No. 95-3911. Bethesda, MD: National Institute on Alcohol Abuse and Alcoholism; 1995. The Drinker Inventory of Consequences (DrInC): An Instrument for Assessing Adverse Consequences of Alcohol Abuse (Test Manual) [Google Scholar]
- Miller WR, Zweben A, DiClemente CC, Rychtarik RG. NIAAA Project MATCH Monograph Series, Vol. 2, DHHS Publication (ADM) 92-1894. Washington: Government Printing Office; 1992. Motivational Enhancement Therapy Manual: A Clinical Research Guide for Therapists Treating Individuals with Alcohol Abuse and Dependence. [Google Scholar]
- Muthén BO. Latent variable analysis: Growth mixture modeling and related techniques for longitudinal data. In: Kaplan D, editor. The Sage Handbook of Quantitative Methodology for the Social Sciences. Thousand Oaks, CA: Sage; 2004. pp. 345–368. [Google Scholar]
- Muthén L, Muthén B. Mplus User’s Guide: Statistical Analysis with Latent Variables, Version 3. Los Angeles, CA: Muthén & Muthén; 2004. [Google Scholar]
- Muthén B, Shedden K. Finite mixture modeling with mixture outcomes using the EM algorithm. Biometrics. 1999;55:463–469. doi: 10.1111/j.0006-341x.1999.00463.x. [DOI] [PubMed] [Google Scholar]
- Nagin D, Tremblay RE. Trajectories of boys’ physical aggression, opposition, and hyperactivity on the path to physically violent and nonviolent juvenile delinquency. Child Devel. 1999;70:1181–1196. doi: 10.1111/1467-8624.00086. [DOI] [PubMed] [Google Scholar]
- Nowinski J, Baker S. The Twelve-Step Facilitation Handbook: A Systematic Approach to Early Recovery From Alcoholism and Addiction. San Francisco, CA: Jossey-Bass; 1992. [Google Scholar]
- Nowinski J, Baker S, Carroll K. NIAAA Project MATCH Monograph Series, Vol. 1, DHHS Publication No. (ADM) 92–1893. Washington: Government Printing Office; 1992. Twelve Step Facilitation Manual: A Clinical Research Guide for Therapists Treating Individuals with Alcohol Abuse and Dependence. [Google Scholar]
- Project MATCH Research Group. Project MATCH: Rationale and methods for a multisite clinical trial matching patients to alcoholism treatment. Alcsm Clin Exp Res. 1993;17:1130–1145. doi: 10.1111/j.1530-0277.1993.tb05219.x. [DOI] [PubMed] [Google Scholar]
- Project MATCH Research Group. Matching alcoholism treatments to client heterogeneity: Project MATCH posttreatment drinking outcomes. J Stud Alcohol. 1997;58:7–29. [PubMed] [Google Scholar]
- Project MATCH Research Group. A study to remember: Response of the Project MATCH Research Group. Addiction. 1999;94:66–69. [PubMed] [Google Scholar]
- Ramaswamy V, DeSarbo WS, Reibstein DJ, Robinson WT. An empirical pooling approach for estimating marketing mix elasticities with PIMS data. Market Sci. 1993;12:103–124. [Google Scholar]
- Rice C, Longabaugh R. Measuring general social support in alcoholic patients: Short forms for perceived social support. Psychol Addict Behav. 1996;10:104–114. [Google Scholar]
- San L. Future research directions and the impact of the MATCH project on research technology in the addictions. Addiction. 1999;94:55–57. [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimension of a model. Ann Stat. 1978;6:461–464. [Google Scholar]
- Spitzer RL, Williams JB. Structured Clinical Interview for DSM-III-R, Patient Version (SCID-P) New York: Biometrics Research Department, New York State Psychiatric Institute; 1988. [Google Scholar]
- Tonigan JS, Connors GJ, Miller WR. The Alcoholics Anonymous Involvement (AAI) scale: Reliability and norms. Psychol Addict Behav. 1996;10:75–80. [Google Scholar]
- Witkiewitz K, van der Maas HLJ, Hufford MR, Marlatt GA. Nonnormality and divergence in posttreatment alcohol use: Reexamining the Project MATCH data “another way”. J Abnorm Psychol. 2007;116:78–394. doi: 10.1037/0021-843X.116.2.378. [DOI] [PMC free article] [PubMed] [Google Scholar]