Skip to main content
PMC home page
Journal of Synchrotron Radiation logoLink to Journal of Synchrotron Radiation
. 2008 Nov 27;16(Pt 1):43–47. doi: 10.1107/S090904950803464X

Hard X-ray phase-contrast imaging with the Compact Light Source based on inverse Compton X-rays

Martin Bech a,*, Oliver Bunk b, Christian David b, Ronald Ruth c,d, Jeff Rifkin c, Rod Loewen c, Robert Feidenhans’l a, Franz Pfeiffer b,e,*
PMCID: PMC2724997  PMID: 19096173

First X-ray phase-contrast imaging results recorded at the Compact Light Source, a laboratory-based inverse Compton X-ray source, are reported.

Keywords: medical X-ray imaging, phase contrast, inverse Compton X-rays

Abstract

The first imaging results obtained from a small-size synchrotron are reported. The newly developed Compact Light Source produces inverse Compton X-rays at the intersection point of the counter propagating laser and electron beam. The small size of the intersection point gives a highly coherent cone beam with a few milliradian angular divergence and a few percent energy spread. These specifications make the Compact Light Source ideal for a recently developed grating-based differential phase-contrast imaging method.

1. Introduction

For more than a hundred years X-rays have been used for medical purposes. X-ray imaging has played a key role in medical diagnosis since the discovery of X-rays in 1895 by Röntgen, and the invention of the CAT scanner for which Hounsfield and Cormack received the Nobel prize in 1972. All modern medical X-ray imaging devices are based on the attenuation through photoelectric absorption of the X-rays penetrating the specimen to be imaged. However, for soft tissue with little absorption, this provides poor contrast. It is well known that X-ray imaging of soft tissue, e.g. mammography screenings, provides little contrast compared with bone images. This problem of low absorption contrast in soft tissue can be overcome with phase-contrast imaging (Fitzgerald, 2000 ▶; Momose, 2005 ▶).

During the last few decades several imaging techniques have been developed based on the phase shift of X-ray waves owing to refraction (Bonse & Hart, 1965 ▶; Ingal & Beliaev­skaya, 1995 ▶; Davis et al., 1995 ▶; Momose et al., 1996 ▶; Wilkins et al., 1996 ▶; Nugent et al., 1996 ▶). Though the specific requirements are different for the techniques, the X-ray source for medical X-ray phase-contrast imaging must fulfill two requirements: there must be some degree of spatial and temporal coherence, and the beam must be large enough to cover a reasonable field of view.

A standard X-ray tube can be used for phase-contrast imaging by grating interferometry (Pfeiffer et al., 2006 ▶, 2008 ▶), and, at X-ray tubes with a fine focus, it is possible to perform propagation-based phase-contrast imaging (Wilkins et al., 1996 ▶; Nugent et al., 1996 ▶). The grating-based method for phase-contrast imaging with standard X-ray tubes is, however, limited by loss of visibility owing to the broad spectrum of the X-ray tube, and, as the propagation-based phase-contrast imaging relies on high-resolution detectors to measure the Laplacian of the phase, it is thus limited in the field of view and does not supply dark-field images (Pfeiffer et al., 2008 ▶).

The best results for high-resolution and high-sensitivity phase-contrast applications are obtained on brilliant and narrow band-pass X-ray sources (Momose et al., 2003 ▶, 2006 ▶; Weitkamp et al., 2005 ▶; Tafforeau et al., 2006 ▶; Pfeiffer, Bunk et al., 2007 ▶; David, Weitkamp et al., 2007 ▶). Third-generation synchrotron radiation sources certainly offer the necessary beam quality and brilliance, but they are far too costly and they are incompatible with a clinical environment. The Compact Light Source (CLS) fulfills both requirements mentioned above, and thus is a promising source for future clinical X-ray phase-contrast imaging applications.

In this paper we will present the first phase-contrast images made with the CLS and show that differential phase-contrast imaging based on a grating interferometer is ideally matched to the CLS X-ray beam.

2. The Compact Light Source

The CLS is a miniature synchrotron for the conventional laboratory developed by Lyncean Technologies Inc. Whereas the insertion devices such as undulators and wigglers on third-generation synchrotron radiation facilities are built with permanent magnets, the CLS produces X-rays in the field of an intense laser undulator [inverse Compton scattering (Huang & Ruth, 1998 ▶)]. The characteristic parameters for undulator radiation are γ (electron energy in units of rest mass) and λu (spatial period of undulator). The fundamental wavelength of X-rays emitted from a magnetic undulator is λu/2γ2 (Als-Nielsen & McMorrow, 2001 ▶), and for magnetic undulators λu is typically a few centimeters, so γ needs to be of the order of 104 to reach a fundamental wavelength in the range of an angstrom. The fundamental wavelength for a laser undulator is λu/4γ2 (Loewen, 2003 ▶), and as the laser undulator at the CLS has a wavelength of ∼1 µm we only need γ ≃ 50 to obtain a fundamental wavelength in the angstrom range. For this reason the electron energy is two orders of magnitude lower than at large-scale synchrotron facilities. This allows the CLS storage ring to be scaled down to a few meters in circumference, making it feasible for use in a conventional laboratory or for clinical use.

The beam divergence of the CLS is much larger than at normal synchrotrons (Loewen, 2003 ▶). This is an advantage in imaging, as a larger field of view can be obtained at shorter source-to-sample distances. In the current set-up, the CLS is operated at an electron energy of 25 MeV, i.e. at γ = 50 and with the beam collimated to α = 4 mrad, giving a roughly circular beam size of diameter 4 cm at 10 m from the source. The X-ray aperture can be opened to increase the beam size by trading off bandwidth, up to a maximum α ≃ 1/γ. For large apertures the angular energy distribution is such that the X-ray energy is high in the forward direction, and falls off with increasing angle, giving a lower E peak at the edges than in the center of the detector. As will be discussed in the Results section of this paper, an energy distribution will have little effect on the image quality.

3. Grating interferometer

In this set-up we have used a grating interferometer for differential phase-contrast imaging as described in detail elsewhere (Momose et al., 2003 ▶; Weitkamp et al., 2005 ▶; David, Bruder et al., 2007 ▶; David, Weitkamp et al., 2007 ▶; Pfeiffer, Kottler et al., 2007 ▶). Two gratings are placed between sample and detector as illustrated in Fig. 1 ▶: a phase grating G1 and an absorption grating G2. A number of images are recorded while stepping the absorption grating transversely over a grating period. This will be referred to as phase stepping. If the phase shift of grating G1 is π, the distance between the gratings must be a fractional Talbot distance d T (Weitkamp et al., 2005 ▶; Momose et al., 2006 ▶). In the case of a parallel beam, d T is given by

3.

where g 1 is the period of grating G1, λ is the wavelength and n is an odd integer. The pitch of G2 should be half that of G1, g 1 = 2g 2. However, in the case of a diverging beam, a magnification occurs along the beam, and a magnification factor must be included in the equations (Engelhardt et al., 2007 ▶),

3.
3.

where L is the distance from the source to G1. For a given set of gratings, these equations can be solved to give values for d T and L. For each pixel the intensity variations during a phase-stepping period are recorded and the changes induced by the specimen are evaluated (Pfeiffer et al., 2008 ▶). From the pixel intensity variations in one data set, both absorption contrast (intensity average) and phase contrast (intensity variation shift) can be extracted, and used for three-dimensional tomographical reconstructions (Pfeiffer, Kottler et al., 2007 ▶). Furthermore, the interference visibility V = (I max − I min)/(I max + I min) provides information on the local coherence of the wavefront (Pfeiffer et al., 2005 ▶), giving an image signal comparable with a dark-field image showing scattered photons (Pfeiffer et al., 2008 ▶). Thus one data set can be processed to give three contrast signals that can be plotted individually as images: a standard absorption image, a differential phase-contrast image and a dark-field image. This is illustrated in Fig. 2 ▶.

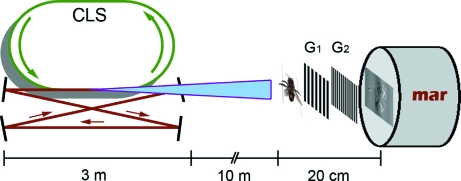
Figure 1.

Figure 1

Open in a new tab

Sketch of the experimental set-up (not to scale). To the left is the Compact Light Source with an electron storage ring and a laser cavity. A conical X-ray beam is produced at the electron–laser intersection point, shining onto the sample. The grating interferometer to the right consists of two gratings, G1 and G2, and a MAR CCD detector.

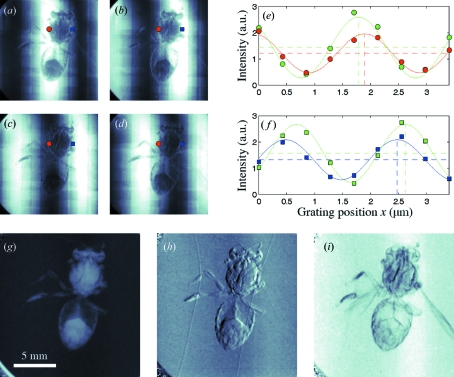
Figure 2.

Figure 2

Open in a new tab

X-ray images of a bee and pixel intensity variations. (a)–(d) Raw images during phase stepping. (e)–(f) Intensity plot of two detector pixels during phase stepping. The green plot is from the flat-field data (without sample present), red and blue plots are with sample present corresponding to the intensity in the red and blue pixels in (a)–(d). Panels (g)–(i) show the three types of contrast obtained from data processing: (g) standard absorption image, (h) differential phase-contrast image, (i) dark-field image.

4. Experiment

For this experiment we have used a grating system consisting of a phase grating G1 with 3.99 µm pitch, and an absorption grating G2 with 2.00 µm pitch. The two gratings have an area of 15 mm × 15 mm, thus limiting the field of view to this area. The distance d T = 22 mm between the two gratings corresponds to the first fractional Talbot distance, n = 1 in equation (2) when L = 8.65 m and λ = 0.92 Å. The CLS was operated at an X-ray energy of E peak = 13.5 keV (λpeak = 0.92 Å), with a full energy spread of ΔE/E peak = 3%. The effective X-ray source size was 70 µm RMS corresponding to 165 µm FWHM, and the angular divergence of the X-ray beam was limited to ±2 mrad by a cylindrical aperture. For each data set, nine phase steps were performed over two grating periods, yielding nine images from which the absorption, differential phase, and dark-field signals were calculated. Each image was recorded with an exposure time of 100 s, hence the total exposure time was 900 s per data set. (We note that the exposure time of 100 s per image, as used for this proof-of-principle experiment, is obviously too long for practical applications. However, provided that the CLS reaches its final design specifications, the total exposure could be reduced to below 1 s.) All images were recorded using a MAR CCD detector with square pixels of size 78 µm × 78 µm.

5. Results

Figs. 2(a)–2(d) ▶ display the first four images of a nine-step phase-stepping series. Two pixels have been marked, and the intensity of these pixels have been plotted in Fig. 2(e) (red circles) and Fig. 2(f) ▶ (blue squares). The three types of contrast are obtained from the components of the Fourier series of measured intensity as a function of grating position. The relevant signals are extracted from the amplitude and phase of the first two Fourier components. The Fourier series of the measured intensity I as a function of grating displacement x can be written as

5.

We are interested in determining the average value a 0, the fringe position shift ϕ1 and the fringe depth a 1. As we perform nine phase steps, and the fringe profile is sufficiently sinusoidal, terms of order n ≥ 2 can be ignored (Momose et al., 2006 ▶) and the equation will read

5.

where the average value a 0 (horizontal dashed line) corresponds to the total transmission in this pixel, the shift ϕ1 (vertical dashed line) corresponds to the differential phase shift, and the modulation amplitude a 1 corresponds to the dark-field signal. In practice the Fourier components a 0, ϕ1 and a 1 are extracted from the data by use of a fast Fourier transform. To take into account the local intensity, curvature, and coherence of the X-ray beam, the raw data are compared with a set of flat-field images with no sample present. The green data points in Figs. 2(e) and 2(f) ▶ are flat-field data. Comparing the sample data with the flat-field data gives the effect on the wavefront caused by the sample. The images obtained from plotting the relative absorption, phase shift, and visibility are shown in Figs. 2(g), 2(h) and 2(i) ▶, referred to as standard absorption (g), differential phase-contrast (h), and dark-field image (i).

A number of different samples have been imaged using the differential phase-contrast technique at the CLS. Fig. 3 ▶ shows three images of a moth obtained from one data set: (a) absorption contrast, (b) differential phase-contrast and (c) dark-field image. The arrows point to two regions where the two new types of image contrast reveals details that are very difficult to see on the standard absorption image. One arrow points to a fishing wire (Fig. 3b ▶) used for suspending the moth, the other arrow points to the leg of the moth (Fig. 3c ▶). Obviously the wings of the moth show up nicely in the dark-field image. It is clearly shown here that the three types of contrast supplement each other well, as each image shows details different from the others.

Figure 3.

Figure 3

Open in a new tab

Three types of image contrast of a moth after data processing. (a) Standard absorption-contrast image. (b) Differential phase-contrast image. (c) Dark-field image. All three images are obtained from the same data set. Arrows indicate regions where the phase-contrast and dark-field images reveal details not visible on the standard X-ray image.

5.1. Beam quality

In the theoretical case of a parallel monochromatic X-ray beam and a perfect absorption-free phase grating giving a π phase-shift, the visibility of the interference pattern created at the first fractional Talbot distance d T would be 100%. However, in practice the visibility is somewhat lower owing to optical limitations such as beam coherence and grating imperfections. The effect of a finite transverse coherence length l c on the expected fringe visibility has been calculated elsewhere (Weitkamp et al., 2006 ▶) to be

5.1.

where n is the fractional Talbot number and g 2 is the grating pitch from equations (2) and (3). The coherence length l c is defined as l c = λL/s, where s is the FWHM of an assumed Gaussian source. In the current set-up we have λ = 0.92 Å, n = 1, g 2 = 2 µm and s = 165 µm, giving a transverse coherence length of l c = 4.8 µm. Inserting these numbers into equation (6) results in an expected visibility of 86%.

On top of the visibility loss owing to a finite transverse coherence length comes losses owing to longitudinal coherence (spectral width) and grating imperfections. When operating at the first fractional Talbot distance, a very broad spectral width is allowed without significant loss of interference visibility. The accepted bandwidth is given by Δλ/λ ≤ 1/n (Weitkamp et al., 2005 ▶). Clearly the 3% bandwidth of the CLS is well below this requirement, and hence this does not limit the interference visibility.

The gratings used for this experiment were of high quality and caused no significant reduction to the visibility. From the images shown in Fig. 2 ▶, a fringe visibility of ∼80% has been calculated. This is in good agreement with the expected value of 86%. The slightly decreased visibility may be caused by the fact that our phase grating G1 had a height of 19.2 µm, corresponding to a π phase-shift at 15 keV X-ray energy, not 13.5 keV, which was the actual energy used. Though this gives rise to a non-perfect interference pattern, it illustrates the very important fact that good visibility can be achieved at the edges of a larger beam where the X-ray energy is decreased, thus allowing the CLS to be used for grating-based phase-contrast imaging with large fields of view.

It should be noted here that the visibility of interference patterns recorded in a similar way at an X-ray tube source is considerably lower owing to the larger energy bandwidth of the polychromatic X-ray bremsstrahlung spectrum and the fact that three, instead of two, gratings have to be used with low-brilliance sources.

6. Outlook

We conclude that the Compact Light Source in combination with grating-based X-ray phase-contrast imaging has the potential to yield images of a quality previously only obtained at large-scale synchrotron radiation facilities. The small size and low cost of the CLS makes it feasible to install it in hospitals and laboratories, with all of the advantages that phase-contrast and dark-field X-ray images can offer. We believe that such an instrument could provide the required image sensitivity and resolution for improved detection of breast carcinomas in mammography applications (Fiedler et al., 2004 ▶; Pisano et al., 2000 ▶; Arfelli et al., 2007 ▶), better differentiation of materials in security screening applications (Pfeiffer et al., 2008 ▶; Harding, 2004 ▶), or biomedical investigations of tumor growth morphology in brains (Pfeiffer, Bunk et al., 2007 ▶; Risser et al., 2007 ▶). In addition, phase-contrast and scattering-based methods may permit a significant reduction in dose per image, since they do not rely on the absorption of an X-ray for the creation of contrast.

Acknowledgments

The authors would like to thank Jens Als-Nielsen for fruitful discussions. Lyncean Technologies Inc would like to thank Rayonix, LLC, for the loan of the marCCD 165 detector. The Compact Light Source is supported by the Protein Structure Initiative, National Institute of General Medical Sciences, grants: R44 GM 66511, R44 GM 074437, and National Institute of General Medical Sciences/National Center for Research Resources, grant U54-GM074961. These contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIGMS or NCRR.

References

  1. Als-Nielsen, J. & McMorrow, D. (2001). Elements of Modern X-ray Physics. New York: John Wiley and Sons.
  2. Arfelli, F. et al. (2007). AIP Conf. Proc.879, 1895–1898.
  3. Bonse, U. & Hart, M. (1965). Appl. Phys. Lett.6, 155–156.
  4. David, C., Bruder, J., Rohbeck, T., Grunzweig, C., Kottler, C., Diaz, A., Bunk, O. & Pfeiffer, F. (2007). Microelectron. Eng.84, 1172–1177.
  5. David, C., Weitkamp, T., Pfeiffer, F., Diaz, A., Bruder, J., Rohbeck, T., Groso, A., Bunk, O., Stampanoni, M. & Cloetens, P. (2007). Spectrochim. Acta B, 62, 626–630.
  6. Davis, T. J., Gao, D., Gureyev, T. E., Stevenson, A. W. & Wilkins, S. W. (1995). Nature (London), 373, 595–598.
  7. Engelhardt, M., Baumann, J., Schuster, M., Kottler, C., Pfeiffer, F., Bunk, O. & David, C. (2007). Appl. Phys. Lett.90, 224101.
  8. Fiedler, S., Bravin, A., Keyrilainen, J., Fernandez, M., Suortti, P., Thomlinson, W., Tenhunen, M., Virkkunen, P. & Karjalainen-Lindsberg, M. L. (2004). Phys. Med. Biol.49, 175–188. [DOI] [PubMed]
  9. Fitzgerald, R. (2000). Phys. Today, 53, 23–26.
  10. Harding, G. (2004). Radiat. Phys. Chem.71, 869–881.
  11. Huang, Z. & Ruth, R. D. (1998). Phys. Rev. Lett.80, 976–979.
  12. Ingal, V. & Beliaevskaya, E. (1995). J. Phys. D, 28, 2314–2317.
  13. Loewen, R. J. (2003). A Compact Light Source: Design and Technical Feasibility Study of a Laser-Electron Storage Ring X-ray Source. SLAC Report 632, Stanford University, USA.
  14. Momose, A. (2005). Jpn. J. Appl. Phys.44, 6355–6367.
  15. Momose, A., Kawamoto, S., Koyama, I., Hamaishi, Y., Takai, K. & Suzuki, Y. (2003). Jpn. J. Appl. Phys.42, L866–L868.
  16. Momose, A., Takeda, T., Itai, Y. & Hirano, K. (1996). Nat. Med.2, 473–475. [DOI] [PubMed]
  17. Momose, A., Yashiro, W., Takeda, Y., Suzuki, Y. & Hattori, T. (2006). Jpn. J. Appl. Phys.45, 5254–5262.
  18. Nugent, K. A., Gureyev, T. E., Cookson, D. F., Paganin, D. & Barnea, Z. (1996). Phys. Rev. Lett.77, 2961–2964. [DOI] [PubMed]
  19. Pfeiffer, F., Bech, M., Bunk, O., Kraft, P., Eikenberry, E. F., Brönnimann, C., Grünzweig, C. & David, C. (2008). Nat. Mater.7, 134–137. [DOI] [PubMed]
  20. Pfeiffer, F., Bunk, O., David, C., Bech, M., Duc, G. L., Bravin, A. & Cloetens, P. (2007). Phys. Med. Biol.52, 6923–6930. [DOI] [PubMed]
  21. Pfeiffer, F., Bunk, O., Schulze-Briese, C., Diaz, A., Weitkamp, T., David, C., van der Veen, J. F., Vartanyants, I. & Robinson, I. K. (2005). Phys. Rev. Lett.94, 164801. [DOI] [PubMed]
  22. Pfeiffer, F., Kottler, C., Bunk, O. & David, C. (2007). Phys. Rev. Lett.98, 108105. [DOI] [PubMed]
  23. Pfeiffer, F., Weitkamp, T., Bunk, O. & David, C. (2006). Nat. Phys.2, 258–261.
  24. Pisano, E. D., Johnston, R. E., Chapman, D., Geradts, J., Iacocca, M. V., Livasy, C. A., Washburn, D. B., Sayers, D. E., Zhong, Z., Kiss, M. Z. & Thomlinson, W. C. (2000). Radiology, 214, 895–901. [DOI] [PubMed]
  25. Risser, L., Plouraboue, F., Steyer, A., Cloetens, P., Duc, G. L. & Fonta, C. (2007). J. Cerebr. Blood F. Met.27, 293–303. [DOI] [PubMed]
  26. Tafforeau, P. et al. (2006). Appl. Phys. A, 83, 195–202.
  27. Weitkamp, T., David, C., Kottler, C., Bunk, O. & Pfeiffer, F. (2006). Proc. SPIE, 6318, 631828.
  28. Weitkamp, T., Diaz, A., David, C., Pfeiffer, F., Stampanoni, M., Cloetens, P. & Ziegler, E. (2005). Opt Express, 12, 6296–6304. [DOI] [PubMed]
  29. Wilkins, S. W., Gureyev, T. E., Gao, D., Pogany, A. & Stevenson, A. W. (1996). Nature (London), 384, 335–337.

Articles from Journal of Synchrotron Radiation are provided here courtesy of International Union of Crystallography

RESOURCES