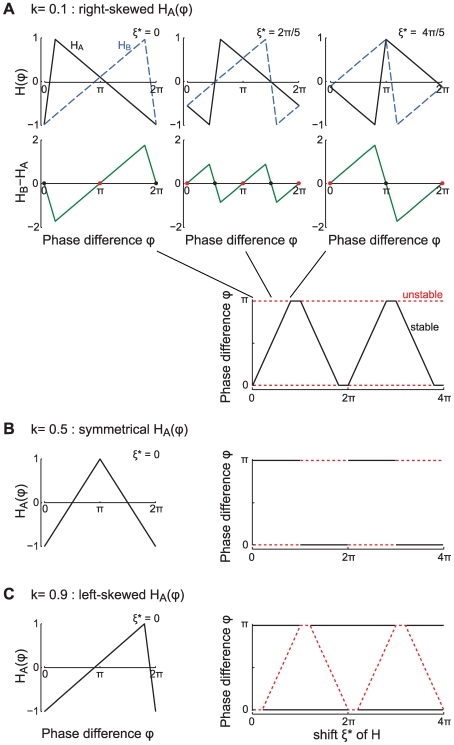
Figure 3. 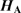skewness controls phase-locking regimes and transitions.

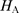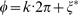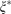The three panels A-B-C show triangular functions with different skewness with their peaks at where is a phase shift that results from the cable coupling. The oscillators are identical so that 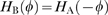. A: Right-skewed 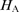with 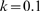(solid black line) plotted from left to right for three values of 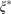together with the corresponding 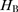(dashed blue line). Below each graph is plotted (green lines) with the stable (black dots) and unstable (red dots) phase-locked solutions. The lower right panel shows the bifurcation diagram with the stable (solid black line) and unstable (dotted red line) phase-locked solutions. The right-skewed 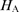yields gradual transitions between the in-phase and anti-phase solutions. B: Symmetrical 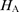with 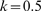yields abrupt transitions between in-phase and anti-phase solutions. C: Left-skewed 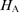with 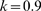yields bistable regions where both the in-phase and the anti-phase solution are stable.