Incorporating model quality information in climate change detection and attribution studies

Abstract

In a recent multimodel detection and attribution (D&A) study using the pooled results from 22 different climate models, the simulated “fingerprint” pattern of anthropogenically caused changes in water vapor was identifiable with high statistical confidence in satellite data. Each model received equal weight in the D&A analysis, despite large differences in the skill with which they simulate key aspects of observed climate. Here, we examine whether water vapor D&A results are sensitive to model quality. The “top 10” and “bottom 10” models are selected with three different sets of skill measures and two different ranking approaches. The entire D&A analysis is then repeated with each of these different sets of more or less skillful models. Our performance metrics include the ability to simulate the mean state, the annual cycle, and the variability associated with El Niño. We find that estimates of an anthropogenic water vapor fingerprint are insensitive to current model uncertainties, and are governed by basic physical processes that are well-represented in climate models. Because the fingerprint is both robust to current model uncertainties and dissimilar to the dominant noise patterns, our ability to identify an anthropogenic influence on observed multidecadal changes in water vapor is not affected by “screening” based on model quality.

Since the mid-1990s, pattern-based “fingerprint” studies have been the primary and most rigorous tool for disentangling the complex causes of recent climate change (1–3). Fingerprinting relies on numerical models of the climate system to provide estimates of both the searched-for fingerprint—the pattern of climate response to a change in one or more forcing mechanisms—and the background “noise” of natural internal climate variability. To date, most formal detection and attribution (D&A) work has used information from only one or two individual models to estimate both the fingerprint and noise (4–6). Relatively few D&A studies have used climate data from three or more models (7–13).

The availability of large, multimodel archives of climate model output has had important implications for D&A research. A prominent example of such an archive is the CMIP-3 (Coupled Model Intercomparison Project) database, which was a key resource for the Fourth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC) (14). The CMIP-3 archive enables D&A practitioners to use information from two dozen of the world's major climate models and to examine the robustness of D&A results to current uncertainties in model-based estimates of climate-change signals and natural variability noise (10–13).

Multimodel databases offer both scientific opportunities and challenges. One challenge is to determine whether the information from each individual model in the database is equally reliable, and should be given equal “weight” in a multimodel D&A study, or in estimating some “model average” projection of future climate change (15). Previous multimodel D&A investigations with atmospheric water vapor (10) and sea-surface temperatures (SSTs) in hurricane formation regions (13) adopted a “one model, one vote” approach, with no attempt made to weight or screen models based on their performance in simulating aspects of observed climate. An important and hitherto unexplored question, therefore, is whether the findings of such multimodel D&A studies are sensitive to model weighting or screening decisions.

To address this question, objective measures of model performance are required. An obvious difficulty is that model errors are highly complex; they depend on the variable considered, the space and timescale of interest, the statistical metric used to compare modeled and observed climatic fields, the exact property of the fields that is being considered (e.g., mean state, diurnal or annual cycle, amplitude and structure of variability, and evolution of patterns), and uncertainties in the observations themselves (16–22). Recent assessments of the overall performance of CMIP-3 models have relied on a variety of statistical metrics and were primarily focused on how well these models reproduce the observed climatological mean state (23, 24).*

Here, we revisit our multimodel D&A study with atmospheric water vapor over oceans (10). We calculate a number of different “model quality” metrics and demonstrate that use of this information to screen models does not affect our ability to identify an externally forced fingerprint in satellite data.

Observational and Model Water Vapor Data

We rely on observational water vapor data from the satellite-based Special Sensor Microwave Imager (SSM/I). The SSM/I atmospheric moisture retrievals commenced in late 1987 and are based on measurements of microwave emissions from the 22-GHz water vapor absorption line (25–27). Retrievals are unavailable over the highly emissive land surface and sea-ice regions. Our focus is therefore on W, the total column water vapor over oceans for a near-global domain.^†

As noted above, fingerprint studies require estimates of both the climate-change signal in response to external forcing and the noise of internal climate variability. We obtain signal estimates from simulations with historical changes in natural and anthropogenic forcings (“20CEN” runs) and noise information from control integrations with no forcing changes.^‡ We use 20CEN and control integrations from 22 different climate models in the CMIP-3 archive. These are the same models that were used in our original water vapor D&A study (10).

Strategy for Assessment of Model Quality

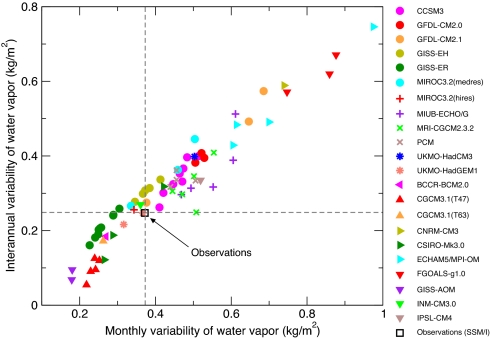
Fig. 1 illustrates why it may be useful to include model quality information in multimodel D&A studies. The figure shows the simulated and observed temporal standard deviation of 〈W〉, the spatial average of atmospheric water vapor over near-global oceans.^§ Results are given for monthly and interannual-timescale fluctuations in 〈W〉. On both timescales, the simulated variability in 20CEN runs ranges from one-third to two-and-a-half times the amplitude of the observed variability.

Fig. 1.

Comparison of the simulated and observed temporal variability of atmospheric water vapor. Observations are from the SSM/I dataset (25, 26); model data are from 71 realizations of 20th century climate change performed with 22 different models (see SI Appendix). All variability calculations rely on monthly mean values of 〈W〉, the spatial average of total atmospheric moisture over near-global oceans. Model and observational 〈W〉 data were first expressed as anomalies relative to climatological monthly means over the period 1988–1999 and then linearly detrended. We computed temporal standard deviations from both the unfiltered and filtered anomaly data. The latter were smoothed by using a filter with a half-power point at ≈2 years. The raw and filtered standard deviations provide information on monthly and interannual-timescale variability, respectively. All calculations were over the 144-month period from January 1988 to December 1999 (the period of maximum overlap between the SSM/I data and most 20CEN simulations). The dashed gray lines are centered on the observations.

Are such variability differences between models and observations of practical importance in multimodel D&A studies? Most D&A studies routinely apply some form of statistical test to check the consistency between observed residual variability (after removal of an estimated externally forced signal) and model control run variability (4, 7–13), and many studies compare power spectra of the observed and modeled variables being analyzed (12, 13). Our focus here is not on formal statistical tests or spectral density comparisons; instead, it is calculating metrics that provide more direct information regarding the fidelity with which models simulate the amplitude and structure of key modes of natural internal variability.

Although our D&A study involves water vapor only, we compute performance metrics for water vapor and SST. We examine SST data because observed SST datasets are 130–150 yr in length and therefore provide a better constraint on model-based estimates of decadal variability than the short (21-yr) SSM/I record. Information on low-frequency variability is crucial for D&A applications, because it constitutes the background noise against which we attempt to identify a slowly evolving anthropogenic signal. All SST-based model quality metrics were calculated using observations from the NOAA Extended Reconstructed SST (ERSST) dataset (28).

We evaluate model performance in simulating W and SST in five different regions. The first is the 50°N–50°S ocean domain used in our previous water vapor D&A work. The next three regions were chosen because they provide information on model errors in simulating three characteristic modes of natural climate variability: the El Niño/Southern Oscillation (ENSO), the Pacific Decadal Oscillation (PDO), and the Atlantic Multidecadal Oscillation (AMO).^¶ The final region comprises tropical oceans (30°N–30°S) and is of interest because of claims that modeled and observed atmospheric temperature changes differ significantly in the tropics.

We analyze model performance in simulating the mean state, annual cycle, and amplitude and structure of variability.^‖ There are 10 mean state diagnostics (two variables × five regions). Each mean state metric is simply a measure of the absolute value of the climatological annual-mean model bias. The 10 annual cycle diagnostics involve the correlations between the simulated and observed climatological mean annual cycle patterns. The 50 variability metrics** are measures of model skill in simulating the amplitude and pattern of observed variability on monthly, interannual, and decadal timescales. The rationale for examining model performance on different timescales is that model variability errors are complex and frequency-dependent (29).

All 70 metrics are normalized by the intermodel standard deviation of the statistical property being considered. This allows us to combine information from the mean, annual cycle, and variability metrics as well as from different climate variables and geographical regions. Details regarding the definition and calculation of our model performance metrics are given in the supporting information (SI) Appendix.

Results from Model Quality Assessment

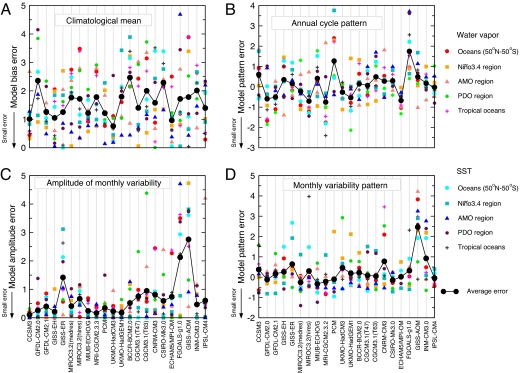
Results for 40 of the 70 individual metrics are shown in Fig. 2. To illustrate the complexity of model errors, we use the example of the UKMO-HadCM3 model (developed at the UK Meteorological Office Hadley Centre). Consider first the results for the absolute bias in the climatological mean state (Fig. 2A). HadCM3 has relatively small bias values for both water vapor and SST, except for SSTs in the PDO region. When models are ranked parametrically on the basis of the “average error” results in Fig. 2A, HadCM3 has the lowest bias values and is therefore ranked first.

Fig. 2.

Results for four different sets of metrics used in the ranking of model performance. The statistics are measures of how well 22 of the models in the CMIP-3 database reproduce key features of observed water vapor and SST behavior in five different geographical regions. The metrics shown here are a subset of the full suite of metrics that we applied for model ranking, and are for the mean state (A), annual cycle pattern (B), amplitude of monthly variability (C), and pattern of monthly variability (D). For models with multiple 20CEN realizations, values of metrics are averaged over realizations. The black dots labeled “average error” represent the arithmetic average (for each model) of the 10 metric values (2 variables × 5 regions). (A and C) Small values of the normalized metrics indicate greater skill in simulating the mean state and the amplitude of monthly variability. (B and D) Negative values of the normalized pattern correlation metrics denote greater skill in simulating the annual cycle and monthly variability patterns.

In terms of its simulation of the climatological annual cycle pattern (Fig. 2B) and the amplitude of monthly variability (Fig. 2C), HadCM3 also performs well relative to its peers and is ranked seventh and fifth, respectively. For the monthly variability pattern, however, HadCM3 has a large error for water vapor in the PDO region (Fig. 2D). This one component has a marked influence on HadCM3's low overall ranking (18th) for the monthly variability pattern. For interannual and decadal variability (not shown), HadCM3 ranks 10th and first in terms of its variability amplitude and 15th and 14th in terms of its variability pattern. As is clear from the HadCM3 example and the other model results in Fig. 2, assessments of the relative skill of the CMIP-3 models are sensitive to a variety of analyst choices.

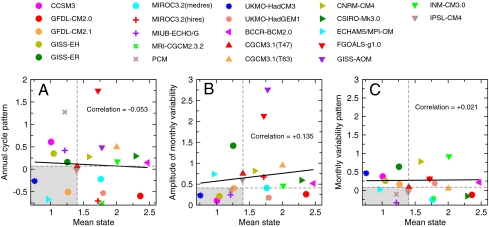
This message is reinforced in Fig. 3, which shows that for our selected variables, regions, and diagnostics, there are no statistically significant relationships between model skill in simulating the climatological mean state and model skill in capturing either the observed annual cycle or the amplitude and pattern of monthly variability. Similar findings have been obtained in related studies (19, 20, 22, 23). One possible interpretation of this result is that the spatial averages of observed climatological annual means provide a relatively weak constraint on overall model performance. Modeling groups attempt to reduce biases in these large-scale climatological averages by adjusting poorly known physical parameters (and by flux correction, which still is used in several of the CMIP-3 models). Observed annual cycle and variability patterns offer more stringent tests of model performance. Reliable reproduction of these more challenging observational targets is difficult to achieve through tuning alone—accurate representation of the underlying physics is of greater importance.

Fig. 3.

Relationship between model skill in simulating the mean state and skill in simulating the annual cycle pattern (A), amplitude of monthly variability (B), and monthly variability pattern (C). Results plotted are the “average errors” shown and described in Fig. 2. The black lines are the fitted least-squares regression lines. Models to the left of the vertical dashed gray line are ranked in the top 10 based on values of the mean state metric α̂. Models below the horizontal dashed gray line are ranked in the top 10 based on values of the annual cycle pattern metric β̂ (A), the variability amplitude metric φ̂ (B), and the variability pattern metric ϕ̂ (C). The gray shaded region indicates the intersection of the two sets of top 10 models plotted in each graph.

The final stage in our model quality assessment is to combine information from different performance metrics, which we accomplish in three different ways. The three combinations involve the 10 mean state and 10 annual cycle diagnostics (M+AC), the 25 variability amplitude and 25 variability pattern metrics (VA+VP), and the 70 mean state, annual cycle, and variability diagnostics (ALL). Individual values of these metrics are averaged, yielding the Q̂₁, Q̂₂, and Q̂₃ statistics, which are used for the parametric ranking of the CMIP-3 models (see SI Appendix). The nonparametric rank is simply the average of the individual ranks rather than the average of individual metric values.

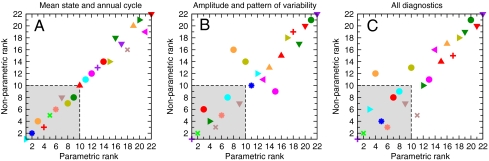
The overall ranking results are shown in Fig. 4. A number of interesting features are evident. First, only three models (MRI-CGCM2.3.2, UKMO-HadGEM1, and IPSL-CM4) are consistently ranked within the top 10 CMIP-3 models based on both ranking approaches and all three sets of performance criteria (M+AC, VA+VP, and ALL). None of the top four models determined with the M+AC metrics (Fig. 4A) is also in the top four based on the VA+VP metrics (Fig. 4B). These results support our previous finding that assessments of model quality are sensitive to the choice of statistical properties used in model evaluation.

Fig. 4.

Parametric and nonparametric ranking of 22 CMIP-3 models. The parametric ranking is based on the Q̂₁, Q̂₂, and Q̂₃ statistics, which are (respectively) measures of model skill in simulating the observed mean state and annual cycle (A), the amplitude and pattern of variability (B), and the combined mean state, annual cycle, and variability properties (C). The Q̂₁, Q̂₂, and Q̂₃ statistics are averages of the normalized values of 20 mean state and annual cycle metrics (M+AC), 50 variability amplitude and variability pattern metrics (VA+VP), and 70 combined metrics (ALL). In the nonparametric ranking procedure, models are ranked from 1 to 22 for each of the 70 metrics, and the individual ranks are then averaged in each of the three groups of metrics (M+AC, VA+VP, and ALL). Full details of the statistics and ranking procedures are given in the SI Appendix. The gray shaded boxes indicate the intersection of the two sets of top 10 models. See Fig. 3 for key.

Second, there is also some sensitivity to the choice of ranking procedure, particularly for the VA+VP and ALL statistics (Fig. 4 B and C). In each of these two cases, the nonparametric and parametric ranking approaches identify slightly different sets of “top 10” models. Only 8 models are in the intersection of these sets.

Third, higher horizontal resolution does not invariably lead to improved model performance. The CMIP-3 archive contains two models (the Canadian Climate Centre's CGCM3.1 and the Japanese MIROC3.2) that were run in both higher- and lower-resolution configurations. The lower-resolution version of CGCM3.1 outperforms the higher-resolution version in terms of the M+AC diagnostics but not for the VA+VP metrics. The reverse applies to the MIROC3.2 model. The lack of a consistent benefit of higher resolution is partly due to our focus on temperature and moisture changes over oceans. The performance improvement related to higher resolution is more evident over land areas with complex topography (30).

Detection and Attribution Analysis

We now apply the same multimodel D&A method used by Santer et al. (10). Instead of employing all 22 CMIP-3 models in the D&A analysis, we restrict our attention to 10-member subsets of the 22 models. These subsets are determined by ranking models on the basis of the three different sets of metrics (M+AC, VA+VP, and ALL) and two different ranking approaches (parametric and nonparametric). From each of these six ranking sets, we select the top 10 and bottom 10 models, yielding 12 groups of 10 models.

Fingerprints are calculated in the following way. For each set of 10 models, we determine the multimodel average of the atmospheric moisture changes over the period 1900–1999.^†† The fingerprint is simply the first empirical orthogonal function (EOF) of the multimodel average changes in water vapor.

Because 10 modeling groups used anthropogenic forcings only, whereas the other 12 applied a combination of anthropogenic and natural external forcings (see SI Appendix), we expect the multimodel fingerprint to down-weight the contribution of natural external forcing to the fingerprint. However, previous work has found that the fingerprints estimated from combined historical changes in anthropogenic and natural external forcing are very similar to those obtained from “anthropogenic only” forcing (10). We infer from this that anthropogenic forcing is the dominant influence on the changes in atmospheric moisture over the 20th century and that the multimodel fingerprint patterns are not distorted by the absence of solar and volcanic forcing in 10 of the 22 models analyzed here.^‡‡

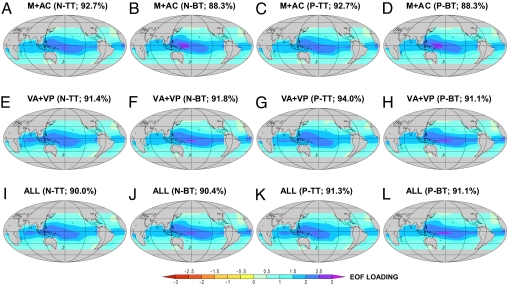
There is pronounced similarity between the fingerprint patterns estimated from the 12 subsets of CMIP-3 models (Fig. 5). All 12 patterns show spatially coherent water vapor increases, with the largest increases over the warmest ocean areas. There are no systematic differences between the fingerprints estimated from different sets of metrics, different ranking procedures, or from the top 10 or bottom 10 models. This indicates that the structure of the water vapor fingerprint is primarily dictated by the zero-order physics governing the relationship between surface temperature and column-integrated water vapor (25, 31).

Fig. 5.

Model fingerprints of externally forced changes in water vapor over near-global oceans. Fingerprints were estimated from 12 different 10-member sets of model 20CEN simulations, as described in Fig. 6 and the SI Appendix. The fingerprint is the leading EOF of the multimodel average change in water vapor over the 20th century. The first four fingerprints (A–D) were estimated from the top 10 (TT) and bottom 10 (BT) models, with nonparametric (N) and parametric (P) rankings based on the M+AC metrics (see Fig. 4). The fingerprints in E–H were estimated from models ranked with the VA+VP pattern statistics. The final four fingerprints (I–L) were calculated from models ranked with a combination of mean state, annual cycle, and variability metrics (ALL). All fingerprint calculations were performed on a common 10° × 10° latitude/longitude grid. The variance explained by the leading mode ranges from 88.3% to 94.0%.

For each of our 12 subsets of CMIP-3 models, estimates of natural internal variability are obtained by concatenating the 10 individual control runs of that subset, after first removing residual drift from each control (Fig. S1 in SI Appendix). The leading EOF patterns estimated from the concatenated control runs are remarkably similar. Each displays the horseshoe-shaped pattern characteristic of the effects of ENSO variability on atmospheric moisture (Fig. S2 in SI Appendix). Unlike the fingerprints, the leading noise modes have both positive and negative changes in water vapor.

The similarity of the noise modes in Fig. S2 occurs despite the fact that individual models can have noticeable differences in the spatial structure of their leading mode of water vapor variability (Fig. S3 in SI Appendix). One possible explanation for this result is that errors in the pattern of the dominant noise mode in individual models are quasirandom; these random error components are reduced when the leading noise mode is estimated from a sufficiently large number of concatenated model control runs (22).

The final step was to repeat the multimodel D&A analysis of Santer et al. (10) with updated SSM/I observations, 12 different fingerprints (Fig. 5), and 12 model-based noise estimates (Fig. S2 in SI Appendix). The D&A analysis was performed 144 times, using each possible combination of fingerprint and noise (Fig. 6). We do not employ any form of fingerprint optimization to enhance signal-to-noise (S/N) ratios (3–7, 10). Our D&A method is fully described in the SI Appendix.

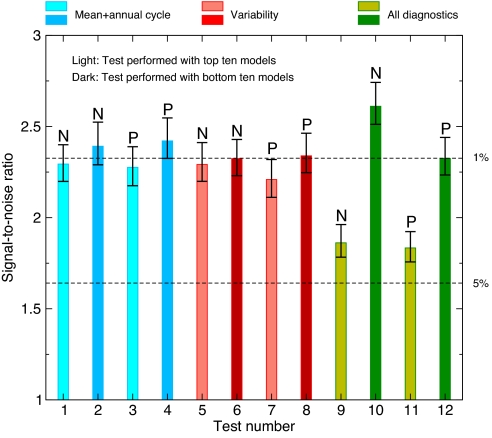
Fig. 6.

Sensitivity of S/N ratios to model quality information. As described in the text, 12 different sets of 10 models were used to calculate 12 externally forced fingerprints and 12 estimates of natural internal variability. The D&A analysis was then performed 144 times, with all possible combinations of fingerprint and noise. In “Test 1,” for example, the D&A analysis was run 12 times, each time with the same concatenated control runs (from the top 10 models determined with the M+AC metrics and nonparametric ranking), but with a different fingerprint (see Fig. 5). The height of each colored bar is the average of the 12 S/N values for the current test. The black error bars denote the maximum and minimum S/N ratios and are a measure of the effects of fingerprint uncertainty on S/N. The signal in the S/N ratio is the linear trend over the period 1988–2008 in Z(t), the projection of the SSM/I water vapor data onto the fingerprint estimated from the current 10-member set of 20CEN runs. The noise is the standard deviation of the sampling distribution of 21-year trends. This distribution is estimated by fitting nonoverlapping 21-year trends to N(t), the time series of the projection of the current set of 10 concatenated control runs onto the fingerprint. Detection of the externally forced fingerprint in observed data occurs when the S/N ratio exceeds and remains above a stipulated 5% significance threshold. The 1% significance threshold also is shown.

In each of the 144 cases, the model-predicted fingerprint in response to external forcing can be positively identified in the observed water vapor data (Fig. 6). S/N ratios for signals calculated over the 21-year period 1988–2008 are always above the nominal 5% significance threshold and exceed the 1% threshold in 62 of 144 cases. These results illustrate that our ability to identify externally forced changes in water vapor is not affected by the “model screening” choices we have made.

Note that there are systematic differences between S/N ratios estimated with top 10 and bottom 10 models, with ratios for the latter larger in all 6 cases (Fig. 6). This result occurs because many of the models ranked in the bottom 10 underestimate the observed variability of water vapor, thereby spuriously inflating S/N ratios (Fig. S4 in SI Appendix). In models with more realistic representations of the mean state, annual cycle, and variability, S/N ratios are smaller but consistently above the stipulated 5% significance threshold.

Conclusions

We have shown that the positive identification of an externally forced fingerprint in satellite estimates of atmospheric water vapor changes is robust to current model uncertainties. Our ability to identify this fingerprint is not affected by restricting our original multimodel D&A study (10) to smaller subsets of models with superior performance in simulating certain aspects of observed water vapor and SST behavior. In fact, we find that even models with noticeable errors in water vapor and SST yield positive detection of an externally forced fingerprint.

The ubiquitous detection of an externally forced fingerprint is due to several factors. First, the structure of the water vapor fingerprint is governed by very basic physics and is highly similar in all 12 of our sensitivity tests (Fig. 5). Second, the fingerprint is characterized by spatially coherent water vapor increases, whereas the dominant noise modes in the model control runs are ENSO-like in structure and do not show coherent water vapor increases over the entire global ocean (Fig. S2 in SI Appendix). Although the structural details of the dominant noise mode differ from model to model (Fig. S3 in SI Appendix), the dissimilarity of the water vapor fingerprint and the leading noise patterns does not. This dissimilarity is the main explanation for the robustness of our D&A results.

The water vapor feedback mechanism is of primary importance in determining the sensitivity of the climate system to external forcing (31, 32). Because our fingerprint estimates are robust across models and relatively insensitive to the model quality metrics calculated here, the contribution of water vapor feedback to projected future climate changes may be similarly insensitive to model skill.^§§

Our study also demonstrates that it is not easy to make an unambiguous identification of “superior” models, even for a very specific application. Model performance assessments are sensitive to the choice of climate variables, analysis regions and timescales, the physical properties of the fields being compared, the comparison metrics, the way in which individual metrics are normalized and combined, and the ranking approaches (see SI Appendix). There is considerable subjectivity in all of these choices. Different sets of choices would yield different model rankings.

In our analysis of water vapor and SST data, we find that model performance in simulating the mean state is virtually uncorrelated with model performance in reproducing the observed annual cycle or the observed amplitude or pattern of variability. This result has implications for attempts to use model performance metrics to weight projections of future climate change. To date, most of these attempts have relied on mean state metrics. Our findings imply that different projection weights would be obtained with annual cycle and variability metrics. Whether different weighting approaches lead to important differences in climate-change projections is currently unclear and may depend on the region, climate variable, and timescale of interest (20, 22). Identification of the best models for making projections of future climate change will likely require metrics that can better constrain current uncertainties in feedback mechanisms (33).

Although we find that incorporating model quality information has little impact on our ability to identify an externally forced water vapor fingerprint, this does not mean that model quality assessment will be of limited value in D&A studies with other variables (8, 11). In the case of water vapor, S/N ratios are invariably above stipulated significance thresholds. If S/N ratios are closer to these thresholds, it may become more important to screen or down-weight models that are deficient in their simulation of the amplitude and structure of natural variability. As we show here, such variability errors can systematically bias D&A results.

In summary, future multimodel D&A studies must deal with the fundamental challenge of how to make appropriate use of the information from a large collection of models of varying complexity and performance levels. Inevitably, model quality assessment will be an integral component of multimodel D&A studies. Although a democratic “one model, one vote” approach was successful for the water vapor D&A problem, this approach may not be adequate in all cases.