Using Two Palpable Measurements Improves the Subject Specific Femoral Modeling

Abstract

Subject-specific musculoskeletal models are essential to biomedical research and clinical applications, such as customized joint replacement, computer-aided surgical planning, gait analysis and automated segmentation. Generating these models from CT or MRI is time and resource intensive, requiring special skills. Therefore, in many studies individual bone models are approximated by scaling a generic template. Thus, the primary goal of this study was to determine a set of clinically available parameters (palpable measures and demographic data) that could improve the prediction of femoral dimensions, as compared to predicting these variables using uniform scaling based on palpable length. Similar to previous non-homogenous anthropometric scaling methods, the non-homogenous scaling method proposed in this study improved the prediction over uniform scaling of five key femoral measures. Homogenous scaling forces all dimensions of an object to be scaled equally, whereas non-homogenous scaling allows the dimensions to be scaled independently. The largest improvement was in femoral depth, where the coefficient of determination (r²) improved from 0.22 (homogenous) to 0.60 (non-homogeneous). In general, the major advantage of this non-homogenous scaling method is its ability to support the accurate and rapid generation of subject specific femoral models since all parameters can be collected clinically, without imaging or invasive methods.

Introduction

Subject-specific musculoskeletal models are essential to biomedical research and clinical applications, such as customized joint replacement (Kessler et al., 2008), computer-aided surgery (Radermacher et al., 1998), gait analysis (Kepple et al., 1998) and automated image segmentation (Yao and Russell, 2003). For example, reliability and wear of implants are dependent upon the stress distribution in the bone (Kerner et al., 1999), which is primarily determined by implant properties (e.g. material, shape and component dimensions). The today’s longer life expectancies requires improving the durability and the reliability of joint implants, especially for younger patients with greater physical activity (Zanetti et al., 2005). Computer-aided orthopaedic surgery requires a geometrical model of the patient’s bone that can reproduce at least its basic morphological aspects and dimensions. In gait analysis, a realistic geometrical model is the first step towards creating an accurate musculoskeletal model (Kepple et al., 1998).

Accurate subject-specific models can be created from high-resolution in vivo imaging modalities, such as CT or MRI, but the creation of these models is expensive, time consuming and requires special skills. Thus, many studies have approximated an individual’s bone shape by scaling a generic template (Adam et al., 2002; Audenino et al., 1996; Bert, 1996; Brand et al., 1982; Lew and Lewis, 1977). The femur has been a particular focus of scaling studies due to its involvement in both the hip and knee joints. Scaling has usually been uniform and isotropic, requiring only a single scale factor, which is likely less accurate than multiple scaling factors. In more advanced studies the bone shape has been deformed by scaling with multiple factors (non-homogenous scaling). Lew et al. (1980) and Brand (1982) used three scale factors to represent femoral size along three orthogonal directions. Similarly, Sommer III et al. (1982) used an affine transformation, which allowed independent scaling along three orthogonal directions. This method was used by Kepple et al. (1998) to generate a 3D database of lower extremity musculotendon insertions and origins. More recent studies have used both x-ray (Gunay et al., 2007) and ultrasound (Rajamani et al., 2007) to generate a sparse subject-specific model. A higher resolution model was then generated by warping a generic high-resolution model to the low-resolution subject-specific model. The shortcomings of these non-homogenous methods are their dependence on internal landmark coordinates, requiring in vivo imaging.

Thus, the primary goal of this study was to determine a set of clinically available parameters (palpable measures and demographic data) that could accurately predict five key anatomic distances on the femur. “Accurately” was define as a coefficient of determination (r²) greater than 0.5.

Materials and method

The study included 76 femurs (52 skeletal femur specimens (cadavers) and 24 volunteers). All femurs were skeletally mature and free from known orthopaedic problems. Demographic data (height, weight, gender and age) were documented for each subject (172.8±8.8cm, 59.7±15.16kg, 42F/34M, 42.2±16.0 years).

Landmark coordinates from the 52 specimens were obtained from an existing database (Kepple et al, 1998). These coordinates were acquired using the Ascension Technologies tracking device (Burlington, VT), having a root-mean-square (RMS) calibration precision of 2 mm. Landmark coordinates from the 24 healthy volunteers’ femurs were obtained from geometric models generated using Geomagic Studio (Research Triangle Park, NC), based on T1-weighted spin echo MR images, segmented in MIPAV (National Institutes of Health, Bethesda, MD). All images had a 0.94 mm in-plane resolution. A slice thickness of 4 mm was used to acquire femoral volumes at the knee and hip where the anatomical landmarks were defined (Figure 1). A slice thickness of 15 mm was used for imaging the femoral shaft. Prior to extracting the anatomical landmarks from geometric models, the models were aligned based on their principal axes.

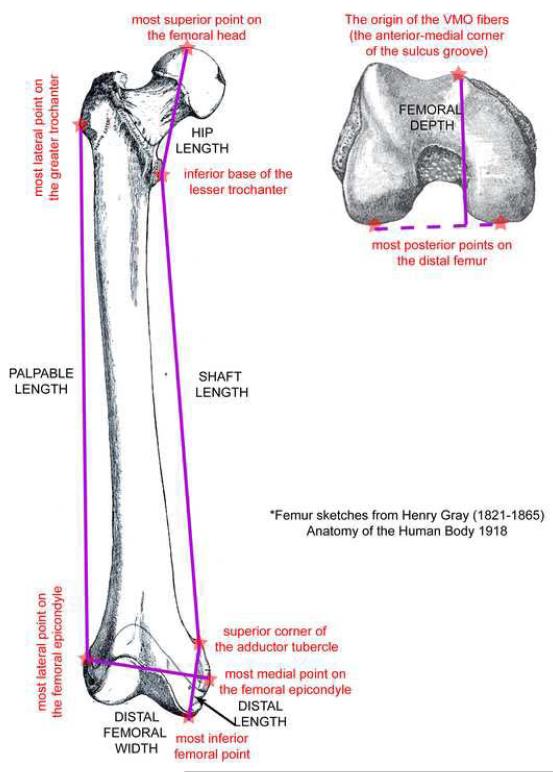
Figure 1.

Key anatomical landmarks (red stars with red lower case labels) that were used to define key anatomic distances and palpable measures, which are listed in all caps. The palpable measures were palpable length, defined as the distance from the most lateral point on the greater trochanter to the most lateral point on the femoral epicondyle and distal femoral width, defined as the distance from the most medial point on the femoral epicondyle to the most lateral point on the femoral epicondyle. The key anatomic distances were hip length, defined as the distance from the most superior point on femoral head to the inferior base of the lesser trochanter; shaft length, defined as the distance between the superior corner of the adductor tubercle to the inferior base of the lesser trochanter; distal length, defined as the distance from the inferior point on the femur to the superior corner of the adductor tubercle; femoral depth, defined as the distance from the origin of the VMO fibers (near the anterior-medial corner of the sulcus groove) to the line connecting the most posterior points on the medial and lateral distal condyle and total length, defined as the distance from the most superior point of the femoral head to the most interior point on the femur.

Seven key measurements were calculated for each femoral dataset. The first two were palpable measures: palpable length and distal femoral width (Figure 1). The next five were key anatomic distances: hip length, shaft length, distal length, femoral depth, and total length (Figure 1). These five measures required in vivo imaging and were not attainable through palpation.

A first analysis was conducted to determine if uniform scaling using only palpable length was sufficient for creating subject-specific models from a normative femoral template (a model generated from one or more femurs that were free from any known defects or abnormalities). Four regression equations (linear with zero intercept, linear with y-intercept, non-linear semilog and non-linear second order polynomial) were calculated for each femoral measure using the palpable length as the independent variable. The methods were compared using the RMS error between the original value and the predicted value for each equation.

A second analysis was used to determine the improvement (over the first analysis) in predicting five of the seven key femoral measures using distal femoral width and subject demographic data (height, weight, and age) in conjunction with palpable length. These measures were added because they are clinical measures (i.e., measures that could be ascertained in a physical exam or demographic information). Stepwise linear regression was used to automatically select a set of parameters that constructed the most accurate predicting equations. The coefficient of determination (r²) determined the quality of fit.

Results

The standard deviation for the femoral measurements ranged from 0.5 to 2.9 cm (Table 1). The standard deviation for each measurement was weakly correlated with its average value (r=0.45, r= regression coefficient). All seven measurements were determined to be normally distributed with Lilliefors significance levels below 5%.

Table 1.

Femoral measurements (n = 76)

	Minimum	Maximum	Mean	SD	SD/Mean
Palpable Measures
Palpable Length (cm)	32.9	44.3	38.1	2.5	6.5%
Distal Width (cm)	7.1	10.8	8.6	0.9	10.4%
Key anatomic distances
Total Length (cm)	40.3	54.7	46.2	2.9	6.3%
Hip Length (cm)	8.0	11.5	9.8	0.9	9.3%
Shaft Length (cm)	26.8	38.5	32.6	2.3	7.0%
Distal Length (cm)	4.0	6.4	4.9	0.5	10.4%
Depth (cm)	5.6	10.1	7.6	1.1	14.0%

Correlations between each of the six dependent measures and the palpable length ranged from 0.47 to 0.97 (Table 2). The quality of the fit was the same among the four regression equations, except for the hip length, which had a slightly higher RMS error for the polynomial function (Table 3).

Table 2. Correlation coefficients (r) among seven key lengths.

All correlations are significant at the 0.001 level (2 —tailed)

	Total length	Hip length	Shaft length	Distal length	Distal Width	Depth
Hip length	0.657
Shaft length	0.931	0.388
Distal length	0.639	0.602	0.455
Distal Width	0.588	0.674	0.421	0.690
Depth	0.549	0.700	0.420	0.610	0.714
Palpable length	0.966	0.524	0.958	0.553	0.509	0.471

Table 3. Comparison of the four fitting techniques for the first analysis (palpable length only).

The first column represents the variable being predicted. The next four represent the RMS error between the original value and the predicted value (as a percentage of the mean value of that variable). The final column lists the average RMS error, across all four analyses.

Fit function Variable	Linear zero- intercept	Linear with intercept	Semilog function	Polynomial function	Average RMS error
Total length (SD)	1.7%	1.6%	1.7%	1.7%	7.7 mm
Hip length (SD)	8.0%	7.9%	7.9%	9.1%	8.0 mm
Shaft length (SD)	2.0%	2.0%	2.0%	2.1%	6.7 mm
Distal length (SD)	8.1%	8.1%	8.1%	8.0%	4.0 mm
Distal Width (SD)	9.0%	8.9%	8.9%	8.9%	7.7 mm
Depth (SD)	12.2%	12.2%	12.2%	12.3%	9.3 mm

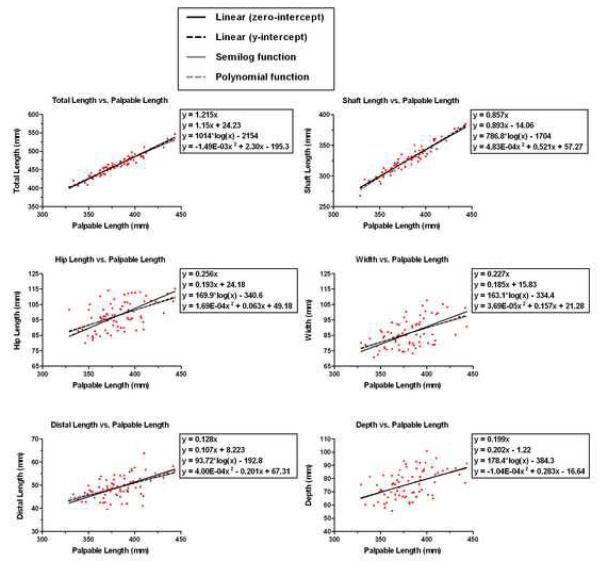
Uniform scaling based on palpable length could not predict four of the six femoral measures (r² < 0.5, Table 4). This, along with the large fluctuations in distal femoral width, depth, and hip length relative to palpable length (Figure 2), suggests that at least two independent variables are needed for accurate femoral scaling. Using additional clinical measures, along with the palpable length, improves the regression equations for each dependent variable and increases the coefficient of determination to above 0.5 in all cases (percent increase ranged from 2.1% to 75.0%, Table 4). Of all additional measures, distal femoral width has the greatest impact on improving prediction error and was the largest contributor to the prediction of distal length and depth (i.e., has the associated r² value, Table 5). Step-wise regression analysis demonstrated r² values, ranging from 0.41 to 1.00, with significance predictability (P<0.05, Table 5). The regression for the female and male populations did not improve the r² values.

Table 4.

Comparison of the coefficient of determination (r²) between single regression with palpable length and stepwise multiple regression.

Dependent Variable	Analysis 1	Analysis 2	Percent Improvement
Total length (SD)	0.93	0.95	2.1%
Hip length (SD)	0.27	0.55	50.9%
Shaft length (SD)	0.92	0.93	1.1%
Distal length (SD)	0.31	0.57	45.6%
Distal Width (SD)	0.25	1.00	75.0%
Femoral Depth (SD)	0.22	0.61	63.9%

Figure 2.

The data distribution is tight for total length and shaft length. The fit for each measurement versus palpable length is shown in a separate graph. The equations listed on each graph are a linear fit with zero-intercept, linear fit with y-intercept, the semi-log function and the polynomial functions (listed in this order from top to bottom). Each graph has an identical x-axis, but the range of the y-axis is different.

Table 5. Stepwise Linear Regression analysis.

based on palpable length, distal femoral width, age and height. When the regression for height was calculated, this variable was switched from a dependent to an independent variable. Column 2 contains the variables used for the regression equation (r² = coefficient of determination), listed in order of contribution to the linear regression equation. The r² value given next to each value defines the quality of the equation based on that variable and those that precede it. Thus, the r² value given for the final variable defines the goodness of fit for the coefficients given in the 3^rd column. Column 3 contains the coefficient of the resultant regression equation. Column 4 contains the t-score and column 5 is the significance of the t-score. The t-score is a guide to determine the usefulness of each individual variable in the regression equation. Normally, a variable is considered as “useful” when its t score is well below -2 or above 2. The final column lists the RMS error of the original value versus the predicted value.

Dependent Variable	Independent Variables	Coefficient	t score	Significance	RMS Error
Total Length	Constant	-35.09	-1.98	0.052
	Palpable length (r2 = 0.94)	0.94	15.08	0.000
	Height (r2 = 0.95)	0.81	4.19	0.000	6.8 mm
Hip Length	Constant	-16.30	-0.98	0.331
	Height (r2 = 0.41)	0.53	4.15	0.000
	Distal Width (r2 = 0.50)	0.36	3.17	0.002
	Weight (r2 = 0.55)	-0.13	-2.53	0.014	6.3mm
Shaft Length	Constant	-16.50	-1.38	0.172
	Palpable length (r2 = 0.93)	0.90	28.62	0.000	6.5mm
Distal Length	Constant	2.22	0.39	0.700
	Distal Width (r2 = 0.48)	0.25	4.91	0.000
	Palpable length (r2 = 0.57)	0.07	3.76	0.000	3.9 mm
Depth	Constant	2.98	0.36	0.723
	Distal Width (r2 = 0.51)	0.74	7.19	0.000
	Age (r2 = 0.61)	0.22	3.87	0.000	6.8mm
Distal Width	Distal Width (r2 = 1.00)				0.0 mm
Height	Constant	62.23	8.26	0.000
	Palpable length (r2 = 0.72)	0.23	9.85	0.000
	Distal Width (r2 = 0.77)	0.24	3.54	0.001

Discussion

This study advances previous work by using multiple scaling factors without requiring invasive measures or advanced high-resolution in vivo imaging. Similar to the non-homogenous anthropometric scaling method (Lewis et al., 1980), the non-homogenous scaling method proposed in this study improved the predictability over homogenous scaling using only palpable length and was able to predict 5 key femoral measures with a coefficient of determination (r²) greater than 0.5. Regression analysis demonstrated that using additional clinically available measurements (distal femoral width, subject height, weight, and age) improved the coefficient of determination from 2.1% to 75.0%. In general, the major advantage of this non-homogenous scaling method is its ability to be implemented quickly and accurately, since all parameters can be collected without imaging or invasive methods. Although, the homogenous method did not perform as well as the non-homogenous, the largest error was still under 12% (depth, average RMS error = 9.3mm). In studies where this is an acceptable level of error, uniform scaling based on palpable length could be implemented, providing a simpler alternative to the non-homogenous method.

Numerous scaling methodologies (Lew and Lewis, 1977; Lewis et al., 1980; Sommer, III et al., 1982) have been developed in an attempt to create subject-specific musculoskeletal models from generic femoral models. These studies focused on mathematical development of scaling techniques and used a minimal set of specimens (<3). Kepple et al (1998), using a larger specimen base (52 cadaver sets), demonstrated that uniform scaling based on subject height provided a RMS error of 6.6 mm for predicting femoral landmark locations. Yet, Lewis et al (1980) demonstrated that non-homogenous scaling reduced RMS errors in identifying anatomical landmark locations, particularly when a large number of points were used in the scaling. Since only a minimal set of anatomical landmarks are available through external palpation, the current work demonstrated that the most efficient application of non-homogeneous affine scaling was attainable through the use of three points, with RMS error of 5.0 mm (averaged over the six distance measures), which is less than the RMS error for individual points (6.5mm) reported by Kepple et al (1998).

The current study demonstrates a simple method to improve scaling by adding a single factor (distal femoral width) that can be easily measured through palpation. The strong correlations between palpable length and two measures of length (shaft length and total length) imply that the superior-inferior direction of the individual femoral sections change size proportionally to the palpable length. The lower correlation between distal femoral width and depth indicates that the two orthogonal dimensions do not. Thus, the use of uniform scaling based on generic models provides less accurate information than the use of multiple scaling factors.

The primary limitations of this study are two-fold. This study was limited to the femur. Yet, by simple extension, the same analysis could be applied to the entire lower extremity. The accuracy of predicting femoral measures is based on visualizing anatomical landmarks directly from a cadaver bone or a MR image. In practice, these landmarks would typically be found through palpation, which would likely introduce higher imprecision.