Abstract
The choriocapillaris is a unique capillary bed that provides nutrients to the retinal photoreceptors. It changes anatomically in diabetes, but the impact of these changes on blood flow is unknown. In this study hemodynamic parameters in individual choriocapillaris vessels were compared in normal and diabetic rats. Three groups were studied: normal buffer-injected control rats, streptozotocin (STZ)-injected mildly hyperglycemic (STZ-MH) rats, and STZ-injected diabetic (STZ-D) rats. 7-8 weeks after STZ injection, the rats were anesthetized, and epifluorescent, intravital microscopy was used to record the flow of fluorescent red blood cells (RBC) in the choriocapillaris. Diameter, RBC flux, and RBC velocity were measured in 153 capillary pathways in five control rats, 98 pathways in four STZ-MH rats, and 153 pathways in seven STZ-D rats. There was no difference in capillary diameter among the groups. RBC flux and velocity were lower in the STZ-injected rats compared to the controls (p≤0.023), which is similar to changes found in other capillary beds. RBC velocity and flux were significantly correlated in all three groups, but the correlations in the STZ-injected rats were much stronger than in the controls. This indicates a more heterogeneous distribution of RBCs at upstream arteriolar branchpoints in hyperglycemic rats, which could lead to a decrease in choriocapillaris hematocrit. These changes in the hyperglycemic choriocapillaris could contribute to impaired oxygen delivery to the photoreceptors in diabetic retina.
Keywords: choriocapillaris, choroid, diabetes, hyperglycemia, erythrocyte flux, blood flow, hemodynamics, retina
INTRODUCTION
The retina is a unique tissue in terms of its vascularization, since it is supplied with blood by two distinct vascular networks, the retinal and choroidal circulations. In general, the retinal circulation supplies the inner half of the retina with blood, while the choroidal circulation is primarily responsible for exchange of nutrients and waste products with the outer retinal cells, including the retinal pigment epithelium and photoreceptors (Linsenmeier and Padnick-Silver, 2000). Anatomically the choroidal blood vessels lie in three layers of the choroid, the highly pigmented vascularized connective tissue that lies between the retina and the sclera. Large and medium-sized arteries and veins lie in Haller’s and Sattler’s layer, while the capillaries of the vascular bed lie in the choriocapillaris, which is separated from the retinal pigment epithelium by the 2-4 μm-thick Bruch’s membrane.
The choriocapillaris is unlike most other capillary beds in the body. The fenestrated capillaries are atypically large, with diameters ranging from12-20 μm (Ring and Fujino, 1967; Wajer et al., 2000). In humans, the vessels are arranged in lobules, and the nature of these lobules varies as a function of retinal eccentricity (McLeod and Lutty, 1994). In general, the lobules are fed by a single short arteriole and drained by a venule. The large bore capillaries and net-like architecture of the choriocapillaris are responsible for the large volume of the choroidal circulation and the low resistance across this vascular bed. Choroidal blood flow is roughly 700-1,000 mg blood/min (Bill, 1984), which is one of the highest in the body on a global volume basis.
Diabetes is known to adversely affect the microcirculation throughout the body, including the ocular circulation. The impact of diabetes on the retinal microcirculation can be especially dramatic, including microaneurysm formation, intraretinal hemorrhages, selective loss of pericytes from retinal capillaries, and subsequent loss of endothelial cells (Frank, 2004). These changes directly or indirectly lead to retinal edema and neovascularization, and eventually blinding diabetic retinopathy. The effects of diabetes on the choroidal circulation are not as well known and are usually regarded as insignificant compared to the changes that occur in the retinal circulation. Nevertheless, anatomical abnormalities have been found in the choroidal vasculature of human patients with diabetes. These alterations include increased tortuosity, microaneurysm formation, choriocapillaris luminal narrowing, endothelial cell loss, and capillary dropout (Cao et al., 1998; Freyler et al., 1986; Fryczkowski et al., 1989; Hidayat and Fine, 1985; McLeod and Lutty, 1994). It has also been reported that overall choroidal blood flow is altered in patients with diabetic retinopathy (Langham et al., 1991; Savage et al., 2004). While these studies have investigated anatomical or histological changes in the choroidal microvessels or global changes in choroidal blood flow, there is no information on the effect of diabetes on blood flow through the choriocapillaris. Since it plays a major role in supplying the photoreceptors with oxygen and other nutrients, alterations in flow through the choriocapillaris could impact metabolism in the avascular outer half of the retina (Linsenmeier and Padnick-Silver, 2000).
In this study we determined the hemodynamic parameters in individual choriocapillaris vessels and in choriocapillaris networks in normal and diabetic rats. We hypothesized that red cell flux and velocity would be lower in the choriocapillaris vessels of diabetic rats compared to those same microvessels in the choroid of normal rats.
MATERIALS AND METHODS
Animals
Male Sprague-Dawley rats of approximately 16 weeks of age (Harlan Sprague-Dawley, Indianpolis, IN) were used in this study for several reasons. First, rats are a common model for the study of diabetes. Second, the rat choriocapillaris has many of the same features found in humans. While the rats do not possess exactly the same lobular structure as is found in the human choriocapillaris (Bhutto and Amemiya, 2001), they do form the same meshwork of large diameter flat capillaries arranged in anastomosing units (Bhutto and Amemiya, 2001; Ninomiya and Kuno, 2001). Third, these particular rats are albino, which allowed choriocapillaris vessels to be viewed using epifluorescence. Finally, we have already described the flow of erythrocytes through larger choroidal vessels in male Sprague-Dawley rats (Braun et al., 1997). All procedures were in accordance with the ARVO Statement for the Use of Animals in Ophthalmic and Vision Research, and the experiments were approved by the local Institutional Animal Care and Use Committee.
Induction of Diabetes with Streptozotocin
Rats were fasted overnight and anesthetized with an intramuscular injection of 54/6 mg/kg ketamine/xylazine. Immediately before the injections, a 10 mg/ml solution of streptozotocin in cold Machelvain’s citrate buffer was made and kept on ice. A drop of blood was taken from the tail vein, and blood glucose was measured (Accu-Chek IIm, Boehringer-Mannheim, Indianapolis, IN). The rats were injected intraperitoneally with streptozotocin (70 mg/kg) or an equivalent volume of citrate buffer. Ten ml of 5% dextrose in lactated Ringer’s was injected subcutaneously in the back. The rats were given 1% dextrose water to drink for the next 24 hours, and blood glucose was monitored the following day and weekly thereafter.
Fluorescent Markers
Several different fluorescent markers were used in this work. Rhodamine-labeled, sterically stabilized, long-circulating, pegylated liposomes were injected to visualize plasma in the blood vessels. These liposomes consisted of egg phosphatidylcholine, cholesterol, 1,2-distearoyl-sn-glycero-3-phosphoethanolamine-N-polyethylene glycol 2000, and lissamine rhodamine B 1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine (rhodamine-DHPE) in a molar ratio of 10:5:0.8:0.1 (Yuan et al., 1995). All lipids except the rhodamine-DHPE were purchased from Avanti Polar Lipids (Alabaster, AL). Rhodamine-DHPE was purchased from Molecular Probes (Eugene, OR). The liposomes were prepared using the lipid film hydration and extrusion method (Hope et al., 1985). The resultant liposomes had a diameter around 200 nm with a final lipid concentration after hydration of 20 mg/ml.
Erythrocytes (RBC) for labeling were obtained from donor rats. The RBC were labeled with 1,1’-dioctadecyl-3,3,3’,3’-tetramethylindocarbo-cyanine perchlorate (DiI, Molecular Probes, Eugene, OR) using a technique that has been described in detail elsewhere (Unthank et al., 1993). Briefly, after blood was removed from the donor rat, erythrocytes were isolated by successive washing and centrifugation. Then 100 μl of RBC were incubated for 30 minutes in a mixture of 10 ml of PBS and 100 μl of 0.5 mg/ml DiI in ethanol. Following washing and centrifugation, 100 μl of DiI-labeled RBC (DiI-RBC) were resuspended to one ml in PBS for a final concentration of 100 μl DiI-RBC/ml.
Videomicroscopy of the Choriocapillaris
Seven to eight weeks after injection with STZ or buffer, the rats were used for an experiment. Before initial anesthesia, a drop of blood was obtained from the tail vein of the restrained rat for determination of blood glucose level (Accu-Chek IIm, Boehringer-Mannheim, Indianapolis, IN). All rats were anesthetized with urethane (1.6 g/kg s.c.; 240 mg/ml urethane in water) subcutaneously in the back, and surgery was only begun after surgical anesthesia had been achieved (1 to 2 hours). The femoral artery and vein were cannulated so that arterial blood pressure could be monitored and the fluorescent markers could be infused, respectively. After the cannulations, hematocrit was determined from a sample of arterial blood drawn from the arterial line. The sclera was then surgically exposed to permit microscopic observation of the choroidal circulation (Braun et al., 1997).
Observation of individual choroidal blood vessels has been described in detail previously (Braun et al., 1997). Briefly, the rat was positioned in a head holder and placed on the stage of a Zeiss intravital microscope (Photomicroscope III, Carl Zeiss, New York, NY). A regulating thermal blanket (Harvard homeothermic blanket, Harvard Apparatus, S. Natick, MA) was placed between the rat and a plexiglass stage to maintain body temperature at 37°C. The arterial line was connected to a mean blood pressure monitor (Digital Manometer, FiberOptic Sensor Technologies, Ann Arbor, MI). The eye was positioned under the 20X long working distance objective. A drop of hydroxypropyl methylcellulose 2.5% (Goniosol, Novartis Ophthalmics, Duluth, GA) was applied to the sclera, and a piece of glass cover slip about 5 × 5 mm was positioned to serve as a contact lens.
Small volumes (0.15-0.20 ml) of rhodamine-labeled liposomes and DiI-RBCs (0.15-0.20 ml) were injected intravenously. Fluorescent microscopy was performed with epi-illumination using a 100-W mercury source with the appropriate filter set. The set had a bandpass excitation filter (λ = 540-550 nm) and a longpass emission filter (λ ≥ 590 nm). Images were recorded via a silicon intensified tube (SIT) video camera (Hamamatsu C2400-08, Hamamatsu, Japan) connected to a S-VHS video recorder (Mitsubishi BV-1000, Mitsubishi Electronics, Japan). A video timer signal (For-A model VTG-55, Los Angeles, CA) was superimposed on the images for record keeping. During epi-illumination a suitable region of the choroid containing a visible field of choriocapillaris vessels was located, and the field was videotaped for at least three minutes for later analysis (Figure 1). A region of choriocapillaris vessels was identified by tracking the path of interconnected vessels to their source or destination. Each vessel path had to be diverging from a feeding vessel (Figure 1) or converging into a draining venule. Using this transscleral approach, only choroid at or proximal to the equator could be visualized, i.e., equatorial and peripheral choroid. Following the experiments, a final hematocrit was determined from an arterial sample, and blood glucose level was measured from a venous sample. Before euthanasia of the rat, another blood sample was taken from the arterial catheter for determination of the labeled fraction of RBCs by flow cytometry (FACScan, Becton Dickinson, Franklin Lakes, NJ). The labeled fraction is the relative number of RBCs that carry the DiI label (number of DiI RBC/total number of RBC).
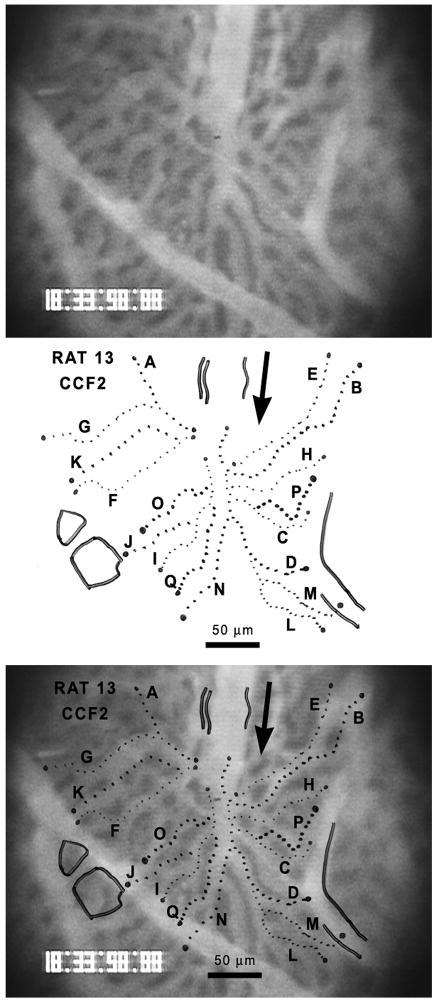
Figure 1.
Epifluorescent image of a field of choriocapillaris vessels in a STZ-D Sprague-Dawley rat (top). The vessels contain fluorescently labeled liposomes. The retina would be located behind these vessels, i.e., into the page. The analyzed pathways of erythrocyte flow have been traced on a transparent sheet (center) and then superimposed on the camera image of the choriocapillaris (bottom). The arrow shows the direction of blood flow through the field.
Analysis of Videotape Images and Determination of Microvascular Parameters
Vascular fields containing regions of choriocapillaris were identified on the videotapes (Figure 1, top). In each field, vascular pathways through the choriocapillaris field were traced onto a sheet of transparency film taped onto a high-resolution video monitor (Figure 1, center), and the number of DiI-RBCs entering each capillary path over a 3-minute period was counted to give the flux of DiI-RBCs per minute. The RBC flux was then determined by dividing the DiI-RBC flux by the labeled fraction. In an earlier study, it was found that exposure of the choroid to light for three minutes had no effect on erythrocyte flux or velocity through larger choroidal vessels (Braun et al., 1997).
The same video image was then viewed in slow motion, and velocities of the DiI-RBC were determined by calculating the transit time of the cells across the length of the capillary path. Velocities were determined for a maximum of 30 DiI-RBCs for the three-minute period, and a mean velocity was calculated. Capillary widths were determined using individual image frames of each vascular field captured and digitized from the videotape (LG-3 Grayscale Scientific PCI Frame Grabber, Catalog #LG3-01 PCI RS170, Scion Corporation, Frederick, MD). The digital image was imported into ImageJ software (National Institutes of Health, Rockville, MD, http://rsb.info.nih.gov/ij/), and the width of each capillary path was measured at four positions along its length. The average of the measurements was used as the vascular diameter for that capillary path.
Statistics
The normality of all distributions was tested using the Kolmogorov-Smirnov test. Since systemic parameters passed normality tests, blood glucose levels, arterial hematocrits, and blood pressure values were compared among the groups using one-way analysis of variance (ANOVA). Likewise, the number of fields per rat and the number of capillaries per rat were also normally distributed and were compared using ANOVA. If significant differences were found among the groups (p < 0.05), the Bonferroni t-test was used to compare the values between any two groups. The Student’s paired t-test was used to compare the systemic parameters obtained before the experiment and those measured after induction of anesthesia.
Since the grouped hemodynamic parameters (capillary diameter, erythrocyte flux, and erythrocyte velocity) all failed normality tests, comparisons among the three groups were made using the nonparametric Kruskal-Wallis one-way analysis of variance on ranks test. If significant differences were found among the groups (p < 0.05), Dunn’s method was used to compare the values between any two groups.
Correlations among hemodynamic parameters or between hemodynamic parameters and vessel diameter were determined using standard linear regression analysis. Regressions were considered significant if p<0.05. The slopes of the regression lines were compared using ANCOVA analysis (Dowdy and Wearden, 1983).
RESULTS
Diabetic Rats
The response of the rats to STZ was variable. Of the 11 rats injected with STZ, seven became extremely hyperglycemic with blood glucose values above 400 mg/dl for the duration of the study. These were designated as STZ-injected diabetic (STZ-D) rats. The other four rats were transiently hyperglycemic, but did not maintain the severe hyperglycemia past the first week. During the course of the study, their blood glucose level was typically between 100 and 200 mg/dl, and they showed no significant weight loss (Table 1). These rats were designated STZ-injected mildly hyperglycemic (STZ-MH) rats. Five rats were injected with buffer and served as control buffer-injected nondiabetic (B-ND) rats.
TABLE 1.
Comparison of systemic parameters in the three study groups: B-ND, STZ-MH, and STZ-D rats.
| Group | Rats | Days Diabetic | Weight (g) | Blood Glucose before urethane (mg/dl) | Blood Glucose after urethane (mg/dl) | Arterial Hematocrit at start of Experiment (%) | Arterial Hematocrit at end of experiment (%) | Arterial Blood Pressure during measurements (mm Hg) |
|---|---|---|---|---|---|---|---|---|
| B-ND | 5 | 0 | 402 ± 43 (356-451) | 86.4 ± 8.6b (74-95) | 175.8 ± 59.8 (132-279) | 49.8 ± 2.5 (45.5-52.0) | 46.9 ± 3.9 (41.8-50.8) | 86.6 ± 11.7 (70-101) |
| STZ-MH | 4 | < 1 week | 394 ± 28 (355-418) | 142.5 ± 44.4a (93-192) | 245.0 ± 48.2 (200-296) | 48.9 ± 2.2 (47.3-52.0) | 48.3 ± 2.3 (46.0-51.3) | 81.8 ± 5.3 (77-90) |
| STZ-D | 7 | 64 ± 4 (59-71) | 293 ± 36a,b (240-345) | 435.4 ± 29.3a,b (389-473) | 466.8 ± 30.1a,b (429-497) | 46.4 ± 2.9 (42.8-50.0) | 45.4 ± 3.2 (38.8-49.0) | 85.5 ± 7.1 (79-95) |
| ANOVA p-value | <0.001 | <0.001 | <0.001 | 0.111 | 0.370 | 0.754 | ||
All values are means ± SD. Values in parentheses represent ranges. The p-value reports the significance of the one-way ANOVA test to compare the values among the three groups. The Bonferroni t-test was used to compare the multiple pairs among the three groups if the ANOVA test showed a significant difference.
p<0.05 compared to B-ND group
p<0.05 compared to STZ-MH group
Systemic Parameters of Rats
The STZ-D rats had increased blood glucose levels for 64 ± 4 days (mean ± SD, n=7, Table 1) at the time of the experiments. The STZ-D rats weighed about 100 g less than the B-ND or STZ-MH rats (p<0.001, Table 1), but there was no difference between the two groups of nondiabetic rats (p=0.770). At the start of the experiment, i.e., before anesthesia induction, there was a significant difference in the blood glucose levels among the three groups (Table 1). The STZ-D rats had the highest blood glucose, which was significantly higher than either nondiabetic group (p<0.001). The blood glucose in the STZ-MH rats was also significantly higher than that in the B-ND rats (p=0.042). In agreement with previous studies (Van der Meer et al., 1975), urethane anesthesia tended to increase blood glucose levels in all three groups, but the increase was only statistically significant in the B-ND and STZ-MH groups (p≤0.025, n=4-5). There was no difference in arterial hematocrit among the groups, either at the beginning or end of the experiment, although these values are higher than the normal hematicrit reported for male Sprague-Dawley rats of this age (Wolford et al., 1986). This higher hematocrit is consistent with the 8% hemoconcentration reported in rats after subcutaneous injection of urethane (Van der Meer et al., 1975). There was no significant difference in arterial blood pressure among the groups (Table 1).
Visualization of Choriocapillaris in Rat
A total of 153 normal choriocapillaris pathways were analyzed in 17 fields in five B-ND rats and in seven STZ-D rats. In the four STZ-MH rats, 11 fields were recorded, and flow through 98 vessel pathways was characterized. There was no difference in the labeled fractions of DiI-RBCs among the groups (Table 2), and the average labeled fraction was 0.0495 ± 0.0114 % (n=16 rats). Likewise, there were no significant differences in the number of fields recorded per rat or in the number of vessels analyzed per rat among the three groups (Table 2).
TABLE 2.
Comparison of hemodynamic parameters in choriocapillaris vessels of B-ND, STZ-MH, and STZ-D rats.
| Group | Rats | Labeled Fraction (% DiI-RBCs) |
Number of Capillary Fields per Rat |
Number of Capillary Pathways per Rat |
Total Number of Capillary Pathways |
Capillary Diameter (μm) |
Erythrocyte Flux (RBC/sec) |
Erythrocyte Velocity (mm/sec) |
|---|---|---|---|---|---|---|---|---|
| B-ND | 5 | 0.046 ± 0.014 (0.025-0.060) | 3.4 ± 0.6 (3-4) | 30.6 ± 8.3 (23-43) | 153 | 13.8 ± 2.4 (9.0-19.5) | 216.5 ± 246.9b (11-1378) | 1.064 ± 0.463b (0.255-3.981) |
| STZ-MH | 4 | 0.054 ± 0.011 (0.042-0.068) | 2.8 ± 0.5 (2-3) | 24.5 ± 4.7 (18-28) | 98 | 14.0 ± 2.4 (9.3-20.1) | 126.7 ± 103.3a (6-451) | 0.894 ± 0.348a (0.352-1.996) |
| STZ-D | 7 | 0.049 ± 0.011 (0.032-0.060) | 2.4 ± 0.8 (1-3) | 21.9 ± 9.7 (8-32) | 153 | 13.4 ± 2.5 (8.9-20.4) | 138.5 ± 132.2a (3-984) | 0.937 ± 0.371a (0.236-2.647) |
| ANOVA p-value | 0.617 | 0.075 | 0.236 | Kruskal-Wallis ANOVA p-value | 0.116 | 0.023 | 0.002 | |
All values are means ± SD. Values in parentheses represent ranges. The p-values report the significance of the one-way ANOVA test or the Kruskal-Wallis One Way Analysis of Variance on Ranks test to compare the values among the three groups. Dunn’s method was used to compare the multiple pairs among the three groups if the Kruskal-Wallis test showed a significant difference.
p<0.05 compared to B-ND group
p<0.05 compared to STZ-MH group
Choriocapillaris Diameter in Normal and Diabetic Rats
There was no difference in the diameter of choriocapillaris vessels among the three groups (Table 2). The diameters ranged from around 9 to 20 μm in all three groups, and the median diameters for the B-ND, STZ-MH, and STZ-D rats were 13.5, 13.6, and 12.9 μm, respectively.
Erythrocyte Flux in Choriocapillaris of Normal and Diabetic Rats
In the choriocapillaris of the B-ND rats, RBC flux varied from 11 to almost 1400 RBC/sec (Table 2, Figure 2A). The median value was 124.7 RBC/sec, and 25% of the capillary pathways had fluxes greater than 300 RBC/sec. The fluxes in both groups of STZ-injected rats were significantly lower than the flux in the buffer-injected rats, but there was no difference between the STZ-MH rats and the STZ-D rats, in which the median fluxes were 100.8 and 105.8 RBC/sec, respectively (Table 2). Less than 6% of the pathways in these two groups had fluxes greater than 300 RBC/sec (Figures 2B and 2C).
Figure 2.
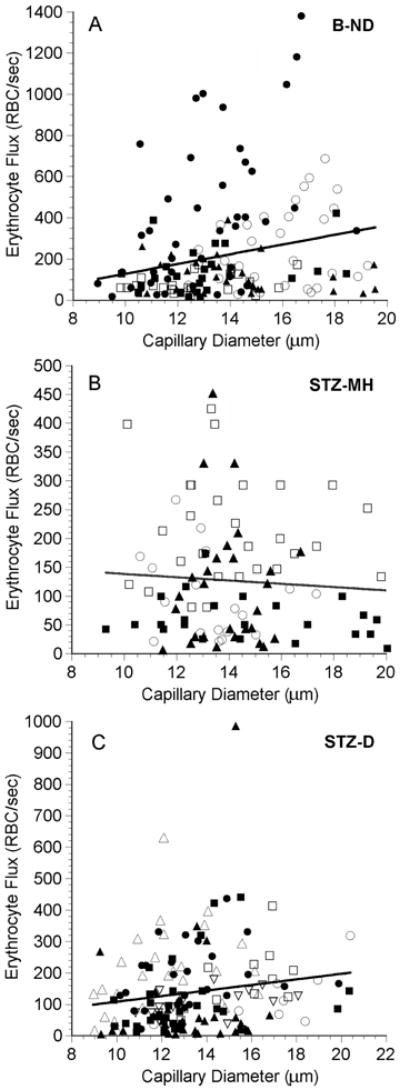
Erythrocyte (RBC) flux as a function of diameter in the choriocapillaris in five B-ND rats (A), four STZ-MH rats (B), and seven STZ-D rats (C). In each panel, each symbol represents a single capillary path, and each symbol type represents values from an individual rat. The line in each plot is the linear regression for the data from all of the rats. A: RBC flux = 23.6 (diameter) − 108.6, n = 153 capillaries in 5 rats, r = 0.231, p = 0.004. B: RBC flux = -2.84 (diameter) + 166.6, n = 98 capillaries in 4 rats, r = 0.065, p = 0.527. C: RBC flux = 8.88 (diameter) + 19.1, n = 153 capillaries in 7 rats, r = 0.166, p = 0.040. Note that there are different scales on the axes.
There was a very weak, but statistically significant, positive correlation between the RBC flux and capillary diameter in the B-ND rats (Figure 2A, r2=0.053, p = 0.004) and STZ-D rats (Figure 2B, r2=0.028, p = 0.040). There was no such correlation in the STZ-MH rats (Figure 2C, r2=0.004, p = 0.527).
Erythrocyte Velocity in Choriocapillaris of Normal and Diabetic Rats
In the normal choriocapillaris, most erythrocytes flowed at a velocity between 0.4 and 2.0 mm/sec (Figure 3A). The medians in the B-ND, STZ-MH, and STZ-D groups were 1.066, 0.824, and 0.907 mm/sec, respectively, and these distributions were statistically different (Table 2). The velocities in the STZ-MH and STZ-D groups were both significantly lower than that in the B-ND group, but were not different from each other (Table 2). In the B-ND group, 22% of the velocities were greater than 1.4 mm/sec, compared to only 9% in the STZ-MH and STZ-D groups (Figures 3B and 3C). There was no correlation between RBC velocity and vessel diameter in any of the groups (Figure 3).
Figure 3.
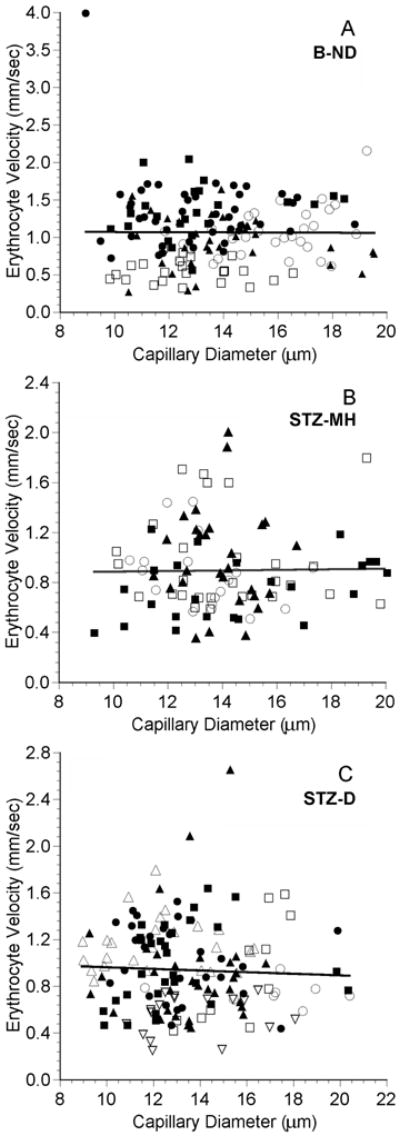
Erythrocyte (RBC) velocity as a function of diameter in the choriocapillaris in five B-ND rats (A), four STZ-MH rats (B), and seven STZ-D rats (C). In each panel, each symbol represents a single capillary path, and each symbol type represents values from an individual rat. The line in each plot is the linear regression for the data from all of the rats. A: RBC velocity = -0.00132 (diameter) + 1.082, n = 153 capillaries in 5 rats, r = 0.007, p = 0.933. B: RBC velocity = 0.00235 (diameter) + 0.861, n = 98 capillaries in 4 rats, r = 0.016, p = 0.876. C: RBC velocity = - 0.00690 (diameter) + 1.030, n = 153 capillaries in 7 rats, r = 0.046, p = 0.574. Note that there are different scales on the axes.
Correlation of Erythrocyte Velocity and Flux in Choriocapillaris of Normal and Diabetic Rats
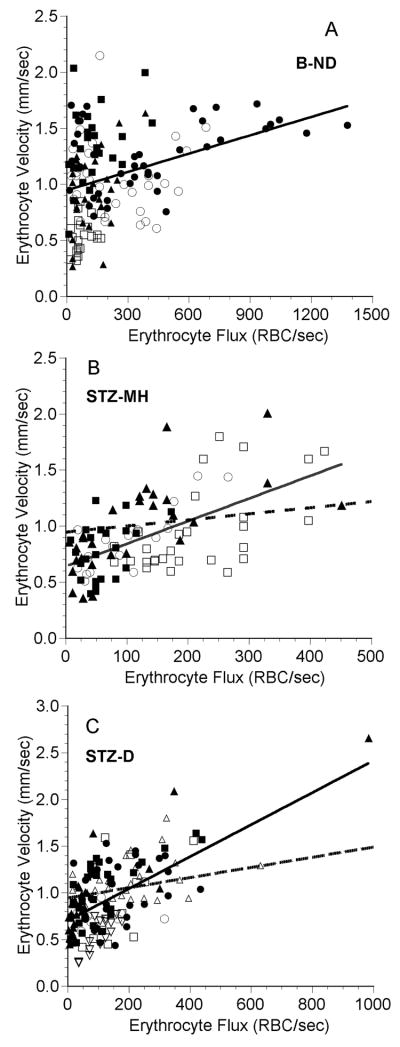
In other capillary beds, erythrocyte flux and velocity are correlated (Ferreira et al., 2006; Kleinfeld et al., 1998). Since the ratio of flux and velocity is proportional to the microvascular hematocrit (Sarelius and Duling, 1982), the slope of this correlation can yield information on the average hematocrit and erythrocyte spacing within the capillaries (Kleinfeld et al., 1998). Because local hematocrit is a key determinant of capillary oxygen delivery (Federspiel and Sarelius, 1984), we examined the relationship between RBC flux and velocity in the choriocapillaris.
Erythrocyte velocity was significantly correlated with RBC flux in all three groups (Figure 4), but there was a significant difference among the three slopes (p<0.001, ANCOVA). Further analysis revealed that the slopes of the lines describing the data from the STZ-MH rats and the STZ-D rats were 3.7 and 3.1 times greater than the slope for the data from the buffer-injected rats, respectively (p<0.001). There was no difference in the slopes for the two STZ-injected groups (p=0.843).
Figure 4.
Erythrocyte velocity as a function of erythrocyte flux in the choriocapillaris in five B-ND rats (A), four STZ-MH rats (B), and seven STZ-D rats (C). Each symbol represents a single capillary path, and each symbol type represents values from an individual rat. The solid line in each plot is the linear regression for the data from all of the rats. In panels B and C, the dashed line is the regression line from panel A. A: RBC velocity = 0.000545 (RBC flux) + 0.946, n = 153 capillaries in 5 rats, r = 0.291, p < 0.001. Point at (76.9, 3.98) not shown for clarity. B: RBC velocity = 0.00202 (RBC flux) + 0.638, n = 98 capillaries in 4 rats, r = 0.600, p < 0.001. C: RBC velocity = 0.00171 (RBC flux) + 0.700, n = 153 capillaries in 7 rats, r = 0.610, p < 0.001. Note that there are different scales on the axes.
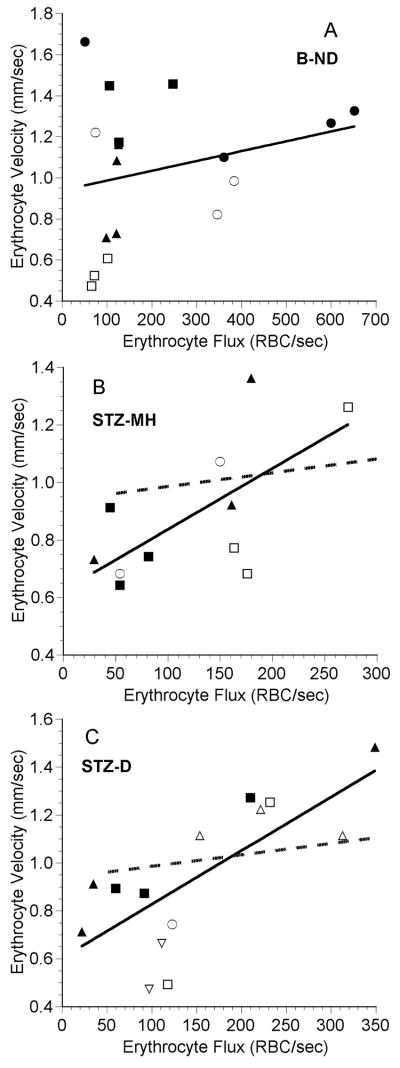
To further investigate this relationship, the mean RBC velocity and RBC flux were calculated for each individual vascular field. There was no significant correlation between average field velocity and flux for the B-ND group (p=0.324, Figure 5A), but these parameters were significantly correlated for the STZ-injected rats (Figures 5B and 5C). The slopes of all three regression lines were very similar to the slopes determined when all of the data were fitted (Figure 4).
Figure 5.
Mean erythrocyte velocity as a function of mean erythrocyte flux in fields of choriocapillaris vessels in five B-ND rats (A), four STZ-MH rats (B), and seven STZ-D rats (C). Each symbol represents the mean value from an individual capillary field, and each symbol type represents values from an individual rat. The line in each plot is the linear regression for the data. In panels B and C, the dashed line is the regression line from panel A. A: RBC velocity = 0.000467 (RBC flux) + 0.937, n = 17 capillary fields in 5 rats, r = 0.254, p = 0.324. B: RBC velocity = 0.00214 (RBC flux) + 0.623, n = 11 capillary fields in 4 rats, r = 0.664, p = 0.026. C: RBC velocity = 0.00224 (RBC flux) + 0.602, n = 17 capillary fields in 7 rats, r = 0.737, p < 0.001. Note that there are different scales on the axes.
DISCUSSION
Although red cell velocity has been previously measured in rat choriocapillaris using scanning laser ophthalmoscopy (Wajer et al., 2000), this is the first time that both erythrocyte flux and velocity have been quantified in the choriocapillaris, allowing us to correlate these parameters with capillary diameter and each other. Since the interaction of erythrocyte flux and velocity is a key determinant of red cell spacing and microvascular hematocrit (Federspiel and Sarelius, 1984; Sarelius and Duling, 1982), quantification of both parameters is necessary to determine the possible impact of choriocapillaris hemodynamics on oxygen delivery to the retina.
Diameter and Hemodynamic Parameters in Choriocapillaris of Normal Rats
The diameter of capillaries in the normal rat choriocapillaris was 13.8 ± 2.4 μm (mean ± SD). The mean value and standard deviation are in good agreement with previous measurements of rat choriocapillaris diameter. Based on measurements from corrosion casts of rat choroid, choriocapillaris vessel diameters were 14.2 ± 2.2 μm near the equator, while toward the periphery they were 12.1 ± 2.1 μm (Bhutto and Amemiya, 2001). A mean diameter of 10.5 ± 3.0 μm was measured from India ink preparations of rat choroid (Wajer et al., 2000). These previous studies also showed a large range of diameters, as indicated by standard deviations between 2 and 3 μm.
The erythrocyte flux measured in the normal choriocapillaris averaged 217 ± 247 RBC/sec, and ranged from 11 to almost 1400 RBC/sec. This is the first measurement of RBC flux in choriocapillaris, and the wide range of fluxes was unexpected. It was not caused by the large spread in vessel diameters, since there was not a strong correlation between flux and diameter (Figure 2A). The heterogeneity in RBC flux is most likely attributable to the extensive interconnectivity of the choriocapillaris, which would result in a complex distribution of driving pressures and resistances throughout the network. Since the choriocapillaris vessels are not formed by simple bifurcations (Figure 1), distribution of RBCs among the choriocapillaris vessels would be more complex than in most other capillary beds.
The mean RBC velocity in the normal choriocapillaris was 1.06 mm/sec, which is in agreement with the value of 1.1 mm/sec reported for rat choriocapillaris using scanning laser ophthalmoscopy (Wajer et al., 2000).
Originally we had planned to calculate capillary hematocrit from these parameters, as we had done for larger choroidal vessels (Braun et al., 1997), using the equation established by Sarelius and Duling (Sarelius and Duling, 1982). Unfortunately, this proved to be impossible for most of the pathways, due to the high level of interconnectivity within the choriocapillaris (Figure 1). The assumptions underlying the calculation of microvascular hematocrit, especially the presence of an unbranched vessel segment, are not valid for most of this capillary bed.
Diameter and Hemodynamic Parameters in Choriocapillaris of Diabetic Rats
There were no differences in capillary diameter among the three groups. These results are consistent with an earlier report, in which electron microscopy revealed no morphometric differences between the choriocapillaris vessels of normal and spontaneously diabetic rats (Caldwell and Fitzgerald, 1991). In human diabetic patients, however, significant narrowing of the vascular lumen in the choriocapillaris has been noted (Cao et al., 1998; Fryczkowski et al., 1989; Fryczkowski et al., 1988; Hidayat and Fine, 1985). Likewise, none of the other morphological changes associated with human diabetic choroidopathy, including vessel tortuosity, microaneurysm formation, capillary dropout, and neovascularization (Cao et al., 1998; Fryczkowski et al., 1988; Hidayat and Fine, 1985), were evident in the current study. The lack of these changes is not surprising, since the duration of diabetes in this study was only two months, and most of these vascular alterations would be expected to be associated with long-term diabetes. Cao et al. observed subtler changes in human diabetics, including choriocapillaris segments without viable endothelial cells that did not support blood flow (Cao et al., 1998). Such diffuse changes could occur earlier in diabetes, since endothelial cell loss in retinal capillaries has been demonstrated in STZ-induced diabetic rats after only one week of diabetes (Joussen et al., 2001). Because we did not assess endothelial viability in this study, we cannot comment whether these changes had already begun in the choriocapillaris and affected the hemodynamic parameters.
In the choriocapillaris of mildly and severely hyperglycemic rats, RBC flux and velocity were both significantly lower than the values in normal choriocapillaris (Table 2). This finding is consistent with previous reports on the effect of diabetes on these parameters in skeletal muscle capillaries in short-term STZ-induced diabetic rats (Kindig et al., 1998) and spontaneously diabetic rats (Padilla et al., 2006). The diabetes-induced decrease of RBC flux of 50 to 67% reported in skeletal muscle capillaries (Kindig et al., 1998; Padilla et al., 2006) was more severe than the decrease in choriocapillaris RBC flux of roughly 40%. Likewise, RBC velocity decreased in diabetic skeletal muscle capillaries by 34 to 65% (Kindig et al., 1998; Padilla et al., 2006), compared to only 12 to 16% in the diabetic choriocapillaris. Since skeletal muscle capillaries are only about 5 μm in diameter (Kindig et al., 1998; Padilla et al., 2006), any diabetes-induced changes in blood rheological properties or in blood vessel characteristics would be expected to have a greater impact on blood flow in these smaller capillaries.
Since the STZ-D and STZ-MH rats exhibited the same differences in RBC flux and velocity compared to the normal B-ND rats, it appears that mild hyperglycemia (< 200 mg/dl) during the 7-8 weeks had the same effect on hemodynamics as severe hyperglycemia (> 400 mg/dl). The present study can shed no light on the mechanism behind the hyperglycemia-induced decrease in capillary hemodynamic parameters, although a likely cause is increased vascular resistance within the choroidal microcirculation. Although smaller vessel diameters could explain the decreases, no change in capillary diameter could be documented in the hyperglycemic rats. Increased resistance of blood flow through the capillaries could be the result of a decrease in erythrocyte deformability and a concominant increase in blood viscosity caused by the hyperglycemia (Fornal et al., 2006; Petropoulos et al., 2007; Tsukada et al., 2001). Increased resistance within the choriocapillaris could also be caused by an increase in adhesion of leukocytes to the endothelium, since there is an increase in the expression of intercellular adhesion molecule-1and P-selectin on the endothelium in human diabetic choroid (McLeod et al., 1995). Since neutrophils are elevated in the choroids of human diabetics (Lutty et al., 1997; McLeod et al., 1995) and leukostasis has been documented in the retinal microcirculation of rats after only one week of STZ-induced diabetes (Joussen et al., 2001), it is possible that leukocytes could play a role in the hemodynamic changes seen in the choriocapillaris. In addition to these diabetes-induced changes in blood cells, damage to the vascular endothelium can also occur, which could increase resistance as well. For example, thinning of the glycocalyx on the endothelium of diabetic microvessels has been demonstrated (Nieuwdorp et al., 2006), which could decrease the repulsive force that normally exists between endothelium and RBCs (Raz et al., 1988). In addition, leukocytes not only accumulate in the choroid, they also damage the endothelium, resulting in choriocapillaris dropout and increased resistance (Cao et al., 1998).
Correlation of Erythrocyte Velocity and Flux in Choriocapillaris
A positive correlation between erythrocyte velocity and flux was found in all three groups, although the correlation between these two parameters in the MH-STZ and D-STZ rats was much stronger than in the normal rats (Figure 4). A positive correlation between erythrocyte velocity and flux has been consistently reported in skeletal muscle capillaries (Ferreira et al., 2006; Kindig and Poole, 1998; Kindig et al., 1998; Padilla et al., 2006; Russell et al., 2003) and has also been found in brain capillaries (Hudetz et al., 1995; Kleinfeld et al., 1998).
The relationship between capillary velocity and flux is a consequence of unequal partitioning of erythrocytes at microvascular bifurcations, resulting in large heterogeneity in microvascular hematocrit and a reduction of the average capillary discharge hematocrit, a phenomenon termed the network Fahraeus effect (Pries et al., 1996). When blood reaches a divergent branch point, more erythrocytes tend to flow into the branch with the higher velocity (Klitzman and Johnson, 1982; Pries et al., 1996), resulting in a positive correlation between RBC flux and velocity. The unequal distribution of red cells is the manifestation of two different hydrodynamic phenomena that occur at bifurcations: plasma skimming and red cell screening (Pries et al., 1996). Plasma skimming was originally described by Krogh (Krogh, 1922) and is the skimming of the plasma-rich marginal layer of the parent vessel into the low-velocity branch at the bifurcation. Phase separation due to plasma skimming does not occur to any significant degree when the feeding vessel is above 40 μm in diameter (Pries et al., 1989). Red cell screening is due to the particulate nature of blood and is caused by fluid forces acting to move the RBC toward the branch with the higher velocity (Pries et al., 1996). Since the effect of red cell screening decreases significantly in vessels greater than about 12 μm in diameter (Pries et al., 1981), it would not be expected to play a direct role in unequal RBC distribution in the relatively large choriocapillaris vessels.
The weak or absent flux-velocity relationship in the normal choriocapillaris (Figures 4A and 5A) is indicative of relatively equal distribution of erythrocytes at most bifurcations upstream. One would predict that this would result in a more homogeneous distribution of RBC flux values in the choriocapillaris, but the standard deviation in RBC flux for the B-ND rats was very large (Table 2). Similarly, there was a large spread in velocity values, especially in capillaries carrying 300 RBC/sec or fewer (Figure 4A). Clearly RBCs did not preferentially flow into capillaries with high velocities, and many high-velocity capillary paths carried relatively few erythrocytes. This apparently random distribution of RBC flux and velocity is most likely due to the absence of velocity-dependent RBC distribution at arteriolar bifurcations upstream and to the complex interconnectivity within the choriocapillaris.
Unlike the situation in the normal choriocapillaris, there was a strong correlation between RBC flux and velocity in the MH-STZ and D-STZ rats (Figures 4B and 4C). This indicates that there was more uneven velocity-dependent distribution of erythrocytes at microvascular branch points in the hyperglycemic rats. Since the strong correlation was maintained even when average values for each vascular field were considered (Figures 5B and 5C), significant redistribution of erythrocytes must have occurred at arteriolar branch points upstream of the choriocapillaris. This hyperglycemia-induced effect may be attributable to differences in normal and nondiabetic arterioles, since defects in the ability of arterioles to vasodilate have been demonstrated in STZ-D rats (Mayhan, 1989) and in human diabetic patients (Goodfellow et al., 1996). In arterioles, uneven RBC distribution is mainly a result of plasma skimming, although any factor that results in asymmetry of the RBC profile in the parent vessel increases the role of red cell screening at the bifurcation and enhances the plasma skimming effect (Pries et al., 1989). Therefore, any diabetes-induced decrease in RBC deformability (Fornal et al., 2006; Petropoulos et al., 2007; Tsukada et al., 2001) or alterations in the interaction between RBCs and the endothelium (Nieuwdorp et al., 2006; Raz et al., 1988) could lead to an increase in plasma skimming at arteriolar bifurcations.
Although we could not directly measure microvascular hematocrit, the velocity-flux relationships in Figure 4 can be used to estimate the relative microvascular hematocrits among the groups. Since no parameters were strongly correlated with vessel diameter and the diameter ranges of the vessels were similar among the groups, the slopes of the lines relating velocity to flux can be considered a rough estimate of the mean RBC spacing within the vessels. These values for the B-ND, STZ-MH, and STZ-D rats are 0.5, 2.0, and 1.7 μm/RBC, respectively. Thus, on average, the erythrocytes in the normal choriocapillaris tend to be more tightly packed, indicative of a higher microvascular hematocrit within the choriocapillaris of normal rats compared to hyperglycemic rats. The lower hematocrit in the STZ-injected rats is attributable to the heterogeneity in RBC distribution and the resultant network Fahraeus effect (Pries et al., 1996). Since capillary oxygen delivery is dependent on erythrocyte spacing (Federspiel and Sarelius, 1984), a high local hematocrit in the choriocapillaris would be consistent with the goal of maximizing oxygen delivery to the photoreceptors by maintaining a steep oxygen gradient from the choriocapillaris into the retina (Linsenmeier and Padnick-Silver, 2000). The high hematocrit in normal choriocapillaris would also agree with our previous data showing that hematocrit in 10-20 μm diameter rat choroidal venules ranged from 15-20% (Braun et al., 1997), much higher than the 8-10% found in similarly sized vessels in cat mesentery (Lipowsky et al., 1980). If the erythrocyte distribution is altered in the diabetic choroid and the average microvascular hematocrit decreases, oxygen delivery to the photoreceptors could be compromised.
Acknowledgments
The authors wish to thank Dr. Mark W. Dewhirst of Duke University for the use of some of the equipment used in portions of this study. This work was supported by National Eye Institute Grant EY11634 to RDB and National Eye Institute Departmental Core Grant P30EY04068.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bhutto IA, Amemiya T. Microvascular architecture of the rat choroid: Corrosion cast study. Anat Rec. 2001;264:63–71. doi: 10.1002/ar.1102. [DOI] [PubMed] [Google Scholar]
- Bill A. Circulation in the eye. In: Renkin E, Michel C, editors. Handbook of Physiology. The Cardiovascular System. Microcirculation. IV. American Physiological Society; Bethesda, MD: 1984. pp. 1001–1034. [Google Scholar]
- Braun RD, Dewhirst MW, Hatchell DL. Quantification of erythrocyte flow in the choroid of the albino rat. Am J Physiol. 1997;272:H1444–1453. doi: 10.1152/ajpheart.1997.272.3.H1444. [DOI] [PubMed] [Google Scholar]
- Caldwell RB, Fitzgerald ME. The choriocapillaris in spontaneously diabetic rats. Microvasc Res. 1991;42:229–244. doi: 10.1016/0026-2862(91)90058-j. [DOI] [PubMed] [Google Scholar]
- Cao J, McLeod DS, Merges CA, Lutty GA. Choriocapillaris Degeneration and Related Pathologic Changes in Human Diabetic Eyes. Arch Ophthalmol. 1998;116:589–597. doi: 10.1001/archopht.116.5.589. [DOI] [PubMed] [Google Scholar]
- Dowdy SM, Wearden S. Statistics for research. Wiley; New York, NY: 1983. [Google Scholar]
- Federspiel WJ, Sarelius IH. An examination of the contribution of red cell spacing to the uniformity of oxygen flux at the capillary wall. Microvasc Res. 1984;27:273–285. doi: 10.1016/0026-2862(84)90059-1. [DOI] [PubMed] [Google Scholar]
- Ferreira LF, Padilla DJ, Musch TI, Poole DC. Temporal profile of rat skeletal muscle capillary haemodynamics during recovery from contractions. J Physiol. 2006;573:787–797. doi: 10.1113/jphysiol.2006.104802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fornal M, Lekka M, Pyka-Fosciak G, Lebed K, Grodzicki T, Wizner B, Styczen J. Erythrocyte stiffness in diabetes mellitus studied with atomic force microscope. Clin Hemorheol Microcirc. 2006;35:273–276. [PubMed] [Google Scholar]
- Frank RN. Diabetic Retinopathy. N Engl J Med. 2004;350:48–58. doi: 10.1056/NEJMra021678. [DOI] [PubMed] [Google Scholar]
- Freyler H, Prskavec F, Stelzer N. Diabetische Chorioidopathie - eine retrospektive fluoreszenzangiographische Studie. Klin Monatsbl Augenheilkd. 1986;189:144–147. doi: 10.1055/s-2008-1050772. [DOI] [PubMed] [Google Scholar]
- Fryczkowski AW, Hodes BL, Walker J. Diabetic choroidal and iris vasculature scanning electron microscopy findings. Int Ophthalmol. 1989;13:269–279. doi: 10.1007/BF02280087. [DOI] [PubMed] [Google Scholar]
- Fryczkowski AW, Sato SE, Hodes BL. Changes in the diabetic choroidal vasculature: scanning electron microscopy findings. Ann Ophthalmol. 1988;20:299–305. [PubMed] [Google Scholar]
- Goodfellow J, Ramsey MW, Luddington LA, Jones CJ, Coates PA, Dunstan F, Lewis MJ, Owens DR, Henderson AH. Endothelium and inelastic arteries: an early marker of vascular dysfunction in non-insulin dependent diabetes. Br Med J. 1996;312:744–745. doi: 10.1136/bmj.312.7033.744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hidayat AA, Fine BS. Diabetic choroidopathy. Light and electron microscopic observations of seven cases. Ophthalmology. 1985;92:512–522. [PubMed] [Google Scholar]
- Hope MJ, Bally MB, Webb G, Cullis PR. Production of large unilamellar vesicles by a rapid extrusion procedure: characterization of size, trapped volume and ability to maintain a membrane potential. Biochim Biophys Acta. 1985;812:55–65. doi: 10.1016/0005-2736(85)90521-8. [DOI] [PubMed] [Google Scholar]
- Hudetz AG, Feher G, Weigle CG, Knuese DE, Kampine JP. Video microscopy of cerebrocortical capillary flow: response to hypotension and intracranial hypertension. Am J Physiol. 1995;268:H2202–2210. doi: 10.1152/ajpheart.1995.268.6.H2202. [DOI] [PubMed] [Google Scholar]
- Joussen AM, Murata T, Tsujikawa A, Kirchhof B, Bursell SE, Adamis AP. Leukocyte-mediated endothelial cell injury and death in the diabetic retina. Am J Pathol. 2001;158:147–152. doi: 10.1016/S0002-9440(10)63952-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kindig CA, Poole DC. A Comparison of the Microcirculation in the Rat Spinotrapezius and Diaphragm Muscles. Microvasc Res. 1998;55:249–259. doi: 10.1006/mvre.1998.2075. [DOI] [PubMed] [Google Scholar]
- Kindig CA, Sexton WL, Fedde MR, Poole DC. Skeletal muscle microcirculatory structure and hemodynamics in diabetes. Respir Physiol. 1998;111:163–175. doi: 10.1016/s0034-5687(97)00122-9. [DOI] [PubMed] [Google Scholar]
- Kleinfeld D, Mitra PP, Helmchen F, Denk W. Fluctuations and stimulus-induced changes in blood flow observed in individual capillaries in layers 2 through 4 of rat neocortex. Proc Natl Acad Sci U S A. 1998;95:15741–15746. doi: 10.1073/pnas.95.26.15741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klitzman B, Johnson PC. Capillary network geometry and red cell distribution in hamster cremaster muscle. Am J Physiol. 1982;242:H211–219. doi: 10.1152/ajpheart.1982.242.2.H211. [DOI] [PubMed] [Google Scholar]
- Krogh A. The anatomy and physiology of capillaries. Yale University Press; New Haven: 1922. [Google Scholar]
- Langham ME, Grebe R, Hopkins S, Marcus S, Sebag M. Choroidal blood flow in diabetic retinopathy. Exp Eye Res. 1991;52:167–173. doi: 10.1016/0014-4835(91)90256-e. [DOI] [PubMed] [Google Scholar]
- Linsenmeier RA, Padnick-Silver L. Metabolic dependence of photoreceptors on the choroid in the normal and detached retina. Invest Ophthalmol Vis Sci. 2000;41:3117–3123. [PubMed] [Google Scholar]
- Lipowsky HH, Usami S, Chien S. In vivo measurements of “apparent viscosity” and microvessel hematocrit in the mesentery of the cat. Microvasc Res. 1980;19:297–319. doi: 10.1016/0026-2862(80)90050-3. [DOI] [PubMed] [Google Scholar]
- Lutty GA, Cao J, McLeod DS. Relationship of polymorphonuclear leukocytes to capillary dropout in the human diabetic choroid. Am J Pathol. 1997;151:707–714. [PMC free article] [PubMed] [Google Scholar]
- Mayhan WG. Impairment of endothelium-dependent dilatation of cerebral arterioles during diabetes mellitus. Am J Physiol. 1989;256:H621–625. doi: 10.1152/ajpheart.1989.256.3.H621. [DOI] [PubMed] [Google Scholar]
- McLeod DS, Lefer DJ, Merges C, Lutty GA. Enhanced expression of intracellular adhesion molecule-1 and P-selectin in the diabetic human retina and choroid. Am J Pathol. 1995;147:642–653. [PMC free article] [PubMed] [Google Scholar]
- McLeod DS, Lutty GA. High-resolution histologic analysis of the human choroidal vasculature. Invest Ophthalmol Vis Sci. 1994;35:3799–3811. [PubMed] [Google Scholar]
- Nieuwdorp M, Mooij HL, Kroon J, Atasever B, Spaan JAE, Ince C, Holleman F, Diamant M, Heine RJ, Hoekstra JBL, Kastelein JJP, Stroes ESG, Vink H. Endothelial Glycocalyx Damage Coincides With Microalbuminuria in Type 1 Diabetes. Diabetes. 2006;55:1127–1132. doi: 10.2337/diabetes.55.04.06.db05-1619. [DOI] [PubMed] [Google Scholar]
- Ninomiya H, Kuno H. Microvasculature of the rat eye: scanning electron microscopy of vascular corrosion casts. Vet Ophthalmol. 2001;4:55–59. doi: 10.1046/j.1463-5224.2001.00143.x. [DOI] [PubMed] [Google Scholar]
- Padilla DJ, McDonough P, Behnke BJ, Kano Y, Hageman KS, Musch TI, Poole DC. Effects of Type II diabetes on capillary hemodynamics in skeletal muscle. Am J Physiol. 2006;291:H2439–2444. doi: 10.1152/ajpheart.00290.2006. [DOI] [PubMed] [Google Scholar]
- Petropoulos I, Margetis P, Antonelou M, Koliopoulos J, Gartaganis S, Margaritis L, Papassideri I. Structural alterations of the erythrocyte membrane proteins in diabetic retinopathy. Graefes Arch Clin Exp Ophthalmol. 2007;245:1179–1188. doi: 10.1007/s00417-006-0500-6. [DOI] [PubMed] [Google Scholar]
- Pries AR, Albrecht KH, Gaehtgens P. Model studies on phase separation at a capillary orifice. Biorheology. 1981;18:355–367. doi: 10.3233/bir-1981-183-605. [DOI] [PubMed] [Google Scholar]
- Pries AR, Ley K, Claassen M, Gaehtgens P. Red cell distribution at microvascular bifurcations. Microvasc Res. 1989;38:81–101. doi: 10.1016/0026-2862(89)90018-6. [DOI] [PubMed] [Google Scholar]
- Pries AR, Secomb TW, Gaehtgens P. Biophysical aspects of blood flow in the microvasculature. Cardiovasc Res. 1996;32:654–667. [PubMed] [Google Scholar]
- Raz I, Havivi Y, Yarom R. Reduced negative surface charge on arterial endothelium of diabetic rats. Diabetologia. 1988;31:618–620. doi: 10.1007/BF00264770. [DOI] [PubMed] [Google Scholar]
- Ring HG, Fujino T. Observations on the anatomy and pathology of the choroidal vasculature. Arch Ophthalmol. 1967;78:431–444. doi: 10.1001/archopht.1967.00980030433005. [DOI] [PubMed] [Google Scholar]
- Russell JA, Kindig CA, Behnke BJ, Poole DC, Musch TI. Effects of aging on capillary geometry and hemodynamics in rat spinotrapezius muscle. Am J Physiol. 2003;285:H251–258. doi: 10.1152/ajpheart.01086.2002. [DOI] [PubMed] [Google Scholar]
- Sarelius IH, Duling BR. Direct measurement of microvessel hematocrit, red cell flux, velocity, and transit time. Am J Physiol. 1982;243:H1018–1026. doi: 10.1152/ajpheart.1982.243.6.H1018. [DOI] [PubMed] [Google Scholar]
- Savage HI, Hendrix JW, Peterson DC, Young H, Wilkinson CP. Differences in Pulsatile Ocular Blood Flow among Three Classifications of Diabetic Retinopathy. Invest Ophthalmol Vis Sci. 2004;45:4504–4509. doi: 10.1167/iovs.04-0077. [DOI] [PubMed] [Google Scholar]
- Tsukada K, Sekizuka E, Oshio C, Minamitani H. Direct Measurement of Erythrocyte Deformability in Diabetes Mellitus with a Transparent Microchannel Capillary Model and High-Speed Video Camera System. Microvasc Res. 2001;61:231–239. doi: 10.1006/mvre.2001.2307. [DOI] [PubMed] [Google Scholar]
- Unthank JL, Lash JM, Nixon JC, Sidner RA, Bohlen HG. Evaluation of carbocyanine-labeled erythrocytes for microvascular measurements. Microvasc Res. 1993;45:193–210. doi: 10.1006/mvre.1993.1018. [DOI] [PubMed] [Google Scholar]
- Van der Meer C, Versluys-Broers JA, Tuynman HA, Buur VA. The effect of ethylurethane on hematocrit, blood pressure and plasma-glucose. Arch Int Pharmacodyn Ther. 1975;217:257–275. [PubMed] [Google Scholar]
- Wajer SD, Taomoto M, McLeod DS, McCally RL, Nishiwaki H, Fabry ME, Nagel RL, Lutty GA. Velocity Measurements of Normal and Sickle Red Blood Cells in the Rat Retinal and Choroidal Vasculatures. Microvasc Res. 2000;60:281–293. doi: 10.1006/mvre.2000.2270. [DOI] [PubMed] [Google Scholar]
- Wolford ST, Schroer RA, Gohs FX, Gallo PP, Brodeck M, Falk HB, Ruhren R. Reference range data base for serum chemistry and hematology values in laboratory animals. J Toxicol Environ Health. 1986;18:161–188. doi: 10.1080/15287398609530859. [DOI] [PubMed] [Google Scholar]
- Yuan F, Dellian M, Fukumura D, Leunig M, Berk DA, Torchilin VP, Jain RK. Vascular permeability in a human tumor xenograft: molecular size dependence and cutoff size. Cancer Res. 1995;55:3752–3756. [PubMed] [Google Scholar]