The frequency of polyploid speciation in vascular plants

Abstract

Since its discovery in 1907, polyploidy has been recognized as an important phenomenon in vascular plants, and several lines of evidence indicate that most, if not all, plant species ultimately have a polyploid ancestry. However, previous estimates of the frequency of polyploid speciation suggest that the formation and establishment of neopolyploid species is rare. By combining information from the botanical community's vast cytogenetic and phylogenetic databases, we establish that 15% of angiosperm and 31% of fern speciation events are accompanied by ploidy increase. These frequency estimates are higher by a factor of four than earlier estimates and lead to a standing incidence of polyploid species within genera of 35% (n = 1,506). Despite this high incidence, we find no direct evidence that polyploid lines, once established, enjoy greater net species diversification. Thus, the widespread occurrence of polyploid taxa appears to result from the substantial contribution of polyploidy to cladogenesis, but not from subsequent increases in diversification rates of polyploid lines.

Polyploidy, the heritable increase in genome copy number, is a central feature of plant diversification (1–3). Polyploidy is captivating as a speciation mechanism for several reasons: (i) it is often associated with the defining features of neospecies, reproductive isolation and morphological differentiation, (ii) it can cause the saltational origin of new species, and (iii) it can have profound effects on subsequent lineage evolution because of genome duplication. Analyses of cytological, fossil and genomic data suggest that 47% to 100% of flowering plant species can be traced to a polyploid event at some point within the diversification of the angiosperm crown group (3–5). In ferns, high chromosome base numbers suggest that most extant taxa are derived from ancient polyploidy (6). However, these inferences tell us relatively little about the frequency of ongoing polyploid speciation, because they are compatible with both rare and frequent polyploid speciation. Current model-based estimates of speciation via polyploidy suggest that it is rare relative to homoploid divergence (7, 8). Here, we use phylogenetic data to obtain the first direct estimate of the frequency of polyploid speciation in flowering plants and ferns and to evaluate whether polyploid lineages diversify more rapidly.

Results and Discussion

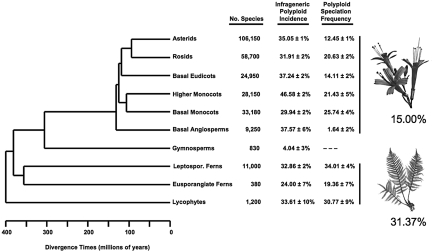
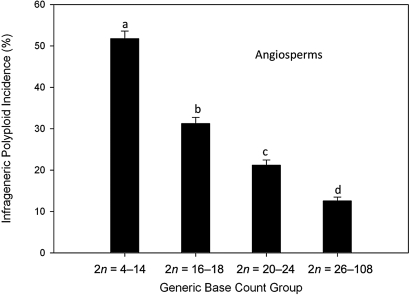
First, following Stebbins (9) and others (10–12), we used published chromosome counts to characterize polyploid incidence across a diverse sample of vascular plant genera. Across the entire dataset, 34.5% (9,795 of 28,406) of species are inferred to be polyploid relative to their generic base (see Materials and Methods and Table S1). We then grouped these data phylogenetically to examine dispersion in this index across the major lineages of vascular plants (13–16; Fig. 1). At this scale, the most striking feature is uniformity of the means across the groups: Phylogenetic taxonomy explains very little of the variation (χ₇² = 380.73, P < 0.0001, R² = 0.010, with the ferns and lycophytes grouped and hereafter referred to as ferns). In contrast, polyploid incidence is distributed less equitably among families (χ₁₉₈² = 4,259.41, P < 0.00001, R² = 0.116). Overall, with the exception of the species-poor gymnosperms, vascular plant species derived from recent polyploid events are ubiquitous and represent a large fraction of named diversity, a pattern that also holds for bryophytes (12). Interestingly, generic base counts are negatively associated with polyploid incidence in angiosperms (χ₃² = 2,798.01, P < 0.00001, R² = 0.085; Fig. 2), but show no association in ferns (χ₃² = 6.61, P = 0.085, R² = 0.002). This result provides the first quantitative support for the hypothesis that chromosome number increase due to polyploidy limits subsequent diversification via genome duplication in flowering plants (3). In addition, this observation may help to explain the stark difference in mean chromosome number between homosporous ferns and angiosperms.

Fig. 1.

Polyploid incidence and speciation frequencies across major groups of vascular plants. Polyploid speciation frequencies are the fractions of branching events that were accompanied by a ploidy shift across the studied phylogenetic trees for each group. The speciation frequencies reported here are based on an irreversible model of polyploid evolution. A binomial standard error follows each incidence and frequency estimate. See Fig. S1 for a diagrammatic explanation of estimation methods for polyploid speciation frequencies. Phylogenetic hypothesis/timescale modified from (13), and based on clades defined in refs. 13–16; clade species richness from refs. 13 and 34. The Higher Monocots are represented by Arecales, Commelinales, Poales, Proteales, Zingiberales; the Basal Monocots by Alistmatales, Asparagales, Dioscoreales, Liliales, Pandanales.

Fig. 2.

Dependence of infrageneric polyploid incidence on the minimum number of chromosomes reported for angiosperm genera (generic base count). Shown are mean percentages (± SE) of polyploid species within genera. Means with different letters are significantly different [P < 0.05 when evaluated within a logistic model and with nonparametric (rank sums) tests]. (N (l − r) = 320, 323, 370, 354).

Assuming no speciation within polyploid lineages, the percentage of species that are infrageneric polyploids can be interpreted as an upper limit to the frequency of polyploid speciation. In contrast, published estimates of the frequency of polyploid speciation for flowering plants [2–4% (ref. 8) and 3.8% (ref. 7)] and ferns [7% (ref. 8)], set an approximate lower limit because they are derived from models that assume a minimum number of infrageneric ploidy shifts. A recent model for predicting polyploid abundance allows multiple, independent transitions to the same ploidy level (17), but it has been applied to only 10 flowering plant genera, all of which have numerous ploidy levels (>4) and are not representative of angiosperms as a whole.

To avoid the above assumptions, we directly estimated the frequency of polyploid speciation by tracking shifts in ploidy level across infrageneric plant phylogenetic trees. For angiosperms, we sampled 1,813 speciation events within 123 phylogenetic trees drawn from the plant systematic literature (Table S2; see Fig. S1 for methodological diagram). Using an irreversible model of polyploid evolution, 272 of the 1,813 events (15.00 ± 0.84%; ± SE) were accompanied by a shift to a higher ploidy level. For ferns, we examined 204 speciation events within 20 infrageneric phylogenetic trees; 64 (31.37 ± 3.26%) involved an increase in ploidy (Table S3). Although less biologically realistic, we also used simple parsimony to map shifts in ploidy level; under this model there were 232 ploidy transitions (12.80 ± 0.78%) across the angiosperm dataset, and 61 (29.90 ± 3.21%) across the ferns.

One concern is that our results may be biased because of uncertainty in the phylogenetic trees analyzed. To obtain a rough estimate of the sensitivity of our angiosperm result to phylogenetic uncertainty, we recorded the minimum number of ploidy transitions across published topologies derived from different data partitions for all studies that reported them and that included 2 or more polyploid species (n = 30). The number of ploidy shifts is slightly lower in the partitioned data (123 versus 139 for the irreversible case), resulting in a ≈3% decrease in the polyploid speciation frequency estimate for angiosperms. This decrease is primarily due to the lower resolution of trees derived from fewer data: Groupings of polyploid/diploid species on trees derived from combined data are collapsed into polytomies, thus fewer shifts are inferred. Given that many of the sampled phylogenetic trees from the full data also contain polytomies, our estimates may be best considered conservative.

Another worry is that aneuploidy can make patterns of chromosomal evolution more complex, and thus, the tracking of ploidy state transitions can become somewhat subjective (see Materials and Methods). Although aneuploid variation was not substantial in the fern dataset, we identified 16 angiosperm groups where significant aneuploidy was present. To validate our inferences of the number of ploidy shifts in these groups, we used a recently developed model to infer the number of ploidy shifts in 12 of the 16 taxa that exhibit substantial aneuploidy (see SI Methods). The number of ploidy shifts inferred with the model-based approach is slightly higher across the 12 groups compared with our more conservative method (62 versus 55; Table S4 and Table S5). This was anticipated because the model-based approach estimates the expected number of polyploid events, taking into account multiple events along a single branch. In addition, even if sister species have the same number of chromosomes, the probabilistic model may infer that they are separated by one or more ploidy transitions, particularly if the branches separating the species are long and the aneuploid and polyploid transition rates are high across the tree (see SI Methods).

The phylogenetic trees used here represent 63 of ≈400 recognized angiosperm families (18) and 10 of ≈40 fern families (16). This broad sample demonstrates that ongoing polyploid speciation is substantially more common in vascular plants than the current estimates suggest (7, 8). Our species-level estimates are bolstered by the frequency of infraspecific polyploidy: 12–13% of angiosperm and 17% of fern species harbor multiple ploidy levels (see Materials and Methods, and ref. 19). But how do polyploid lineages fare over longer timeframes?

Several researchers have presented a positive relationship between generic species richness and polyploid incidence in angiosperms as indirect evidence that genome doubling is associated with increased net diversification rate (8, 20, 21), a result we corroborate here across 1,271 genera. However, polyploid incidence explains only a small portion of the variance in generic species richness across the entire angiosperm dataset (F_1,1269 = 73.90, P < 0.0001, R² = 0.055), although the relationship is tighter when only those genera for which we have chromosome counts for ≥50% of the species are included (F_1,488 = 82.86, P < 0.0001, R² = 0.145). In ferns, polyploid incidence is not a significant predictor of generic species richness (F_1,94 = 2.16, P = 0.145, R² = 0.022). Earlier workers have treated the angiosperm result cautiously (8, 17, 20, 21), arguing that genera with high species richness and polyploid incidence may simply be older than genera with comparatively fewer species and lower polyploid incidence. Alternatively, this relationship may arise because polyploid lines do not contribute to morphological disparity (22) and thus are less likely to be segregated as genera. Instead, the reproductive isolation that often attends ploidy shifts may allow the accumulation of more species within genera than would otherwise occur in the absence of polyploidy. Both age and taxonomy may thus influence the positive association between generic species richness and infrageneric polyploid incidence. Consequently, this relationship cannot be taken as direct evidence that polyploidy leads to increased net species diversification.

To evaluate the taxonomic influence, we worked at a slightly larger scale to assess the degree to which polyploidy is an infrageneric phenomenon. For angiosperms, we mapped ploidy shifts across 34 intrafamilial phylogenetic trees where the terminal branches typically represent genera. Although it can be difficult to determine that a genus is wholly polyploid because of incomplete cytogenetic sampling, we estimated the number of angiosperm genera that are polyploid relative to near allies (Table S6). The origins of 64 of 435 genera (15.6 ± 1.74%) were associated with an increase in ploidy, a fraction that is strikingly similar to the frequency of polyploid speciation. However, this estimate is biased upward, because it is likely that some genera scored as polyploid contain unsampled, extant diploid species.

Therefore, we conducted a more direct test of the relative success of polyploid versus diploid lines. If polyploidy has increased net diversification rates, then polyploid species would tend to group together on phylogenetic trees, and these groups would contain more species than their lower-ploid sister groups. Based on this logic, we tested for differences in species richness between angiosperm sister groups, each invariant for ploidy level but separated by a ploidy shift, to determine whether such shifts accelerate diversification (Table S7 and Fig. S1). Of 59 comparisons involving greater than 2 species, 23 polyploid lineages contain more species, whereas 30 do not (6 ties). The marginal difference in species richness in these polyploid by diploid contrasts is not significant when evaluated by both parametric and nonparametric tests (n = 59, t = 0.4561, P = 0.650, 2-tailed matched pairs t test; n = 59, z = −1.169, P = 0.2425, Wilcoxon/Kruskal–Wallis Test). The symmetry in species richness between polyploid-diploid sister groups in this broader survey is in accord with a similar analysis conducted at the intergeneric level within the Rosaceae (21). Overall, single ploidy transitions that separate reasonably large lineages are rare, indeed most ploidy transitions in this analysis (92 of 151) separate 2 species (1:1 ties).

By necessity, the above contrasts were often drawn from the tips of the trees. To use more of the information contained within our sample of trees, we evaluated diversification rate variation with SymmeTREE (23). This method assesses whole trees for significant asymmetry and identifies nodes at which significant shifts in net diversification occur. We examined 26 topologies that contained 2 or more polyploid species. Twelve of these exhibited significant diversification rate variation based on at least 1 whole-tree statistic, and 6 of these 12 trees had at least 1 node that could be linked to a diversification rate shift. However, ploidy shifts could be implicated in only 2 of the topologies. In one of these 2 trees, the single significant node subtends a clade that is polymorphic for ploidy (5 polyploids, 2 diploids and 3 species with no count data). Thus, although polyploidy clearly contributes to the clade imbalance identified by the model, we cannot infer that polyploids within this group have diversified at an elevated rate. In the second case, the model identified 4 significant nodes. Two of these represent branching events within a polyploid lineage and one is deep in the tree and is not near a ploidy shift. The 4th shift occurs along a branch that supports 27 polyploid species, 9 diploid species and 15 species of unknown ploidy level. The sister group to this clade is a single species of unknown ploidy level. Although these results do not provide a clear answer, they are consistent with our conclusion based on the sister group contrasts. Both of the comparative approaches used here demonstrate that ploidy lability limits our ability to evaluate differences in speciation rate between polyploid and diploid lines within angiosperm genera; and clearly, attempts to establish individual ploidy shifts in deep time as causal to diversity radiations (24) are tenuous.

In conclusion, our results indicate that the frequency of polyploid speciation in vascular plants is higher by a factor of four compared with previous estimates. These new estimates may be conservative because: (i) incomplete phylogenetic resolution, common in our phylogeny dataset, will lead, on average, to fewer inferred ploidy shifts than truly occurred, and (ii) multiple polyploid speciation events that share one or both parents may appear to represent a single event in phylogenetic trees (25). Also, our estimates do not include unnamed, intraspecific polyploid cytotypes, which may often represent cryptic biological species (19). Although we detect no diversification advantage associated with genome duplication, the high frequency of polyploid speciation in angiosperms, coupled with loss of chromosomes in polyploid lines (26), helps to explain the initially surprising evidence that even flowering plant species with low chromosome numbers have a polyploid ancestry (27).

Materials and Methods

Polyploid Incidence Within Genera.

We assembled a chromosome count database from the portion of the Index of Plant Chromosome Numbers (IPCN) that was available in digital form (28). Two data files were constructed, 1 for seed plants and 1 for ferns. For the latter, the IPCN data were augmented by hand with chromosome counts from a different compendium (29), all earlier IPCN print volumes (28), and several recent primary sources. The numbers of infrageneric polyploid species in both the seed plant and fern datasets were computed with a Perl script, where sporophytic (2n) counts greater than or equal to 3.5 times the lowest haploid (n) count of the host genus were tabulated as polyploid. Genera with counts that fell between the lowest count and the polyploid threshold were checked by hand, and those genera for which there was dysploid continuity between the lowest count and species tagged as polyploid were removed. In addition, genera with data for 3 or fewer species and for which the lowest count was not corroborated by a second count were also removed from the seed plant analysis. The ferns were treated in the same way except that genera with singleton base counts were included when this count was deemed accurate. Angiosperm genera with lowest counts inferred from 2 records from only 1 species were checked against data from Federov (30) to ensure accuracy. When there were conflicts between these 2 sources, the genera were removed. Finally, 3 groups (Cyperaceae, Cuscuta, Luzula) known to possess holocentric chromosomes were removed from the analysis. The number of species within a genus with chromosome count data are positively correlated with generic species richness. Thus, weighted averages of the percentage of polyploid species are reported as they more accurately reflect the group-level expectation of drawing a polyploid species at random from the dataset or from nature. Data from the above Perl analyses were used to compare polyploid incidence among clades identified by molecular systematists (13–16). In addition, we grouped angiosperm and fern genera separately into 4 base count categories, low to high and each with approximately the same number of genera, to determine whether generic base count is a predictor of polyploid incidence. Because polyploid incidence is a proportion, we used a logistic model to evaluate statistical significance. Statistical analyses, including those below, were performed using JMP versions 5 or 7 (ref. 31). The polyploid incidence data are reported in Table S1.

Polyploid Incidence Within Species.

The incidence of infraspecific polyploidy was estimated by calculating the fraction of named species that contain multiple ploidy levels. This fraction has been estimated on a smaller scale elsewhere for angiosperms (19, 32). We used the chromosome count datasets described above to estimate this fraction for both ferns and angiosperms. Triploid counts are excluded from these estimates. We report the fern and angiosperm estimates in the results as single point estimates.

Polyploid Incidence and Species Richness.

The relationship between polyploid incidence and generic species richness estimates was evaluated with ANOVA. Species richness was natural log transformed. In cases where the number of species in the richness estimate was lower than the number of species for which we had count data, we set species richness equal to the number of species with data. The data used for this analysis are included in Table S1.

Phylogenetic Analysis of the Frequency of Polyploid Speciation.

Angiosperms.

We selected published phylogenetic trees from the plant systematic literature: American Journal of Botany (2004–2006), Plant Systematics and Evolution (2004–2005), Systematic Botany (2001–2006), and Taxon (2003–2004). Those studies that included ≈25% or more of the recognized taxa of the most intensively sampled group (e.g., a section of a genus) were included. On average 44.5% of recognized species of the focal groups were sampled for phylogenetic analysis and had chromosome counts (sampling intensity). Regression of the number of ploidy shifts per speciation event on sampling intensity is not significant (F_1,122 = 1.03, P = 0.313, R² = 0.008).

Most studies were based on multiple data partitions and presented more than one topology; when possible, we selected the tree that was inferred from the most data. We used chromosome counts from the seed plant dataset, the IPCN volume 1975–78 (28), and Federov (30), and counts reported with the phylogenetic analyses to infer ploidy level. In the few cases where there was a conflict between counts reported with the phylogenetic analysis and those from compendia, we used exclusively the count data reported with the phylogenetic analysis to infer ploidy level.

We coded ploidy states by treating each discrete group of counts separated by a gap more than or equal to to the lowest count as a separate ploidy state. For example, n = 9 and n = 18 coded as 2 different ploidy states (0, 1); n = 9–13 and n = 22 coded as 2 different ploidy states (0, 1); n = 8, n = 16, and n = 24 coded as 3 different ploidy states (0, 1, 2). The numbers of character state transitions were inferred with unordered optimization. Thus, for the last, 3-state example, if a species with state 0 (for n = 8) were sister to a species with state 2 (for n = 24), this was counted as a single step, i.e., a single polyploid event. Speciation events that did not involve doubling but that were inferred to involve an addition of a complete chromosome set, were counted as polyploid events, e.g., transitions from state 1 to state 2 in the 3-state example.

For most taxa, the above methods were sufficient; however, for some groups (n = 16), aneuploid variation (loss or gain of chromosomes without change in ploidy) was substantial and made ploidy state inference more difficult because gaps between ploidy states were blurred. For a subset of these phylogenetic trees (n = 12), we used a likelihood approach that assessed the fit of various models that allowed for both aneuploid (gain or loss of single chromosomes) and polyploid changes to infer the number of ploidy shifts across a tree (see SI Methods for details). In general, the best-fit model inferred more ploidy shifts than our approach based on more subjective scoring of ploidy states in groups with aneuploidy. A comparison of the results is presented in Table S4. The results reported in Fig. 1 are based on the scoring approach described in the previous paragraph rather than the likelihood model results, because the model could not be applied to all phylogenies.

In this analysis, the number of speciation events per phylogenetic hypothesis is equal to the number of species with count data minus one. Thus, our estimate of the frequency of polyploid speciation is the fraction of speciation events that are accompanied by a transition in ploidy. This method ignores extinction and assumes that ploidy transitions are directly associated with speciation, an assumption that is consistent with the observation that ploidy transitions are accompanied by reproductive isolation. However, by ignoring extinction, we may be overestimating the contribution of polyploidy to cladogenesis.

We first determined the numbers of ploidy transitions with an irreversible model with unordered states, where the deepest node in the tree was constrained to the lowest ploidy state in the group and ploidy level decreases were not allowed. This model is in accord with the consensus view that polyhaploidy is likely very rare in nature. When necessary, we used MacClade 4.06 to determine the number of ploidy state changes (33). Because the irreversible model cannot be implemented in MacClade unless all nodes are dichotomous, we resolved polytomies to minimize ploidy state changes (most parsimonious solution of a “soft” polytomy). We also inferred the number of ploidy transitions with parsimony, again with unordered states. We report a binomial standard error for our estimates of the frequency of polyploid speciation. Table S2 lists the phylogenies, with associated data, used for this analysis.

Ferns and lycophytes.

We identified published phylogenetic trees using a variety of scientific indices and chose twenty studies for inclusion. All of the selected phylogenetic trees contained at least 4 species with count data. In all but 1 case (Dryopteris), the studies were focused on small genera or small clades within genera. On average, 83.1% of recognized species of the focal groups were sampled for phylogenetic analysis and had chromosome counts (sampling intensity). In most cases, the authors of the study considered ploidy variation explicitly, and we used the count data presented in the study to infer the number of ploidy transitions. In this sample, aneuploid variation was not significant. In some cases, the comprehensive dataset used for the Perl analysis was used as a supplement, and, as with the angiosperm analysis, we resolved conflicts between data reported in the article and in our dataset in favor of the former. The frequency of polyploid speciation was calculated as for the angiosperms. For this sample, there is a significant, positive relationship between polyploid speciation frequency and sampling intensity (F_1,19 = 5.08, P = 0.037, R² = 0.22). The leverage comes from 4 phylogenetic trees with no polyploid events and incomplete chromosome count data. In total, these 4 studies contain 25 speciation events. Table S3 lists the phylogenetic studies and associated data used for this analysis.

Polyploidy and the Evolution of Genera.

We performed this analysis in the manner described above for the phylogenetic analyses of polyploid speciation frequencies. Phylogenies were drawn from the American Journal of Botany (2004–2006) and International Journal of Plant Sciences (2006) and represent 28 families. It is expected that a portion of the genera scored as polyploid contain unsampled diploid species, thus our estimate of the number of polyploid genera is biased upward. Table S6 lists the phylogenies and associated data used for this analysis.

Polyploidy and Net Diversification Rate.

Nonnested sister group contrasts.

We examined all angiosperm phylogenies included in the polyploid speciation frequency analysis for contrasts between sister lineages that were each monomorphic for ploidy level but separated by a ploidy shift. To increase sample size, we then searched for phylogenetic hypotheses for genera that were relatively well characterized cytogenetically within the first half of Federov (30) and/or in our chromosome count dataset (these studies constitute the “Nonrandom” (NR) studies in Table S7). For many of the studies examined, sampling is incomplete: Either all species within a clade were not sampled, or cytogenetic data were not available for all species; or sampling was incomplete in both respects. In general, we only included contrasts where chromosome count data were available for all sampled taxa on either side of a single ploidy shift. In the included studies with missing count data, the sign of the contrast (e.g., more polyploid species) is robust to new data, although the species numbers may not be (e.g., 5:1 may change to 2:1). We do include contrasts where phylogenetic sampling is incomplete (all recognized species not included). When these latter studies are excluded, the difference between polyploid and diploid lineages remains insignificant. Table S7 lists the studies and associated data used for this analysis.

Whole-tree asymmetry.

We used SymmeTREE to determine whether a subset of the published angiosperm trees used to track ploidy changes contain statistically significant shifts in diversification rates (23). This program compares species diversity differences across all nodes within a topology and compares these differences, based on a variety of asymmetry metrics, to a null distribution derived from simulations. If a given tree contained a significant shift in diversification rate based on any one of the test statistics (without correcting for multiple tests), we then identified the node at which this shift occurred to determine whether it coincides with a ploidy shift. For this analysis we focused on those trees for which ≥80% of recognized species were sampled and which contained ≥2 polyploid species. SymmeTREE can accommodate polytomies by resolving them randomly, however, trees that exhibited significant asymmetry only within randomly resolved polytomies were not scored as asymmetric.