Modeling Aging Effects on Two-Choice Tasks: Response Signal and Response Time Data

Abstract

In the response signal paradigm, a test stimulus is presented, and then at one of a number of experimenter-determined times, a signal to respond is presented. Response signal, standard response time (RT), and accuracy data were collected from 19 college-age and 19 60- to 75-year-old participants in a numerosity discrimination task. The data were fit with 2 versions of the diffusion model. Response signal data were modeled by assuming a mixture of processes, those that have terminated before the signal and those that have not terminated; in the latter case, decisions are based on either partial information or guessing. The effects of aging on performance in the regular RT task were explained the same way in the models, with a 70- to 100-ms increase in the nondecision component of processing, more conservative decision criteria, and more variability across trials in drift and the nondecision component of processing, but little difference in drift rate (evidence). In the response signal task, the primary reason for a slower rise in the response signal functions for older participants was variability in the nondecision component of processing. Overall, the results were consistent with earlier fits of the diffusion model to the standard RT task for college-age participants and to the data from aging studies using this task in the standard RT procedure.

Response times (RTs) are generally longer for older participants than young participants. Interpretations of this have been difficult, in part because of differences in participants' speed–accuracy criterion settings. It is well known that participants can trade speed for accuracy or accuracy for speed (Luce, 1986; Pachella, 1974; Reed, 1973; Swensson, 1972; Wickelgren, 1977). Variations in criterion settings can also interact with task difficulty, with some participants showing large RT differences across levels of difficulty and other participants showing smaller differences. The problem becomes especially acute if different groups of participants, such as the young and older participants of interest in this article, adopt systematically different tradeoff settings. When this is the case, differences in settings lead to difficulties in the interpretation of processing speed.

In a standard two-choice decision task, each participant can choose his or her own tradeoff setting and therefore his or her own accuracy values and RTs. In contrast, in a response signal task, participants are instructed to respond at times set by the experimenter. In the response signal procedure (see Corbett & Wickelgren, 1978; Dosher, 1976, 1979, 1981, 1982, 1984; McElree & Dosher, 1993; Ratcliff, 1978, 1980, 1981; Reed, 1973, 1976; Schouten & Bekker, 1967; Wickelgren, 1977; Wickelgren & Corbett, 1977), each test stimulus is followed by a signal to respond, and participants are trained to respond within 300 ms of the signal. Stimulus-to-signal times are chosen to produce a range of accuracy values from chance performance to asymptotic performance, producing a function that shows how accuracy increases with processing time. For example, in lexical decision, test strings of letters could be followed by response signals at 50 ms up to 1,800 ms. Participants would perform at chance at the 50-ms lag and near 100% correct at the 1,800-ms lag.

In the response signal paradigm, accuracy values are usually converted to d′ values, with one experimental condition taken as baseline and the other conditions scaled against it. The d′ functions allow estimates of the point in time at which accuracy begins to rise above chance, the rate at which accuracy grows, and the asymptotic value of accuracy. Such time course data are most often obtained by fitting an exponential growth function to the data and using parameters of the fit as measures of these aspects of performance (onset, growth rate, and asymptote). For the research presented here, I used both the standard task with speed and accuracy instructions and a response signal task. The goals were to place more constraints on the ability of the diffusion model to explain data, to use both kinds of procedures to see whether a consistent view of the effects of aging on performance is obtained across the tasks, and to better understand performance in the response signal task. Furthermore, because the diffusion model is a process model, it can predict the time course of the increase in proportion correct for every condition rather than having to scale one condition against another.

In sequential sampling models like the diffusion model, the problems of separating speed and accuracy effects from each other and from effects of task difficulty are handled theoretically. Speed, accuracy, and task difficulty are mapped jointly onto theoretically defined components of processing. In this study, the diffusion model is applied jointly to the data from speed and accuracy instructions in the standard RT task and to response signal data, as in Ratcliff (2006). The aim is to identify components of processing that differ between young and older participants.

When the same stimuli are used in the standard two-choice procedure and in the response signal procedure with the same participants, the underlying components of processing should be plausibly related between the two procedures. The important difference between the tasks is that responses in the standard procedure are governed by the information in the stimulus coupled with participants' speed–accuracy tradeoff settings, whereas responses in the response signal procedure are governed by stimulus information coupled with experimenter-determined response signal times. Until recently, there have been few attempts to relate data from the two procedures to each other. In part, this is because integrating the two kinds of data—RT distributions and accuracy values for correct and error responses from the standard procedure plus accuracy values as a function of time from the response signal procedure—cannot be done empirically. However, as pointed out above, it can be done by interpreting the data through sequential sampling models.

There is an alternative procedure, called the deadline procedure, that is like the response signal procedure except that the time between the stimulus onset and the signal to respond is constant for each block of trials. Reed (1973) argued that the response signal procedure is superior to the deadline procedure because in the deadline procedure, participants can adjust their criteria across blocks of trials. In fact, I ran a companion set of deadline sessions with the response signal sessions in the experiments reported in Ratcliff (2006) and found that the average RT for a particular deadline varied significantly across sessions of the experiment, producing significant differences in accuracy across sessions. Also, because the deadline was predictable, participants produced fast guesses. In contrast, because the response signal procedure has the lag variable from trial to trial, participants cannot anticipate the signal and so cannot produce fast guesses.

I present an experiment using a numerosity discrimination experiment. This task has the advantage that there is no limitation on perceptual information or on memory so it serves as a baseline against which to compare other tasks. Two versions of the diffusion model were tested against data from both the standard procedure, with speed and accuracy instructions, and the response signal procedure. The question was whether the models could explain the data: accuracy values and the distributions of correct and error RTs for the standard task, as well as the growth of proportion correct as a function of lag for the response signal task. Fitting all of these data simultaneously is a significant challenge. The crucial questions are whether the interpretation of the data from the two tasks is the same within the diffusion model framework, ascribing empirical effects to the same components of processing, and whether the effects of aging are attributed to the same components of processing.

In the experiment presented here, the stimuli were arrays of dots. On each trial, participants were asked to decide whether the number of dots was large or small, with the number of dots ranging from 31 to 70. The same participants were tested on both the standard RT task and the response signal task. In the standard task, there were blocks of trials for which participants were instructed to respond as quickly as possible and alternating blocks for which they were instructed to respond as accurately as possible. In the response signal task, six response signal lags were used, ranging from 50 to 1,800 ms with lags randomly assigned to trials.

Diffusion Model

In the diffusion model, noisy evidence is accumulated over time toward one of two response criteria corresponding to the two possible responses. A response is executed when a criterion is reached. Different processes from the same experimental condition with the same mean rate of accumulation of evidence reach the correct criterion at highly variable times, thus producing RT distributions, and they sometimes reach the wrong criterion, thus producing an error. Evidence is a single quantity so that one criterion corresponds to positive evidence and the other to negative evidence.

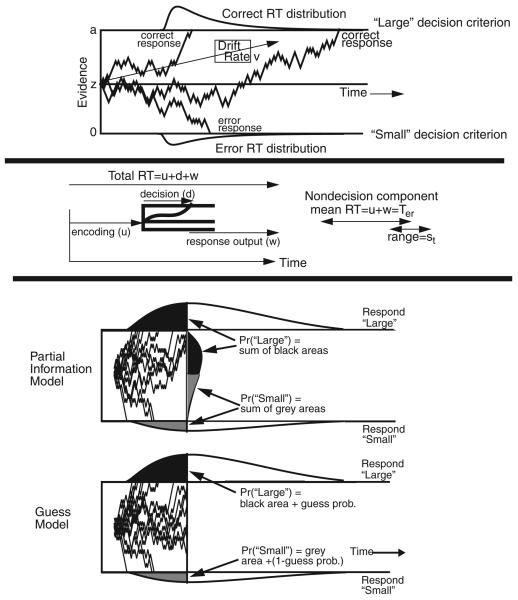
The top panel of Figure 1 illustrates the diffusion model (see Busemeyer & Townsend, 1993; Diederich & Busemeyer, 2003; Gold & Shadlen, 2001; Laming, 1968; Link, 1992; Link & Heath, 1975; Palmer, Huk, & Shadlen, 2005; Ratcliff, 1978, 1981, 1988, 2006; Ratcliff, Cherian, & Segraves, 2003; Ratcliff & McKoon, 2008; Ratcliff & Rouder, 1998; Ratcliff & Smith, 2004; Ratcliff et al., 1999; Roe, Busemeyer, & Townsend, 2001; Smith, 1995, 2000; Smith, Ratcliff, & Wolfgang, 2004; Stone, 1960; Voss, Rothermund, & Voss, 2004) and its noisy accumulation of evidence from a starting point (z) toward one or the other of the boundaries (a or 0). The mean rate of accumulation of evidence is called drift rate (v). In perceptual tasks, drift rate is determined by the quality of the information extracted from a stimulus; in recognition memory and lexical decision tasks, it is determined by the quality of the match between a test item and memory. Within-trial variability (noise) causes processes with the same drift rate to terminate at different times (producing RT distributions) and sometimes to terminate at the wrong boundary (producing errors). The values of the components of processing vary from trial to trial. Drift rate is assumed to be normally distributed across trials with a standard deviation of η. Starting point is assumed to be uniformly distributed across trials with range s_z (which is equivalent to variability in decision criteria if the variability is not too large).

Figure 1.

An illustration of the diffusion model. The top panel illustrates the diffusion model with starting point z, boundary separation a, and drift rate v. Three sample paths are shown illustrating variability within the decision process, and correct and error RT distributions are illustrated. The middle panel illustrates the components of processing besides the decision process d with the duration of the encoding process u and the duration of processes after the decision process w. These two components are added to give the duration of nondecision component T_er, and it is assumed to have range s_t. The bottom panel shows terminated and nonterminated processes in the diffusion model for partial information and guessing models. The upper figure shows the distributions for “large” and “small” responses for terminated and nonterminated processes at some time T. It also shows the probability of a “large” response if decision processes have access to partial information; it is the combination of the two black densities. The probability of a “small” response is the combination of the two gray densities. The lower figure shows the probabilities of “large” and “small” responses if partial information is not available and nonterminated processes lead to guesses.

The middle panel of Figure 1 shows encoding and response execution processes, processes that occur before and after the decision process, respectively. The nondecision processes are combined, with a mean RT for the combination that is labeled T_er. Also, the nondecision component is uniformly distributed with range s_t. The uniform distribution does not affect the overall shape of the RT distributions because it is combined (convolved) with the much wider decision process distribution (see Ratcliff & Tuerlinckx, 2002, Figure 11, for more details).

In signal detection theory, all variability would be attributed to the numerosity estimate (the estimate of whether the number of dots was larger or smaller than 50) with variability normally distributed across trials. In the diffusion model, this corresponds to variability in drift rate across trials. However, in the diffusion model, the different sources of variability within trial, starting point, and the nondecision component are separately identified when the model is fit to data (see Ratcliff & Tuerlinckx, 2002). If predicted data are generated from the model, the parameter values were recovered accurately so that, for example, high variability in drift across trials is not misidentified as high variability in starting point.

In the response signal procedure, when a signal is presented participants have to respond within 200–300 ms. There are two ways that this can be accommodated in the diffusion model. One is to assume that the response criteria are removed and decisions are determined according to whether the accumulated amount of evidence at the time the signal is presented is above or below the starting point (i.e., partial information). This assumption leads to a relatively simple expression for the growth of accuracy over time, and the function fits data well (e.g., Ratcliff, 1978, 1980, 1981; Ratcliff & McKoon, 1982). However, this version of the model, when simultaneously fit to regular RT and accuracy data, does not fit the data well (Ratcliff, 2006; also, poor fits to go–no-go paradigms were obtained with the same boundary removal assumption [Gomez, Ratcliff, & Perea, 2007]).

The other way to explain response signal data is to assume that responses represent a mixture of processes: those that have already terminated at a boundary when the signal is presented and those that have not. For processes that have not terminated, a decision can be made on the basis of the position of the process (partial information) or simply by guessing (e.g., De Jong, 1991; Ratcliff, 2006).

The assumption that responses for nonterminated processes are based on partial information or guesses is shown in the bottom panel of Figure 1. The mean drift rate is toward the top boundary which corresponds to a “large” response. The vertical line between the two response boundaries and RT distributions is the point in time at which the signal is given. In the partial information model, if the accumulated evidence is above the starting point, a positive “large” decision is made, and if it is below the starting point, a negative decision is made. In the guessing model, any process that has not terminated is assigned to a “large” response with a guessing probability (an additional parameter). This guessing assumption is consistent with the view that to use information from the stimulus in making an explicit decision, the process must reach a criterion. Those processes that have terminated correctly before the signal form the black distribution at the top boundary in Figure 1 and those that have terminated at the incorrect boundary form the gray distribution at the bottom boundary. As shown in the figure, correct and error responses are mixtures of the proportions of terminated processes and proportions of nonterminated processes based on partial information or guesses.

Ratcliff (2006) compared implementations of the diffusion model for the response signal task, first, with no boundaries; second, with boundaries and guessing; and third, with boundaries and partial information. In Ratcliff's experiment, 7 participants were tested with both speed and accuracy instructions in the standard task and with six lags in the response signal task. The models were fit to the data from the two tasks simultaneously. It was assumed that the drift rate and standard deviation in drift across trials were the same for the two tasks. All the other parameters were free to be different. With the no-boundary assumption for the response signal task, the models did not fit the data well. In contrast, when there were boundaries on the decision process, the models did fit well. The fits of the models to the data were about equally as good when responses for nonterminated processes were based on partial information and when they were guesses.

Numerosity Discrimination Experiment

The numerosity discrimination task was chosen because it has few perceptual or memory limitations and so provides a good baseline for other response signal experiments. The procedure is similar to tasks previously tested on older participants that have shown little effect on drift rates as a function of age, so there should be no floor effects on performance with older participants. Another reason for choosing the numerosity task is its simplicity; we thought that training for the response signal task might be easier with the simplicity of numerosity discrimination.

The stimuli were 10 × 10 arrays containing between 31 and 70 randomly placed dots. Participants were instructed to give “large” responses when the number of dots was larger than 50 and to give “small” responses when the number of dots was fewer than or equal to 50. On each trial, a participant was told whether his or her response was correct, with “large” being the correct response for more than 50 dots and “small” being the correct response for 50 dots or fewer.¹ The lags between stimulus and signal to respond varied from 50 to 1,800 ms. Participants were instructed to respond within 250 ms of the signal.

Method

Participants

Nineteen undergraduate students were recruited from the Bryn Mawr undergraduate population by means of flyers posted around campus; each was paid $15 per session. Nineteen 60- to 75-year-old adults were recruited from local senior centers and were paid $15 per session. Each participant participated in 12 sessions of the standard procedure. The 60- to 75-year-olds also participated in 10 sessions of response signal trials and the college students in 8 sessions of response signal trials. One 60- to 75-year-old participant was unable to learn the response signal task, so this participant was replaced.

All participants had to meet the following criteria to participate in the study: a score of 26 or above on the Mini-Mental State Examination (Folstein, Folstein, & McHugh, 1975), a score of 20 or less on the Center for Epidemiological Studies Depression Scale (Radloff, 1977), and no evidence of disturbances in consciousness, medical, or neurological diseases causing cognitive impairment, head injury with loss of consciousness, or current psychiatric disorder. Participants had normal or corrected-to-normal vision (20/30 or better) as measured by a Snellen “E” chart. All participants completed the Information subtest and the Digit Symbol–Coding subtest of the Wechsler Adult Intelligence Scale—III (Wechsler, 1997), and estimates of full-scale IQ were derived from the scores of the two subtests (Kaufman, 1990). The means and standard deviations for these background characteristics are presented in Table 1.

Table 1.

Subject Characteristics

	Older adults		Younger adults
Measure	M	SD	M	SD
Mean age	69.2	4.5	20.8	1.3
Years of education	17.3	1.7	13.4	1.5
MMSE	28.6	1.3	29.1	1.0
WAIS–III information	13.3	2.4	14.6	1.4
WAIS–III digit-symbol coding	12.6	3.4	12.1	1.8
CES-D: Total	8.4	6.9	9.9	9.2

Note. MMSE = Mini-Mental State Examination (Folstein, Folstein, & McHugh, 1975); WAIS–III = Wechsler Adult Intelligence Scale—III (Wechsler, 1997); CES-D = Center for Epidemiological Studies Depression Scale (Radloff, 1977).

Stimuli

The stimuli were dots placed in a 10 × 10 grid in the upper left corner of a VGA monitor, subtending a visual angle of 4.30° horizontally and 7.20° vertically. The dots were clearly visible, light characters displayed against a dark background. When the response signal was displayed, dots in the sixth row were replaced by a row of capital Rs. The VGA monitors were driven by IBM Pentium II microcomputers that controlled stimulus presentation time and recorded responses and RTs. The stimuli were divided into eight groups of five numbers of dots each (31–35, 36–40, etc.) for data analysis to reduce the number of conditions and to increase the number of observations per condition.

Procedure

For the standard RT procedure, blocks of trials for which participants were instructed to respond as quickly as possible (without guessing or hitting the wrong response key too often) alternated with blocks of trials for which they were instructed to respond as accurately as possible (while still making a single global judgment about the number of dots). A test item remained on the screen until a response was made by pressing the “?/” key for “large” responses and the “Z” key for “small” responses. After a response, RT and accuracy feedback were provided for 500 ms and then there was a 400-ms delay before the next stimulus. If a response was shorter than 250 ms, a message saying “too fast” was displayed for 500 ms before the 400-ms delay preceding the next stimulus. There were 40 test items in each block, one for each of the possible numbers of dots, in random order. There were a total of 16 blocks with accuracy instructions and 16 blocks with speed instructions in each session, with a participant-timed rest between each block. Data from the first session or both the first and second sessions were discarded, depending on when performance became stable. This was done informally by observing when accuracy did not change by more than a few percentages and RT by less than 20 or 30 ms. With two speed–accuracy conditions and eight stimulus conditions, there were about 80 observations per condition per session.

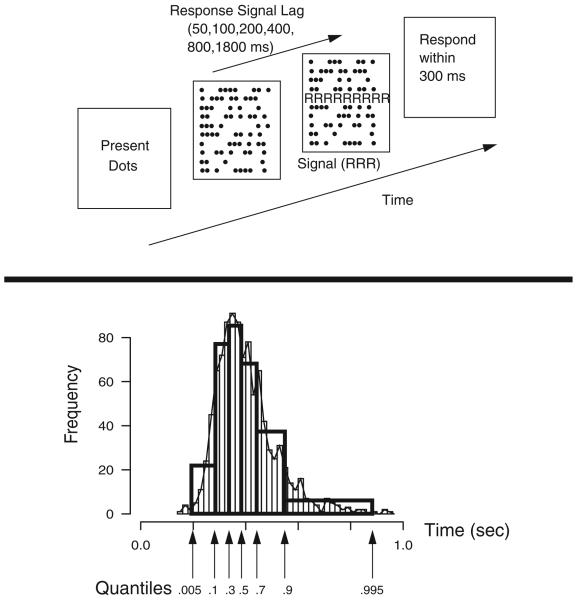
The top panel of Figure 2 shows the sequence of events for each test item for the response signal procedure. There were 26 blocks of 40 trials in each session, again with a participant-timed rest between each block. The 40 trials tested all the possible numbers of dots, in random order. There were six response signal lags: 50, 100, 200, 400, 800, and 1,800 ms, randomly assigned to test items. After each response, accuracy feedback was displayed for 250 ms, a blank screen for 400 ms, RT feedback for 500 ms, a blank screen for 300 ms, and then the next array of dots. With six lags and eight stimulus conditions, there were on average 22.5 observations per condition per session.

Figure 2.

The top panel shows the time course of events in the experimental paradigm. The bottom panel shows how a response time (RT) distribution can be constructed from quantile RTs (on the x-axis) drawing equal area rectangles between the .1, .3, .5, .7, and .9 quantile RTs and rectangles of half the area at the extremes.

Each participant participated in 20 or 22 sessions. The first 8 and the last 4 used the standard RT task. In between, there were 8 sessions with the response signal task for college students and 10 sessions with the response signal task for 60- to 75-year-old participants. For the college students, the first 1 or 2 sessions of response signal data were eliminated, and for the 60- to 75-year-old participants, between 1 and 4 sessions were eliminated, depending on how many sessions were required to achieve stable performance. Summing across the sessions that were not discarded, there were about 850 observations per condition (i.e., for each of the eight groups of numbers of dots) for each participant with the standard task, and there were between 140 and 200 observations per condition for each response signal lag with the response signal task.

It has been an informal belief that many older participants are unable to perform the response signal task. In the experiment reported here, the older participants did learn how to do it, but special training was required. First, our research assistant is talented in having the patience and persistence to cajole older participants into performing quickly. Second, training was implemented by instructing participants on initial trials to pay no attention to the stimulus, to simply respond to the signal by hitting one of the two response keys randomly. Then after RTs to the signal speeded up sufficiently, the participants were instructed to gradually start paying attention to the stimulus. They were told to first improve accuracy for the easier stimuli (very large or very small numbers of dots) without allowing their RTs to increase, and then they were told to gradually increase accuracy for the more difficult items. If a participant started to slow down, he or she was again instructed to pay attention only to the response signal (or even extremely, to squint their eyes so they could see only the signal to respond). For most participants, one to two sessions of training were required, although some 60- to 75-year-old participants took as many as four sessions.

It is possible to verify that participants were following instructions in the response signal procedure by examining RT distributions for the response signal procedure. If processing is terminated by the signal, RT distributions would be approximately symmetric. But if participants are simply behaving as in the standard task, the RT distributions would be skewed (i.e., a lot of responses in the usual right skewed tail would be outside the 100- to 500-ms window at the short lags). Inspection of the data showed that the RT distributions in the response signal task were symmetric even at the shortest lags.

Results and Discussion

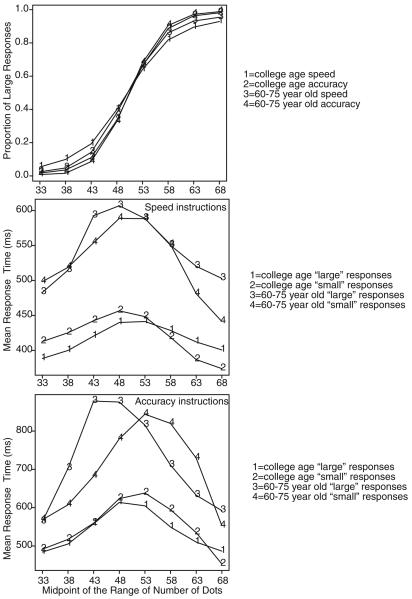
In the speed and accuracy blocks of trials in the regular RT task, I eliminated responses from the first block of each session, short and long outlier RTs in all blocks, and the first response in each block from data analyses. Summaries of the basic data from the standard RT task are shown in Figure 3. The top panel shows accuracy as a function of the eight conditions (eight groups of numbers of dots) for speed and accuracy instructions for college-age and 60- to 75-year old participants. As in other studies (Ratcliff, Thapar, & McKoon, 2001), the 60- to 75-year old participants were somewhat more accurate than the college-age participants. Probability correct with speed instructions was about .08 less than with accuracy instructions. The second panel shows mean RT as a function of condition for “large” and “small” responses and college-age versus 60- to 75-year-old participants for speed instructions. The mean RTs for correct responses for college-age participants increased by about 50 ms from easy to difficult conditions, and error responses were faster than correct responses. The RTs for correct responses for the 60- to 75-year-old participants increased by about 80 ms from easy to difficult conditions. Overall, the 60- to 75-year-old participants were about 100 ms slower than the young participants. The 60- to 75-year-old participants' error responses were slower than their correct responses at low accuracy levels (e.g., the 43- to 58-dot conditions) and faster than their correct responses at extreme values of accuracy (e.g., 31–35 and 66–70 dots; cf. Ratcliff et al., 1999). The third panel, for the data with accuracy instructions, shows the same patterns as the second panel. With accuracy instructions, the college-age participants slowed by 100–150 ms and the 60- to 75-year-old participants slowed by 100–250 ms. Unlike with speed instructions, both groups of participants showed the crossover of error versus correct RTs—errors responses slower than correct responses at low accuracy levels but faster at higher accuracy levels. Except for the occurrence of fast errors in the most extreme conditions, these results replicate the results from Ratcliff et al. (2001).

Figure 3.

Plots of accuracy and mean RT averaged over participants in each age group.

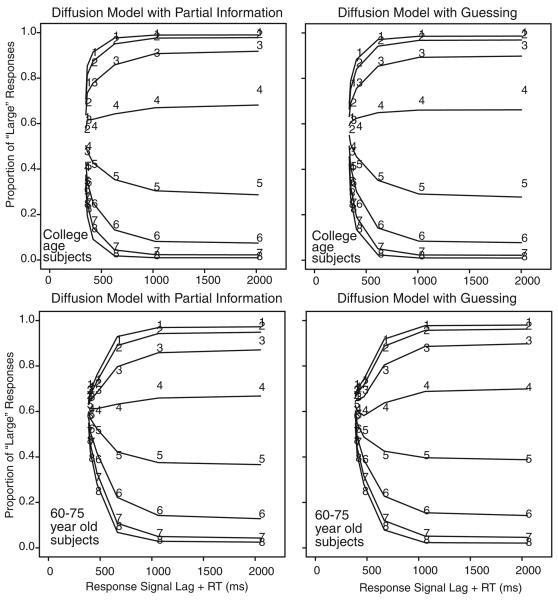
Summaries of the data from the response signal procedure (Figure 6) are discussed later. Only responses within a window between 100 ms and 500 ms after the signal were used in analyses. These cutoffs resulted in elimination of 7% of the data for college-age participants and of 10% of the data for 60- to 75-year-old participants. In general, 60- to 75-year-old participants had a slower rise to asymptote compared with college-age participants, a slightly higher time intercept, and about the same level of asymptotic accuracy.

Figure 6.

Proportion of “large” and “small” responses in the response signal procedure as a function of response signal lag. The digits 1–8 refer to the experimental conditions, namely dot groups for 31–35, 36–40, 41–45, 46–50, 51–55, 56–60, 61–65, and 66–70 dots. The lines represent the fits of the diffusion models to the data.

Fits of the Models to the Data

The two kinds of data, response signal data and RT distributions and accuracy from the regular RT task, were fit simultaneously. As many of the parameters as possible were kept constant across the two tasks, as discussed below.

For the diffusion model, predictions for the response signal data were computed using an explicit expression for the distribution of evidence for nonterminated processes within the decision process at each point in time (Ratcliff, 1988, 2006). The expression is an infinite sum, and it provides an exact numerical solution. The standard expressions for RT distributions and accuracy also have exact numerical solutions (Ratcliff, 1978). The expressions for terminated and nonterminated processes together provide the probability that a process has terminated at one or the other of the response boundaries by time T or, if it has not terminated at time T, the probability that the process is above or below the starting point. For the response signal procedure, this latter probability determines which response is executed for the partial information model. It should be pointed out that the solutions to the expressions are not simple because they require infinite sums of sine and exponential terms that must be integrated over distributions of parameter values, specifically a normal distribution of drift rates and uniform distributions of starting point and nondecision component of processing; for details, see Ratcliff (2006).

Fitting Data From the Standard RT Task

The models were fit to accuracy values and quantile RTs for correct and error responses for each stimulus condition (the eight groups of stimuli). Ratcliff and Tuerlinckx (2002) evaluated several methods of fitting the models and showed that using RT quantiles as the basis of a chi-square statistic provides a good compromise between robustness to outlier data and accurate recovery of parameter values. Typically, the .1, .3, .5, .7, and .9 RT quantiles are used, one set of quantiles for each of the two responses for each condition. Binning the data in this way has the advantage that the presence of a few extreme values does not affect the computed quantiles.

Quantiles provide a good summary of the overall shape of the distribution; in particular, they describe the shape one sees when looking at a histogram, that is, where the distribution peaks and how wide its left and right tails are. The bottom panel of Figure 2 illustrates this by showing a sample RT histogram with quantiles plotted on the time axis and equal area rectangles drawn between the quantiles.

The models were used to generate the predicted cumulative distributions of response probabilities from the explicit expressions for the diffusion model (Ratcliff, 1978, 2006; Ratcliff & Smith, 2004; Ratcliff & Tuerlinckx, 2002; Ratcliff et al., 1999). Subtracting the cumulative probabilities for each successive quantile from the next higher quantile gives the probability mass between them (i.e., the probabilities of responses between them) for the expected values. The expected and observed probabilities were then used to construct the chi-square statistic. The observed proportion of responses between each pair of quantiles is the proportion of the probability distribution that is between them: .2 between the .1, .3, .5, .7, and .9 quantiles and .1 above the .9 and below the .1 quantiles. These proportions are multiplied by the proportion of correct or error responses so that the proportions across the two responses and all the quantiles add to 1. These were then multiplied by the number of observations to give the observed frequencies (O) and expected frequencies (E) and χ² = ∑(0 − E)²/E. The number of degrees of freedom for the RT task is calculated as follows: For a total of k experimental conditions and a model with m parameters, the degrees of freedom are k(12 − 1) − m, where 12 comes from the number of bins between and outside the RT quantiles for correct and error responses for a single condition (minus 1 because the total probability mass must be 1, which reduces the number of degrees of freedom by 1). There were 16 conditions in the experiment, 8 number-of-dots conditions for each of the two types of instructions, so the degrees of freedom equal 176 − m.

Fitting Response Signal Data

For the partial information model, the probability of a “large” response is the sum of the proportion of processes that have terminated at the “large” boundary and the proportion of processes that have not terminated but are above the center of the process (a/2), that is, the sum of the black areas in the bottom panel of Figure 1. The center of the process is selected for the cutoff instead of the starting point because this allows an initial bias in the proportion of responses. If the starting point is near one boundary, then with the variability in starting point it is possible to get a relatively small proportion of the distribution of starting points below the halfway point leading to the initial bias. The proportion of processes that have not terminated is given by Equation 6 in Ratcliff (2006). Note that the expression for the proportion must be integrated over the distributions of drift rate, starting point, and nondecision component and over distance between the center and a boundary in the process to compute the proportion between the center and a boundary.

For the guessing model, the probability of a “large” response is the sum of the proportion of processes that have terminated at the “large” boundary and the proportion that have not terminated multiplied by the guessing probability (see the bottom panel of Figure 1). For both models, at a particular response signal lag the proportion of processes that have terminated at the “large” boundary is assumed to be the cumulative proportion of “large” responses that have terminated by that time in the standard RT task (but with different parameters other than drift rates).

One further constraint was needed for fitting the data for the individual 60- to 75-year-old participants and that was a constraint on the values of T_er for the response signal trials. In initial fits to individual participants, this parameter became implausibly small (below 200 ms) or implausibly large (more than 100 ms greater than the value of T_er for the regular RT task) because of the relatively low numbers of observations for an individual participant. Because of this, for the 60- to 75-year-old participants, the values of T_er for the response signal trials was constrained to be above 350 ms and below T_er for the regular RT task. This had a minimal effect on the goodness of fit.

The models were tested using the data for the six response signal lags for all eight conditions; the dependent measure was the proportion of “large” responses (which is equal to 1 – the proportion of “small” responses). For the models, the 48 observed and 48 predicted proportions were multiplied by the number of observations per condition to form a chi-square statistic. With 48 conditions, 48 degrees of freedom were added to the 176 degrees of freedom for the data from the standard RT task. Note that the data from both tasks were fit simultaneously.

Constraints on Components of Processing Across Paradigms

The easiest conditions (very large and very small numbers of dots) have the most extreme values of drift rate (strongly positive and strongly negative). The more difficult conditions (intermediate numbers of dots) have lower drift rate values (near zero for the most difficult conditions). Following Ratcliff (2006), it was assumed that difficulty of stimuli does not differ between the standard RT and the response signal tasks and that the difficulty does not vary with speed versus accuracy instructions in the standard RT task. Therefore, the eight drift rates were held constant across the response signal task and across the speed and accuracy conditions for the standard task. Also, variability in drift rate within and across trials was held constant.

Although the drift rates were assumed to be the same across tasks, it is possible for them to be biased for one task relative to another. For example, drift rates of 0.3 and −0.2 in the regular task might be biased to be 0.25 and −0.25 in the response signal task. All drift rates might have a constant added or subtracted, in direct analogy to a change in criterion in signal detection theory. In the models, this is represented by a drift criterion, which was added to the drift rates in the response signal paradigm relative to the standard RT task; in other words, the zero point of drift was free to differ between the two tasks. It was assumed that participants can change the values of decision criteria and starting points (a and z) between tasks and between speed–accuracy instructions, so these parameters were also free to vary when the models were fit to the data.

Variability in the starting point across trials (s_z) was the same for the speed and accuracy instruction conditions, as has been assumed in other applications, but was allowed to be different for the response signal task. The nondecision component of processing (T_er) was assumed to be the same for speed and accuracy instructions, but different for the response signal task because the response signal (the row of Rs) is highly salient and demands an immediate response. Variability in the nondecision component s_t was assumed to be the same across tasks (fits were performed allowing s_t to vary across tasks, but the value turned out to be similar across the tasks).

Response Time and Accuracy Fits for the Standard RT Task

The standard RT task and the response signal task jointly constrain applications of the models, and so the data from the two tasks were fit simultaneously. The partial information and guessing models were fit to the average data across participants (average response proportions and average quantile RTs) and separately to the data from individual participants. Below, it is shown that the parameter values were about the same for fits to average data and the averages of parameter values across participants.

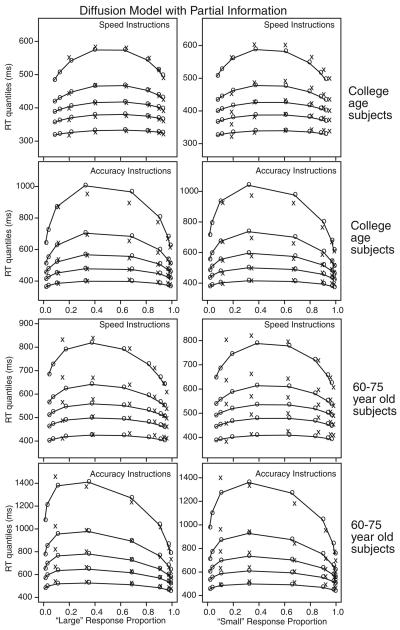
The data from the standard task are presented in Figures 4 and 5 as quantile probability functions (the xs are the data). There are four panels for each group of participants: “large” responses with speed and accuracy instructions and “small” responses with speed and accuracy instructions. For each of the eight conditions in the experiment, the .1, .3, .5 (median), .7, and .9 quantiles of the RT distribution are plotted as a function of response proportion. The proportions on the right of each panel come from correct responses, and the proportions on the left come from error responses. For example, for the most difficult condition, the probability of a correct response for young participants with speed instructions is .6, on the right, and the probability of an error was .4, on the left. The advantage of quantile probability functions over other ways of displaying the data is that they show information about all the data from the experiment: the proportions of correct and error responses and the shapes of the RT distributions for correct and error responses. This means, for example, that the change in shape of RT distributions can be examined as a function of difficulty, and comparisons can be made between correct and error responses. Figure 4 shows fits of the partial information model and Figure 5 shows fits of the guessing model.

Figure 4.

Quantile probability functions for “large” and “small” responses for speed and accuracy instructions for the two participant groups. The quantile response times (RTs) in order from the bottom to the top are the .1, .3, .5, .7, and .9 quantiles in each vertical line of xs. The xs are the data and the os are the predicted quantile RTs from the best-fitting diffusion model with partial information, joined with lines. The vertical columns of xs for each of the eight conditions (dot groups for 31–35, 36–40, 41–45, 46–50, 51–55, 56–60, 61–65, and 66–70 dots) are the five quantile RTs and the horizontal position is the response proportion corresponding to that condition. Note that extreme error quantiles could not be computed because there were too few observations (fewer than five) for some participants for some of the conditions and so these are not shown.

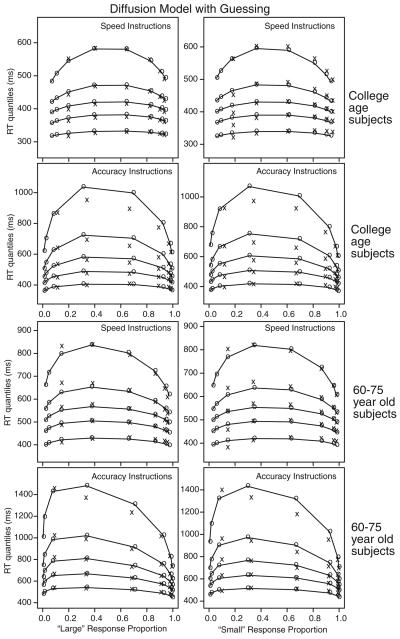
Figure 5.

The same quantile-probability plots as in Figure 4 but for the guessing model. Quantile probability functions for “large” and “small” responses for speed and accuracy instructions for the two participant groups. The quantile response times (RTs) in order from the bottom to the top are the .1, .3, .5, .7, and .9 quantiles in each vertical line of xs. The xs are the data and the os are the predicted quantile RTs from the best-fitting guessing model with partial information, joined with lines. The vertical columns of xs for each of the eight conditions (dot groups for 31–35, 36–40, 41–45, 46–50, 51–55, 56–60, 61–65, and 66–70 dots) are the five quantile RTs and the horizontal position is the response proportion corresponding to that condition. Note that extreme error quantiles could not be computed because there were too few observations (fewer than five) for some participants for some of the conditions and so these are not shown.

The os in the figures (connected by the lines) are the predictions from the diffusion model using the best-fitting parameters. With only boundary separation (a and z) changing between speed and accuracy instructions, the model captures almost all aspects of the data. The horizontal position of the columns of xs and os shows how well the model fits the accuracy data, and the inverted-U–shaped functions for the os show how well the model fits the RT quantile data (the xs). The .1 quantile RTs change little across levels of difficulty, but change by 50–80 ms from the speed to the accuracy conditions. The .9 quantile RTs change by between 100–300 ms across difficulty for college-age participants and by 200–500 ms for the 60- to 75-year-old participants. Response proportion changes a little, by less than 10%, as a function of speed–accuracy instruction. The partial information and guessing models produce about the same quality of fits.

Response Signal Fits

For the response signal task, Figure 6 shows the probabilities of “large” responses for the eight conditions for college-age participants and 60- to 75-year-old participants for the partial information and guessing models. The numbers are the data, and the lines are the best-fitting values under the assumption that partial information is available. The figures show the changes in probability of a “large” response across response signal lags, with the asymptotic probability highest for the conditions with the largest numbers of dots and lowest for the conditions with the smallest numbers of dots. Remarkably, there are no systematic misses between predictions and data. This is especially noteworthy because the same drift rates were used as in the standard RT task. The partial information and guessing models fit the data about equally well.

Table 2 shows chi-square values for the partial information and guessing models when the models were fit to the standard task and the response signal task simultaneously. It also shows the total chi-square divided into the contribution from the standard RT task and the contribution from the response signal data.

Table 2.

Chi-Square Goodness of Fit for the Models

Participants' variant	χ2 from all data	χ2 from RT	χ2 from response signal	χ2 from RT data alone	Average χ2 over individual participant fits	df
College age
Partial	6,180	5,553	627	5,471	1,009	203
Guess	6,603	5,802	801	5,471	986	202
60- to 75-year-olds
Partial	10,355	8,883	1,472	8,282	1,212	203
Guess	10,343	9,177	1,165	8,282	1,008	202

The results largely replicate those of Ratcliff (2006). The partial information and guessing diffusion models fit about equally well, and the response signal and RT data are consistent with each other. That is, the chi-square value for the fit of the RT data alone is only a little better (smaller) than the chi-square for the RT portion of the joint fit to the response signal and RT data. In other words, the fit to the RT data is not altered when the response signal data are jointly fit with the RT data.

Aging Effects and Parameter Values

The key question is how the college students and 60- to 75-year-olds differ in terms of components of processing as represented by model parameter values. All comparisons were carried out by means of t tests using parameter values from the 19 participants in each group. First, drift rates were a little larger for the 60- to 75-year-old participants (not significantly so), but across trial variability in drift rate was significantly larger for the 60- to 75-year-old participants. This means that college-age participants were less variable from trial to trial in obtaining an estimate of numerosity. For the standard RT task, the nondecision component was a little slower (by about 70 ms) and boundary separation was larger with both speed and accuracy instructions for 60- to 75-year-olds relative to college-age participants (see Tables 3 and 4). These results hold for both the partial information and guessing versions of the model, and they replicate the results of earlier studies with numerosity judgments (Ratcliff et al., 2001; Ratcliff, Thapar, & McKoon, 2006). They are also consistent with the results from other two-choice tasks that show small or no differences in drift rates between young and older participants (Ratcliff, Thapar, Gomez, & McKoon, 2004; Ratcliff, Thapar, & McKoon, 2003, 2004, 2007; Spaniol, Madden, & Voss, 2006; but see Thapar, Ratcliff, & McKoon, 2003). In addition, the range in the nondecision component of processing is larger for the 60- to 75-year-old participants. All the variability parameter values were typical of those obtained in the references cited above.

Table 3.

Diffusion Model Parameters

Model, participants, data, and measure	ar	zr	szr	aa	za	as	zs	sz	η	Ter response times (seconds)	Ter signal (seconds)	st (seconds)	Guess probability (“small” response)
Partial information
College age
Average data	0.129	0.064	0.026	0.121	0.063	0.071	0.037	0.032	0.072	0.330	0.330	0.133
Participant average	0.135	0.072	0.023	0.121	0.063	0.072	0.038	0.023	0.059	0.326	0.303	0.133
Participant SD	0.017	0.013	0.013	0.026	0.012	0.013	0.009	0.012	0.031	0.021	0.019	0.023
60- to 75-year-olds
Average data	0.143	0.070	0.067	0.148	0.069	0.092	0.042	0.042	0.118	0.389	0.400	0.186
Participant average	0.135	0.069	0.031	0.147	0.069	0.092	0.044	0.025	0.099	0.398	0.384	0.187
Participant SD	0.031	0.019	0.020	0.030	0.016	0.012	0.010	0.011	0.029	0.029	0.028	0.052
Guess
College age
Average data	0.113	0.057	0.013	0.118	0.061	0.070	0.036	0.032	0.073	0.330	0.250	0.130	0.605
Participant average	0.112	0.053	0.023	0.123	0.064	0.072	0.038	0.026	0.076	0.328	0.259	0.137	0.638
Participant SD	0.015	0.010	0.013	0.028	0.014	0.014	0.010	0.012	0.046	0.021	0.014	0.023	0.130
60- to 75-year-olds
Average data	0.112	0.057	0.052	0.148	0.068	0.093	0.042	0.040	0.108	0.400	0.356	0.185	0.590
Participant average	0.128	0.059	0.029	0.153	0.072	0.094	0.045	0.028	0.119	0.401	0.367	0.193	0.614
Participant SD	0.036	0.020	0.021	0.034	0.019	0.014	0.010	0.014	0.041	0.030	0.019	0.043	0.156

Note. The parameters of the model are a_r = boundary separation for the response signal experiment (z_r, z_a, and z_s are the corresponding starting points); s_zr = range of the distribution of starting point (z) across trials for the response signal experiment; a_a = boundary separation for accuracy instructions; a_s = boundary separation for speed instructions; s_z = range of the distribution of starting point (z) across trials; η = standard deviation in drift across trials; T_er = nondecision component of response times; s_t = range of the distribution of nondecision times across trials.

Table 4.

Diffusion Model Drift Rates and Drift Criterion

Model, participants, data, and measure	v1	v2	v3	v4	v5	v6	v7	v8	Signal trial drift criterion
Partial information
College age
Average data	−0.410	−0.330	−0.217	−0.069	0.88	0.230	0.340	0.404	−0.018
Participant average	−0.414	−0.341	−0.230	−0.083	0.059	0.201	0.310	0.373	−0.005
Participant SD	0.072	0.062	0.046	0.021	0.027	0.046	0.066	0.071	0.026
60- to 75-year-olds
Average data	−0.405	−0.331	−0.202	−0.056	0.089	0.229	0.340	0.406	0.001
Participant average	−0.425	−0.340	−0.207	−0.053	0.085	0.229	0.348	0.421	0.000
Participant SD	0.098	0.075	0.048	0.027	0.023	0.038	0.060	0.080	0.037
Guess
College age
Average data	−0.381	−0.304	−0.192	−0.042	0.115	0.259	0.370	0.434	−0.053
Participant average	−0.442	−0.360	−0.242	−0.086	0.072	0.224	0.339	0.407	−0.003
Participant SD	0.085	0.072	0.057	0.035	0.037	0.061	0.087	0.096	0.030
60- to 75-year-olds
Average data	−0.433	−0.345	−0.211	−0.046	0.102	0.237	0.372	0.442	−0.028
Participant average	−0.476	−0.381	−0.230	−0.059	0.100	0.257	0.388	0.473	−0.008
Participant SD	0.118	0.083	0.063	0.035	0.041	0.066	0.092	0.109	0.090

Note. The drift criterion values are added to drift rates to reflect bias differences between the two procedures. v= drift rate. v₁−v₈ = drift rates for 31–35, 36–40, 41–45, 46–50, 51–55, 56–60, 61–65, and 66–70 dots, respectively.

In the response signal task, boundary separation was about the same for college-age and 60- to 75-year-old participants and was similar to the size of boundary separation in the accuracy version of the standard RT task. The nondecision component of processing was significantly larger by 80–90 ms for 60- to 75-year-old participants than for college-age participants and was a little smaller for the response signal task compared with the RT task for the partial information model, but quite a bit smaller (69 and 34 ms) for the guessing model. In terms of the mechanics of the model, this is because in the partial information model, accuracy of both terminated and nonterminated processes increases with time, but for the guessing model, accuracy can only grow from terminated processes. This means that for the guessing model, processes must start terminating earlier than for the partial information model to achieve the same level of accuracy. One plausible reason for the smaller value of the nondecision component for the guessing model for both age groups is that in the response signal task, when the signal is presented, either a response is prepared or a guess has to be made. When a response is prepared, the boundary has already been crossed; when a guess has to be made, then the process does not have to cross the boundary. Both of these processes could be faster than evaluating boundary crossing. (This is a possible explanation for the guessing model; for the partial information model, the duration for executing the prepared response and for evaluating partial information would be about the same as for evaluating boundary crossing.)

Figure 6 shows that the growth of accuracy is faster for college-age participants than for 60- to 75-year-old participants. Ratcliff (2006, Figure 7) showed that two parameters that could give rise to such differences were boundary separation and standard deviation in drift rate across trials. In this study, the differences in these parameter values are not large enough to produce the difference in growth rate in Figure 6. The two parameters that are responsible for the difference in growth rate between young and older participants in this study are the nondecision component and variability in the nondecision component.

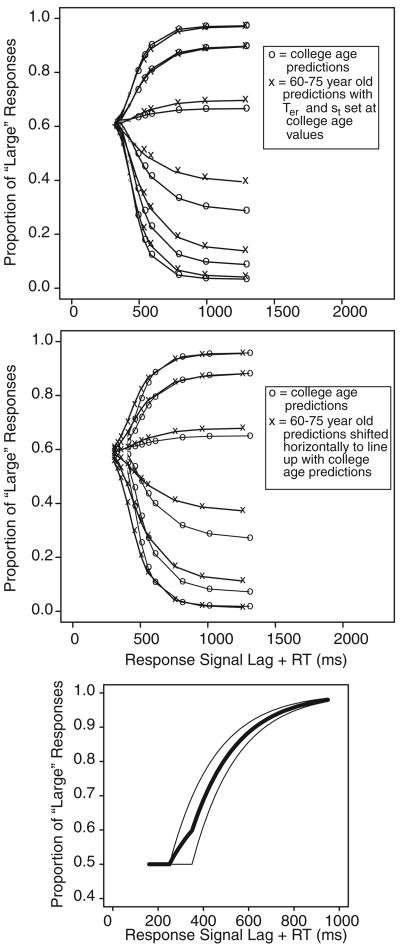
Figure 7.

The top panel shows predictions from the diffusion model with guessing (for fits to group data) for the college-age participant parameter values (os) and for the 60- to 75-year-old parameter values with the values of T_er and s_t set to the values for the young participants. This shows that the response signal functions have the same shape, and all that differs are the parameters T_er and s_t. The middle panel shows the same predictions for the college-age participants with the functions truncated at the shortest response signal lag plus response time. This is all that can be observed from data. Also shown are predictions from 60- to 75-year-old participants shifted to the left (to align for comparison), illustrating that both the difference in s_t and the truncation are responsible for the differences in rate of rise to asymptote. The bottom panel shows the result of averaging two exponential approaches to limit with the same rate and different time intercepts (thin lines). The result is a slower rise to asymptote (in this example, with the average of two functions, there is an initial slow rise followed by steeper rise).

The top panel of Figure 7 shows response signal functions predicted from the guessing model using parameter values for college-age participants (os) and using parameter values for the 60- to 75-year-old participants (xs) with T_er and s_t set to the values for the college-age participants (note the two extreme conditions were eliminated for clarity, and the vertical scales were stretched a little so that predictions for the 60- to 75-year-old participants would overlap). The two sets of curves lie virtually on top of each other, which shows that in the model, it is only differences in these two parameters that produce differences in growth rate. The middle panel of Figure 7 shows the predictions from the two sets of parameter values with the 60- to 75-year-old participants' predictions shifted to the left to align with the college-age participants' predictions. The increase in s_t produces a slightly more gradual increase for the 60- to 75-year-old participant functions. Additionally, the value of T_er for the college-age participants is smaller than the shortest response signal lag plus RT, which means that the initial gradual increase that the model predicts (shown in the top panel of Figure 7) is cut off and the functions start later than the point at which they would converge.

There are also larger individual differences in T_er and s_t for the 60- to 75-year-old participant data than the college-age participant data. This means that the 60- to 75-year-old participant data will have a wider spread of growth functions across participants than the college-age participant data. The bottom panel of Figure 7 shows two exponential growth functions that might represent two different participants with the same growth rate but different time intercepts (the thin lines) and a mixture of the two (the thick line). Because the two exponentials begin to rise at different times, the mixture first tracks the earlier one and then tracks the average of the two after the later one begins to rise. This leads to a more gradual initial rise for the mixture than either of the individual functions. This is another factor that contributes to the more gradual initial rise for the average data for the 60- to 75-year-old participants.

For the results just described, the diffusion model was fit to the means across participants of the response proportions and the RT quantiles. We also fit the data to each participant individually and then averaged the best-fitting parameter values. The resulting values were close to those obtained with the fits to the mean data. The close match between the two methods of fitting has been observed in other studies (Ratcliff, Thapar, Gomez, & McKoon, 2004; Ratcliff et al., 2001; Ratcliff, Thapar, & McKoon, 2003, 2004; Thapar et al., 2003). To decide whether differences in parameter values were significantly different or not, t tests were used with participants as the random variable, but the sizes of the differences can also be examined by using standard errors computed across participants, that is, the standard deviations in Tables 3 and 4 divided by the square root of 19 (the number of participants in each group).

A possible limitation of the models is that the rate of growth of the response signal functions in the models is quite sensitive to the boundary separation used for the response signal task and the standard deviation in drift rate across trials. The growth rate and asymptotic accuracy change substantially if the boundary separation or standard deviation in drift rate across trials is changed (Figure 7; Ratcliff, 2006), and we have yet to find a way to manipulate the boundary separation in the response signal task.

Conclusions

The experiment presented here demonstrates that older participants can, with some effort, be trained to perform the response signal task. The results of fitting the diffusion model to the data show effects of aging on performance that are consistent with those on other tasks similar to the one used here (Ratcliff et al., 2001, 2006). The results are also consistent between the regular RT task and the response signal task. The two versions of the diffusion model, partial information and guessing, fit the data equally well, and as in Ratcliff (2006), there is no way to discriminate between them on the basis of goodness of fit.

To use the response signal procedure with older adults, several aspects of the method of training are important. In our study, only 1 out of 20 participants was unable to perform the task. First, the participants have to be convinced that they can make mistakes and that everyone does. Second, they have to learn how to hit the response keys quickly, within a time window of 100–500 ms. Initially, they are instructed to pay no attention to the stimuli, rather to just hit a key when the response signal is presented. Third, when they have reached a reasonable speed, they are told to pay attention to the easier stimuli and attempt to become more accurate. This training can take from one to four sessions to reach acceptable levels of performance.

Laver (2000) conducted one of the few other published response signal experiments with older adults. Participants performed a lexical decision task with primed and unprimed words and non-words, and the growth of d′ as a function of lag was examined. One potential problem with Laver's experiment is that the participants might not have been fully trained. There were only two sessions, and a great many responses were outside the 100- to 400-ms window he used to include responses for analysis. In fact, at a 100-ms response signal lag, about 45% of the older adults' data were excluded. In the present study, 15% of the data would have been excluded with a window of 100–400 ms, and only 6% were excluded with our 100- to 500-ms window.

In addition to the response signal method, there is another method of examining the growth of information over time, the time–accuracy method (e.g., Kliegl, Mayr, & Krampe, 1994). In a time–accuracy experiment, stimulus presentation time is manipulated and accuracy at each of the presentation durations is measured. The growth of accuracy as a function of presentation time is compared for young and older adults, providing a comparison of the relative rate of information uptake.

The time–accuracy method and response signal methods measure two different aspects of processing. In the context of the diffusion model, presentation duration determines drift rate, which is the amount of information extracted from the stimulus. Response signal lag determines the amount of time available for the accumulation of evidence in the decision process (see Smith et al., 2004, for a model that combines the two; also Ratcliff & Rouder, 2000; Ratcliff, Thapar, & McKoon, 2003; Thapar et al., 2003).

The research described in this article emphasizes that experimental data must be approached from a theoretical perspective. Theory is necessary because there are three dependent variables in the standard RT paradigm—accuracy and correct and error RTs—plus there is accuracy as a function of time in the response signal paradigm. RT and accuracy have two different scales. Accuracy can range only from 0.0 to 1.0, and variability in accuracy is maximum when accuracy is 0.5. RTs can range from 0 to infinity, and the variability in RTs increases as RT increases. The accuracy and RT measures are also different in that the distribution of accuracy response proportions is binomial, whereas RT distributions are right skewed. These differences make it unlikely that some empirical measure can, by itself, disentangle tradeoff settings from task difficulty effects. What is needed to understand performance is a way to combine RT and accuracy values from the standard task and accuracy values from the response signal task. I argue that this can only be done with a model of processing that relates the measures by theoretical constructs such as the quality of evidence entering the decision process, the amount of evidence needed to make a decision, and the duration of other components of processing. The diffusion model accomplishes this, as do some other sequential sampling models (e.g., Ratcliff, Thapar, Smith, & McKoon, 2004).

Although the interpretation of the response signal data from the experiment reported here did not add substantially to conclusions drawn from the standard RT task, there are other situations in which response signal data can give information that the standard task cannot (see Ratcliff, 1980, for early modeling). For example, if the rate of evidence accumulation changes over time in the diffusion process, then an appropriately designed response signal experiment can show a nonmonotonic growth of accuracy. Such nonmonotonic d′ functions are obtained in paradigms in which two sources of information become available at different times during the time course of evidence accumulation (e.g., Dosher, 1984; Gronlund & Ratcliff, 1989; McElree, Dolan, & Jacoby, 1999; Ratcliff & McKoon, 1982, 1989). Also, in a serial process in which the order can be determined, if one process produces a decision on some trials, but other trials require two or three or more serial processes to complete, then a time intercept difference will be obtained in the response signal paradigm (e.g., McElree & Dosher, 1993). This will mirror a shift in the leading edge of RT distributions that is too big for diffusion models to accommodate. Note that each comparison in the serial process might be modeled as a diffusion process, but the RT predictions would be dominated by the combinations of processes and would not be particularly sensitive to the choice of the diffusion model to represent RT distribution shape. In several articles, diffusion model analyses have been used to make claims about how performance on simple two-choice tasks changes with age. The standard result that performance slows with age has been interpreted in many tasks using the diffusion model as resulting from more conservative decision criteria with a smaller effect of slowing of nondecision components of processing (Ratcliff, Thapar, Gomez, & McKoon, 2004; Ratcliff et al., 2001, 2004, 2006, 2007). In these tasks, drift rate (evidence from the stimulus) is the same for college-age participants through to 75- to 90-year-old participants.

The results from this study are consistent with this interpretation and provide additional indirect evidence that decision criteria have a large contribution to slowing. First, drift rates, which are the same in the regular RT task and the response signal task, do not differ significantly for college-age and 60- to 75-year-old participants. This is consistent with the contention that this numerosity discrimination task has little memory or perceptual load.

Second, boundary separation for the regular RT task trials (with both speed and accuracy instructions) is more conservative (larger) for 60- to 75-year-old participants relative to college-age participants. Because speed–accuracy setting is under the control of participants, it should be possible to find situations in which older participants are not slower than young participants. Figure 3 shows such a case; the speed instruction condition for 60- to 75-year-old participants has RTs about the same as the accuracy instruction condition for the college-age participants. Boundary separation for the response signal trials is about the same for the two participant groups. This suggests that when participants are free to adjust their decision criteria, older participants value accuracy more than speed, even when they are encouraged to respond quickly. However, when the task requires a response immediately after the signal, both groups select a setting at about the same value. This provides additional evidence that decision criteria settings in the regular RT task are set strategically.

Third, the duration of the nondecision component of processing is longer for the 60- to 75-year-old participants relative to college-age participants by amounts similar to those found in other studies (Ratcliff et al., 2001). Also, variability in the nondecision component is a little larger for 60- to 75-year-old participants relative to college-age participants. Differences in these two parameters are responsible for the slower rise in the response signal function for 60- to 75-year-old participants relative to college-age participants. By the time college-age participants are able to respond, accuracy has grown to above chance, but because 60- to 75-year-old participants have slower nondecision components with more variability, the growth of accuracy is both delayed and the rate is slowed because of increased variability in the nondecision component (see Figure 7 and the discussion about it).

The result of this study is quite counterintuitive. For these response signal data from this numerosity discrimination paradigm, most of the information processes of college-age and 60- to 75-year-old participants are the same, the quality of evidence extracted from the stimulus is the same, and decision criteria are set to approximately the same value. What appears to be a slower growth of evidence empirically for 60- to 75-year-old participants turns out to be the result of an increased smearing of growth functions that are otherwise the same as those for college-age participants.

These results show the generality of the diffusion model in accounting for results from different experimental paradigms within a single task (numerosity discrimination). They also show the value of modeling to substantive domains such as the effects of aging on speed of processing.