Two-dimensional Strain Imaging of Controlled Rabbit Hearts

Abstract

Ultrasound strain imaging using two-dimensional (2-D) speckle tracking has been proposed to quantitatively assess changes in myocardial contractility due to ischemia. Its performance must be demonstrated in a controlled model system as a step toward routine clinical application. In this study, a well-controlled 2-D cardiac elasticity imaging technique was developed using two coplanar and orthogonal linear probes simultaneously imaging an isolated retroperfused rabbit heart. Acute ischemia was generated by left anterior descending (LAD) artery ligation. An excitation-contraction decoupler, 2,3-butanedione monoxime, was applied at a 4mM concentration to reversibly reduce myocardial contractility. Results using a single probe demonstrate that directional changes in the in-plane principal deformation axes can help locate the bulging area due to LAD ligation, which matched well with corresponding Evans Blue staining, and strains, or strain magnitude, based on principal stretches can characterize heart muscle contractility. These two findings using asymmetric displacement accuracy (i.e., normal single probe measurements with good axial but poor lateral estimates) were further validated using symmetric displacement accuracy (i.e., dual probe measurements using only accurate axial tracking estimates from each). However, the accuracy of 2-D cardiac strain imaging using a single probe depends on the probe’s orientation due to the large variance in lateral displacement estimates.

INTRODUCTION

Myocardial ischemia and infarction due to the occlusion of coronary arteries alter the contractility of cardiac muscle, producing segmental akinesis or systolic bulging (dyskinesis) (Akaishi et al. 1986, Holmes et al. 2005). This regional wall motion abnormality has become one of the key indicators for visual interpretation and diagnosis of heart disease using echocardiography (Heger et al. 1979). However, this method is observer-dependent (Thomas and Popovic 2006).

Ultrasound strain and strain rate imaging have been proposed to quantitatively assess regional myocardial deformation (D’hooge et al. 2002, Kaluzynski et al. 2001, Uematsu et al. 1995, Urheim et al. 2000). Doppler tissue imaging (DTI) derived elasticity imaging (D’hooge et al. 2002, Uematsu et al. 1995, Urheim et al. 2000) and correlation-based two-dimensional (2-D) speckle tracking (Kaluzynski et al. 2001, Lee et al. 2007, Leitman et al. 2004, Notomi et al. 2005) are two major ultrasound techniques to measure myocardial strain (D’hooge et al. 2000, Thomas and Popovic 2006).

DTI-derived strain imaging has been investigated in phantom experiments (Matre et al. 2003), animal experiments (Urheim et al. 2000), and human experiments (Edvardsen et al. 2002, Pellerin et al. 2003), demonstrating the feasibility of clinical application (Sutherland et al. 2004). However, these methods are severely limited by angle dependency because only one component of the symmetric strain tensor (3 and 6 components in 2-D and three-dimensional tensors, respectively) can be measured along the beam direction (D’hooge et al. 2000, Edvardsen et al. 2002, Thomas and Popovic 2006). The second limitation is that DTI-derived strain estimates suffer from low signal-to-noise ratio (SNR) (Chen et al. 2005, Hanekom et al. 2007) because relatively high repetition frequencies are required to minimize decorrelation due to multi-dimensional motion. Axial displacement images estimated using DTI-derived methods are visually noisier than those using phase-sensitive 2-D speckle tracking (Chen et al. 2005).

An alternative approach to strain imaging using 2-D non-Doppler speckle tracking can minimize the angle dependency problems of Doppler-based methods by estimating in-plane 2-D strain components. Non-Doppler speckle tracking can be divided into two categories according to different input data: phase-insensitive speckle tracking using B-mode gray-scale images (Leitman et al. 2004, Migrino et al. 2007) and phase-sensitive speckle tracking using radio frequency (RF) data (Brusseau et al. 2008, D’hooge et al. 2002, Kaluzynski et al. 2001, Konofagou and Ophir 1998, Lee et al. 2007, Lopata et al. 2006, Maurice and Bertrand 1999). Phase-insensitive 2-D tracking has poor precision in both dimensions whereas phase-sensitive tracking has good precision along the propagation direction and relatively poor precision orthogonal to the propagation direction (Lubinski et al. 1999).

It has been shown that phase-insensitive tracking can overcome Doppler based DTI-derived strain imaging’s angle dependence in animal experiments (Migrino et al. 2007, Rappaport et al. 2008) and clinical patient investigations (Cho et al. 2006, Leitman et al. 2004, Perk et al. 2007). Without phase information, however, the results depend highly on spatial and temporal smoothing, and traces of strain components only represent the overall behavior of large segments.

In contrast, phase-sensitive speckle tracking using RF images can refine tracking results along the propagation direction using the calculated phase zero-crossing position (Lubinski et al. 1999), and this improvement in one direction leads to higher accuracy in the accumulated results in both directions (see section on 2-D speckle tracking under Materials and Methods). Therefore, phase-sensitive speckle tracking not only can overcome the angle limitation of Doppler-based methods, but also provide more accurate results with higher spatial resolution for each strain component, an important feature to derive coordinate-independent principal axes and strains based on the principal stretches along these axes. The accuracy and higher spatial resolution is valuable to detect the transmurality of myocardial ischemia or infarction. In this study, phase-sensitive speckle tracking is used to estimate myocardial deformation.

In continuum mechanics, deformation at one point in a solid body can be fully characterized by strains based on the principal stretches along the principal axes, where a proper coordinate rotation is applied to eliminate all shear components (Atkin and Fox 1980). These parameters are only related to the deformation status at that point and are theoretically independent of coordinates. In this study, we propose to use in-plane strains based on the principal stretches along the principal axes to characterize the contractility of heart muscle and the directional change of the principal axes to detect abnormal motion. In the remainder of this paper we will often refer to deformation estimated in this way simply as strains.

Note that strains (Chen 2004, Jia et al. 2007) obtained by deriving the principal stretches from the right Cauchy deformation tensor are different from the principal strains (Zervantonakis et al. 2007) calculated using the finite Lagrange deformation tensor. The latter includes a second order term in the fractional deformation, where the former is more precise and direct when estimating the fractional deformation compared to the original length in large strain situations, such as the accumulated deformation at the end of the systole, as shown in the Appendix.

Estimation of strains based on principal stretches and their principal axes is independent of the coordinate system or the orientation of the probe. These strains are derived from the eigenvalues and eigenvectors of the right Cauchy deformation tensor. The tensor captures the deformation status at that point and that moment regardless of the probe’s orientation. However, the accuracy and precision of estimated strains and their principal axes depend on the probe’s orientation. Because displacements used to estimate the right Cauchy deformation tensor are estimated by multi-dimensional, phase-sensitive speckle tracking, they exhibit higher variance in the lateral direction than the axial direction due to the availability of phase information only along the ultrasound propagation direction (Lubinski et al. 1996). The unequal estimation variances between displacements along the beam and those perpendicular to it lead to the unequal estimation variances of the components in the right Cauchy deformation tensor. Therefore, the accuracy and precision of estimated strains and their principal axes derived from the right Cauchy deformation tensor depend on the direction of ultrasound propagation relative to the principal axes.

In this paper, we describe a well controlled in-vitro experiment on an isolated rabbit heart paced from the apex. Two coplanar and orthogonal linear probes were used to acquire RF data. Left ventricle (LV) pressure and electrocardiogram (ECG) signals were recorded and synchronized with ultrasound RF data acquisition using a field programmable gate array (FPGA). Acute ischemia was generated by ligating the left anterior descending (LAD) coronary artery on an isolated Langendorff retroperfused rabbit heart. Results from a single probe show that systolic bulging of the heart wall due to LAD ligation can be detected by significant directional changes (about 90°) in the principal axes. As indicated by the principal axes, muscle fibers during systole actively shorten primarily along the heart’s circumferential direction producing heart wall thickening primarily along the heart’s radial direction before LAD ligation. After ligation, fibers are passively stretched primarily along the heart’s circumferential direction by surrounding muscles, leading to heart wall thinning approximately along the heart’s radial direction in the area perfused by the LAD. In addition, decreased myocardial contractility due to 2,3-butanedione monoxime (BDM) was detected by decreased strain magnitude. Results derived using asymmetric displacement accuracy from a single probe were also compared to those derived using symmetric displacement accuracy (i.e., dual probe measurements using only accurate axial tracking information from each). Identification of the ischemic region using directional changes of the principal axes was further validated by Evans Blue staining.

MATERIALS and METHODS

Langendorff Rabbit Heart Preparations

One adult New Zealand white rabbit was used. The experiment was performed according to a protocol approved by the University of Michigan Committee on the Use and Care of Animals. The rabbit received veterinary care provided by the University of Michigan Unit for Laboratory Animal Medicine. The University of Michigan is authorized by the American Association of Accreditation of Laboratory Animal Health Care and the animal care use program is in compliance with the standards in The Guide for the Care and Use of Laboratory Animals.

The rabbit was anesthetized by intramuscular injection of Ketamine (35mg/kg) and Xylazine (5mg/kg). As soon as the rabbit was euthanized by injecting sodium pentobarbital (100 mg/kg), heparin (500U/kg) was injected into the left marginal ear vein to prevent clot formation. The heart was rapidly excised and mounted on a Langendorff setup. It was retroperfused with modified, oxygenated Krebs-Henseleit (K-H) buffer (pH 7.4; 37°C; 95% O₂/5% CO₂) through the aorta with perfusion pressure 35 – 40 mmHg. The modified K-H buffer (Tanhehco et al. 2000) contained in mM: 117 NaCl, 4 KCl, 1.2 MgCl₂•6H₂O, 1.1 KH₂PO₄, 5.0 glucose, 25 NaHCO₃, and 2.6 CaCl₂•2H₂O.

Experimental Setup

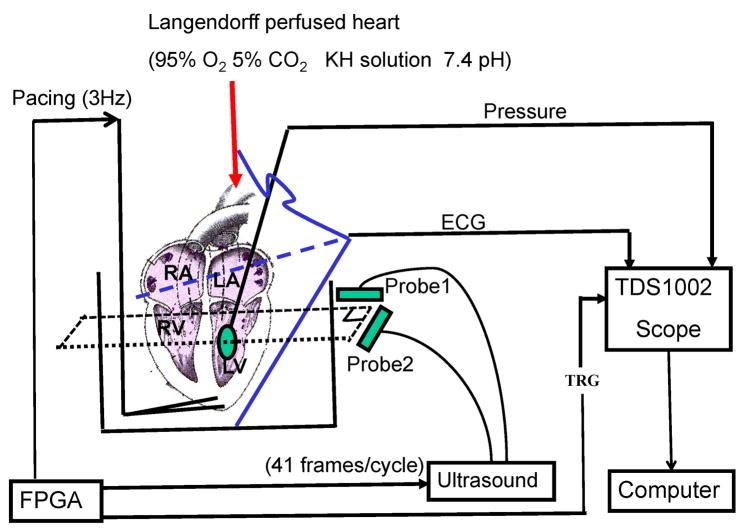
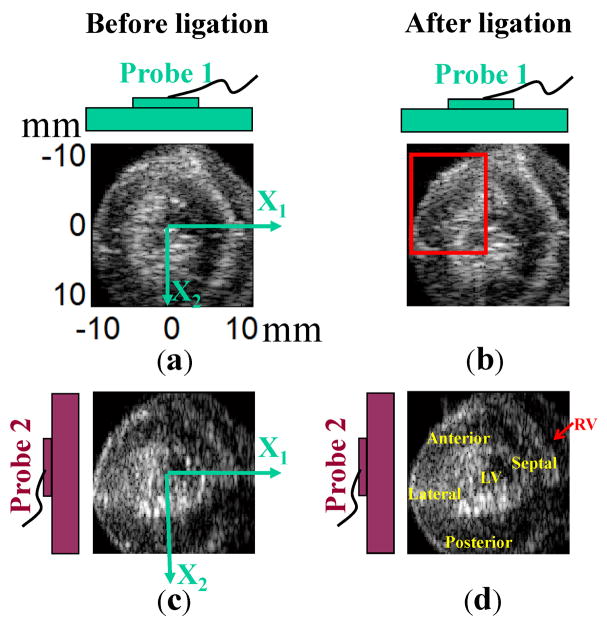
To overcome the rabbit’s natural heart beat and synchronize data acquisition, the heart was paced at 3Hz from its apex with two electrodes (Fig. 1). They were made of Teflon insulated tungsten wires (A-M System Inc., Carlsborg, WA, USA) and attached to a function generator (5V, 500μs square pulse, HP33120A, Agilent Technologies, Santa Clara, CA, USA). The ECG signal was recorded using three electrodes; two, made of Teflon insulated tungsten wires, were placed at the top and bottom of the bath; the third silver wire was submerged in the perfusion solution near the aorta. The ECG signal was filtered through a differential amplifier with gain of 1000 and bandwidth of 1–3000 Hz (AM502, Tektronix, Richardson, TX, USA).

Fig. 1.

Schematic of the experimental setup: The rabbit heart was retroperfused with modified K-H buffer (pH 7.4; 37°C; 95% O₂/5% CO₂) through the aorta. Two electrodes paced the heart from its apex at 3Hz. The ECG signal was recorded using three electrodes. Two wires were placed at the top and bottom of the bath. The third silver wire was submerged in the perfusion solution right before the aorta. LV pressure was measured through a latex balloon filled with water. Two linear arrays were coplanar and orthogonally positioned outside the tank to acquire RF data. An FPGA chip helped synchronize the pacing signal, LV pressure, ECG signal, and RF data capturing.

The LV pressure was recorded with a pressure meter (Alicat Scientific Inc., Tucson, AZ) through a latex balloon. The balloon was inserted via the left atrium into the LV, secured with a silk string at the left atrial appendage, and then expanded with a small amount of water to achieve an LV end-diastolic pressure of 10 mmHg. Measured LV pressure was 10–60mmHg, well within the heart’s physiological working range. The balloon itself, however, was not fully inflated and with the water inside was still deformable. Therefore the balloon introduced minimal elasticity effects on myocardial deformation. The measured LV pressure was filtered through a second differential amplifier with gain of 50 and bandwidth of 0.1–3000 Hz (AM502, Tektronix). Both ECG and LV pressure signals were digitized simultaneously using an oscilloscope (TDS1002, Tektronix) and transferred to a computer using a general purpose interface bus (GPIB).

Two linear array probes connected to a commercial ultrasound (US) scanner (SonixRP, Ultrasonix, Richmond, BC, Canada) were coplanar and orthogonally positioned below the LAD ligation position to acquire RF data from a short-axis view (Fig. 2). An FPGA chip (ezFPGA-C6-6, Dallas Logic, Plano, TX, USA) was programmed to synchronize the pacing signal, LV pressure, ECG signal, and RF data capture. The frame rate of the US machine in this experiment was 123 Hz (41 frames per heart cycle). This was the highest frame rate available with this commercial scanner for the field of view used and the requirement of full synchrony with the pacing signal. This frame rate is not as high as cited in other studies (Luo and Konofagou 2008), but it is sufficient here because out-of-plane motion was minimized by attaching the heart to the fixed pacing wire at the apex. The average correlation coefficient for frame to frame tracking was above 0.8 except for one interval of high strain rate during early systole in which the average coefficient fell to about 0.7.

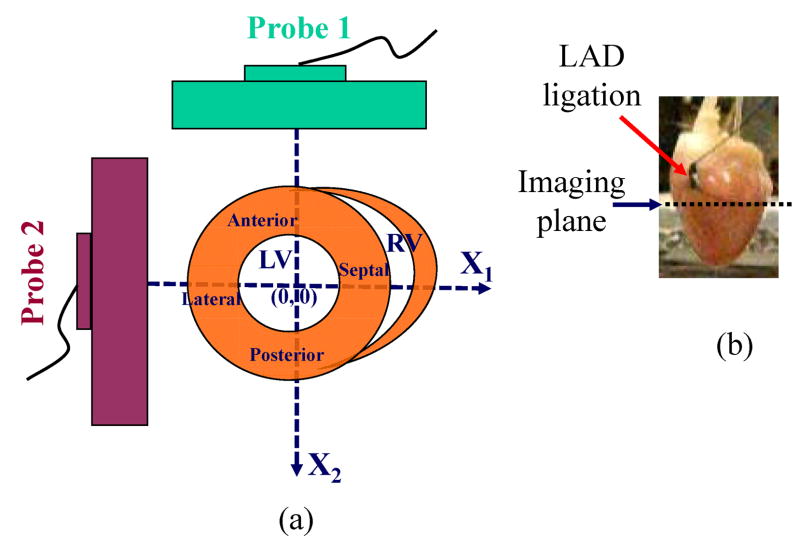
Fig. 2.

Probe orientation in global coordinates for short-axis view of the heart. Two linear probes were coplanar and oriented 90° apart within a plane just below the LAD was ligation (as shown in (b)). RF data in the short-axis view were acquired from two probes, with higher resolution along the axial direction and lower resolution along the lateral direction for each probe. As shown in (a), the X₁-axis is the lateral direction of probe 1 and axial direction of probe 2. The X₂-axis is the axial direction of probe 1 and lateral direction of probe 2.

To co-register the two fields of view, a wire perpendicular to the image plane was used to register the image planes from each probe after the probes were clamped in a holder with two 90° legs. The wire was first placed in the lateral center of each probe, then translated 3 steps in x and y directions independently with a step size of 5mm (i.e., nine total positions). Images were recorded at each position and used to construct a 3x3 composite point image for each probe. The center point was used to locate the image center. One 3 by 3 point image from one probe was also rotated 90° to check if it would overlap the other 3 by 3 point image from the second probe. Alignment was maintained to 0.15 mm and orthogonality to 0.5°.

Both linear probes used in this setup have a central frequency of 5 MHz, sampling frequency of 40MHz, and 128 elements with a pitch of 0.3 mm. Two coordinate systems (global coordinates and scanner coordinates) were used, as shown in Fig. 2 with the anterior wall on the upper left corner (Fig. 2(a)). In global coordinates, the X₁-axis was defined as the horizontal direction and the X₂-axis is defined as the vertical direction. In scanner coordinates, the axial direction is defined along the beam propagation direction, and the lateral direction is perpendicular to the beam propagation direction for each probe. Since the probes were orthogonal to each other, the X₁-axis in global coordinates is the lateral direction of probe 1 and the axial direction of probe 2; the X₂-axis is the axial direction of probe 1 and the lateral direction of probe 2.

Experimental Procedure

The experimental procedure was divided into four stages. In the first three, LV pressure, ECG and RF data were monitored and recorded. In the final stage, Evans Blue staining was used to find the nonperfused area (area at risk) due to LAD ligation.

Stage 1: The rabbit heart was retroperfused with modified K-H solution. The heart wall contracted synchronously with the pacing signal.

Stage 2: The rabbit heart was retroperfused with both K-H solution and 4mM BDM. Maximum contraction was decreased with BDM.

Stage 3: Acute ischemia was produced by ligating the LAD with a silk suture. The heart was retroperfused with only K-H solution or K-H solution including 4mM BDM, which will be discussed in the next section (BDM regulation). RF data were acquired from both probes several minutes after LAD ligation. RF data obtained in stages 1, 2 and 3 were processed offline. Strains and their corresponding principal axes were estimated from these RF data obtained before and after ligation.

Stage 4: Evans Blue staining was used to identify nonperfused areas: areas at risk. The heart was detached from the Langendorff perfusion system. 2ml of 0.4% Evans Blue was retroperfused into the heart for about 10 seconds until the heart was stained uniformly (Booth et al. 2005). The heart was then cut around the imaging plane corresponding to the short-axis view used for all experiments. Optical images of the stained cross section were used to validate the abnormal region determined by principal axes analysis. The unstained area was the area at risk due to LAD ligation (Booth et al. 2005).

BDM Regulation

BDM is an excitation-contraction decoupler, 2,3-butanedione monoxime, which can reversibly reduce the maximum deformation (Kettlewell et al. 2004). In other words, BDM can reduce heart muscles’ contractility. The higher the concentration of BDM, the more contractility will be reduced. In the experiment, 4mM BDM was retroperfused into the heart along with oxygenated modified K-H solution to partially reduce the heart muscles’ contractility.

2-D Speckle Tracking

As mentioned above, each of two coplanar, orthogonal linear probes acquired forty one frames (one RF data set) in one heart cycle. Correlation-based phase-sensitive 2-D speckle tracking (Lubinski et al. 1999) was applied to estimate the cardiac contraction between every two consecutive frames in each data set. The tracking algorithm first calculated the complex cross-correlation coefficient between speckle-sized blocks from two consecutive frames. The correlation coefficient functions were then filtered using a 2-D Hanning window to reduce tracking error and peak hopping.

In this study, the correlation kernel, corresponding to one speckle spot, was 1.50 mm × 0.24 mm (lateral x axial) and the filter size was 2.10 mm × 1.22 mm (lateral x axial). Axial and lateral displacements were initially estimated by finding the peak position of the magnitude of the filtered correlation coefficient function using a parabolic fit. The axial displacement was further refined by calculating the position of the phase zero-crossing around the peak correlation coefficient. Since there is no phase information in the lateral direction, lateral displacement estimates have much larger variance than axial ones (Lubinski et al. 1996).

Estimated displacements between two consecutive frames were then integrated frame by frame to obtain the accumulated displacements relative to a reference frame. In this study, the reference frame was chosen at the beginning of systole (downward arrow in Fig. 3(c) and (d)) and displacements were accumulated until peak systole (upward arrow in Fig. 3(c) and (d)). Ultimately, the axial displacement estimate had a higher spatial resolution of about 1.24 mm and the lateral displacement estimate had a resolution of about 2.58 mm, considering the combined effects of kernel and filter sizes. The thickness of heart wall was about 4–5mm. Finally, the deformation gradient tensor was computed using Eq. (A-1) by spatially differentiating accumulated displacements to derive principal axes and strains based on the principal stretches along these axes. Details are described in the next section.

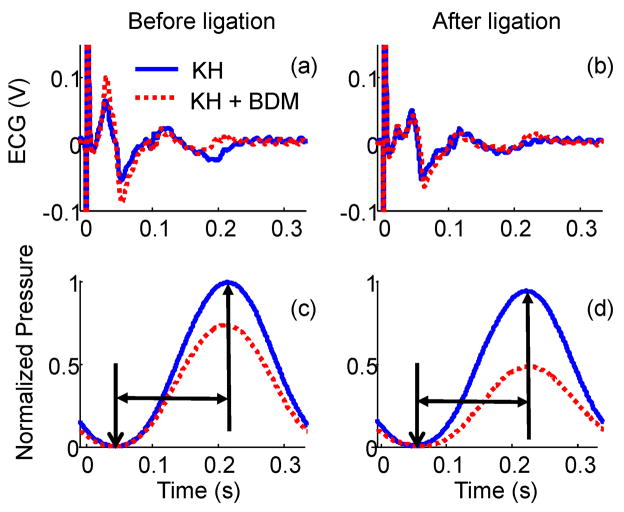
Fig. 3.

(a) ECG measured before LAD ligation; (b) ECG measured after LAD ligation; (c) Normalized LV pressure before LAD ligation; (d) Normalized LV pressure after LAD ligation. The heart was perfused with two different solutions: only modified K-H solution (blue solid line), and modified K-H solution with 4 mM BDM (red dotted line). The big signal at t=0 in (a) and (b) is a triggering artifact. The duration between the two arrows in (c) and (d) is defined as systole in this experiment. The first frame over this period was used as the reference frame for displacement accumulation.

Strains Based on the Principal Stretches and Corresponding Principal Axes

In continuum mechanics, deformation at one point in a solid body can be fully characterized by strains based on the principal stretches along the principal axes, where a proper coordinate rotation eliminates all shear components. The principal axes and corresponding strains fully describe the deformation at that point independent of coordinate system. In this study, we use strains based on the principal stretches to characterize contractility and directional changes of their principal axes to detect abnormal motion due to LAD ligation.

As shown in the appendix, the deformation gradient tensor using Eq. (A-1) is calculated by first spatially differentiating accumulated displacements estimated using phase-sensitive speckle tracking. Then, the right Cauchy deformation tensor C was calculated using Eq. (A-2). As shown in Eqs. (A-3) and (A-4), by calculating the eigenvalues and eigenvectors of this tensor, the square of two in-plane principal stretches (λ₁ and λ₂) and their principal axes (v₁ and v₂) in the orthogonal matrix Ω are obtained. Note that principal axes defined here are bidirectional. That is, v₁and −v₁ represent the same axis.

The strains based on the principal stretches at a point within the solid body are defined as (λ₁ −1) and (λ₂ −1) at that point along the principal axes v₁and v₂, respectively. If one strain is larger than zero, then the solid body at this point lengthens along the corresponding principal axis. If negative, the solid body at this point shortens along the principal axis. Note that the strains (λ₁ −1) and (λ₂ −1) based on the principal stretches have the same corresponding principal axes as the principal strains (ε₁ and ε ₂) calculated using Eqs. (A-5) and (A-6). However, they have different values as shown in Eqs. (A-7) and (A-8) and different physical meanings.

As illustrated in Fig. A-1 and Eq. (A-9), strains based on principal stretches (λ₁ −1) and (λ₂ −1) quantify the shortening (−) or lengthening (+) of the original element along the principal axes as a fraction of the original length. Principal strains ε₁ and ε₂ as shown in Eq. (A-8) include a second order term in the fractional length change which is significant at large strain amplitude. When the deformation is small, the principal strains approximately equal the strains based on the principal stretches along the principal axes.

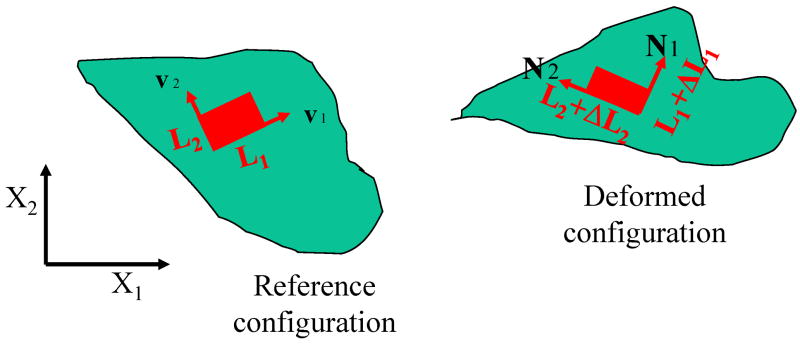
Fig. A-1.

The deformation of an infinitesimal 2-D element at a point in a solid body illustrated in the reference configuration and deformed configuration. X₁ and X₂ are the coordinate’s axes for the reference configuration. v₁ and v₂ are the principal axes of this 2-D element in the reference configuration. The original size of this element is L₁ by L₂ along the principal axes. After deformation, the element was reshaped into (L₁ + ΔL₁) by (L₂ + ΔL₂). The principal axes are rotated into N₁ and N₂ in the deformed configuration.

$$\begin{array}{l}{\epsilon }_1\approx {\lambda }_1-1\\ {\epsilon }_2\approx {\lambda }_2-1.\end{array}$$ (1)

However, the accumulated strain at the end of systole is not small. Strains based on the principal stretches (λ₁ −1) and (λ₂ −1) along the principal axes are more direct and precise parameters for characterizing cardiac deformation. Consequently we propose to use the strains (λ₁−1) and (λ₂−1) along the principal axes v₁ and v₂ to characterize heart muscle contractility in this study. For convenience, we define λ₁ > λ₂ for the rest of the paper.

The accuracy and resolution of axial and lateral displacements estimated by speckle tracking will affect the accuracy of principal axes estimates and corresponding strains, because displacements are used directly to calculate deformation gradient tensor components, as shown in Eq. (A-1). As mentioned above, the lateral component has lower spatial resolution and less estimation precision than the axial component. To further investigate the effects of asymmetric displacement estimation and explore optimal methods using multi-dimensional speckle tracking, we also compare single probe results with those derived using both axial displacements from two orthogonal and coplanar linear probes.

In summary, three methods were used:

Method 1: lateral and axial displacements derived exclusively from probe 1 data. u₁ and u₂ in Eq. (A-1) are the lateral and axial displacement components of probe 1, respectively, as shown in Fig. 2.

Method 2: lateral and axial displacements derived exclusively from probe 2 data. u₁ and u₂ in Eq. (A-1) are the axial and lateral displacement components of probe 2, respectively, as shown in Fig. 2.

Method 3: axial displacements from probe 1 and probe 2 are used. u₁ is the axial displacement of probe 2 and u₂ is the axial displacement of probe 1, as shown in Fig. 2.

RESULTS

ECG Signal and LV Pressure

ECG and LV pressure before and after LAD ligation are shown in Fig. 3 for two perfusion conditions: only modified K-H solution (blue) and modified K-H solution with 4 mM BDM (red). Note that the peak at time zero in the ECG figures is a pacing artifact. When the heart was correctly paced, each cycle was 1/3 second. The time lag between excitation, indicated by the ECG signal, and contraction, indicated by LV pressure, remained the same for all conditions (as shown in Fig. 3(a) and (c), Fig. 3(b) and (d)). The morphology of ECG signals in Fig. 3(a) was similar for different BDM concentrations before LAD ligation. The same phenomena can also be observed in Fig. 3(b) after LAD ligation. However, the morphology of the ECG signals before and after ligation was slightly different. The reason is probably that muscle fibers perfused by the LAD no longer actively contracted and conduction was altered after ligation.

As discussed in the previous section (BDM Regulation), BDM was used to reduce heart muscles’ contractility. This effect of BDM was clearly demonstrated by the LV pressure. As shown in Fig. 3(c), LV pressure was reduced by about 25% in the heart retroperfused with K-H solution including 4 mM BDM (red) compared to that measured when the heart was retroperfused with only K-H solution (blue). After ligation, LV pressure was reduced by about 50% by BDM as shown in Fig. 3(d). The duration between the two arrows in Fig. 3(c) and (d) was defined as systole in this study.

Strains Based on the Principal Stretches and Corresponding Principal Axes

Results from a single probe presented in this section were further validated using the results from two probes. To closely compare single probe to dual probe performance, we present results from both systems together.

B-mode images acquired using the two linear arrays before and after ligation when the heart was perfused in modified K-H solution are registered in the global coordinates shown in Fig. 4 with the anterior wall on the upper left corner as shown in Fig. 4(d). The first column presents B-mode images before ligation, while the second column contains B-mode images after ligation. The first row was acquired with probe 1 at the top and the second row was acquired with probe 2 on the left. After LAD ligation, abnormal motion in the anterior wall highlighted in Fig. 4(b) was observed in the B-mode movie (B_mode_movie.avi). Compared to the synchronous global contraction of the heart before ligation, the anterior wall in the highlighted area after LAD ligation lost its local active contraction and bulged out during systole instead of thickening in the radial direction. This abnormal area matched the perfusion area of the LAD.

Fig. 4.

B-mode images acquired using the two linear arrays before and after ligation in global coordinates displayed with respect to probe orientation: The first column shows B-mode images before ligation, while the second shows images after ligation. The first and second rows were acquired using probes 1 and 2, respectively. Bulging can be observed from the B-mode movie (B_mode_movie.avi) in the area highlighted by the box in (b).

Results at the end of systole referenced to the first frame at the beginning of systole are presented and analyzed in the rest of section. To avoid being distracted by surrounding artifacts, masks are manually generated according to the contour of the corresponding first B-mode image during systole and applied to subsequent results.

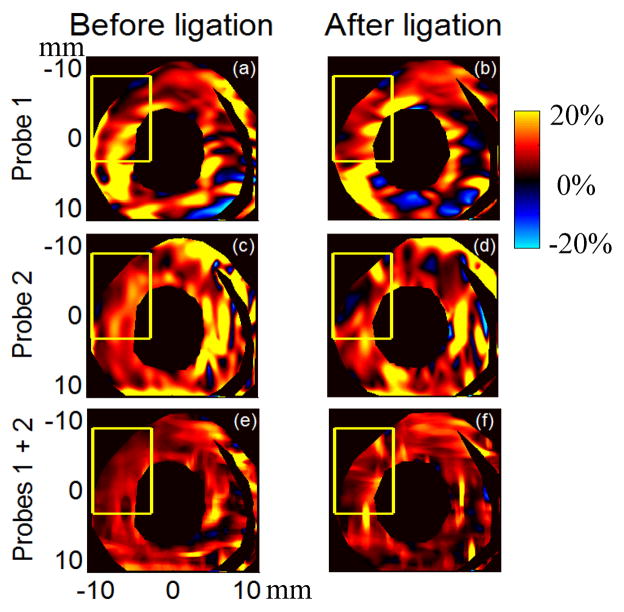
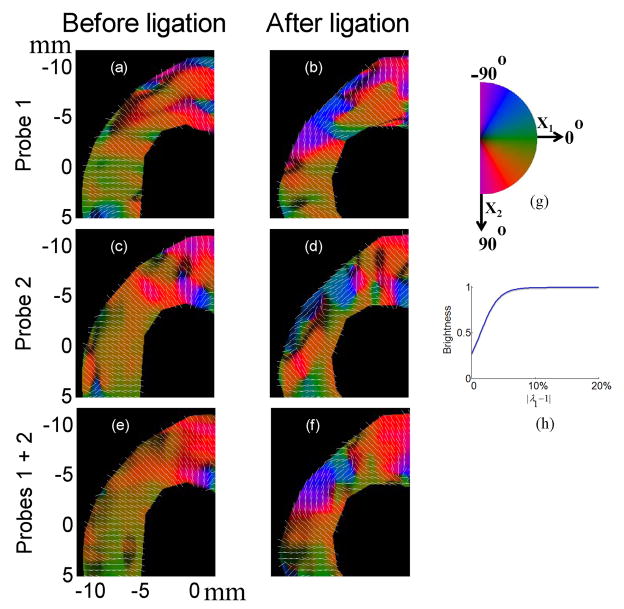
As discussed in the corresponding section under Materials and Methods, the deformation at any position within the heart wall can be characterized by principal axes (v₁and v₂) with corresponding strains based on the principal stretches along them ((λ₁ −1) and (λ₂ −1) with λ₁ > λ₂) derived from accumulated Lagrangian displacement estimates using 2-D speckle tracking. The strain (λ₁ −1) before and after ligation at the end of the systole is presented in Fig. 5 for different probe combinations when the heart was perfused with only modified K-H perfusion solution. The first column shows results before ligation, and the second column after ligation. The first row presents results from probe 1, the second row from probe 2, and the third row from combined axial displacement estimates from both probes. The highlighted area denotes the region of abnormal motion observed in the B-mode movie. The accumulation of strain (λ₁ −1) during systole for three probe combinations is also presented in three separate movies: KH_Probe1_strain1.avi, KH_Probe2_strain1.avi, and KH_Probe1and2_strain1.avi, which correspond to rows 1, 2 and 3 in Fig. 5, respectively. As is evident from these figures and movies, (λ₁ −1) is positive over most of the heart wall, especially when axial displacement estimates from both probes are combined. Positive values mean the myocardium lengthens along the principal axis v₁. Images of this principal axis’s direction in the upper left corner of Fig. 5 are shown in Fig. 6 and color coded from −90° to 90° as shown in the colormap in Fig. 6(g). The brightness of each color was modulated by the magnitude of the strain using the shifted sigmoid function shown in Fig. 6(h). A vector presenting the direction of the principal axis is superimposed on the color-coded image (the corresponding movies KH_Probe1_v1_highlighted.avi, KH_Probe2_v1_highlighted.avi, and KH_Probe1and2_v1_highlighted.avi). The principal axis v₁ is primarily in a direction perpendicular to the heart wall before ligation and changes to be primarily in a direction parallel to the heart wall after ligation. In other words, the heart wall thickens primarily in a direction perpendicular to the heart wall before ligation due to active shortening of muscle fibers, and changes to be passively stretched by surrounding muscles primarily in a direction parallel to the heart wall after ligation in this highlighted area. This is consistent with findings by Villarreal (Villarreal et al. 1991) that myocardium in ischemic regions will change from radial directional thickening to circumferential directional stretching during systole. Note that estimation of strains based on principal stretches and principal axes does not require a centroid; it is only related to the deformation condition at that point.

Fig. 5.

Strain based on the principal stretch (λ₁ −1) at the end of systole before (left column) and after (right column) ligation for different probe combinations when the heart was perfused with only modified K-H perfusion solution. The first row presents results using only probe 1 data (KH_Probe1_normal_strain1.avi), the second row presents results using only probe 2 data (KH_Probe2_normal_strain1.avi), and the third row presents results combining axial displacement estimates from both probes (KH_Probe1and2_normal_strain1.avi).

Fig. 6.

The angle of principal axis v₁ for strain based on the principal stretch (λ₁ −1) in the upper left corner of Fig. 5 at the end of systole before (left column) and after (right column) ligation for different probe combinations when the heart was perfused with K-H perfusion solution. On the left side, the first row presents results using only probe 1 data, the second row presents results using only probe 2 data and the third row presents results combining axial displacement estimates from both probes.. On the right side, (g) presents the cyclic colormap for the angle of principal axis ranging from −90° to 90°; (h) presents the shifted sigmoid function describing the relationship between each color’s brightness and the magnitude of the strain. Vector showing the direction of the principal axis v₁ is superimposed.

These results match those obtained from two probes (Fig. 6(f) versus Fig. 6(e)). However, the shapes of the area with this direction change in single probe images are slightly different from that in the two probe image. This is mainly due to the large variation in lateral displacement estimation from single probe data.

The second strain ((λ₂ −1) and their principal axis v₂ also provide the complementary information that myocardium in the highlighted area actively shortens approximately parallel to the heart wall before ligation but changes to thinning approximately perpendicular to the heart wall after ligation due to stretching by surrounding muscles.

Similar trends are observed when the heart was retroperfused with K-H perfusion solution including 4 mM BDM, but with expected reduced overall deformation magnitude. Under both perfusion conditions, muscle fibers in the highlighted region during systole actively shorten primarily along the heart’s circumferential direction and thicken primarily along the heart’s radial direction before LAD ligation. After ligation, fibers are passively stretched primarily along the heart’s circumferential direction by surrounding muscles, leading to the heart wall’s thinning approximately along the heart’s radial direction.

The decrease of the overall myocardium’s contractility due to BDM is observed by the decrease of strains along their principal directions. This decrease can also be found quantitatively in the averaged strains (λ₁ −1), (λ₂ −1) and strain magnitude ( $\sqrt{{({\lambda }_1-1)}^2+{({\lambda }_2-1)}^2}$) in the highlighted region (shown in Fig. 5) at the end of systole before ligation for both types of solution shown in Table 1. The averaged strains for K-H solution including 4 mM BDM decrease to 40%–60% of that for only K-H solution. The variance of the calculation is relatively large partly because the segment covers the entire heart wall from endocardium to epicardium.

Table 1.

Strains based on the principal stretches along principal axes in the highlighted area before ligation

	Probe1		Probe 2		Probes 1 and 2
	KH	KH+BDM	KH	KH+BDM	KH	KH+BDM
strain 1 based on the principal stretches (%)	−7.7±3.5	−4.4±2.0	−8.4±4.4	−4.9±2.4	−6.4±2.6	−4.0±1.5
strain 2 based on the principal stretches (%)	10.1±8.6	5.3±4.8	8.6±4.8	4.0±2.2	5.1±2.3	3.6±1.5
strain magnitude based on the principal stretches (%)	13.7±7.6	7.5±4.3	12.7±5.0	6.8±2.3	8.5±2.7	5.5±1.8

Directional changes of the principal axes also can be presented as the dot product of principal axes v₁ before and v₁ after LAD ligation in the highlighted region, as shown in Fig. 7(a)–(c) for only K-H solution. A value of one in these images means that the principal axes before ligation and after ligation are the same/parallel while zero means they are perpendicular to each other. The region with the directional changes of principal axes can be observed in the upper left corner for different probe combinations. Compared to Fig. 7(c) using two probes, the single probe results (Fig. 7(a) and (b)) have more shape variation because of the large variance in the lateral displacement estimates for single probe data. In other words, the accuracy and precision of single probe results tends to be sensitive to probe orientation.

Fig. 7.

The dot product of the first principal axes before and after ligation for heart perfused using only K-H solution: (a) Probe 1; (b) Probe 2; (c) Probes 1+2 (d) Evans Blue staining result after the ultrasound experiment. The highlighted region is the area at risk due to LAD ligation.

Evans Blue Staining

Fig. 7(d) presents an optical photograph of the heart stained with Evans Blue at the cross section corresponding to the ultrasound results presented above. The upper left area has substantially less staining due to LAD ligation. This area at risk identified by Evans Blue staining matches well to the abnormal area (Fig. 7(a)–(c)) estimated by measurements of the directional change in the principal axis.

DISCUSSION and CONCLUSIONS

In this study, a well-controlled 2-D cardiac elasticity imaging technique was developed to test the capability of multi-dimensional speckle tracking for detection of deformation abnormalities due to myocardial ischemia. Two coplanar and orthogonal linear probes were used to simultaneously image an isolated retroperfused rabbit heart. A segmental dyskinesis (i.e., systolic bulging) due to acute ischemia was produced by LAD ligation and a reversible decrease in the myocardium’s contractility was also achieved by adding 4 mM BDM into modified K-H perfusion solution. Initial results in this study have demonstrated two possibilities for potential clinical application of this 2-D cardiac elasticity imaging technique.

First, the results from a single probe demonstrate the feasibility of sensitively detecting abnormal wall deformation using directional changes of the principal axes - the results from two probes further validate this feasibility. Under two perfusion conditions (only modified K-H solution and K-H solution including 4 mM BDM) as shown in Fig. 6, and corresponding movies during systole (KH_Probe1_v1_highlighted.avi, KH_Probe2_v1_highlighted.avi, and KH_Probe1and2_v1_highlighted.avi for only modified KH), muscle fibers during systole actively shorten primarily along the heart’s circumferential direction producing heart wall thickening primarily along the heart’s radial direction before LAD ligation. After ligation, fibers are passively stretched primarily along the heart’s circumferential direction by surrounding muscles, leading to the heart wall’s thinning approximately along the heart’s radial direction in the area perfused by the LAD. The region detected by this directional change matches well with the area at risk identified by Evans Blue staining. The continuous transition of principal axes at the boundary of the region is also found in Fig. 6. This is consistent with previously reported findings describing the tethering effects of surrounding normal myocardium on segments which have lost active contraction (Bijnens et al. 2007).

We also repeated the experiment in a second rabbit heart perfused with K-H solution to demonstrate the coordinate-independence of strains based on principal stretches and corresponding principal axes. Compared to the first heart (Fig. 7), the region with abnormal contractility was rotated about 45° clockwise as shown in the dot product images of principal axes before and after LAD ligation for different probe combinations (Fig. 8(a), (b) and (c)). As expected, the results from single probes (Fig. 8(a) and (b)) show more variation than those using two probes (Fig. 8(c)). The detected abnormal region also matched well with the corresponding Evans Blue staining shown in Fig. 8(d). Similar coordinate-independence was also proposed using principal strains by Zervantonakis (2007). However, strains based on the principal stretches are more direct and precise to quantify cardiac contractility, as shown in the Appendix.

Fig. 8.

The dot product of the first principal axes before and after ligation for the second heart: (a) Probe 1; (b) Probe 2; (c) Probes 1+2 (d) Evans Blue staining result after the ultrasound experiment. The highlighted region is the area at risk due to LAD ligation.

Second, the results from a single probe also demonstrated the feasibility of quantifying myocardial contractility using strains, or stain magnitude, based on the principal stretches along principal axes. In this experiment, 4 mM BDM was used to reversibly reduce overall myocardial contractility, which decreases the heart’s global function as measured by LV pressure. As expected for the 4 mM BDM case, strains based on the principal stretches along the principal axes decrease along with the decrease of the myocardium’s contractility, as shown in table 1. Therefore, the strains, or strain magnitude, along the principal axes can be used as an indicator of myocardial contractility. It may be possible to sensitively detect segmental changes in contractility (such as segmental akinesis) from the locally decreased magnitude of strains along the principal axes.

The above two conclusions derived using asymmetric displacement accuracy (i.e., normal single probe measurements with good axial and poor lateral estimates) were further validated using symmetric displacement accuracy (i.e., dual probe measurements using only accurate axial tracking estimates from each). The location of the abnormality and general trends in contractility detected with a single probe are similar to those obtained with two probes. However, the size and shape of the abnormal region are different for the different probe combinations. This difference is due primarily to the large variance in lateral displacement estimates and their position in the deformation tensor F as shown in Eq. (A-1). This leads to dependency of the accuracy of 2-D cardiac strain imaging using a single probe on the probe’s orientation, even though the principal axes and their corresponding strains are theoretically only related to the deformation status at that point and independent of coordinates.

Initial results using a single probe in this study suggest that this method may be clinically useful for diagnosing cardiac diseases related to abnormal wall deformation by finding the abnormal principal axis directions of myocardium during systole. That is, a possible regional dyskinesis can be found by a single probe when the principal axis of positive strain in this area during systole is not primarily along the radial direction of the heart wall. This method reduces the angle limitation of Doppler based strain imaging and has potential for detecting the transmurality of myocardial ischemia or infarction with higher accuracy and spatial resolution than B-mode image based tracking.

The results obtained with this method using a single probe must be used with special care for clinical interpretation since the accuracy of the region at risk depends on the probe’s orientation relative to the heart wall. Analysis of single probe data acquired from multiple views on the suspected region during examination is also recommended if possible. If the location of the detected suspect region is independent of probe rotation, the confidence in myocardial abnormality will increase. Nonetheless, imaging the same suspect region from different views is subject to limited probe windows among the ribs and requires more operator expertise.

Finally, this technique may also be applicable to stress echocardiography in the future. During stress echocardiography, images obtained at rest and during peak exercise or pharmacologic stress are compared to identify areas at risk for ischemia. The same conclusions made between K-H solution and K-H solution including 4 mM BDM in this study can be applied to strain images acquired during a stress test compared to those acquired at rest. The dot product map of principal axes can be used as another visual presentation to detect the area at risk. However, correct registration of the heart wall between rest and stress images is required to use the dot product image as a potential clinical tool. In addition, a stress test will increase heart rate, producing fewer frames per cardiac cycle at a given frame rate. High frame rate (D’hooge et al. 2000, Luo and Konofagou 2008) is usually preferred to reduce decorrelation due to out-of-plane motion when correlation-based 2-D tracking is applied. Therefore, interframe interpolation with proper weighting must be developed to properly compare images acquired at different effective frame rates (i.e. frames per cardiac cycle). Moreover, the SNR of clinical data is usually lower than that of controlled animal experiments, which will affect the accuracy of this method when applied clinically.

APPENDIX: Principal Stretch and Principal Strain

In continuum mechanics, deformation is often quantified by the deformation gradient tensor F (Malvern 1969). It compares the size and shape of material elements in the deformed configuration. Let x and X be the coordinates in the reference and deformed configuration, respectively. F in 2-D is defined as:

$$\mathbf{F}\equiv \left(\begin{array}{cc}\frac{\partial x_1}{\partial X_1}& \frac{\partial x_1}{\partial X_2}\\ \frac{\partial x_2}{\partial X_1}& \frac{\partial x_2}{\partial X_2}\end{array}\right)=\left(\begin{array}{cc}\frac{\partial u_1}{\partial X_1}+1& \frac{\partial u_1}{\partial X_2}\\ \frac{\partial u_2}{\partial X_1}& \frac{\partial u_2}{\partial X_2}+1\end{array}\right),$$ (A-1)

where u₁ and u₂ are the displacement components due to deformation. F can be expressed as F = RU, where R is a rotation matrix and U is a symmetric deformation matrix. The right Cauchy deformation tensor

$$\mathbf{C}\equiv {\mathbf{F}}^{\mathbf{T}}\mathbf{F}={\mathbf{U}}^T\mathbf{U}$$ (A-2)

is independent of rotation and fully characterizes the deformation. C is a symmetric tensor and can be decomposed as:

$$\mathbf{C}=\mathbf{\Omega }\left(\begin{array}{cc}{({\lambda }_1)}^2& 0\\ 0& {({\lambda }_2)}^2\end{array}\right){\mathbf{\Omega }}^T$$ (A-3)

where

$$\mathbf{\Omega }=\left(\begin{array}{cc}{\mathbf{v}}_1& {\mathbf{v}}_2\end{array}\right)=\left(\begin{array}{cc}{\text{v}}_{11}& {\text{v}}_{12}\\ {\text{v}}_{21}& {\text{v}}_{22}\end{array}\right)$$ (A-4)

is a unitary matrix, and v₁ and v₂ are the eigenvectors of C corresponding to the eigenvalues ${\lambda }_1^2$ and ${\lambda }_2^2$, respectively, and orthogonal to each other.

Because tissues do not have high compressibility, ${\lambda }_1^2={\lambda }_2^2$ holds only if the deformation is small. Therefore, in this study where large deformation is typical, it suffices to consider only ${\lambda }_1^2\ne {\lambda }_2^2$. When ${\lambda }_1^2\ne {\lambda }_2^2$, the eigenvectors are uniquely determined to within a factor of 1 or −1 (Malvern 1969). In continuum mechanics, λ₁ and λ₂ are defined as principal stretches, and v₁ and v₂ represent the principal axes of these principal stretches. Note that the principal axes defined here are bidirectional. That is, v₁ and −v₁ represent the same axis. A principal stretch represents the length ratio of a segment along the corresponding principle axis in the deformed configuration to its original segment along the corresponding principal axis in the reference configuration. That is, (λ₁ −1) and (λ₂ −1) describe how much the original segment shortens (−) or lengthens (+) along the principal axis directions as a fraction of the original lengths. In this study, we use (λ₁ −1) and (λ₂ −1) to characterize cardiac contractility and the principal axes to characterize contraction direction. We label (λ₁ −1) and (λ₂ −1) as the strains based on the principal stretches along the principal axes. They differ from the principal strains.

The commonly used Lagrangian (Green) strain tensor for finite deformation is:

$$\mathbf{E}=\frac{1}{2}(\mathbf{C}-\mathbf{I}).$$ (A-5)

E is a symmetric tensor and can be also decomposed as:

$$\mathbf{E}=\mathbf{Q}\left(\begin{array}{cc}{\epsilon }_1& 0\\ 0& {\epsilon }_2\end{array}\right){\mathbf{Q}}^T.$$ (A-6)

where ε₁ and ε₂ are the eigenvalues of E and are called principal strains. They were proposed for view-independent myocardial strain mapping by Zervantonakis (2007).

Comparing (A-3), (A-5) and (A-6) further reveals that strains based on the principal stretches (λ₁ −1) and (λ₂ −1) have the same principal axes as principal strains ε₁ and ε₂. However, in general ${\epsilon }_1=\frac{1}{2}\left({({\lambda }_1)}^2-1\right)\ne ({\lambda }_1-1)$ and ${\epsilon }_2=\frac{1}{2}\left({({\lambda }_2)}^2-1\right)\ne ({\lambda }_2-1)$.

To understand the physical meaning of these parameters, the deformation at a point in a solid body can be illustrated by an infinitesimal 2-D element at that point (Fig. A-1). X₁ and X₂ are the coordinate’s axes for the reference configuration. v₁ and v₂ are the principal axes of this 2-D element in the reference configuration. The original size of this element is L₁ by L₂ along the principal axes. After deformation, the element was reshaped into (L₁ + ΔL₁) by (L₂ + ΔL₂). The principal axes are rotated into N₁ and N₂ in the deformed configuration, as illustrated in Fig. A-1.

The principal stretches and principal strains at this point are written as

$$\begin{array}{l}{\lambda }_1=\frac{\mathrm{\Delta }{L}_1+L_1}{L_1}\\ {\lambda }_2=\frac{\mathrm{\Delta }{L}_2+L_2}{L_2}\end{array}$$ (A-7)

$$\begin{array}{l}{\epsilon }_1=\frac{1}{2}\left({({\lambda }_1)}^2-1\right)=\frac{1}{2}\left({(\frac{\mathrm{\Delta }{L}_1+L_1}{L_1})}^2-1\right)=\frac{\mathrm{\Delta }{L}_1}{L_1}+\frac{1}{2}{(\frac{\mathrm{\Delta }{L}_1}{L_1})}^2\\ {\epsilon }_2=\frac{1}{2}\left({({\lambda }_2)}^2-1\right)=\frac{1}{2}\left({(\frac{\mathrm{\Delta }{L}_2+L_2}{L_2})}^2-1\right)=\frac{\mathrm{\Delta }{L}_2}{L_2}+\frac{1}{2}{(\frac{\mathrm{\Delta }{L}_2}{L_2})}^2\end{array}$$ (A-8)

After rewriting Eq.(A-7), we see that

$$\begin{array}{l}{\lambda }_1-1=\frac{\mathrm{\Delta }{L}_1}{L_1}\\ {\lambda }_2-1=\frac{\mathrm{\Delta }{L}_2}{L_2}\end{array}$$ (A-9)

As shown in Eq. (A-8), principal strains ε₁ and ε ₂ include a second order term in the fractional deformation compared to strain based on principal stretch (λ₁ −1) and (λ₂ −1). Since we want to quantify the fractional change of element length in large strain cases, such as the deformation at the end of systole in this study, principal stretches are more direct and precise.