Abstract
Motivation: Predictions of protein local structure, derived from sequence alignment information alone, provide visualization tools for biologists to evaluate the importance of amino acid residue positions of interest in the absence of X-ray crystal/NMR structures or homology models. They are also useful as inputs to sequence analysis and modeling tools, such as hidden Markov models (HMMs), which can be used to search for homology in databases of known protein structure. In addition, local structure predictions can be used as a component of cost functions in genetic algorithms that predict protein tertiary structure. We have developed a program (predict-2nd) that trains multilayer neural networks and have applied it to numerous local structure alphabets, tuning network parameters such as the number of layers, the number of units in each layer and the window sizes of each layer. We have had the most success with four-layer networks, with gradually increasing window sizes at each layer.
Results: Because the four-layer neural nets occasionally get trapped in poor local optima, our training protocol now uses many different random starts, with short training runs, followed by more training on the best performing networks from the short runs. One recent addition to the program is the option to add a guide sequence to the profile inputs, increasing the number of inputs per position by 20. We find that use of a guide sequence provides a small but consistent improvement in the predictions for several different local-structure alphabets.
Availability: Local structure prediction with the methods described here is available for use online at http://www.soe.ucsc.edu/compbio/SAM_T08/T08-query.html. The source code and example networks for PREDICT-2ND are available at http://www.soe.ucsc.edu/~karplus/predict-2nd/ A required C++ library is available at http://www.soe.ucsc.edu/~karplus/ultimate/
Contact: karplus@soe.ucsc.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
1.1 Protein local structure
The original definition of protein secondary structure was based on the work of Linus Pauling and Robert Corey (Pauling et al., 1951), who predicted the existence of α-helices and β-sheets. After the structures of proteins began to be solved with X-ray crystallography to atomic resolution, more nuanced variants of these two original patterns emerged, such as particular types of turns, β-bulges and so on.
As the number of solved structures published in the PDB (Bernstein et al., 1977) increased, it became necessary to define such structures by means of computer algorithms. In these definitions, each residue of a protein is associated with one letter of a secondary structure alphabet. The most commonly employed algorithms are dssp, an eight-letter alphabet due to Kabsch and Sander (1983) and stride, a seven-letter alphabet due to Frishman and Argos (1995).
These secondary structure alphabets are often reduced to the three states of helix, sheet and coil. But, since the coil category accounts for ∼45% of all assigned residues in a protein (Fetrow et al., 1997), it is likely that such first-order definitions, while easily interpreted and possessing an intuitive appeal, fail to capture much of the information available in the atomic coordinates of protein structures.
Even if one is restricted to assigning one alphabet letter per residue, it is possible to more broadly define local structure alphabets, which can capture much of this missing information. Among the properties that can be encoded in such an alphabet are
participation in hydrogen bonding with neighboring residues, which can either collapse (dsspehl2) or expand (str2) the helix-sheet-coil paradigm,
torsion angles of the backbone at the residue,
torsion angles between Cα atoms,
ad hoc definitions based on unsupervised learning techniques, such as the protein blocks of de Brevern et al. (2000) and
measures of the exposure of the residue to the solvent.
Among alphabets that capture some of the above properties, we have previously (Karchin et al., 2003, 2004) explored the use of, and relationships among, numerous local structure alphabets. These can be categorized into backbone geometry alphabets and burial alphabets. The definition of the backbone geometry and burial alphabets can be found in the Supplementary Materials.
For this work, we evaluated eight different local structure alphabets—six backbone alphabets: alpha, bys, dssp, str2, stride and dssp-ehl2 and two burial alphabets: burial-cb-14-7 and near-backbone-11. Our main interest here is in the robustness of the training protocol, as Karchin's work has previously examined the usefulness of these alphabets (except for near-backbone-11) (Karchin et al., 2003, 2004).
1.2 Inputs and outputs of local structure predictors
The key attribute of a local structure prediction algorithm is that it uses as input sequence information from the protein—no structural information is assumed. Rather than just a simple sequence, however, most algorithms use a profile of the target sequence as the starting point. Such profiles are usually derived from a multiple alignment of sequences that share some degree of similarity with the target protein and presumably represent either close or distant homologs. It is presumed that conservation of structure is a feature of the evolution of homologs, so that the multiple sequence alignment represents a sampling by nature of the sequences that can adopt that structure. The more that distant homologs can be included in such a profile, the more information we have about what sequences can adopt the structure, and the more reliably we should be able to predict the structure.
On the other hand, too much generality can include noise (sequences adopting different local structures) that may swamp the signal that is sought. Thus one may need to carefully tune the threshold used to define similarity when including sequences in a multiple alignment to be used as input to a local structure prediction. An alternative to such tuning however, is to use a fairly loose definition of similarity, but also use the actual sequence of the target protein as an auxiliary input.
We call this the guide sequence and describe below our experience with using it in local structure prediction.
The output of a local structure prediction can be just a single letter from the predicted alphabet, corresponding to each position in the target sequence. However, a more general output consists of a probability distribution over the letters of the alphabet at each position. This form conveys more information, is often more useful for subsequent tools, and if desired, can easily be reduced to a single output per position by choosing the letter with the highest probability.
1.3 Uses of predicted local structure
In the following subsections, we describe some typical uses of local structure predictions.
1.3.1 Fold-recognition efforts
In the community-wide experi-ment for protein structure prediction known as casp (Lawrence Livermore National Laboratory, 2002; Moult et al., 1997, 1999), our group has concentrated on remote fold-recognition with fairly good results (Karplus et al., 1997, 1999, 2001). In 2000, we started incorporating secondary structure prediction in our fold-recognition method for casp4 (Karplus et al., 2001).
The suite of tools for sequence alignment and modeling (SAM) developed at UCSC (Hughey and Krogh, 1995, 1996; Hughey et al., 1999) is based on hidden Markov models (hmms). While, the original versions of SAM represented an amino acid profile via the emission probabilities of the amino acid types at each position in the sequence, more recent versions have implemented so-called multi-track hmms (Karplus et al., 2003). In these models, additional parameters are added, representing emission probabilities at each position of one or more local structure alphabet letters.
Among the uses of these hmms are fold recognition, pairwise alignments of sequences and generation of the fragments to be used in fragment replacement programs such as undertaker (Karplus et al., 2003) or rosetta (Bonneau et al., 2001; Bradley et al., 2005). When building such an hmm for a target protein of unknown structure, the emission probabilities for the alphabets other than the primary amino acid sequence are taken from a local structure prediction.
1.3.2 Cost functions for tertiary predictions
We have developed the undertaker program that performs three-dimensional (3D) protein structure prediction. It employs a genetic algorithm, with numerous tunable cost functions and conformation generation operators, including fragment replacement, as in the rosetta program. Cost functions based on predicted local structure have been found to be among the most powerful of the cost functions for determining the quality of resulting conformations.
1.3.3 Alphabet logos
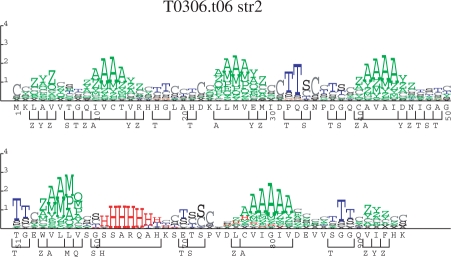
For a protein that appears to contain a novel structure, having no close homologs in PDB, and for which the full panoply of 3D structure tools fails to generate a structure with high confidence, a reasonable prediction of local structure can still be useful. For example, a biologist can derive insight by looking at the logo representation of the local structure prediction, as in Figure 1. These logos are similar to sequence logos (Schneider and Stephens, 1990), but use the predicted probability of the structure alphabet letters, rather than observed frequency of amino acids or bases. At each position in the sequence, the total height of all the letters is proportional to the relative entropy between the predicted probabilities 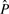 and the background distribution of the alphabet (P0):
and the background distribution of the alphabet (P0):
Fig. 1.
This is a logo of a prediction of the str2 alphabet for a casp7 protein sequence that had no close PDB homologs, but which was predicted to consist almost entirely of anti-parallel β-strands and one α-helix. See text for explanation of heights of letters. The bars below the sequence positions represent segments of a single contiguous predicted letter of the full str2 alphabet. When the structure was solved, it turned out that this predicted secondary structure was very accurate.
The individual predicted letters at a position are displayed such that the total height is distributed according to the predicted probabilities of the letters at that position. For example, if a single letter is predicted with absolute certainty (even if the prediction turns out to be wrong!), the logo will show the predicted letter at maximal height.
In Figure 1, the prediction consists almost entirely of anti-parallel (β)-strands, separated either by regions of low-confidence predictions, or by more definite short turn regions. Even though no high-confidence full structure prediction for this protein could be made, a biologist looking at the logo can get an immediate feel for the likely type of protein this is, and could make a decision on whether or not to invest significant effort in pursuit of the structure (or other properties) of the protein. Similarly, when making detailed structure predictions, a human analyst can gain insight by looking at such a representation and can then guide machine-based methods towards more likely solutions.
1.4 Neural nets for local structure prediction
As soon as there began to be sufficient protein structures in PDB, the preferred implementation of predictions of secondary structure focused on neural nets. As more and more protein sequences became available it was recognized that using multiple sequence alignments as the inputs to the neural nets leads to more accurate results (Rost and Sander, 1993). In the psipred method (Jones, 1999), the position-specific scoring matrices that are available from psi-blast (Altschul et al., 1997) are used directly, rather than the multiple alignments that are the usual output from that program.
The architecture of many of the neural net programs currently in widespread use (Jones, 1999; Rost, 1996) is relatively straight-forward. A window is applied to the input profile, so that a fixed number (say 15, as in psipred) of positions in the sequence are examined simultaneously at the input level. For the 20 amino acids (and one additional letter to indicate the ends of the sequence), this requires 315 input units in the network (for psipred). There typically follows a single hidden layer (psipred used 75 units for that layer). Finally, the three output units representing helix, sheet and coil produce the secondary structure sequence. In order to deliver slightly improved accuracy, this first network is usually connected in tandem to a second network of similar architecture. The second network differs from the first in that its inputs use the same secondary structure alphabet as its outputs, and it thus can be termed a structure-to-structure predictor (Rost and Sander, 1993).
As is described in more detail below, the predict-2nd imple-mentation differs from the above paradigm in several respects. First of all, rather than relying on a tandem pair of neural networks, we have implemented a fully general scheme that allows an arbitrary number of hidden layers. At each layer, a window of units from the previous layer can be used as input, with the window widths, like the number of hidden layers and the number of units per layer, selected at run time. Another difference from the usual methods is that we do not use the (Qn) measure (percentage of correct predictions in the whole sequence) as the objective function to be optimized during training. Instead, we focus on the bits saved or information-gain measure (defined in Section 2.1) for an arbitrary local structure alphabet.
One relatively recent addition to predict-2nd is the optional inclusion of a guide sequence (defined above) in the input. This is intended to counteract the possibility of overgeneralization of the input profile due to inclusion of too distantly related sequences.
It is worth noting that like all the other layers, the number of outputs from predict-2nd is also easily varied, which enables us to quickly generate predictions for arbitrary local structure alphabets. This allows us to evaluate their predictability, as well as to use such alphabets in our other programs for improved results.
We have also improved our training protocol by using multiple random starts. Neural net training often gets trapped in local optima, and using multiple starts with different initial weights helps us find a good local optimum.
1.5 Other tools for local structure prediction
Neural networks have not been the only methods applied to the local structure prediction problem—others include Bayesian statistics and various machine learning methods. For example, the GOR V method uses a combination of information theory, Bayesian statistics and evolutionary information for local structure predictions (Klockzkowski et al., 2002). A recently popular machine learning method for predicting local structure has been support vector machines (Cortes and Vapnik, 1995; Hua and Sun, 2001). Both of these methods have been used to predict a three-letter reduced state alphabet from DSSP and do comparably to neural networks when predicting this kind of local structure alphabet.
2 METHODS
The following sections described how we generate, given an amino acid sequence for a protein of unknown structure, a residue-by-residue prediction for an arbitrary local structure alphabet. See Figure 2.
Fig. 2.
Overview of our local structure prediction method. Starting with the target amino acid sequence as input, a single track HMM is constructed and updated by the SAM program during an iterative search for homologous sequences. After convergence, the SAM HMM is used to generate a multiple sequence alignment of the homologous sequences that were found. This alignment is input to the predict-2nd multilayer neural network which generates predictions of the letters of a local structure alphabet for each position in the input alignment.
2.1 Objective functions
In evaluating the performance of neural nets for prediction of classic secondary structure, most practitioners have concentrated on the so-called Qn measure, which is simply the percentage of correct predictions in the entire sequence. Thus if one is predicting helix, strand or coil, a choice is made at each position and is scored in a binary fashion as being either right or wrong when compared to the alphabet in use (usually a collapsed version of dssp or stride).
When one is concerned with fold-prediction, the segment overlap (SOV) measure (Rost et al., 1994; Zemla et al., 1999) is often used. In this measure a pairwise alignment of the predicted sequence and the actual sequence is used to calculate the fraction of segments (runs of one letter in the alphabet) that are correctly found. In Figure 1, the bars that appear below the position-by-position letters represent the predicted segments for use in SOV measures. The SOV measure was intended primarily for use with a simple three-state secondary structure alphabet and may have no useful meaning in alphabets that do not result in long runs of the same letter.
Because we are interested in examining different local structure alphabets, we prefer to use a measure that is not intrinsically dependent on the number of letters in the alphabet. We also are interested in the confidence of our predictions (the probability assigned to the outputs) rather than just whether the most probable output is correct or not, which discards much of the information in the prediction. For these reasons, we have taken an information-based approach to prediction. For each alphabet, the information content (entropy) can be calculated, which is defined as
where P(xi) is the probability of a certain letter occurring based on the background distribution of the alphabet. An alphabet with a higher entropy value carries more information, and we can expand the idea of information for use in our prediction methods. We focus on the probability assigned by our prediction to the correct letter at each position in the sequence, and calculate the average number of bits saved per position, relative to the background distribution of the alphabet. The bits-saved measure can also be considered the information gain from predicting letters of the alphabet. For a sequence with n positions, if ci is the correct letter at position i, and the background and predicted probabilities are P0 and  , then our measure is
, then our measure is
Assume one had an alphabet of four letters, and wished to double the size of that alphabet by splitting each category in two. If the original prediction of four letters is extended to eight by randomly assigning each prediction to one of its two new subclasses, then the Q8 score would be roughly half of the Q4 score. In contrast, even though the entropy of the new alphabet is increased by one full bit, since both the background and predicted probability of the correct letter at every position would be halved, the bits saved by the original prediction would be nearly unchanged.
Thus, although we report the Qn and SOV results of our predictions, and in fact sometimes use an objective function that is a weighted mixture of all three measures to choose a network, we train our networks by maximizing the following function (which contains the network-dependent part of bit-saved):
2.2 Creating multiple alignments
To generate multiple alignments, we use the SAM suite of HMMs tools to do iterated search, using any of several different protocols we have developed (Hughey and Krogh, 1996; Karplus et al., 2001, 2005). The multiple alignments are thinned so that the resulting set has no pair of sequences with more than 90% identity on the aligned columns. For a more detailed discussion about how we generate multiple alignments for use with local structure prediction, see the Supplementary Materials.
2.3 Converting multiple alignments to profiles
For input to the neural nets, predict-2nd converts the SAM alignments into profiles, assigning a probability vector over the amino acids at each position in the sequence. The probability vector is computed by using a Dirichlet mixture regularizer (Sjölander et al., 1996) applied to weighted counts of the amino acids at that position. The relative sequence weights are computed using a method due to Henikoff and Henikoff (1996, 1994).
Dirichlet mixture regularizers are sensitive to the total weight of the sequences, as well as the relative weights, and we have experimented with two different ways to set the total weight. In one method, the total weight is simply the number of sequences in the alignment. In the other method, the total weight is adjusted so that the average relative entropy of the resulting distribution compared to the background distribution is ∼1.3 bits. As it turns out, both weighting schemes seem to work equally well, and the details of the sequence weighting may not be of much importance. See the Supplementary Materials for a more detailed description of the weighting methods.
2.4 Neural net architectural features
The predict-2nd implementation is script driven and has the ability to write out and read back in a neural net description that comprises a set of interfaces and layers of essentially arbitrary size. Based on our earlier experience, we have focused in the current work on neural nets with three hidden layers, varying the number of units in each hidden layer and the windowing used in each interface.
The number of input units is 42 if a guide sequence is used: a one-hot encoding (this is the guide sequence) of the amino acid in the target sequence (20), a probability for each amino acid from the multiple alignment (20) and probabilities of insertion and deletion (2). The number of output units is just the number of distinct letters in the local structure alphabet to be predicted.
To calculate the output of each unit in each layer, we use a soft max function so that all of the outputs of a given layer represent a valid probability distribution (summing to unity) over that layer's units. Thus, if a unit j receives weighted inputs wijxi from the set of units i with values xi in the previous layer, and has a bias value bj, then its output is calculated as
In each layer, every unit actually takes as inputs a window of outputs from the previous layer's set of units. So in the previous formula, the range of i should be taken to include NW values, where N is the number of unique units in the previous layer and W is the window width used. This windowing feature gives the net the ability to capture local structure information that is not encoded in a single amino acid position. We would normally expect the weights to be highest in the center of the window, but there is nothing in the current neural net training paradigm to enforce this.
Because the number of paths from input position i to output position j decreases as |i−j| increases, the influence of residues further away from the position being predicted is automatically reduced by the multi-layer windowing. The multilayer windowing also allows propagation of information from a fairly large set of inputs with relatively few parameters to train in the neural net, reducing the dangers of overfitting the training data.
In our work with three hidden layers, we usually use between 10 and 15 units in each layer, with window widths varying from about 5 at the input layer to as high as 13 for the layer before the outputs.
2.5 Training the nets
Our training data are a set we call dunbrack-30pc-1763, which is a set of 1763 non-homologous chains. It is derived from a culled PDB set of 1875 chains, with resolution of 1.8 Å or better, maximum R-factor 0.25 and maximum sequence identity of 30%, using Dunbrack's PISCES server (Wang and Dunbrack, 2003). We removed 112 chains from the set:
77 chains because length <50
26 chains that were non-globular (fragments of a protein that had been entered in PDB as separate chains, chains with very long breaks, chains with topological problems such as bad knots, or non-compact monomers from a multimeric complex). Because the desired labeling for burial alphabets was determined from chains in isolation, without other parts of multimeric complexes or crystal contacts, we did not want to include too many examples of chains that were not independently folding. In retrospect, we probably should have removed even more of the chains that are unlikely to fold independently to the experimentally observed structure.
nine chains that had very bad clashes as determined by the clash detector in our undertaker program.
We used 3-fold cross-validation to test the neural networks, that is, we split the dunbrack-30pc-1763 set into three sets of chains, trained networks on two-thirds of the data and tested on the remaining third. Results are reported on the average of three networks, one for each of the three test sets.
To train the networks, we started by training 100 networks each with different random values for the weights wij and bias bj in each neuron. After 50 epochs of training, we chose the 10 best networks and trained these networks for 100 more epochs. We then trained the top three networks for a final 100 epochs, and chose the best of those.
All the training and choices were based strictly on the training set. We then used the reserved test data to test the finally chosen network. More details about our training protocol can be found in the Supplementary Materials.
3 RESULTS
To date, we have explored the space of architectures to a limited extent, with preliminary experiments (not reported here) indicating that architectures with two or three hidden layers outperformed architectures with zero or one hidden layer, but that the arrangement of window widths and number of hidden units was not critical.
In this article, we focus on two architectures for which we did extensive testing, described in Table 1. One network is chosen from the class of architectures using a guide sequence in addition to a profile for input; the other uses the profile only. Each architecture was selected based on preliminary testing of a small number of architectures on one alphabet and one set of multiple sequence alignments (data not shown). Note that they have the same number of hidden layers (3), with comparable window sizes and number of units in the hidden layers.
Table 1.
Architectures for the neural nets compared in this article.
| IDaaHr | IDGaaH13 | |
|---|---|---|
| Use guide seq? | no | yes |
| Total seq. weight | # of seqs | to get 1.3 bits |
| Input units | 22 | 42 |
| Layer 1 window | 5 | 3 |
| Layer 1 units | 15 | 13 |
| layer 2 window | 7 | 7 |
| Layer 2 units | 15 | 13 |
| layer 3 window | 9 | 9 |
| Layer 3 units | 15 | 13 |
| Output window | 13 | 11 |
| Output units | 11 (for BYS) | 11 (for BYS) |
| Degrees of freedom | 6850 (for BYS) | 5438 (for BYS) |
The IDaaHr network uses amino acid probabilities and insert/delete probabilities from a multiple sequence alignment as inputs. The IDGaaH13 uses those inputs plus a one-hot encoding of the amino acid of the target sequence. The sequence weighting for computing the probabilities differs between the two networks, but this is probably irrelevant (Table 4).
The number of units in each layer and the window of inputs from the previous layer is shown. The number of output units is equal to the number of letters in the output alphabet being predicted. The degrees of freedom represents the number of parameters to be trained (downward adjusted for the parameters which could be subsumed in other parameters, due to the normalization of the soft-max function) and is shown for the case of the bys alphabet, which has 11 output units. The nets for other alphabets will have slightly different degrees of freedom as the output layer will have different numbers of parameters, based on the number of outputs.
Due to its smaller windows and number of units, the IDGaaH13 network has slightly fewer total degrees of freedom (number of parameters to be trained, downward adjusted for the parameters which could be subsumed in other parameters because of the normalization by the soft-max function), than the IDaaHr network, despite having more inputs. If the guide sequence did not matter, one might expect the IDaaHr network to outperform the IDGaaH13 network with its fewer degrees of freedom, but the opposite is apparently true for all alphabets tested, as shown in Table 2.
Table 2.
Comparison of results for several alphabets with the two architectures specified in Table 1, using SAM-T06 multiple alignments
| Alphabet | bits saved |
Qn |
||
|---|---|---|---|---|
| IDaaHR | IDGaaH13 | IDaaHR | IDGaaH13 | |
| str2 | 1.05 | 1.12 | 0.54 | 0.56 |
| dssp | 0.92 | 0.98 | 0.63 | 0.64 |
| stride | 0.89 | 0.94 | 0.66 | 0.67 |
| bys | 0.70 | 0.83 | 0.58 | 0.59 |
| dssp-ehl2 | 0.75 | 0.79 | 0.77 | 0.78 |
| alpha | 0.67 | 0.74 | 0.46 | 0.47 |
| burial CB14 | 0.55 | 0.57 | 0.35 | 0.35 |
| near-backbone-11 | 0.49 | 0.54 | 0.24 | 0.25 |
The bits-saved measure is the one used for training, as Qn (the fraction of most probable letters that are correct) is not really comparable between different alphabets. Note that the backbone alphabets carry more predictable information than the burial alphabets (CB14 and near-backbone-11).
The (Qn) value for the dsspehl2 alphabet is included in Table 2 to show that predict-2nd is comparable to other methods of local structure prediction. However, the Qn measure can vary greatly depending on the training and test data, so this measure does not show that predict-2nd is considerably better or worse than other prediction methods.
In Table 3, we show the results in bits saved after each stage of training. We report the average over all neural nets trained after 50, 150 and 250 epochs of training. Because we do 3-fold cross-validation and select fewer networks for training in later stages, the number of neural networks used in the averages are 300, 30 and 9, respectively. These results indicate that using a guide sequence in our training helps improve the results from the neural network. For example, for the near-backbone-11 alphabet, after 50 epochs, the average without a guide sequence is only 0.05 bits saved while the average with a guide sequence is 0.33 bits saved.
Table 3.
Comparison of the average training results for the str2 and near-backbone-11 alphabets for two architectures specified in Table 1 trained for 50, 150 and 250 epochs
| epochs | 50 | 150 | 250 |
|---|---|---|---|
| str2 | mean bits saved | ||
| IDaaHr | 0.84 | 1.02 | 1.08 |
| IDGaaH13 | 0.94 | 1.10 | 1.16 |
| near-backbone-11 | mean bits saved | ||
| IDaaHr | 0.05 | 0.47 | 0.50 |
| IDGaaH13 | 0.33 | 0.51 | 0.56 |
The architecture with the guide sequence (IDGaaH13) is consistently superior at all stages of training.
In Table 4, we show the results for the str2 alphabet using different weighting methods for generating the profiles from the multiple sequence alignments. For both architectures, changing the total weight of the sequences made essentially no difference in the average quality of the results.
Table 4.
The IDaaHr and IDGaaH13 neural nets in Table 3 differ in both architecture and sequence weighting
| Architecture | Weighting | Mean bits saved |
|---|---|---|
| IDaaHr | # of seq | 1.05 |
| IDaaH13 | 1.3 bits/col | 1.05 |
| IDGaaHr | # of seq | 1.12 |
| IDGaaH13 | 1.3 bits/col | 1.12 |
In this table, we compare the effect of the architecture change and the weighting change separately for the str2 alphabet, using the SAM-T06 alignments. IDaaH13 has the same architecture as IDaaHr, but uses a different sequence weighting. IDGaaHr has the same architecture as IDGaaH13, but with a different sequence weighting. The choice of weighting method does not seem to have an effect on the bits-saved measure, while the choice of architecture does.
In Table 5, we present the results for comparison across three iterated search methods for generating the multiple alignments: SAM-T2K, SAM-T04 and SAM-T06. The differences between the architectures is consistent across all the different multiple sequence alignments.
Table 5.
Comparison of results for the str2 and near-backbone-11 alphabets for two architectures specified in Table 1 trained on multiple alignments created with three different protocols
| Alignment | SAM-T2K | SAM-T04 | SAM-T06 |
|---|---|---|---|
| str2 | mean bits saved | ||
| IDaaHr | 1.07 | 1.02 | 1.05 |
| IDGaaH13 | 1.10 | 1.09 | 1.12 |
| near-backbone-11 | mean bits saved | ||
| IDaaHr | 0.51 | 0.48 | 0.49 |
| IDGaaH13 | 0.54 | 0.52 | 0.55 |
The difference between architectures is consistent across the different multiple alignments, with the IDGaaH13 architecture (which uses a guide sequence) consistently outperforming the IDaaHr architecture.
In Figure 3, we plot histograms of the bits saved for each chain of the test sets for the str2 alphabet test. The distributions of bits saved for the two architectures are quite similar, and the difference in the means is only about 0.2 standard deviations, but is almost 10 times the standard error of the mean.
Fig. 3.
Histogram of bits saved in cross-validation tests using the two architectures, one with and one without guide sequence for prediction of str2 alphabet. IDGaaH13 has a mean of 1.14, standard deviation of 0.31 and standard error of the mean of 0.007. IDaaHr has a mean of 1.08, standard deviation of 0.33 and standard error of the mean of 0.008. Most of the outliers with negative bits saved are short chains that are part of multimeric complexes and which probably do not fold independently to the experimentally observed conformation.
4 APPLICATIONS AND DISCUSSION
We use the predictions of various local structure alphabets produced by predict-2nd in several of our software tools. We find that reasonably accurate predictions of novel alphabets are important for extending the performance of those tools, and that improvements in local structure prediction result in improvements in fold recognition and alignment.
A key improvement to the ability of SAM to find remote homologs has come from the extension of the hmms, first to two tracks, and more recently to three tracks. For three-track hmms our current preferred set of alphabets is amino acid, str2 and near-backbone-11. We continue to optimize the weighting of the tracks for various applications including finding templates and making alignments to these templates.
Another use of predicted local structure is in the undertaker program, which uses local structure predictions in its cost function. There are two distinct uses, one only for backbone alphabets and the other for any alphabet that undertaker can assign to a conformation. For backbone alphabets (such as DSSP, Stride, str2, alpha, …), confident helix and strand predictions can be converted to helix and strand constraints for undertaker. For any alphabet, undertaker can include a cost function that is just the sum of the log odds ratios, 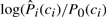 , for each position of the conformation.
, for each position of the conformation.
5 CONCLUSION
From the initial rough predictions of the classically defined secondary structure of the protein backbone, much progress has been made in optimizing neural nets to predict local structure on a residue-by-residue basis. Among the significant previous advances in these efforts were the use of amino acid profiles (or multiple alignments) as the input to the neural nets, and the cascading of two neural nets (each with one hidden layer), to produce the final predictions.
Our predict-2nd program generalizes these paradigms by allowing for arbitrary local structure alphabets, and arbitrary numbers of hidden layers, units per layer and window size at each layer. We have added a guide sequence as an additional input and found small but consistent improvements from doing so.
We have developed a multiple-random-start training protocol to get consistently good results from neural network training, despite the tendency for neural nets to get trapped in local optima.
By optimizing for information gain, rather than fraction correct, we have been able to compare alphabets with quite different sizes and background probabilities.
Funding: National Institutes of Health (grant R01 GM068570); Department of Energy (DOE) (grant DE-FG0395-99ER62849); National Physical Sciences Consortium graduate fellowship.
Conflict of Interest: none declared.
Supplementary Material
REFERENCES
- Altschul S, et al. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein F, et al. The Protein Data Bank: a computer-based archival file for macromolecular structures. J. Mol. Biol. 1977;112:535–542. doi: 10.1016/s0022-2836(77)80200-3. [DOI] [PubMed] [Google Scholar]
- Bonneau R, et al. Rosetta in CASP4: progress in ab initio protein structure prediction. Proteins Struct. Funct. Genet. 2001;45:119–126. doi: 10.1002/prot.1170. [DOI] [PubMed] [Google Scholar]
- Bradley P, et al. Free modeling with Rosetta in CASP6. Proteins Struct. Funct. Bioinform. 2005;61:128–134. doi: 10.1002/prot.20729. [DOI] [PubMed] [Google Scholar]
- Cortes C, Vapnik V. Support vector networks. Mach. Learn. 1995;20:273–297. [Google Scholar]
- de Brevern A, et al. Bayesian probabilistic approach for predicting backbone structures in terms of protein blocks. Proteins Struct. Funct. Genet. 2000;41:271–287. doi: 10.1002/1097-0134(20001115)41:3<271::aid-prot10>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- Fetrow J, et al. Patterns, structures, and amino acid frequencies in structural building blocks, a protein secondary structure classification scheme. Proteins Struct. Funct. Genet. 1997;27:249–271. [PubMed] [Google Scholar]
- Frishman D, Argos P. Knowledge-based protein secondary structure assignment. Proteins Struct. Funct. Genet. 1995;23:566–579. doi: 10.1002/prot.340230412. [DOI] [PubMed] [Google Scholar]
- Henikoff JG, Henikoff S. Using substitution probabilities to improve position-specific scoring matrices. Comput. Appl. Biosci. 1996;12:135–143. doi: 10.1093/bioinformatics/12.2.135. [DOI] [PubMed] [Google Scholar]
- Henikoff S, Henikoff JG. Position-based sequence weights. J. Mol. Biol. 1994;243:574–578. doi: 10.1016/0022-2836(94)90032-9. [DOI] [PubMed] [Google Scholar]
- Hua S, Sun Z. A novel method of protein secondary structure prediction with high segment overlap measure: support vector machine approach. J. Mol. Biol. 2001;308:397–407. doi: 10.1006/jmbi.2001.4580. [DOI] [PubMed] [Google Scholar]
- Hughey R, Krogh A. Technical Report UCSC-CRL-95-7. UC Santa Cruz, CA: University of California, Santa Cruz, Computer Engineering; 1995. SAM: sequence alignment and modeling software system. [Google Scholar]
- Hughey R, Krogh A. Hidden Markov models for sequence analysis: extension and analysis of the basic method. Comput. Appl. Biosci. 1996;12:95–107. doi: 10.1093/bioinformatics/12.2.95. Information on obtaining SAM is available at http://www.soe.ucsc.edu/research/compbio/sam.html(last accessed date September 19, 2008). [DOI] [PubMed] [Google Scholar]
- Hughey R, et al. Technical Report UCSC-CRL-99-11. UC Santa Cruz, CA: University of California, Santa Cruz, Computer Engineering; 1999. SAM: sequence alignment and modeling software system, version 3. Available from http://www.soe.ucsc.edu/research/compbio/sam.html(last accessed date September 19, 2008). [Google Scholar]
- Jones D. Protein secondary structure prediction based on position-specific scoring matrices. J. Mol. Biol. 1999;292:195–202. doi: 10.1006/jmbi.1999.3091. [DOI] [PubMed] [Google Scholar]
- Kabsch W, Sander C. Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers. 1983;22:2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
- Karchin R, et al. Hidden Markov models that use predicted local structure for fold recognition: alphabets of backbone geometry. Proteins Struct. Funct. Genet. 2003;51:504–514. doi: 10.1002/prot.10369. [DOI] [PubMed] [Google Scholar]
- Karchin R, et al. Evaluation of local structure alphabets based on residue burial. Proteins Struct. Funct. Genet. 2004;55:508–518. doi: 10.1002/prot.20008. doi:10.1002/prot.2008. [DOI] [PubMed] [Google Scholar]
- Karplus K, et al. Predicting protein structure using hidden Markov models. Proteins Struct. Funct. Genet. 1997;(Suppl. 1):134–139. doi: 10.1002/(sici)1097-0134(1997)1+<134::aid-prot18>3.3.co;2-q. [DOI] [PubMed] [Google Scholar]
- Karplus K, et al. Predicting protein structure using only sequence information. Proteins Struct. Funct. Genet. 1999;(Suppl. 3):121–125. doi: 10.1002/(sici)1097-0134(1999)37:3+<121::aid-prot16>3.3.co;2-h. [DOI] [PubMed] [Google Scholar]
- Karplus K, et al. What is the value added by human intervention in protein structure prediction. Proteins Struct. Funct. Genet. 2001;45:86–91. doi: 10.1002/prot.10021. [DOI] [PubMed] [Google Scholar]
- Karplus K, et al. Combining local-structure, fold-recognition, and new-fold methods for protein structure prediction. Proteins Struct. Funct. Genet. 2003;53:491–496. doi: 10.1002/prot.10540. [DOI] [PubMed] [Google Scholar]
- Karplus K, et al. SAM-T04: what's new in protein-structure prediction for CASP6. Proteins Struct. Funct. Bioinform. 2005;61:135–142. doi: 10.1002/prot.20730. [DOI] [PubMed] [Google Scholar]
- Klockzkowski A, et al. Combining the GOR V algorithm with evolutionary information for protein secondary structure prediction from amino acid sequence. Proteins Struct. Funct. Genet. 2002;49:154–166. doi: 10.1002/prot.10181. [DOI] [PubMed] [Google Scholar]
- Lawrence Livermore National Laboratory. CASP5 experiment web site. [(last accessed data September 19, 2008)];2002 Available at http://predictioncenter.org/casp5/
- Moult J, et al. Critical assessment of methods of protein structure prediction (CASP): round II. Proteins Struct. Funct. Genet. 1997;(Suppl. 1):2–6. [PubMed] [Google Scholar]
- Moult J, et al. Critical assessment of methods of protein structure prediction (CASP): round III. Proteins Struct. Funct. Genet. 1999;(Suppl. 3):2–6. [PubMed] [Google Scholar]
- Pauling L, et al. The structure of proteins: two hydrogen-bonded helical conformations of the polypeptide chain. Proc. Natl Acad. Sci. USA. 1951;37:205–211. doi: 10.1073/pnas.37.4.205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rost B. Phd: predicting one-dimensional protein structure by profile-based neural networks. Methods Enzymol. 1996;266:525–539. doi: 10.1016/s0076-6879(96)66033-9. [DOI] [PubMed] [Google Scholar]
- Rost B, Sander C. Improved prediction of protein secondary structure by use of sequence profiles and neural networks. Proc. Natl Acad. Sci. USA. 1993;90:7558–7562. doi: 10.1073/pnas.90.16.7558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rost B, et al. Redefining the goals of protein secondary structure prediction. J. Mol. Biol. 1994;235:13–26. doi: 10.1016/s0022-2836(05)80007-5. [DOI] [PubMed] [Google Scholar]
- Schneider T, Stephens R. Sequence logos: a new way to display consensus sequences. Nucleic Acids Res. 1990;18:6097–6100. doi: 10.1093/nar/18.20.6097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sjölander K, et al. Dirichlet mixtures: a method for improving detection of weak but significant protein sequence homology. Comput. Appl. Biosci. 1996;12:327–345. doi: 10.1093/bioinformatics/12.4.327. [DOI] [PubMed] [Google Scholar]
- Wang G, Dunbrack RL., Jr PISCES: a protein sequence culling server. Bioinformatics. 2003;19:1589–1591. doi: 10.1093/bioinformatics/btg224. [DOI] [PubMed] [Google Scholar]
- Zemla A, et al. A modified definition of Sov, a segment-based measure for protein secondary structure prediction assessment. Proteins Struct. Funct. Genet. 1999;34:220–223. doi: 10.1002/(sici)1097-0134(19990201)34:2<220::aid-prot7>3.0.co;2-k. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.