A practical algorithm for finding maximal exact matches in large sequence datasets using sparse suffix arrays

Abstract

Motivation: High-throughput sequencing technologies place ever increasing demands on existing algorithms for sequence analysis. Algorithms for computing maximal exact matches (MEMs) between sequences appear in two contexts where high-throughput sequencing will vastly increase the volume of sequence data: (i) seeding alignments of high-throughput reads for genome assembly and (ii) designating anchor points for genome–genome comparisons.

Results: We introduce a new algorithm for finding MEMs. The algorithm leverages a sparse suffix array (SA), a text index that stores every K-th position of the text. In contrast to a full text index that stores every position of the text, a sparse SA occupies much less memory. Even though we use a sparse index, the output of our algorithm is the same as a full text index algorithm as long as the space between the indexed suffixes is not greater than a minimum length of a MEM. By relying on partial matches and additional text scanning between indexed positions, the algorithm trades memory for extra computation. The reduced memory usage makes it possible to determine MEMs between significantly longer sequences.

Availability: Source code for the algorithm is available under a BSD open source license at http://compbio.cs.princeton.edu/mems. The implementation can serve as a drop-in replacement for the MEMs algorithm in MUMmer 3.

Contact: zkhan@cs.princeton.edu;mona@cs.princeton.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

With the advent of high-throughput sequencing technologies, the possibility that genome sequencing and re-sequencing will become a routine experiment in a genetics lab is increasingly becoming a reality. These new sequencing technologies place ever increasing demands on existing algorithms for sequence analysis. The demands originate from sheer sequence output due to relatively inexpensive short read sequencing technologies and the growing number of relatively similar sequenced genomes (Pop and Salzberg, 2008). Further computational challenges are expected from experimental sequencing technologies that promise read lengths that are thousands of base pairs in length within a decade (Eid et al., 2009). Assembly of genomes using these technologies and comparison of the resulting closely related genomes will be critical for new discovering new biology, from uncovering genes, regulatory elements and large-scale genomic reorganization to identifying variations between related species and individuals.

Maximal exact matches (MEMs) are exact matches between two strings that cannot be extended in either direction towards the beginning or end of two strings without allowing for a mismatch. Algorithms for computing MEMs between sequences appear in two contexts where high-throughput sequencing will vastly increase the volume of sequence data: (i) seeding alignments of high-throughput sequencing reads for genome assembly and (ii) designating anchor points for genome–genome comparisons when the two genomes are relatively similar. These two tasks may be performed in a variety of ways, with different strategies preferred for different situations. Putative alignments between reads for genome assembly are typically found using a seed, typically a short, fixed-length exact match (Myers et al., 2000). MEMs become computationally advantageous seeds when reads share long subsequences; alignments seeded using fixed-length exact matches will process many seeds from these subsequences and run relatively slower. In genome comparison, the prevailing strategy for comparing similar genomes involves finding anchor points containing stretches of exact or near exact matches between the two genomes (Bray and Pachter, 2004; Choi et al., 2005; Istrail et al., 2004; Kurtz et al., 2004; Schwartz et al., 2003). Algorithms differ in the type of anchor points they use and how they process these anchor points. Their performances vary depending on the genome comparison task at hand. MEMs are one type of anchor point that is best suited for comparing closely related genomes (Bray and Pachter, 2004; Choi et al., 2005; Kurtz et al., 2004).

The classical approach to finding MEMs between sequences S and P involves creating a concatenated sequence S#P, indexing the resulting string in a suffix tree, and searching for maximal repeats that span the special character # (Gusfield, 1997). Indexing both strings is costly in terms of space because of the large amount of memory occupied by the suffix tree. As a result, this approach has given way to a technique that involves indexing only one reference sequence in a suffix tree (Abouelhoda et al., 2004, 2006; Kurtz et al., 2004). Even though indexing is only the smaller of the two sequences in a suffix tree saves a considerable amount of memory, the size of the index still remains a significant problem. Practical implementations use highly engineered suffix trees to save even more memory (Kurtz, 1999; Kurtz et al., 2004).

Recent work has focused on using the SA, a space-efficient alternative to the suffix tree, to further decrease the memory occupied by the index (Manber and Myers, 1993). Augmented with additional information, the ‘enhanced’ suffix array (ESA) provides the same functionality as the suffix tree and can be used to find MEMs between sequences (Abouelhoda et al., 2004). The ESA can be used to find MEMs using the classical approach in which both sequences are indexed (Höhl et al., 2002) or by indexing only a reference sequence (Abouelhoda et al., 2006). However, even the ESA requires a significant amount of engineering in order to limit the size of the index (Abouelhoda et al., 2004).

One of the key features of MEMs is the absence of a constraint on the cardinality of the match. We observe that the lack of this constraint allows the use of a sparse index. In contrast to a full-text index, a sparse index stores only a subset of positions of the text, saving a significant amount of memory. If the subset of positions indexed is not ‘too’ sparse, a sparse index can act like a full-text index (Kärkkäinen and Ukkonen, 1996). By sifting through and confirming partial matches, an algorithm that uses a sparse index trades memory for additional computation.

Our main contribution is an algorithm for finding MEMs using a sparse SA. Our approach adapts several existing ESA techniques to find MEMs using sparse SAs and introduces a new technique that helps simplify the algorithm (Abouelhoda et al., 2004, 2006; Kurtz et al., 2004). Instead of storing precomputed suffix links as typically done on suffix trees and ESAs, our second contribution is a practical method for simulating suffix links in the sparse SA. Suffix links play a key role in accelerating algorithms for locating MEMs. Our third contribution is a new technique for parallelizing the computation of MEMs that uses properties specific to a sparse SA. We show how this new technique can be used to offset the additional computational cost associated with the sparse index. We compare our parallel sparse suffix array algorithm with MUMmer (Kurtz et al., 2004), which finds MEMs using suffix trees, and vmatch (Abouelhoda et al., 2004), which finds MEMs using an ESA. By finding MEMs between sequences ranging in length from 5 Mb to 3 Gb, we show that it is possible to use sparse SAs to obtain MEMs between significantly longer sequences.

2 PRELIMINARIES

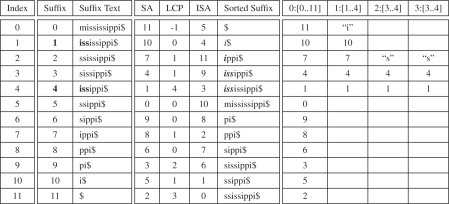
We assume the reference string S[0,…, n − 1] of size n over an alphabet Σ={ $, A, C, G, T} (e.g. DNA) has a termination character S[n − 1] = $ that occurs nowhere else in the string and is lexicographically less than all the characters that occur in the alphabet. The suffixes of the reference string are zero indexed by their position in the original string (Fig. 1, left). The SA is an array of these suffix positions where the corresponding suffixes have been ordered by a suffix sorting algorithm (Fig. 1, middle). That is, SA[i] gives the suffix specified by position which is i-th in lexicographical ordering.

Fig. 1.

The suffix indexes of the reference text S = mississippi$ listed in order (left). The SA is an array of integers where these indices are listed in lexicographical order. LCP and ISA designate the longest common prefix (LCP) array and inverse SA, respectively (see text) (middle). Search for the occurrences of P = iss in the SA by a top-down search one character at a time (right).

Because the prefix of any suffix is the occurrence of a substring match in the original reference string, SAs accelerate searches for exact matches. Binary search locates the right and left interval containing the matching suffix and hence the positions of substring occurrences. We use a top-down approach to SA searching. For a query string (or genome) P[0,…, m − 1] of length m, top- down search starts from some character position p in the query P advancing one character at a time to successively narrow down an interval [s..e] with start index s and end index e in the suffix array. The interval contains the positions of these exact matches in the original reference string. We use the 3-tuple d:[s..e] to record the next position p+d to match in the query P and current interval [s..e] in the SA. Note d corresponds to the length of the match starting from position p. As matches grow by calls to binary search, d increases and the interval [s..e] becomes smaller.

An example of top-down search for the query P = iss at p=0 is shown in Figure 1 (right). The initial interval is always the entire SA 0:[0..11]. Binary search for the first character ‘i’ in the query narrows the interval to 1:[1..4] and the search for ‘ss’ leads to the interval 3:[3..4], which gives the positions 4 and 1 of P = iss in the original reference string.

Top-down search requires two key elements: binary search for left and right ends of intervals (Supplementary Fig. 1). Binary search relies on a single character comparison of the d-th character of the middle suffix S[SA[(s + e)/2]+d] with the P[p + d] character of the query. Successive calls to the binary search for left and right interval ends allow the algorithm to narrow down the interval containing the query. If the current character P[p+d] in the query does not occur in the next interval, a null ⊥ value is returned to designate that the query is not found. We opt for this approach because it requires no additional information, other than the SA itself and the input string, and enables matching a query up until a mismatch is found, a key operation in searching for MEMs.

MEMs require two additional arrays, namely the inverse SA (ISA) and the LCP array. The is a mapping from a particular suffix index to its position in the SA (Fig. 1, middle); that is, ISA[i] gives the lexicographically ordered position of the i-th suffix. The ISA can be constructed in linear time by scanning the SA along each position j = 0,…, n − 1 and storing in the ISA the corresponding position ISA[SA[j]]=j. The LCP array contains the length of the LCP between successive sorted suffixes in the SA (i.e. LCP[i] is the length of the LCP shared between SA[i] and SA[i − 1] and if i = 0, it is set to −1 (Fig. 1, middle). The LCP array can be computed in O(n) time (Kasai et al., 2001).

3 SPARSE SA

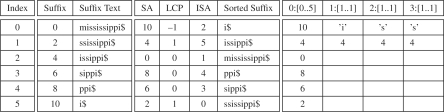
In contrast to full-text SAs, sparse SAs store every K-th suffix of the text. Even though the idea of sparse suffix tree is over a decade old, only recently have simple, practical algorithms been introduced constructing sparse SAs (Ferragina and Fischer, 2007; Kärkkäinen and Ukkonen, 1996). We review the techniques presented in Ferragina and Fischer (2007) for constructing sparse SAs here: (i) Use America flag sort, a type of radix sort, to sort each suffix up to the K-th character (McIlroy et al., 1993). (ii) Construct a new reference text of length n/K, where each character is the bucket number obtained by American flag sort. (iii) Build a SA, intSA, of the new text using an algorithm that handles integer alphabets (Larsson and Sadakane, 2007). (iv) Convert the SA into the sparse SA of the original reference string S by multiplying each value in the computed SA by K for i = 0,…, n/K − 1 (i.e. SA[i]=intSA[i]· K).

For all positions j = 0,…;, n/K−1, one can also construct an inverse SA ISA[SA[j]/K] = j and, using a modified LCP construction algorithm, the corresponding LCP array (Ferragina and Fischer, 2007). An example of a sparse SA and the corresponding ISA and LCP arrays are shown in Figure 2. In total, the sparse SA index and the text will occupy 12n/K + n bytes, assuming integers take 4 bit and text takes 1 byte. Even though they index every K-th suffix in the text, we show in the remainder of the article that sparse SAs can be used to find MEMs between two strings.

Fig. 2.

Sparse SA example. The sparse suffix indexes for K = 2 of the reference text S= mississippi$ listed in order (left). Compare to Figure 1. The corresponding sparse SA, ISA and LCP arrays (middle). Search for the occurrences of P = iss in the sparse SA locates only one string match (right).

4 MEMS

MEMs are exact matches between two sequences that cannot be extended in either direction toward the end or the beginning of the sequences without introducing a mismatch (Abouelhoda et al., 2006; Kurtz et al., 2004). The only constraint on MEMs is a minimum length L. Without this constraint, a large number of matches consisting of a small number of characters will be returned. To find MEMs between a query string P and the reference string S, the algorithm advances through each character position p in the query string and attempts to find MEMs of sufficient length that begin at p in the query string.

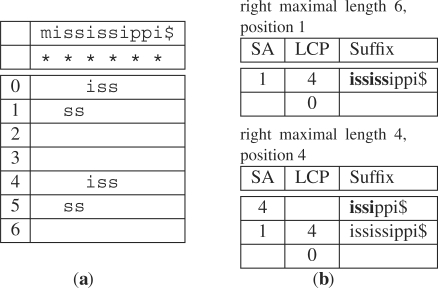
In order to find MEMs using sparse SAs, we adapt several existing techniques for finding MEMs in full-text SAs. Specifically, we use an approach where MEMs are found by maintaining two intervals (Abouelhoda et al., 2006). These intervals are obtained by top-down binary search at position p in the query string P. The first interval d : [s‥e] is found by matching at most L−(K − 1) characters (Supplementary Algorithm 1). For this interval, d is the length of the current match, s is the start of the interval in the SA and e is the end of the interval in the SA. By allowing for matches that are K − 1 characters <L in length, the entire match can be recovered by scanning regions in between the sparsely indexed suffix positions (Fig. 3a). The second interval q:[l..r] is found by matching as many characters as possible, the longest possible match. For this interval, q is the length of the current match, l is the start of the interval in the SA and r is the end of the interval in the SA. Note that q:[l..r] is a subinterval of d:[s..e], i.e. s ≤ l, r ≤ e, and q ≥ d.

Fig. 3.

(a) Partial matches at successive locations in the query P = issxiss and K = 2 sparsely indexed string S = mississippi$. The asterisk indicates an indexed position and the numbers in the left column designate positions in the query P. A match of ‘ss’ can be used to recover the MEM ‘iss’ by scanning left of the match and checking for left maximality. (b) Here, we consider another query P = ississ to find MEMs of length ≥4 in the full text K = 1 SA. At the initial position in the query p = 0, the interval of a right maximal match of length 6 at position 1 in the reference is found by top-down search. Examining neighboring LCP values, the algorithm ‘unmatches’ the characters ‘iss’ to find a second right maximal match ‘issi’ of length 4.

If there are at least d≥L−(K − 1) matched characters at position p in the query P, the algorithm uses both intervals to scan for MEMs of length L. The use of these intervals is based on the observation that every suffix corresponding to the first interval d:[s..e] has a prefix of length L−(K − 1) which matches the query string P at position p. To determine whether each of these prefixes corresponds to a MEM of length L, we need to find its left and right maximal boundaries.

In order to find these MEMs, we use an approach that differs from the maintenance of a stack and reliance on the structure of the suffix tree present in traditional approaches for finding MEMs (Abouelhoda et al., 2006; Kurtz et al., 2004). Using both intervals, d:[s..e] and q:[l..r], we determine the length and position of right MEMs. Right MEMs are matches between S and P that cannot be extended any further towards the end of the strings.

The algorithm finds these right MEMs by ‘unmatching’ characters in the maximum length match using LCP values at the start LCP[l] and end LCP[r + 1] of the interval (Supplementary Algorithm 3; Fig. 3b). The first-right MEMs of length q are obtained directly from the interval q:[l..r]. Observe that the LCP of the set of suffixes indexed between l and r corresponds to the maximum length q, and that both LCP[l] and LCP[r + 1] must be less than this value, or otherwise the interval corresponding to the maximum length match could be expanded. Thus, q′ =max(LCP[l], LCP[r + 1]) is the length of the next longest match and the minimum LCP value of the interval with characters unmatched.

Using the new LCP value, the interval can be expanded to the left l=l − 1 until LCP[l|<q′ and the right r = r + 1 until LCP[r + 1]<q′. Each array index visited as these intervals are expanded has a corresponding suffix position in the SA, and each of these suffixes in the SA must be right maximal matches of length q′. This expansion process continues as long as q′≥d the length of the right maximal matches collected are greater than the minimum-length match.

Once a right maximal match and its corresponding length is found, the algorithm determines left maximality by scanning to the left of the right maximal match (Supplementary Algorithm 4). Because, the reference string S is indexed at every K-th suffix position, the algorithm must scan up to K characters to the left of the match. The scan is stopped at a mismatch or at the beginning of either string. The resulting left maximal match is stored only if it meets the length constraint ≥L.

Approaches that rely on the structure of the suffix tree, such as the ESA approach in Abouelhoda et al., (2006), have complexity O(m + R), where m is the length of matched query sub-string and R is the number of right maximal matches. In contrast, our approach has complexity O(mlog n+Q) where Q is the number of length m = L−(K − 1) matches of a query sub-string in the sparse SA.

At this point, the algorithm can advance to the next position p +1 of the query P and reset the minimum length interval d:[s..e] and the maximum length interval q:[l..r] both to be 0:[0..n/K − 1] the maximum- and minimum-length intervals, and match again from this new query string prefix. However, this naive algorithm will repeat all the work required to obtain the d − 1 and q − 1 characters of the minimum- and maximum-length matches, respectively. Suffix links offer a way of avoiding the additional work of matching these characters again. In the next section, we describe an approach that does not rely on having pre-computed and stored suffix links, but instead uncovers them with extra computation.

5 SIMULATING SUFFIX LINKS

Suffix links are explicitly represented in a suffix tree. A suffix link, along with some counting information, allows any algorithm to jump from the node in the suffix tree that is reached by matching P[p… p+d] to the node in the suffix tree is reached by the match P[p+1…s(p + 1)+(d−1)], completely eliminating the O(d) time required to re-match starting from position p + 1. Suffix links are by-products of classical algorithms for suffix tree construction, and they are key to accelerating algorithms for finding MEMs (Gusfield, 1997).

In contrast to the suffix tree, an SA does not contain any explicit suffix link information. In order to address this limitation, the approach used by the ESA attempts to mimic the structure of the suffix tree to recover suffix link information (Abouelhoda et al., 2004). By augmenting intervals in the SA with child and sibling data, the ESA mimics the structure of nodes and edges of a suffix tree. This allows top-down traversal of the underlying suffix tree structure and forms the basis computing the equivalent of suffix links (Abouelhoda et al., 2004); Section 7.1). Unfortunately, storing this additional information without ballooning the size of the index requires a complex scheme that relies on the storage of small numbers and bucketed positions along the SA [see end of Section 6.1 and Section 8.1 in Abouelhoda et al. (2004)].

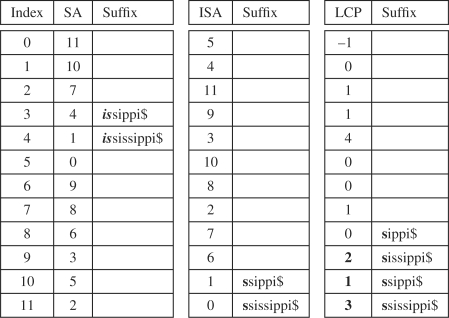
Instead of mimicking the structure of a suffix tree, we use an alternate approach to simulating suffix links in the SA. The approach we adopt is much simpler than the techniques used by the ESA. We assume we have a next match query position and interval d:[l..r] having matched from query position P[p]. We use the ISA to compute the left l = ISA[SA[l]/K + 1] and right r = ISA[SA[r]/K + 1] ends of a new interval in the SA. Using the ISA, the algorithm obtains the position in the SA corresponding to the suffix with the first K characters of the matched part of the query removed. The key problem with using the ISA is that the new interval q:[l… r] where q = d − K may not correspond to the same interval obtained by top-down search with the P[p + K…s(p + K)+(d − K)]. In particular, this interval q:[l..r] is only guaranteed to be a contained in the interval obtained by the top-down search.

In order to solve this problem, we expand the interval by a process we call LCP expansion (Fig. 4). The approach preserves q = d − K characters that have been matched already in the query P. We advance the left l = l − 1 and right r = r + 1 ends of the interval until the end of the array is reached or until a value <q is reached at the left LCP[l] and right LCP[r + 1] end of the interval. In addition, we limit this process to 2qlog n steps to assure the algorithm runs in O(m²log n) time where m is the length of the query and n is the length of the reference (i.e. no worse than the naive algorithm for finding MEMs using top-down binary search). Inspite of its poor worst case performance, we found this simple approach to simulating suffix links works much faster in practice.

Fig. 4.

Suffix link simulation for the full text K = 1, example in Figure 1. Top-down binary search for the query P = ‘is’ narrows down the interval [3..4] (left). From [3..4], we can use the ISA for K = 1 to compute a new interval l = ISA[SA[l] + 1]=10 and r=ISA[SA[r]+1]=11(middle). However, the interval does not correspond to the interval [8..11], obtained by top-down search of the single character P = ‘s’ query. The interval is obtained by expanding the left side of the interval using values ≥1 (in bold) in the LCP array (right).

6 NEW PARALLELIZATION TECHNIQUE

The sequential version of the algorithm, as presented above, trades extra computation for memory. The index occupies much less memory since only a subset of the suffixes are stored. The extra computation primarily originates from the additional scanning required to locate left maximal matches after right maximal matches are found and from the number of matches of length L − (K − 1) that must be examined for right and left maximality. By decreasing the threshold on the length of these matches, a much larger number of these matches must be processed with increasing values of K.

The primary way to offset this additional computation is to use parallel processing. If there are multiple query sequences, one clean and simple way to apply parallel processing is to distribute the computation of each query sequence to individual processors. In fact, the recent implementation MUMmerGPU uses such a parallelization scheme to take advantage of the many specialized CPUs on modern graphics processors (Schatz et al., 2007). Our algorithm, including other approaches such as MUMmer and vmatch, can also be parallelized by assigning query sequences to multiple CPUs on a multi-core machine or, with the requisite modifications, a graphics processor.

When there is only one query sequence, one can try to split the query sequence and assign each part to a processor. Unfortunately, this approach has the property that it will miss MEMs that span this split. In the case of genomic sequences, this data may be split by chromosome; however single choromosomes as long as 1 GB are known (Paux et al., 2008). To better deal with longer sequences, we introduce a simple parallelization technique that exploits how suffix links are applied in sparse SAs. Specifically, we focus on the first set of positions p = 0,…,(K − 1) in the query P that must be matched. For values K > 1, the acceleration provided by the suffix link simulation technique advances the algorithm p = p + K characters in the query string. If the algorithm starts at p = 0, then it must advance to p = K, skipping all of K − 1 initial positions of the query P. Consequently, the algorithm must be run for all of the initial positions p = 0,…, K − 1 in the query string P. This leads to a simple way to design a parallel version of the algorithm: run an independent process for each value initial prefix p = 0,…,(K − 1) and combine the results.

This parallelization technique works best for small values of K because of diminishing returns from the suffix link acceleration. The simulated suffix link advances K characters at every step, but it also requires at least K characters to be matched before the suffix link acceleration can be applied. If a region of the query P contains few short matches with the reference sequence S, this acceleration will rarely be applied.

7 EXPERIMENTAL RESULTS

7.1 Genome comparison anchor points

We now describe how our approach performs in uncovering MEMs in a wide range of genome comparison scenarios. We compare the parallel version of our sparse SA implementation for K = 2, 3, 4, using 2, 3 and 4 processors, respectively, against our sequential, full SA implementation (K = 1). We compare these approaches to two sequential algorithms for computing MEMs: MUMmer which is based on suffix trees, and vmatch which is based on an ESA. For K = 2, 3, 4, we use the parallel version of our algorithm in order to demonstrate that our new parallelization technique can effectively use multiple CPUs to offset the additional computation required by the sparse SA. Our experiments show how close these parallel version can come to the upper bound provided by the sequential full-text algorithms.

For our approach, we implemented the algorithm described above with just three additional optimizations: (i) We stored the LCP array in just over 1 byte, storing values ≥255 in an index sorted array. The large values in the sorted array were accessed by binary search (Abouelhoda et al., 2004). (ii) We used a modified top-down search that saves the information from binary search for the left interval to speed up search of the right interval (Ferragina and Fischer, 2007). In addition, the parallelization was implemented using the POSIX threads library.

We compared our approach with the open-source MUMmer version 3.20 and the closed-source vmatch version 2.0. We used the following command line for MUMmer 3.20: mummer -b -l L -maxmatch -n ref.fasta query.fasta >output for reference genome and query fasta files, respectively. We used the following two commands for vmatch 2.0: mkvtree -db ref.fasta -allout -v -pl -dna -indexname index; vmatch -qspeedup 2 -l L -d -p -q query.fasta index > output. We used the 32 bit version of vmatch to ensure vmatch would use 4 bit integers for storing suffix positions. The commands assured that MEMs of length L, including reverse complement MEMs, were computed by both implementations. All methods were run on a 4-core Intel Xeon 2 GHz machine with 16 GB of RAM. Total run time was measured using the GNU time command. The peak memory was measured by calling ps to determine resident memory usage every second during the program's extion. In order to assure fair comparison, our implementation used 1 byte characters for sequence data. We did not make the additional optimization of encoding DNA sequences using 2 bit per base.

First, we considered the genomes present in the original MUMmer 3 paper (Kurtz et al., 2004). We selected a minimum MEM length L so that the run time was not dominated by writing the MEM positions to disk. The timing and memory results are shown in Table 1. Furthermore, as a sanity check, we confirmed that the same exact MEMs were found by all of the algorithms tested. For K = 1, a sequential full SA, our approach is faster than open source MUMmer while using considerably less memory, and is competitive with the closed-source vmatch. Modifications to our open-source software may enable further optimizations to the full SA option. For values of K = 2 and 3, the sparse MEM algorithm uses significantly less memory than the full-text approaches; while the sparse SA approach relies on extra computation, part of this computation can be offset using the parallelization scheme described above. For K = 4, we no longer are able to offset the extra computation using parallelism, with the run time becoming almost twice slower than MUMmer. However, the memory used by our approach is a factor of 4 less than the memory used by MUMmer.

Table 1.

Total run time in seconds on a 4-core 2 GHz Intel Xeon CPU on the DNA sequences benchmarked in Kurtz et al. (2004) [panel (a)] and memory usage in megabytes on the same sequences [panel (b)]

Reference	Size	Query	Size	L	MUMmer	vmatch	K = 1	K = 2	K = 3	K = 4
Panel (a) Run time in seconds (K -core/1-core)
Escherichia coliK12	4.6 Mbp	E.coliO157:H7	5.5 Mbp	20	13.75	9.86	10.54	7.72/15.86	9.83/31.46	14.98/53.88
Aspergillus fumigatus	28.0 Mbp	A.nidulans	30.1 Mbp	20	109.72	75.71	82.17	61.93/119.06	79.48/184.89	177.90/272.01
Saccharomyces cerevisiae	13.0 Mbp	S.pombe	13.8 Mbp	20	38.58	31.85	30.93	24.15/35.90	32.27/91.63	54.10/162.98
Drosophila melanogaster2L	22.2 Gbp	D.pseudoobscura	150.0 Gbp	25	400.42	360.89	337.14	266.31/525.87	402.70/879.34	774.03/2090.30
Homo sapiens21	44.7 Gbp	Mus musculus16	99.2 Gbp	50	316.08	244.22	267.72	166.91/354.17	239.78/703.02	479.04/1305.70
Panel (b) Memory usage in megabytes
Escherichia coliK12	4.6 Mbp	E.coliO157:H7	5.5 Mbp	20	77.38	44.78	59.84	39.21	32.46	29.07
Aspergillus fumigatus	28.0 Mbp	A.nidulans	30.1 Mbp	20	478.88	259.38	312.23	176.64	130.88	108.98
Saccharomyces cerevisiae	13.0 Mbp	S.pombe	13.8 Mbp	20	200.03	116.31	153.24	95.39	76.97	67.70
Drosophila melanogaster2L	22.2 Gbp	D.pseudoobscura	150.0 Gbp	25	502.67	460.62	299.67	188.82	153.26	136.27
Homo sapiens21	44.7 Gbp	M.musculus16	99.2 Gbp	50	639.28	452.87	431.45	278.93	196.22	170.84

The minimum length L of the MEM is indicated in the corresponding column. K = 1 corresponds to a full text SA. K > 1 designates the use of a sparse SA that samples every Kth position. Mbp denotes million base pairs. For K = 2,3,4 the respective 2, 3, and 4 CPU core run time is paired with the single core run time (i.e. K-core/1-core).

Second, we tested our algorithm on four full genomes from the Drosophila 12 genomes project (Table 2) (Drosophila 12 Genomes Consortium, 2007). We selected the genomes based on their increasing evolutionary distance to examine any effects on run time and memory usage that might be caused by decreasing sequence similarity. As expected, the closest test case between D.simulans and D.sechellia had the fastest run time using our algorithm. Again, for values of K = 2 and 3, the parallel version of the sparse MEM algorithm achieved the same performance in run time as the full-text sequential algorithms while using significantly less memory. For the algorithm that used the least memory (K = 4), we observed a factor of 3 decrease in memory with an almost factor of 3 increase in run time from the full text K = 1 version. As before, we confirmed that the same exact MEMs were found by all of the algorithms tested, providing a sanity check of the results.

Table 2.

Total run time 4-core 2 GHz Intel Xeon CPU on full genomes [panel (a)] and memory usage in gigabytes on the same genomes [panel (b)]

Reference	Size	Query	Size	L	MUMmer	vmatch	K = 1	K = 2	K = 3	K = 4
Panel (a) Run time
Drosophila simulans	139 Mbp	D.sechellia	168 Mbp	50	10m1s	9m2s	8m0s	6m39s	8m37s	17m40s
Drosophila melanogaster	170 Mbp	D.sechellia	168 Mbp	50	9m32s	10m8s	9m56s	8m14s	12m27s	23m14
Drosophila melanogaster	170 Mbp	D.yakuba	167 Mbp	50	13m11s	11m56s	9m26s	8m29s	12m45s	28m15s
Mouse	2.6 Gbp	Human	3.1 Gbp	100	F	F	F	F	3h46m51s	9h1m38s
Human	3.1 Gbp	Chimp	3.4 Gbp	100	F	F	F	F	3h15m3s	6h41m36s
Panel (b) Memory usage in gigabytes
Drosophila simulans	139 Mbp	D.sechellia	168 Mbp	50	2.19	1.30	1.44	0.79	0.57	0.47
Drosophila melanogaster	170 Mbp	D.sechellia	168 Mbp	50	2.68	1.59	1.77	0.97	0.69	0.56
Drosophila melanogaster	170 Mbp	D.yakuba	167 Mbp	50	2.68	1.60	1.81	0.98	0.70	0.57
Mouse	2.6 Gbp	Human	3.1 Gbp	100	F	F	F	F	11.09	9.10
Human	3.1 Gbp	Chimp	3.4 Gbp	100	F	F	F	F	12.97	10.47

F designates the program failed to run on the inputs. h, m, s designate hours, minutes and seconds, respectively. Mbp denotes million base pairs and Gbp denotes billion base pairs. K = 2,3,4, use 2, 3 and 4 cores, respectively.

Finally, we scaled the inputs up to large mammalian genomes (see also Table 2). We computed all MEMs of length L = 100 or greater for two test cases: (i) mouse genome (mm9) as the reference and human genome (hg18) as the query; (ii) the human genome as the reference (hg18) and the chimpanzee genome (panTro2) as the query. We attempted to use MUMmer 3.20 and the 32 bit version of vmatch 2.0 to compute MEMs, but both failed to load the entire reference genomes, printing error messages. The 64 bit version of vmatch attempted to build a full text index on the entire reference genomes, but quickly ran out of memory in both cases. In contrast, the parallel version our algorithm succeeded in computing MEMs between these large sequences for K = 3 and 4. Interestingly, the algorithm ran in less time for the larger human and chimp inputs. Because of the long stretches of sequence similarity known to exist between these sequences, the suffix link acceleration was applied more frequently.

7.2 High-throughput short read sequences

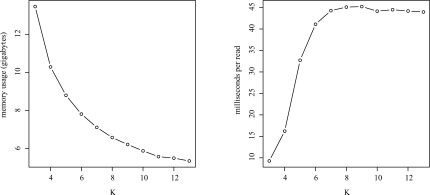
Using increasing values of K, we examined how memory usage improved and run time increased when computing MEMs between unpaired 454 reads from a 1000 Genomes Pilot Project and the 3.1 Gbp human genome (hg18) (Fig. 5). The computed MEMs represent the first step of seeding alignments during assembly with a reference genome and subsequent genotyping. The unpaired reads were collected by the 454 contract sequencing center using a 454 GS FLX instrument, which generates reads on average of ∼ 500 bp in length. The 1 330 318 reads were obtained from run SRR003636, sample NA19240, population YRI₁.

Fig. 5.

Effect of increasing values of K on memory usage and MEM computation time using unpaired 454 reads from thae 1000 Genomes Project and the 3.1 Gbp human genome (hg18). For this evaluation L = 100, we computed MEMs of length ≥100. Total memory usage in gigabytes on a 4-core 2 GHz Intel Xeon CPU with 16 GB of RAM (left) and corresponding average per read computation time in milliseconds (right).

With increasing values of K, we found that memory usage diminished with the expected inverse of K pattern. The most gains were provided at K = 3 and diminished approaching K = 10 (Fig. 5, left). In contrast, we were surprised to see that the time to compute MEMs leveled off at K = 7 (Fig. 5, right). We believe this occurred because the simulated suffix link requires at least K characters to be matched before the MEMs algorithm uses the link to advance in the query and ‘un-match’ K characters. Because of this requirement, with increasing values of K, the suffix link acceleration is applied less frequently. In effect, the algorithm was approaching the performance of the naive O(m²log n) algorithm for computing MEMs. Interestingly, if the naive algorithm is fast enough for the given application, the LCP array and the ISA arrays can be eliminated entirely, saving a significant amount of space.

8 DISCUSSION

The algorithm presented in this work provides a computation versus space trade-off to find MEMs between two or more sequences. We show this trade off can be offset in part by introducing a parallel version of the algorithm. Further, we emphasize that even though we use a sparse index, the output of a full text index algorithm and our sparse SA algorithm is the same as long as the index is not ‘too’ sparse L > K. In other words, the space between the indexed suffixes is not greater than the minimum length L constraint on MEMs. The sparse SA algorithm does not lose any MEMs because it relies on partial matches and extra computation to recover all of the MEMs.

In addition the length constraint L, several approaches have added further restrictions on MEMs. Maximally unique matches add a restrictive cardinality constraint (Kurtz et al., 2004). The MEM must occur once in both the query and reference sequences, while rare MEMs loosen this cardinality constraint slightly to find better anchor points in genome comparison and EST alignment (Ohlebusch and Kurtz, 2008). Enforcing cardinality constraints efficiently using sparse SAs will be more computationally inefficient than enforcing it using a full-text index since each partially matched position must be checked to determine cardinality. In addition to cardinality, MEMs have been restricted to occur at least once in all indexed genomes or sequences, and again, full text indexing allows these to be discovered more efficiently. We note that both of these filters, or even more complex filters such as those used in Choi et al. (2005), can be applied in a post-processing step after computing all MEMs.

The approach used by our algorithm is not the only approach for trading memory for extra computation when the index on the reference sequences occupies too much memory. Splitting the reference sequence into parts and running an algorithm for computing MEMs on each part one after the other is another way to make this trade-off. This approach has two main downsides. First, it assumes a way to split sequences that guarantees no MEM will span the split. Second, it requries two or more separate large text indexes to be loaded into memory one after the other in order to compute MEMs for a single query sequence. This might be undesirable if queries for MEMs are submitted one at a time or in small batches (e.g. online database search or a client/server system). Each query would require loading each half of the index when a sparse SA could keep the entire index in memory. We emphasize that sparse SA techniques presented in this work can also be combined with this approach to enable the computation of MEMs in sequence datasets even larger than those tested in this work.

We also comment on two future research directions. The first relates to the LCP expansion process used for simulating suffix links. The process requires both the ISA and the LCP array. We speculate that perhaps these two arrays can be replaced by a single array that allows the computation of suffix links. We note that using a modified version of the algorithm in Manzini (2004), we can compute the LCP array directly from the SA, a process requiring 8n/K + n bytes for the LCP array, text and SA. It might be possible to convert the LCP array in-place into this new array for computing suffix links, thereby reducing memory usage and improving the speed of the algorithm. Second, one limitation of compressed text indexes is that they lack suffix links, which are key to accelerating the computation of MEMs (Ferragina et al., 2009). If these compressed indexes can be augmented with suffix links, sparse indexes and compressed indexes can be compared directly.

Lastly, we contribute an open-source implementation of our algorithm that can serve as a drop-in replacement for the suffix tree based MEMs algorithm in the popular MUMmer 3 system (Kurtz et al., 2004). MUMmer 3 provides fast alignment of large-scale DNA and protein sequences for genome–genome comparison and, more recently, genome assembly. We expect that our initial code base for SAs and sparse SAs can be further optimized and improved, either within the context of MUMmer or within other systems.