Abstract
The perceived position of a stationary Gaussian window of a Gabor target shifts in the direction of motion of the Gabor’s carrier stimulus, implying the presence of interactions between the specialized visual areas that encode form, position and motion. The purpose of this study was to examine the temporal and spatial properties of this illusory motion-induced position shift (MIPS). We measured the magnitude of the MIPS for a pair of horizontally separated (2 or 8°) truncated-Gabor stimuli (carrier = 1 or 4 cpd sinusoidal grating, Gaussian envelope SD = 18 arc min, 50% contrast) or a pair of Gaussian windowed random-texture patterns that drifted vertically in opposite directions. The magnitude of the MIPS was measured for drift speeds up to 16 deg/s and for stimulus durations up to 453 ms. The temporal properties of the MIPS depended on the drift speed. At low velocities, the magnitude of the MIPS increased monotonically with the stimulus duration. At higher velocities, the magnitude of the MIPS increased with duration initially, then decreased between approximately 45 and 75 ms before rising to reach a steady state value at longer durations. In general, the magnitude of the MIPS was larger when the truncated-Gabor or random-texture stimuli were more spatially separated, but was similar for the different types of carrier stimuli. Our results are consistent with a framework that suggests that perceived form is modulated dynamically during stimulus motion.
Keywords: Motion-form interaction, perceived position, dynamics of form perception, illusion
INTRODUCTION
When an array of dots moves behind a stationary window of random dots, the position of the stationary motion-defined window appears to be shifted in the direction of motion (Ramachandran & Anstis, 1990). In accordance with this observation, the perceived position of a stationary Gaussian window of a Gabor stimulus also is shifted in the direction of motion of the Gabor’s carrier grating (DeValois & DeValois, 1991). These illusory position shifts, along with several other phenomena in which motion influences the perceived position of a stationary object (Snowden, 1998; Nishida & Johnston, 1999; Whitney, 2002; Bressler & Whitney, 2006), suggest the presence of interactions between the specialized visual areas that encode form, position and motion.
Many studies, using different experimental paradigms, have examined the properties of the illusory motion-induced position shift (MIPS) of stationary objects (DeValois & DeValois, 1991; Whitaker, McGraw and Pearson, 1999; McGraw, Whitaker, Skillen & Chung, 2002; Mussap and Prins, 2004; Fu, Shen, Gao & Dan, 2004; Durant & Johnston, 2004; Shim & Cavanagh, 2004; Watanabe, 2005; Whitney, 2005; Arnold & Johnston, 2005; Yokoi & Watanabe, 2005; Sundberg, Fallah & Reynolds, 2006; Bressler & Whitney, 2006). For instance, using a pair of first-order Gabor patterns with carrier gratings that drifted continuously in opposite directions, DeValois and DeValois (1991) found that the magnitude of the illusory MIPS depends both on the spatial and temporal frequency of the stimuli. However, they did not find a proportional relationship between the magnitude of the illusory MIPS and the carrier speed. Whitaker et al. (1999) asked observers to judge the relative size of expanding vs. contracting carrier patterns and documented an illusory motion-induced size change of the unvarying stimulus envelope. This size change could be described adequately by a square-root function of the radial carrier velocity.
Recently, Bressler and Whitney (2006) showed that the magnitude of the illusory MIPS for drifting first-order Gabor stimuli increases with the carrier velocity, before reaching a plateau that depends on the carrier spatial frequency. Using a motion-adaptation paradigm, McGraw et al. (2002) also found that the illusory position shift for a stationary first-order Gabor stimulus increases as a function of carrier speed, until leveling off at a velocity of approximately 1 deg/s.
Unlike the results of DeValois and DeValois (1991), McGraw et al. (2002) reported that the magnitude of the illusory MIPS does not depend on the spatial frequency of the carrier stimulus, implying that the illusory shift might depend on either the temporal frequency or the velocity of carrier motion. Indeed, the maximum position shift occurs at a nearly constant temporal frequency, for carrier gratings of both intermediate (DeValois & DeValois, 1991) and low spatial frequency (Bressler & Whitney, 2006). However, DeValois & DeValois (1991) showed that the illusory MIPS is absent if the carrier grating is flickered instead of drifting, which indicates that motion of the carrier is necessary for an illusory position shift to occur. Bressler and Whitney (2006) found that drifting second-order Gabor stimuli also exhibit an illusory MIPS. However, the temporal frequency dependence of the second-order MIPS is band-pass, as opposed to the more high-pass frequency characteristic of the MIPS that they found using first-order carrier stimuli.
The magnitude of the illusory MIPS for a drifting first-order Gabor increases monotonically with the target’s retinal eccentricity, at a rate of about 1-2 arc-min per degree of eccentricity (DeValois & DeValois, 1991; Fu et al., 2004). The illusion does not depend on stimulus contrast (McGraw et al., 2002) and is virtually absent if the luminance window of a drifting first-order Gabor stimulus is changed from a Gaussian to a rectangular profile (Whitney, Goltz, Thomas, Gati, Menon & Goodale, 2003; Arnold & Johnston, 2005). Similarly, Ramachandran and Anstis (1990) reported that the magnitude of the illusory MIPS for a motion-defined window decreases if luminance contrast is added to the boundary between regions of moving and non-moving dots.
Recent studies suggest that the MIPS may be caused by an interaction between the processing of motion and form information (Whitney et al., 2003, Arnold & Johnston, 2005). A determination of how this illusion develops in time should produce insight into the temporal characteristics of the neural mechanisms that are involved in these interactions. Further, although it is clear that the MIPS depends on the space constant of the Gabor envelope (Whitney et al., 2003; Arnold & Johnston, 2005), it is not known how the spatial content (narrow-band vs. broadband) of the carrier stimulus contributes to the magnitude of the illusion.
To investigate the temporal properties of the MIPS, we measured the magnitude of the perceived position shift between a pair of Gabor stimuli as a function of their drift speed, for a range of stimulus durations. To clarify the spatial properties of the MIPS, we measured the perceived position shift as a function of drift speed for Gabor stimuli with (1) sinusoidal carrier gratings of 1 or 4 cpd and (2) a Gaussian windowed gray-scale random-texture pattern. Because the illusory position shift increases with the retinal eccentricity of the target (DeValois & DeValois, 1991; Fu et al., 2004), we compared the spatial and temporal properties of the illusion for two separations of the drifting stimuli. We will discuss the results in the context of possible models to describe the interactions between the processing of motion, position, and form.
METHODS
Apparatus
Stimuli were generated on a Macintosh G3 computer using custom-written software, and were displayed on a Dell 17″ (model M991) monitor at a mean luminance of 20 cd/m2. The luminance of the display was measured using a Minolta LS-100 photometer. Stimuli were displayed within the central region of the monitor, measuring 26.7° × 20°. Unless otherwise stated, the video frame rate was 75 Hz. Observers sat at 65 cm from the display during testing. At this viewing distance, each pixel subtended 2 arc min.
Stimuli and Psychophysical Procedures
The stimuli used in Experiment 1 of this study (Figure 1) were “Gabor” patches like those used by DeValois and DeValois (1991). Each “Gabor” was a patch of horizontal sine wave grating (the carrier) windowed by a Gaussian envelope (SD = 18 arc min). The contrast of the stimuli was 50%. In order to minimize processing time, each patch was drawn within a 1° × 1° square. At the edges of this square window, the Gaussian envelope did not fade completely to the mean luminance, thereby producing noticeable edges. Consequently, we shall refer to this stimulus as a truncated-Gabor. Although the noticeable edges were primarily on the right and left sides, the residual contrast of the upper and lower edges of the truncated-Gabor patches may have reduced the measured magnitude of the MIPS (Whitney et al., 2003; Arnold & Johnston, 2005). To produce drifting motion of the truncated-Gabor carrier, the spatial phase of the carrier grating was updated in each video frame. For all experiments, the initial relative phase of all stimuli was zero, unless otherwise stated. The highest drift speed was limited to one quarter-cycle phase shift per video frame.
Figure 1.
Stimulus configuration for the experiments. a. In experiments that used truncated-Gabor stimuli, a pair of horizontal sinusoidal patterns drifting vertically in opposite directions within a stationary Gaussian luminance window were presented on either side of fixation. b. In experiments that used random-texture stimuli, a pair of random-texture patterns drifting vertically in opposite direction within a stationary Gaussian luminance window were presented on either side of fixation.
In Experiment 2, we measured the perceived position shift for Gaussian-windowed random-texture stimuli. As shown in Figure 1, each presentation consisted of two images, one on each side of the fixation cross. To minimize feature cues, we used a method that is analogous to that used to generate limited-lifetime random-dot motion (Newsome & Pare, 1988), with the difference that, here, the limited-lifetime applies to the spatial frequency components of the random-texture stimulus. The random-texture stimulus was generated from an initial frame that consisted of 16 arc-min random dots, corresponding to 8×8 pixels. In subsequently presented frames, the motion in each image was produced by shifting the spatial phase of randomly selected spatial frequencies (up to 15 cpd) from the discrete 2D Fourier spectrum in a manner consistent with a coherent vertical position shift of the carrier dots. In other words, the phase shift was scaled appropriately to the spatial frequency and orientation of each selected frequency component. The spatial phases of the unselected spatial frequencies did not change. As for the truncated-Gabor stimuli, the window was not shifted during the motion of these stimuli. For each image, half of the spatial frequency components in the discrete Fourier spectrum carried the motion signal.
During testing, the observer sat in a dimly lit room. Viewing was binocular. At the start of each trial, the observer fixated a 16 arc-min fixation cross in the center of the homogeneous gray screen. After 1 s, two identical stimulus patches (truncated-Gabor or Gaussian-windowed random-texture stimuli, see Figure 1) appeared on opposite sides of the central fixation cross, with a horizontal center-to-center separation of either 2 or 8° (corresponding to retinal stimulus eccentricities of 1 and 4°). The two stimulus patches were presented for a fixed duration (see below for details), during which the carriers drifted in opposite directions (upward or downward) from one another. The task of the observer was to judge, after stimulus offset, whether the position of the right patch was higher or lower than that of the left patch. From trial to trial, the initial position of the right patch was randomly chosen from a set of seven positions according to the Method of Constant Stimuli, such that a psychometric function could be constructed from the observer’s responses. The point of subjective equality (where the right patch was judged equally often to be higher or lower than the left one) defined the perceived position shift that was induced by the carrier motion (as noted in the Results, this procedure actually defines twice the spatial shift of each stimulus). Each block of trials consisted of 140 trials, with 10 repeated presentations of each combination of motion direction and the vertical position of the right patch. The spatial characteristics of the carrier stimuli, the speed of the carrier motion, and the presentation durations tested are given in the sections below that describe each experiment.
Experiment 1: Effect of stimulus duration on the illusory MIPS
The goal of Experiment 1 was to examine how the illusory MIPS develops over time, for a range of stimulus velocities. Stimuli were truncated-Gabor patches with velocities ranging from 0 to 4 deg/s, and presented for durations of 53, 107 and 453 ms. The carrier spatial frequency was 4 cpd. In a separate condition, we assessed the MIPS at even shorter stimulus durations using a carrier with a spatial frequency of 1 cpd and a drift velocity of 16 deg/s. Note that because of the 1° × 1° truncated Gaussian window, the mean luminance of the drifting 1 cpd stimuli modulated with time. However, this luminance modulation provided no information about the direction of motion and therefore should not influence the perceived position shift (DeValois & DeValois, 1991). To allow a finer sampling of stimulus durations in this condition, the video frame rate was changed to 85 Hz. The stimulus durations tested ranged from 23.5 to 94.1 ms (i.e., from 2 to 8 video frames) in steps of 1 video-frame.
Experiment 2: Effect of carrier type on the illusory MIPS
The goal of this set of experiments was to determine the role played by the spatial characteristics of the carrier stimulus in the illusory MIPS. Data were obtained for pairs of truncated-Gabor stimuli with a carrier spatial frequency of 1 cpd and for pairs of Gaussian-windowed random-texture patches, drifting at velocities that ranged from 0.25 to 16 deg/s. In this experiment, the duration of the stimuli was fixed at 453 ms.
Observers
The three authors and one observer who was unaware of the purpose of the study, participated in Experiment 1. Authors SC and SP participated in Experiment 2. During the experiments, each observer wore either spectacles or contact lenses to achieve the best optical correction of his or her refractive errors. All of the observers have corrected visual acuity of at least 20/20 in each eye and no known ocular pathology. Written informed consent was obtained from each observer after the procedures of the experiment were explained, and before the commencement of data collection.
RESULTS
Effect of stimulus duration on the illusory MIPS
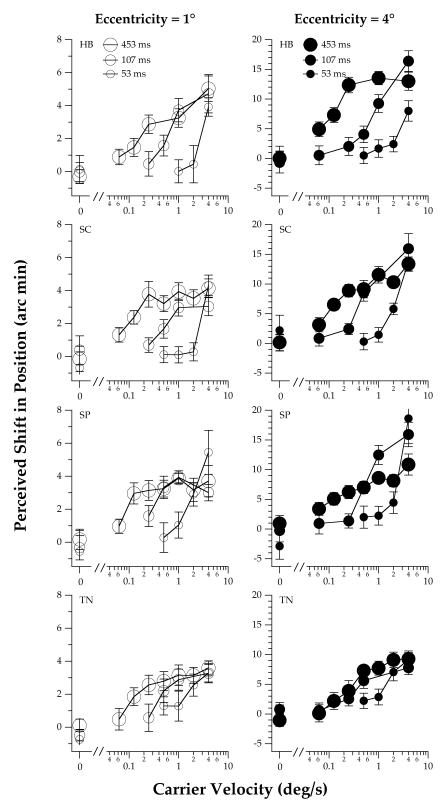
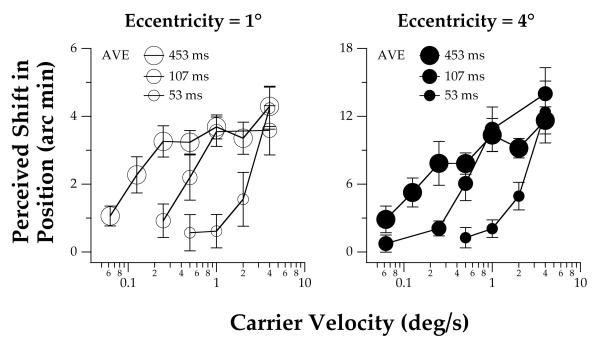
The perceived position shift of a 4 cpd drifting truncated-Gabor is plotted for three stimulus durations as a function of the carrier velocity for individual observers in Figure 2. Group-averaged data are presented in Figure 3. Because the observers’ task was to compare the vertical positions of a pair of truncated-Gabor patches on opposite sides of the fixation target, we assume that each plotted point represents twice the illusory position shift that would be produced if one moving truncated-Gabor patch were presented by itself. The left and right panels in each figure show data for stimulus eccentricities of 1 and 4° (corresponding to a center-to-center spatial separation of 2 and 8°), respectively. At both eccentricities, the perceived position shift increases monotonically as the velocity of the carrier grating increases. In agreement with previous studies (DeValois & DeValois, 1991), the magnitude of the MIPS is substantially larger for the more eccentric truncated-Gabor stimuli. Here, we found that the absolute magnitude of the illusory position shift is approximately 3 times larger for stimuli presented at an eccentricity of 4° than at 1° (note the difference in the vertical scales in the left and right panels of Figures 2 - 5).
Figure 2.
Effect of stimulus duration and eccentricity on the illusory MIPS for low carrier velocities of the truncated-Gabor stimuli. Data are shown for four observers for carrier velocities ranging from 0 to 4 deg/s, durations of 53, 107 and 453 ms and eccentricity of 1 and 4°. The spatial frequency of the carrier was 4 cpd. The error bars represent ±1 SEM across runs.
Figure 3.
Effect of stimulus duration and eccentricity on the average illusory MIPS for low carrier velocities of the truncated-Gabor stimuli. Data shown in Figure 2 are averaged across all the observers. The error bars represent ±1 SEM across observers.
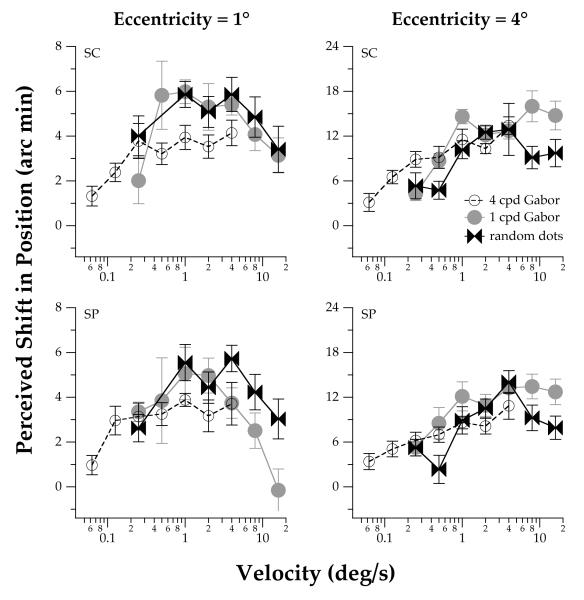
Figure 5.
Effect of the type of carrier on the illusory MIPS for a range of carrier velocities. Data are shown for two observers for truncated-Gabor stimuli of 1 and 4 cpd and random-texture stimuli, and eccentricities of 1 and 4°. The duration of the stimulus was 453 ms. Data for 4 cpd truncated-Gabor stimuli are re-plotted from those in Figure 2. The error bars represent ±1 SEM across runs.
The rate of change of the perceived position shift with velocity is not the same for the three stimulus durations, as shown by the different shapes of the functions in each panel of Figures 2 and 3. Specifically, for stimulus durations of 107 and 453 ms, the perceived position shift reaches an asymptotic value at a velocity of approximately 1 deg/s. In contrast, for a stimulus duration of 53 ms, the perceived position shift continues to increase for the range of carrier velocities tested. Close examination of the data also reveals that the temporal properties of the illusion depend on the carrier velocity. Consistent with previous data (Arnold & Johnston, 2005), the illusory position shift increases monotonically as a function of the stimulus duration at lower velocities. However, as the velocity of the carrier grating increases, the perceived position shift grows most quickly for stimuli of short duration. At a carrier velocity of 4 deg/s, the data in Figures 2 and 3 suggest that the magnitude of the perceived position shift varies non-monotonically as a function of duration.
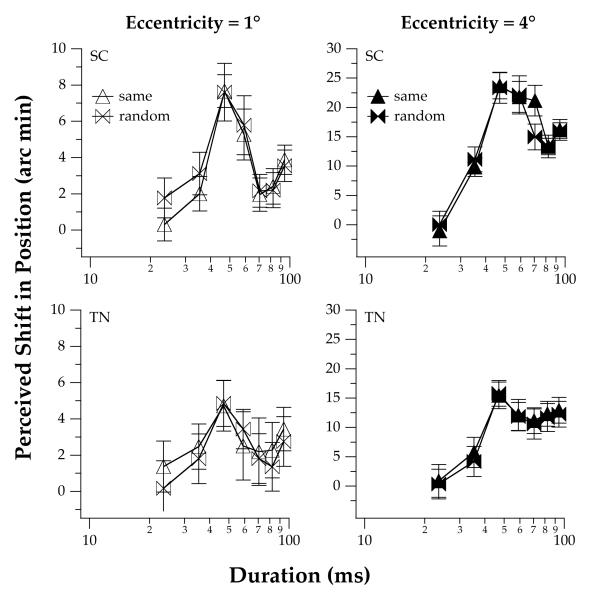
The oscillatory behavior of the MIPS with stimulus duration is more apparent in Figure 4, which presents data obtained for two observers at a carrier velocity of 16 deg/s. In particular, the perceived position shift increases monotonically with stimulus duration up to approximately 45 ms, then decreases for stimulus durations between 45 and approximately 75 ms, before rising again for longer durations. The magnitude of the induced position shift for the longest stimulus duration tested in this experiment (94.1 ms) is similar to that obtained in Experiment 2, which used the same carrier spatial frequency and velocity and a duration of 453 ms (see Figure 5, below). This comparison suggests that, for a carrier velocity of 16 deg/s, the illusory MIPS reaches a steady-state value when the stimulus duration is approximately 100 ms. For both observers, the difference between the magnitude of the perceived position shift at the initial temporal peak (ca. 45 ms) and the ultimate plateau is a larger fraction of the ultimate plateau for stimuli at an eccentricity of 1° than 4°.
Figure 4.
Effect of stimulus duration and eccentricity on the average illusory MIPS for a high carrier velocity of the truncated-Gabor stimuli. Data are shown for two observers for a carrier velocity of 16 deg/s, durations ranging from 23.5 to 94.1 ms, eccentricities of 1 and 4°, and, same vs. random initial phases of the carriers in the two stimuli. The spatial frequency of the carrier was 1 cpd. The error bars represent ±1 SEM across runs.
To ensure that observers’ judgments did not depend on the phase of the truncated-Gabor carriers, we re-tested them using truncated-Gabor stimuli in which the initial phase of the carrier gratings was randomized. As shown in Figure 4, the data obtained for stimuli with fixed vs. random starting phase are very similar, indicating that the magnitude of the illusory position shift depends on the duration of the drifting truncated-Gabor stimulus and not on the relative phases of the left and right carrier stimuli.
Effect of carrier type on the illusory MIPS
The magnitudes of perceived position shift are qualitatively similar for 1 and 4 cpd truncated-Gabor stimuli as a function of the carrier velocity (Figure 5), rather than as a function of temporal frequency. Further, the magnitudes of perceived position shift are qualitatively similar for truncated-Gabor stimuli and for Gaussian-windowed random-texture patches (Figure 5). The data in Figure 5 were obtained for a stimulus duration of 453 ms, by which time we assume that the illusory MIPS has reached a steady-state condition. Although the magnitude of the perceived position shift increases similarly for the grating and random-texture carrier stimuli up to a velocity of approximately 4 deg/s, a quantitative difference exists for higher velocities when the stimuli are at an eccentricity of 4°. These data are not consistent with the data of DeValois and DeValois (1991) and Bressler and Whitney (2006), which indicate that the maximum magnitude of perceived position shift occurs for a constant temporal frequency for carriers of different spatial frequency. Whereas the perceived position shift decreases at velocities greater than 4 deg/s for the Gaussian-windowed random-texture patches (similar to the results obtained for both types of carrier stimuli at an eccentricity of 1°), no change occurs in the illusory position shift at higher velocities for 1 cpd truncated-Gabor stimuli.
DISCUSSION
Possible explanations for the illusory MIPS
Ramachandran and Anstis (1990) suggested that the illusory MIPS that they observed in their experiments was caused by an inappropriate application of motion signals from the carrier dots to the stationary kinetic edge of their stimulus. However, the resulting position shift cannot be expected to increase indefinitely as the positions of the carrier elements are displaced further and further during motion. Rather, if the illusory position shift results from a misapplication of the carrier position signals, then one can assume that the magnitude of this shift should be limited by the veridical position signals that are associated with the stationary stimulus window (Ramachandran and Anstis, 1990; Patel, Chung & Bedell, 2004). These veridical position signals have a precision that can be estimated by the threshold for discriminating position offset in a pair of physically stationary windows. Consequently, the mean perceived position of the stationary window can be approximated as:
| (1) |
where, Pwindow, Swindow, k, Thwindow, v and Δt are the mean perceived position of the window, the physical position of the window, a constant, the position threshold for a static windowed stimulus, thespeed of carrier motion, and the duration of carrier motion, respectively. This explanation implies that the magnitude of the MIPS should vary linearly with the speed of a fixed-duration carrier stimulus, up to an upper limit. Beyond this limit, the magnitude of the MIPS should be independent of speed. Similarly, for a carrier stimulus that moves at a fixed speed, the magnitude of the MIPS should increase linearly with the stimulus duration, until an upper asymptote is achieved. This explanation also implies that the magnitude of the MIPS should increase monotonically with stimulus manipulations that reduce the precision of position resolution for the stimulus window.
The data shown in Figure 3 are consistent with these predictions in the following ways: (a) the magnitude of the MIPS becomes asymptotic as the drift speed increases, especially if the stimulus duration is long enough that the position information from motion mechanisms can reasonably be expected to achieve its steady-state value, and (b) the asymptotic magnitude of MIPS increases with the separation between the stimuli, which is known to adversely affect the precision of visual position judgments (e.g. Sullivan, Oatley & Sutherland, 1972; Klein & Levi, 1987; Levi & Klein, 1990; Waugh & Levi, 1998; Bedell, Chung & Patel, 2000). On the other hand, data in Figures 4 and 5 clearly show that, under some conditions, the MIPS varies non-monotonically with both the velocity and duration of the moving carrier stimulus. These results indicate that the mechanism underlying the MIPS has complex dynamic properties that are not described by the simple model embodied in Eq. 1. Finally, judgments of position for stationary separated targets are based upon the location of the centroids of their luminance distributions (e.g. Watt, Morgan & Ward, 1983; Whitaker & Walker, 1988; Patel, Bedell & Ukwade, 1999). The explanation above recognizes no influence of carrier motion on the perceived contrast distribution of a windowed moving stimulus, which is at odds with findings that the perceived contrast of such stimuli are altered at the leading and trailing edges, thereby altering the location of the stimulus centroid (Whitney et al., 2003; Arnold & Johnston, 2005).
In most studies of the illusory MIPS, the stationary window and the carrier occupy the same spatial locations. However, in an experiment by Mussap and Prins (2002), the stationary window and the carrier motion signals were spatially dissociated. A perceived shift of the stationary window occurred despite this spatial dissociation. Mussap and Prins (2002) concluded from these results that the perceived shift of the stationary window cannot be attributed readily to an erroneous application of carrier’s motion signals to the perceived location of the stationary window. Similarly, Whitaker et al. (1999) concluded that a weighted sum of conflicting position cues from the radial motion of the carrier stimulus and from the stationary stimulus envelope cannot account completely for the magnitude of the illusory size changes that they observed in their experiments.
A potentially simple explanation for the MIPS is that successive stimulus frames are averaged temporally, such that the centroids of the time-averaged stimuli are shifted in the direction of motion. This explanation predicts that the perceived shift would vary systematically with the duration of stimulus motion. However, this explanation predicts also that the direction of the illusory MIPS should depend on the initial phase of the moving truncated-Gabor stimulus, which is not supported by the data shown in Figure 4.
Fu et al. (2004) proposed that illusory MIPS results from a motion-induced displacement in the location of cortical receptive fields. They found that the receptive fields that they mapped for neurons in cat primary visual cortex underwent a shift in the direction opposite to the direction of stimulus motion. Under the assumption that each neuron conveys a fixed position label to subsequent visual processing, stimulation at a given retinal location during motion should be interpreted as originating from a visual location that is shifted from the true location in the direction of motion. A property of the illusory MIPS is that it occurs only when the stationary window of a drifting stimulus has sufficiently blurry edges, and is absent when the edges of the window are sharp (e.g. Whitney et al., 2003). In the absence of additional mechanisms, it is unclear how a fixed receptive-field structure can produce such a dramatic dependence on the smoothness of the window’s edges. Further, as pointed out by Arnold and Johnston (2005), a receptive field shift should cause a perceived shift in the entire spatial extent of the drifting stimulus. Contrary to this prediction, Arnold and Johnston (2005) found that the central part of a drifting Gabor stimulus remains largely unshifted, despite a substantial illusory MIPS of the Gabor as a whole. Lastly, if cortical receptive fields shifted during motion as modeled by Fu et al. (2004), then the perceived spatial position of a moving object should be extrapolated forward in the direction of motion (Berry et al. 1999), a proposal that has been rejected by numerous studies of the flash-lag phenomenon (Baldo & Klien, 1995; Purushothaman, Patel, Bedell & Ogmen, 1998b; Patel, Ogmen, Bedell & Sampath, 2000; Brenner & Smeets, 2000; Whitney, Murakami & Cavanagh, 2000; Krekelberg & Lappe, 2001; Ogmen, Patel, Bedell & Camuz, 2004; Kirschfeld, 2006).
A framework to account for the illusory MIPS
Several authors considered the possibility that the illusory shift of a stationary stimulus, such as the envelope of a drifting Gabor, results from an interaction between motion processing in areas such as MT and the representation of the stimulus in early cortical areas such as V1 (e.g. McGraw et al., 2002; Watanabe, 2005; Nishida and Johnston, 1998; Snowden, 1998). However, the exact nature of these interactions was not described adequately. Recently, Whitney et al. (2003) and Arnold and Johnston (2005) showed that, during motion, the perceived contrast of a Gabor patch increases at its leading edge and decreases at its trailing edge, suggesting that the illusory MIPS could result from a shift in the perceived centroid of the stimulus window. However, neither study proposed a specific mechanism to account for the observed modulations of perceived contrast, and neither showed how various characteristics of the illusory MIPS could be explained using the reported interaction between motion and contrast. Here, we present a formal framework to show how the illusory MIPS and its phenomenal properties can be explained based on the motion-dependant modulation of perceived stimulus form.
To obtain insight into the possible neural basis of the MIPS, consider a spatially windowed sinusoidal stimulus that drifts rightward beneath a stationary window or envelope. Figure 6 illustrates how the perceived position of a stationary Gaussian window would shift due to drifting motion of its carrier. Note that when the carrier stimulus drifts, these envelopes attenuate the amplitude of temporal luminance modulation in the carrier stimulus in a spatially dependent manner. On the other hand, the temporal frequency of luminance modulation remains equal to the product of the carrier spatial frequency and velocity at all spatial locations within each envelope. We assume that the luminance profile of the windowed drifting stimulus is encoded in a form map by an array of retinotopically arranged neurons and that the gains of these neurons are modulated by signals from neighboring neurons in a direction dependent manner. We also assume that motion mechanisms are organized retinotopically to form a motion map (not illustrated in the figure) and that signals from this map activate the direction-dependent interactions in the form map. The spatial distribution of gain-control signals that are generated at each neuron in the form map by its neighbors is defined as the motion activated gain field of that neuron. Note that the concept of gain control of a neuron by signals from neighboring neurons is well established in the literature on luminance and contrast perception (Sperling & Sondhi, 1968; Sperling, 1970; Grossberg, 1973; Lu & Sperling, 1996). Also note that the concept of a gain field is distinct from the concept of a classical receptive field (RF) in the following important way: a visual RF defines a spatial region over which a neuron’s response can be modulated by a visual input whereas a gain field defines a spatial region over which a neuron’s gain can be modulated by a visual input. The spatial interactions within a RF can produce activity in the target neuron, but a gain-field interaction can only modulate the target neuron’s ongoing activity. In general, the instantaneous gain of a neuron in a one-dimensional form map is given by:
| (2) |
| (3) |
where, Gi, α, β, xp, Ip, J and K are the gain of the ith neuron in the form map where i ∈ set of all neurons in the form map, the gain-increase weight from neighboring neurons, the gain-decrease weight from neighboring neurons, the input of the pth neuron in the form map where p ∈ set of all neurons in the form map, the output amplitude of the pth neuron in the form map, the set of neurons that send gain increase signals, and the set of neurons that send gain decrease signals. Note that the specific neighboring neurons that are included in sets J and K depend on the direction of stimulus motion.
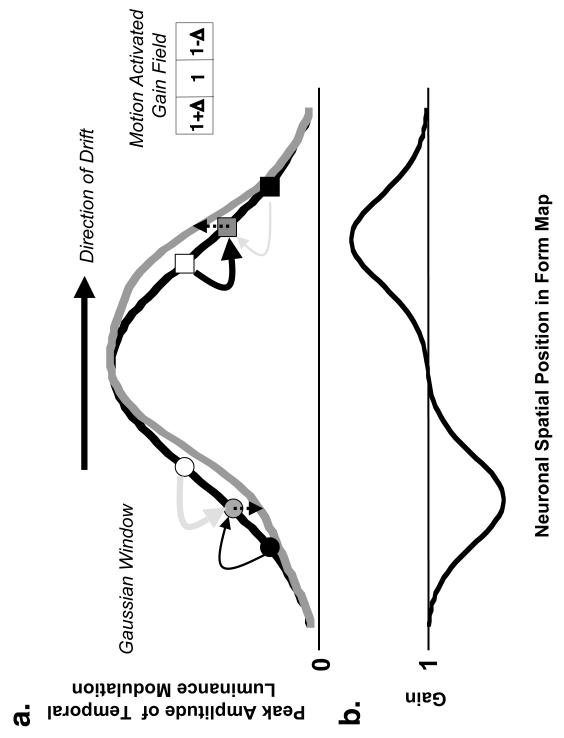
Figure 6.
Illustration of a motion activated gain field and its possible role in generating the MIPS. a. This figure illustrates the influence of a motion activated gain field (e.g. inset at top right) on the peak amplitude of temporal luminance modulation at various spatial locations in the form map produced by a Gaussian windowed drifting sinusoidal carrier (thick black curve). We assume that the gain of a neuron is the sum of all the gain change signals received from its neighbors, a concept similar to the combination of excitatory and inhibitory signals within receptive fields. Note that the gain change signals are activated by the retinotopically corresponding motion signals in a motion map (not shown). The long arrow at the top represents the direction of drift. The curved arrows represent the gain change (or control) signals that a single neuron receives from its neighbors. The thickness of the arrow represents the magnitude of the gain change signal. Black arrows represent gain-increase (amplification) signals while gray arrows represent gain-decrease (attenuation) signals. Two example locations are illustrated: one within the leading (filled gray square) and another within the trailing (filled gray circle) half of the drifting Gabor stimulus. At the location within the trailing half of the drifting stimulus (filled gray circle), the gain-increase signal is lower than the gain decrease signal and thus the net effect is to reduce the peak amplitude of luminance modulation at that location (downward dotted arrow). The opposite effect (upward dotted arrow) occurs for the location within the leading half of the drifting stimulus (filled gray square). The thick gray curve represents the peak amplitude of luminance modulation after the gain changes in the form map have reached steady-state (e.g. curve in b). This curve illustrates the distortion of the form map and the shift in centroid of the activity pattern, which leads to a shift in the perceived position of the drifting Gabor stimulus in the direction of motion. b. An example of the steady-state gains of the neurons in the form map. Gains are lower (greater) than unity within the trailing (leading) half of the drifting stimulus. The gain is minimum (or maximum) near the spatial regions where the slope of the Gaussian window of the drifting Gabor is steepest. Conversely, the gains are close to unity near the spatial regions where the slope of the Gaussian window of the drifting Gabor is close to zero. The thick gray curve in panel a is computed by multiplying the thick black curve in panel a by the gain curve in this panel. Note that for a rectangular window, the steady-state gains for all the neurons in the form map will be constant everywhere (if the gain increase signals truly balance the gain decrease signals, the gains will be close to unity) except in the small region at the stimulus edges.
For simplicity, consider that a rightward drifting stimulus produces a motion-activated gain field, as shown in the inset in the upper right of Figure 6. According to this motion-activated gain field, a neuron in the form map receives a signal to increase (or decrease) its gain from neighboring neurons that are retinotopically to the left (or right). The gain-increase signal can be viewed as a signal that prepares the neurons in the form map that are likely to be excited by a moving stimulus in the future, in order to increase the speed of this response. Temporal facilitation in the direction of motion has been proposed as a mechanism that could underlie a shorter latency for moving objects, compared to stationary flashed objects (Whitney, Cavanagh & Murakami, 2000). The gain-decrease signal can be viewed as a means to quickly remove persisting signals in the form map, that would otherwise be left over from an object that has moved to another location on the retina (Bex, Edgar & Smith, 1995; Chen, Bedell & Ogmen, 1995; Purushothaman, Ogmen, Chen & Bedell, 1998a). When gain-increase and gain-decrease signals are combined together, a motion-activated gain field can improve both the spatial and temporal resolution of the visual system in representing the form of a moving stimulus. Although we illustrate this idea here using a one-dimensional discrete motion-activated gain field, the motion-activated gain fields in the visual system are assumed to be two-dimensional and spatially graded, based on the likely future directions of a moving object.
A distinction between a discrete moving object and a windowed drifting stimulus, such as a grating, becomes apparent. A moving object would normally activate the gain-increase interactions before the gain decrease interactions at each retinotopic location, an order of activation that optimizes the benefits that are provided by these interactions. On the other hand, a windowed drifting stimulus can activate both types of interactions simultaneously at a single retinotopic locus, which results in little or no net benefit for the perception of form. Gain interactions may not be very important for correctly perceiving the form of a drifting stimulus, partly because other spatio-temporal interactions reduce the perception of motion smear for these stimuli (Burr, 1980; Purushothaman et al., 1998a; Hammett & Bex, 1996).
How, specifically, does the concept of the motion-activated gain fields explain the illusory MIPS phenomenon and its properties? For the Gaussian-windowed stimulus, the neural responses in the form map in the presence of the motion-activated gain field (as shown in the inset of Figure 6) differ for the leading and trailing sides of the stimulus. In Figure 6, we illustrate this difference for two representative neurons in the form map (indicated by the grey circle and square), which sample spatial locations on opposite sides of the drifting Gabor. Because the amplitude of temporal luminance modulation is lower near the edges than near the center of the Gaussian window, a neuron that samples the trailing side of the stimulus (the grey circle) will receive stronger gain-decrease (Ik; the thick gray arrow) than gain-increase (Ij; thin black arrow) signals from its neighboring neurons. As a result, the net temporal luminance modulation of this neuron will be reduced (shown by the downward dotted arrow), compared to its response in the absence of any motion-activated gain-field interactions. For a neuron that samples the leading side of the drifting stimulus (grey square), the gain-increase signals (Ij; thick black arrow) will be stronger than the gain-decrease signals (Ik; thin grey arrow) and the temporal luminance modulation of the neuron will therefore increase (shown by theupward dotted arrow), compared to its response in the absence of motion-activated gain-field interactions. These asymmetrical gain-field interactions in the leading and trailing halves of the stimulus therefore shift the centroid of the neural activity in the form map, and hence the perceived position of the drifting Gabor stimulus, in the direction of motion. Note that the asymmetric gain-field interactions are presumed to be local, dynamic and stimulus dependant, as opposed to the static asymmetric receptive fields interactions proposed by Fu et al. (2004).
When the stimulus window is rectangular, the motion-activated gain-field interactions for neurons that sample the leading and trailing parts of the drifting stimulus are largely similar. In particular, the uniform amplitude of temporal luminance modulation across the drifting stimulus results in a balance between the gain-increase and the gain-decrease signals from neighboring neurons, regardless of which region of the stimulus the neuron samples, with the exception of the small stimulus regions at the sharp edges of the window. Consequently, the activity pattern of the neurons in the form map should be similar with or without the presence of motion-activated gain-field interactions. This analysis therefore predicts only a minimal illusory position shift when the window is rectangular, in agreement with experimental data (Whitney et al., 2003; Arnold & Johnston; 2005). Note that the same explanation can account for the illusory position shift found by Fu et al. (2001), who showed that the position of a blurred moving object is shifted forward in the direction of motion if the motion stops and the stationary target is left visible for 100 ms. For the gain-field explanation to account for this result, the persistence of gain field connections must be assumed to approximate 100 ms, the duration that the stimulus used by Fu et al. remained stationary before disappearing.
Because the motion-activated gain-field interactions shown in Figure 6 depend primarily on the amplitude but not the temporal frequency of luminance modulation, the illusory MIPS is expected to be largely independent of the carrier characteristics, in agreement with our results. In our experiments, a four-fold increase in the spatial frequency of the truncated-Gabor carrier stimulus left the magnitude of the illusory position shift largely unchanged (see Figure 5). Further, the magnitude of the illusory position shift for a windowed random-texture stimulus is similar to that for a drifting truncated-Gabor stimulus. The lack of a dependence of the illusory MIPS on spatial properties of the carrier was shown also by McGraw et al. (2002). The similarity between the results for grating and limited-lifetime random-texture carriers implies that motion energy is sufficient to produce the illusory MIPS and that the physical movement of stimulus features is not necessary, a conclusion also drawn by Mussap and Prins (2002). However, illusory position offsets do not occur for a stationary windowed stimulus or a flickering stimulus (DeValois and DeValois, 1991), indicating that a temporal component of luminance modulation that results in motion is required to produce an illusory perceptual shift.
Consistent with the results of DeValois and DeValois (1991), we found that the illusory MIPS increases as a function of the eccentricity of the moving targets (see Figures 2-5). This increase may be related to the shift that occurs with retinal eccentricity in the spatial scale of visual analysis. In other words, as eccentricity increases the spatial interactions that underlie the illusory MIPS would be expected to occur over an increasingly larger visual space. In the context of the framework outlined above, we suggest that gain field sizes increase as the eccentricity of the stimulus increases. This possibility is consistent with the fact that both retinal and cortical sampling become coarser as the visual-field eccentricity increases. Previously, the systematic coarsening of sampling with retinal eccentricity was invoked to account for the increased region that contributes to spatial crowding as the eccentricity of the targets increases (Toet & Levi, 1992).
Two other possible explanations for the increase in the MIPS with eccentricity can be discounted on the basis of our data. One possibility is that an increase in the magnitude of internal motion signals (i.e., saliency) is responsible for the increase in the illusory MIPS as a function of eccentricity. An increase in the saliency of motion signals with an increase in eccentricity could be a consequence of greater transience of peripheral compared to foveal visual responses (see Solomon, Martin, White, Ruttiger & Lee, 2002). However, as shown in Table 1, our observers’ thresholds to detect stimulus motion are higher at an eccentricity of 4° than 1° (also see, e.g., van de Grind, van Doorn & Koenderink, 1983; Johnston & Wright, 1985). Consequently, if the magnitude of internal motion signals increases as a function of the stimulus eccentricity, then the internal noise (which limits the motion thresholds) must increase at an even greater rate. This would imply that not just the magnitude but the variability of the MIPS should increase with the eccentricity of the stimulus. Contrary to this expectation, the data in Figures 2-5 show no evidence for a relative increase in the variability of the MIPS as the eccentricity of the stimuli increases.
Table 1.
Average motion thresholds (deg/s) for a stimulus duration of 453 ms.
| Stimulus | Gap Separation = 120′ | Gap Separation = 480′ |
|---|---|---|
| 4 cpd truncated-Gabor | 0.02 ± 0.003 | 0.04 ± 0.01 |
| 1 cpd truncated-Gabor | 0.01 ± 0.002 | 0.02 ± 0.004 |
| Random-Texture | 0.08 ± 0.02 | 0.16 ±0.03 |
A second possible explanation for the increase in the MIPS with eccentricity is that the presence of neural blur effectively increases the space constant of the Gaussian stimulus window. To address this possibility, we filtered the luminance distribution of the Gaussian window that we applied to our stimuli (space constant = 18 arc-min) using two filters: (1) a spatial band-pass filter representing the foveal contrast sensitivity function and (2) a spatial low-pass filter representing the contrast sensitivity function at a retinal eccentricity of 10 deg. These contrast sensitivity functions were obtained from Chung, Legge and Tjan (2002). We found that the luminance distribution of the Gaussian window is completely unchanged by these two filters, suggesting that the increased magnitude of MIPS with stimulus eccentricity and the variation in the MIPS with the space constant of the Gaussian stimulus window result from different mechanisms.
Presumably, the dynamic aspects of the illusory MIPS represent the dynamics of the circuits that are responsible for the motion-activated gain-field interactions. For all stimulus velocities tested, the magnitude of the illusory MIPS reaches a plateau when the duration of the drifting stimulus is sufficiently long. This result suggests that the mechanism responsible for the illusory MIPS has the properties of a temporal low-pass filter. This filtering, as indicated by the temporal properties of the illusory MIPS, should not be confused with the temporal filtering applied to the stimulus. When the stimulus velocity is low, the magnitude of the MIPS increases monotonically with an increase in stimulus duration until it reaches a plateau. However, when the stimulus velocity is higher, the magnitude of the MIPS oscillates before reaching a plateau, suggesting that the underlying mechanism is non-linear with respect to the stimulus velocity.
The dynamics exhibited by the illusory MIPS could reflect either the dynamics of the motion mechanisms that respond to the carrier stimulus, the dynamics of the network that produces the hypothesized motion-activated gain-field interactions, or both. In fact, the dynamics exhibited by the illusory MIPS are consistent with the dynamics of motion-sensitive neurons in cortical area MT. Lisberger and Movshon (1999) recorded the responses of MT neurons to a step change in target speed as a function of time for a range of step amplitudes (0 to 128 deg/s). They found that a large proportion of these neurons exhibited both a transient and a sustained change in their firing rate in response to a step change (from zero) in the stimulus speed. All neurons had a preferred speed, which yielded the largest transient or sustained response. In general, the preferred speeds for transient and sustained responses were similar. For the majority of the neurons (see Figures 2B and 20 in Lisberger and Movshon, 1999) the responses were more (or less) transient for speeds higher (or lower) than the preferred speeds. Because the population of MT cells has a largely uniform distribution of preferred speeds and because the speed tuning of individual cells is broad, the population activity in MT becomes increasingly transient as the step of stimulus speed increases (see Figure 20 in Lisberger and Movshon, 1999). This change in the population dynamics of cortical MT neurons as a function of the stimulus speed is qualitatively similar to the temporal variation of the MIPS illusion that we observed at low vs. high velocities. We therefore suggest that the transient dynamics of the MIPS illusion is more likely to be a reflection of the dynamics of the motion signal that controls the gain fields.
Bressler and Whitney (2006) showed recently that a MIPS occurs also for second-order motion stimuli. They found that the second-order MIPS is largely independent of the spatial frequency of the carrier. However, in their experiments the MIPS that resulted from first-order motion stimuli generally increased for lower spatial frequencies of the carrier. Although these data appear to contradict our results, the spatial frequencies used by Bressler and Whitney’s (2006) experiments ranged from 0.2 to 0.7 cpd, substantially lower than those in our experiments. Lowering the spatial frequency below a certain value may increase in the first-order MIPS, similar to increasing the eccentricity of the stimulus. To account for the existence of second-order MIPS, the framework that is outlined above requires that signals from second- as well as first-order motion mechanisms activate the postulated gain fields. The construction of a second-order motion mechanism requires only the addition of a rectification stage to an otherwise first-order motion mechanism (Lu & Sperling, 1995). However, based on Bressler and Whitney’s (2006) results, second-order motion signals would presumably need to be band-pass filtered with respect to temporal frequency prior to activating the gain fields.
Recently, Kirschfeld (2006) proposed an explanation for the illusory position shift of a moving object observed in the motion-offset paradigm (Kanai, Sheth & Shimojo, 2004) that is based on attentional processing and meta-contrast masking. Kirschfeld noted that a moving object would produce a sequence of focal attention and meta-contrast masking operations in the direction of motion. He assumed that focal attention operates ahead of and meta-contrast masking operates behind the instantaneous position of the object. Further, he suggested that these operations provide only modulatory influences and do not generate any activity that would result directly in their perception. Kirschfeld proposed that the successive modulatory influences of focal attention and meta-contrast would distort the perceived form of a moving object, such that the centroid of the activity pattern corresponding to its instantaneous position would be shifted in the direction of motion.
Although Kirschfeld’s explanation has several features in common with the framework presented above, it is unclear whether his explanation can explain the illusory MIPS. Meta-contrast masking is largely symmetrical spatially (see the masking models in Ogmen, Brietmeyer & Melvin, 2003 and Breitmeyer, Kafaligonul, Ogmen, Mardon, Todd & Ziegler, 2006); hence, the masking effect should propagate equally in front of and behind the instantaneous position of the masking target. However, because the peak of meta-contrast masking occurs temporally after the mask is presented, the masking that is generated by a discrete moving target should lag spatially behind the physical position of the target. An analysis of the masking produced by a Gaussian windowed drifting stimulus is more complicated because, unlike classical meta-contrast masking, the mask and target do not occupy distinct spatial locations. As a first approximation, we estimate that the steady-state effect of self-induced meta-contrast masking on a windowed drifting stimulus would be to decrease its contrast symmetrically at all spatial locations. Similarly, in the steady state condition, focal attention generated by a windowed drifting stimulus would be expected to increase its contrast uniformly at all spatial locations. Therefore, unlike the conceptual framework that we presented above to account for the illusory MIPS, the processes of meta-contrast masking and focal attention are not well suited to generate a substantial asymmetry in the represented form of a windowed drifting stimulus. Although a contribution of additional higher-level processes cannot be ruled out completely, low-level cortical mechanisms appear to be sufficient to explain most aspects of the illusory MIPS for stimuli that drift within a physically stationary spatial window.
Finally, it is useful to consider how the conceptual framework that we present above to account for the illusory MIPS might be implemented mechanistically in the brain. A mechanistic model must be dynamic, and preferably capable of accounting for the perceptual responses to a range of spatio-temporal visual stimuli. Previously, the RECOD model (Ogmen, 1993) was shown to account successfully for human psychophysical data on motion deblurring (Purushothaman et al, 1998a) and visual masking (Ogmen et al., 2003; Brietmeyer et al., 2006), which represent temporal changes in the visibility of dynamic stimuli. We speculate that by including the connectivity required to produce direction-dependent gain fields and by fine tuning the temporal parameters of the model, the RECOD model should be able to account also for the non-linear temporal properties of the MIPS with respect to stimulus velocity.
Acknowledgments
Supported by research grants R01 EY12810, R01 EY05068, and R01 MH 49892 from NIH.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Arnold DH, Johnston A. Sub-threshold motion influences apparent position. Journal of Vision. 2005;5:202a. [Google Scholar]
- Baldo MV, Klein SA. Extrapolation or attention shift? Nature. 1995;378:565–566. doi: 10.1038/378565a0. [DOI] [PubMed] [Google Scholar]
- Bedell HE, Chung STL, Patel SS. Elevation of Vernier thresholds during image motion depends on target configuration. Journal of the Optical Society of America A. 2000;17:947–954. doi: 10.1364/josaa.17.000947. [DOI] [PubMed] [Google Scholar]
- Berry MJ, 2nd, Brivanlou IH, Jordan TA, Meister M. Anticipation of moving stimuli by the retina. Nature. 1999;398:334–338. doi: 10.1038/18678. [DOI] [PubMed] [Google Scholar]
- Bex PJ, Edgar GK, Smith AT. Sharpening of drifting, blurred images. Vision Research. 1995;35:2539–2546. doi: 10.1016/0042-6989(95)00060-d. [DOI] [PubMed] [Google Scholar]
- Breitmeyer BG, Kafaligonul H, Ogmen H, Mardon L, Todd S, Ziegler R. Meta- and paracontrast reveal differences between contour- and brightness-processing mechanisms. Vision Research. 2006;46:2645–2658. doi: 10.1016/j.visres.2005.10.020. [DOI] [PubMed] [Google Scholar]
- Brenner E, Smeets JB. Motion extrapolation is not responsible for the flash-lag effect. Vision Research. 2000;40:1645–1648. doi: 10.1016/s0042-6989(00)00067-5. [DOI] [PubMed] [Google Scholar]
- Bressler DW, Whitney D. Second-order motion shifts perceived position. Vision Research. 2006;46:1120–1128. doi: 10.1016/j.visres.2005.10.012. [DOI] [PubMed] [Google Scholar]
- Burr D. Motion smear. Nature. 1980;284:164–165. doi: 10.1038/284164a0. [DOI] [PubMed] [Google Scholar]
- Chen S, Bedell HE, Ogmen H. A target in real motion appears blurred in the absence of other proximal moving targets. Vision Research. 1995;35:2315–2328. doi: 10.1016/0042-6989(94)00308-9. [DOI] [PubMed] [Google Scholar]
- Chung STL, Legge GE, Tjan BS. Spatial-frequency characteristics of letter identification in central and peripheral vision. Vision Research. 2002;42:2137–2152. doi: 10.1016/s0042-6989(02)00092-5. [DOI] [PubMed] [Google Scholar]
- DeValois RL, DeValois KK. Vernier acuity with stationary moving Gabors. Vision Research. 1991;31:1619–1626. doi: 10.1016/0042-6989(91)90138-u. [DOI] [PubMed] [Google Scholar]
- Durant S, Johnston A. Temporal dependence of local motion induced shifts in perceived position. Vision Research. 2004;44:357–366. doi: 10.1016/j.visres.2003.09.022. [DOI] [PubMed] [Google Scholar]
- Fu YX, Shen Y, Dan Y. Motion-induced perceptual extrapolation of blurred visual targets. Journal of Neuroscience. 2001;21:172–176. doi: 10.1523/JNEUROSCI.21-20-j0003.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu YX, Shen Y, Gao H, Dan Y. Asymmetry in visual cortical circuits underlying motion-induced perceptual mislocalization. Journal of Neuroscience. 2004;24:2165–2171. doi: 10.1523/JNEUROSCI.5145-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grossberg S. Contour enhancement, short term memory, and constancies in reverberating neural networks. Studies in Applied Mathematics. 1973;52:217–257. [Google Scholar]
- Hammett ST, Bex PJ. Motion sharpening: evidence for the addition of high spatial frequencies to the effective neural image. Vision Research. 1996;36:2729–2733. doi: 10.1016/0042-6989(96)00009-0. [DOI] [PubMed] [Google Scholar]
- Johnston A, Wright MJ. Lower thresholds of motion for gratings as a function of eccentricity and contrast. Vision Research. 1985;25:179–185. doi: 10.1016/0042-6989(85)90111-7. [DOI] [PubMed] [Google Scholar]
- Kanai R, Sheth BR, Shimojo S. Stopping the motion and sleuthing the flash-lag effect: Spatial uncertainity is the key to perceptual mislocalization. Vision Research. 2004;44:2605–2619. doi: 10.1016/j.visres.2003.10.028. [DOI] [PubMed] [Google Scholar]
- Kirschfeld K. Stopping motion and the flash-lag effect. Vision Research. 2006;46:1547–1551. doi: 10.1016/j.visres.2005.07.010. [DOI] [PubMed] [Google Scholar]
- Klein SA, Levi DM. Position sense of the peripheral retina. Journal of the Optical Society of America A. 1987;4:1543–1553. doi: 10.1364/josaa.4.001543. [DOI] [PubMed] [Google Scholar]
- Krekelberg B, Lappe M. Neuronal latencies and the position of moving objects. Trends in Neuroscience. 2001;24:335–339. doi: 10.1016/s0166-2236(00)01795-1. [DOI] [PubMed] [Google Scholar]
- Levi DM, Klein SA. The role of separation and eccentricity in encoding position. Vision Research. 1990;30:557–585. doi: 10.1016/0042-6989(90)90068-v. [DOI] [PubMed] [Google Scholar]
- Lisberger SG, Movshon JA. Visual motion analysis for pursuit eye movements in area MT of macaque monkeys. Journal of Neuroscience. 1999;19:2224–2246. doi: 10.1523/JNEUROSCI.19-06-02224.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu ZL, Sperling G. The functional architecture of human visual motion perception. Vision Research. 1995;35:2697–2722. doi: 10.1016/0042-6989(95)00025-u. [DOI] [PubMed] [Google Scholar]
- Lu ZL, Sperling G. Contrast gain control in first- and second-order motion perception. Journal of the Optical Society of America A. 1996;13:2305–2318. doi: 10.1364/josaa.13.002305. [DOI] [PubMed] [Google Scholar]
- McGraw PV, Whitaker D, Skillen J, Chung STL. Motion adaptation distorts perceived visual position. Current Biology. 2002;12:2042–2047. doi: 10.1016/s0960-9822(02)01354-4. [DOI] [PubMed] [Google Scholar]
- Mussap AJ, Prins N. On the perceived location of global motion. Vision Research. 2002;42:761–769. doi: 10.1016/s0042-6989(01)00304-2. [DOI] [PubMed] [Google Scholar]
- Newsome WT, Pare EB. A selective impairment of motion perception following lesions of the middle temporal visual area (MT) Journal of Neuroscience. 1988;8:2201–2211. doi: 10.1523/JNEUROSCI.08-06-02201.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishida S, Johnston A. Influence of motion signals on the perceived position of spatial pattern. Nature. 1999;397:610–612. doi: 10.1038/17600. [DOI] [PubMed] [Google Scholar]
- Ogmen H. A neural theory of retino-cortical dynamics. Neural Networks. 1993;6:245–273. [Google Scholar]
- Ogmen H, Breitmeyer BG, Melvin R. The what and where in visual masking. Vision Research. 2003;43:1337–1350. doi: 10.1016/s0042-6989(03)00138-x. [DOI] [PubMed] [Google Scholar]
- Ogmen H, Patel SS, Bedell HE, Camuz K. Differential latencies and the dynamics of the position computation process for moving targets, assessed with the flash-lag effect. Vision Research. 2004;44:2109–2128. doi: 10.1016/j.visres.2004.04.003. [DOI] [PubMed] [Google Scholar]
- Patel SS, Bedell HE, Ukwade MT. Vernier judgments in the absence of regular shape information. Vision Research. 1999;39:2349–2360. doi: 10.1016/s0042-6989(98)00265-x. [DOI] [PubMed] [Google Scholar]
- Patel SS, Chung STL, Bedell HE. Motion-induced position shifts are limited by conflicting relative position information. Journal of Vision. 2004;4:577a. [Google Scholar]
- Patel SS, Ogmen H, Bedell HE, Sampath V. Flash-lag effect: differential latency, not postdiction. Science. 2000;290:1051. doi: 10.1126/science.290.5494.1051a. [DOI] [PubMed] [Google Scholar]
- Purushothaman G, Ogmen H, Chen S, Bedell HE. Motion deblurring in a neural network model of retino-cortical dynamics. Vision Research. 1998a;38:1827–1842. doi: 10.1016/s0042-6989(97)00350-7. [DOI] [PubMed] [Google Scholar]
- Purushothaman G, Patel SS, Bedell HE, Ogmen H. Moving ahead through differential visual latency. Nature. 1998b;396:424. doi: 10.1038/24766. [DOI] [PubMed] [Google Scholar]
- Ramachandran VS, Anstis SM. Illusory displacement of equiluminous kinetic edges. Perception. 1990;19:611–616. doi: 10.1068/p190611. [DOI] [PubMed] [Google Scholar]
- Shim WM, Cavanagh P. The motion-induced position shift depends on the perceived direction of bistable quartet motion. Vision Research. 2004;44:2393–2401. doi: 10.1016/j.visres.2004.05.003. [DOI] [PubMed] [Google Scholar]
- Snowden RJ. Shifts in perceived position following adaptation to visual motion. Current Biology. 1998;8:1343–1345. doi: 10.1016/s0960-9822(07)00567-2. [DOI] [PubMed] [Google Scholar]
- Solomon SG, Martin PR, White AJ, Ruttiger L, Lee BB. Modulation sensitivity of ganglion cells in peripheral retina of macaque. Vision Research. 2002;42:2893–2898. doi: 10.1016/s0042-6989(02)00414-5. [DOI] [PubMed] [Google Scholar]
- Sperling G. Model of visual adaptation and contrast detection. Perception & Psychophysics. 1970;8:143–157. [Google Scholar]
- Sperling G, Sondhi MM. Model of visual luminance discrimination and flicker detection. Journal of the Optical Society of America. 1968;58:1133–1145. doi: 10.1364/josa.58.001133. [DOI] [PubMed] [Google Scholar]
- Sullivan GD, Oatley K, Sutherland NS. Vernier acuity as affected by target length and separation. Perception & Psychophysics. 1972;12:438–444. [Google Scholar]
- Sundberg KA, Fallah M, Reynolds JH. A motion-dependent distortion of retinotopy in area V4. Neuron. 2006;49:447–457. doi: 10.1016/j.neuron.2005.12.023. [DOI] [PubMed] [Google Scholar]
- Toet A, Levi DM. The two-dimensional shape of spatial interaction zones in the parafovea. Vision Research. 1992;32:1349–1357. doi: 10.1016/0042-6989(92)90227-a. [DOI] [PubMed] [Google Scholar]
- van de Grind WA, van Doorn AJ, Koenderink JJ. Detection of coherent movement in peripherally viewed random-dot patterns. Journal of the Optical Society of America. 1983;73:1674–1683. doi: 10.1364/josa.73.001674. [DOI] [PubMed] [Google Scholar]
- Watanabe K. The motion-induced position shift depends on the visual awareness of motion. Vision Research. 2005;45:2580–2586. doi: 10.1016/j.visres.2005.03.001. [DOI] [PubMed] [Google Scholar]
- Watt RJ, Morgan MJ, Ward RM. Stimulus features that determine the visual location of a bright bar. Investigative Ophthalmology & Visual Science. 1983;24:66–71. [PubMed] [Google Scholar]
- Waugh SJ, Levi DM. Visibility and Vernier acuity for separated targets. Vision Research. 1993;33:539–552. doi: 10.1016/0042-6989(93)90257-w. [DOI] [PubMed] [Google Scholar]
- Whitaker D, Walker H. Centroid evaluation in the vernier alignment of random dot clusters. Vision Research. 1988;28:777–784. doi: 10.1016/0042-6989(88)90024-7. [DOI] [PubMed] [Google Scholar]
- Whitaker D, McGraw PV, Pearson S. Non-veridical size perception of expanding and contracting objects. Vision Research. 1999;39:2999–3009. doi: 10.1016/s0042-6989(99)00010-3. [DOI] [PubMed] [Google Scholar]
- Whitney D. The influence of visual motion on perceived position. Trends in Cognitive Sciences. 2002;6:211–216. doi: 10.1016/s1364-6613(02)01887-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitney D. Motion distorts perceived position without awareness of motion. Current Biology. 2005;15:324–326. doi: 10.1016/j.cub.2005.04.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitney D, Murakami I, Cavanagh P. Illusory spatial offset of a flash relative to a moving stimulus is caused by differential latencies for moving and flashed stimuli. Vision Research. 2000;40:137–149. doi: 10.1016/s0042-6989(99)00166-2. [DOI] [PubMed] [Google Scholar]
- Whitney D, Cavanagh P, Murakami I. Temporal facilitation for moving stimuli is independent of changes in direction. Vision Research. 2000;40:3829–3839. doi: 10.1016/s0042-6989(00)00225-x. [DOI] [PubMed] [Google Scholar]
- Whitney D, Goltz HC, Thomas CG, Gati JS, Menon RS, Goodale MA. Flexible retinotopy: motion-dependent position coding in the visual cortex. Science. 2003;302:878–881. doi: 10.1126/science.1087839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yokoi K, Watanabe K. Distortion of positional representation of visual objects by motion signals. Journal of Vision. 2005;5:206a. [Google Scholar]