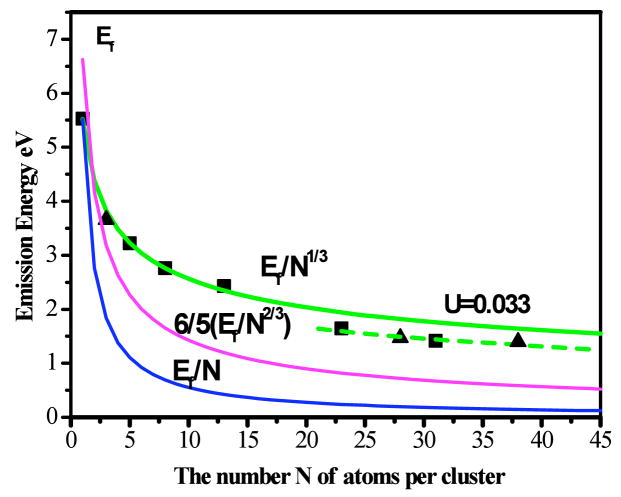
Figure 4.

Correlation of the number of atoms, N, per cluster with emission energy. Emission energy decreases with increasing number of atoms. The correlation of emission energy with N is quantitatively fit with E_fermi/N^1/3, as predicted by the jellium model (1, 2). When N is equal to 1, the energy of valence electron is equal to Fermi energy because the valence electron is at the HOMO level. Emission energies of Au₂₃ and Au₃₁ exhibit slight deviations from the E_fermi/N^1/3 scaling. Consistent with the narrow excitation and emission spectra, the potential confining the free electrons flattens slightly for Au₂₃ and Au₃₁, with anharmonicity parameter U=0.033 (42). The experimental values for the emission energies of Au₃ (82), Au₂₈ (9)and Au₃₈ (71) are 3.66, 1.55, and 1.44 eV respectively (represented by ▲), which are all consistent with the observed scaling relations. Kubo’s predicted model E_f/N (12) and the square potential box model (6/5E_f/N^2/3 (1) are also shown in the figure. Obviously these models can not accurately fit the emission energy scalings of the gold clusters.