An overview of statistical decomposition techniques applied to complex systems

Abstract

The current state of the art in applied decomposition techniques is summarized within a comparative uniform framework. These techniques are classified by the parametric or information theoretic approaches they adopt. An underlying structural model common to all parametric approaches is outlined. The nature and premises of a typical information theoretic approach are stressed. Some possible application patterns for an information theoretic approach are illustrated. Composition is distinguished from decomposition by pointing out that the former is not a simple reversal of the latter. From the standpoint of application to complex systems, a general evaluation is provided.

Introduction

Decomposition is a process of breaking up into constituent elements. In mathematical analysis, it means factorization and/or finding summands of a real number or a matrix. In systems science, decomposition consists of finding an optimal partition of a system in terms of its subsystems. Decompositions in real-life applications are motivated by a need to obtain a much simpler body of constituents that can best represent a given system of unmanageable size and/or complex structure. Complexity is a lack of information about a system, and unmanageable size means high dimensionality (Donoho, 2000; Fan and Li, 2006). Optimality of decomposition is evaluated by means of some adopted criteria, such as a dispersion measure of observables (for instance, higher eigenvalues or singular values of covariance matrix) or their conformity with prior knowledge on network structure or an entropic measure (information content) involved, etc.

Here we aim to discuss the current state of the art in decomposition within a uniform framework of approach. We do not intend this to be a full-fledged survey. For illustrations and examples on some known techniques, readers will be referred elsewhere. Because decomposition has a vast spectrum of application areas, finding a common framework of interest to all is challenging. The case is the same with determining the type of audience to be addressed. We have chosen a general statistical and information theoretic framework without dwelling on specifics of a certain area, for example, technicalities of statistical inference issues relating to the models discussed. Apart from taking care to introduce a conceptual framework for decomposition on the basis of partitions and except for the two illustrations provided on applications of the last technique and our efforts to find a common framework for exposition, we do not claim originality:

A close study of the relevant literature has led us to conclude that applications of decomposition and relevant techniques fit into two categories of approaches: The first category handles the problem in terms of a structural formal model representing the real-world phenomenon to be considered. The second category uses information theoretic treatment of systems without specifying such a structure. The first four well-known techniques to be discussed can be placed within the first category and are also used for dimension reduction: principal component analysis (PCA), singular value decomposition (SVD), independent component analysis (ICA), and network component analysis (NCA). The final technique, which may be called decomposition with information transfer function (ITF), falls in the second category. Although it is one of the earliest approaches found in literature, ITF is little known and the least explored. In the exposition below, both random vectors and matrices are shown in bold uppercase letters whereas bold italic uppercase letters are used for random vectors only. The superscript t stands for transposition.

A common framework of structure for the first category of techniques can be set up in terms of a linear model such as

$$\left(\begin{array}{c}{X}_1\\ X_2\\ ⋮\\ X_n\end{array}\right)=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \dots & a_{1\text{m}}\\ a_{21}& a_{22}& \dots & a_{2\text{m}}\\ ⋮& ⋮& ⋮& ⋮\\ a_{n1}& a_{n1}& \dots & a_{nm}\end{array}\right]\left(\begin{array}{c}{Z}_1\\ Z_2\\ ⋮\\ Z_m\end{array}\right)+\left(\begin{array}{c}{E}_1\\ E_2\\ ⋮\\ E_n\end{array}\right)$$ (1)

In information theory, for instance, this model represents a simple formal communication channel without encoding and decoding (Ash, 1990, Chapter I). The model (1) will shortly be expressed as

$$\mathit{X}=\mathbf{A}\mathit{Z}+\mathit{E}$$

The column vector X = (X₁, X_2,…, X_n)^t of the model (1) has n observable random variables X₁, X₂,…, X_n such as phenotypes in biology. The coordinates of the column vector Z stand for m non-observable random factors Z₁, Z_2,…, Z_m, with n ≤ m, where m denotes the number of arrays into which these latent factors (say, genotypes in the case of the given biological example) can be placed. The (n×1) vector E contains n unobserved residuals E₁, E₂,…, E_n, which are sometimes called noise factors. When E₁, E₂,…, E_n are missing in the model, i.e., when E=0, (1) becomes a noise-free or noiseless model. Setting Y = AZ and having hence X = Y + E for (1), one easily obtains an initial decomposition {Y, E} of X underlying the model (1). The assumption behind the decomposition {Y, E} is that these two vectors or factors have additive (independent or at least orthogonal) effects on X. Y = AZ is a linear approximation to any differentiable non-linear function (correspondence) Y = Ψ(Z) at a certain point of Z. The general setup (1) outlined above is different from the classical multivariate regression model. In the multivariate regression model, the matrix A is observable and the vector Z is unobservable. Furthermore, under the regression model, the noise vector E cannot obviously be neglected.

The vectors Z and X are related to each other though an unknown mixing matrix A, the rows of which correspond to the coordinates of X, i.e., phenotypes in biology, and the columns correspond to the elements of Z. In physical terms, matrix A stands for a system or a network (i.e., gates) through which, for example, genotypes or similar latent factors are connected to phenotypes or observable outputs. Often, these matrices give some idea about the underlying structure of a system. Such matrices are sometimes given special names like design structure matrices, dependency structure matrices, problem solving matrices, or design precedence matrices (Browning, 2001). In fact, a lower triangular matrix A corresponds to a hierarchical structure and diagonal or block diagonal matrices indicate independence or block-wise independence of components. Generally, matrix cells contain real or complex numbers. In a bipartite network system (e.g., a network between two different groups such as the phenotypes and genotypes in our biology example), however, they are composed of non-negative integers only. Irrespective of their numerical nature, estimation of or information on such matrices becomes of utmost importance for the study of complex systems.

The main statistical problem tackled by the structural approach in (1) is thus to obtain a statistically significant estimate of the matrix A and hence the vector Z by using the information contained in the observable X. In the statistical identification and estimation of matrix A, vector X is assumed generally to have a statistical distribution with non-spherical contours on its domain (e.g., if the variance-covariance matrix of a multivariate normal distribution has distinct eigenvalues, the corresponding probability density function traces ellipsoids in its domain whereas a covariance matrix with identical eigenvalues produces spheroids in its domain). PCA and SVD are basically designed for distributions with non-spherical contours; ICA works well with non-normal distributions. Furthermore, normal distributions have maximum entropy among other distributions with an identical mean and variance and therefore are inappropriate for entropic analyses that seek minimum entropy.

The first four techniques to be discussed below aim at obtaining matrix A from parameters of relevant distributions or at estimating it in terms of some observational phenomena. For the purpose of estimation, some finite number of observations like X₁, X_2,…, X_N, n < N, on X are obtained. The condition n < N is obviously required for non-singularity. Hence, ignoring the corresponding residual vectors E₁, E_2,…, E_N for the corresponding vectors Z₁, Z_2,…, Z_N for the time being, we have the observational phenomenon

$$\left[\begin{array}{cccc}{X}_{11}& X_{12}& \dots & X_{1\text{N}}\\ X_{21}& X_{22}& \dots & X_{2\text{N}}\\ ⋮& ⋮& ⋮⋮⋮& ⋮\\ X_{\text{n}1}& X_{\text{n}2}& \dots & X_{\text{nN}}\end{array}\right]=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \dots & a_{1\text{m}}\\ a_{21}& a_{22}& \dots & a_{2\text{m}}\\ ⋮& ⋮& ⋮& ⋮\\ a_{n1}& a_{n1}& \dots & a_{nm}\end{array}\right]\left[\begin{array}{cccc}{Z}_{11}& Z_{12}& \dots & Z_{1\text{N}}\\ Z_{21}& Z_{22}& \dots & Z_{2\text{N}}\\ ⋮& ⋮& ⋮⋮⋮& ⋮\\ Z_{\text{m}1}& Z_{\text{m}2}& \dots & Z_{\text{mN}}\end{array}\right]$$ (2)

In matrix notation, (2) can be re-expressed as

$$\mathbf{X}=\mathbf{AZ}$$ (3)

The matrix X corresponds to a set of N observations on n genes, for instance. The objective for the first four techniques is to obtain an estimate of the unknown structure matrix A by means of the observable X and hence to obtain information on Z with the model (2).

As mentioned earlier, ITF does not involve such a structure as (1) above. Instead, an input process like the latent Z of the above discussion is assumed to be transformed to an output process like the observable Y (or X) above with the understanding that Z and Y (or X) may not necessarily obey vector space algebra or any other space algebra with certain topological properties. Both the input and the output of transformation are assumed to be stochastic. We denote a system with S ={X₁, X₂,…,X_n}, meaning that X₁, X₂,…,X_n are just components of the system; S does not represent a functional notation. As it is the case with a structural model as in (1), X₁, X₂,…,X_n usually correspond to output. Because we are interested in the nature of a system, this output feature of X₁, X₂,…,X_n is often overlooked. Further discussion on systems can be found in the treatment of ITF below. The objective of this final technique is thus to find a partition p{S₁, S₂, …,S_q}, q ≤ n (e.g., a set of exhaustive disjoint subsets S₁, S₂, …,S_q), that provides the same information as S.

Principal Component Analysis

Although the underlying mathematical tool of PCA is not new, its application to statistical problems and its subsequent independent development are attributed to Pearson (1901) and Hotelling (1933). This mathematical tool is known as spectral decomposition of nonsingular (positive- or negative-definite) symmetrical square matrices and is sometimes referred as the Hoteling or Karhunen-Loève transform. Because a variance-covariance of a random vector satisfies these square-symmetry and positive-definiteness properties, spectral decomposition can also apply to the variance-covariance matrix V(X) = Σ = ε(X− ε (X))(X− ε (X))^t of the observable vector X in model (1) or its estimate Σ̂ obtained from observation matrix X in (2) in the usual way:

$$\widehat{\mathbf{\sum }}=\frac{1}{N}(\mathbf{X}-\frac{1}{N}\mathbf{X}l){(\mathbf{X}-\frac{1}{N}\mathbf{X}l)}^t$$

where l is an (N×1) sum vector, i.e., l =(1,1,…,1)^t, and as pointed out above, we have the condition n < N for Σ̂ to be positive definite (Seber, 1984, p. 59). We shall henceforth deal with such positive-definite cases and shall refer to them as standard PCA. The symbol ^ above any character that denotes a parameter stands (conventionally) for the corresponding estimate.

Spectral decomposition of Σ or Σ̂ is then the factoring-out of these matrices such as

$$\mathbf{\sum }=\mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^t\text{and}\widehat{\mathbf{\sum }}=\widehat{\mathbf{Q}}\widehat{\mathbf{\Lambda }}{\widehat{\mathbf{Q}}}^t$$

where Q is an n× n matrix with orthonormal columns Q₁, Q_2,…, Q_n that are basically the eigenvectors of Σ, and Λ is a diagonal matrix with positive diagonal elements λ₁, λ₂,…, λ_n consisting of the corresponding eigenvalues. We also have similar matrices Q̂ and Λ̂ for Σ̂. In view of the orthonormality of Q₁, Q_2,…, Q_n, the following obvious results are obtained:

$$\mathbf{Q}{\mathbf{Q}}^t={\mathbf{Q}}^{\text{t}}\mathbf{Q}=\mathbf{I}=\left[\begin{array}{cccc}1& 0& \dots & 0\\ 0& 1& \dots & 0\\ .& .& \dots & .\\ 0& 0& \dots & 1\end{array}\right]$$ (4)

The same results will obviously hold for its sample counterpart Q̂. The spectral decomposition of Σ can be re-expressed in the better known way as

$$\mathbf{\sum }=\mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^{\text{t}}=\sum _{k=1}^n{\lambda }_k{\mathit{Q}}_k{{\mathit{Q}}_k}^t=\underset{k=1}{\overset{n}{‡"}}{\mathbf{\sum }}_{\text{k}}$$ (5)

The last equality shows that the variance-covariance matrix can also be decomposed as the sum of n matrices Σ_k= λ_k Q_kQ_k^t, (k=1,2,…,n), which are orthogonal to each other so that Σ_iΣ_j= 0 for i ≠ j. Obviously, the matrices Q_k = Q_k Q^t_k are idempotent (orthogonal projection) matrices because

$$\mathbf{Q}{\mathbf{Q}}^t=\underset{k=1}{\overset{n}{‡"}}{\mathbf{Q}}_k=\underset{k=1}{\overset{n}{‡"}}{\mathit{Q}}_k{{\mathit{Q}}^t}_k=\mathbf{I}$$ (6)

The spectral decomposition Σ = QΛQ^t introduces further computational conveniences for inversion and squaring the variance-covariance matrix Σ, i.e.,

$${\mathbf{\sum }}^2=\underset{k=1}{\overset{n}{‡"}}{({\lambda }_k)}^2{\mathit{Q}}_k{{\mathit{Q}}_k}^t\text{and}{\mathbf{\sum }}^{-1}=\underset{k=1}{\overset{n}{‡"}}{({\lambda }_k)}^{-1}{\mathit{Q}}_k{{\mathit{Q}}_k}^t$$

Parallel statements will be valid for the sample counterpart Σ̂ of Σ as well. (For other aspects of spectral decomposition of variance-covariance matrices, see Jolliffe, 2002).

Such decomposition has some implications in statistical applications for the case that n = m. In fact, when Σ or Σ̂ is known, and in consequence when Q or Q̂ can be obtained, we can replace the structure matrix A in (1) with Q or Q̂ to have X = QZ or X = Q̂ Ẑ, depending on the availability Q or Q̂, so that, because n = m, the unobserved Z

$$\mathit{Z}={\mathbf{Q}}^{\text{t}}\mathit{X}\text{or}\widehat{Z}={(\widehat{\mathbf{Q}})}^{\text{t}}\mathit{X}$$

can be obtained. The variance-covariance matrix of Z is now given by matrix Λ, which contains eigenvalues of Σ on the diagonal, i.e.,

$$\begin{array}{l}\text{V}(\mathit{Z})=\mathit{\epsilon }(\mathit{Z}-\mathit{\epsilon }(\mathit{Z})){(\mathit{Z}-\mathit{\epsilon }(\mathit{Z}))}^{\text{t}}={\mathbf{Q}}^{\text{t}}\times \mathit{\epsilon }(\mathit{X}-\mathit{\epsilon }(\mathit{X})){(\mathit{X}-\mathit{\epsilon }(\mathit{X}))}^{\text{t}}\times \mathbf{Q}=\mathbf{\Lambda }\\ =\left[\begin{array}{cccc}{\lambda }_1& 0& \dots & 0\\ 0& {\lambda }_2& \dots & 0\\ .& .& \dots & .\\ 0& 0& \dots & {\lambda }_n\end{array}\right]=\left[\begin{array}{cccc}\text{V}({\text{Z}}_1)& \text{Cov}({\text{Z}}_1,{\text{Z}}_2)& \dots & \text{Cov}({\text{Z}}_1,{\text{Z}}_{\text{n}})\\ \text{Cov}({\text{Z}}_2,{\text{Z}}_1)& \text{V}({\text{Z}}_2)& \dots & \text{Cov}({\text{Z}}_2,{\text{Z}}_{\text{n}})\\ .& .& \dots & .\\ \text{Cov}({\text{Z}}_{\text{n}},{\text{Z}}_1)& \text{Cov}({\text{Z}}_{\text{n}},{\text{Z}}_2)& \dots & \text{V}({\text{Z}}_{\text{n}})\end{array}\right]\end{array}$$

with the implication that the new transformed variables

$${\text{Z}}_1={{\mathit{Q}}^{\mathit{t}}}_{\mathit{1}}\mathit{X},{\text{Z}}_2={{\mathit{Q}}^{\mathit{t}}}_{\mathit{2}}\mathit{X},\dots ,{\text{Z}}_{\text{n}}={{\mathit{Q}}^{\mathit{t}}}_{\mathit{n}}\mathit{X}$$

are uncorrelated and have the respective eigenvalues of V(X) = Σ as their variances, i.e.,

$$\text{V}({\text{Z}}_{\text{i}})={\lambda }_{\text{i}}\text{and}\text{Cov}({\text{Z}}_{\text{i}},{\text{Z}}_{\text{j}})=0,\text{for}\text{all}i,j=1,2,\dots ,\text{n}\text{and}i\ne j$$

Note that sums of the variances of Z₁, Z₂,…, Z_n and X₁, X₂,…, X_n are identical:

$$\text{tr}(\mathbf{\sum })=\sum _{k=1}^n\text{V}(X_k)=\text{tr}(\mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^t)=\text{tr}({\mathbf{Q}}^t\mathbf{Q}\mathbf{\Lambda })=\text{tr}(\mathbf{\Lambda })=\sum _{k=1}^n\text{V}(Z_k)$$

From a geometric point of view, metric properties of both the transformed variables Z₁, Z₂,…, Z_n and the original variables X₁, X₂,…, X_n are identical. For instance, |Z| =(X^tQ^tQX)^1/2= |X|, which means the vectors X and Z have identical lengths. Furthermore, inner products in both spaces are identical: X_i^tX_j = (QZ_i)^t(QZ_j)= Z_i^tQ^tQZ_j = Z_i^tZ_j. Hence, both X_i^tX_j = Z_i^tZ_j and |Z| = |X| imply that the pairs (X_i, X_j) and (Z_i, Z_j) have the same positions with respect to each other in both the original and transformed spaces because X_i^tX_j = cos θ × |X_i|×|X_j| and Z_i^tZ_j = cos ρ×|Z_i|×|Z_j| result in θ = ρ. Similarly, the corresponding areas and volumes are identical in both spaces. Because multiplication from the left of the vector X by an orthogonal matrix Q^t or multiplication of Z by the orthogonal Q yields rotations of these vectors, the original X and the transformed Z are but rotated vectors with all other metric properties being left intact (i.e., they are so-called rigid motions of each other). For that reason, PCA is sometimes presented as a simple rotation. All of the above discussion applies to sample counterparts that result from replacing A with Q̂ except, of course, for relevant statistical inferential issues.

If these eigenvalues are ranked as λ_(n) ≤ λ_(n−1) ≤…≤ λ₍₂₎ ≤ λ₍₁₎ and the corresponding eigenvectors Q_(n), Q_(n−1),…, Q₍₁₎ are ordered accordingly, then the uncorrelated transformed variables Z_(n)= Q^t_(n)X, Z_(n−1) = Q^t_(n−1)X_,…, Z₍₁₎ = Q^t₍₁₎X can be ordered in terms of the magnitude of their variances. The same ordering also holds for the factorized matrices

$${\mathbf{\sum }}_{(\text{k})}={\lambda }_{(\text{k})}{\mathbf{Q}}_{(k)}{{\mathbf{Q}}_{(k)}}^t$$

which can be ordered in a decreasing fashion for k=1,2,…,n

$$\mathbf{\sum }={\mathbf{\sum }}_{(1)}+{\mathbf{\sum }}_{(2)}+\dots +{\mathbf{\sum }}_{(\text{n}-1)}+{\mathbf{\sum }}_{(\text{n})}$$

Practically, this means that some reduction of dimension can be obtained on the basis of the magnitude of decomposed variances by cutting out small-ordered ones as negligible. For instance, the number of significant Z_(i)’s can be restricted to the first k variables, k < n, satisfying ${\displaystyle \sum _{i=1}^k}{\lambda }_{(i)}=\delta$ for some predetermined δ level of variance. There are some inferential issues on determination of the number k of significant variables (Anderson, 1984, pp. 468–479).

The decomposition in (5) is sometimes referred to as eigen decomposition to distinguish it from other decompositions such as Cholesky decomposition, etc. (Anderson, 1984, p. 586; Press et. al., 1992). When matrices are defined over complex numbers, orthogonal matrices become unitary matrices and their transposes naturally are conjugate transposes of these matrices. Because the matrix Σ is symmetric, resulting eigenvalues will always be real.

The formal setup of the PCA analysis is based on a structural model such as the model (1) above. Therefore, its validity depends on the validity of the model as compared with the real phenomenon that it models. For instance, data that do not involve a location parameter and/or a scale factor are hardly suitable for a framework like (1). Also, as an alternative to a complex unmanageable system based on X₁, X₂,…, X_n, the analysis aims at obtaining some system based on variables Z₁, Z₂,…, Z_k that are smaller in number (k < n), simpler in nature, and bear the same information (eigenvalues). However, this is achieved at the expense of orthogonality and/or un-correlatedness restrictions imposed on Z₁, Z₂,…, Z_k. These impositions may not be realistic for some applications areas such as biological systems. Application of the technique is restricted to phenomena with distributions tracing non-spherical contours in their domains because little will be gained in the spherical case. Finally, the mathematical tool on which standard PCA is based applies to nonsingular decompositions, which requires that n = m in the model (1). Most real-life phenomena, however, seem to present a singular structure. The last restriction is alleviated by the next technique in the sequel: SVD. PCA does not seem to have lost its attractiveness despite prevailing high-dimensionality problems observed recently (Hastie et al., 2000). It is interesting further to note that PCA can be used for such a theoretical issue as construction of bivariate distributions (Gurrera, 2005). The use of Q̂ for A invites further inferential issues such as sampling distributions of eigenvalues and eigenvectors of Σ̂ (Anderson, 1984, pp.465–468, pp. 473–477, Chapter 13; Seber, 1984, pp. 35–38; Joliffe, 2002; Kendall, 1975, Chapter 2; Johnson and Wichern, 2002, Chapter 8).

Singular Value Decomposition

SVD is based on a matrix factorization technique that dates from the 19th century and was developed by several mathematicians in linear algebra and differential geometry (Stewart, 1993; Eckart. and Young, 1936). The technique warrants factorization of any real matrix in a way similar to spectral decomposition of square matrices. As such, given an (n×m) rectangular matrix C, SVD is actually a spectral decomposition of symmetric square positive semi-definite matrices C^tC and CC^t. For any (n×m) rectangular matrix C, the products C^tC and CC^t are known to be symmetric and positive semi-definite (Scheffe, 1959, p. 399) with real non-negative eigenvalues, and these products are thus suitable for spectral decomposition explained above in connection with PCA. Assume hence that an (n×m) matrix C is factored out the way that the matrix Σ is decomposed as in (5) above with Q now being represented by U when it is positioned on the left of the diagonal matrix and Q^t by V when it is on the right:

$$\mathbf{C}={\mathbf{UDV}}^{\text{t}}=\sum _{i=1}^{min\{n,m\}}{\lambda }_i{\mathit{U}}_{\text{i}}{{\mathit{V}}^{\text{t}}}_{\text{i}}$$ (7)

where U_i ’s and V_i ’s are orthonormal columns of U and V, respectively, and D is diagonal with real nonnegative entries λ_i’s. The factorization (7) is sometimes interpreted as C being orthogonally (unitarily) equivalent or similar to the diagonal matrix D. There are various modes of SVD for the dimensions of the matrices involved. For instance, (i) the matrix U can be (n×n) with n orthonormal (unitary) columns U_i, called left singular (eigen array) vectors, and V is an (m×m) matrix with m orthonormal columns V_i, called right singular vectors (eigen genes in the biological example considered above) such that

$${\mathbf{U}}^{\text{t}}\mathbf{U}={\mathbf{I}}_{\text{n}}\text{and}{\mathbf{V}}^{\mathbf{t}}\mathbf{V}={\mathbf{I}}_{\text{m}}$$

D is an (n×r), r = min{n,m}, diagonal matrix with positive diagonal entries called singular values (eigen expressions) of C. (ii) A second mode corresponds to the case where the dimensions of the matrix U are (n×m) with n orthonormal left singular vectors and the (m×m) matrix V itself is orthogonal with m right singular vectors, such that

$${\mathbf{U}}^{\text{t}}\mathbf{U}={\mathbf{V}}^{\mathbf{t}}\mathbf{V}={\mathbf{I}}_{\text{m}}$$

Hence, D becomes a (m×m) diagonal matrix with non-negative real singular values of C on its diagonal. The thin, compact, and truncated types of SVD are not discussed here because of space considerations.

To explain technicalities in SVD, we denote the real non-negative eigenvalues of the matrices C^tC and CC^t with κ₁, κ₂, …,κ_r with r being min{n,m}. Given the decomposition C = UDV^t as in (7) with dimensions given for instance as in (i) above, we obtain

$${\mathbf{C}}^{\text{t}}\mathbf{C}=\mathbf{VD}{\mathbf{U}}^{\text{t}}\mathbf{UD}{\mathbf{V}}^{\text{t}}=\mathbf{V}{\mathbf{D}}^2{\mathbf{V}}^{\text{t}}$$

from which, by multiplication with V on the right, we have

$${\mathbf{C}}^{\text{t}}\mathbf{C}\mathbf{V}=\mathbf{V}{\mathbf{D}}^2{\mathbf{V}}^{\text{t}}\mathbf{V}=\mathbf{V}{\mathbf{D}}^2$$ (8)

Setting G= C^tC and noting that V= [V₁, V₂, …, V_m] and D² = diag (κ₁, κ₂, …, κ_r), (8) yields

$$\mathbf{G}{\mathit{V}}_i={\kappa }_{\text{i}}{\mathit{V}}_{\text{i}},i=\text{1},\text{2},\dots ,r$$

which suggests that eigenvectors V_i of the matrix G = C^tC are the right singular vectors of the matrix G, and the singular values of C are given by absolute square roots of the corresponding eigenvalues of G = C^tC. When these non-negative singular values are ranked in terms of their descending magnitudes, i.e., $\sqrt{{\kappa }_{(r)}}\le \sqrt{{\kappa }_{(r-1)}}!\ddot{\text{U}}\cdots !\ddot{\text{U}}\sqrt{{\kappa }_{(1)}}$, then corresponding singular vectors can also be ordered in descending degree of importance such as ,…,U₍₁₎,…, U_(r−1), U_(r) and V₍₁₎,…,V_(r−1), V_(r). For clarity, matrix D can be rearranged, i.e., for n < m and m<n, giving respectively

$$\mathbf{D}=\left[\begin{array}{cccccccc}\sqrt{{\kappa }_{(1)}}& 0& \dots & 0& ⋮& 0& \dots & 0\\ 0& \sqrt{{\kappa }_{(2)}}& \dots & 0& ⋮& 0& \dots & 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& \dots & \sqrt{{\kappa }_{(\text{n})}}& ⋮& 0& \dots & 0\end{array}\right]\text{and}\mathbf{D}=\left[\begin{array}{cccc}\sqrt{{\kappa }_{(1)}}& 0& \dots & 0\\ 0& \sqrt{{\kappa }_{(2)}}& \dots & 0\\ ⋮& ⋮& ⋮& ⋮\\ 0& 0& \dots & \sqrt{{\kappa }_{(\text{n})}}\\ \dots & \dots & \dots & \dots \\ 0& 0& \dots & 0\\ ⋮& ⋮& ⋮& ⋮\\ 0& 0& \dots & 0\end{array}\right]$$

Note also that (7) can also be re-expressed as

$$\mathbf{C}={\mathbf{UDV}}^{\text{t}}=\sum _{i=1}^{min\{n,m\}}\sqrt{{\kappa }_{(i)}}{\mathit{U}}_{(\text{i})}{\mathit{V}}_{(\text{i})}^{\text{t}}=\sum _{i=1}^{min\{n,m\}}{\mathbf{C}}_{(\text{i})},{\mathbf{C}}_{(\text{i})}=\sqrt{{\kappa }_{(i)}}{\mathit{U}}_{(\text{i})}{\mathbf{V}}_{(\text{i})}^{\text{t}}$$ (9)

with C_(i) C^t_(j) = 0 for i ≠ j, i.e., the matrices C_(i) and C_(j) are orthogonal and hence matrix C can be decomposed in an additive way as well. The matrices C_(i) in (9) are uncorrelated “modes” of the original matrix C. Because of the ordering of singular values, the modes (C_(i)’s) in (9) are also ordered, so that C_(i)’s corresponding to negligible (small) singular values are sometimes loosely defined as noise and can thus be ignored in the analysis.

Simple arithmetic reveals, on the other hand, that the eigenvalues and eigenvectors of the matrix F= CC^t will now be κ₁, κ₂,…, κ_m and U₁,U₂, ,U_m, respectively. Accordingly, by definition of these values and vectors, we will have

$$\mathbf{F}{\mathit{U}}_i={\kappa }_i{\mathit{U}}_i,\text{i}=1,2,\dots ,\text{m}$$

The decomposition will then be

$$\mathbf{C}={\mathbf{UDV}}^{\text{t}}=\underset{i=1}{\overset{m}{‡"}}\sqrt{{\kappa }_{(\text{i})}}{\mathit{U}}_{(\text{i})}{\mathit{V}}_{(\text{i})}^{\text{t}}=\underset{i=1}{\overset{m}{‡"}}{\mathbf{Y}}_{(i)},{\mathbf{Y}}_{(\text{i})}=\sqrt{{\kappa }_{(\text{i})}}{\mathit{U}}_{(\text{i})}{\mathit{V}}_{(\text{i})}^{\text{t}}$$ (9)

Note that the matrices Y_(i) of the decomposition (9) are orthogonal in the sense that for all i ≠ j, we have

$${\mathbf{Y}}_{(\text{i})}{{\mathbf{Y}}^{\text{t}}}_{(\text{j})}=\sqrt{{\mathit{\kappa }}_i{\mathit{\kappa }}_j}{\mathit{U}}_{(\text{i})}{\mathit{V}}_{(\text{i})}^{\text{t}}{\mathit{V}}_{(\text{j})}{\mathit{U}}_{(\text{j})}^{\mathit{t}}=\mathbf{0}$$

Furthermore, as it is the case with spectral decomposition in PCA, it is possible to obtain a pseudo (Monroe-Penrose) inverse C⁻ of C as

$${\mathbf{C}}^{-}=\mathbf{U}{\mathbf{D}}^{-}{\mathbf{V}}^{\text{t}}$$

where D⁻ is the corresponding pseudoinverse of D. Because D is a diagonal matrix, its pseudoinverse will be also diagonal and will correspond thus to its transposition. So that, for the matrix D given earlier, i.e.,

$$\mathbf{D}=\left[\begin{array}{cccc}\sqrt{{\kappa }_{(1)}}& 0& \dots & 0\\ 0& \sqrt{{\kappa }_{(2)}}& \dots & 0\\ ⋮& ⋮& ⋮& ⋮\\ 0& 0& \dots & \sqrt{{\kappa }_{(\text{n})}}\\ \dots & \dots & \dots & \dots \\ 0& 0& \dots & 0\\ ⋮& ⋮& ⋮& ⋮\\ 0& 0& \dots & 0\end{array}\right]$$

the generalized inverse looks like

$${\mathbf{D}}^{-}=\left[\begin{array}{cccccccc}{a}_{(1)}& 0& \dots & 0& 0& 0& \dots & 0\\ 0& a_{(2)}& \dots & 0& 0& 0& \dots & 0\\ .⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ 0& 0& \cdots & a_{(n)}& 0& 0& \dots & 0\end{array}\right]=[{\mathbf{D}}^{-\mathbf{1}},\mathbf{0}]$$

where $a_{(i)}=\frac{1}{\sqrt{{\kappa }_{(i)}}}$, i = 1,2,…,n.

This much SVD algebra is suffient for this brief review. There are various applications of SVD in different areas of statistical analysis, but its main use is in general regression analyses yielded by

$$\underset{\mathbf{A},\mathbf{Z}}{min}{\Vert \mathbf{X}-\mathbf{AZ}\Vert }^2$$

where the noiseless version of the model (3) above is considered and the norm is the Frobenius (Euclidean) matrix norm defined for any rectangular matrix M as

$$\Vert \mathbf{M}\Vert =\sqrt{\underset{i}{‡"}\underset{j}{‡"}{\mid {\text{m}}_{\text{ij}}\mid }^2}\mid =\sqrt{\mathit{trace}({\mathbf{M}}^t\mathbf{M})}$$

This particular use shows how SVD was first used (Lawson and Hanson, 1995).

Another use of SVD in the sense of three-matrix factorization as in (7) relates to decomposition of the observation matrix X and is usually observed in biology, where the matrix U is used for bioassay, elements of the matrix D are called singular values, and elements of the matrix V are interpreted as eigen genes. Matrix X is broken thus down to orthogonal summands, i.e.,

$$\mathbf{X}={\mathbf{UDV}}^{\text{t}}=\sum _{i=1}{d}_{(i)}{\mathit{U}}_{(i)}{{\mathit{V}}_{(i)}}^{\text{t}}=\sum _{i=1}{\mathbf{X}}_{(i)},{\mathbf{X}}_{(i)}=d_i{\mathbf{U}}_{(i)}{{\mathbf{V}}_{(i)}}^t$$

Matrix U is thus functionally identical to matrix A of the structural models in (1) and (2).

One of the main uses of SVD in the current context is for decomposition of covariance matrices. Because the covariance matrix of two differing vectors of distinct dimensions is rectangular, it is decomposable in the sence of SVD. Let a pair of vectors such as the (n×1) vector X and the (m×1) vector Y be given. Their covariance

$$\text{Cov}(\mathit{X},\mathit{Y})=\mathbf{M}=\mathit{\epsilon }(\mathit{X}-\mathit{\epsilon }(\mathit{X})){(\mathit{Y}-\mathit{\epsilon }(\mathit{Y}))}^{\text{t}}$$

is an (n×m) rectangular matrix and is therefore decomposable singularly as

$$\mathbf{M}={\mathbf{UDV}}^{\text{t}}$$

Consequently, as in PCA, the variance-covariance matrix of any transformed vector Z = U^tX will then be

$$\mathit{\epsilon }(\mathit{Z}-\mathit{\epsilon }(\mathit{Z})){(\mathit{Z}-\mathit{\epsilon }(\mathit{Z}))}^{\text{t}}={\mathbf{U}}^{\text{t}}\text{V}(\mathit{X})\mathbf{U}={\mathbf{U}}^{\text{t}}(\mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^{\text{t}})\mathbf{U}=\mathbf{\Phi }\mathbf{\Lambda }{\mathbf{\Phi }}^{\text{t}}={\mathbf{\Lambda }}^{\ast }$$

where

$${\mathbf{\Lambda }}^{\ast }=\left[\begin{array}{cccc}{\lambda }_{(1)}& 0& \dots & 0\\ 0& {\lambda }_{(2)}& \dots & 0\\ ⋮& ⋮& \dots & ⋮\\ 0& 0& \dots & {\lambda }_{(\text{r})}\end{array}\right]\text{and}\mathbf{\Phi }={\mathbf{U}}^{\text{t}}\mathbf{Q}$$

with r = min {n,m}. We then use the spectral decomposition QΛQ^t for V(X), and in the last equality, we utilize the fact that multiplication of two orthogonal matrices such as U^t and Q yields again an (m×n) matrix Φ with orthonormal columns:

$$\mathbf{\Phi }={\mathbf{U}}^{\text{t}}\mathbf{Q}=\left(\begin{array}{c}{U^t}_{(1)}\\ {U^t}_{(2)}\\ ⋮\\ {U^t}_{(m)}\end{array}\right)(Q_{(1)},Q_{(2)},\cdots ,Q_{(n)})=\left[\begin{array}{cccc}{U^t}_{(1)}{Q}_{(1)}& {U^t}_{(1)}{Q}_{(2)}& \dots & {U^t}_{(1)}{Q}_{(n)}\\ {U^t}_{(2)}{Q}_{(1)}& {U^t}_{(2)}{Q}_{(2)}& \dots & {U^t}_{(2)}{Q}_{(n)}\\ ⋮& ⋮& ⋮& ⋮\\ {U^t}_{(m)}{Q}_{(1)}& {U^t}_{(m)}{Q}_{(2)}& \dots & {U^t}_{(m)}{Q}_{(n)}\end{array}\right]$$

so that a typical element of ΦΛΦ^t becomes

$${{\mathit{U}}^{\text{t}}}_{(\text{i})}[\sum _{k=1}^n{\lambda }_{(k)}{\mathit{Q}}_{(\text{k})}{{\mathit{Q}}^{\text{t}}}_{(\text{k})}]{\mathit{U}}_{(\text{j})}=\{\begin{array}{cc}{\lambda }_{(k)},& i=j=k\\ 0,& i\ne j.\end{array}$$

The latter conclusion is obviously identical to the result that can be obtained from PCA.

In sum, SVD is more general than PCA because it is applicable to cases where PCA is applied but the converse is not valid. Furthermore, as mentioned earlier, an appropriate type of SVD (thin, compact, and truncated) can be chosen for a problem. Like PCA, SVD is also used for data reduction. As is the case with PCA, the application of SVD is restricted to phenomena that have statistical distributions with non-spherical contours. All in all, SVD has the same drawbacks as PCA because it is based on the same structural approach, which may be restrictive in some application areas. Also, the orthogonality restriction imposed by the analysis may not be suitable for some types of data. An interesting illustrative application is in Chung and Seabrook (2004). The next approach that we discuss goes to a further extreme in the last direction.

Independent Component Analysis (Blind Source Separation)

ICA seems to have been proposed by several authors from various disciplines in the last quarter of a century (Comon, 1994). However, the main areas of origin are signal processing and neural network analyses. ICA is also known as blind (myopic) source separation. The qualifiers “blind” or “myopic” are used to point out the property that the sole observable of the system is its output, i.e., the vector X of the model (1). “Independence” is affixed to the name, because of technical reasons concerning input, i.e., the vector Z of the model can satisfy certain contrast functions in signal processing when its coordinates are independent. The name “independent component analysis” seems to have been suggested by Jutten and Herault (1991) with respect to “principal component analysis”; they also refer to it as “blind source separation”.

In model (1) and/or (2) the variables X₁, X_2,…, X_n represent random observable variables and the variables Z₁, Z_2,…, Z_m represent unobservable (latent) variables with A being a mixing matrix. When the matrix A is orthogonal as in PCA and SVD, the variables Z₁, Z_2,…, Z_m become orthogonal transformations (projections) of the variables X₁, X_2,…, X_n. The orthogonality property results in mutual uncorrelatedness of Z₁, Z_2,…, Z_m (see covarience matrix Λ above). Uncorrelatedness does not imply independence, which is obviously a stronger requirement than orthogonality. In terms of the method-of-moments terminology, orthogonality relates only to second moments (or cumulants) whereas independence also involves higher moments (or cumulants). ICA is based on the assumption that the generating sources for the variables X₁, X_2,…, X_n are independent. The joint distribution of X₁, X_2,…, X_n may be known or unknown. The objective of the analysis is to determine an unknown A and the corresponding unobservable vector Z=(Z₁, Z_2,…, Z_m)^t through some observations on X = (X₁, X_2,…, X_n)^t.

Gaussian distributions are not appropriate for that objective, because, A cannot be identified and is therefore not estimable by these distributions. In fact, when X and Y are two vectors with each being an orthogonal transformation of the other, their metrics |X| and |Y| will thus be identical, i.e., |X| = |Y|. When both X and Y are assumed further to be Gaussian distributions with identical means and variances (for instance, when they have zero mean vectors and when their variances are equal to identity matrices of the same dimension), their densities will look like

$$k\mathit{exp}\{-\frac{1}{2}\mid \mathit{X}{\mid }^2\}=k\mathit{exp}\{-\frac{1}{2}\mid \mathit{Y}{\mid }^2\}$$

Setting X = AZ and Y = AZ as in the model (1),

$$k\mathit{exp}\{-\frac{1}{2}\mid \mathbf{A}\mathit{Z}{\mid }^2\}=k\mathit{exp}\{-\frac{1}{2}\mid \mathbf{A}\mathit{Z}{\mid }^2\}$$

which shows that neither A nor Z can be identified by these densities.

Furthermore, Gaussian distributions are proved to have the largest entropy among the distributions of random variables with identical means and variances (Papoulis and Pillai, 2002, p.669). If we set H(X) for the entropy of a random vector X with coordinates X_i’s and H(S) stands for a system S with components X_i’s, the entropy corresponding to the whole vector X or to the system S is then given as

$$H(\mathit{X})=\left\{\begin{array}{c}\underset{i=1}{-‡"}P(X=x_i)\times logP(X=x_i)\\ -f(x)logf(y)dx\end{array}\right\}=H(S)$$

where P stands for the joint probability density function (pdf) for the discrete X, f denotes the joint pdf in the continuous case, and the logarithm is with respect to 2 or e base. The concept of entropy discussed here corresponds to Schroedinger’s (1944, p.73) concept of negative entropy. As such, it is an information measure. Thus, if H(X_Gaus) stands for the entropy of a random vector X_Gaus, which has a Gaussian distribution, and H(X) denotes the entropy of a distribution of non-Gaussian random variables represented by the vector X, then the non-negative magnitude

$$J(\mathit{X})=H({\mathit{X}}_{\mathit{Gaus}})-H(\mathit{X})$$

yields the discrepancy of entropies between the Gaussian-distributed X_Gaus and any other X supposed to be different from X_Gaus. Accordingly, the larger J(X) is the more different X_Gaus will be from X. One method for checking non-normality of the distribution involved consists of maximizing J(X) = J((X₁, X₂, …, X_n). Obviously, J(X) is a variation of negentropy (not to be confused with Schroedinger’s concept), which is shown to be invariant under linear transformations. The negentropy function J(X) can be considered as the initial technical process for estimating matrix A in the model (1) on the basis of joint distribution of X₁, X_2,…, X_n. However, if this estimation requires prior knowledge on the relevant pdf or its estimate, then this technique will be computationally difficult.

Before matrix A is estimated, statistically independent components of or statistically independent sources for the rows (or columns) of the matrix X in (1) must be checked (Lee et. al., 1998). A method used for that purpose is based on minimization of the mutual information function of Papoulis and Pillai (2002, p.647) or the transmission function of Conant (1968, p.11) defined as

$$T(\mathit{X})=\underset{i=1}{\overset{n}{‡"}}H(X_i)-H(X_1,X_2,\dots ,X_n)=\underset{i=1}{\overset{n}{‡"}}H(X_i)-H(\mathit{X})$$ (10)

where H(X_i) is the entropy of each individual random variable X_i of an n-dimensional column vector X = (X₁, X₂,…,X_n)^t. T(X) is a non-negative quantity indicating discrepancy between entropies of the dependence case, i.e., H(X₁, X₂,…,X_n), and the n independence case, i.e., $\underset{i=1}{\overset{n}{‡"}}H(X_i)$; the latter is always larger than the former (Papoulis and Pillai, 2002, p.646). (The proof given by these authors corresponds to the two-subsystem [two-variable] case but can be easily extended to the n-variable case as well.) The larger the quantity T(X) in (10), the more dependent X₁, X₂,…,X_n become, in which case X₁, X₂,…,X_n are not appropriate for estimating matrix A. Obviously, to be able to minimize T(X), marginal and joint distributions of X₁, X₂,…,X_n must be known and, as previously remarked, estimation of pdf values is difficult. Methodological developments by Conant (1968 and 1972) allow all computations involved in T(X) to be easily based on empirical frequencies.

The essential method for estimating matrix A in (1) is a maximum likelihood technique that is applicable when the relevant densities are known (Hyvarinen and Oja, 2000; Comon, 1994; Hyvarinen et al., 2001). Before the application of this method, to be on the safer side, the required non-normality of the distribution involved and the necessary independence conditions used for estimation must be checked through the two methods previously discussed.

In sum, ICA has a well-founded statistical basis. The analysis displays the same drawbacks as PCA and SVD because its foundation is a structural approach that may not fit the data of some areas of the application. ICA evidently eliminates the orthogonality requirement of PCA and SVD by introducing the independence condition, but the latter actually is stricter than the former (for an illustrative comparative review of the above three techniques, see, Srinivasan et. Al.). Application of this technique seems to be restricted to non-Gaussian distributions. All three previous decomposition techniques are designed to choose matrix A of model (1) from among the matrices that satisfy orthogonality and independence properties imposed on real data. Such matrices may not be appropriate for biological data. We have thus another technique as proposed by the decomposition approach: NCA.

Network Component Analysis

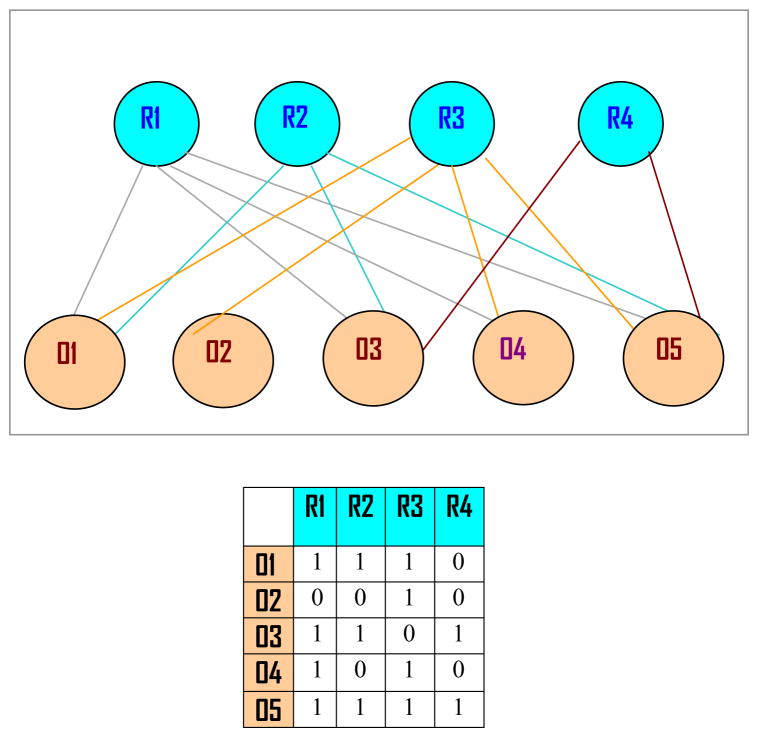
Some recent discussions (Liao et. al., 2003) concerning PCA, SVD, and ICA note that the hypothesized relationship between Z and X (assumed to exist by these three techniques for the models (1) or (3)) imposes some statistical constraints on data; for example, orthogonality (orthonormality) and independence of unobservable variables are not warranted in some applications, such as biological experimentation. These methods obtain a (random) value of matrix A from a class of all real (complex)-valued matrices satisfying the hypothesized relationship. In an actual case, X is maintained to be produced by Z according to a bipartite network system between two distinct groups of phenomena such as phenotype and genotype (Figure 1).

FIGURE 1. A Pictorial Example for Network Design.

Depicted in the upper part is a bipartite network between four regulatory agents (gene knock-outs, drugs etc.) denoted by R1 through R4 and five outputs (e.g., growths of certain organisms) designated with O1 through O5. Connections between regulatory nodes and output nodes are shown as usual. The rectangular table just underneath the network represents the connectivity matrix B with columns corresponding to regulatory agents and rows to outputs. The regulatory matrix C is not shown in the picture. When there are no connections between output nodes (rows) and regulatory nodes (columns), the corresponding cells contain zero. Obviously, all other cells are composed of ones for the network shown here.

The (n×N) observation matrix X on the left side of (3) can be reconstructed as

$$\mathbf{X}=\mathbf{BC}$$ (11)

where the (m × N) matrix C, which replaces matrix Z in (3) above and is now called ‘regularity matrix’, consists of N samples of m signal inputs (genotypes) with the condition m < N. The (n × m) connectivity matrix B, which replaces matrix A in (3) above, indicates the number of ways by which input signals (genotypes) are connected to signal outputs (phenotypes) in X so that each input may or may not be connected to each output. Thus, a typical entry (b_ij) of B shows how many times the j^th signal input is connected to the i^th output; it is zero when there is no connectivity between the relevant inputs and outputs. Regularity matrix C is assumed to be of full row rank (i.e., r(C) = m); connectivity matrix B is of full column rank (i.e., r(B) = m) with each column of B containing at at least (m − 1) zeros. By (3) and (10), we have

$$\mathbf{X}=\mathbf{AZ}=\mathbf{BC}$$ (12)

As follows from (12), the statistical assumptions concerning orthogonality or independence on the constituent factors Z work through the regularity matrix C on the right side of (11) in such a way as to make C comply with these orthogonality and/or independence criteria. The decompositions corresponding to the right side of (11) are unique up to a nonsingular transformation P such as A^*=AP; Z^*=P⁻¹Z, B^*=BP and C^*= P⁻¹C, which yields

$$\mathbf{X}={\mathbf{A}}^{\ast }{\mathbf{Z}}^{\ast }=\mathbf{AP}{\mathbf{P}}^{-1}\mathbf{Z}=\mathbf{AZ}\text{and}{\mathbf{B}}^{\ast }{\mathbf{C}}^{\ast }=\mathbf{BP}{\mathbf{P}}^{-1}\mathbf{C}=\mathbf{BC}=\mathbf{X}$$

As is proven in Liao et al. (2003, Appendix 1), when on the conditions C is of full row rank, the rank of B equals the number of its columns, and each column of B contains at least (m − 1) zeros, the transformation matrix P can only be a diagonal matrix so that the decomposition X = BC is unique up to a diagonal scalar. This ensures identifiability of a system up to diagonal scalar in the sense that, corresponding to certain regularity C, only one connectivity (network) matrix B produces the observations X.

From a computational standpoint, the matrix decomposition BC of X is obtained through an iterative optimization (minimization with respect to matrices B and C), an algorithm applied to the square of Frobenius (Euclidean) matrix norm mentioned earlier, e.g.,

$$\Vert \mathbf{M}\Vert =\sqrt{\underset{i}{‡"}\underset{j}{‡"}{\mid {\text{m}}_{\text{ij}}\mid }^2}\mid$$

of the rectangular matrix M = X − BC. Hence, B and C are estimated from X by using a two-step least-squares algorithm using the objective function

$$\underset{\mathbf{BC}}{min}{\Vert \mathbf{X}-\mathbf{BC}\Vert }^2$$

subject to the side condition that the connectivity pattern B belongs to a manifold of matrices with a certain pattern (e.g., entries representing connectivity are arbitrary non-zero natural numbers initially and non-connectivity is represented by zero). The detailed algorithm of estimation itself is summarized and can be found in Liao et al. (2003, Appendix 2).

To sum up, NCA has fundamentally the same foundation as the previous analyses: It has a structural and therefore a parametric approach, the only difference being the estimate of matrix A from a narrower class of matrices satisfying a certain network configuration. It therefore displays the same drawbacks as PCA, SVD, and ICA.

Decomposition by Information Transfer

As it is the case with the previous approaches, the idea behind the decomposition by ITF is to find a much simpler system than a given system, simplicity being defined as lack of complexity of systems (especially for hierarchical systems that are composed of some layers of subsystems). Unlike PCA, SVD, ICA, and NCA, ITF does not specify a structural model and analysis is not carried out in terms of such a model. Ignoring the specific natures of components that make up a system, a measure of complexity of a system can be related to the earlier-defined entropy H(S) and transmission T(S) functions for a system S = {X₁, X₂,…,X_n} with n ordered components X₁, X₂,…,X_n.. For technical reasons, S is not necessarily a vector with coordinates X₁, X₂,…,X_n but represents a system with ordered components in the sense that, unless stated otherwise, all permutations of {X₁, X₂,…,X_n} stand for distinct systems. Thus, because complexity is related to information (actually, a lack of information), the following non-negative magnitude, which is in fact a measure of information,

$$\underset{i=1}{\overset{n}{‡"}}H(X_i)$$

can be used to measure lack of complexity of a system when n individuals (components) are taken one by one and their inherent potentials (measured in terms of entropy) are added up arithmetically. The underlying assumption for such measure is that individuals act independently and do not exhibit a coherent body. Similarly,

$$H(X_1,X_2,\dots ,X_n)=H(S)$$

is also a measure of information (lack of complexity) when interactive behavior of n components is taken into account, i.e., when individuals form a coherent body of a system.

The transfer function T(X) already defined as a difference of the two foregoing measures of information in (10) is now designated by T(S, p) and will be defined in terms of the components of S:

$$T(S,\mathit{P})=\underset{i=1}{\overset{n}{‡"}}H(X_i)-H(X_1,X_2,\dots ,X_n)$$ (13)

This obviously is a non-negative measure of change in information between a system composed of a random collection of n independent individuals and a system composed of an integrated body of these n individuals. In a way, the transfer function indicates useable information that exists in components for the system. The larger the magnitude, the more remote the system S will be from the chaotic case of n components being unable to form a system. The symbol p, expressed precisely as p {X₁, X₂,…,X_n}, represents a partition of S. The notation T(S, p) hence emphasizes that information transformation depends on the given system S as well as the specific partition p of S under consideration. Roughly, the contribution of p to T(S, p) n corresponds to the sum ${\displaystyle \underset{i=1}{\overset{n}{‡"}}}H(X_i)$ on the right side of (13), and that of the S-part is given by H(X₁, X₂,…,X_n) on the same side of the equation. Because we now are dealing with a system rather than the vector X, we now bring in the system symbol S into (10) to have the notation in (13). By a partition p {S₁, S₂,…, S_q} of S, we mean a collection of disjoint subsets S₁, S₂,…, S_q, (q ≤ n) of S that exhaust S, i.e., $S={\displaystyle \underset{i=1}{\overset{q}{\cup }}}{S}_i$. The simplest partition is p {X₁, X₂,…, X_n} as in (13), where q = n with S_i ={X_i} and is called the element partition. A trivial partition is p {S}, i.e., p {S}=S with q=1 whereas numerous partitions correspond to 1< q < n, the well known of which is the dichotomous partition p {S₁,S₂}. With partition notation p {S₁, S₂,…, S_q}, the ITF becomes

$$T(S,\mathit{P})=T(S_1,S_2,\dots ,S_q,\mathit{P})=\underset{i=1}{\overset{q}{‡"}}H(S_i)-H(S_1,S_2,\dots ,S_q)$$ (14)

where H(S₁,S₂,…,S_q) is equal to H(X₁, X₂,…,X_n) because ${\displaystyle \underset{i=1}{\overset{q}{\cup }}}{S}_i=S=\{X_1,X_2,\dots ,X_n\}$ and H(S₁), H(S₂), …, H(S_q) are the corresponding entropies of the individual elements of the partition. Equation (14) can be interpreted as unused information in p {S₁, S₂,…, S_q} for the system S. As noted earlier, (10) and its variations as in (13) and (14) are specifically discussed in Papoulis and Pillai (2002) and Conant (1968, 1972). For applications in classical statistical inference, a parallel information theoretic approach is adopted by Kullback (1959, Chapters 1 through 3).

To emphasize the interaction between these two sets when a dichotomous partition p {S₁, S₂} and their transmission is involved, the function T is sometimes indexed by the subscript B, i.e.,

$$T_B(S_1,S_{2,}\mathit{P})=H(S_1)+H(S_2)-H(S_1,S_2)=T(S_1,S_2,\mathit{P})$$

Similarly, to emphasize interaction within the system S ={X₁, X₂,…,X_n} with an element partition p, the magnitude T(S, p) can also be tagged as T_W(S, p), where the subscript W stands for the interaction within the system S. Because a coherent system can only be composed of a series system, a parallel system, or a mixture of both (Barlow and Prochan, 1975, Chapter 2), then the probability corresponding to the partition can range from the probability of the former, i.e., P(S₁, S₂) = P(S₁) × P(S₂) with its entropy being H(S₁,S₂) = H(S₁) + H(S₂), to the probability of the latter, i.e., P(S₁, S₂) = min{P(S₁), P(S₂)} with the corresponding entropy of the latter being H(S₁, S₂) = min{H(S₁), H(S₂)}. We have thus a maximum value for T(S₁,S₂, p) that is obtained when H(S₁, S₂) = min{H(S₁), H(S₂)} and the minimum value of T_B(S₁,S₂, p) is reached when H(S₁,S₂) = H(S₁) + H(S₂), in which case T_B(S₁,S₂, p) = 0. The minimum value of the transfer function indicates that S₁ and S₂ are independent in statistical terms. If we let T^U_B(S₁:S₂) stand for the maximal value of T_B(S₁,S₂, p),

$$0\le T_{12}=\frac{T_B(S_1,S_2,\mathit{P})}{{T^U}_B(S_1,S_2)}\le 1$$ (15)

For all systems partitioned as S₁ and S₂ and having joint distributions with fixed marginal distributions for S₁ and S₂ (i.e., systems with the given marginal distributions of S₁ and S₂), T₁₂ will be closer to one as the underlying sub-systems S₁ and S₂ get more and more integrated to form a whole system and will approach to zero as S₁ and S₂ become disintegrated to form separate systems. T₁₂ is actually some version of the absolute value of the usual correlation coefficient when S₁ and S₂ are singletons like S = {X₁}and S₂ = {X₂}. Hence, T₁₂ = 0 means non-relatedness of subsets S₁ and S₂, and T₁₂ = 1 implies that S₁ and S₂ depend completely on each other. This latter aspect of transfer functions is amply emphasized in Conant (1968, 1972).

For comparison of the complexities of pairs of subsystems, Conant (1968) introduced an additional instrumental index called the interaction measure:

$$Q_{S_i}(S_j)=T_{S_i}(S_j)-T(S_j,\mathit{P})i\ne j=1,2,\dots ,q$$ (16)

which is useful in detecting a change in the complexity of S_j when it is integrated into the subsystem S_i, so that the interdependence among the components of S_j are evaluated against their joint conditional interdependence, given the integration of the elements of S_i. T_Si (S _j, p) in (16) denotes the conditional transmission over S_j ={X_j1, X_j2,…, X_jr} and given the interrelatedness of the elements of S_i, and is defined as

$$T_{S_i}(S_j)=\underset{i=j_1}{\overset{j_r}{‡"}}{H}_{S_i}(X_i)-H_{S_i}(X_{j_1},X_{j_2},\dots ,X_{j_r})$$

where

$$H_{S_i}(S_j)=H(S_i,S_j)-H(S_j)$$

Unlike the T(.) transfer functions that are always positive, the interaction measure Q(.) in (16) can be negative (i.e., the sets S_i and S_j interact negatively), positive (i.e., S_i and S_j interact positively), or zero (i.e., S_i and S_j are stochastically independent).

The usefulness of the information transfer function in (13) or (14) for applications of systems is two-fold. When we have no usable information or conversely when we have full information on both S and p, the function T(S, p) ceases to be useful. Its use becomes accentuated when we have partial information on S and/or p. In fact, we may be in a position to obtain a system with some given subsystems or to derive some subsystems from a given system. The former problem is composition (integration) and latter is decomposition. In composition, p is known but we have no information on S. In decomposition, we have information on S but none about p. Information on p and/or S means knowledge about the distributions involved as well; “information” as used here is either in the theoretic sense, e.g., the information transfer function, or is in the daily usage sense, i.e., knowledge. Thus, for solution of the integration problem, the information transfer function is maximized over all possible systems 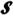={S|S• 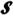} that yield the given common partition p. In other words, H(S)= H(S₁,S₂,…,S_q) or H(X₁, X₂,…,X_n) is minimized. Conversely, a solution for decomposition (partition p) is obtained by minimizing the transfer function over all possible partitions π = { p: p • π } of the given system S. In other words, ${\displaystyle \underset{i=1}{\overset{q}{‡"}}}H(S_i)$ or ${\displaystyle \underset{i=1}{\overset{n}{‡"}}}H(X_i)$ is minimized. Composition is not simply a reversal of decomposition because, in addition to the required knowledge on relevant partition, the so-called blueprint of composition must also be known, i.e., compatibility of all marginal distributions with the given joint distribution of S must be checked (Dall’Aglio, 1972; Butterfly et. al., 2005; Arnold et al., 1999). However, the current work is only interested in decomposition.

All foregoing discussions and indices are undoubtedly relevant when distributions are known. When such information is unavailable, empirical distributions can be used as consistent estimates. Collecting observations for this purpose is costly and difficult. This is basically true for empirical assessment of joint distributions when we are interested in obtaining estimates of multivariate distributions for large sets of components. The following illustrate the initial stages where observations on element partition and pair-wise partition of the system are available:

Illustration One

A simple empirical case corresponds to the availability of observations on each individual component. Let S ={Y₁, Y₂,…,Y_n} hence be a system with n ordered components and with the given matrix X of discrete observations

$$\mathbf{Y}=\left[\begin{array}{cccc}{y}_{11}& y_{12}& \cdots & y_{1\text{n}}\\ y_{21}& y_{22}& \cdots & y_{2\text{n}}\\ ⋮& ⋮& ⋮⋮⋮& ⋮\\ y_{{\kappa }_1}& y_{{\kappa }_2}& \cdots & y_{{\kappa }_{\text{n}}}\end{array}\right]=(y_{ij})$$

where y_ij denotes the i^th functional value (i=1,2,…, κ) taken up by the j^th component of the system S = {Y₁, Y₂,…,Y_n}. The number (say, κ) of functional values is identical for each random component for the convenience of notation. The values y_ij are not necessarily identical for all components. Assume further that these values are observed with the frequencies in Table 1:

Table 1.

Observations on element partitioning

	Y1	Y2	…	Yn
yi1	m11	m12	…	m1n
yi2	m21	m22	…	m2n
⋮	⋮	⋮	⋮	⋮
yiκ	mκ1	mκ2	…	mκn
Marginal Sums	m ∘1	m ∘2	…	m ∘n	m

By definition, the magnitudes m_∘j and m in Table 1 are ${\displaystyle \sum _{i=1}^{\kappa }}{m}_{ij}={\mathit{m}}_{\circ \mathit{j}}$ and ${\displaystyle \sum _{j=1}^n}{m}_{\circ j}=m$. These observations are sufficient for obtaining estimates for marginal distributions of the individual components Y₁, Y₂,…,Y_n. A real-life example for this case corresponds to frequency of long-distance phone calls m_ij placed at a certain geographical location Y_i at some given time unit y_ij.

Consider the element partition p {S₁, S₂,…,S_n}of S where S_j={Y_j} for each component Y_i. Thus, the marginal probability of each component S_j={Y_j} is P(S_j) = π_j, which can be consistently estimated by ${\widehat{\pi }}_j=\frac{m_{\circ j}}{m}$. For each component Y_i,, the probability of the event {Y_j=y_ij} is represented by P(Y_j=y_ij|S_j) = π_i|j, which will, similarly be estimated by ${\widehat{\pi }}_{i\mid j}=\frac{m_{ij}}{m_{\circ j}}$. However, after observing the system S, the probability for the same event {Y_j=y_ij} becomes P(Y_i=y_ij|S) = π_ij and is estimated with ${\widehat{\pi }}_{ij}=\frac{m_{ij}}{m}$. Accordingly, estimates for the entropies of individual components are

$$\mathit{H}({\widehat{\mathit{S}}}_{\mathit{j}})=-\sum _{\mathit{i}=1}^{\kappa }\frac{{\mathit{m}}_{\mathit{ij}}}{{\mathit{m}}_{\circ \mathit{j}}}log(\frac{{\mathit{m}}_{\mathit{ij}}}{{\mathit{m}}_{\circ \mathit{j}}}),j=1,2,\dots ,\text{n}$$

and the estimate for the system entropy is given by

$$H(S_1,\widehat{S_2},\dots ,S_n)=-\sum _{j=1}^n\sum _{i=1}^{\kappa }\frac{m_{ij}}{m}\left((\mathit{log}\frac{m_{ij}}{m})\right).$$

By (11), the estimated information transfer will be

$$\begin{array}{l}Tr(\widehat{S},P)=\sum _{j=1}^{\mathit{n}}\mathit{H}({\widehat{\mathit{S}}}_{\mathit{j}})-H(S_1,\widehat{S_2},\dots ,S_n)\\ =-\sum _{i=1}^{\kappa }\frac{{\mathit{m}}_{\mathit{ij}}}{{\mathit{m}}_{\circ \mathit{j}}}log(\frac{{\mathit{m}}_{\mathit{ij}}}{{\mathit{m}}_{\circ \mathit{j}}})+\sum _{j=1}^n\sum _{i=1}^{\kappa }\frac{m_{ij}}{m}\left((\mathit{log}\frac{m_{ij}}{m})\right)\end{array}$$ (17)

A vanishing value of this non-negative real number in (17) provides some evidence that the partition p {S₁, S₂,…,S_n} conforms well with the given system S, so that the degree of its divergence from zero is a clue that there is still some unused information in p {S₁, S₂,…,S_n} for S. When Tr(Ŝ,P)= 0, observations suggests that the system cannot be decomposed further than the element decomposition p {S₁,S₂,…,S_n}. A non-vanishing value of the empirical information transfer function Tr(Ŝ,P)thus suggests that it is worthwhile to seek decompositions other than p {S₁,S₂,…,S_n}. We can partition S in some other way such as p {S₁, S₂,…,S_q} where 1< q < n. The foregoing analysis can be repeated using (14) to check whether p {S₁, S₂,…,S_q} has some information for S. In that case, the system entropy estimate $H(S_1,\widehat{S_2},\dots ,S_n)$ will stay put, but estimates of entropies H (Ŝ_ℓ) of individual subsets S_ℓ will change.

The given observations in the Table 1 are clearly not sufficient for obtaining a conclusion beyond the result obtained above. For further conclusions we need more sophisticated observations and experiments. Hence, we have the next illustration:

Illustration Two

The second illustration relates to a case where empirical data for pairs of components are available. This case is more general in the sense that availability of empirical observations (frequencies) on pairs of random variables also implies availability of observations on individual variables. Assume again, for simplicity of exposition, that the random components Y₁, Y₂,···, Y_n−1 and Y_n are discreet and the number of functional values taken by each Y_i is r_i, (i=1,2,…,n) with these values ranging over the whole numbers

$$y_{i1},y_{i2},\dots ,y_{i{r}_i}$$

For notational convenience and without a loss of generality, we can assume that r_i = r for all i=1,2,…,n. In accordance with a certain pattern, the joint event {Y_i=y_ih, Y_j=y_jk}, i• j, takes values in the discrete (r(n−1))× (r(n − 1)) matrix layout set up as in Table 2. This layout is now our observational system T, which is a proper subset of S×S.

Table 2.

Pair-wise observations

	Y1	Y2	…	Yi	…	Yj	…	Yn
Y1
Y2
⋮
Yi
⋮
Yj
⋮
Yn

Because we are interested in cross pairs of variables like Y_i and Y_j with i ≠ j, the diagonal cells (darker gray) are irrelevant and we therefore have (n−1) rows and (n−1) columns of interest. Hence, off-diagonal cells become a center of interest. Each off-diagonal cell is composed of an (r×r) matrix of observations on the bi-variable event such as {Y_i=y_ih, Y_j=y_jk}, i ≠ j = 1,2,…,n and h,k = 1,2,…,r. When the two events {Y_i=y_ih, Y_j=y_jk} and {Y_j=y_jk,Y_i=y_ih} are identical, i.e., when they are symmetrical, only the upper or lower off-diagonal part of the table can be used. For convenience of visualization, the unused part (for instance, the lower part) is shaded in light gray. In this latter case, the upper off-diagonal block cells become the system T of observations to be considered below. The bottom row and the last column shaded in blue are empty and the cell in the southeast corner contains one single element marked m representing total number of observations.

To aid exposition, the cell corresponding to the observational frequencies on the i^th and j^th variables (orange) is reproduced in Table 3 with the same color. For the specific pair of Y_i and Y_j, the symbol m _i(h)j(k) in stands for the frequency with which the bi-variable event {Y_i=y_ih, Y_j=y_jk} is observed empirically. The last column and the bottom row present marginal frequencies involved (column-wise and row-wise sums of the frequencies in the table): For observations on

Table 3.

Frequencies of {Y_i=y_ih, Y_j=y_jk} in Table 2 for the highlighted pair of i and j

mi(1)j(1)	mi(1)j(2)	…	mi(1)j(r)	mi(1)j
mi(2)j(1)	mi(2)j(2)	…	mi(2)j(r)	mi(2) j
⋮	⋮	⋮	⋮	⋮
mi(r)j(1)	mi(r)j(2)	…	mi(r)j(r)	mi(r) j
mi j(1)	mi j(2)	…	mi j(r)	mi j

{Y_i=y_is} corresponding to a certain s =1,2,…,r we have

$$m_{i(s)j}=\underset{k=1}{\overset{r}{‡"}}{m}_{i(s)j(k)},i\ne j$$

and similarly, for a certain t =1,2,…,r we have

$$m_{ij(t)}=\underset{h=1}{\overset{r}{‡"}}{m}_{i(h)j(t)},i\ne j$$

Thus,

$$m_{ij}=\sum _{i=1}^r{m}_{i(s)j}=\sum _{i=1}^r{m}_{ij(t)}$$

with

$$m=\sum _{i=1}\sum _{i<j}{m}_{ij}.$$

As it is designated in Table 2, m is located in the southeast cell of the table.

The $q=\frac{n(n-1)}{2}$ upper off-diagonal block cells of Table 2 can now be labeled T₁, T₂, …,T_q. p {T₁, T₂, …,T_q} is a proper partition of T. Labeling starts from the top leftmost cell of the table and then goes to the leftmost off-diagonal block cell of the second row and so on as in the lexicographical ordering: T₁ for {Y₁,Y₂}, T₂ for {Y₁,Y₃},…, T_q for {Y_n−1,Y_n}. For each partition ℓ= (i,j), i < j, estimates of the marginal probabilities

$$P(Y_i=y_{ih},Y_j=y_{jk})={\pi }_{i(h)j(k)},j>i=1,2,\dots ,\text{n}\text{and}h,k=1,2,\dots ,\text{n}$$

are given by

$${\widehat{\mathit{\pi }}}_{i(h)j(k)\mid \ell }=\frac{m_{i(h)j(k)}}{m_{ij}}$$

For the whole system the same estimate becomes

$${\widehat{\mathit{\pi }}}_{i(h)j(k)}=\frac{m_{i(h)j(k)}}{m},$$

so that, as before,

$$\begin{array}{l}H({\widehat{T}}_{\ell }))=-\sum _{h=1}^r\sum _{k=1}^r\frac{m_{i(h)j(k)}}{m_{ij}}\mathit{log}(\frac{m_{i(h)j(k)}}{m_{ij}})\\ H(T_1,\widehat{T_2},\dots ,T_q)=-\sum _{i=1}^n\sum _{i<j}^n\sum _{h=1}^r\sum _{k=1}^r\frac{m_{i(h)j(k)}}{m}\mathit{log}(\frac{m_{i(h)j(k)}}{m})\end{array}$$

The estimated transfer function

$$\widehat{T}r(T,P)=\sum _{\ell =1}^{q}H({\widehat{T}}_{\ell })-H(T_1,\widehat{T_2},\dots ,T_q)$$

will have small values close to zero when a pair-wise partition is enough for decomposition whereas its higher values will produce evidence that there is further information to be utilized in T for a further partition p {T₁, T₂, …,T_r}, q ≠ r.

ITF seems to be free from restrictions of structural modeling and does not depend on the type of distribution of the random variables involved. It also does not require any restriction on the type of interaction of variables such as their uncorrelatedness, independence, etc. It therefore is a flexible technique but need a great deal of care and designing efforts before being applied empirically. As it is the case with previous approaches, high dimensionality of data may at times be a deterrent factor in its application.

Concluding Remarks

This work is an attempt to provide a uniform body of exposition for available techniques of decomposition in the literature. Because of prevailing high-dimensionality issues, these techniques have increased in importance for the past two decades. Except for some comments and the two illustrations of the use of information transfer and for our efforts to present a unified standpoint, we do not claim originality. Our unifying framework has been probability theory and multivariate statistics as well as information theory. We have not dwelt on inferential issues concerning use of statistical estimates because of our intension to provide a general text that will apply to a large spectrum of application areas.

Regarding the applicability of the five techniques reviewed: All of the four techniques PCA, SVD, ICA, and NCA are based on structural modeling of a real-life phenomenon; they are dependent upon some assumptions concerning interactive nature of real-life events such as uncorrelatedness or independence which may be restrictive for data; they are analytically well-founded, which paves the way for their preference; and they have dimension reduction properties in their favor. The last technique, ITF, is free from all such drawbacks but requires challenging tasks of design and computation. Unlike the first three techniques, it is not particularly used for data reduction purposes. All five techniques confront high-dimensionality problems and seem to need care in applications involving Gaussian distributions.