Abstract
The liver is perfused through the portal vein and the hepatic artery. When its perfusion is assessed using PET and 15O-labeled water (H215O), calculations require a dual blood input function (DIF), i.e., arterial and portal blood activity curves. The former can be generally obtained invasively, but blood withdrawal from the portal vein is not feasible in humans. The aim of the present study was to develop a new technique to estimate quantitative liver perfusion from H215O-PET images with a completely noninvasive approach. We studied normal pigs (n=14), in which arterial and portal blood tracer concentrations and Doppler ultrasonography flow rates were determined invasively to serve as reference measurements. Our technique consisted of using model DIF to create tissue model function, and the latter to simultaneously fit multiple liver time-activity curves from images. The parameters obtained reproduced the DIF. Simulation studies were performed to examine the magnitude of potential biases in the flow values, and to optimize the extraction of multiple tissue curves from the image. The simulation showed the error associated with assumed parameters was <10%, and the optimal number of tissue curves was between 10 and 20. The estimated DIFs were well reproduced against the measured ones. In addition, the calculated liver perfusion values were not different between the methods and showed a tight correlation (r=0.90). In conclusion, our results demonstrate DIF can be estimated directly from tissue curves obtained through H215O-PET imaging. This suggests the possibility to enable completely noninvasive technique to assess liver perfusion in patho-physiological studies.
Keywords: Algorithms; Animals; Blood Flow Velocity; physiology; Hepatic Artery; physiology; Image Interpretation, Computer-Assisted; methods; Liver; blood supply; physiology; Oxygen Radioisotopes; diagnostic use; Positron-Emission Tomography; methods; Reproducibility of Results; Sensitivity and Specificity; Swine; Water; diagnostic use
Keywords: Hepatic blood flow, Input function, Portal vein, Positron emission tomography, H215O
Introduction
The quantitative determination of hepatic blood flow has the potential to provide important information in the assessment and follow-up of liver disorders, which are almost invariably accompanied by abnormalities in organ perfusion, representing a prognostic indicator and responding to disease amelioration (Blomley et al 1995; Henderson et al 1992; Leen et al 1993; Martin-Comin et al 1988; Taniguchi et al 1993, 1996a, b, 1999; Ziegler et al 1996). Positron emission tomography (PET) and 15O-labeled water (H215O) enable to assess hepatic perfusion quantitatively (Taniguchi et al 1996a,b; Ziegler et al 1996), as based on tracer kinetic modeling, requiring the notion of the time variation of radiotracer concentrations in the liver tissue and in the blood entering the organ (input function).
The liver is characterized by a dual blood supply, comprising the hepatic artery and the portal vein, draining venous blood from the gastrointestinal tract. Thus, in the modeling of PET data from liver two blood time-activity curves are required to represent the input function (dual input function, DIF). However, blood withdrawal from a peripheral artery (Kanno et al 1987; Erikson et al. 1988; Eriksson et al. 1991; Ruotsalainen, et al 1997; Votaw et al. 1998; Kudomi et al 2003) is not always successful and risk-free, and it requires careful correction in time delay between the sampling site and the tissue. More important, the portal vein cannot be accessed from any peripheral site, making its blood collection impractical in humans.
The aim of the present study was to develop a new technique to estimate the two components of the DIF non-invasively from dynamic H215O PET images. The present method was characterized by use of a model input function to create a tissue model function, which was used to simultaneously fit multiple tissue curves from PET image. The parameter obtained in the input function model reproduced the input function. Computer simulation studies were performed to examine the magnitude of potential biases in the parameter estimates caused by the inherent assumptions, and to optimize the extraction of multiple tissue curves from the image. The present investigation was conducted in pigs because the comparison between measured and estimated values necessitated deep catheterization and invasive Doppler flow measurements.
Materials and Methods
Theory and computation of non-invasive DIF
A model function was created to shape the input function according to the dose of tracer, administration process, body weight and physiological state in each subject (Kudomi et al 2006). The model function introduced is:
| (1) |
Details of the model function are given in Appendix. Briefly, A indicates the height, and t1 and t2 − t1 indicate the appearance time of tracer and administration duration. Ke (ml/min) and Ki (= αKe)(ml/min), represent the tracer bidirectional diffusion rates between arterial blood and whole body interstitial spaces, respectively.
The portal vein blood model function was generated by introducing the gut compartment model (Ziegler et al 1996; Taniguchi et al 1996a, b, 1999), that is, a single compartment model between arterial blood and gut compartment, assuming no difference in appearance time between arterial and portal blood (or delay time of portal input), with diffusion rate kg in the gut system as:
| (2) |
Using these arterial and portal input model functions, the tissue response function can be expressed by assuming a single tissue compartment model (Ziegler et al 1996; Taniguchi et al 1999a, b) and that tracers in arterial and portal blood were well mixed before exchange with liver tissue as:
| (3) |
where k2 is defined as (fa+fp)/VL, and VL (ml/g) is the distribution volume of water between blood and tissue. In the present study, VL was fixed to 0.7 ml/g, which was suggested to fix in a sensitivity analysis by Ziegler et al (Ziegler et al 1996) and was obtained as 0.71 ± 0.03 ml/g for same subjects in our preliminary evaluation using measured blood input functions. Including a blood volume term into this equation, the model function for liver tracer concentrations, as measured by PET (CPET) can be expressed as:
| (4) |
where Cinput(t) is defined as:
| (5) |
where ra and rp are arterial (fa ml/min/g) and portal vein blood flow (fp ml/min/g) ratios to total hepatic flow, i.e., ra= fa/( fa+ fp) and rp= fp/( fa+ fp) (Ziegler et al 1996). The flow chart to estimate input functions in this procedure is simplified in Figure 1. Multiple tissue time activity curves (TAC) from liver image were used to estimate the input functions. First, the model function in Eq (4) was individually fitted to tissue TACs assuming that kg in Eq (2) is constant, by a non-linear fitting method (variable-metric method in the PAW environment: version 2.13/08 (http://wwwasd.web.cern.ch/wwwasd/paw/)), and the set of seven parameters of A, t1, t2, Ke(1+α), fa, fp and V0 in Eqs (1) and (4) was obtained for each tissue TAC. Then, means and standard deviations of t1, t2, and ra (= fa/( fa+ fp)) were calculated, and the tissue TACs with values of t1 or t2 > one standard deviation of respective means were excluded to avoid the potential influence of TACs outside the liver. In the second step, assuming that all parts of the liver share the same input functions, values of t1, t2, and ra were fixed to their means and the other two parameters (A and Ke(1+α)) were estimated by minimizing the following equation:
| (6) |
where CPETi,k is the tissue TAC for kth frame in ith tissue region of interest, t is the corresponding time of kth frame, and fai, fpi(=fa(1−ra)/ra) and V0i are values of arterial and portal vein blood flows, and of blood volume for ith tissue, respectively. In this procedure, S2 was minimized by the grid search method to avoid dependency of initial guess, where S2 was calculated for 1000 discrete values of both A and Ke(1+α) between ranges of three standard deviations from respective mean values, omitting the negative value. In this procedure, for a given input function, i.e., given A and Ke(1+α), fa and V0 for each TAC were computed by the grid search method, with acceptable ranges of 0–100 ml/min/g and 0–1 ml/ml, and steps of 1 ml/min/g and 0.01 ml/ml, respectively, and then substituted in Eq (6). Finally, the image based input function was obtained by substituting the estimated parameters into equation (1).
Fig 1.
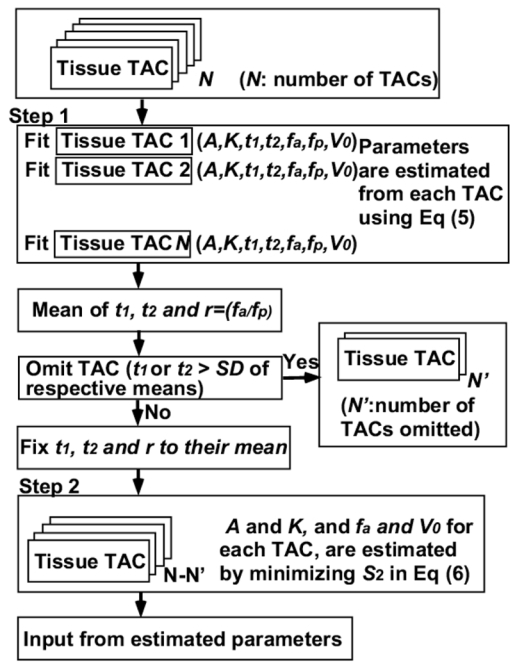
A schematic diagram of the procedure to estimate the input functions using multiple tissue TACs. (Step 1) the model function (Eq (4)) was individually fitted to N tissue time activity curves (TAC). Then, means and standard deviations of t1, t2, and ra were calculated, and the tissue TACs with values of t1 or t2 > one standard deviation of respective means were excluded (indicated as N′ TACs) to avoid the potential influence of TACs outside the liver. In the second step, assuming that all parts of the liver share the same input functions, values of t1, t2, and ra were fixed to their means and the other two parameters (A and Ke(1+α)) were estimated by minimizing the Eq (6) by the grid search method. Finally, the image based input function was obtained by substituting the estimated parameters into Eq (1).
Simulation Study
The present method for generating portal vein input assumes that the diffusion rate in the gut system, kg is a fix constant, and there is no time delay between portal and arterial blood. It is not a priori known how these assumed factors degrade the accuracy of estimated DIF and flow. Moreover, tissue TACs from PET images convey some degree of noise, and the accuracy of the estimated input function might depend on either the degree of noise or the applied number of tissue TACs or both. A simulation study was designed to reveal the influence of the above elements on the accuracy of the current method.
To this purpose, we selected one arterial curve from one of the present experiments. First, a portal input curve was created by assuming kg = 0.5/min, corresponding to the estimated mean in all animals. The combination of these arterial and portal vein curves was treated as the ‘true DIF’. In the present experimental study, the average of activity concentrations in an area of the summed image was distributed with a 20% range around the mean for the whole liver, and this percentage was independent of the size of the selected areas in regions >50 pixels. This supports the assumption that flow values in the liver distribute around a 20% range around a mean of arterial flow of 15 ml/min/100g (Materne et al 2000). Thus, by assuming ten values of fa as 13, 13.5, 14, 14.5, 15, 15, 15.5,16, 16.5 and 17 ml/min/100g, and ratio r(=fp/fa)=6 (Materne et al 2000), one set of ten hepatic tissue TACs was generated from the true DIF using Eq (6).
The propagation of an error in kg and delay time to blood flow estimation was simulated. The sequence of steps in this procedure is simplified in Figure 2(A) and (B). For kg, simulated portal input curves were created from the selected arterial curve by changing kg from 0.35 to 0.65/min for error simulation in kg, and combinations of the arterial and simulated portal vein curves were used as the simulated DIF. Sets of tissue TACs were generated from these simulated DIFs, with the same assumptions of fa and r as given above. In turn, each set for each kg was used to back-estimate DIF (arterial and portal components) fixing kg as 0.5/min in this process as presented above. Finally, fa and fp were calculated from estimated DIFs for each kg by the Gauss-Newton nonlinear fitting method in the interactive modeling and data analysis system called PyBLD (http://homepage2.nifty.com/peco/pybld/pybld.html) (Carson 1986) using Eq (4). For delay time, simulated portal input curves were created from the selected arterial curve by shifting the time from 0 to 10 sec, and combinations of the arterial and simulated portal vein curves were used as the simulated DIF. Sets of tissue TACs were generated as above. In turn, each set for each delay time was used to back-estimate DIF fixing time delay as 0.0 sec. Finally, fa and fp were calculated from estimated DIFs for each delay time. Mean of % difference between computed and assumed (‘true’) flow values are presented as a function of kg and delay time.
Fig 2.
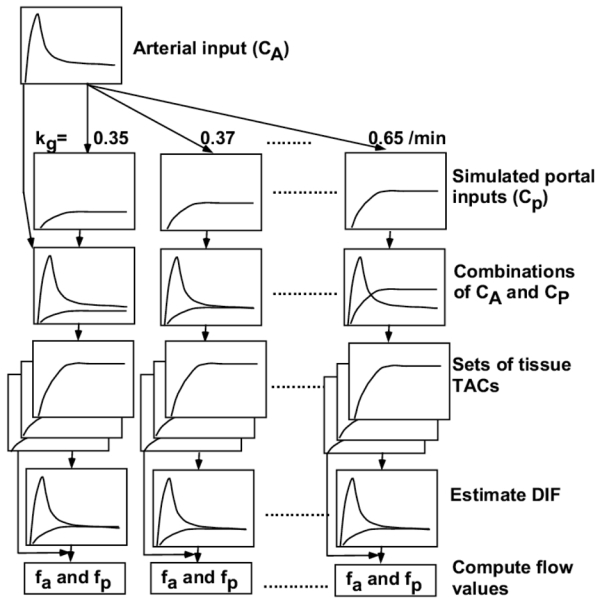
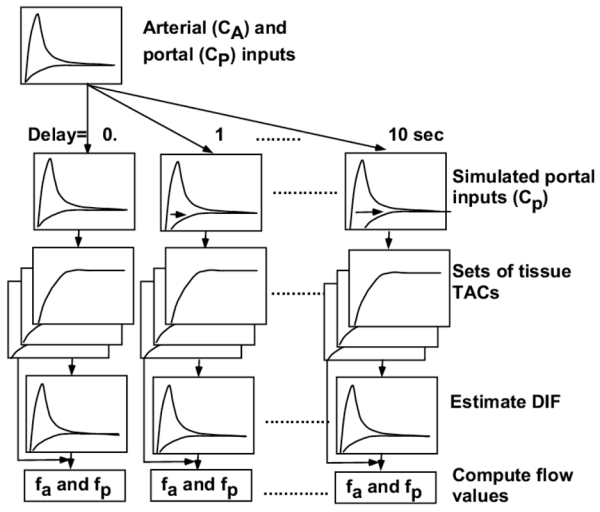
Schematic diagram of the procedure to analyze error sensitivity in hepatic arterial (fa) and portal flow (fp) values against assumed kg (A) and time delay (B). Portal input curves were created by changing the value of kg from 0.35 to 0.65/min in (A) and by shifting the time from 0 to 10 sec in (B), respectively, and combinations of the arterial (CA) and simulated portal (CP) curves were used as the simulated dual input functions (DIF). Sets of tissue time acticity curves (TAC) were generated from these simulated DIFs, by assuming ten values of fa from 13 to 17 ml/min/100g. In turn, each set of tissue TACs was used to back-estimate DIF fixing kg as 0.5/min and time delay as 0.0 sec. Finally, fa and fp were calculated from estimated DIFs for each kg and delay time. TAC: time activity curve, DIF: dual input function.
The influence of noise versus number of TACs on the accuracy of the method was explored. As shown by Edward et al (Edward et al 1999), as the noise on tissue TACs increased, the standard deviation of uptake ratio of tracer increased; as more regions were used, the standard deviation tended to decrease. However, if the number of TACs is larger the noise on tissue is also large and viceversa. Our simulation was intended to reveal an optimal number of tissue TACs to be extracted from the whole region of the liver. The procedure is summarized in Figure 3. First, tissue TACs with noise were generated as follows. Gaussian noise at peak was imposed on the set of ten hepatic tissue TACs generated above. Two levels of noise were introduced, corresponding to 10 and 20% of counts at the level of the peak, and 10 and 20% each of the square root of counts at the other points. This procedure was repeated 100 times and 100 sets of noisy tissue TACs, embracing a total of 1000 pixels, were obtained. Next, the ith set of tissue TACs, in kth frame with fa defined as Cfai,k were summed for same fa as:
| (8) |
where NT indicates the summed number of tissue TACs and corresponds to the summed number of pixels. NT were set to 5, 10, 20, 50, 100 and 200, corresponding to a number of tissue TACs (Ntis) of 200, 100, 50, 20, 10, and 5, respectively. Here, when NT was 200, the 100 tissue TACs were summed as NT=100 and additionally combinations of fa= 13. and 13.5, 14. and 14.5, 15. and 15., 15.5 and 16. and 16.5, and 17. ml/min/100g were summed. For each Ntis and each level of noise, DIF was estimated, as described. Then, arterial and portal vein blood flow values were computed as above, using estimated DIF and tissue TACs with fa of 15 ml/100g/min. This procedure was repeated 100 times and the bias and deviation in values of arterial and portal vein flow results were calculated. Their bias and deviation was presented as a function of Ntis.
Fig 3.
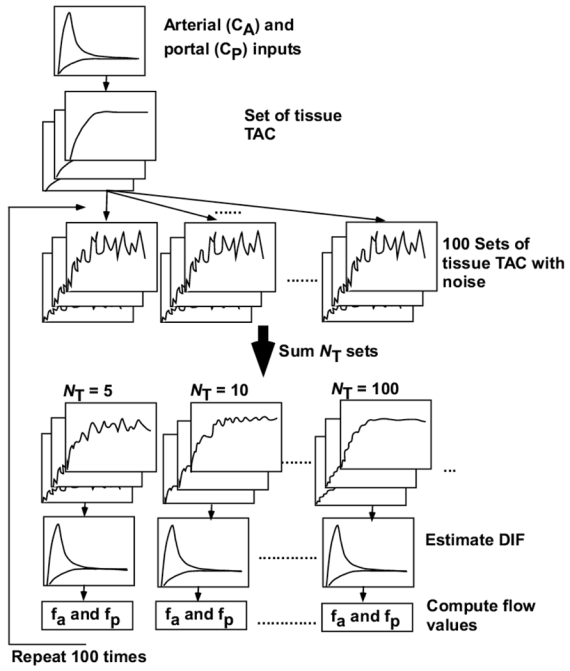
Schematic diagram of the procedure to analyze statistical accuracy of hepatic arterial (fa) and portal flow (fp) values against noise on tissue curves., First, tissue time activity curves (TAC) with noise were generated by imposing Gaussian noise on the set of ten hepatic tissue TACs. This procedure was repeated 100 times and 100 sets of noisy tissue TACs were obtained. Next, the NT (= 5, 10, 20, 50, 100 and 200) sets of tissue TACs with the same flow value were summed. For each NT, dual input function (DIF) was estimated. Then, arterial (fa) and portal blood flow (fb) values were computed using estimated DIF and tissue TACs. This procedure was repeated 100 times.
Experimental Study
PET experiment
Fourteen pigs with weight 30.0±1.1 kg were studied under anaesthesia. Data on glucose metabolism in these animals have been previously reported (Iozzo et al 2006, Iozzo et al 2007). Animals were deprived of food on the day prior to the study at 5:00 pm. Anaesthesia was induced with ketamine (1.0 g) into neck muscles and maintained by intravenous ketamine and pancuronium (total of 1.5 g and 40 mg, respectively) during the experiment. Animals were intubated through a tracheostomy and their respiration was controlled by a ventilator providing oxygen and normal room air (regulated ventilation, 16 breaths per min). Catheters were inserted into the carotid artery for arterial blood sampling and the femoral vein for administration of H215O. Splanchnic vessels were accessed by sub-costal incision; after dissection of the hepato-gastric ligament, purse string sutures were allocated to allow catheter insertion via a small incision in the portal vein. A catheter was inserted directly in the portal vein for portal vein blood sampling. Ultrasound based flow-probes (Medi-Stim Butterfly Flowmeter, Medi-Stim AS) were placed around the portal vein and hepatic artery to determine blood velocity in each vessel. The diameter of the hepatic artery and portal vein were measured off-line from B-mode ultrasound images acquired using an Acuson Sequoia 512 mainframe with a 13 MHz B-mode linear array transducer. The area of the vessel was calculated assuming circular shape. Then, blood flow was obtained for each vessel during the PET scans. The surgical access was closed, and the distal catheter extremities were secured to the abdominal surface to avoid tip displacement. The animals were then transported to the PET centre for tracer administration, liver imaging and blood sampling. Vital signs, blood pressure and heart rate were monitored throughout the study.
PET acquisition was carried out in 2D mode using an ECAT 931-08/12 scanner (CTI Inc, Knoxville, TN) with a 10.5 cm axial field of view and a resolution of 6.7 mm (axial) × 6.5 mm (in-plane) full width at half maximum (FWHM). After transmission scan for attenuation correction, the dynamic scan was started after the injection of H215O (274 MBq, 30 sec bolus injection), consisting of 20 frames with gradually increasing individual durations (6 × 5 sec, 6 × 15 sec and 8 × 30 sec).
During PET scanning, blood was withdrawn continuously from the carotid artery and portal vein, through catheters (1.4 mm in inner diameter, length of tube was 900 mm to the detector and 60 mm in the detector sensitive region), by using a peristaltic pump (Scanditronix, Uppsala, Sweden) with a withdraw speed of 6 mL/min. Radioactivity concentrations in blood were measured with a BGO coincidence monitor system. The detectors had been cross-calibrated to the PET scanner via ion chamber (Ruotsalainen, et al 1997).
At the end of the experimental period, animals were sacrificed by potassium chloride injection and anaesthetic overdose, the abdominal cavity was rapidly accessed, and the whole liver was explanted and weighed and its volume was measured by water displacement; liver density was calculated as the ratio of organ weight-to-volume, to derive the ultrasound based flow to PET-equivalent unit (i.e., flow per unit of tissue volume).
The protocol was reviewed and approved by the Ethical Committee for Animal Experiments of the University of Turku.
Data processing
Dynamic sinogram data were corrected for dead time in each frame in addition to detector normalization. Tomographic images were reconstructed from corrected sinogram data by the median root prior reconstruction algorithm with 150 iterations and Bayesian coefficient of 0.3 (Alenius S and Ruotsalainen U. 1997). Attenuation correction was applied with transmission data. A reconstructed image had 128×128×15 matrix size with a pixel size of 2.4 mm × 2.4 mm and 6.7 mm with 20 frames.
Measured arterial and portal vein blood TACs were corrected for physical decay and dispersion (Iida et al 1986) as: τ=2.5 sec, which was experimentally obtained and usually applied in our centre. The arterial TAC corrected for decay and dispersion was then corrected for delay by fitting to a whole-liver tissue TAC (Iida et al, 1988). The arterial curve obtained, Ca(t), was used as the measured arterial input function. Then, the portal vein curve, corrected for dispersion (τ=2.5 sec) and delay with the same delay time for arterial TAC, CP(t), was fitted according to the following equation:
| (9) |
to obtain kg, and to account for the appearance time (Δtp sec) via the gut system. Obtained measured curves were directly fitted with Eqs (1) and (2) to examine adequacy for a usage of model functions.
A region of interest (ROI) was placed on the whole region of the liver in a summed image, and subsequently divided plane-by-plane into sub-regions of 700 pixels each, corresponding to 11–22 sub-regions. Sub-regions were created by extracting pixels firstly from horizontal then vertical directions inside the whole ROI in each slice. Each sub-region consisted of a single area with the same number of pixels. Tissue TACs in the sub-regions were extracted from dynamic images. Then, DIF was estimated according to the procedure introduced above. In the first step, initial values and boundary conditions for the non-linear fitting (PAW environment) for each parameter were 20000 between 0.0000002 and 200000000 Bq/ml for A, 5 between 2 and 20 ml/min for Ke(1+α), 1 between −10 and 100 sec for t1, 20 between 1 to 60 sec for t2 − t1, 20 between 1 and 100 ml/min/g for fa, 100 between 1 and 400 ml/min/g for fb, and 0.05 between 0 and 1 ml/ml for V0, respectively. In the second step, S2 value in Eq (6) was minimized, and the image based input function was obtained. Areas under the curves (AUC) for measured and image based inputs were calculated for 0 to 180 sec. Their % difference was calculated.
Perfusion values fa and fp were calculated by non-linear Gauss-Newton fitting method (PyBLD environment). Results obtained with the new technique were compared with a) those obtained with the measured input function, and b) the ones from our independent reference method, i.e., ultrasonography, after their normalization to the organ volume to derive PET-equivalent units.
Statistical analysis
Data are shown individually or as mean±SD. The Student’s paired t-test was used for intra-individual comparisons of flow values. Regression analyses were performed according to standard techniques. A p <0.05 was considered to be significant. Differences between the flow values were calculated as: (fX−fY)/fY, where fX and fY are flow values from the noninvasive method, and from the measured input or ultrasonography, respectively and plotted in Bland-Altman plot (Bland and Altman 1986).
Results
Simulation Study
The biases in values of arterial, portal vein and total blood perfusion due to a fixed kg and delay time are presented in Figure 4(A) and (B) as a function of the value of kg and delay time, respectively. The error in total flow results did not exceed 10% for a ≤20% (i.e., 0.4–0.6 min−1) difference between the fixed and the assumed (‘true’) kg and for a <10 sec time delay.
Fig 4.
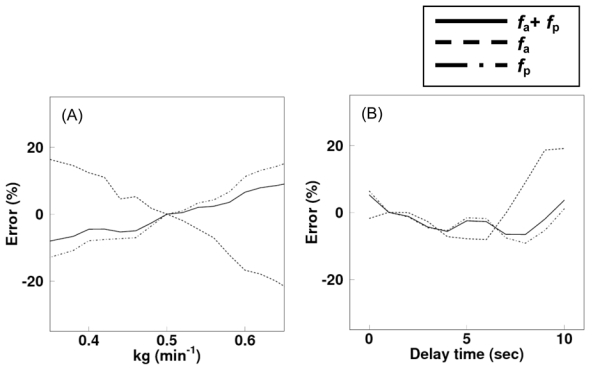
Error in values of arterial (fa), portal vein (fp) and total (fa+fp), blood flow propagated from error in kg (A) and delay time (B).
The influence of noise and number of tissue TACs, i.e., the bias and deviation on both arterial and portal blood flow values, showed to be minimal, for a number of tissue TACs of 10 to 20 at both noise levels (Figure 5). As shown in Fig. 5, if the number of tissue TACs is increased, noise on each curve for input estimation becomes larger. On the other hand, a smaller number of tissue TAC corresponds to less information from tissue TAC in terms of variation of flow values. This result suggested that the optimal number of tissue TACs to be applied to preserve accuracy is in the above range, which is independent of the two noise levels. Among five parameter composing the model input functions, the three parameters t1, t2, and ra were determined with same accuracy, i.e., both the difference and deviation in those values were less than 1 sec for t1 and t2 and 5 % for ra, respectively, for the noise level of 10 %, independent of the number of tissue TACs. Bias and deviation of the remaining two parameters A and Ke(1+α) depended on the number of tissue TACs following the same tendency as the bias and deviation on blood flow values, as described above.
Fig 5.
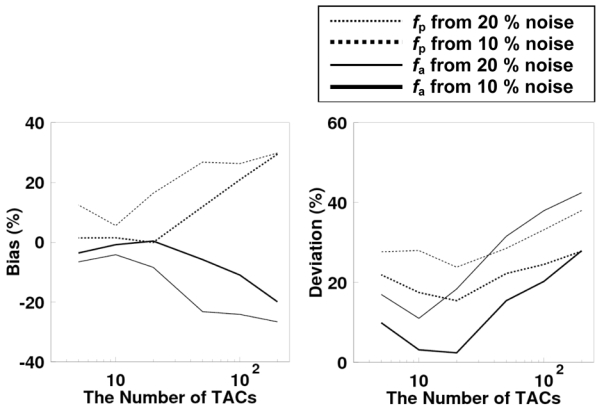
Bias (left) and deviation (right) in the arterial and portal vein blood flow values as a function of the number of time activity curves applied to the estimation of the input function.
Experimental Study
Reconstructed images are shown in Figure 6, together with divided sub-regions. In the first step of our procedure, the obtained value of t1 from TACs extracted from sub-regions overlapping the vena cava (e.g., lower sub-region at upper left side image in Figure 6) was 10 to 13 sec earlier than the mean, and these TACs were omitted from further processing. The estimated t2 − t1 was 27±3 sec, which was similar to the tracer administration duration.
Fig 6.
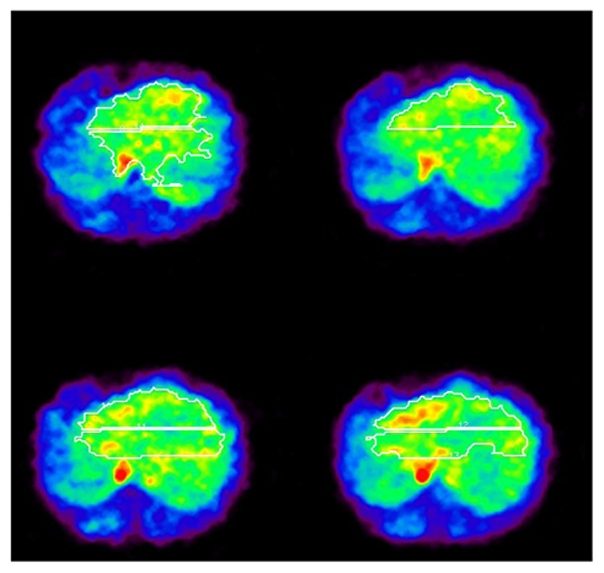
View of liver H215O-PET images in four slices and sub-regions (solid line). The small area with high activity levels on the mid-right and -left side of the image corresponds to the vena cava and aorta, respectively.
Figure 7 shows the curves of the model arterial and portal input functions (Eqs (1) and (2)) directly fitted to measured curves. The model functions for those were superimposable to measured curves, although both modeled curves slightly overestimated at the late times. This result suggested the model function was almost adequate to use for the estimation of input.
Fig 7.
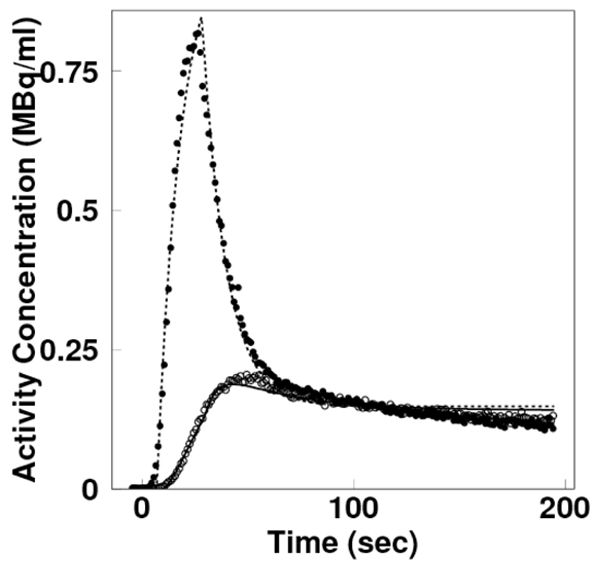
Time-activity curves representing the arterial (broken line) and portal (solid line) model input functions (Eqs (1) and (2)), in comparison with the measured arterial (black circles) and portal (open circles) input functions.
The mean ±SD of kg was 0.497±0.153 ml/min/g and that of Δtp, was 0.7 ± 5.1 sec obtained by fitting the portal TAC using arterial TAC by Eq (9).
Estimated, image-derived arterial and hepatic input functions were almost superimposable to the measured curves (Figure 8). The mean ± SD and range of difference of AUCs were −3.15 ± 8.73% ranging from −13.5 to 17.9% and 1.47 ± 8.87 % ranging from −13.5 to 10.2% for arterial and portal input functions, respectively. The coefficient of variation of the estimated flow ratio between artery and portal vein in the first step across sub-regions was 26±9%. The mean ± SD of that ratio across subjects was 0.15 ± 0.07 and those from ultrasonography was 0.16 ± 0.06, and paired t-test showed no significant difference between them. This suggests supporting the assumption that the ratio between arterial and portal input defined in Eq (5) relates to the flow values.
Fig 8.
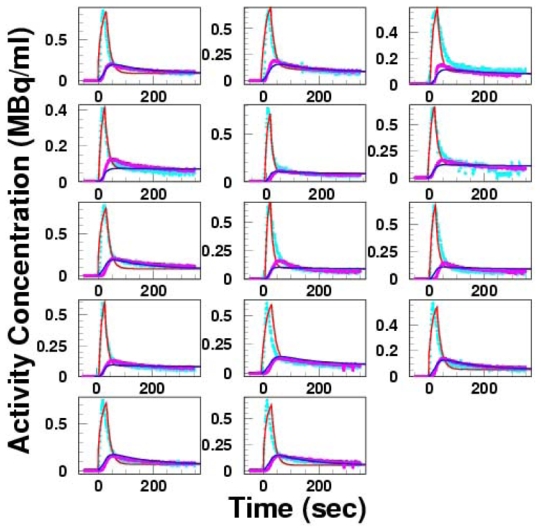
Estimated arterial (red line) and portal vein (blue line) input functions from PET images, and their comparison with measured arterial (plot in light blue) and portal input (plot in pink) functions.
The Bland-Altman plot between values of hepatic arterial, portal and total perfusion, as estimated by using the image-derived versus the measured blood curves is shown in Figure 9. This plot demonstrates a small overestimation by image derived method with a bias of 0.01 and 0.07 ml/min/g for arterial and portal flow respectively, and that 0.08 ml/min/g for total flow. Respective regression lines were: y = 0.00 + 1.09 x (r=0.97, p<0.001), y = 0.05 + 1.02 x (r=0.87, p<0.001) and y = 0.02 + 1.06 x (r=0.90, p<0.001). Paired t-test showed no significant difference between the methods. Differences were, −6.8 ± 20.0, −4.9 ± 14.3 and −5.8 ± 15.6 % for arterial, portal and total blood flow values, respectively.
Fig 9.
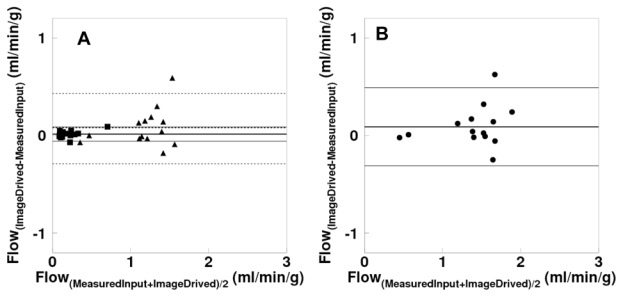
(A) Bland-Altman plot for arterial (square), portal (triangle) and (B) total hepatic blood flow differences between measured and image derived input functions.
The Bland-Altman plot between values of hepatic arterial, portal and total perfusion, as estimated by using the current method versus ultrasonography is given in Figure 10. This plot demonstrates an overestimation by image derived method with a bias of 0.02 and 0.22 ml/min/g for arterial and portal flow respectively, and that 0.24 ml/min/g for total flow. Respective regression lines were: y = 0.06 + 0.69 x (r=0.69, p=0.12), y = 0.41 + 0.98 x (r=0.54, p=0.025) and y = 0.24 + 0.97 x (r=0.60, p=0.022). Again, paired t-test showed no significant difference between the methods. Differences were, 3.6 ± 52.0, 15.5 ± 31.3 and 16.9 ± 33.0 % for values of arterial, portal and total blood flow, respectively.
Fig 10.
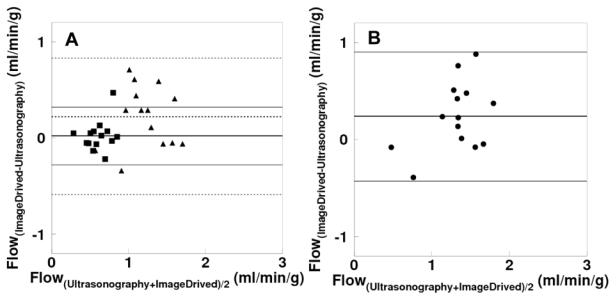
(A) Bland-Altman plot for arterial (square), portal (triangle) and (B) total hepatic blood flow differences between ultrasonography and kinetic modeling using image derived input functions.
The total flow values ranged from 0.5 to 2 ml/min/g in the animals (Figures 9 and 10). However, only two out of fourteen showed smaller values of 0.5 ml/min/g (i.e., approximately 500 ml in the whole organ), which is still physiologically reasonable, while the great majority clustered between 1 and 2 ml/min/g.
Discussion
In the current work, we developed and validated a method to estimate the two components of the hepatic dual input function from liver H215O-PET images, and quantify hepatic perfusion. Computer simulations were used to evaluate the influence of assumptions, noise in raw data, and number and size of the regions of interest to be used in the analysis. After demonstrating that kg can be assumed within a 20% range by introducing a negligible error in perfusion estimates, and that 10–20 regional time-activity curves appear optimal, the method was validated experimentally, by showing its coherence with measured blood tracer levels and with liver perfusion results obtained by an independent technique.
The current approach estimated the hepatic arterial and portal input functions from multiple tissue curves to calculate respective and total organ perfusion. A high degree of overlap and tight correlations were observed between the estimated input functions and those obtained during online blood sampling/counting. Consequently, calculated flow values were consistent between the methods. Alternative to the present procedure, a region of interest (ROI) based input extraction from PET images has been used for the carotid artery in [11C]Flumazenil brain studies (Sanabria-Bohorquez et al 2003), abdominal artery for kidney blood flow quantification with H215O (Juillard et al 2000), and aorta for cardiac 18F-FDG metabolism (Van deer Weerdt et al 2001), and for tumor blood using H215O (Watabe et al 2001). In these approaches, ROIs are drawn in visible vessels, and the partial volume effect must be taken into account by testing different ROI sizes or by thresholding the pixels inside arterial ROIs; the need for partial volume correction remains a necessary limitation. Closer to the current analysis, Edward et al applied multiple tissue curves to estimate quantitative kinetic parameters in the brain (Edward et al 1999), and well reproduced the input function for H215O. However, their formula did not take into account the radioactivity from the blood component inside the tissue ROI, and the validity of their method may not be directly extrapolated to the liver, because of the large proportion of blood, which is typically ranging between 0.27 and 0.40 ml/ml (Munk et al 2001) in this organ. The present method showed that the height of the estimated input is almost doubled if the blood volume is not included in the formula and if the arterial volume contributes 10% of radioactivity in the tissue TACs in our preliminary study (data not shown). The shape of an arterial input function from multiple tissue TACs has been well reproduced in brain 18FDG or [11C]MPDX studies, by using an independent component analysis based method (Extraction of the Plasma TAC using Independent Component Analysis, EPICA) (Naganawa et al 2005a, b), still requiring one arterial blood sample, and the combination of the latter and the current techniques may be of further simplification and deserves investigation, since it would entail neither a model function nor direct blood measurements.
One advantage of introducing a model function was to shape the model input function by imposing constrains to the parameters range, allowing overcome noise problems caused by limited scan duration and short half-life of 15O. The present approach may be applicable to a study group including subjects with hepatic disorders as far as measurement conditions are equivalent and the shape of the input function can be expected to be similar, though the validity of the present method was tested in normal animals. We expect no relevant limitation in the extension of the assumptions concerning the shape to other species, and in a majority of hepatic conditions. A drawback in the use of a model function, however, is that the feasibility is unknown for a group in which the shape of input functions could be extremely different or cannot be expressed by the present model function. This is not a commonly expected case. In this situation, the present method would require to, and may still be adapted, by introducing group specific parameter constraints or a modified model function. The present model function was created by assuming the model, namely, tracer bidirectional diffusion to whole body as in differential equation (A-1). The solution was derived as equation (A-10), and the model function was modified to avoid the one order term of t, which would complicate calculations in the following procedures, i.e., model function for portal input and for tissue response functions. This modification could deteriorate the physiological mean of parameters, such as Ke and Ki, however, the input functions obtained in the present study using this modified equation well reproduced the shape of measured inputs. The modified model function and derived portal model function seemed to be superimposable to measured blood TACs, although there were slight, few-second systematic misalignments in the peak of arterial blood and overestimations at the late phase. This suggested that the error in the position of the peak and in late phase in the estimated input function against measured ones (Figure 7 and 8) is due to a limitation in the description of the model function.
The present estimation procedure followed two steps, as designed to fit tissue curves individually, and then simultaneously. The first step allowed careful exclusion of tissue TACs showing t1 or t2 values over one standard deviation from the mean, to eliminate the influence of radioactivity outside the liver region. In fact, in the experimental procedure, H215O was injected in the femoral vein, draining into the vena cava, which is not distant from the liver. Other adjacent high-perfusion organs include the kidneys. The influence of ROIs drawn in proximity of these regions was not included in the model. Thus, special attention was paid at excluding confounding tissue TACs, by examining t1 and t2. In the above examples, the tracer was expected to show an early peak in case of an anatomical overlap with the vena cava, and the extracted TAC covering this region was omitted in this step. The second step was introduced to facilitate the achievement of the convergence, by fixing the values of t1, t2 and ra to their calculated means (as obtained above) to estimate the remaining two parameters. Generally, if many parameters are estimated in a fitting procedure such as in the present method, there could be many local minima and uniqueness of parameter solution might not be guaranteed. As shown in the simulation study, the three parameters t1, t2 and ra were estimated independent of the number of tissue TACs, however, the remaining two parameters A and Ke(1+α) were dependent on that. This suggests that correlation among parameters due to their numerosity could not be prevented. However, the shapes of input functions were reproduced and flow values were consistent with other two methods, i.e., those computed from measured inputs and from ultrasonography. Thus, the correlation among parameters did not seem to affect the estimation of flow values, although further study is required for optimization.
We used a fixed value of kg to represent the diffusion rate of water between arterial blood and the gut compartment in the estimation of the portal input. The deviation in this rate constant was about 26% in the current study group. The simulation analysis showed that values within 20% of the assumed ‘true’ kg number corresponded to a propagated error of 10% in the final estimation of hepatic perfusion. The value of kg used in our final computations is in accordance with the recently reviewed concept that (Lindstedt and Schaeffer 2002) in mammals, the general biological rate (uptake ratio) varies approximately in proportion to the 3/4 power of body size, and, given a body mass of ~60 kg, kg, which is uptake rate of water in the gut system, can be predicted to fall around 0.45 min−1 in humans. This number is consistent with a mean figure of 0.5 min−1, as obtained in this study, suggesting that the present assumption could be implemented to obtain the liver input function in humans. We also assumed a time delay of portal input to be zero against the arterial one. The deviation in this time was about 0.7 sec in the current study group. The simulation analysis showed that an error in this value within 10 sec corresponded to a propagated error of less than 10% in the final estimation of hepatic perfusion. Of further strength, a close agreement was shown between estimated and measured blood activity curves and estimated and Doppler determined liver flow results. The larger difference of the latter against the former might be due to the model assumptions in flow calculations, as well as in the assumption of circular shape when estimating the area of the arterial and portal vessels by ultrasonography and in the accuracy of ultrasonography data (from multiple measurements of flow data, coefficient of variation was 13±5% for portal flow, and 18±10% for hepatic arterial flow with this study (data not shown)). In this study, the flow values were calculated assuming the dual input, single compartment model (Ziegler et al 1996, Taniguchi et al 1996a 1996b; Becker et al 2005). Altogether, the above observations support the use of a fixed kg and the current model in the fully non-invasive quantification of liver perfusion.
The validation of the current approach, as obtained in this study, is especially valuable in the liver for multiple reasons. First, the inaccessibility of the portal vein prevents its direct blood sampling in humans. Arterial blood can be obtained, (Kanno et al 1987; Erikson et al. 1988; Eriksson et al. 1991; Ruotsalainen, et al 1997; Votaw et al. 1998; Kudomi et al 2003), but blood counting requires corrections for dispersion, delay between target organ and sampling device, and cross calibration between PET scanner and radioactivity counter, which are all potential sources of errors, in the same magnitude as that expected with the current method. Second, liver perfusion can be compromised both as consequence and cause of hepatic disease, and is considered a prognostic indicator and useful marker during progression or treatment follow-up (Johnson et al 1985; Materne et al 2000). Third, the possibility to distinctly quantify portal and arterial perfusion is important because their reciprocal compensation may be masked once only total hepatic flow is measured.
The present simulation study allowed establish that the optimal number of tissue TACs for DIF estimation was 10 to 20, independent of the noise levels, among the ones selected in this investigation. As pointed out by Edward et al (Edward et al 1999), as the noise on tissue TACs increased, the standard deviation of uptake ratio of tracer increased. Also, they suggested, that the standard deviation tended to decrease when more regions were used. The present study intended to investigate the optimal number of tissue TACs from the whole region of liver. The noise in the liver can be minimized, by placing a ROI to cover the whole organ, and subsequently dividing it in a number of sub-regions, corresponding to 10–20, under the conditions of the current experiments. The present results may depend on the reconstruction method. However, as far as the PET image is calculated quantitatively and the distribution of flow values in the extracted TACs is in the same order of magnitude as the present study, the results of optimization in this study would be applicable because those two conditions were assumed in the present simulation study. We assumed that the ratio of blood flow between the hepatic artery and the portal vein was uniform in the whole organ, as supported by an extended literature on the healthy liver, and on a majority of metabolic disorders involving the organ. Conversely, the quantification of flow in hepatic tumors - in which perfusion from arterial blood is predominant - may be best approximated by simplifying the procedure to a single input, or by fitting the relative vascular (arterial and portal) contributions as additional parameters in the model. The current procedure was validated for the determination of liver perfusion with H215O PET data. Required conditions were a model function to describe the input function and a kinetic model for tracer exchange between blood and tissue. In theory, the present method might be adapted to other tracers and organs, if tracer kinetics in the tissue can be described with a model function.
In conclusion, our results demonstrate that arterial and portal vein concentrations of labeled water can be estimated directly from tissue time-activity curves obtained through dynamic H215O PET imaging. The calculated hepatic arterial, portal and total perfusion values using estimated or measured input functions were similar, and consistent with ultrasonography measurements.
Acknowledgments
The authors thank the technical staff of the Turku PET Centre for the efforts and skills dedicated to this project. This work is part of the project Hepatic and Adipose Tissue and Functions in the Metabolic Syndrome (HEPADIP, see http://www.hepadip.org/), which is supported by the European Commission as an Integrated Project under the 6th Framework Programme (contract LSHMCT-2005-018734). The study was further supported by grants from the Academy of Finland (206359 to P.N.), Finnish Diabetes Foundation (P.I.), EFSD/Eli-Lilly (P.I.), Sigrid Juselius Foundation (N.K. and P.I.), and Novo Nordisk Foundation (P.N.).
Appendix
A model function for AIF was created, by assuming a two-compartment model, in which the tracer is administered in a rectangular form and diffuses bi-directionally between arterial and interstitial space in whole body peripheral tissue compartments. Differential equations for the model function (CA(t)) can be expressed as;
| (A-1) |
| (A-2) |
| (A-3) |
where t1 and t2 assumes the appearance time of administered tracer and t2−t1 represents the administration duration, A corresponds to the given amount of tracer. The equation: F (equation (A-3)), represents the bolus administration of tracer in the rectangular form with duration: t2−t1. CWB(t) is the expected tracer concentration in interstitial spaces in whole body peripheral tissues, Ke and Ki are bidirectional tracer diffusion rates between blood and peripheral tissue compartments, respectively. Solving equation (A-2) for CWB gives:
| (A-4) |
Sum of equation (A-1) and (A-2) is:
| (A-5) |
Thus:
| (A-6) |
Substitution of CWB from equation (A-4) into (A-6) after multiplying eKi·t, gives:
| (A-7) |
Differentiation with respect to t after arranging gives;
| (A-8) |
where α=Ki/Ke. Thus:
| (A-9) |
Solving equation (A-9), we obtain:
| (A-10) |
The first term in the second equation for t1<t<t2, i.e., Keα(1+α)(t1−t2) would complicate further calculations (such as tissue response and portal input), thus this term was omitted, and the model function (A-10) was modified to set the CA value as 0 at t=t1, as continuous at t=t2, and as non zero value at the equilibrium, i.e., at t=∞. Thus, following equation was derived:
| (A-11) |
References
- Alenius S, Ruotsalainen U. Bayesian image reconstruction for emission tomography based on median root prior. Eur J Nucl Med . 1997;24:258–65. doi: 10.1007/BF01728761. [DOI] [PubMed] [Google Scholar]
- Becker GA, Muller-Schauenburg W, Spilker ME, Machulla HJ, Piert M. A priori identifiability of a one-compartment model with two input functions for liver blood flow measurements. Phys Med Biol . 2005;50:1393–404. doi: 10.1088/0031-9155/50/7/004. [DOI] [PubMed] [Google Scholar]
- Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet . 1986;1:307–10. [PubMed] [Google Scholar]
- Blomley MJ, Coulden R, Dawson P, et al. Liver perfusion studied with ultrafast CT. J Comput Assist Tomogr. 1995;19:424–433. doi: 10.1097/00004728-199505000-00016. [DOI] [PubMed] [Google Scholar]
- Carson RE. Parameter estimation in positron emission tomography. In: Phelps ME, Mazziotta JC, Schelbert HR, editors. Positron Emission Tomography and Autoradiography: Principles and Applications for the Brain and Heart. New York, NY: Raven Press; 1986. pp. 347–390. [Google Scholar]
- Johnson DJ, Muhlbacher F, Wilmore DW. Measurement of hepatic blood flow. J Surg Res. 1985;39:470–81. doi: 10.1016/0022-4804(85)90102-7. [DOI] [PubMed] [Google Scholar]
- Edward VR, Di Bella EV, Clackdoyle R, Gullberg GT. Blind estimation of compartmental model parameters. Phys Med Biol. 1999;44:765–80. doi: 10.1088/0031-9155/44/3/018. [DOI] [PubMed] [Google Scholar]
- Eriksson L, Holte S, Bohm Chr, Kesselberg M, Hovander B. Automated blood sampling system for positron emission tomography. IEEE Transaction on Nuclear Science. 1988;35:703–707. [Google Scholar]
- Eriksson L, Kanno I. Blood sampling devices and measurements. Med Prog Technol. 1991;17:249–57. [PubMed] [Google Scholar]
- Henderson JM, Gilmore GT, Mackay GJ, Galloway JR, Dodson TF, Kutner MH. Hemodynamics during liver transplantation: the interactions between cardiac output and portal venous and hepatic arterial flows. Hepatology. 1992;16:715–718. doi: 10.1002/hep.1840160316. [DOI] [PubMed] [Google Scholar]
- Iida H, Kanno I, Miura S, Murakami M, Takahashi K, Uemura K. Error analysis of a quantitative cerebral blood flow measurement using H215O autoradiography and positron emission tomography, with respect to the dispersion of the input function. J Cereb Blood Flow Metab. 1986;6:536–545. doi: 10.1038/jcbfm.1986.99. [DOI] [PubMed] [Google Scholar]
- Iida H, Higano S, Tomura N, Shishido F, Kanno I, Miura S, Murakami M, Takahashi K, Sasaki H, Uemura K. Evaluation of regional differences of tracer appearance time in cerebral tissues using [15O] water and dynamic positron emission tomography. J Cereb Blood Flow Metab. 1988;8:285–288. doi: 10.1038/jcbfm.1988.60. [DOI] [PubMed] [Google Scholar]
- Iozzo P, Gastaldelli A, Järvisalo MJ, Kiss J, Borra R, Buzzigoli E, Viljanen A, Naum G, Viljanen T, Oikonen V, Knuuti J, Savunen T, Salvadori PA, Ferrannini E, Nuutila P. 18F-FDG assessment of glucose disposal and production rates during fasting and insulin stimulation: a validation study. J Nucl Med. 2006;47:1016–22. [PubMed] [Google Scholar]
- Iozzo P, Järvisalo MJ, Kiss J, Borra R, Naum GA, Viljanen A, Viljanen T, Gastaldelli A, Buzzigoli E, Guiducci L, Barsotti E, Savunen T, Knuuti J, Haaparanta-Solin M, Ferrannini E, Nuutila P. Quantification of liver glucose metabolism by positron emission tomography: validation study in pigs. Gastroenterology. 2007;132:531–42. doi: 10.1053/j.gastro.2006.12.040. [DOI] [PubMed] [Google Scholar]
- Juillard L, Janier M, Fouque D, et al. Renal blood flow measurement by positron emission tomography using 15O-labeled water. Kidney International. 2000;57:2511–2518. doi: 10.1046/j.1523-1755.2000.00110.x. [DOI] [PubMed] [Google Scholar]
- Kanno I, Iida H, Miura S, Murakami M, Takahashi K, Sasaki H, Inugami A, Shishido F, Uemura K. A system for cerebral blood flow measurement using an H215O autoradiographic method and positron emission tomography. J Cereb Blood Flow Metab . 1987;7:143–53. doi: 10.1038/jcbfm.1987.37. [DOI] [PubMed] [Google Scholar]
- Kudomi N, Choi E, Watabe H, Kim KM, Shidahara M, Ogawa M, Teramoto N, Sakamoto E, Iida H. Development of a GSO Detector Assembly for a Continuous Blood Sampling System. IEEE TNS. 2003;50:70–73. [Google Scholar]
- Kudomi Nobuyuki, Watabe Hiroshi, Hayashi Takuya, Iida Hidehiro. Non-invasive estimation of arterial input function for water and oxygen from PET dynamic images. J Nucl Med. 2006;47(Supplement 1):361. [Google Scholar]
- Leen E, Goldberg JA, Anderson JR, et al. Hepatic perfusion changes in patients with liver metastases: comparison with those patients with cirrhosis. Gut. 1993;34:554–557. doi: 10.1136/gut.34.4.554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindstedt, Schaeffer Use of allometry in predicting anatomical and physiological parameters of mammals. Laboratory Animals. 2002;36:1–19. doi: 10.1258/0023677021911731. [DOI] [PubMed] [Google Scholar]
- Martin-Comin J, Mora J, Figueras J, et al. Calculation of portal contribution to hepatic blood flow with 99m-Tc-microcolloids. A noninvasive method to diagnose liver graft rejection. J Nucl Med. 1988;29:1776–1780. [PubMed] [Google Scholar]
- Materne R, Van Beers BE, Smith AM, Leconte I, Jamart J, Dehoux JP, Keyeux A, Horsmans Y. Non-invasive quantification of liver perfusion with dynamic computed tomography and a dual-input one-compartmental model. Clin Sci (Lond) . 2000;99:517–25. [PubMed] [Google Scholar]
- Munk OL, Bass L, Roelsgaard K, Bender D, Hansen SB, Keiding S. Liver kinetics of glucose analogs measured in pigs by PET: importance of dual-input blood sampling. Nucl Med . 2001;42:795–801. [PubMed] [Google Scholar]
- Naganawa M, Kimura Y, Nariai T, et al. Omission of serial arterial blood sampling in neuroreceptor imaging with independent component analysis. NeuroImage. 2005a;26:885–890. doi: 10.1016/j.neuroimage.2005.02.025. [DOI] [PubMed] [Google Scholar]
- Naganawa M, Kimura Y, Ishii K, Oda K, Ishiwata K, Matani A. Extraction of a Plasma Time-Activity Curve From Dynamic Brain PET Images Based on Independent Component Analysis. IEEE Trans on Bio-Med Eng. 2005b;52:201–210. doi: 10.1109/TBME.2004.840193. [DOI] [PubMed] [Google Scholar]
- Ruotsalainen U, Raitakari M, Nuutila P, Oikonen V, Sipilä H, Teräs M, Knuuti MJ, Bloomfield PM, Iida H. Quantitative blood flow measurement of skeletal muscle using oxygen-15-water and PET. J Nucl Med. 1997;38:314–9. [PubMed] [Google Scholar]
- Sanabria-Bohorquez SM, Maes A, Dupont P, Bormans G, de Groot T, Coimbra A, Eng W, Laethem T, De Lepeleire I, Gambale J, Vega JM, Burns HD. Image-derived Input Function for [11C]Flumazenil Kinetic Analysis in Human Brain. Mol Img Biol. 2003;5:72.78. doi: 10.1016/s1536-1632(03)00046-5. [DOI] [PubMed] [Google Scholar]
- Taniguchi H, Oguro A, Takeuchi K, Miyata K, Takahashi T, Inaba T, Nakahashi H. Difference in regional hepatic blood flow in liver segments--non-invasive measurement of regional hepatic arterial and portal blood flow in human by positron emission tomography with H2(15)O. Ann Nucl Med. 1993;7:141–5. doi: 10.1007/BF03164957. [DOI] [PubMed] [Google Scholar]
- Taniguchi H, Oguro A, Koyama H, Masuyama M, Takahashi T. Analysis of models for quantification of arterial and portal blood flow in the human liver using PET. J Comput Assist Tomogr. 1996a;20:135–44. doi: 10.1097/00004728-199601000-00025. [DOI] [PubMed] [Google Scholar]
- Taniguchi H, Koyama H, Masuyama M, Takada A, Mugitani T, Tanaka H, Hoshima M, Takahashi T. Angiotensin-II-induced hypertension chemotherapy: evaluation of hepatic blood flow with oxygen-15 PET. J Nucl Med . 1996b;37:1522–3. [PubMed] [Google Scholar]
- Taniguchi H, Yamaguchi A, Kunishima S, Koh T, Masuyama M, Koyama H, Oguro A, Yamagishi H. Using the spleen for time-delay correction of the input function in measuring hepatic blood flow with oxygen-15 water by dynamic PET. Ann Nucl Med . 1999;13:215–21. doi: 10.1007/BF03164895. [DOI] [PubMed] [Google Scholar]
- Van der Weerdt A, Klein LJ, Boellaard R, Visser CA, Visser FC, Lammertsma AA. Image-derived Input Functions for Determination of MRGlu in Cardiac 18F-FDG PET Scans. J Nucl Med. 2001;42:1622–1629. [PubMed] [Google Scholar]
- Votaw JR, Shulman SD. Performance evaluation of the Pico-Count flow-through detector for use in cerebral blood flow PET studies. J Nucl Med. 1998;39:509–515. [PubMed] [Google Scholar]
- Watabe H, Channing MA, Riddell C, Jousse F, Libutti SK, Carrasquillo JA, Bacharach SL, Carson RE. Noninvasive estimation of the aorta input function for measurement of tumor blood flow with. IEEE Trans Med Imaging. 2001;20:164–74. doi: 10.1109/42.918468. [DOI] [PubMed] [Google Scholar]
- Ziegler SI, Haberkorn U, Byrne H, Tong C, Kaja S, Richolt JA, Byrne H, Tong C, Schosser R, Krieter H, Kaja S, Richolt JA, Lammertsma AA. Price P Measurement of liver blood flow using oxygen-15 labelled water and dynamic positron emission tomography: limitations of model description. Eur J Nucl Med . 1996;23:169–77. doi: 10.1007/BF01731841. [DOI] [PubMed] [Google Scholar]


