Figure 5.

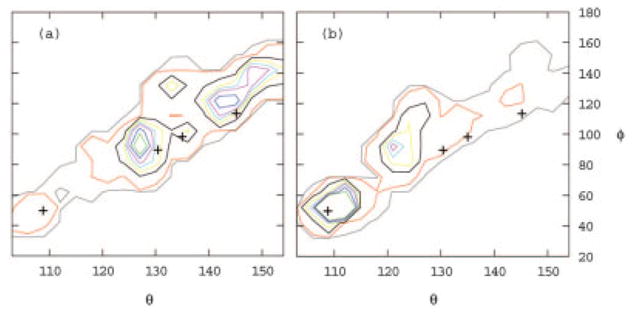
Calculated population distribution of (a) ribose-free and (b) ribose-bound RBP as a function of the interdomain bending angle θ and twisting angle φ (see Fig. 4). Contours are drawn at 0.08 (green), 0.06 (blue), 0.04 (magenta), 0.03 (sky blue), 0.02 (yellow), 0.01 (brown), 0.001 (red), and 0.0001(gray) relative populations. The crosses indicate the (θ, φ) coordinates of the crystal structures of, with increasing angle θ, the closed ribose-bound (2dri) and open ribose-free (1urp) conformations of RBP, and open ribose-free conformations of a single-point mutant of RBP (1ba2). The angle θ is defined as the angle formed between the centers of mass of the C- and N-terminal domains and the center of mass of the hinge region. The angle φ is defined as the dihedral angle formed by the center of mass of the N-terminal domain, the center of mass of the residues on the N-terminal domain side of each of the three hinge strands, the center of mass of the corresponding residues on the C-terminal domain side of the three hinge strands, and the center of mass of the C-terminal domain. Angles are expressed in degrees. Highly populated conformations generally correspond to experimental crystal conformations. In agreement with experiments, the predicted population of the closed conformation (θ ≈ 110°, φ ≈ 50°) in the presence of ribose (b) is larger than in the absence of ribose (a). Similarly, the population of open conformations (θ >115°) is larger in the absence of ribose. The population peak at (θ ≈ 122°, φ ≈ 95°) in the presence of ribose (b) corresponds to a partially open conformation not yet observed experimentally postulated to play a role in the mechanism of ribose transport.