Tomosynthesis via Total Variation Minimization Reconstruction and Prior Image Constrained Compressed Sensing (PICCS) on a C-arm System

Abstract

Recently, foundational mathematical theory, compressed sensing (CS), has been developed which enables accurate reconstruction from greatly undersampled frequency information (Candes et. al. and Donoho). Using numerical phantoms it has been demonstrated that CS reconstruction (e.g. minimizing the ${\ell }_1$ norm of the discrete gradient of the image) offers promise for computed tomography. However, when using experimental CT projection data the undersampling factors enabled were smaller than in numerical simulations. An extension to CS has recently been proposed wherein a prior image is utilized as a constraint in the image reconstruction procedure (i.e. Prior Image Constrained Compressed Sensing - PICCS). Experimental results are demonstrated here from a clinical C-arm system, highlighting one application of PICCS in reducing radiation exposure during interventional procedures while preserving high image quality. In this study a range of view angles has been investigated from very limited angle aquisitions (e.g. tomosythesis) to undersampled CT acquisitions.

1. INTRODUCTION

The research presented here is based upon recent foundational mathematical theory, compressed sensing (CS), that allows for accurate reconstruction from highly undersampled frequency data.^1,2 In tests with numerical phantoms CS has provided accurate reconstruction with very impressive undersampling factors for computed tomography.³ However, in the case that experimental CT projection data is utilized the undersampling factors feasible without significant degredation in image quality are smaller than in the numerical phantom experiments.^4,5 An extension to CS has recently been proposed wherein a prior image is utilized as a constraint in the image reconstruction procedure (i.e. Prior Image Constraint Compressed Sensing - PICCS).⁵ The additional sparsification transform of subtracting the prior image from the current image estimate has enabled significant increases in the undersampling factors enabled.⁵ In this work we demonstrate experimental results from a clinical C-arm system (GE Healthcare's Innova 4100). The application proposed here is to utilize PICCS in order to reduce radiation exposure during interventional procedures without sacraficing image quality.

We will first review the basis of the PICCS algorithm and demonstrate the differences between this new algorithm and current CS algorithms. For a given image X, the compressed sensing minimization problem^1,2 may be expressed as

$$\underset{X}{\text{min}}{\mid \Psi X\mid }_{{\ell }_1},s.t.AX=Y,$$ (1)

where ${\mid \mathbf{z}\mid }_{{\ell }_1}={\Sigma }_{i=1}^N\mid {\mathbf{z}}_i\mid$ is the ${\ell }_1$ norm of an N-dimensional vector z, and Ψ is a sparsifying transform. In the compressed sensing literature sparsifying transforms include the discrete gradient transform and wavelet transforms. In this work we have used the discrete gradient transform which is defined as

$${\nabla }_{m,n}X(m,n)=\sqrt{{\left(D_{x}X\right)}^2+{\left(D_{y}X\right)}^2}$$ (2)

where X(m, n) is the intensity value at (m, n) and D_xX = X(m + 1, n) – X(m, n) and D_yX = X(m, n + 1) – X(m, n). When the gradient transform is utilized in this framework the minimization problem becomes that of minimizing the total variation (TV) in the image. A new framework was recently proposed by our group⁵ where the objective function has been modified to include some apriori infomation about the image volume.

$$\underset{X}{\text{min}}[\alpha {\mid {\Psi }_1(X-X_p)\mid }_{{\ell }_1}+(1-\alpha ){\mid {\Psi }_{2}X\mid }_{{\ell }_1}],s.t.AX=Y.$$ (3)

Thus, this new reconstruction framework is referred to as Prior Image Constrained Compressed Sensing (PICCS), and comparisons with compressed sensing (CS) will be performed using the same parameters (e.g. setting α = 0 in the Eq. 3).

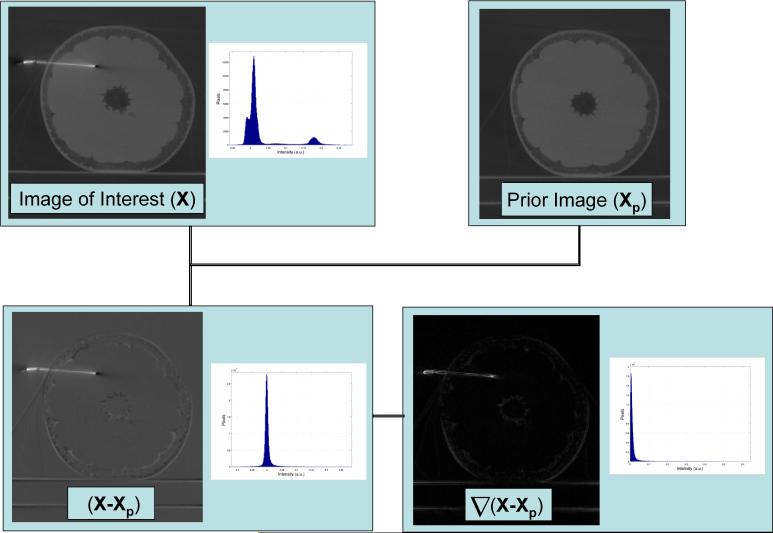
To illustrate the significant increase in image sparseness Flat-Panel Cone-beam CT (FP-CBCT) images of a grapefruit before and after needle insertion have been subjected to the sparcification transforms used in PICCS (Figure 1). First a subtraction with a prior image then a discrete gradient transform. From the images and corresponding histograms there is a clear increase in image sparsity as the number of significant image voxels (e.g. image voxels which are above the level of noise) has significantly decreased after applying the sparsification tranformations.

Figure 1.

Demonstration of the sparsifying transforms used in this work. Upper left: a FP-CBCT image containing both a grapefruit and a needle. Upper right: a possible prior image for this case which is the grapefruit before needle insertion. Lower left: the difference image between the image of interest and the prior. Lower right: the magnitude of the gradient of the difference image. In each case the histograms plotted beside the images plot the number of pixels in each given intensity bin. Note, that after the sparsification transforms there are many more pixels with values near zero.

We will motivate the clinical problem addressed here with the PICCS algorithm through a demonstration from clinical research being conducted at our institution (Figure 2), where a needle has been placed within a simulated tumor in a porcine model. Intra-operative three dimensional imaging via FP-CBCT offers both high spatial resolution and the ability to image low contrast structures such as soft-tissue. Thus, it provides a realistic alternative to pre-operative CT/MR imaging combined with fiducial markers or bony anatomical references. Intra-operative imaging also has the advantage that it takes into account changes in the anatomy occuring before and during the intervention. Siewerdsen's group has proposed using tomosynthesis to supplement cone-beam CT during the intervention.⁶ In this work we propose that as multiple FP-CBCT acquisitions may be used during a procedure that the radiation dose may be reduced for the entire procedure by using an initial intra-operative planning FP-CBCT to constrain subsequent acquisitions used for monitoring or verifying purposes.

Figure 2.

One possible application of CS and PICCS on the C-arm system is to provide reduced dose for intra-operative CT/tomosynthesis monitoring by using known information from a prior image (e.g. a planning FP-CBCT).

2. METHODS

2.1. PICCS for interventional guidance

The schematic illustration (Figure 3 (a)) demonstrates the proposed data flow to generate reconstructed images for surgical guidance with undersampled/incomplete data, where a fully sampled FP-CBCT is used as the prior image in the PICCS algorithm. The data may come from undersampled cone-beam CT (short-scan range) or a tomosynthetic acquisition. A range of tomo angles has been studied here as given in Figure 3, where the total exposure is kept constant by fixing the total number of frames used to 20. This represents a 20 fold dose reduction from the fully sampled acquisition (400 views over 200°). In this study the entire dose reduction was achieved by using fewer view angles for the PICCS reconstruction, but one may also use reduced exposure from each view angle to achieve dose reduction with the PICCS algorithm.

Figure 3.

The illustration given in (a) demonstrates the suggested pipeline where a fully sampled FP-CBCT scan is used as the prior image volume for image reconstruction with PICCS using either a subsequent tomosynthesis acquisition or subsequent undersampled CT data. In (b) we describe the range of tomosynthesis angles studied from a short scan acquisition (e.g. 200°) to a very limited tomo angle (e.g. 10°).

2.2. Implementation of PICCS on a C-arm system

When implementing these algorithms with ideal systems in numeric simulations the forward-projection and back-projection operations can be implemented using the simple geometric equations relating the source and detector positions. However, on experimental/clinical systems the ideal imaging geometry is typically not realized. Despite these deviations from the ideal trajectory the actual trajectory and the projection operator from view to view is repeatable on this system.⁸ Therefore, the projection operators for each view may estimated via a calibration scan, and then used for later acquisitions. For this purpose we have used a geometrical phantom consisting of 41 ball bearings in a known helical geometry was scanned, from which 3 × 4 projection matrices (P-matrices) were calculated using a view by view minimization procedure.^7,8 Each point in image space is mapped to the detector space by multiplication with the P-matrix from a given view,

$$\left[\begin{array}{c}\hfill s\cdot u\hfill \\ \hfill s\cdot v\hfill \\ \hfill s\hfill \end{array}\right]=\mathbf{P}\left[\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \\ \hfill z\hfill \\ \hfill 1\hfill \end{array}\right]$$ (4)

where u, v are the detector coordinates, and x, y, z are the image coordinates as seen in Figure 4. The P-matrix based backprojection operation in the filtered backprojection (FBP) reconstruction is voxel driven⁹ using the efficient implementation which does not require the full matrix multiplication for each voxel. The P-matrix based forward and backprojection operations in the iterative methods are ray driven, where the entry and exit points to the reconstructed volume are calculated directly from the P-matrix rather than using estimations of the source and detector positions calculated from the P-matrices.¹⁰ After calculating the entry and exit points in the reconstruction volume the standard Siddon method was utilized to calculate the overlap with each image voxel.¹¹ Data consistency, AX = Y, was enforced using the algebraic reconstruction technique (ART).¹² The projection based enforcement of the data consistency condition was choosen here for this geometry. Note that a frequency space enforcement may also be feasible for planar tomosynthesis acquisitions such linear and circular tomosynthesis. This would be accomplished using the concept of a virtual image object, where parallel projections of the virtual image object are directly related to divergent projections of the real object.^13,14 The TV/PICCS minimization procedure was carried out using a standard steepest decent minimization.¹⁵ The parameter ‘numberSDIterations’ refers to the number of steepest decent iterations used in approaching the solution to the minimization problem before enforcing the data consistency condition AX = Y . The parameters used in this minimization procedure were determined emperically and a systematic optimization of these parameters has not yet been conducted. The pseudo-code for our implementation used in this work is given below.

Xp ← FBP Reconstruction (Prior)

X0 ← Xp

while (||Xk - Xk-1||2 < ε)

foreach Raypath [ART Iteration]

Forward project through Xk

Compare the forward projection with the measured detector data

Backproject the difference (ray-driven)

end foreach

for( i=1:numberSDIterations ) [using the CS or PICCS objective]

Take a step in the steepest decent minimization

end for

end while

Figure 4.

Illustration of the geometry for our C-arm system which is modeled using projection matrices. The ray passing through a point $\overrightarrow{x}$ from the source point $\overrightarrow{y}$(t) has overlap with the image volume as shown in red.

2.3. Experimental Parameters

The projection data was acquired from a GE Innova 4100 flat panel based C-arm system with the physical parameters given in Figure 5a. Standard pre-processing^8,16 and reconstruction was performed using in house software written in C++ with the parameters given in the Figure 5b. The ‘planning image’ was of a grapefruit before needle insertion and the ‘verification image’ was after needle insertion. Rapid convergence was observed for both the CS and PICCS algorithms; thus all results presented here used only five ART iterations for both the CS and PICCS algorithms.

Figure 5.

(a) The physical parameters used when scanning the grapefruit for the experiments given here. (b) The reconstruction parameters used to achieve the results presented below, where the normalized TV step is given in terms of the maximum value in the prior images.

3. RESULTS

A comparison of the axial image slices for the short scan acquisition (e.g. 20 views over 200°). The distracting streaking artifacts present in the FBP image have been supressed with the PICCS algorithm and more detail is present in the background anatomy of the PICCS image (e.g. examine the center of the image). There is a slight glarring around the needle in the CS and PICCS results, but the needle remains well visualized in each case (Figure 6).

Figure 6.

The axial reconstruction results for the undersampled FP-CBCT acquisition where the data range satisfies the short-scan criteria.

The reconstruction results in Figure 7 show coronal image planes (i.e. standard for PA tomosynthesis). All images presented here are displayed over the full range of intensity values. Note that even for small tomo angles the PICCS results maintain the proper background anatomy while the standard tomosynthesis results display the well known trend of through plane blurring and enhancing high spatial frequencies in plane. The CS algorithm here was initialized with a zero image. The CS results reduce the contribution of the high spatial frequencies compared with the FBP results but do not fully recover the background anatomy as in the PICCS results.

Figure 7.

The coronal reconstructions spanning the range of tomo angles from 10° to 200° comparing the FBP, CS and PICCS reconstructions from the 20 views of projection data.

As expected with a limited angle acquisition the ability to properly reconstruct the needle in axial slices is dependent on the scan data used. When the needle is parallel to the standard tomo planes it can not be properly recovered, but when it is perpendicular to the tomo planes it can be recovered (Figure 8). Thus, if the object introduced is of known shape one may tailor the tomosynthesis trajectory. In the case of unknown changes in the images from the planning images the undersampled CT acquisition is the safest bet.

Figure 8.

The comparison between PA and Lateral tomosynthesis for a relatively small tomo angle of 40°. The measured projection information is insufficient for depth localizaion with either the FBP or PICCS reconstruction for the PA tomosynthesis.

4. CONCLUSION

Compressed Sensing(CS) and Prior Image Constrained Compressed Sensing (PICCS) were compared to standard FBP reconstruction for undersampled/limited angle acquisitions. The PICCS algorithm enabled reconstruction of a needle introduced into a grapefruit from few views, while maintaining the ‘background anatomy’. If a tomosynthesis acquisition is choosen the orientation of the arc with respect to the anatomy is no less important than with standard image reconstruction. Experimental data in simplistic phantoms indicates that a significant undersampling is acceptable (e.g. a factor of 20 dose reduction) when using the PICCS reconstruction algorithm.

The results demonstrated here are from a well controlled experiment where motion was minimal between the prior image and subsequent imaging. In the clinical setting this may not always be the case as the patient is frequently repositioned for optimal fluoroscopic/cine imaging. Therefore, a robust implementation of this technique will require either 2D-3D registration for each projection or a transform of the prior image into the current space of the subsequent image volumes. For instance with the undersampled CT acquisition this may be accomplished by registering the undersampled acquisition to the prior image volume. For neurological applications a rigid affine transform will be used to align the prior image volume with the undersampled FBP before begining the PICCS iterations. We also plan to study the robustness of the technique to non-ideal prior images, such as using a contrast enhanced prior image to contrain a subsequent acquisition which is non contrast enhanced. Additionally, we are exploring the application of this new algorithm to dynamic contrast enhanced acquisitions on C-arm systems.