Mapping Ancient Forests: Bayesian Inference for Spatio-temporal Trends in Forest Composition Using the Fossil Pollen Proxy Record

Abstract

Ecologists use the relative abundance of fossil pollen in sediments to estimate how tree species abundances change over space and time. To predict historical forest composition and quantify the available information, we build a Bayesian hierarchical model of forest composition in central New England, USA, based on pollen in a network of ponds. The critical relationships between abundances of taxa in the pollen record and abundances as actual vegetation are estimated for the modern and colonial periods, for which both pollen and direct vegetation data are available, based on a latent multivariate spatial process representing forest composition. For time periods in the past with only pollen data, we use the estimated model parameters to constrain predictions about the latent spatio-temporal process conditional on the pollen data. We develop an innovative graphical assessment of feature significance to help to infer which spatial patterns are reliably estimated. The model allows us to estimate the spatial distribution and relative abundances of tree species over the last 2500 years, with an assessment of uncertainty, and to draw inference about how these patterns have changed over time. Cross-validation suggests that our feature significance approach can reliably indicate certain large-scale spatial features for many taxa, but that features on scales smaller than 50 km are difficult to distinguish, as are large-scale features for some taxa. We also use the model to quantitatively investigate ecological hypotheses, including covariate effects on taxa abundances and questions about pollen dispersal characteristics. The critical advantages of our modeling approach over current ecological analyses are the explicit spatio-temporal representation, quantification of abundance on the scale of trees rather than pollen, and uncertainty characterization.

1 Introduction

Scientific inference about forest composition in the past relies heavily on sediment records of fossil pollen taken from ponds and other depositional environments (Davis 1981; Delcourt and Delcourt 1987). Fossil pollen collected from multiple sites over time acts as a proxy for the abundance of different tree taxa (species or genera), telling us about spatiotemporal vegetation dynamics over thousands of years. Paleoecologists ask questions such as the following: How have relative population abundances and range boundaries changed over time? Do stable assemblages of species exist for long periods of time or are forest compositions constantly shifting? How have forest communities changed in response to past climate shifts and what can forest composition tell us about climate? Practical environmental questions relate to how human manipulation of forests compares to natural forest change.

However, inferring tree abundance on the landscape from pollen abundance in sediments is not straightforward, because the relationship between the relative abundance of trees near a pond and pollen in the sediment of that pond is not simple. Different tree species produce different amounts of pollen on average (Jackson 1990), and the representation of any individual tree in deposited pollen is a complex function of distance to the deposition basin, size of the deposition basin, landscape openness, forest structure, wind regime, and preservation in sediments (Prentice 1985; Jackson and Lyford 1999; Nielsen and Sugita 2005). Our understanding of the timing of sediment deposition depends on indirect and inexact measurements of sediment age (through radiometric dating and strati-graphic markers). The aggregate effect of these sources of uncertainty is pollen assemblages that are noisy reflections of the trees in the surrounding landscape.

Because of these uncertainties, most paleoecological studies do not attempt to make explicit inference about the distribution of trees based on fossil pollen data. Instead, they assume that robust changes in pollen abundances over space and time generally correspond to changes in vegetation at the scales described above, primarily using multivariate time series at one or more sites (Fuller et al. 1998). Efforts to explicitly correct for differential pollen production across taxa range from primarily statistical (Tauber 1965; Prentice et al. 1987) to more mechanistic approaches (Bunting and Middleton 2005). These studies highlight the difficulty of inferring a complicated spatial pattern of pollen source contributions across the landscape from pollen proportions in a single deposition site. The power to disentangle this spatial signal using a network of sites was explored by Webb (1974) and Sugita (1993, 1994, 2007a,b). Our work provides a statistical framework to estimate the signal and quantify the uncertainty in this process based on a spatial network of noisy data.

Building on recent work in Bayesian spatio-temporal statistics (e.g., Wikle et al. 2001; Banerjee et al. 2004; Fuentes and Raftery 2005; Royle and Wikle 2005; Gelfand et al. 2006; Haslett et al. 2006), we develop an approach for modelling forest composition based on vegetation data from two key time points and pollen data from sediment cores, using a multivariate latent spatio-temporal process representing the relative abundances of different taxa. The model allows inference across space and time, based on modeling the relationship between forest composition and pollen composition for locations and times at which both vegetation and pollen data are available. Assuming consistency in the relationships over time, the model then predicts vegetation in the past using proxy pollen data. The statistical challenges are in computationally-efficient and sufficiently-resolved representation of the latent spatio-temporal surfaces, modelling spatially correlated compositional data, and carefully borrowing strength across space, time and taxa. We seek to allow the pollen data to provide as much information as possible, avoiding oversmoothing, while constraining the model sufficiently to achieve reasonable prediction that accounts for bias and noisiness. Finally, this high-dimensional model must be fit; MCMC in such situations is often time-consuming and prone to mixing difficulties (Knorr-Held and Rue 2002; Christensen et al. 2006; Paciorek 2007). There has been recent fruitful collaborative work between statisticians and ecologists in understanding patterns of species distributions (e.g., Hooten et al. 2003; Royle and Wikle 2005; Gelfand et al. 2006). Our work is in this tradition, but differs in its consideration of a multi-taxon spatial process and its use of proxy data to predict distributions over time, as well as through careful consideration of how to assess the significance of predicted spatial patterns.

Our analysis focuses on central New England in the northeastern United States over the past 2500 years. The network of pollen sites that we model is amongst the most dense sets of pollen data in existence and and has taken decades to produce. Our goals are both particular to this domain and quite general. In particular, we first want to understand the relationship between the pollen record in a pond and vegetation in the surrounding area. Second, we want to estimate and compare vegetation in our space-time domain in the colonial and modern eras. Third, our key application goal is to predict, and quantify uncertainty in, spatio-temporal patterns in tree abundances over the past 2500 years. More generally, we want to explore the ability of the pollen record to inform vegetation composition and dynamics spatially and temporally and create a modelling infrastructure useful in different areas and time periods.

Section 2 describes the pollen and vegetation data available from central New England. In Section 3 we build an estimation model to calibrate pollen to vegetation at times at which both types of data are available and then present a prediction model that uses parameter estimates from the estimation model to make predictions when only pollen data are available. We assess the model, considering the consistency and strength of the association between the proxy pollen composition and forest vegetation composition, as well as using cross-validation, and then use the model for prediction over the past 2500 years (Section 4). We also introduce innovative graphics that take advantage of the rich information in the posterior samples to assess a variety of contrasts of interest. The discussion in Section 5 highlights the contributions of the modeling approach to the ecological problem. Additional ecological analysis of model results is currently underway and will be presented in the ecological literature. Additional details on model performance and results are provided in a technical report that expands upon this manuscript (Paciorek and McLachlan 2008), noted in several places in the text.

2 Data

2.1 Study area and study taxa

Our study area extends from 43°, 21′ N, 73°, 30′ W in the northwest to 41°, 37′ N, 71°, 13′ W in the southeast corner in south-central New England, USA, focusing on central and western Massachusetts, west of the Boston metropolitan area. In projected coordinates, this defines a region, 192 × 192 km², which for computational reasons we divide into a 16 by 16 grid, with each grid cell 12 km on a side. All computations are done at the resolution of the grid cell.

We focus on 9 particular taxa (genus or species), including the most common taxa in the area: oak (Quercus spp.), pine (Pinus spp.), maple (Acer spp.), hemlock (Tsuga canadensis), and beech (Fagus grandifolia); as well as several additional taxa of particular interest, namely hickory (Carya spp.), birch (Betula spp.), spruce (Picea spp.), and chestnut (Castanea dentata). Other tree taxa, excluding taxa that are primarily shrubs and small trees, are grouped into a tenth category and included in the analysis as a tenth reference ’taxon’. Note that due to chestnut blight there have been essentially no adult pollen-producing chestnut in the study area in the last 100 years, so many of our figures omit chestnut.

2.2 Pollen data

Plant pollen from trees, shrubs and herbaceous plants falls on the surfaces of ponds, sinks to the bottom, and accumulates in sediment. Over time, these sediments are buried by layers from successive time periods, creating a sediment record of what fell into the pond. The scale of vegetation that corresponds most closely to the composition of pollen in the sediments of small ponds and depositional environments is generally vegetation within one to two km (Jackson 1990; Jackson and Lyford 1999; Nielsen and Sugita 2005), but more than half of the total pollen in those sediments may originate beyond that distance (Sugita 1994; Sugita et al. 1998; Sugita 2007b).

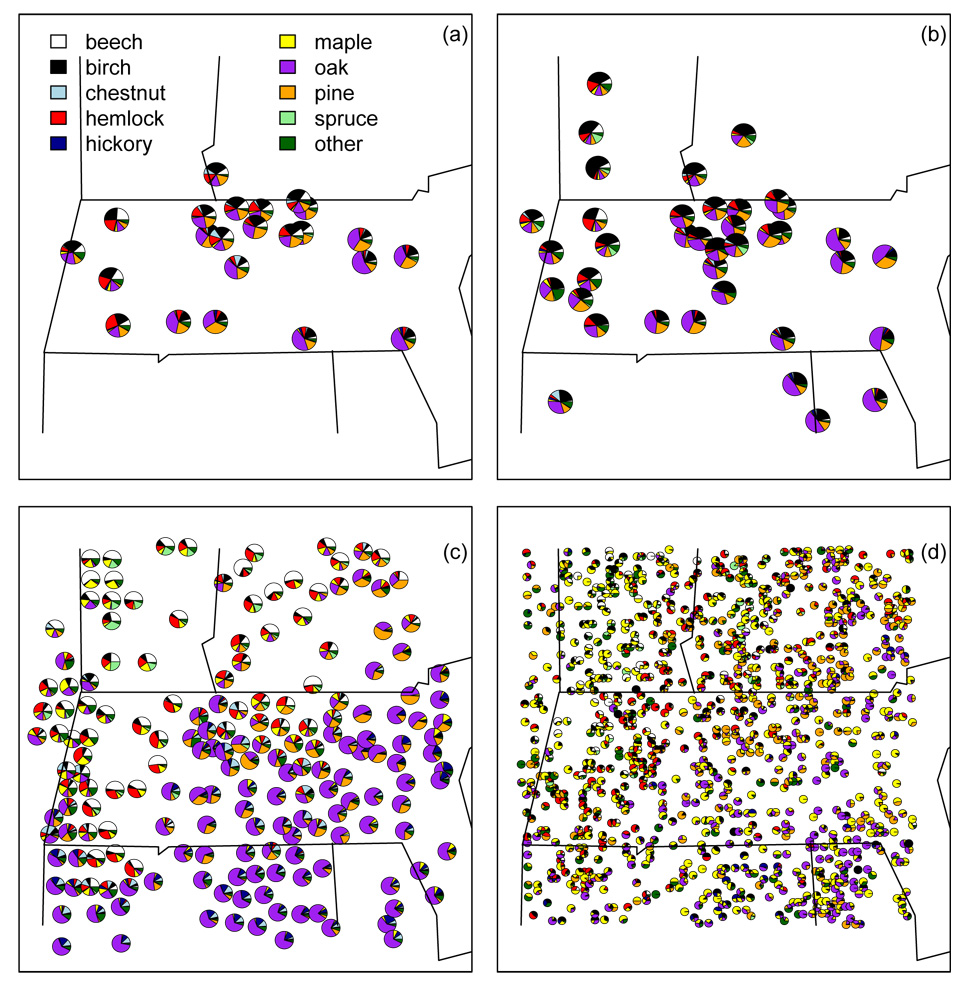
As described below, the period of colonial settlement and the modern period are times when vegetation and pollen data can be compared. While separated only by a few hundred years, these periods are likely to be as disparate in forest structure and composition as any two time periods considered, because of the drastic ecological effects of post-settlement land use (Foster et al. 1998; Fuller et al. 1998; Oswald et al. 2007). Colonial era surveys provide historical vegetation data, but the surveys occurred at different times in different parts of the study region. Therefore, we used the appearance of agricultural weed pollen to select pollen samples (~500 grains) at individual times from 23 ponds with archived sediment cores to best match the time at which the survey in the township encompassing each pond was completed (Fig. 1a). Because settlement occurred over a period of time, the colonial era data do not represent a fixed snapshot in time, but rather a reasonably consistent window within the settlement process, stretching over the years ca. 1635–1800. Because of the long lifespans of trees and the relatively quick settlement, we consider this treatment of the colonial data to be reasonable. For the modern era we use surface sediment samples to best represent current vegetation, taken from 38 ponds (Fig. 1b).

Figure 1.

(a) Pollen composition by pond for the colonial era. (b) Pollen composition by pond for the modern era. (c) Witness tree vegetation composition for the colonial era (plotted at the centroids of colonial townships). (d) Forest service plot vegetation composition for the modern era.

To make predictions back in time, we make use of the full archived cores from the 23 ponds. The temporal coverage varies, with ponds having records of length varying between the most recent 1000 years and the most recent 15000 years, with the most recent 2500 years being our full period of interest. Each core is divided into intervals and approximately 500 grains from a sample of sediment in each interval are identified and counted. A subset of samples is dated using radiocarbon dating, with linear interpolation providing dates for all samples, resulting in samples at different and irregular times for each pond. The uncertainties in the dating include the natural stochasticity of radioactive decay, the linear interpolation, uncertainty in the calibration of radiocarbon to calendar years, and uncertainty in the assignment of calendar age to the appearance of weed pollen in the cores, in addition to uncertainty in the lead-210 dating used for the most recent 150 years. Paciorek and McLachlan (2008) outline a potential approach to extend the Bayesian calibration methods of Blaauw and Christen (2005) to the spatial context. We do not account for the dating uncertainties here, in part because of our focus on changes at time scales of several hundred years or more, for which uncertainties in dating should have limited impact.

Some sediment mixing occurs in upper sediments, so any individual sample represents pollen deposited over a period of years, naturally smoothing the data. The long lifespan of trees also causes smoothness. Accordingly, in our spatio-temporal predictions, we aggregate all samples into intervals of 100 calendar years and base the prediction model on this set of discrete times. The first interval is centered on 1950 (defined to be the ’present’ or year 0 in the paleoecological dating scheme) and the last is centered on 550 B.C. (denoted henceforth as year -2500).

2.3 Vegetation data

2.3.1 Colonial witness tree data

During settlement of central New England in the 17th and 18th centuries, colonial surveyors surveyed lots of size 0.5–65 ha for settlement, citing ’witness’ trees as permanent markers of the lot corners within townships (approximately 6-mile square). Records of these witness trees have been recovered from town archives, and surveyor identifications have been mapped to modern taxonomic classification (Cogbill et al. 2002). These data are available aggregated to the township, with between 26 and 3149 trees per township for 183 townships with known boundaries in our study region, providing 87,114 trees in total (Fig. 1c).

2.3.2 Modern vegetation data

The U.S. Forest Service (USFS) Forest Inventory Analysis (FIA: www.fia.fs.fed.us) program samples vegetation using randomly-located plots on both public and private land, counting and identifying (to species) all trees in four 7.3 m radius subplots located 36.6 m apart. Our data consist of FIA tree counts of individuals greater than 10 cm diameter at breast height (1.3m) from 1990 for 1094 plots in the study area, with individuals aggregated into our ten taxa (Fig. 1d). Because of privacy concerns, USFS randomizes the plot locations to within 1.6 km of actual location. The plots contain between one and 115 trees per plot, with 29,938 trees in total.

3 Model description

3.1 Notation

Let p = 1, …, P (for population) index the P = 10 tree taxa. The subscript i indexes the vegetation plots or townships. We work on a regular grid, with s = 1, …, S indexing the S = 16² spatial locations on the grid and t = 1,…, T indexing the T time points, discretized in 100 year intervals. To simplify the notation, we suppress the dependence on t when considering the modern and colonial periods.

3.2 Overview

Our modelling proceeds in two basic steps. First, in ’estimation runs’, we use the modern and colonial data to estimate key parameters describing the pollen-vegetation relationships and critical hyperparameters that constrain the model structure, borrowing strength across multiple ponds based on the spatial process structure. Second, in ’prediction’ runs, we use only pollen data and the estimated key parameter values to make predictions in the past. The critical hyperparameters reflect the general structure of vegetation and parameterize spatial process variability, regression coefficient variability, and long-distance pollen dispersal. They serve to constrain the model to produce reasonable predictions with only a small number of ponds.

An alternative is to fit a coherent Bayesian model to all the pollen and vegetation data at all points in time. However, with a complicated model and multiple data sources, model misspecification and difficulty in model development and assessment are major concerns that would be exacerbated in a single integrated analysis. Our approach also allows us to carefully control what information is used to inform and constrain the inference at different points in time, for example, making inference about parameters related to the general structure of the vegetation based only on the vegetation data (Section 3.3.4). It also eases the computational burden.

We note that our multivariate non-normal outcome prevents conjugate updates of the latent process values and analytic integration over these process values, greatly affecting MCMC mixing and limiting our ability to fit complicated structure in the model hierarchy. This stands in contrast to much recent work with normal data that extends simple Bayesian spatial models to spatio-temporal, multivariate, nonseparable, and other settings. This constraint, combined with sparse, noisy, and complicated data, necessitates careful attention to deciding upon the key aspects of reality to represent in the model structure.

3.3 Estimation model

3.3.1 Likelihood terms

Our likelihood terms are conditional on a latent multivariate spatial process, which provides the the composition vector for each grid cell, r (s) = (r₁(s), …, r_P (s)), described in Section 3.3.2. Here we define the separate likelihoods for modern plot data, colonial witness tree data, and pollen data.

Vegetation

For the vegetation, our basic strategy is to use a Dirichlet-multinomial (𝒟ℳ) structure (also known as the compound multinomial distribution, a generalization of the beta-binomial) (Dey and Maiti 2002) to account for overdispersion in the vegetation data due to heterogeneity of vegetation within grid cells. First, consider the FIA plot data. We associate each plot, i, with the grid cell in which the plot falls, s(i). The likelihood for the vector of tree counts, conditionally independent between plots, is υ_i = {υ_1,i, …, υ_P,i} ~ 𝒟ℳ (n_i, α_FIAr(s(i))), where n_i = Σ_p υ_p,i. The scalar Dirichlet precision parameter, α_FIA, is multiplied by each element of the composition vector for the grid cell in which the plot falls, r(s(i)). For the witness trees, the structure is similar, except that the tree counts are aggregated into townships, which are generally larger than the grid cells and are misaligned with respect to the grid. To account for this, we consider the count of trees in a township, i, to represent a weighted average of the trees in the grid cells that the township overlaps, s ∈ O(i), where O(i) is the set of overlapped grid cells. The weighting is based on the proportion of the township falling in each grid cell, w_i (s). This gives us the likelihood for the ithe township, υ_i ~ 𝒟ℳ (n_i, α_WTr̄(i))), where r̄(i) = (r̄₁(i), … , r̄_P(i)) and the proportion of the pth taxa in the ith township is r̄p(i) = Σ_s∈O(i) w_i(s)r_p(s). In other words, the composition for the township is calculated as the integral over the gridded piecewise composition surface. Other approaches are possible, such as using the intersections of the grid cells and townships (Mugglin et al. 2000) in the discretization of the spatial domain, but seem unlikely to materially affect the results.

Pollen

For the pollen, the likelihood must account for the fact that pollen production and dispersal vary by taxon, which causes the proxy pollen data to be biased for the local vegetation, even if one were to directly measure pollen falling to the ground. We again use the Dirichlet-multinomial form for the pollen count data for the modern and colonial eras, but we differentially scale the vegetation composition in the grid cell to account for the bias. The likelihood for the vector of pollen counts at location i, c_i, is,

$${\mathit{c}}_{\mathit{i}}=\left\{c_{1,i},\dots ,c_{P,i}\right\}~𝒟ℳ(n_i,\varphi •\mathit{r}(\mathit{s}(\mathit{i}))),$$ (1)

where ϕ is a vector of taxon-specific scaling factors that relate pollen to vegetation and r(s(i)) is the vegetation composition of the grid cell in which the pond lies. Note that the multiplication is done element-wise (i.e., a Hadamard product). Because of chestnut blight, there are essentially no pollen-producing chestnut adults in the modern era, so we cannot estimate ϕ for chestnut in the modern era and assume this value is the same as for the ’other’ category.

An added complication is that examination of the pollen data suggests a substantial fraction of pollen is derived from long-distance dispersal. Based on nearby vegetation data in the modern and colonial periods and on site visits by the authors, many ponds have taxa present despite little evidence that the taxa exist locally in sufficient quantity to explain the pollen abundance. The model assumes that 0 ≤ γ ≤ 1 of the proportion of pollen produced in a cell remains in the cell and the remaining 1 − γ distributes in a distance-weighted fashion in a 15 by 15 grid of cells (some of which extend beyond our core grid) centered around each cell (see also Nielsen and Sugita 2005 for a similar decomposition of local and long-distance dispersal). The result is to replace r_p(s(i)) in (1) with

$$\gamma r_p(s(i))+(1-\gamma )\frac{1}{C}{\displaystyle \sum _{s_k\ne s(i)}{r}_p(s_k)w(s(i),s_k),}$$ (2)

where C is a normalization term calculated by summing w(s(i), s_j) over cells s_j in the 15 by 15 grid surrounding the focal cell. The second term is a weighted average of the vegetation composition in the core grid cells other than s(i), where weights,

$$w(s(i),s_k)=\text{exp}\left(-\frac{d{(s(i),s_k)}^2}{{\psi }^2}\right),$$

are calculated based on the distance between the cell in which the pond resides and the other cells based on the grid cell centroids, d(s(i), s_k), scaled by a dispersal distance parameter ψ. The result is that the model attempts to distinguish the portion of the pollen data that is informative about the cell vegetation, ignoring pollen that reflects vegetation similar to the region as a whole, and essentially attempting a deconvolution.

The induced Dirichlet precision parameter for the pollen data depends on the scaling parameters and varies between ponds in different grid cells,

$${\alpha }_{\text{pollen}}(i)={\displaystyle \sum _p{\varphi }_p\left(\gamma r_p(s(i))+(1-\gamma )\frac{1}{C}{\displaystyle \sum _{s_k\ne s(i)}{r}_p(s_k)w(s(i),s_k)}\right),}$$ (3)

with somewhat lower values and therefore lower precision for ponds on the periphery of the domain because of the lack of modelled pollen input from cells outside the domain.

Ideally we would use an anisotropic, skewed dispersal kernel that reflects the effects of prevailing wind direction, but we were not able to find a reasonable skewed kernel parameterization. It would also be preferable to extend the domain to include vegetation at fairly large distances in all directions from the study ponds to limit boundary effects.

3.3.2 Spatially-correlated vegetation composition process

Using the spatial representation described below, which provides an approximate thin plate spline-based spatial process, g_p(·), for each taxon, we define the proportions of the ten taxa at a given location using the additive log-ratio transformation (Aitchison 1986, p. 113), where the proportion of taxon p at location s is

$$r_p(s)=\frac{\text{exp}(g_p(s))}{{\displaystyle {\sum }_{k=1}^P\text{exp}(g_k(s))}}\Rightarrow {\displaystyle \sum _p{r}_p(s)=1.}$$ (4)

This approach allows us to use standard spatial models, yet create a multivariate framework for compositional data, and is very similar to the approach of Haslett et al. (2006). Note that the Aitchison (1986, p. 113) model has a one in the denominator in place of the contribution to the sum from the tenth, ’other’, category, as well as replacing the numerator with one for p = P. For our MCMC implementation (Section 3.5), we specify g_P (·) in order to improve mixing. The result is that the processes are not fully identifiable, but the vegetation compositions are, because of the sum to one constraint (4).

Latent processes

We take the P = 10 latent spatial processes to be independent spatial processes , gp(·), defined at each grid cell location as g_p(s), using a knot-based radial basis function approximation to a thin plate spline (Ruppert et al. 2003, Ch. 13). The value of the process at the 256 grid locations is

$${\mathit{g}}_{\mathit{p}}={\beta }_{0,p}\mathbf{1}+{\displaystyle \sum _k{\mathit{x}}_{\mathit{k}}{\beta }_{k,p}+\mathit{\Psi }{\mathit{u}}_{\mathit{p}}.}$$ (5)

Here, ψ is a reduced-rank basis matrix constructed using thin plate spline generalized covariance matrices on an equally-spaced 9 by 9 grid of knots. The 81 basis coefficients are taken to have prior distribution u_p ~ 𝒩 (0, σ² I), with the single variance component controlling the amount of smoothing. The covariates are described below.

We recognize that vegetation is likely to be nonstationary, while the construction is stationary, but believe that by including key covariates in the mean structure, in particular elevation, we have accounted for a major source of nonstationarity. Our approach avoids the computational difficulties of nonstationary processes and recognizes the limitations on resolution caused by the sparseness of the pollen data. The inclusion of covariates also helps to justify our use of a single σ² common to all taxa (an approach that Haslett et al. (2006) also find to be sufficient) reflecting that taxon abundances tend to change in tandem spatially.

Also note that our model assumes prior dependence between taxa only to the extent induced by a sum to one constraint, reflecting our desire to avoid a dependence structure that because of data sparsity would need to be implausibly constant over space. Critically, for every pond we have a large multinomial sample and direct information on each taxon from its count. Borrowing strength across taxa through a dependence structure introduces potential for bias from misspecification of the dependence structure, while the balanced sampling of data provides limited opportunity for variance reduction.

Landscape covariates

Vegetation abundance is strongly related to covariates such as elevation, soil type and climate. Covariates are represented in the spatial process representation (5), where x_k is a vector of values of the kth covariate at each grid cell, and β_k,p is the coefficient for the pth taxon. To predict in the past, we are limited to covariates whose values are known at every time point, generally those that have not changed much over time. In particular, we use elevation (averaged over the grid cell) and latitude (after projection) in the current model, as these are readily available and are the covariates most likely to influence vegetation at the spatial resolution of our grid. Note that latitude (at the cell centroid) is merely a linear spatial term. We include only a linear term in latitude and not in longitude because vegetation is likely to vary most substantially with climate differences that vary most strongly with latitude, and for the prediction runs, with 23 or fewer ponds, we wanted to estimate as few parameters as possible, leaving any variability by longitude to be accounted for in the radial basis portion of the spatial process. Both covariates are centered about their means, with elevation scaled to units of 1 km and latitude to 100 km.

3.3.3 Hyperparameter representation, prior distributions, and shrinkage

The goal for our prior distributions for the various parameters is to allow the data to play the primary role in estimating the parameters, while borrowing strength as necessary in contexts in which the data provide limited information. This is particularly relevant for the prediction runs, for which the small number of ponds provides limited information about spatial structure and covariate effects.

For the covariate effects, we use exchangeable prior structures to allow us to estimate hyperparameters in the estimation runs that can be used to constrain the relevant parameters in the prediction runs. We take β₁ and β₂, the coefficients for elevation and latitude, respectively, as ${\mathit{\beta }}_{\mathit{k}}~𝒩(\mathbf{0},s_{{\beta }_k}^2\mathit{I}),k=1,2$. In the estimation runs, the coefficient for each taxon could be estimated individually with independent prior distributions with little difficulty based on the dense vegetation data, but the variance components allow us to stabilize the estimates of the coefficients in the prediction runs, while still allowing the coefficients to vary in time. Note that the coefficients are taken to have mean zero because (4) causes the mean to not be identifiable; only relative differences can be estimated.

For the remaining parameters, $\{{\beta }_0,\varphi ,\gamma ,{\sigma }^2,{\alpha }_{\text{FIA}},{\alpha }_{\text{WT}},\psi ,s_{{\beta }_1}^2,s_{{\beta }_2}^2\}$, we use non-informative, but proper priors, with the components of β₀ and ϕ taken to be independent. In particular, for variance components, we have used uniform priors on the standard deviation scale to avoid the use of diffuse inverse gamma priors (Gelman 2006), which have sharp spikes in density at small values, and decay extremely rapidly to zero density at values smaller than the location of the spike. For all the parameters, we impose lower and upper limits on the parameter values to prevent the MCMC sampler from wandering in areas of the parameter space in which the data provide little information and ensure propriety. In all cases of non-informative priors, the posterior distributions were concentrated away from the limits, suggesting that the diffuseness of the prior is not of particular concern (see the considerations of Berger et al. 2001).

3.3.4 Model misspecification and model incoherence

With regard to model misspecification, we know that sediment pollen records are an error-prone and biased proxy for vegetation, while the modern plot data, and likely the colonial vegetation data to a lesser extent, are relatively error-free. Thus in doing the estimation runs, we would like to estimate the key parameters used to constrain predictions in such a way that our vegetation surface estimates are informed primarily by the vegetation data. In our joint estimation model for vegetation and pollen data, in cells with limited vegetation data, the vegetation estimates in a cell can overfit to the pollen data. To avoid this, in the estimation runs, our MCMC samples of parameters used to construct the latent vegetation process, r(s), are done conditional only on the vegetation data, ’cutting feedback’ in a manner recently introduced into the BUGS software (Spiegelhalter et al. 2003) and discussed in detail in Rougier (2008). Yucel and Zaslavsky (2005) have also considered this issue in models with multiple data sources in which one data source directly informs a parameter, but a second, larger, set of data can also influence the inference more strongly than desired because of model misspecification. In our setting the pollen dataset acts as the ’larger’ dataset within individual grid cells with ponds because of the large number of pollen grains compared to the tree counts. A sensitivity analysis suggested that the coherent model without cutting feedback overfits to some degree, but not a substantial amount, with increased estimates of the precision in the pollen data and of the proportion of grid-cell pollen, γ.

3.4 Prediction model

After fitting the model in the estimation runs for the colonial and modern eras, we use fixed parameter values from those runs in the prediction runs, which have the same model form as the estimation runs, but with temporal autocorrelation introduced as described below. To account for uncertainty in the parameters from the estimation runs, we compute separate predictions conditional on samples from the posterior of the parameters from a given estimation run. In the prediction runs, only β_0,p(t), β_1,p(t), β_2,p(t), and u_p(t), which are the parts of the model that directly determine the vegetation composition at each time, and autocorrelation parameters for these time series, are estimated. This approach ensures that the vegetation predictions are primarily informed by the pollen proportions at the time of interest, but that structural information that is well-informed only with rich vegetation data is based on the estimation runs.

The temporal structure gives us the ability to smooth over time to better estimate r_p(s, t) and assess how the relationships between taxon abundances and covariates have changed over time (e.g., Williams et al. 2001) as inferred from the pollen data. For each of the temporally-varying terms, we include an overall mean that we integrate over for better MCMC mixing, giving us two temporal variance components. For example,

$${\mathit{\beta }}_{\mathbf{0},\mathit{p}}~𝒩(\mathbf{0},{\sigma }_0^2({\delta }_0\mathit{J}+1-{\delta }_0)\mathit{R}({\rho }_0)))$$

where δ₀ ∈ (0, 1) is the proportion of variance for the long-term mean, J is a matrix of ones, ${\sigma }_0^2$ is the overall variance, and R(ρ₀) is the correlation matrix, a function of decay parameter is ρ₀ and the relevant time lags. We use a Matérn correlation function with υ = 2 but also consider the exponential (i.e., AR(1)) correlation function. The priors for β_1,p and β_2,p are analogous but with $s_{{\beta }_1}^2\text{and}{s}_{{\beta }_2}^2$ in place of ${\sigma }_0^2$, and ρ₁ and ρ₂ in place of ρ₀. We choose ${\sigma }_0^2$ to be large, imposing no constraints on the overall mean, β₀, while using the variance components for β₁ and β₂ from the estimation runs to stabilize their estimation. To provide for residual spatio-temporal structure, we specify an analogous temporal correlation structure for the basis coefficients

$${\mathit{u}}_{\mathit{k},\mathit{p}}~𝒩(\mathbf{0},{\sigma }^2(\delta \mathit{J}+(1-\delta )\mathit{R}(\rho ))),$$

again independent between coefficients for different knots and where σ² is taken from the estimation runs. This constraint ensures that the amount of spatial heterogeneity is based on information from the rich vegetation data in the estimation runs. Nonseparability may come into play, particularly at times of range expansion and contraction, but would be difficult to estimate based on the small number of sites, and would add even more complexity to the modeling. For the proportion of variance and the decay parameters we use uniform priors, where for the latter we impose upper and lower bounds based on the discrete time lag and length of the time period.

Because vegetation changed markedly upon European settlement (Fuller et al. 1998), introducing a likely nonstationarity in time, we run the prediction model separately for the pre-settlement (2500 to 300 years before present) and post-settlement periods (500 to 0 years before present). Note the inclusion of a buffer on either side of the settlement period for both runs to avoid boundary effects.

In our prediction runs, we make use of the posterior distributions for all parameters, except those mentioned above, from either the modern or colonial estimation run. To incorporate uncertainty in these parameters, we fit the prediction model using 50 draws from the joint posterior distribution of $\{\varphi ,\gamma ,\psi ,{\sigma }^2,s_{{\beta }_1}^2,s_{{\beta }_2}^2\}$ from the chosen estimation run, running a separate MCMC for each draw, and combining the iterations from the 50 chains to estimate posterior quantities. In this way we incorporate parameter uncertainty into our predictions, but we do not update these distributions as the pollen data alone do not contain sufficient information to inform the parameters.

3.5 Implementation

Details on MCMC implementation, including sampling schemes and evidence of adequate mixing are provided in Paciorek and McLachlan (2008). We note that the lack of conjugacy and inability to integrate over the latent processes in our hierarchical multivariate space-time model with a non-normal likelihood seriously affect mixing and require long run times, even with the simplifications in our model structure. One critical detail is that dependence between the hyperparameters and associated random effects (e.g., between σ² and u or between $s_{{\beta }_1}^2$ and β₁) can greatly slow mixing (Knorr-Held and Rue 2002; Rue and Held 2005; Paciorek 2007), so we use joint proposals for hyperparameters and their random effects following Paciorek (2007). The posterior estimates for a given estimation run (modern or colonial era) are based on three separate chains, while for the prediction runs, they are based on the aforementioned 50 separate chains.

4 Model results and assessment

Results from the model come in several forms. In Section 4.1 we use the estimation runs to learn about the relationship between pollen and vegetation in the modern and colonial periods. We consider the ecological implications of parameter estimates and contrast results from the modern and colonial estimation runs to understand potential differences in vegetation structure. In Section 4.2, we assess the use of the model for prediction in a cross-validatory fashion. Having argued that our model performs reasonably, in Section 4.3, we apply the prediction model to pollen data over the past 2500 years. Additional details on model performance and results are provided in Paciorek and McLachlan (2008).

4.1 Estimation model results

4.1.1 Pollen as proxy for vegetation

Differential pollen production and dispersal

The estimation runs allow us to characterize the relationship between pollen in sediments and local vegetation, thereby informing us about the ability of pollen to serve as proxy data for vegetation. Our model attempts to find the best fit between pollen and vegetation across a regional network of sites. As a residual diagnostic, we compare pollen composition in each pond to the spatially-smoothed estimated vegetation composition of the encompassing grid cell from the model. While differences between pollen and vegetation composition may arise because the grid-scale vegetation is poorly estimated, most ponds fall in areas with nearby FIA plots or town-ship data (see Figure 1), so we expect that most differences are due to long-distance pollen transport and local (within grid cell) vegetation heterogeneity.

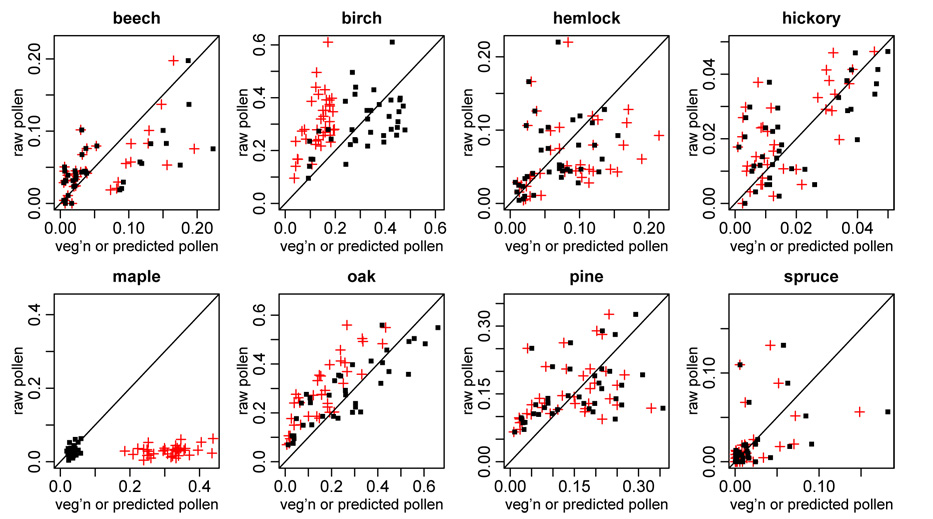
For the modern era, Fig. 2 plots relative pollen abundance in ponds versus model-smoothed grid cell relative vegetation abundance for each taxon (red crosses). Most taxa show increasing relationships. The lack of 1:1 relationship shows the importance of including ϕ to adjust for differential pollen production and dispersal. After scaling the smoothed vegetation by the estimated values of ϕ, we see the values falling around the 1:1 line in Fig. 2 (black squares), albeit with some taxa, such as oak and hickory, showing more consistent relationships than others, such as spruce. The substantial remaining variability makes it difficult to precisely estimate ϕ. Results are similar for the colonial era (not shown).

Figure 2.

For the modern era, scatterplots by taxa of pollen proportions in each pond against both the model-smoothed vegetation proportions in the grid cell of the pond (red crosses) or model-predicted pollen proportions based on scaling the smoothed vegetation in the cell by ϕ (black squares).

Based on plots by pond rather than by taxon (not shown), most ponds show an increasing relationship between relative abundance of each taxon in the pollen and in pollen as predicted from vegetation, scaling by ϕ, although some ponds show sharp differences, particularly for some of the more abundant taxa. Fortunately, in almost all cases, taxa with low abundance in the vegetation can be distinguished from taxa with high abundance in the vegetation based on the pollen. Further exploration has not indicated any relationships with covariates or spatial patterns that might explain which ponds have more noisy relationships between the pollen and smoothed vegetation proportions. Nor are the ponds with the noisy relationships consistent between the modern and colonial eras. This makes more sophisticated error modeling difficult.

The estimation runs also allow us to investigate differential taxon-specific pollen production and dispersal. For both the modern and colonial parameter estimates, large uncertainties prevent us from readily distinguishing among most taxa based on ϕ, but the two taxa whose estimates are clearly different than the others are maple, with low production/dispersal, and birch, with high production/dispersal, agreeing with previous finer-scale analyses of the relationship between trees and pollen assemblages in the eastern U.S. (e.g., Jackson 1990).

Long-distance dispersal

Based on diagnostic plots similar to Figure 2, the full model accounting for long-distance dispersal produced smaller deviations between the raw pollen proportions and pollen as predicted from vegetation than a model without long-distance dispersal, setting γ ≡ 1. The simpler model fits substantially worse than allowing γ to be estimated in the estimation runs, with a ΔDIC of 307 (427) for the modern (colonial era). Not surprisingly, the estimated precision of the pollen data is smaller when γ ≡ 1, with values of ᾱ_pollen of 35 compared to 60 for the modern run and 27 compared to 97 for the colonial run, as the additional unexplained heterogeneity is accounted for in the Dirichlet heterogeneity parameter. Further assessment using cross-validation supported the use of the mixture model, with the model without long-distance dispersal producing predicted vegetation surfaces with much less distinct spatial patterns (not shown) and less posterior confidence about feature significance, as we would expect with the smaller estimated Dirichlet heterogeneity parameter for the pollen data. In future ecological analyses we will consider different approaches for pollen source contributions in more detail, as this is an issue of critical paleoecological importance and others have attempted to infer relative contributions by various methods (e.g., Jackson and Lyford 1999; Nielsen and Sugita 2005).

For the pollen data, γ represents the proportion of pollen data consistent with vegetation estimated in the encompassing grid cell, with 1 − γ the proportion based on weighting the composition in the other grid cells in the domain. In both the colonial and modern eras, γ is about one-half, 0.48 for the modern era (with a 95% credible interval of 0.30, 0.61) and 0.50 (0.41, 0.59) for the colonial era, indicating that much of the pollen in the ponds is not consistent with the grid-cell-estimated vegetation. The pollen could be associated with long-distance transport, reflecting the vegetation in other grid cells, or with local sub-grid-scale vegetation that happens to be more similar to the region-wide vegetation than the model-estimated vegetation in the grid cell of the pond. While local variability and lack of identifiability in the model surely contribute to some extent, site visits by the authors suggest that many of the ponds visited had few nearby trees of the type indicated by the anomalous pollen, suggesting that much of the pollen may be due to long-distance transport. Our results are consistent with previous paleoecological work (Jackson and Lyford 1999; Davis 2000; Nielsen and Sugita 2005), which suggests that mixing of pollen sources makes it difficult to distinguish local from regional sources. For taxa that are at high abundance in most locations, such as maple in the modern era, it is particularly difficult to distinguish pollen from the grid cell compared to long-distance transport. Additional vegetation data from field surveys near ponds could help estimate local vegetation, thereby distinguishing long-distance from local pollen and improving our estimation of ϕ and γ. A strength of the model is that it synthesizes already-existing data, but it could readily incorporate local vegetation data.

Ecologists expect that the contribution of local pollen dispersal,γ, and the distance-based decay in dispersal,ψ, may differ by taxa (Jackson 1990), but a model with γ and ψ varying by taxa, both parameterized by exchangeable priors, showed little ability to distinguish differences between taxa, albeit with a small improvement in DIC (6.7 for the modern era and 9.0 for the colonial). These parameters are difficult to estimate, because the model involves a deconvolution of the deposited pollen, so all taxa show high levels of posterior uncertainty.

4.1.2 Spatial smoothing of composition data

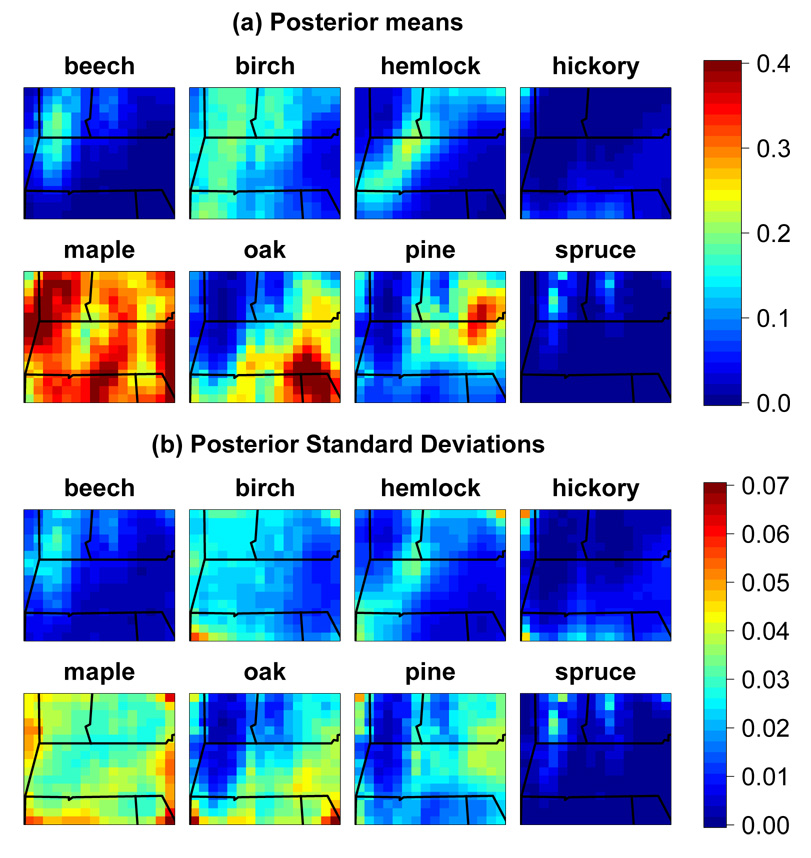
By running the model for the modern and colonial eras, we can smooth the available vegetation data and provide estimates of colonial and modern vegetation in a visually appealing fashion, with associated uncertainty. In accounting for the count data structure, this simple application of the model has advantages over non-statistical smoothing and graphical display, allowing us to consider the ecological differences since European settlement in light of the estimated uncertainty. In Fig. 3a, we see the smoothed composition estimates for the modern era. Spatial gradients in vegetation appear to have become less distinct with European settlement (not shown). Fig. 3b shows uncertainty estimates for each taxon, suggesting that with the rich vegetation data of the FIA surveys we have reasonably precise estimates. However note that this is done at the grid level, and there is certainly a large amount of within-cell heterogeneity that causes individual stands of trees to have compositions that differ drastically from the composition estimate in a cell. The standard deviations are larger for more common taxa, but this reflects only that we can be quite certain in absolute terms that less common taxa are uncommon; the coefficient of variation (not shown) indicates that relative uncertainty is greater for the less common taxa and, for a given taxon, in locations in which the taxon is less common.

Figure 3.

Posterior means (a) and standard deviations (b) of vegetation estimates from modern estimation runs. Note that some maple and oak proportions are truncated to 0.4.

Our model relies on key parameters to translate between pollen data and vegetation predictions in the prediction runs. In particular, the variance component for the basis coefficients of the spatial process representation influences the amount of smoothing, which not only influences point predictions by determining the degree of local averaging, but perhaps more importantly determines the degree of uncertainty, with uncertainty increasing rapidly with increasing distance from ponds when the smoothing parameters specify more unsmooth spatial processes. As expected because of changes in vegetation post-settlement and sparser data in the modern surveys, the estimated heterogeneity is less in the modern era with an estimate of σ of 1.8 (1.2, 2.5) compared to 5.9 (4.1, 8.2) in the colonial era. This difference and the difference in the estimates of ϕ highlight the importance of choosing between the estimation parameters estimated for the modern and colonial periods when predicting in the past.

4.2 Cross-validation

Our estimation runs allow us to compare reasonable model specifications, but the true test of the model is its ability to predict and provide good uncertainty estimations for vegetation when only pollen data are available. Our next assessment uses cross-validation, first using modern parameter estimates to predict in the colonial period and then using colonial parameter estimates to predict in the modern period. Note that while only several hundred years apart, the modern and colonial eras are separated by vast ecological changes induced by European settlement, as great as any differences expected over the past 2500 years (Fuller et al. 1998; Oswald et al. 2007), so this provides an important check on the model.

4.2.1 Feature Significance

Uncertainty assessment is a major concern for a complicated model with an ambitious prediction goal. Pointwise standard deviations of prediction for each taxon provide some information about how certain we can be about our point predictions of vegetation composition, including which taxa are most reliably predicted and at which spatial locations we can be most certain. However, this does not give us a complete picture concerning our certainty about spatial features of the predictive surfaces. Our primary interest lies in determining which spatial areas can be reliably determined to have higher or lower abundances of a given taxon than other areas, although detection of gradients and extrema may also be of interest. We also want to compare abundances of individual taxa across time and between taxa at individual times and spatial locations.

To make assessments about relative abundances of a single taxon across locations at fixed time, we make use of the posterior distributions of contrasts between different locations. We take a graphical approach focused on pointwise comparisons, hoping to provide approximate inference about all the locations at the expense of some loss of information about joint properties. In general, the use of exchangeable prior distributions with the resulting shrinkage justifies not adjusting for multiplicity (Berry and Hochberg 1999, Carlin and Louis 2000, p. 339, Gelman et al. 2008). We do not adjust for multiplicity because our spatial model has this flavor of exchangeability through the spatial process structure for the vegetation processes that smooths abundances towards each other, potentially giving flat surfaces (σ² ≈ 0) if the data suggest little spatial variability. The prediction model also smooths in time.

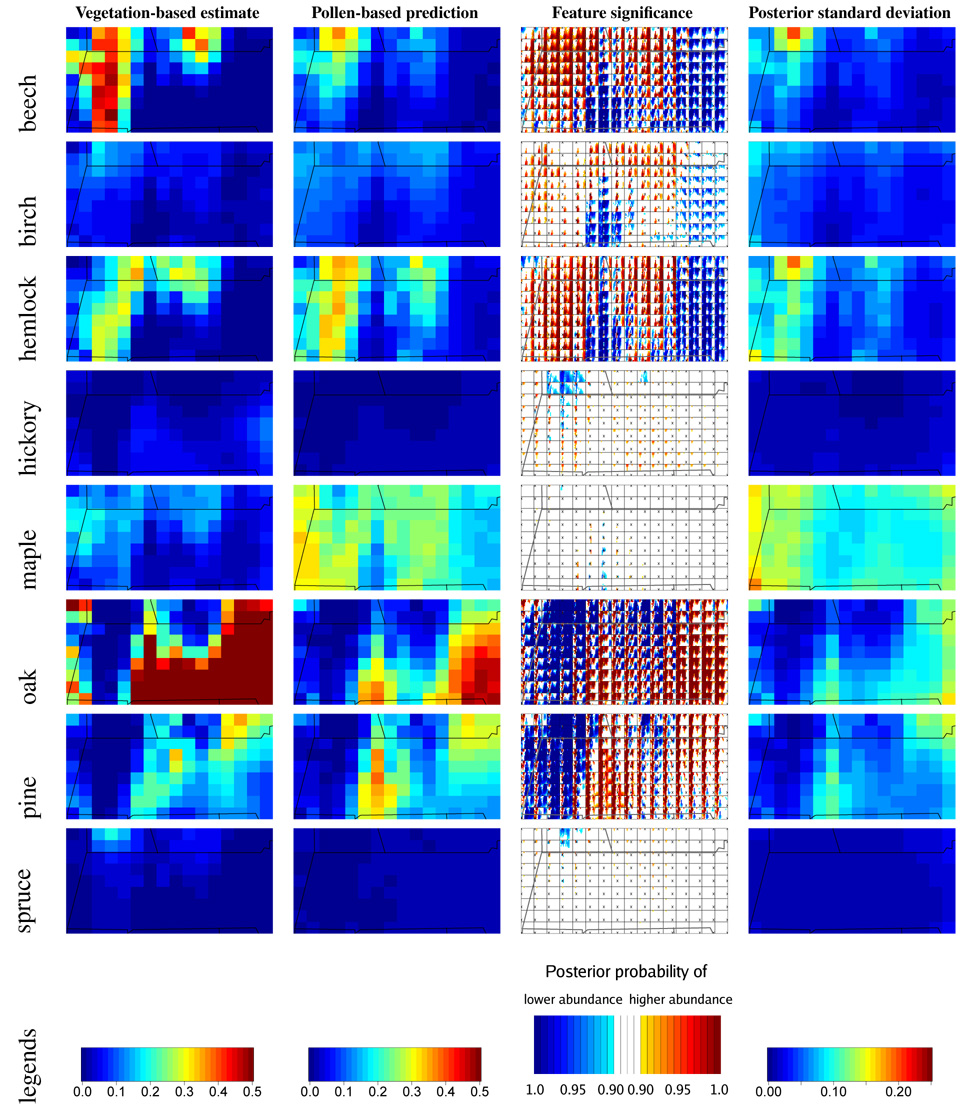
Our approach is to consider pairwise posterior probabilities of differential abundance for a given taxon and plot the results in an informative way, demonstrated in the third column of plots in Fig. 4. For each pair of grid cells, we compute the posterior probability that the abundance of the taxon in one grid cell is higher than the abundance in the other grid cell. We sequentially consider each grid cell as the focal cell, making a subplot in which we color the other grid cells for which pairwise differences between the focal cell and the other cell have at least 90% posterior probability of lying on one side of zero. The colors indicate the sign of the difference and the posterior probability of lying on that side of zero. Finally we make a mosaic of the subplots, with the subplot placed on a map in the position of the focal grid cell and an ’x’ marking the relative position of the focal location within the subplot. By tiling the subplots into a full plot, we present a color map of pointwise, pairwise probabilities of differential abundance. Viewing the mosaic of subplots as a single plot, areas of substantial probability of differential abundance from other areas show themselves as deep colors, while individual subplots can still be examined to assess differences between a given focal location and all other locations. In Fig. 4 we see that for beech, the northwestern and north-central areas indicated in dark red show high probability of higher abundance than the south-central and eastern areas. In contrast, for hickory, the evidence is less strong, with moderate probability of a small area in the northwest (in blue) having lower abundance than most of the rest of the region.

Figure 4.

For the colonial period, vegetation estimated in the colonial estimation run (making use of witness tree vegetation data) (first column), vegetation predicted in the colonial prediction run based on colonial pollen and modern parameter estimates (second column), feature significance for the prediction run (third column) and posterior prediction standard deviations (fourth column). In the first column some cell abundances are truncated at 0.5.

4.2.2 Assessment of Predicted Surfaces and Uncertainty Characterization

In Fig. 4 for the colonial period (and in Paciorek and McLachlan (2008) for the modern period), we compare our best estimate of vegetation, from the colonial estimation run, with predictions based on pollen from the colonial period and parameter estimates from the modern period. We also show feature significance plots and plots of posterior standard deviations of prediction to assess uncertainty. Based on comparisons of the vegetation-predicted surfaces with the pollen-predicted surfaces, interpreted in light of the feature significance plots, it appears the model is doing a reasonably good job of predicting spatial patterns. For the colonial period, the features are quite similar in the prediction and estimation runs, and patterns detected in the feature significance plots are seen in the vegetation-predicted surfaces when considered at a fairly coarse resolution, suggesting minimal type one error, with few non-existent patterns detected. For the modern predictions, the results are not as good, particularly for hemlock. The model fails to capture some large-scale patterns and is overly confident about the patterns it does estimate. The poorer results in predicting modern vegetation may more strongly reflect difficulties in predicting modern vegetation than problems with the colonial parameter estimates per se. Land-use change post-colonization makes spatial patterns in modern vegetation less distinct and less strongly associated with the covariates than in the colonial era (Foster et al. 1998; Fuller et al. 1998), making prediction more difficult. The larger precision of the pollen data as a proxy for vegetation in the colonial estimation runs than in the modern estimation runs causes overconfidence in the modern predictions. Given that vegetation structure in the past is very likely to be more similar to the colonial vegetation than the modern vegetation, the success of the model in predicting colonial patterns gives us confidence in the ability of the model to make predictions.

In terms of absolute abundance, the model generally indicates the taxa with high and low abundance reasonably (maple is an exception) but often incorrectly predicts overall relative abundance of a taxon (Fig. 4). This relates to whether the estimated values of ϕ are appropriate for the time period. In particular, maple is overpredicted in the colonial era and underpredicted in the modern, while the reverse is true for oak and beech. This occurs because the estimated values of ϕ for the two taxa are different for the two eras; use of the parameter estimate from estimation runs for the same era as the prediction runs improves prediction of the overall level, indicating the sensitivity of predictions to this key parameter. Given that we expect vegetation before settlement to be more similar to the colonial vegetation than the modern vegetation, this suggests we should focus on the colonial parameter estimates for prediction before settlement.

Posterior uncertainty varies widely between taxa and across space (Fig. 4). Uncertainty is the greatest far from ponds, as should be the case. Maple is particularly uncertain, because the low pollen production/dispersal of maple causes inference about maple to rely on a small number of pollen grains in each pond, creating a large signal to noise ratio.

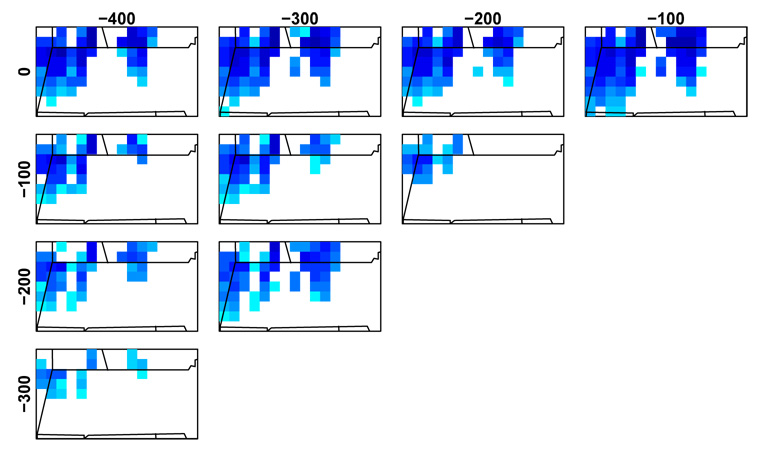
To assess temporal changes, we can contrast abundance estimates for each taxon between any pair of time points on a pointwise cell by cell basis, again without post hoc correction for multiple testing because of the temporal smoothing done by the model. The comparison takes the simple form, at each grid cell, of computing the posterior probability for the chosen taxon that the abundance is greater in one period than a second period. If this posterior probability exceeds a threshold (we use 90% in our plots) for either period, we plot the posterior probability as the color shade in the cell. As an example, Fig. 5 shows distinct changes in beech over time when comparing the present (i.e., 1950), with the years 100 to 400 years before present. The areas of predicted robust decrease in beech match estimated declines based on the colonial and modern vegetation data (but note that this is not full cross-validation given our use of the modern estimation run parameters). Assessment of this and other such contrast plots in light of the modern and colonial vegetation data suggests the model can detect changes over time with reasonable specificity and some sensitivity to real changes in composition.

Figure 5.

Posterior probabilities of differences in recent beech abundance between pairs of time points 0 to 400 years before present (1950) based on modern parameter estimates. Each cell indicates the posterior probability (with a threshold of 90%) that the cell has lower (blue) or higher (red - no examples here) abundance in the later time period than the earlier time period. See Fig. 4, third column for color legend.

These results suggest that our model is performing as well as may reasonably be expected, able to resolve many spatial patterns and temporal changes at coarse scale but missing the fine-scale details of vegetation and some coarse patterns.

4.3 Operational prediction model results

Here we describe initial results from the prediction runs over the past 2500 years. Many other uses of the full posterior distribution are possible. For display purposes, we use predictions based on colonial parameter estimates; more detailed ecological analysis will assess robustness with respect to the estimation run used.

The parameter estimates for the temporal variance components indicate that changes over time occur smoothly, particularly for the regression coefficients, but also for the residual spatio-temporal structure.

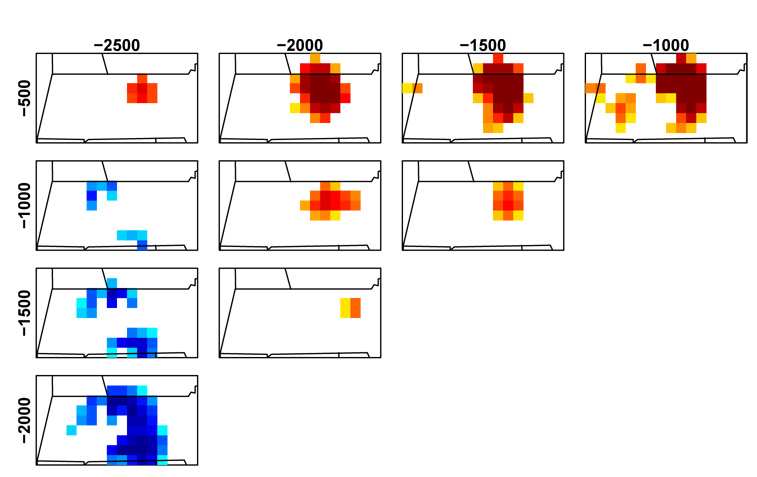
Surface predictions and posterior standard deviations, as well as feature significance plots, are possible for each prediction time point, allowing inference about spatial patterns, but are not shown for brevity. In Fig. 6, we show temporal contrast plots for the pre-settlement period, which suggest that there was a trend toward increased oak abundance in higher-elevation areas in central Massachusetts in the period 1000 to 500 years before present and a decreasing trend in roughly the same area 2500 to 2000 years before present. There are no detectable trends in areas furthest to the east that have high oak abundance.

Figure 6.

Posterior probabilities of differences in pre-settlement oak abundance between pairs of time points 500 to 2500 years before present (1950) based on colonial parameter estimates. Each cell indicates the posterior probability (with a threshold of 90%) that the cell has lower (blue) or higher (red) abundance in the later time period than the earlier time period. See Fig. 4, third column for color legend.

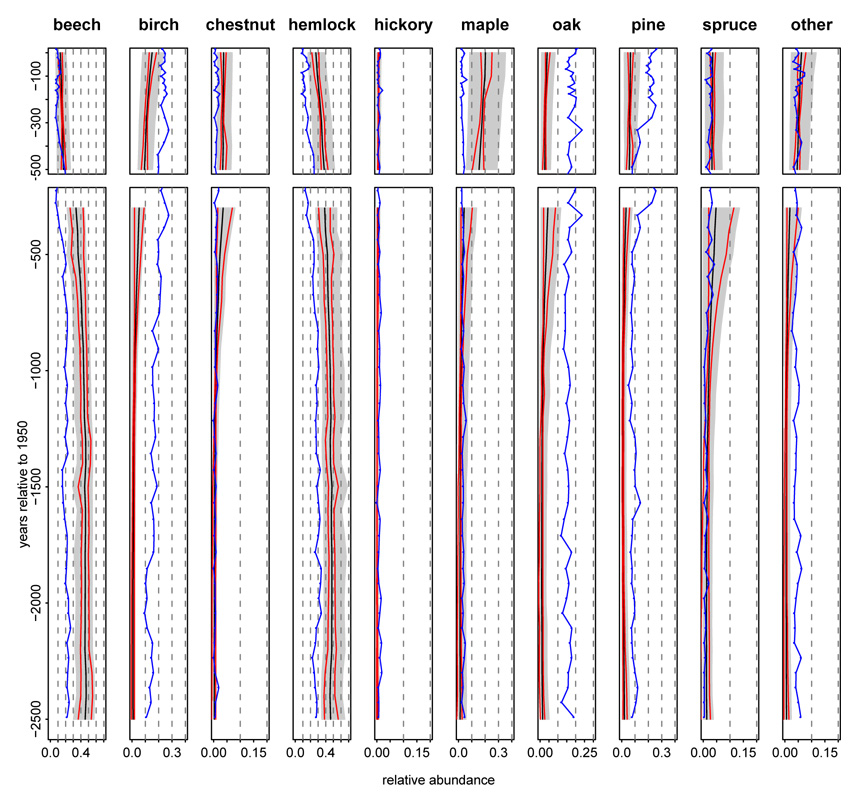
A common presentation of pollen data is in the form of a pollen diagram showing changes in pollen composition in a pond over time. An analogous presentation using model output is to estimate vegetation composition and associated uncertainty in a given grid cell, demonstrating the ability of the model to estimate and characterize uncertainty in vegetation based on pollen. In Fig. 7 we compare pollen composition to model-estimated vegetation, including a decomposition into the average across time and temporal deviation from that average that allows assessment of contrasts across time. Maple, chestnut, spruce, and hickory pollen are all represented at low abundance throughout the period of interest. After accounting for taxon-specific biases in pollen representation and borrowing strength both spatially and based on environmental covariates, the model provides some evidence that birch, chestnut, maple, oak, and spruce increased over time pre-settlement, while the more common beech and hemlock do not show a robust trend. In general the model-estimated trends in the grid cell match those from the pollen in the single pond, but spatial smoothing in the model can cause differences between raw pollen and estimated vegetation, such as seen for maple.

Figure 7.

Vegetation diagrams for the grid cell encompassing pond 20 (Snake Pond) with the recent period based on modern parameter estimates (top; 0 to 500 years before present) and the pre-settlement period based on colonial parameter estimates (bottom, 300 to 2500 years before present). Black lines represents the posterior mean and gray shading the 95% credible intervals for vegetation abundance, r_p(s, t), with blue lines showing corresponding pollen proportions from Snake Pond. Red lines represent 95% pointwise credible intervals for the deviations over time in the vegetation (r_p (s, t) − r̄_p (s)), which are plotted as offsets relative to the posterior mean of r̄_p(_s). Plotting the credible interval for the deviation in this way removes the effect of uncertainty in ϕ_p, which affects all times in the same way, and avoids the overly conservative contrasts of abundance across time indicated by the gray shading.

Plots of the elevation and latitude regression coefficients over time (not shown) show little trend for most taxa, suggesting a lack of stark changes in the relationships of vegetation to abiotic factors.

We also considered running the prediction model at time intervals of 50 years and with an exponential temporal correlation function. For most aspects of the predictions these changes had little effect, but there was some sensitivity in the temporal contrasts.

5 Discussion

Almost 100 years ago, von Post (1917) described the problem of interpreting forest composition from fossil pollen assemblages. Long-distance pollen dispersal, differential pollen production, and a generally high level of process noise have continued to be major obstacles for the interpretation of paleoecological data since. Analyses of pollen data have identified important trends in the data (Berglund 1991; Davis et al. 1998; Fuller et al. 1998; Soepboer et al. 2007), but they have not quantified these trends in an inferential framework that explicitly accounts for the various sources of uncertainty and the natural spatial context of the data. Although theory and models about pollen production, dispersal, and accumulation have continuously evolved (Webb 1974; Jackson 1990; Davis 2000; Haslett et al. 2006; Sugita 2007a,b), most paleoecological literature simply presents raw pollen percentages and asks the reader to understand that these are rough and unquantified approximations of the forest composition, which is the real variable of interest.

Our work tackles this problem, building a statistical framework for inferring historical forest composition based on proxy pollen sediment data. We present a multivariate spatiotemporal model for compositions. We build the model in stages, allowing easier model assessment. Under a set of simple assumptions about the relationship between trees and pollen through space and time, our model adds a quantitative estimate of uncertainty to inference about changing vegetation, providing the first spatially-explicit statistical analysis of paleoecological data, and borrowing strength across multiple ponds and across time in a coherent way. Innovative graphical assessments of feature significance based on the full posterior distribution suggest that the pollen data can reliably indicate certain large-scale spatial features for some taxa, but that features on scales smaller than ~50 km are not possible to distinguish, nor are large-scale features for some taxa, such as those with low pollen production/dispersal relative to other taxa. The model does not resolve the substantial problems involved in using pollen data to estimate forest composition, but does suggest which inferences are more reliable and what additional data would be most helpful.

Specific results from the model demonstrate the advantages of the spatially-explicit modeling approach that calibrates pollen to vegetation. For example, Fig. 7 estimates the extent to which a classic pollen diagram misrepresents changing forest composition. Most paleoecological studies (e.g., Fuller et al. 1998) would show only the blue pollen proportions and interpret forest change by acknowledging that the representation of certain tree taxa is likely to be biased in pollen data. Our analysis quantifies this in a coherent probabilistic framework. The recent decrease in beech trees suggested in Fig. 7 is depicted in a regional context in Fig. 6. Previous studies (Fuller et al. 1998; Oswald et al. 2007) have identified this regional decrease, but were unable to describe this trend in a continuous spatial setting. Graphical representations of output from our model allow a resolution of spatial analysis previously unavailable to paleoecologists. More importantly, confidence in the strength of the inferences is articulated. A similar set of maps for maple (not shown) shows very little significant trend, due to the large uncertainty about maple abundance. Given the amount of noise in the pollen representation and the relative sparseness of fossil pollen datasets, it is important that paleoecologists are able to confidently detect patterns emerging above the noise in their data.

The long-term and broad-scale nature of modern environmental problems ensures that networks of paleoecological sites will continue to provide important benchmarks for environmental change (Botkin et al. 2007). Our model provides the framework for testing ecological theory through the incorporation of covariates and through its ability to distinguish important spatial and temporal trends from noise. The mode was designed with few biological assumptions, but it could be modified to incorporate such constraints, as well as additional data such as more finely-specified pollen dispersal data, environmental covariates, or spatial genetic information, as these data become available. We anticipate that our work, along with parallel efforts by others to interpret paleoecological data in better articulated statistical terms (Haslett et al. 2006; Sugita 2007a,b), will allow this longstanding data source to be better integrated into modern environmental analysis.