Abstract
Chain graphs present a broad class of graphical models for description of conditional independence structures, including both Markov networks and Bayesian networks as special cases. In this paper, we propose a computationally feasible method for the structural learning of chain graphs based on the idea of decomposing the learning problem into a set of smaller scale problems on its decomposed subgraphs. The decomposition requires conditional independencies but does not require the separators to be complete subgraphs. Algorithms for both skeleton recovery and complex arrow orientation are presented. Simulations under a variety of settings demonstrate the competitive performance of our method, especially when the underlying graph is sparse.
Keywords: chain graph, conditional independence, decomposition, graphical model, structural learning
1. Introduction
Graphical models are widely used to represent and analyze conditional independencies and causal relationships among random variables. Monographs on this topic include Cowell et al. (1999), Cox and Wermuth (1996), Edwards (2000), Lauritzen (1996), Pearl (1988) and Spirtes et al. (2000). Two most well-known classes of graphical models are Markov networks (undirected graph) and Bayesian networks (directed acyclic graph). Wermuth and Lauritzen (1990) introduced the broader class of block-recursive graphical models (chain graph models), which includes, but is not limited to, the above two classes.
Among a multitude of research problems about graphical models, structural learning (also called model selection in statistics community) has been extensively discussed and continues to be a field of great interest. There are primarily two categories of methods: score-based methods (using AIC, BIC, posterior score, etc.) and constraint-based methods (using significance testing). Lauritzen (1996, Section 7.2) provides a good summary of the most important works done in the last century. Recent works in this area include Ravikumar et al. (2008), Friedman et al. (2007), Kalisch and Bühlmann (2007), Meinshausen and Bühlmann (2006), Tsamardinos et al. (2006), Ellis and Wong (2006), Friedman and Koller (2003), Chickering (2002), Friedman et al. (1999), etc. However, most of these studies are exclusively concerned with either Markov networks or Bayesian networks. To our limited knowledge, Studený (1997) is the only work that addresses the issue of learning chain graph structures in the literature. Recently, Drton and Perlman (2008) studied the special case of Gaussian chain graph models using a multiple testing procedure, which requires prior knowledge of the dependence chain structure.
Chain graph models are most appropriate when there are both response-explanatory and symmetric association relations among variables, while Bayesian networks specifically deal with the former and Markov networks focus on the later. Given the complexity of many modern systems of interest, it is usually desirable to include both types of relations in a single model. See also Lauritzen and Richardson (2002).
As a consequence of the versatility, chain graph models have received a growing attention as a modeling tool in statistical applications recently. For instance, Stanghellini et al. (1999) constructed a chain graph model for credit scoring in a case study in finance. Carroll and Pavlovic (2006) employed chain graphs to classify proteins in bioinformatics, and Liu et al. (2005) used them to predict protein structures. However, in most applications, chain graphs are by far not as popular as Markov networks and Bayesian networks. One important reason, we believe, is the lack of readily available algorithms for chain graph structure recovery.
To learn the structure of Bayesian networks, Xie et al. (2006) proposed a ‘divide-and-conquer’ approach. They showed that the structural learning of the whole DAG can be decomposed into smaller scale problems on (overlapping) subgraphs. By localizing the search of d-separators, their algorithm can reduce the computational complexity greatly.
In this paper, we focus on developing a computationally feasible method for structural learning of chain graphs along with this decomposition approach. As in structural learning of a Bayesian network, our method starts with finding a decomposition of the entire variable set into subsets, on each of which the local skeleton is then recovered. However, unlike the case of Bayesian networks, the structural learning of chain graph models is more complicated due to the extended Markov property of chain graphs and the presence of both directed and undirected edges. In particular, the rule in Xie et al. (2006) for combining local structures into a global skeleton is no longer applicable and a more careful work must be done to ensure a valid combination. Moreover, the method for extending a global skeleton to a Markov equivalence class is significantly different from that for Bayesian networks.
In particular, the major contribution of the paper is twofold: (a) for learning chain graph skeletons, an algorithm is proposed which localizes the search for c-separators and has a much reduced runtime compared with the algorithm proposed in Studený (1997); (b) a polynomial runtime algorithm is given for extending the chain graph skeletons to the Markov equivalence classes. We also demonstrate the efficiency of our methods through extensive simulation studies.
The rest of the paper is organized as follows. In Section 2, we introduce necessary background for chain graph models and the concept of decomposition via separation trees. In Section 3, we present the theoretical results, followed by a detailed description of our learning algorithms. Moreover, we discuss the issue of how to construct a separation tree to represent the decomposition. The computational analysis of the algorithms are presented in Section 4. Numerical experiments are reported in Section 5 to demonstrate the performance of our method. Finally, we conclude with some discussion in Section 6. Proofs of theoretical results and correctness of algorithms are shown in Appendices.
2. Definitions and Preliminaries
In this section, we first introduce the necessary graphical model terminology in Section 2.1 and then give the formal definition of separation trees in Section 2.2.
2.1 Graphical Model Terminology
For self-containedness, we briefly introduce necessary definitions and notations in graph theory here, most of which follow those in Studený (1997) and Studený and Bouckaert (2001). For a general account, we refer the readers to Cowell et al. (1999) and Lauritzen (1996).
A graph  = (V, E) consists of a vertex set V and an edge set E. For vertices u, v ∈ V, we say that there is an undirected edge u – v if (u, v) ∈ E and (v, u) ∈ E. If (u, v) ∈ E and (v, u) ∉ E, we say that there is a directed edge from u to v and write u → v. We call undirected edges lines and directed edges arrows. The skeleton
= (V, E) consists of a vertex set V and an edge set E. For vertices u, v ∈ V, we say that there is an undirected edge u – v if (u, v) ∈ E and (v, u) ∈ E. If (u, v) ∈ E and (v, u) ∉ E, we say that there is a directed edge from u to v and write u → v. We call undirected edges lines and directed edges arrows. The skeleton  ′ of a graph
′ of a graph  is the undirected graph obtained by replacing the arrows of
is the undirected graph obtained by replacing the arrows of  by lines. If every edge in graph
by lines. If every edge in graph  is undirected, then for any vertex u, we define the neighborhood ne
is undirected, then for any vertex u, we define the neighborhood ne (u) of u to be the set of vertices v such that u − v in
(u) of u to be the set of vertices v such that u − v in  .
.
A route in  is a sequence of vertices (v0, ···, vk), k ≥ 0, such that (vi−1, vi) ∈ E or (vi, vi−1) ∈ E for i = 1, ···, k, and the vertices v0 and vk are called terminals of the route. It is called descending if (vi−1, vi) ∈ E for i = 1, ···, k. We write u ↦ v if there exists a descending route from u to v. If v0, ···, vk are distinct vertices, the route is called a path. A route is called a pseudocycle if v0 = vk, and a cycle if further k ≥ 3 and v0, ···, vk−1 are distinct. A (pseudo) cycle is directed if it is descending and there exists at least one i ∈ {1, ···, k}, such that (vi, vi−1) ∈ ∉ E.
is a sequence of vertices (v0, ···, vk), k ≥ 0, such that (vi−1, vi) ∈ E or (vi, vi−1) ∈ E for i = 1, ···, k, and the vertices v0 and vk are called terminals of the route. It is called descending if (vi−1, vi) ∈ E for i = 1, ···, k. We write u ↦ v if there exists a descending route from u to v. If v0, ···, vk are distinct vertices, the route is called a path. A route is called a pseudocycle if v0 = vk, and a cycle if further k ≥ 3 and v0, ···, vk−1 are distinct. A (pseudo) cycle is directed if it is descending and there exists at least one i ∈ {1, ···, k}, such that (vi, vi−1) ∈ ∉ E.
A graph with only undirected edges is called an undirected graph (UG). A graph with only directed edges and without directed cycles is called a directed acyclic graph (DAG). A graph that has no directed (pseudo) cycles is called a chain graph.
By a section of a route ρ = (v0, ···, vk) in  , we mean a maximal undirected subroute σ: vi –··· –vj, 0 ≤ i ≤ j ≤ k of ρ. The vertices vi and v j are called the terminals of the section σ. Further the vertex vi (or vj) is called a head-terminal if i > 0 and vi−1 → vi in
, we mean a maximal undirected subroute σ: vi –··· –vj, 0 ≤ i ≤ j ≤ k of ρ. The vertices vi and v j are called the terminals of the section σ. Further the vertex vi (or vj) is called a head-terminal if i > 0 and vi−1 → vi in  (or j < k and vj ← vj+1 in
(or j < k and vj ← vj+1 in  ), otherwise it is called a tail-terminal. A section σ of a route ρ is called a head-to-head section with respect to ρ if it has two head-terminals, otherwise it is called non head-to-head. For a set of vertices S ⊂ V, we say that a section σ: vi – ··· –vj is outside S if {vi, ···, vj}∩ S = ∅. Otherwise we say that σ is hit by S.
), otherwise it is called a tail-terminal. A section σ of a route ρ is called a head-to-head section with respect to ρ if it has two head-terminals, otherwise it is called non head-to-head. For a set of vertices S ⊂ V, we say that a section σ: vi – ··· –vj is outside S if {vi, ···, vj}∩ S = ∅. Otherwise we say that σ is hit by S.
A complex in  is a path (v0, ···, vk), k ≥ 2, such that v0 → v1, vi − vi+1 (for i = 1, ···, k− 2) and vk−1 ← vk in
is a path (v0, ···, vk), k ≥ 2, such that v0 → v1, vi − vi+1 (for i = 1, ···, k− 2) and vk−1 ← vk in  , and no additional edge exists among vertices {v0, ···, vk} in
, and no additional edge exists among vertices {v0, ···, vk} in  . We call the vertices v0 and vk the parents of the complex and the set {v1, ···, vk−1} the region of the complex. The set of parents of a complex κ is denoted by par(κ). Note that the concept of complex was proposed in Studený (1997) and is equivalent to the notion of ‘minimal complex’ in Frydenberg (1990).
. We call the vertices v0 and vk the parents of the complex and the set {v1, ···, vk−1} the region of the complex. The set of parents of a complex κ is denoted by par(κ). Note that the concept of complex was proposed in Studený (1997) and is equivalent to the notion of ‘minimal complex’ in Frydenberg (1990).
An arrow in a graph  is called a complex arrow if it belongs to a complex in
is called a complex arrow if it belongs to a complex in  . The pattern of
. The pattern of  , denoted by
, denoted by  *, is the graph obtained by turning the arrows that are not in any complex of
*, is the graph obtained by turning the arrows that are not in any complex of  into lines. The moral graph
into lines. The moral graph  m of
m of  is the graph obtained by first joining the parents of each complex by a line and then turning arrows of the obtained graph into lines.
is the graph obtained by first joining the parents of each complex by a line and then turning arrows of the obtained graph into lines.
Studený and Bouckaert (2001) introduced the notion of c-separation for chain graph models. Hereunder we introduce the concept in the form that facilitates the proofs of our results. We say that a route ρ on  is intervented by a subset S of V if and only if there exists a section σ of ρ such that:
is intervented by a subset S of V if and only if there exists a section σ of ρ such that:
either σ is a head-to-head section with respect to ρ, and σ is outside S; or
σ is a non head-to-head section with respect to ρ, and σ is hit by S.
Definition 1
Let A, B, S be three disjoint subsets of the vertex set V of a chain graph  , such that A, B are nonempty. We say that A and B are c-separated by S on
, such that A, B are nonempty. We say that A and B are c-separated by S on  , written as
, if every route with one of its terminals in A and the other in B is intervented by S. We also call S a c-separator for A and B.
, written as
, if every route with one of its terminals in A and the other in B is intervented by S. We also call S a c-separator for A and B.
For a chain graph  = (V, E), let each v ∈ V be associated with a random variable Xv with domain
= (V, E), let each v ∈ V be associated with a random variable Xv with domain 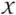 v and μ the underlying probability measure on Πv∈V
v and μ the underlying probability measure on Πv∈V  v. A probability distribution P on Πv∈V
v. A probability distribution P on Πv∈V 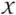 v is strictly positive if dP(x)/dμ > 0 for any x ∈ Πv∈V
v is strictly positive if dP(x)/dμ > 0 for any x ∈ Πv∈V 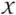 v. From now on, all probability distributions considered are assumed to be strictly positive. A probability distribution P on Πv∈V
v. From now on, all probability distributions considered are assumed to be strictly positive. A probability distribution P on Πv∈V 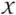 v is faithful with respect to
v is faithful with respect to  if for any triple (A, B, S) of disjoint subsets of V such that A and B are non-empty, we have
if for any triple (A, B, S) of disjoint subsets of V such that A and B are non-empty, we have
| (1) |
where XA = {Xv: v ∈ A} and XA╨XB|XS means the conditional independency of XA and XB given XS; P is Markovian with respect to  if (1) is weakened to
if (1) is weakened to
In the rest of the paper, A╨B|S is used as short notation for XA╨XB|XS when confusion is unlikely.
It is known that chain graphs can be classified into Markov equivalence classes, and those in the same equivalence class share the same set of Markovian distributions. The following result from Frydenberg (1990) characterizes equivalence classes graphically: Two chain graphs are Markov equivalent if and only if they have the same skeleton and complexes, that is, they have the same pattern. The following example illustrates some of the concepts that are introduced above.
Example 1
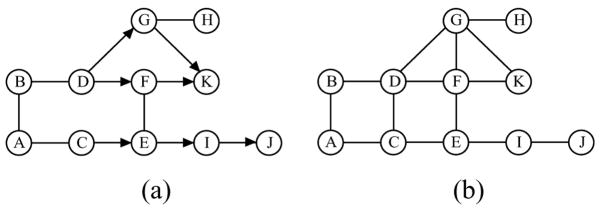
Consider the chain graph  in Fig. 1(a). D → F – E ← C and F → K ← G are the two complexes. The route ρ = (D, F, E, I, E, C) is intervented by an empty set since the head-to-head section (E →)I(←E) is outside the empty set. It is also intervented by E since the non head-to-head section (D →)F – E(→ I) is hit by E. However, D and C are not c-separated by E since the route (D, F, E, C) is not intervented by E. The moral graph
in Fig. 1(a). D → F – E ← C and F → K ← G are the two complexes. The route ρ = (D, F, E, I, E, C) is intervented by an empty set since the head-to-head section (E →)I(←E) is outside the empty set. It is also intervented by E since the non head-to-head section (D →)F – E(→ I) is hit by E. However, D and C are not c-separated by E since the route (D, F, E, C) is not intervented by E. The moral graph  m of
m of  is shown in Fig. 1(b), where edges C – D and F – G are added due to moralization.
is shown in Fig. 1(b), where edges C – D and F – G are added due to moralization.
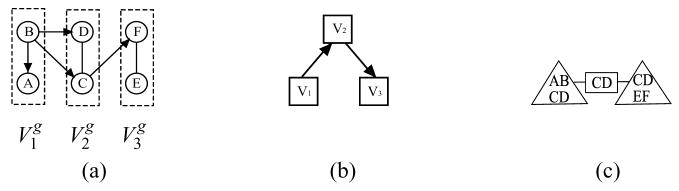
Figure 1.
(a) a chain graph  ; (b) its moral graph
; (b) its moral graph  m.
m.
2.2 Separation Trees
In this subsection, we introduce the notion of separation trees which is used to facilitate the representation of the decomposition. The concept is similar to the junction tree of cliques and the independence tree introduced for DAG as ‘d-separation trees’(Xie et al., 2006).
Let 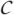 = {C1, ···, CH} be a collection of distinct variable sets such that for h = 1, ···, H, Ch ⊆ V. Let
= {C1, ···, CH} be a collection of distinct variable sets such that for h = 1, ···, H, Ch ⊆ V. Let  be a tree where each node corresponds to a distinct variable set in
be a tree where each node corresponds to a distinct variable set in  , to be displayed as a triangle (see, for example, Fig. 2). The term ‘node’ is used for a separation tree to distinguish from the term ‘vertex’ for a graph in general. An undirected edge e = (Ci,Cj) connecting nodes Ci and Cj in
, to be displayed as a triangle (see, for example, Fig. 2). The term ‘node’ is used for a separation tree to distinguish from the term ‘vertex’ for a graph in general. An undirected edge e = (Ci,Cj) connecting nodes Ci and Cj in  is attached with a separator S = Ci ∩ Cj, which is displayed as a rectangle. A separator S is connected to a node C if there is some other node C′, such that S attaches to the edge (C,C′). Removing an edge e or equivalently, removing a separator S from
is attached with a separator S = Ci ∩ Cj, which is displayed as a rectangle. A separator S is connected to a node C if there is some other node C′, such that S attaches to the edge (C,C′). Removing an edge e or equivalently, removing a separator S from  splits
splits  into two subtrees
into two subtrees  1 and
1 and  2 with node sets
2 with node sets  1 and
1 and  2 respectively. We use Vi = ∪C∈
2 respectively. We use Vi = ∪C∈ iC to denote the unions of the vertices contained in the nodes of the subtree
iC to denote the unions of the vertices contained in the nodes of the subtree  i for i = 1, 2.
i for i = 1, 2.
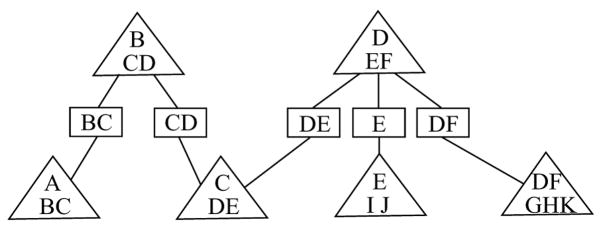
Figure 2.
A separation  of the graph
of the graph  in Fig. 1(a).
in Fig. 1(a).
Definition 2
A tree  with node set
with node set 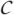 is said to be a separation tree for a chain graph
is said to be a separation tree for a chain graph  = (V, E) if
= (V, E) if
∪C∈
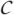 C = V, and
C = V, andfor any separator S in
 with V1 and V2 defined as above by removing S, we have
.
with V1 and V2 defined as above by removing S, we have
.
Notice that a separator is defined in terms of a tree whose nodes consist of variable sets, while the c-separator is defined based on a chain graph. In general, these two concepts are not related, though for a separation tree its separator must be some corresponding c-separator in the underlying chain graph.
Example 1. (Continued)
Suppose that
is a collection of vertex sets. A separation tree  of
of  in Fig. 1(a) with node set
in Fig. 1(a) with node set 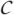 is shown in Fig. 2. If we delete the separator {D, E}, we obtain two subtrees
is shown in Fig. 2. If we delete the separator {D, E}, we obtain two subtrees  1 and
1 and  2 with node sets
2 with node sets 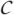 1 = {{A, B,C}, {B,C, D}, {C, D, E}} and
1 = {{A, B,C}, {B,C, D}, {C, D, E}} and 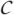 2 = {{D, E, F}, {E, I, J}, {D, F, G, H, K}}. In
2 = {{D, E, F}, {E, I, J}, {D, F, G, H, K}}. In  , the separator S = {D, E} c-separates V1\S = {A, B,C} and V2\S = {F, G, H, I, J, K}.
, the separator S = {D, E} c-separates V1\S = {A, B,C} and V2\S = {F, G, H, I, J, K}.
Not surprisingly, the separation tree could be regarded as a scheme for decomposing the knowledge represented by the chain graph into local subsets. Reciprocally, given a separation tree, we can combine the information obtained locally to recover the global information, an idea that will be formalized and discussed in subsequent sections.
The definition of separation trees for chain graphs is similar to that of junction trees of cliques, see Cowell et al. (1999) and Lauritzen (1996). Actually, it is not difficult to see that a junction tree of a chain graph  is also its separation tree. However, we point out two differences here: (a) a separation tree is defined with c-separation and it does not require that every node is a clique or that every separator is complete on the moral graph; (b) junction trees are mostly used as inference engines, while our interest in separation trees is mainly derived from its power in facilitating the decomposition of structural learning.
is also its separation tree. However, we point out two differences here: (a) a separation tree is defined with c-separation and it does not require that every node is a clique or that every separator is complete on the moral graph; (b) junction trees are mostly used as inference engines, while our interest in separation trees is mainly derived from its power in facilitating the decomposition of structural learning.
3. Structural Learning of Chain Graphs
In this section, we discuss how separation trees can be used to facilitate the decomposition of the structural learning of chain graphs. Theoretical results are presented first, followed by descriptions of several algorithms that are the summary of the key results in our paper. It should be emphasized that even with perfect knowledge on the underlying distribution, any two chain graph structures in the same equivalence class are indistinguishable. Thus, we can only expect to recover a pattern from the observed data, that is, an equivalence class to which the underlying chain graph belongs. To this end, we provide two algorithms: one addresses the issue of learning the skeleton and the other focuses on extending the learned skeleton to an equivalence class. We also discuss at the end of the section the problem of constructing separation trees. Throughout the rest of the paper, we assume that any distribution under consideration is faithful with respect to some underlying chain graph.
3.1 Theoretical Results
It is known that for P faithful to a chain graph  = (V, E), an edge (u, v) is in the skeleton
= (V, E), an edge (u, v) is in the skeleton  ′ if and only if Xu╨̷Xv|XS for any S ⊆ V\{u, v} (see Studený 1997, Lemma 3.2 for a proof). Therefore, learning the skeleton of
′ if and only if Xu╨̷Xv|XS for any S ⊆ V\{u, v} (see Studený 1997, Lemma 3.2 for a proof). Therefore, learning the skeleton of  reduces to searching for c-separators for all vertex pairs. The following theorem shows that with a separation tree, one can localize the search into one node or a small number of tree nodes.
reduces to searching for c-separators for all vertex pairs. The following theorem shows that with a separation tree, one can localize the search into one node or a small number of tree nodes.
Theorem 3
Let  be a separation tree for a chain graph
be a separation tree for a chain graph  . Then vertices u and v are c-separated by some set Suv ∪ V in
. Then vertices u and v are c-separated by some set Suv ∪ V in  if and only if one of the following conditions hold:
if and only if one of the following conditions hold:
u and v are not contained together in any node C of
 ,
,u and v are contained together in some node C, but for any separator S connected to C, {u, v} ⊈ S, and there exists such that ,
u and v are contained together in a node C and both of them belong to some separator connected to C, but there is a subset of either ⋃u∈C′ C′ or ⋃v∈C′ C′ such that .
For DAGs, condition 3 in Theorem 3 is unnecessary, see Xie et al. (2006, Theorem 1). However, the example below indicates that this is no longer the case for chain graphs.
Example 1. (Continued)
Consider the chain graph in Fig. 1(a) and its separation tree in Fig. 2. Let u = D and v = E. The tree nodes containing u and v together are {C, D, E} and {D, E, F}. Since the separator {D, E} is connected to both of them, neither condition 1 nor 2 in Theorem 3 is satisfied. Moreover, u╨̷v|S for S =∅, {C} or {F}. However, we have u╨v|{C, F}. Since {C, F} = S′ is a sub-set of both ⋃u∈C′ C′ = {B,C, D}∪{C, D, E}∪{D, E, F}∪{D, F, G, H, K} = {B,C, D, E, F, G, H, K} and ⋃v∈C′C′ = {C, D, E}∪{D, E, F}∪{E, I, J} = {C, D, E, F, I, J}, condition 3 of Theorem 3 applies.
Given the skeleton of a chain graph, we extend it into the equivalence class by identifying and directing all the complex arrows, to which the following result is helpful.
Proposition 4
Let  be a chain graph and
be a chain graph and  a separation tree of
a separation tree of  . For any complex κ in
. For any complex κ in  , there exists some tree node C of
, there exists some tree node C of  such that par(κ) ⊆C.
such that par(κ) ⊆C.
By Proposition 4, to identify the parents for each complex, we need only pay attention to those vertex pairs contained in each tree node.
3.2 Skeleton Recovery with Separation Tree
In this subsection, we propose an algorithm based on Theorem 3 for the identification of chain graph skeleton with separation tree information.
Let  be an unknown chain graph of interest and P be a probability distribution that is faithful to it. The algorithm, summarized as Algorithm 1, is written in its population version, where we assume perfect knowledge of all the conditional independencies induced by P.
be an unknown chain graph of interest and P be a probability distribution that is faithful to it. The algorithm, summarized as Algorithm 1, is written in its population version, where we assume perfect knowledge of all the conditional independencies induced by P.
Algorithm 1.
Skeleton Recovery with a Separation Tree.
Algorithm 1 consists of three main parts. In part 1 (lines 2–10), local skeletons are recovered in each individual node of the input separation tree. By condition 1 of Theorem 3, edges deleted in any local skeleton are also absent in the global skeleton. In part 2 (lines 11–16), we combine all the information obtained locally into a partially recovered global skeleton which may have extra edges not belonging to the true skeleton. Finally, we eliminate such extra edges in part 3 (lines 17–22).
The correctness of Algorithm 1 is proved in Appendix B. We conclude this subsection with some remarks on the algorithm.
Remarks on Algorithm 1
Although we assume perfect conditional independence knowledge in Algorithm 1, it remains valid when these conditional independence relations are obtained via performing hypotheses tests on data generated over P as in most real-world problems. When this is the case, we encounter the problem of multiple testing. See Sections 3.4 and 5 for more details.
The c-separator set
 is not necessary for skeleton recovery. However, it will be useful later in Section 3.3 when we try to recover the pattern based on the learned skeleton.
is not necessary for skeleton recovery. However, it will be useful later in Section 3.3 when we try to recover the pattern based on the learned skeleton.Part 3 of Algorithm 1 is indispensable as is illustrated by the following example.
Example 1. (Continued)
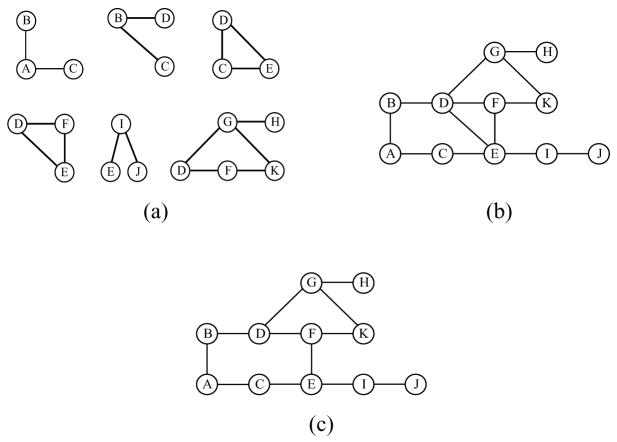
We apply Algorithm 1 to the chain graph  in Fig. 1(a) and the corresponding separation tree given in Fig. 2. The local skeletons recovered in part 1 of the algorithm are shown in Fig. 3(a). The c-separators found in this part are SBC = {A}, SCD = {B}, SEJ = {I}, SDK = {F, G}, SDH = {F, G}, SFG = {D}, SFH = {G} and SHK = {G}. In part 2, the local skeletons are combined by deleting the edges that are absent in at least one of the local skeletons, leading to the result in Fig. 3(b). The edge B –C is deleted since it is absent in the local skeleton for the tree node {A, B,C}. In part 3, we need to check D – E and D – F. D – E is deleted since D╨E|{C, F}, and we record SDE = {C, F}. The recovered skeleton is finally shown in Fig. 3(c).
in Fig. 1(a) and the corresponding separation tree given in Fig. 2. The local skeletons recovered in part 1 of the algorithm are shown in Fig. 3(a). The c-separators found in this part are SBC = {A}, SCD = {B}, SEJ = {I}, SDK = {F, G}, SDH = {F, G}, SFG = {D}, SFH = {G} and SHK = {G}. In part 2, the local skeletons are combined by deleting the edges that are absent in at least one of the local skeletons, leading to the result in Fig. 3(b). The edge B –C is deleted since it is absent in the local skeleton for the tree node {A, B,C}. In part 3, we need to check D – E and D – F. D – E is deleted since D╨E|{C, F}, and we record SDE = {C, F}. The recovered skeleton is finally shown in Fig. 3(c).
Figure 3.
(a) local skeletons recovered in part 1 of Algorithm 1 for all nodes of  in Fig. 2; (b) partially recovered global skeleton of
in Fig. 2; (b) partially recovered global skeleton of  in part 2 of Algorithm 1; (c) completely recovered global skeleton of
in part 2 of Algorithm 1; (c) completely recovered global skeleton of  in part 3 of Algorithm 1.
in part 3 of Algorithm 1.
3.3 Complex Recovery
In this subsection, we propose Algorithm 2 for finding and orienting the complex arrows of  after obtaining the skeleton
after obtaining the skeleton  ′ in Algorithm 1. We call this stage of structural learning complex recovery. As in the previous subsection, we assume separation tree information and perfect conditional independence knowledge. For simplicity, let Sc denote V\S for any vertex set S ⊆ V.
′ in Algorithm 1. We call this stage of structural learning complex recovery. As in the previous subsection, we assume separation tree information and perfect conditional independence knowledge. For simplicity, let Sc denote V\S for any vertex set S ⊆ V.
Algorithm 2.
Complex Recovery.
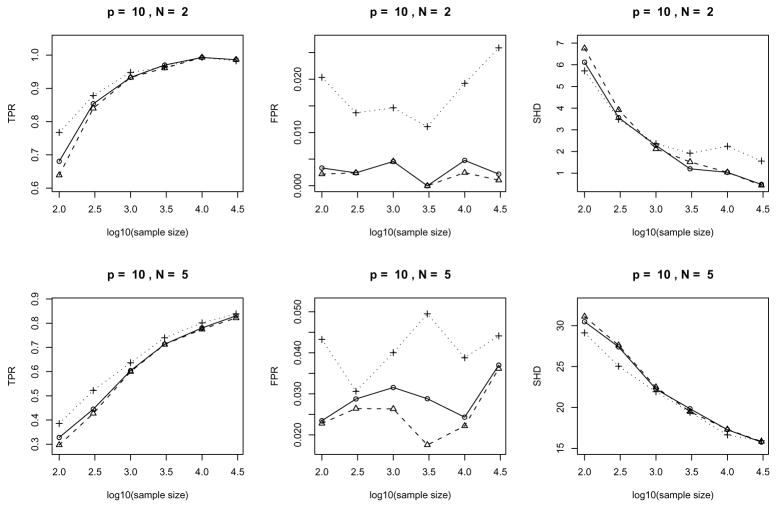
Example 1. (Continued)
After performing Algorithm 1 to recover the skeleton of  , we apply Algorithm 2 to find and orient all the complex arrows. For example, when we pick [C, D] in line 2 of Algorithm 2 and consider C – E in line 3 for the inner loop, we find SCD = {B} and C╨̷D|SCD ∪{E}. Therefore, we orient C → E in line 5. Similarly, we orient D → F, F → K and G → K when considering [D,C] with D – F (in the inner loop), [F, G] with F – K and [G, F] with G – K and observing that C╨̷D|SCD ∪{F} and F╨̷G|SFG ∪{K}, where the c-separators SCD = {B} and SFG = {K} were obtained during the execution of Algorithm 1. We do not orient any other edge in Algorithm 2. The resulting graph is shown in Fig. 4, which is exactly the pattern for our original chain graph
, we apply Algorithm 2 to find and orient all the complex arrows. For example, when we pick [C, D] in line 2 of Algorithm 2 and consider C – E in line 3 for the inner loop, we find SCD = {B} and C╨̷D|SCD ∪{E}. Therefore, we orient C → E in line 5. Similarly, we orient D → F, F → K and G → K when considering [D,C] with D – F (in the inner loop), [F, G] with F – K and [G, F] with G – K and observing that C╨̷D|SCD ∪{F} and F╨̷G|SFG ∪{K}, where the c-separators SCD = {B} and SFG = {K} were obtained during the execution of Algorithm 1. We do not orient any other edge in Algorithm 2. The resulting graph is shown in Fig. 4, which is exactly the pattern for our original chain graph  in Fig. 1(a).
in Fig. 1(a).
Figure 4.
The pattern of  recovered by applying Algorithm 2.
recovered by applying Algorithm 2.
The correctness of Algorithm 2 is guaranteed by Proposition 4. For the proof, see Appendix B.
Remarks on Algorithm 2
As Algorithm 1, Algorithm 2 is valid when independence test is correctly performed using data and again, multiple testing becomes an important issue here.
In Algorithm 2, the set
 obtained in Algorithm 1 helps avoid the computationally expensive looping procedure taken in the pattern recovery algorithm in Studený (1997) for complex arrow orientation.
obtained in Algorithm 1 helps avoid the computationally expensive looping procedure taken in the pattern recovery algorithm in Studený (1997) for complex arrow orientation.Line 9 of Algorithm 2 is necessary for chain graphs in general, see Example 2 below.
To get the pattern of
 * in line 9, at each step, we consider a pair of candidate complex arrows u1 → w1 and u2 → w2 with u1 ≠ u2, then we check whether there is an undirected path from w1 to w2 such that none of its intermediate vertices is adjacent to either u1 or u2. If there exists such a path, then u1 → w1 and u2 → w2 are labeled (as complex arrows). We repeat this procedure until all possible candidate pairs are examined. The pattern is then obtained by removing directions of all unlabeled arrows in
* in line 9, at each step, we consider a pair of candidate complex arrows u1 → w1 and u2 → w2 with u1 ≠ u2, then we check whether there is an undirected path from w1 to w2 such that none of its intermediate vertices is adjacent to either u1 or u2. If there exists such a path, then u1 → w1 and u2 → w2 are labeled (as complex arrows). We repeat this procedure until all possible candidate pairs are examined. The pattern is then obtained by removing directions of all unlabeled arrows in  *.
*.
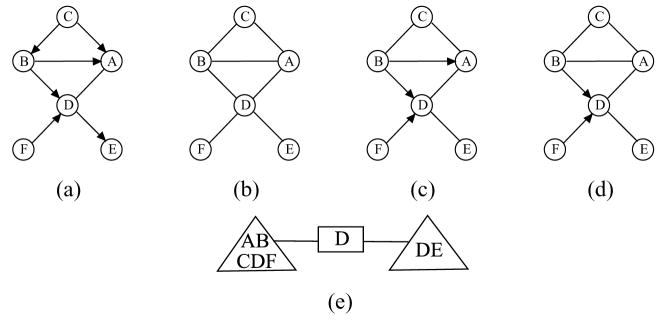
Example 2
Consider the chain graph  ˜ in Fig. 5(a) and the corresponding separation tree
˜ in Fig. 5(a) and the corresponding separation tree  ˜ in Fig. 5(e). After applying Algorithm 1, we obtain the skeleton
˜ in Fig. 5(e). After applying Algorithm 1, we obtain the skeleton  ˜′ of
˜′ of  ˜. In the execution of Algorithm 2, when we pick [B, F] in line 2 and A in line 3, we have B╨F|∅, that is, SBF = ∅, and find that B╨̷F|A. Hence we orient B – A as B → A in line 5, which is not a complex arrow in
˜. In the execution of Algorithm 2, when we pick [B, F] in line 2 and A in line 3, we have B╨F|∅, that is, SBF = ∅, and find that B╨̷F|A. Hence we orient B – A as B → A in line 5, which is not a complex arrow in  ˜. Note that we do not orient A – B as A → B: the only chance we might do so is when u = A, v = F and w = B in the inner loop of Algorithm 2, but we have B ∈ SAF and the condition in line 4 is not satisfied. Hence, the graph we obtain before the last step in Algorithm 2 must be the one given in Fig. 5(c), which differs from the recovered pattern in Fig. 5(d). This illustrates the necessity of the last step in Algorithm 2. To see how the edge B → A is removed in the last step of Algorithm 2, we observe that, if we follow the procedure described in Remark 4 on Algorithm 2, the only chance that B → A becomes one of the candidate complex arrow pair is when it is considered together with F → D. However, the only undirected path between A and D is simply A – D with D adjacent to B. Hence B → A stays unlabeled and will finally get removed in the last step of Algorithm 2.
˜. Note that we do not orient A – B as A → B: the only chance we might do so is when u = A, v = F and w = B in the inner loop of Algorithm 2, but we have B ∈ SAF and the condition in line 4 is not satisfied. Hence, the graph we obtain before the last step in Algorithm 2 must be the one given in Fig. 5(c), which differs from the recovered pattern in Fig. 5(d). This illustrates the necessity of the last step in Algorithm 2. To see how the edge B → A is removed in the last step of Algorithm 2, we observe that, if we follow the procedure described in Remark 4 on Algorithm 2, the only chance that B → A becomes one of the candidate complex arrow pair is when it is considered together with F → D. However, the only undirected path between A and D is simply A – D with D adjacent to B. Hence B → A stays unlabeled and will finally get removed in the last step of Algorithm 2.
Figure 5.
(a) the chain graph  ˜ in Example 2; (b) the skeleton
˜ in Example 2; (b) the skeleton  ˜′ of
˜′ of  ˜; (c) the graphical structure
˜; (c) the graphical structure  ˜* before executing the last line in Algorithm 2; (d) the graphical structure
˜* before executing the last line in Algorithm 2; (d) the graphical structure  ˜* obtained after executing Algorithm 2; (e) a separation tree
˜* obtained after executing Algorithm 2; (e) a separation tree  ˜ for
˜ for  ˜ in (a).
˜ in (a).
3.4 Sample Versions of Algorithms 1 and 2
In this section, we present a brief description on how to obtain a sample version of the previous algorithms and the related issues.
To apply the previous methods to a data set, we proceed in the exactly same way as before. The only difference in the sample version of the algorithms lies in that statistical hypothesis tests are needed to evaluate the predicate on line 5, 13 and 19 in Algorithm 1 and on line 4 in Algorithm 2. Specifically, conditional independence test of two variables u and v given a set C of variables is required. Let the null hypothesis H0 be u╨v|C and alternative H1 be that H0 may not hold. Generally we can use the likelihood ratio test statistic
where L(θ|D) is the likelihood function of parameter θ with observed data D. Under H0, the statistic G2 asymptotically follows the χ2 distribution with df degrees of freedom being equal to the difference of the dimensions of parameters for the alternative and null hypothesis (Wilks, 1938).
Let Xk be a vector of variables and N be the sample size. For the case of a Gaussian distribution, the test statistic for testing Xi╨Xj|Xk can be simplified to
which has an asymptotic χ2 distribution with df = 1. Actually, the exact null distribution or a better approximate distribution of G2 can be obtained based on Bartlett decomposition, see Whittaker (1990) for details.
For the discrete case, let be the observed frequency in a cell of Xs = m where s is an index set of variables and m is category of variables Xs. For example, denotes the frequency of Xi = a, Xj = b and Xk = c. The G2 statistic for testing Xi╨Xj|Xk is then given by
which is asymptotically distributed as a χ2 distribution under H0 with degree of freedom
where #(X) is the number of categories of variable X.
3.4.1 The Multiple Testing Problem
As mentioned in the remarks of Algorithms 1 and 2, when perfect knowledge of the population conditional independence structure is not available, we turn to hypotheses testing for obtaining these conditional independence relations from data and run into the problem of multiple testing. This is because we need to test the existence of separators for multiple edges, and we typically consider more than one candidate separators for each edge.
Although a theoretical analysis of the impact of the multiple testing problem on the overall error rate (see, for example, Drton and Perlman 2008) for the proposed method is beyond the scope of this paper, simulation studies are conducted on randomly generated chain graphs to show the impact of choices of different significance levels on our method in Section 5.1. Based on our empirical study there, we feel that choosing a small significance level (e.g., α = 0.005 or 0.01) for the individual tests usually yields good and stable results when the sample size is reasonably large and the underlying graph is sparse.
3.5 Construction of Separation Trees
Algorithms 1 and 2 depend on the information encoded in the separation tree. In the subsection, we address the issue of how to construct a separation tree.
As proposed by Xie et al. (2006), one can construct a d-separation tree from observed data, from domain or prior knowledge of conditional independence relations or from a collection of databases. Their arguments are also valid in the current setting. In the rest of this subsection, we first extend Theorem 2 of Xie et al. (2006), which guarantees that their method for constructing a separation tree from data is valid for chain graph models. Then we propose an algorithm for constructing a separation tree from background knowledge encoded in a labeled block ordering (Roverato and La Rocca, 2006) of the underlying chain graph. We remark that Algorithm 2 of Xie et al. (2006), which constructs d-separation trees from hyper-graphs, also works in the current context.
3.5.1 From Undirected Independence Graph to Separation Tree
For a chain graph  = (V, E) and a faithful distribution P, an undirected graph
= (V, E) and a faithful distribution P, an undirected graph 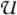 with a vertex set V is an undirected independence graph (UIG) of
with a vertex set V is an undirected independence graph (UIG) of  if for any u, v ∈ V,
if for any u, v ∈ V,
| (2) |
We generalize Theorem 2 of Xie et al. (2006) as follows.
Theorem 5
Let  be a chain graph. Then a junction tree constructed from any undirected independence graph of
be a chain graph. Then a junction tree constructed from any undirected independence graph of  is a separation tree for
is a separation tree for  .
.
Since there are standard algorithms for constructing junction trees from UIGs (see Cowell et al. 1999, Chapter 4, Section 4), the construction of separation trees reduces to the construction of UIGs. In this sense, Theorem 5 enables us to exploit various techniques for learning UIGs to serve our purpose.
As suggested by relation (2), one way of learning UIGs from data is testing the required conditional independencies. Agresti (2002) and Anderson (2003) provides general techniques for discrete and Gaussian data respectively. Recently, there are also works on estimating UIGs via ℓ1-regularization, see, for instance, Friedman et al. (2007) for Gaussian data and Ravikumar et al. (2008) for the discrete case. Edwards (2000, Chapter 6) presents some other established methods for UIG learning, including those that are valid when XV includes both continuous and discrete variables. All these methods can be used to construct separation trees from data.
3.5.2 From Labeled Block Ordering to Separation Tree
When learning graphical models, it is a common practice to incorporate substantive background knowledge in structural learning, mostly to reduce the dimensionality of the search spaces for both computational and subject matter reasons.
Recently, Roverato and La Rocca (2006) studied in detail a general type of background knowledge for chain graphs, which they called labeled block ordering. We introduce this concept here and investigate how it is related to the construction of separation trees.
By summarizing Definitions 5 and 6 in Roverato and La Rocca (2006), we define the labeled block ordering as the following.
Definition 6
Let V1, ···, Vk be a partition of a set of vertices V. A labeled block ordering ℬ of V is a sequence (
, i = 1, ···, k) where li ∈ {u, d, g} and with the convention that
. We say a chain graph  = (V, E) is ℬ-consistent if
= (V, E) is ℬ-consistent if
every edge connecting vertices A ∈ Vi and B ∈ Vj for i ≠ j is oriented from A → B if i < j;
for every li = u, the subgraph
 Vi is a UG;
Vi is a UG;for every li = d, the subgraph
 Vi is a DAG;
Vi is a DAG;for every li = g, the subgraph
 Vi may have both directed and undirected edges.
Vi may have both directed and undirected edges.
Example 1. (Continued)
Let V1 = {A, B,C, D, E, F}, V2 = {G, H, K} and V3 = {I, J}. Then Fig. 6 shows that for a labeled block ordering
,  in Fig. 1(a) is ℬ-consistent.
in Fig. 1(a) is ℬ-consistent.
Figure 6.
A labeled block ordering
for which  in Fig. 1(a) is ℬ-consistent.
in Fig. 1(a) is ℬ-consistent.
To show how labeled block ordering helps learning separation trees, we start with the following simple example.
Example 3
Suppose that the underlying chain graph is the one in Fig. 7(a) which is ℬ-consistent with . Then for V1 = {A, B}, V2 = {C, D} and V3 = {E, F}, we have V1╨V3|V2. Together with the total ordering on them, we can construct the DAG in Fig. 7(b) with vertices as blocks Vi, i = 1, 2, 3, which depicts the conditional independence structures on the three blocks. By taking the junction tree of this DAG and replacing the blocks by the vertices they contain, we obtain the tree structure in Fig. 7(c). This is a separation tree of the chain graph in Fig. 7(a).
Figure 7.
(a) a chain graph with a labeled block ordering; (b) the DAG constructed for the blocks; (c) the tree structure obtained from the junction tree of the DAG in (b).
Below we propose Algorithm 3 for constructing a separation tree from labeled block ordering knowledge. The idea is motivated by the preceding toy example. By omitting independence structures within each block, we can treat each block as a vertex in a DAG. The total ordering on the blocks and the conditional independence structures among them enable us to build a DAG on these blocks. By taking the junction tree of this particular DAG, we obtain a separation tree of the underlying chain graph model.
Algorithm 3.
Separation Tree Construction with Labeled Block Ordering.
| Input: A labeled block ordering of V; perfect conditional independence knowledge. | |
Output: A separation tree  of of  . . |
|
| 1 | Construct a DAG  with blocks Vi, i = 1, ···, k; with blocks Vi, i = 1, ···, k; |
| 2 | Construct a junction tree  by triangulating by triangulating  ; ; |
| 3 | In  , replace each block Vi by the original vertices it contains. , replace each block Vi by the original vertices it contains. |
We note that a labeled block ordering gives a total ordering of the blocks Vi, i = 1, ···, k. Given a total ordering of the vertices of a DAG, one can use the Wermuth-Lauritzen algorithm (Spirtes et al., 2000; Wermuth and Lauritzen, 1983) for constructing (the equivalence class of) the DAG from conditional independence relations. Spirtes et al. (2000) also discussed how to incorporate the total ordering information in the PC algorithm for constructing DAGs from conditional independence relations. Since these approaches rely only on conditional independence relations, they can be used in Algorithm 3 for constructing the DAG  . The only difference is that each vertex represents a random vector rather than a random variable now. The correctness of Algorithm 3 is proved in Appendix B.
. The only difference is that each vertex represents a random vector rather than a random variable now. The correctness of Algorithm 3 is proved in Appendix B.
3.5.3 Separation Tree Refinement
In practice, the nodes of a separation tree constructed from a labeled block ordering or other methods may still be large. Since the complexities of our skeleton and complex recovery algorithms are largely dominated by the cardinality of the largest node on the separation tree, it is desirable to further refine our separation tree by reducing the sizes of the nodes. To this end, we propose the following algorithm.
If the current separation tree contains a node whose cardinality is still relatively large, the above algorithm can be repeatedly used until no further refinement is available. However, we remark that the cardinality of the largest node on the separation tree is eventually determined by the sparseness of the underlying chain graph together with other factors including the specific algorithms for constructing undirected independence subgraphs and junction tree. The correctness of the algorithm is proved in Appendix B.
4. Computational Complexity Analysis
In this section, we investigate the computational complexities of Algorithms 1 and 2 and compare them with the pattern recovery algorithm proposed by Studený (1997). We divide our analysis into two stages: (a) skeleton recovery stage (Algorithm 1); (b) complex recovery stage (Algorithm 2). In each stage, we start with a discussion on Studený’s algorithm and then give a comprehensive analysis of ours.
4.1 Skeleton Recovery Stage
Let  = (V, E) be the unknown chain graph, p the number of vertices and e the number of edges, including both lines and arrows. In Studený’s algorithm, to delete an edge between a vertex pair u and v, we need to check the independence of u and v conditional on all possible subsets S of V\{u, v}. Therefore, the complexity for investigating each possible edge in the skeleton is O(2p) and hence the complexity for constructing the global skeleton is O(p22p).
= (V, E) be the unknown chain graph, p the number of vertices and e the number of edges, including both lines and arrows. In Studený’s algorithm, to delete an edge between a vertex pair u and v, we need to check the independence of u and v conditional on all possible subsets S of V\{u, v}. Therefore, the complexity for investigating each possible edge in the skeleton is O(2p) and hence the complexity for constructing the global skeleton is O(p22p).
For Algorithm 1, suppose that the input separation tree has H nodes {C1, ···, CH} where H ≤ p and m = max{card(Ch), 1 ≤ h ≤ H}. The complexity for investigating all edges within each tree node is thus O(m22m). Thus, the complexity for the first two parts of Algorithm 1 is O(Hm22m). For the analysis of the third step, suppose that k = max{card(S), S ∈  } is the cardinality of the largest separator on the separation tree. Since the tree with H nodes has H − 1 edges, we also have H − 1 separators. Thus, the edge to be investigated in step 3 is O(Hk2). Then, let d be the maximum of the degrees of vertices in the partially recovered skeleton obtained after step 2. By our algorithm, the complexity for checking each edge is O(2d). Hence, the total complexity for step 3 is O(Hk22d). Combining all the three parts, the total complexity for our Algorithm 1 is O(H(m22m + k22d)). It is usually the case that m, k and d are much smaller than p, and therefore, our Algorithm 1 is computationally less expensive than Studený’s algorithm, especially when
} is the cardinality of the largest separator on the separation tree. Since the tree with H nodes has H − 1 edges, we also have H − 1 separators. Thus, the edge to be investigated in step 3 is O(Hk2). Then, let d be the maximum of the degrees of vertices in the partially recovered skeleton obtained after step 2. By our algorithm, the complexity for checking each edge is O(2d). Hence, the total complexity for step 3 is O(Hk22d). Combining all the three parts, the total complexity for our Algorithm 1 is O(H(m22m + k22d)). It is usually the case that m, k and d are much smaller than p, and therefore, our Algorithm 1 is computationally less expensive than Studený’s algorithm, especially when  is sparse.
is sparse.
4.2 Complex Recovery Stage
For complex arrow orientation, Studený’s algorithm needs to first find a candidate complex structure of some pre-specified length l and then check a collection of conditional independence relations. Finding a candidate structure can be accomplished in a polynomial (of p) time. The complexity of the algorithm is determined by the subsequent investigation on conditional independence relations. Actually, the number of conditional independence relations to be checked for each candidate structure is 2p−2 − 1. Hence, the complexity of Studený’s algorithm is exponential in p.
In Algorithm 2, the computational complexity of the large double loop (lines 2–8) is determined by the number of conditional independence relations we check in line 4. After identifying u, w and v, we need only to check one single conditional independence with the conditioning set Suv ∪{w}, which can be done in O(1) time. The pair {u, w} must be connected on  ′, thus the number of such pairs is O(e). Since the number of v for each {u, w} pair is at most p, we execute line 4 at most O(pe) times. The complexity for the double loop part is thus controlled by O(pe). Next we show that the complexity for taking the pattern of the graph is O(e2(p + e)). As in the remarks on Algorithm 2, in each step, we propose a pair of candidate complex arrows u1 → w1 and u2 → w2 and then check whether there is an undirected path from w1 to w2 whose intermediate vertices are adjacent to neither u1 nor u2. This can be done by performing a graph traversal algorithm on an undirected graph which is obtained by deleting all existing arrows on the current graph with the adjacency relations checked on the original graph. By a breadth-first search algorithm, the complexity is O(p + e) (Cormen et al., 2001). Since the number of candidate complex arrow pairs is controlled by O(e2), the total complexity for finding the pattern is O(e2(p + e)). Since pe = O(e2(p + e)), the total complexity for Algorithm 2 is O(e2(p + e)).
′, thus the number of such pairs is O(e). Since the number of v for each {u, w} pair is at most p, we execute line 4 at most O(pe) times. The complexity for the double loop part is thus controlled by O(pe). Next we show that the complexity for taking the pattern of the graph is O(e2(p + e)). As in the remarks on Algorithm 2, in each step, we propose a pair of candidate complex arrows u1 → w1 and u2 → w2 and then check whether there is an undirected path from w1 to w2 whose intermediate vertices are adjacent to neither u1 nor u2. This can be done by performing a graph traversal algorithm on an undirected graph which is obtained by deleting all existing arrows on the current graph with the adjacency relations checked on the original graph. By a breadth-first search algorithm, the complexity is O(p + e) (Cormen et al., 2001). Since the number of candidate complex arrow pairs is controlled by O(e2), the total complexity for finding the pattern is O(e2(p + e)). Since pe = O(e2(p + e)), the total complexity for Algorithm 2 is O(e2(p + e)).
By incorporating the information obtained in the skeleton recovery stage, we greatly reduce the number of conditional independence tests to be checked and hence obtain an algorithm of only polynomial time complexity for the complex recovery stage. The improvement is achieved with additional cost: we need to store the c-separator information Suv’s obtained from Algorithm 1 in the set  . The possible number of {u, v} combinations is O(p2), while the length of Suv is O(p). Hence, the total space we need to store
. The possible number of {u, v} combinations is O(p2), while the length of Suv is O(p). Hence, the total space we need to store  is O(p3), which is still polynomially complex.
is O(p3), which is still polynomially complex.
4.3 Comparison with a DAG Specific Algorithm When the Underlying Graph is a DAG
In this subsection, we compare our algorithm with Algorithm 1 in Xie et al. (2006) that is designed specifically for DAG structural learning when the underlying graph structure is a DAG. We make this choice of the DAG specific algorithm so that both algorithms can have the same separation tree as input and hence are directly comparable.
Combining the analyses in the above two subsections, we know that the total complexity of our general algorithm is O(H(m22m + k22d) + e2(p + e)), while the complexity of the DAG specific algorithm is O(Hm22m) as claimed in Xie et al. (2006, Section 6). So the extra complexity in the worst case is O(Hk22d + e2(p + e)). The term that might make a difference is O(Hk22d), which occurs as the complexity of step 3 in our Algorithm 1 and involves an exponential term in d. Note that d is defined as the maximum degree of the vertices in the partially recovered skeleton  ′ obtained after step 2 of Algorithm 1, where
′ obtained after step 2 of Algorithm 1, where  ′ is exactly the skeleton for the underlying DAG in the current situation (i.e., step 3 of Algorithm 1 does not make any further modification to
′ is exactly the skeleton for the underlying DAG in the current situation (i.e., step 3 of Algorithm 1 does not make any further modification to  ′ when
′ when  is a DAG). Hence, if the underlying graph is sparse, d is small and the extra complexity O(Hk22d + e2(p + e)) is well under control.
is a DAG). Hence, if the underlying graph is sparse, d is small and the extra complexity O(Hk22d + e2(p + e)) is well under control.
Therefore, if we believe that the true graph is sparse, the case where our decomposition approach is most applicable, we can apply our general chain graph structural learning algorithm without worrying much about significant extra cost even when the underlying graph is indeed a DAG.
5. Simulation
In this section, we investigate the performance of our algorithms under a variety of circumstances using simulated data sets. We first demonstrate various aspects of our algorithms by running them on randomly generated chain graph models. We then compare our methods with DAG-specific learning algorithms on data generated from the ALARM network, a Bayesian network that has been widely used in evaluating the performance of structural learning algorithms. The simulation results show the competitiveness of our algorithms, especially when the underlying graph is sparse. From now on, we refer to our method as the LCD (Learn Chain graph via Decomposition) method. Algorithms 1 and 2 have been implemented in the R language. All the results reported here are based on the R implementation.
5.1 Performance on Random Chain Graphs
To assess the quality of a learning method, we adopt the way Kalisch and Bühlmann (2007) used in investigating the performance of PC algorithm on Bayesian networks. We perform our algorithms on randomly generated chain graphs and report summary error measures.
5.1.1 Data Generation Procedure
First we discuss the way in which the random chain graphs and random samples are generated. Given a vertex set V, let p = |V| and N denote the average degree of edges (including undirected and pointing out and pointing in) for each vertex. We generate a random chain graph on V as follows:
Order the p vertices and initialize a p × p adjacency matrix A with zeros;
For each element in the lower triangle part of A, set it to be a random number generated from a Bernoulli distribution with probability of occurrence s = N/(p − 1);
Symmetrize A according to its lower triangle;
Select an integer k randomly from {1, ···, p} as the number of chain components;
Split the interval [1, p] into k equal-length subintervals I1, ···, Ik so that the set of variables falling into each subinterval Im forms a chain component Cm;
Set Aij = 0 for any (i, j) pair such that i ∈ Il, j ∈ Im with l > m.
This procedure then yields an adjacency matrix A for a chain graph with (Ai j = Aji = 1) representing an undirected edge between Vi and Vj and (Aij = 1, Aji = 0) representing a directed edge from Vi to Vj. Moreover, it is not hard to see that  [vertex degree] = N where an adjacent vertex can be linked by either an undirected or a directed edge.
[vertex degree] = N where an adjacent vertex can be linked by either an undirected or a directed edge.
Given a randomly generated chain graph  with ordered chain components C1, ···, Ck, we generate a Gaussian distribution on it via the incomplete block-recursive regression as described in Wermuth (1992). Let Xm be the |Cm| × 1 random vector, and
. Then we have the block-recursive regression system as
with ordered chain components C1, ···, Ck, we generate a Gaussian distribution on it via the incomplete block-recursive regression as described in Wermuth (1992). Let Xm be the |Cm| × 1 random vector, and
. Then we have the block-recursive regression system as
where
Let
be the block-diagonal part of B*. Each block diagonal element Σi,i.i+1···k of B* is the inverse covariance matrix of Xi conditioning on (Xi+1, ···, Xk), an element of which is set to be zero if the corresponding edge within the chain component is missing. The upper triangular part of B* has all the conditional covariances between Xi and (X1, ···, Xi−1). The zero constraints on the elements correspond to missing directed edges among different components. Finally, W* ~ N(0, T).
For the chain component Ci, suppose the corresponding vertices are Vi1, ···, Vir, and in general, let B*[Vl,Vm] be the element of B* that corresponds to the vertex pair (Vl,Vm). In our simulation, we generate the B* matrix in the following way:
For the diagonal block Σi,i.i+1···k of B*, for 1 ≤ j < j′ ≤ r, we fix B*[Vij, Vij] = 1 and set B*[Vij, Vij′] = 0 if the vertices Vij and Vij′ are non-adjacent in Ci and otherwise sampled randomly from (−1.5/r, −0.5/r) ∪(0.5/r, 1.5/r), and finally we symmetrize the matrix according to its upper triangular part.
For Σi, j,i+1···k, 1 ≤ j ≤ i−1, an element B*[Vl,Vm] is set to be zero if Vl ∈ Ci is not pointed to by an arrow starting from Vm ∈ C1 ∪···∪Ci−1, and sampled randomly from −1.5/r, −0.5/r) ∪ (0.5/r, 1.5/r) otherwise.
If any of the block diagonal elements in B* is not positive semi-definite, we repeat Step (1) and (2).
After setting up the B* matrix, we take its block diagonal to obtain the T matrix. For fixed B* and T, we first draw i.i.d. samples of W* from N(0, T), and then pre-multiply them by (B*)−1 to get random samples of X. We remark that faithfulness is not necessarily guaranteed by the current sampling procedure and quantifying the deviation from the faithfulness assumption is beyond the scope of this paper.
5.1.2 Performance under Different Settings
We examine the performance of our algorithm in terms of three error measures: (a) the true positive rate (TPR) and (b) the false positive rate (FPR) for the skeleton and (c) the structural Hamming distance (SHD) for the pattern. In short, TPR is the ratio of # (correctly identified edge) over total number of edges, FPR is the ratio of # (incorrectly identified edge) over total number of gaps and SHD is the number of legitimate operations needed to change the current pattern to the true one, where legitimate operations are: (a) add or delete an edge and (b) insert, delete or reverse an edge orientation. In principle, a large TPR, a small FPR and a small SHD indicate good performance.
In our simulation, we change three parameters p (the number of vertices), n (sample size) and N (expected number of adjacent vertices) as follows:
p ∈ {10, 40, 80},
n ∈ {100, 300, 1000, 3000, 10000, 30000},
N ∈ {2, 5}
For each (p, N) combination, we first generate 25 random chain graphs. We then generate a random Gaussian distribution based on each graph and draw an identically independently distributed (i.i.d.) sample of size n from this distribution for each possible n. For each sample, three different significance levels (α= 0.005, 0.01 or 0.05) are used to perform the hypothesis tests. We then compare the results to access the influence of the significance testing level on the performance of our algorithms. A separation tree is obtained through the following ‘one step elimination’ procedure:
We start from a complete UIG over all p vertices;
We test zero partial correlation for each element of the sample concentration matrix at the chosen significance level α and delete an edge if the corresponding test doesn’t reject the null hypothesis;
An UIG is obtained after Step 2 and its junction tree is computed and used as the separation tree in the algorithms.
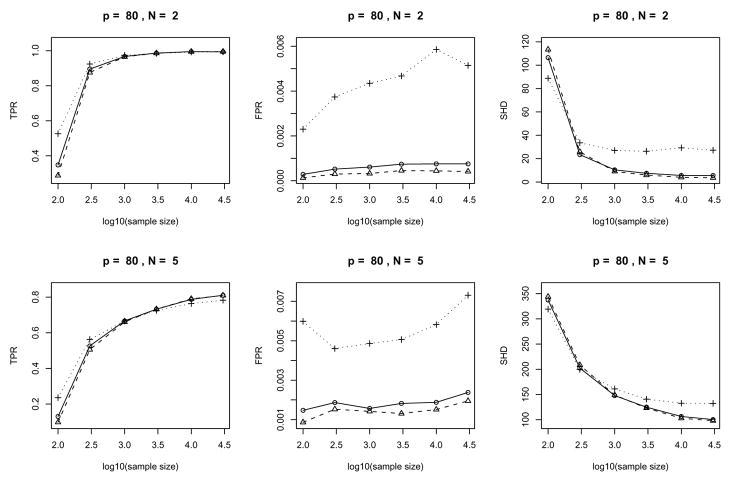
The plots of the error measures are given in Fig. 8, 9 and 10. From the plots, we see that: (a) our algorithms yield better results on sparse graphs (N = 2) than on dense graphs (N = 5); (b) the TPR increases with sample size while the SHD decreases; (c) the behavior of FPR is largely regulated by the significance level α used in the individual tests and has no clear dependence on the sample size (Note that FPRs and their variations in the middle columns of Fig. 8, 9 and 10 are very small since the vertical axes have very small scales); (d) large significance level α(=0.05) typically yields large TPR, FPR and SHD while the advantage in terms of a larger TPR (compared to α= 0.005 or 0.01) fades out as the sample size increases and the disadvantage in terms of a larger SHD becomes much worse; (e) accuracy in terms of TPR and SHD based on α= 0.005 or α= 0.01 is very close while choosing α= 0.005 does yield a consistently (albeit slightly) lower FPR across all the settings in the current simulation. Such empirical evidence suggests that in order to account for the multiple testing problem, we can choose a small value (say α= 0.005 or 0.01 for the current example) for the significance level of individual tests. However, the optimal value for a desired overall error rate may depend on the sample size and the sparsity of the underlying graph.
Figure 8.
Error measures of the algorithms for randomly generated Gaussian chain graph models: average over 25 repetitions with 10 variables. The two rows correspond to N = 2 and N = 5 cases and the three columns give three error measures: TPR, FPR and SHD in each setting respectively. In each plot, the solid/dashed/dotted lines correspond to significance levels α= 0.01/0.005/0.05.
Figure 9.
Error measures of the algorithms for randomly generated Gaussian chain graph models: average over 25 repetitions with 40 variables. Display setup is the same as in Fig. 8.
Figure 10.
Error measures of the algorithms for randomly generated Gaussian chain graph models: average over 25 repetitions with 80 variables. Display setup is the same as in Fig. 8.
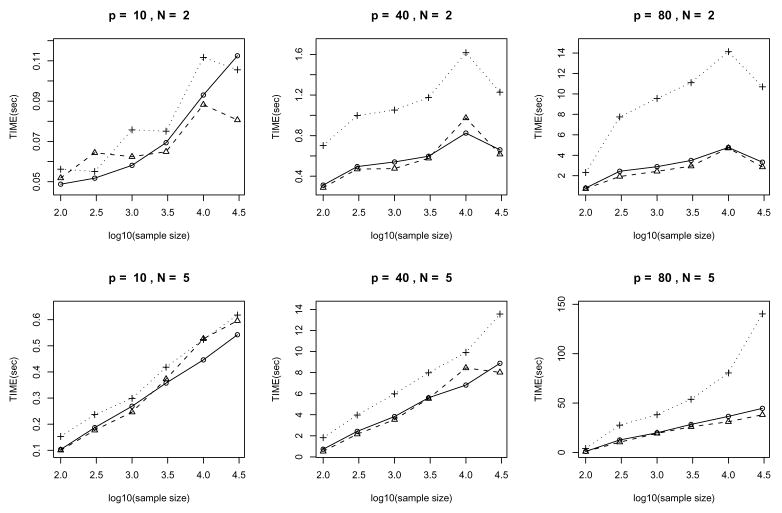
Finally, we look at how our method scales with the sample size, which is not analyzed explicitly in Section 4. The average running times vs. the sample sizes are plotted in Fig. 11. It can be seen that: (a) the average run time scales approximately linearly with log(sample size); and (b) the scaling constant depends on the sparsity of the graph. The simulations were run on an Intel Core Duo 1.83GHz CPU.
Figure 11.
Running times of the algorithms on randomly generated Gaussian chain graph models: average over 25 repetitions. The two rows correspond to N = 2 and 5 cases and the three columns represent p = 10, 40 and 80 respectively. In each plot, the solid/dashed/dotted lines correspond to significance levels α = 0.01/0.005/0.05.
5.2 Learning the ALARM Network
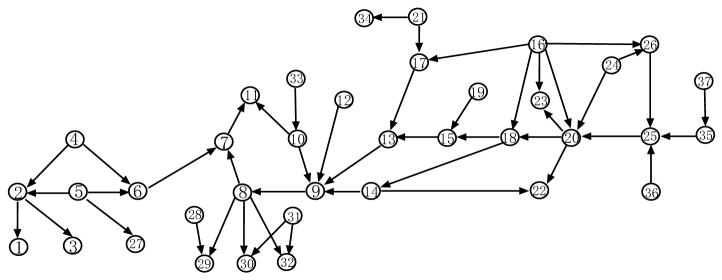
As we have pointed out in Section 1, Bayesian networks are special cases of chain graphs. It is of interest to see whether our general algorithms still work well when the data are actually generated from a Bayesian network. For this purpose, in this subsection, we perform simulation studies on both Gaussian and discrete case for the ALARM network in Fig. 12 and compare our algorithms for general chain graphs with those specifically designed for Bayesian networks. The network was first proposed in Beinlich et al. (1989) as a medical diagnostic network.
Figure 12.
The ALARM network
5.2.1 The Gaussian Case
In the Gaussian case, for each run of the simulation, we repeat the following steps:
A Gaussian distribution on the network is generated using a recursive linear regression model, whose coefficients are random samples from the uniform distribution on (−1.5, −0.5) ∪ (0.5, 1.5) and residuals are random samples from N(0, 1).
A sample of size n is generated from the distribution obtained at step 1.
We run the LCD algorithms, the DAG learning algorithms proposed in Xie et al. (2006) and the PC algorithm implemented in the R package pcalg (Kalisch and Bühlmann, 2007) all with several different choices of the significance level α. The one step elimination procedure described in Section 5.1.2 was used to construct the separation trees for the LCD and DAG methods.
We record the number of extra edges (FP), the number of missing edges (FN) and the structural Hamming distance (SHD) compared with the true pattern for all the three learned patterns.
We performed 100 runs for each sample size n ∈ {1000, 2000, 5000, 10000}. For each sample, we allow three different significance levels α ∈ {0.05, 0.01, 0.005} for all the three methods. Table 1 documents the averages and standard errors (in parentheses) from the 100 runs for each method-parameter-sample size combination.
Table 1.
Simulation results for Gaussian samples from the ALARM network. Averages and standard errors for (FP, FN, SHD) from 100 runs.
| Alg (Level α) | n = 1000 | n = 2000 | n = 5000 | n = 10000 |
|---|---|---|---|---|
| DAG | (3.09, 4.05, 17.3) | (3.17, 3.14, 15.2) | (3.48, 2.07, 12.4) | (3.16, 1.62, 10.5) |
| (0.05) | (0.18, 0.19, 0.61) | (0.16, 0.16, 0.54) | (0.18, 0.16, 0.55) | (0.17, 0.11, 0.46) |
| DAG | (0.87, 3.41, 12.2) | (0.87, 2.60, 9.90) | (0.71, 1.60, 6.02) | (0.58, 1.24, 5.23) |
| (0.01) | (0.08, 0.19, 0.64) | (0.09, 0.17, 0.54) | (0.08, 0.14, 0.41) | (0.08, 0.10, 0.36) |
| DAG | (0.61, 3.34, 11.4) | (0.54, 2.50, 8.77) | (0.36, 1.49, 5.43) | (0.33, 1.08, 4.14) |
| (0.005) | (0.08, 0.19, 0.60) | (0.07, 0.16, 0.52) | (0.07, 0.12, 0.38) | (0.06, 0.11, 0.39) |
| LCD | (2.06, 5.19, 19.0) | (2.10, 4.25, 16.7) | (2.5, 3.07, 14.0) | (2.15, 2.38, 11.3) |
| (0.05) | (0.16, 0.19, 0.58) | (0.15, 0.17, 0.53) | (0.15, 0.15, 0.50) | (0.15, 0.14, 0.39) |
| LCD | (0.41, 4.93, 15.8) | (0.34, 4.01, 12.9) | (0.44, 2.82, 9.79) | (0.30, 2.10, 7.11) |
| (0.01) | (0.06, 0.21, 0.61) | (0.06, 0.17, 0.50) | (0.07, 0.15, 0.41) | (0.05, 0.13, 0.40) |
| LCD | (0.22, 4.86, 15.3) | (0.12, 3.85, 12.2) | (0.13, 2.85, 9.14) | (0.14, 1.95, 6.49) |
| (0.005) | (0.05, 0.21, 0.61) | (0.03, 0.16, 0.52) | (0.04, 0.14, 0.41) | (0.03, 0.13, 0.40) |
| PC | (4.72, 7.98, 38.4) | (5.03, 6.79, 38.5) | (4.94, 5.19, 35.2) | (4.41, 4.21, 31.9) |
| (0.05) | (0.22, 0.23, 0.73) | (0.23, 0.23, 0.73) | (0.24, 0.20, 0.79) | (0.26, 0.19, 0.89) |
| PC | (3.45, 9.23, 37.9) | (3.11, 7.78, 34.8) | (3.27, 5.88, 31.5) | (2.98, 4.87, 30.9) |
| (0.01) | (0.19, 0.26, 0.78) | (0.19, 0.22, 0.76) | (0.20, 0.21, 0.79) | (0.22, 0.20, 0.88) |
| PC | (3.14, 9.61, 38.1) | (2.95, 8.05, 35.6) | (3.03, 6.15, 31.4) | (2.88, 5.13, 30.4) |
| (0.005) | (0.20, 0.27, 0.69) | (0.18, 0.23, 0.79) | (0.20, 0.21, 0.78) | (0.22, 0.20, 0.79) |
As shown in Table 1, compared with the DAG method (Xie et al., 2006), the LCD method consistently yields a smaller number of false positives and the differences in false negatives are consistently smaller than two on recovering the skeleton of the network. The SHDs obtained from our algorithms are usually comparable to those from the DAG method when α = 0.05 and the difference is usually less than five when α = 0.01 or 0.005. Moreover, we remark that as sample size grows, the power of the significance test increases, which leads to better performance of the LCD method as in the case of other hypothesis testing based methods. However, from Table 1, we find that the LCD performance increases more rapidly in terms of SHD. One plausible reason is that in Algorithm 2, we identify complex arrows by rejecting conditional independence hypotheses rather than direct manipulation as in the algorithms specific for DAG and hence have some extra benefit in terms of accuracy as the power of the test becomes greater.
Finally, the LCD method consistently outperforms the PC algorithm in all three error measures. Such simulation results confirm that our method is reliable when we do not know the information that the underlying graph is a DAG, which is usually untestable from data.
5.2.2 The Discrete Case
In this section, a similar simulation study with discrete data sampled from the ALARM network is performed. The variables in the network are allowed to have two to four levels. For each run of the simulation, we repeat the following steps:
-
For each variable Xi and fixed configuration pai of its parents, we define the conditional probability , where L is the number of levels of Xi and {r1, ···, rL} are random numbers from the Uniform(0,1) distribution.
2. A sample of size n is generated from the above distribution.
3. We run three algorithms designed specifically for DAG that have been shown to have a good performance: MMHC (Max-Min Hill Climbing: Tsamardinos et al., 2006), REC (Recursive: Xie and Geng, 2008) and SC (Sparse Candidate: Friedman et al., 1999) with several different choice of parameters. We also perform the LCD learning algorithm with different choices of the significance level. For the LCD method, a grow-shrink Markov blanket selection is performed on the data to learn the UIG and the junction tree of the UIG is supplied as the separation tree for the algorithm.
4. For each algorithm, we recorded the FP, FN and SHD of the recovered pattern under each choice of the learning parameter.
We performed 100 runs for each of the four different sample sizes n ∈ {1000, 2000, 5000, 10000}, and in each run, we allow the following choices of the learning parameters:
For MMHC, REC and LCD, we allow three different significance levels α ∈ {0.05, 0.01, 0.005}; and
For SC, we allow the learning parameters to be either 5 or 10.
The means and standard errors from the 100 runs of all the four learning methods are summarized in Table 2. It can be seen that REC could yield the best result when the learning parameter is appropriately chosen. However, all the other methods are more robust against the choice of learning parameters. For the LCD method, all the three error measures: FP, FN and SHD are consistently comparable to those of methods specifically designed for DAG. Moreover, as in the Gaussian case, the power of the tests used in the LCD method grows as the sample size become larger, which makes the LCD method even more competitive, especially in terms of SHD. For example, when the sample size reaches 10000, the LCD method with α = 0.01 or 0.005 outperforms the sparse candidate method with parameters 5 or 10.
Table 2.
Simulation results for discrete samples from the ALARM network. Averages and standard errors for (FP, FN, SHD) from 100 runs.
| Alg (Level α) | n = 1000 | n = 2000 | n = 5000 | n = 10000 |
|---|---|---|---|---|
| MMHC | (0.27, 7.77, 34.0) | (0.16, 5.15, 27.9) | (0.08, 2.61, 20.6) | (0.03, 1.53, 16.0) |
| (0.05) | (0.05, 0.25, 0.57) | (0.04, 0.19, 0.48) | (0.03, 0.15, 0.47) | (0.02, 0.10, 0.45) |
| MMHC | (0.13, 8.39, 34.6) | (0.08, 5.53, 28.2) | (0.07, 2.96, 21.2) | (0.00, 1.64, 16.1) |
| (0.01) | (0.04, 0.26, 0.57) | (0.03, 0.19, 0.48) | (0.03, 0.16, 0.46) | (0.00, 0.10, 0.45) |
| MMHC | (0.13, 8.79, 35.3) | (0.09, 5.77, 28.6) | (0.06, 3.09, 21.4) | (0.01, 1.75, 16.3) |
| (0.005) | (0.04, 0.26, 0.57) | (0.03, 0.18, 0.51) | (0.03, 0.16, 0.47) | (0.01, 0.11, 0.46) |
| REC | (6.20, 4.95, 40.1) | (6.49, 3.52, 35.9) | (6.20, 1.77, 28.9) | (6.39, 0.80, 25.1) |
| (0.05) | (0.24, 0.19, 0.71) | (0.24, 0.13, 0.74) | (0.23, 0.11, 0.68) | (0.23, 0.08, 0.73) |
| REC | (1.57, 5.52, 33.2) | (1.82, 3.64, 27.2) | (2.06, 1.80, 20.0) | (2.31, 0.86, 16.2) |
| (0.01) | (0.13, 0.22, 0.58) | (0.13, 0.14, 0.48) | (0.12, 0.11, 0.56) | (0.14, 0.09, 0.52) |
| REC | (1.02, 5.72, 32.9) | (1.23, 3.76, 26.3) | (1.20, 1.86, 18.6) | (1.64, 0.90, 14.6) |
| (0.005) | (0.10, 0.22, 0.55) | (0.10, 0.15, 0.49) | (0.08, 0.12, 0.49) | (0.12, 0.09, 0.47) |
| SC | (0.63, 7.35, 34.2) | (0.50, 4.71, 27.8) | (0.59, 2.50, 21.7) | (0.81, 1.53, 18.1) |
| (5) | (0.07, 0.26, 0.60) | (0.09, 0.18, 0.49) | (0.09, 0.14, 0.53) | (0.11, 0.10, 0.56) |
| SC | (0.85, 7.30, 34.5) | (0.76, 4.65, 28.3) | (0.94, 2.36, 22.0) | (1.30, 1.32, 18.1) |
| (10) | (0.09, 0.25, 0.64) | (0.09, 0.18, 0.52) | (0.09, 0.14, 0.53) | (0.13, 0.10, 0.59) |
| LCD | (2.92, 8.49, 38.9) | (2.50, 5.94, 32.17) | (2.18, 3.41, 25.17) | (1.99, 2.18, 19.8) |
| (0.05) | (0.17, 0.21, 0.53) | (0.16, 0.18, 0.51) | (0.14, 0.13, 0.46) | (0.12, 0.10, 0.50) |
| LCD | (1.07, 8.16, 37.8) | (0.97, 5.63, 31.7) | (0.80, 3.40, 23.1) | (0.68, 2.11, 17.2) |
| (0.01) | (0.09, 0.20, 0.46) | (0.09, 0.16, 0.42) | (0.09, 0.13, 0.46) | (0.09, 0.09, 0.42) |
| LCD | (0.69, 8.14, 38.4) | (0.67, 5.84, 31.8) | (0.40, 3.31, 23.2) | (0.41, 2.09, 17.1) |
| (0.005) | (0.08, 0.19, 0.41) | (0.08, 0.17, 0.43) | (0.07, 0.13, 0.45) | (0.07, 0.09, 0.40) |
6. Discussion
In this paper, we presented a computationally feasible method for structural learning of chain graph models. The method can be used to facilitate the investigation of both response-explanatory and symmetric association relations among a set of variables simultaneously within the framework of chain graph models, a merit not shared by either Bayesian networks or Markov networks.
Simulation studies illustrate that our method yields good results in a variety of situations, especially when the underlying graph is sparse. On the other hand, the results also reveal that the power of the significance test has an important influence on the performance of our method. With fixed number of samples, one can expect a better accuracy if we replace the asymptotic test used in our implementation with an exact test. However, there is a trade-off between accuracy and computational time.
The results in this paper also raised a number of interesting questions for future research. We briefly comment on some of those questions here. First, the separation tree plays a key role in Algorithms 1 and ****2. Although the construction of separation trees has been discussed in Xie et al. (2006) and Section 3.5 here, we believe that there is room for further improvements. Second, we have applied hypothesis testing for the detection of local separators in Algorithm 1 and also in complex arrow determination in Algorithm 2. It shall be interesting to see whether there exists some alternative approach, preferably not based on hypothesis testing, to serve the same purpose here. A theoretical analysis of the effect of multiple testing on the overall error rate of the procedure is also important. In addition, it is a common practice to incorporate prior information about the order of the variables in graphical modelling. Therefore, incorporation of such information into our algorithms is worth investigation. Finally, our approach might be extendible to the structural learning of chain graph of alternative Markov properties, for example, AMP chain graphs (Andersson et al., 2001) and multiple regression chain graphs (Cox and Wermuth, 1996).
An R language package lcd that implements our algorithms is available on the first author’s website: www.stanford.edu/~zongming/software.html.
Acknowledgments
The authors would like to thank two referees for their valuable suggestions and comments which improve the presentation of the previous version of the paper. We would also like to thank Professor John Chambers and Xiangrui Meng for their help on the simulation study. This research was supported by NSFC (10771007, 10431010, 10721403), 863 Project of China (2007AA01Z437), MSRA and MOE-Microsoft Key Laboratory of Statistics and Information Technology of Peking University. The first author was also supported in part by grants NSF DMS 0505303 and NIH EB R01 EB001988.
Appendix A. Proofs of Theoretical Results
In this part, we give proofs to theorems and propositions. We first give a definition and several lemmas that are to be used in later proofs.
Definition 7
Let  be a separation tree for a CG
be a separation tree for a CG  with the node set
with the node set  = {C1, ···, CH}. For any two vertices u and v in
= {C1, ···, CH}. For any two vertices u and v in  , the distance between u and v in the tree
, the distance between u and v in the tree  is defined by
is defined by
where d(Ci,Cj) is the distance between nodes Ci and Cj in  . We call Ci and Cj minimizers for u and v if they minimize the distance d(Ci,Cj).
. We call Ci and Cj minimizers for u and v if they minimize the distance d(Ci,Cj).
Lemma 8
Let ρ be a route from u to v in a chain graph  , and W the set of all vertices on ρ (W may or may not contain the two end vertices). Suppose that ρ is intervented by S ⊂ V. If W ⊂ S, ρ is also intervented by W and any vertex set containing W.
, and W the set of all vertices on ρ (W may or may not contain the two end vertices). Suppose that ρ is intervented by S ⊂ V. If W ⊂ S, ρ is also intervented by W and any vertex set containing W.
Proof
Since ρ is intervented by S and W ⊂ S, there must be a non head-to-head section σ of ρ that is hit by S and actually every non head-to-head section of ρ is hit by S. Thus, σ is also hit by W and any vertex set containing W. Hence, ρ is intervented.
Lemma 9
Let  be a separation tree for a chain graph over vertex set V and K a separator of
be a separation tree for a chain graph over vertex set V and K a separator of  which separates
which separates  into two subtrees
into two subtrees  1 and
1 and  2 with variable sets V1 and V2. Suppose that u ∈ V1\K, v ∈ V2\K and ρ is a route from u to v in
2 with variable sets V1 and V2. Suppose that u ∈ V1\K, v ∈ V2\K and ρ is a route from u to v in  . Let W denote the set of all vertices on ρ (W may or may not contain the two end vertices). Then ρ is intervented by W ∩ K and by any vertex set containing W ∩ K.
. Let W denote the set of all vertices on ρ (W may or may not contain the two end vertices). Then ρ is intervented by W ∩ K and by any vertex set containing W ∩ K.
Proof
Since u ∈ V1\K and v ∈ V2\K, there must be a sequence from s (may be u) to y (may be v) in ρ = (u, ···, s,t, ···, x, y, ···, v) such that s ∈ V1\K, y ∈ V2\K and all vertices from t to x in this sequence are contained in K. Otherwise, every vertex of ρ is either in V1\K or in V2\K. This implies that there exists w ∈ V1\K and z ∈ V2\K on ρ that are adjacent, which is contradictory to the fact that . Without loss of generality, we can suppose that y is the first vertex (from the left) of ρ that is not in V1.
Let ρ′ be the sub-route of the sequence (s,t, ···, x, y), and W ′ be the vertex set of ρ′ excluding s and y. Since W ′ ⊂ K, we know from Lemma 8 that there is at least one non head-to-head section (w.r.t. ρ′) on ρ′ and every non head-to-head section of ρ′ is hit by W ′. We are to show that there is at least one non head-to-head section of ρ that is hit by K and hence W ∩ K as well as any set containing W ∩ K.
The only problem arises when ρ′ is part of a head-to-head section of ρ. Otherwise, there is some non head-to-head section of ρ′ that is (part of) a non head-to-head section of ρ.
Thus, we suppose that the head-to-head section of ρ is
By our assumption on y, we know that s′ ∈ V1. If s′ ∈ K, then the non head-to-head section containing s′ is hit by K. If s′ ∈ V1\K and y′ ∈ K, then the non head-to-head section containing y′ gives the result. If s′ ∈ V1\K and y′ ∈ V1\K, then we can consider the sub-route starting from y′. This is legitimate since every non head-to-head section of that sub-route is also non head-to-head w.r.t. ρ. Hence, we need only consider the case that s′ ∈ V1\K and y′ ∈ V2\K. In this case, let t′ be the last (from left) vertex in this section that is adjacent to s′ and x′ the first vertex after t′ in this section that is adjacent to y′. Since chain graphs cannot have directed pseudocycles, we know that s′ → t′ and y′ → x′. Then we have s′╨̷y′|K, which is contradictory to the property of separation trees that . This completes our proof.
Lemma 10
Let u and v be two non adjacent vertices in a chain graph  and ρ a route from u to v in
and ρ a route from u to v in  . If ρ is not contained in An(u) ∪ An(v), then ρ is intervented by any subset S of An(u) ∪ An(v).
. If ρ is not contained in An(u) ∪ An(v), then ρ is intervented by any subset S of An(u) ∪ An(v).
Proof
Since ρ is not contained in An(u) ∪ An(v), there exist four vertices s,t, x and y, such that ρ = (u, ···, s,t, ···, x, y, ···, v), with {s, y}⊂ An(u) ∪An(v) and {t, ···, x}∩[An(u) ∪An(v)] = ∅. Then we have s → t and x ← y, since otherwise t and/or x must be in An(u) ∪An(v). Thus, there exists at least one head-to-head section between s and y on ρ such that it is not hit by any subset of An(u) ∪ An(v). Hence, ρ is intervented by any subset S of An(u) ∪ An(v).
Lemma 11
Let  be a separation tree for a chain graph
be a separation tree for a chain graph  over V and C a node of
over V and C a node of  . Let u and v be two vertices in C which are non adjacent in
. Let u and v be two vertices in C which are non adjacent in  . If u and v are not contained simultaneously in any separator connected to C, then there exists a subset S of C which c-separates u and v in
. If u and v are not contained simultaneously in any separator connected to C, then there exists a subset S of C which c-separates u and v in  .
.
Proof
Define
We show below that .
To this end, let ρ be any fixed route from u to v in  . If ρ is not contained in An(u) ∪ An(v), by Lemma 10, ρ is intervented by S. Otherwise, we divide the problem into the following six possible situations:
. If ρ is not contained in An(u) ∪ An(v), by Lemma 10, ρ is intervented by S. Otherwise, we divide the problem into the following six possible situations:
u –···– u′ ← x, x ≠ v, x ∈ C, where u –···– u′ means the first (from left) section of ρ that contains u;
u –···– u′ → x –···– x′ → y, x ≠ v, x ∈ C;
u –···– u′ → x –···– x′ y, x ≠ v, x ∈ C, y ∈ C;
u –···– u′ → x –···– x′ ← y, x ≠ v, x ∈ C, y ∉ C;
u – u′ ···– v′ – v, u – u′ –···– v′ → v or u – u′ –···– v′ ← v;
u –···– u′ → x or u –···– u′ ← x, x ∉ C.
We prove the desired result situation by situation.
For situation 1, we have that x ∈ An(u), which, together with x ∈ C implies that x ∈ S. The non head-to-head section containing x is hit by S, and ρ is thus intervented.
For situation 2, since x ∈ An(u) ∪ An(v) and x ∉ An(u), we have x ∈ An(v). Together with x ∈ C, this gives x ∈ S and the non head-to-head section containing x is hit by S.
For situation 3, since chain graphs do not admit directed pseudocycles, we know that x ∉ An(u) and y ≠ v. Similar to situation 2, we have x ∈ An(v) and hence y ∈ An(v). The non head-to-head section containing y is hit by S.
For situation 4, suppose that C′ is one of the nodes on  that contains y. Consider first the case when v belongs to the separator K connected to C and the next node on the path from C to C′ on
that contains y. Consider first the case when v belongs to the separator K connected to C and the next node on the path from C to C′ on  . By our assumption, u ∉ K. We divide the problem into the following three cases:
. By our assumption, u ∉ K. We divide the problem into the following three cases:
{u, ···, u′}∩S ≠ ∅: u –···– u′ is hit by S and ρ is hence intervented;
{u, ···, u′}∩S = ∅, {x, ···, x′}∩S = ∅: the head-to-head section x –···– x′ is not hit by S and ρ is intervented;
{u, ···, u′}∩S = ∅, {x, ···, x′}∩S ≠ ∅: there must exist some x*∈ {x, ···, x′} such that x* ∈ C ∩ An(v) and x* ≠ = v. Since {u, ···, u′}∩S = ∅ and u ╨y|K, there should be no complex in the induced subgraph of (u, ···, u′, x, ···, x′, y). Otherwise, there exists some u* ∈ {u, ···, u′}, such that (u*, y) is an edge on (
 An(u,y,K))m, which implies u╨̷y|K since {u, ···, u′}∩K = ∅. However, this requires that there is some u** ∈ {u, ···, u′} such that (u**, y) is an edge on
An(u,y,K))m, which implies u╨̷y|K since {u, ···, u′}∩K = ∅. However, this requires that there is some u** ∈ {u, ···, u′} such that (u**, y) is an edge on  , which again implies that u╨̷y|K. Hence, this case can never happen.
, which again implies that u╨̷y|K. Hence, this case can never happen.
Next, we consider the case that v ∉ K. The assumption that {x, ···, x′}⊂ An(v) implies that there exists at least one ′ →′ on the sub-route l′ of ρ from y to v. Consider the rightmost one of such arrows, there is no further ′ ← ′ closer to the right end v than it is. Otherwise, any vertex w between them satisfies w ∈ An(u) and w ∈ de(v), which is contradictory to the fact that v ∈ de(u) here. Thus, this case reduces to one of the situations 1, 5 and 6 with u replaced by v.
For situation 5, since u and v are non adjacent, we know that v′ ≠ u and u′ ≠ v. If {u′, ···, v′}∩ S = ∅, then {u′, ···, v′}∩C ⊂ {u, v}. We can eliminate vertices from the left such that {u′, ···, v′}∩ C ⊂ {v}. This will not influence our result since any non head-to-head section of the sub-route is (part of) a non head-to-head section of ρ. Since u′ ≠ v and {u′, ···, v′} ∩C ⊂ {v}, we have u′ ∉ C. Suppose that u′ ∈ C′ and K is the separator related to C and the next node on the path from C to C′ on  . Then u ∈ K, v ∉ K and u′ ╨ v|K. However, since {u′, ···, v′} ∩ C ⊂ {v}, we have {u, ···, u′}∩K = ∅, which is impossible. Hence {u′, ···, v′}∩S ≠ ∅ and ρ is intervented.
. Then u ∈ K, v ∉ K and u′ ╨ v|K. However, since {u′, ···, v′} ∩ C ⊂ {v}, we have {u, ···, u′}∩K = ∅, which is impossible. Hence {u′, ···, v′}∩S ≠ ∅ and ρ is intervented.
For situation 6, consider first the case that u –···– u′ ← x. If {u, ···, u′} ∩ S ≠ ∅, then ρ is intervented by S. Otherwise, suppose that x ∈ C′ and K is the separator connected to C and the next node on the path from C to C′ in  . If v ∈ K, then u ∉ K and {u, ···, u′} ∩ K ⊂ {v}. If {u, ···, u′}∩K = {v}, then it reduces to situation 5. If {u, ···, u′}∩K = ∅, then u╨̷x|K, which is contradictory to the definition of separation tree. If v ∉ K, then by the above argument, we must have u ∈ K. Consider the sub-route of ρ starting with x. It is legitimate to do so since any non head-to-head section of the sub-route is also non head-to-head in ρ. By Lemma 9, at least one non head-to-head section is hit by W ∩ K where W is the vertex set of the sub-route excluding the two end vertices. We know that W ∩ K ⊂ S ∪ {u, v}. If the non head-to-head section is hit at u or v, we can consider the further sub-route starting at that point and it is again legitimate by the same reason. Finally, we can reduce to the case where W ∩K ⊂ S. Thus, ρ is intervented by S. This also completes the proof of situation 4. For the other case in this situation, all the argument is the same up to the point where v ∉ K and u ∈ K. We can consider reversing the vertex sequence, then with u replaced by v, it must be in one of the situations 1 to 4, the second case in situation 6 or the first case in situation 6 with u ∉ K. This complete the proof of the lemma.
. If v ∈ K, then u ∉ K and {u, ···, u′} ∩ K ⊂ {v}. If {u, ···, u′}∩K = {v}, then it reduces to situation 5. If {u, ···, u′}∩K = ∅, then u╨̷x|K, which is contradictory to the definition of separation tree. If v ∉ K, then by the above argument, we must have u ∈ K. Consider the sub-route of ρ starting with x. It is legitimate to do so since any non head-to-head section of the sub-route is also non head-to-head in ρ. By Lemma 9, at least one non head-to-head section is hit by W ∩ K where W is the vertex set of the sub-route excluding the two end vertices. We know that W ∩ K ⊂ S ∪ {u, v}. If the non head-to-head section is hit at u or v, we can consider the further sub-route starting at that point and it is again legitimate by the same reason. Finally, we can reduce to the case where W ∩K ⊂ S. Thus, ρ is intervented by S. This also completes the proof of situation 4. For the other case in this situation, all the argument is the same up to the point where v ∉ K and u ∈ K. We can consider reversing the vertex sequence, then with u replaced by v, it must be in one of the situations 1 to 4, the second case in situation 6 or the first case in situation 6 with u ∉ K. This complete the proof of the lemma.
Proof of Theorem 3
The sufficiency of condition 1 is given by Lemma 9. The sufficiencies of conditions 2 and 3 are trivial by the definition of c-separation.
Now we show the necessity part of the theorem. If d(u, v) > 0, by Lemma 9, any separator K on the path from minimizers Ci to Cj c-separates u and v. If d(u, v) = 0, we consider the following two possible cases: (1) u and v are not contained simultaneously in any separator connected to C for some node C on  containing both u and v; (2) otherwise. For the first case, Lemma 11 shows that there exists some S′ ⊂ C that c-separates u and v. Otherwise, since
, bd
containing both u and v; (2) otherwise. For the first case, Lemma 11 shows that there exists some S′ ⊂ C that c-separates u and v. Otherwise, since
, bd (u) ⊂ ⋃u∈C C and bd
(u) ⊂ ⋃u∈C C and bd (v) ⊂ ⋃v∈C C, we know that at least one of the conditions 2 and 3 holds.
(v) ⊂ ⋃v∈C C, we know that at least one of the conditions 2 and 3 holds.
Proof of Proposition 4
We verify Proposition 4 by contradiction. Let us suppose that u and v are parents of a complex κ = (u, w1, ···, wk, v), k ≤ 1 in  and that for any node C on
and that for any node C on  , {u, v}∩ C ≠ {u, v}. Now suppose that u ∈ C1, v ∈ C2 and K is the separator related to C1 and the next node on the path from C1 to C2 on
, {u, v}∩ C ≠ {u, v}. Now suppose that u ∈ C1, v ∈ C2 and K is the separator related to C1 and the next node on the path from C1 to C2 on  . If u ∉ K and v ∉ K, we must have that {w1, ···, wk}∩ K ≠ ∅. This implies that u╨̷ v|K, which is contrary to the definition of separation trees. Hence, without loss of generality, we may suppose that u ∈ K, and this enables us to go one node closer to C2 on the path. Then after finite steps, we will consider two adjacent nodes on
. If u ∉ K and v ∉ K, we must have that {w1, ···, wk}∩ K ≠ ∅. This implies that u╨̷ v|K, which is contrary to the definition of separation trees. Hence, without loss of generality, we may suppose that u ∈ K, and this enables us to go one node closer to C2 on the path. Then after finite steps, we will consider two adjacent nodes on  . Repeating the above argument ensures that {u, v} belongs to one of these two nodes.
. Repeating the above argument ensures that {u, v} belongs to one of these two nodes.
Appendix B. Proofs for Correctness of the Algorithms
Before proving the correctness of the algorithms, we need several more lemmas.
Lemma 12
Suppose that u and v are two adjacent vertices in  , then for any separation tree
, then for any separation tree  for
for  , there exists a node C in
, there exists a node C in  which contains both u and v.
which contains both u and v.
Proof
If not, then there exists a separator K on  , such that u ∈ V1\K and v ∈ V2\K where Vi denotes the variable set of the subtree
, such that u ∈ V1\K and v ∈ V2\K where Vi denotes the variable set of the subtree  i induced by removing the edge attached by the separator S, for i = 1 and 2. This implies u╨v|K, which is impossible.
i induced by removing the edge attached by the separator S, for i = 1 and 2. This implies u╨v|K, which is impossible.
Lemma 13
Any arrow oriented in line 5 of Algorithm 2 is correct in the sense that it is an arrow with the same orientation in  .
.
Proof
We prove the lemma by induction. If we don’t orient any arrow in line 5, then the lemma holds trivially. Otherwise, suppose u → w is the first arrow we orient by considering the ordered triple 〈u, v, w〉, then we show that it cannot be u − w or u ← w in  . If it is u − w in
. If it is u − w in  , then by Lemma 11, if u and v are not in any separator simultaneously, there exists some Suv ⊂ Ch such that u╨v|Suv and w ∈ Suv. Otherwise, u╨v|bd
, then by Lemma 11, if u and v are not in any separator simultaneously, there exists some Suv ⊂ Ch such that u╨v|Suv and w ∈ Suv. Otherwise, u╨v|bd (u) ∪ bd
(u) ∪ bd (v), and we know that w ∈ bd
(v), and we know that w ∈ bd (u) ∪ bd
(u) ∪ bd (v) ⊂ bd
(v) ⊂ bd ′(u) ∪ bd
′(u) ∪ bd ′(v). Thus we won’t orient it as u → w. A similar argument holds for the case when u ← w in
′(v). Thus we won’t orient it as u → w. A similar argument holds for the case when u ← w in  .
.
Now suppose that the k-th arrow we orient is correct, let’s consider the k + 1-th. Suppose it’s u′ → w′ by considering the order triple 〈u′, v′, w′〉. Then the above argument holds exactly with u, v and w substituted by u′, v′ and w′. However, for here, the claim that bd (u′) ∪ bd
(u′) ∪ bd (v′) ⊂ bd
(v′) ⊂ bd ′(u′) ∪ bd
′(u′) ∪ bd ′(v′) holds by the induction assumption.
′(v′) holds by the induction assumption.
Lemma 14
Suppose that ℋ is a graph, if we disorient any non-complex arrow in ℋ, the pattern of ℋ does not change.
Proof
First, we note that we will not add or delete edge in ℋ, so the skeleton of ℋ does not change.
Second, we only disorient non-complex arrows, and hence those complexes in ℋ before disorientation remain complexes after disorientation since the subgraph induced by any complex does not change.
Finally, we show that there will not be new complex. If there appears a new complex, say u → w1 –···, –wl ← v, we must have l ≥ 2. Since it was not a complex before disorientation, one of the lines in w1 – ··· – wl must be the arrow disoriented. Suppose we have wi → wi+1 before disorientation, then wi → wi+1 – ··· –wl ← v was a complex before disorientation. Hence, the disoriented arrow wi → wi+1 was a complex arrow, which contradicts our assumption.
Correctness of Algorithm 1
On the one hand, by Studený (1997, Lemma 3.2), we know that for any chain graph  , there is an edge between two vertices u and v if and only if u╨̷v|S for any subset S of V. Thus, line 6 of Algorithm only deletes those edges that cannot appear in the true skeleton. So do lines 14 and 19.
, there is an edge between two vertices u and v if and only if u╨̷v|S for any subset S of V. Thus, line 6 of Algorithm only deletes those edges that cannot appear in the true skeleton. So do lines 14 and 19.
On the other hand, if u and v are not adjacent in  , by Theorem 3, it must be under one of the three possible conditions. If it is in condition 1, we will never connect them since we do not connect any vertex pair that is never contained in any node simultaneously. If it is in condition 2, then we will disconnect them in line 6 and line 14. Finally, if it is in condition 3, then either u╨v|bd
, by Theorem 3, it must be under one of the three possible conditions. If it is in condition 1, we will never connect them since we do not connect any vertex pair that is never contained in any node simultaneously. If it is in condition 2, then we will disconnect them in line 6 and line 14. Finally, if it is in condition 3, then either u╨v|bd (u) or u╨v|bd
(u) or u╨v|bd (v). By our previous discussion, we know that before starting line 17, we have bd
(v). By our previous discussion, we know that before starting line 17, we have bd (u) ⊂ ne
(u) ⊂ ne  ′(u) and bd
′(u) and bd (v) ⊂ ne
(v) ⊂ ne ′(v) for the
′(v) for the  ′ at that moment. Thus, we will disconnect u and v in line 19.
′ at that moment. Thus, we will disconnect u and v in line 19.
Correctness of Algorithm 2
By Proposition 4, Lemma 12 and the correctness of Algorithm 1, we know that every ordered vertex triple 〈u, v, w〉 in  with u → w a complex arrow and v the parent of (one of) the corresponding complex(es) is considered in line 4 of Algorithm 2. If the triple 〈u, v, w〉 is really in this situation, then we know that u╨̷v|Suv ∪{w}, and hence we orient u − w as u → w. Moreover, Lemma 13 prevents us from orienting u − w as w → u during the execution of Algorithm 2. This proves that we will orient every complex arrow right before starting line 9 in Algorithm 2.
with u → w a complex arrow and v the parent of (one of) the corresponding complex(es) is considered in line 4 of Algorithm 2. If the triple 〈u, v, w〉 is really in this situation, then we know that u╨̷v|Suv ∪{w}, and hence we orient u − w as u → w. Moreover, Lemma 13 prevents us from orienting u − w as w → u during the execution of Algorithm 2. This proves that we will orient every complex arrow right before starting line 9 in Algorithm 2.
Then by Lemma 13, the  *before starting line 9 is a hybrid graph with the same pattern as
*before starting line 9 is a hybrid graph with the same pattern as  . Thus Lemma 14 guarantees that we obtain the pattern of
. Thus Lemma 14 guarantees that we obtain the pattern of  after line 9.
after line 9.
Correctness of Algorithm 3
First of all, we show that any conditional independence relation represented by  is also represented by
is also represented by  . This is straightforward by noting the following two facts:
. This is straightforward by noting the following two facts:
assuming positivity, both DAG models and chain graph models are closed subset of graphoids under 5 axioms, see Pearl (1988) and Studený and Bouckaert (2001);
any conditional independence relation used in constructing
 is represented by
is represented by  .
.
Then by Xie et al. (2006, Theorem 2), the  in line 2 is a separation tree of
in line 2 is a separation tree of  . With the block vertices substituted, by the definition of separation trees, the output
. With the block vertices substituted, by the definition of separation trees, the output  of Algorithm 3 is a separation tree of
of Algorithm 3 is a separation tree of  .
.
Correctness of Algorithm 4
Algorithm 4.
Separation Tree Refinement.
Input: A crude separation tree  c for c for  ; perfect conditional independence knowledge. ; perfect conditional independence knowledge. |
|
Output: A refined separation tree  for for  . . |
|
| 1 | Construct an undirected independence subgraph over each node of  c; c; |
| 2 | Combine the subgraphs into a global undirected independence graph  ¯ whose edge set is the union of all edge sets of subgraphs; ¯ whose edge set is the union of all edge sets of subgraphs; |
| 3 | Construct a junction tree  of of  ¯. ¯. |
Xie et al. (2006, Theorem 3) guarantees the correctness of Algorithm 4.
Contributor Information
Zongming Ma, Email: ZONGMING@STANFORD.EDU.
Xianchao Xie, Email: XXIE@FAS.HARVARD.EDU.
Zhi Geng, Email: ZGENG@MATH.PKU.EDU.CN.
References
- Agresti A. Categorical Data Analysis. 2. John Wiley & Sons; Hoboken, NJ: 2002. [Google Scholar]
- Anderson TW. An Introduction to Multivariate Statistical Analysis. 3. John Wiley & Sons; Hoboken, NJ: 2003. [Google Scholar]
- Andersson SA, Madigan D, Perlman MD. Alternative Markov properties fror chain graphs. Scand J Statist. 2001;28:33–85. [Google Scholar]
- Beinlich I, Suermondt H, Chevaz R, Cooper G. The alarm monitoring system: A case study with two probabilistic inference techniques for belief networks. Proceedings of the 2nd European Conference on Artificail Intelligence in Medicine; Berlin: Springer-Verlag; 1989. pp. 247–256. [Google Scholar]
- Carroll S, Pavlovic V. Protein calassification using probabilistic chain graphs and the gene ontology structure. Bioinformatics. 2006;22(15):1871–1878. doi: 10.1093/bioinformatics/btl187. [DOI] [PubMed] [Google Scholar]
- Chickering DM. Learning equivalence classes of bayesian-network structures. J Mach Learn Res. 2002;2:445–498. [Google Scholar]
- Cowell RG, Dawid AP, Lauritzen SL, Spiegelhalter DJ. Probabilistic Networks and Expert Systems. Springer-Verlag; New York: 1999. [Google Scholar]
- Cox DR, Wermuth N. Multivariate Dependencies: Models, Analysis and Interpretation. Chapman and Hall; London: 1996. [Google Scholar]
- Drton M, Perlman M. A sinful approach to gaussian graphical model selection. J Stat Plan Infer. 2008;138:1179–1200. [Google Scholar]
- Edwards D. Introduction to Graphical Modelling. 2. Springer-Verlag; New York: 2000. [Google Scholar]
- Ellis B, Wong WH. Learning bayesian network structures from experimental data. 2006 URL http://www.stanford.edu/group/wonglab/doc/EllisWong-061025.pdf.
- Friedman J, Hastie T, Tibshirani R. Sparse inverse covariance estimation with the graphical lasso. Biostatistics. 2007 doi: 10.1093/biostatistics/kxm045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman N, Koller D. Being bayesian about network structure: a bayesian approach to structure discovery in bayesian networks. Mach Learn. 2003;50:95–126. [Google Scholar]
- Friedman N, Nachmana I, Pe’er D. Learning bayesian network structure from massive datasets: The “sparse candidate” algorithm. Proceedings of the Fifteenth Conference on Uncertainty in Artificail Intelligence; Stockholm, Sweden: 1999. pp. 206–215. [Google Scholar]
- Frydenberg M. The chain graph markov property. Scand J Statist. 1990;17:333–353. [Google Scholar]
- Kalisch M, Bühlmann P. Estimating high-dimensional directed acyclic graphs with the pc-algorithm. J Mach Learn Res. 2007;8:616–636. [Google Scholar]
- Lauritzen SL. Graphical Models. Claredon Press; Oxford: 1996. [Google Scholar]
- Lauritzen SL, Richardson TS. Chain graph models and their causal interpretations (with discussion) J R Statist Soc B. 2002;64:321–361. [Google Scholar]
- Liu Y, Xing EP, Carbonell J. Predicting protein folds with structural repeats using a chain graph model. Proceedings of the 22nd International Conference on Machine Learning; 2005. [Google Scholar]
- Meinshausen N, Bühlmann P. High-dimensional graphs and variable selection with the lasso. Ann Statist. 2006;34:1436–1462. [Google Scholar]
- Pearl J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Morgan Kaufmann; San Francisco, CA: 1988. [Google Scholar]
- Ravikumar P, Wainwright MJ, Lafferty J. Technical Report 750. Department of Statistics, University of California; Berkeley: 2008. High-dimensional graphical model selection using ℓ1-regularized logistic regression. URL http://www.stat.berkeley.edu/tech-reports/750.pdf. [Google Scholar]
- Roverato A, La Rocca L. On block ordering of variables in graphical modelling. Scand J Statist. 2006;33:65–81. [Google Scholar]
- Spirtes P, Glymour C, Scheines R. Causation, Prediction and Search. 2. MIT Press; Cambridge, MA: 2000. [Google Scholar]
- Stanghellini E, McConway KJ, Hand DJ. A discrete variable chain graph for applicants for credit. J R Statist Soc C. 1999;48:239–251. [Google Scholar]
- Studený M. A recovery algorithm for chain graphs. Int J Approx Reasoning. 1997;17:265–293. [Google Scholar]
- Studený M, Bouckaert RR. On chain graph models for description of conditional independence structures. Ann Statist. 2001;26:1434–1495. [Google Scholar]
- Tsamardinos I, Brown LE, Aliferis CF. The max-min hill-climbing bayesian network structure learning algorithm. Mach Learn. 2006;65:31–78. [Google Scholar]
- Wermuth N. On block-recursive linear regression equations. Revista Brasileira de Probabilidade e Estatistica. 1992;6:1–56. [Google Scholar]
- Wermuth N, Lauritzen SL. Graphical and recursive models for contingency tables. Biometrika. 1983;72:537–552. [Google Scholar]
- Wermuth N, Lauritzen SL. On substantive research hypotheses, conditional independence graphs and graphical chain models. J R Statist Soc B. 1990;52:21–50. [Google Scholar]
- Whittaker J. Graphical Models in Applied Multivariate Statistics. John Wiley & Sons; 1990. [Google Scholar]
- Wilks S. The large-sample distribution of the likelihood ratio for testing composite hypotheses. Ann Math Stat. 1938;20:595–601. [Google Scholar]
- Xie X, Geng Z. A recursive method for structural learning of directed acyclic graphs. J Mach Learn Res. 2008;9:459–483. [PMC free article] [PubMed] [Google Scholar]
- Xie X, Geng Z, Zhao Q. Decomposition of structural learning about directed acyclic graphs. Artif Intell. 2006;170:442–439. [Google Scholar]