Abstract
The pathways responsible for flowering time in Arabidopsis thaliana comprise one of the best characterized genetic networks in plants. We harness this extensive molecular genetic knowledge to identify potential flowering time quantitative trait genes (QTGs) through candidate gene association mapping using 51 flowering time loci. We genotyped common single nucleotide polymorphisms (SNPs) at these genes in 275 A. thaliana accessions that were also phenotyped for flowering time and rosette leaf number in long and short days. Using structured association techniques, we find that haplotype-tagging SNPs in 27 flowering time genes show significant associations in various trait/environment combinations. After correction for multiple testing, between 2 and 10 genes remain significantly associated with flowering time, with CO arguably possessing the most promising associations. We also genotyped a subset of these flowering time gene SNPs in an independent recombinant inbred line population derived from the intercrossing of 19 accessions. Approximately one-third of significant polymorphisms that were associated with flowering time in the accessions and genotyped in the outbred population were replicated in both mapping populations, including SNPs at the CO, FLC, VIN3, PHYD, and GA1 loci, and coding region deletions at the FRI gene. We conservatively estimate that ∼4–14% of known flowering time genes may harbor common alleles that contribute to natural variation in this life history trait.
A major ecological trait in Arabidopsis thaliana is the timing of the transition to flowering, which defines the shift from vegetative to reproductive development (Koornneef et al. 2004; Engelmann and Purugganan 2006). Flowering time in A. thaliana is a complex trait that is responsive to multiple environmental cues, including photoperiod, vernalization, ambient temperature, and nutrient status (Engelmann and Purugganan 2006). The range of variation in flowering time can be large, with a significant amount of this diversity arising from heritable genetic variation (Van Berloo and Stam 1999; Ungerer et al. 2003).
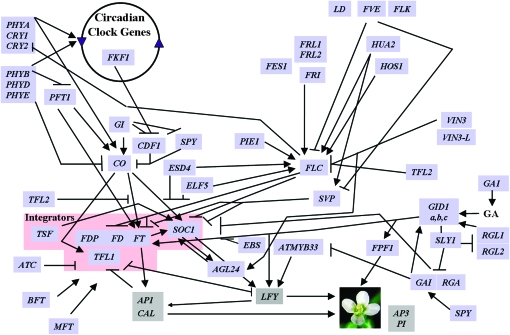
Flowering time in this species has become a model for understanding complex trait genetics in plants, in part because of how extensively it has been characterized via forward genetic approaches (Simpson and Dean 2002). The flowering time genes represents one of the best studied functional genetic networks in plants, as geneticists have identified >60 genes that regulate flowering time (Mouradov et al. 2002; Komeda 2004; Baurle and Dean 2006) (see Figure 1 and supporting information, Figure S1). Understanding the evolutionary ecology of flowering time, however, requires us to determine not only the genes that control this trait, but also the specific genes that cause natural variation in flowering time.
Figure 1.—
The flowering time genetic network. The genes included in this study (in blue) and their interactions are depicted. Also, included in gray at the base of the network are the ABC genes, which are essential in the determination of floral meristems. Description of the construction of the network is described in Figure S1.
Flowering time has thus been the subject of an intensive quantitative trait locus (QTL) mapping effort by the community of A. thaliana researchers, with numerous QTL mapping studies published in the last 15 years (Clarke et al. 1995; Jansen et al. 1995; Kuittinen et al. 1997; Stratton 1998; El-Assal et al. 2001; Maloof et al. 2001; Ungerer et al. 2002, 2003; Weinig et al. 2002, 2003; Bandaranayake et al. 2004; El-Lithy et al. 2004; Juenger et al. 2005; Werner et al. 2005b). QTL mapping studies of flowering time have defined at least 28 loci that affect natural variation in flowering time among individual accessions of this species under different conditions. Molecular studies have conclusively shown that CRYPTOCHROME2 (CRY2) (El-Assal et al. 2001), FRIGIDA (FRI) (Johanson et al. 2000), FLOWERING LOCUS C (FLC) (Werner et al. 2005a), FLM (Werner et al. 2005b), PHYTOCHROME A (PHYA) (Maloof et al. 2001), PHYB (Filiault et al. 2008), PHYC (Balasubramanian et al. 2006), and PHYD (Aukerman et al. 1997) all harbor natural polymorphisms that alter flowering time. Nearly half of the polymorphisms at these genes are rare, with the minor allele frequency (MAF) of the causal polymorphism at <10%, and some of these polymorphisms are accession specific.
Despite the wealth of knowledge about the population and quantitative genetics of flowering time in A. thaliana, a substantial amount of natural variation in flowering time remains unexplained (Werner et al. 2005a). In recent years, structured association mapping has emerged as a major tool in the search for genes that underlie quantitative trait variation (e.g., Yu et al. 2006), including natural variation in flowering time in A. thaliana. Although genomewide association studies have gained prominence in recent years (Hirschhorn and Daly 2005), candidate gene association studies remain a key approach to gene mapping (Tabor et al. 2002). Whereas genomewide studies scan large numbers of markers across the entire genome, candidate gene studies specifically target genes with known functions in the trait of interest, with the expectation that doing so may enrich for the number of meaningful trait associations.
The candidate gene approach has proven successful in many instances, such as in the identification of genes for trait variation in wild and cultivated maize (Wilson et al. 2004; Weber et al. 2007, 2008), pine (Gonzalez-Martinez et al. 2007), and human diseases (Vaisee et al. 2000; Ueda et al. 2003). In model organisms, such as A. thaliana, candidate gene studies are a potentially powerful approach, because many of the genetic pathways underlying ecologically significant traits have been dissected through forward genetic approaches, providing strong candidates for genes and pathways that might underlie natural trait variation (Ehrenreich et al. 2007).
The large number of known flowering time genes identified through molecular developmental genetics makes flowering time a particularly attractive trait for candidate gene association studies. There have been attempts to use candidate gene approaches to identify flowering time quantitative genes in A. thaliana (e.g., Caicedo et al. 2004; Olsen et al. 2004), but a comprehensive analysis using a large set of candidate loci has yet to be undertaken. Using candidate gene haplotype tagging SNPs (htSNPs), we conduct networkwide structured association mapping using 51 A. thaliana flowering time genes and compare our candidate gene results to those from randomly selected background loci. We then retest a subset of our significant associations in an independent panel of inbred lines derived from the intercrossing of 19 accessions, which were genotyped at about half of the flowering time htSNPs. This two-stage approach of association mapping in the natural accessions and the inbred lines allows us to identify several novel candidates for flowering time variation.
MATERIALS AND METHODS
Resequencing data:
The resequencing data used in this article are from several sources. Resequencing data for 48 of the flowering time candidate genes for 24 accessions are detailed in Flowers et al. (2009). These data encompass the entire gene, including ∼1 kb of the promoter region and ∼500 bp of the 3′ flanking region. The genes and accessions are listed in Table S1 and Table S2. These same accessions are among the 96 used by Nordborg et al. (2005) in generating their data, from which we selected 319 background fragments for inclusion in our study. For the Nordborg et al. (2005) data, we used only alleles from the 24 accessions overlapping those used by Flowers et al. (2009) in addition to the Columbia reference allele. Previously published resequencing data were used for the genes CRY2, FLC, and FRI (Caicedo et al. 2004; Olsen et al. 2004; Stinchcombe et al. 2004), and the specific accessions and the total number of accessions used in these studies are variable and different from the Flowers et al. (2009) data. All flowering time gene alignments are provided in File S1. A list of the Nordborg et al. (2005) fragments used in this study are included in Table S3.
Haplotype-tagging SNP selection:
HtSNPs were chosen using an algorithm similar to one proposed by Carlson et al. (2004) that grouped all common SNPs (MAF ≥ 0.1) in a multiple sequence alignment for a locus into bins on the basis of their patterns of linkage disequilibrium, with the threshold for binning being r2 = 1. Sites with gaps or missing data were ignored by the binning procedure. From each bin, one SNP was randomly selected to be the htSNP representing that bin. The median and mean numbers of htSNPs identified per candidate gene were 8 and 9.8, respectively; for the background fragments, the median and mean numbers of htSNPs were 2 and 2.7, respectively. One hundred eighty-seven of these background fragments were genotyped at all identified htSNPs, while 131 were genotyped at only one randomly selected htSNP. The identified htSNPs were genotyped in a panel of 475 accessions (listed in Table S4). The DNA used for genotyping was isolated from the leaves of plants grown under 24-hr light for 3 weeks at New York University. QIAGEN 96-well DNAeasy kits were used to extract the DNA. Genotyping was done using the Sequenom MassArray technology and was conducted by Sequenom (http://www.sequenom.com). Overall, ∼87% of the htSNPs were successfully genotyped in ≥375 accessions, resulting in the genotyping of 574 background htSNPs and 383 flowering time htSNPs. The SNP genotypes are available in Table S5.
Population structure assessment:
Two programs—STRUCTURE (Pritchard et al. 2000; Falush et al. 2003) and InStruct (Gao et al. 2007)—were used to determine the extent of population structure in our panel of accessions. These programs are very similar, with the primary difference being that InStruct explicitly estimates selfing rates along with population structure. In these analyses, one SNP from each of the 319 background loci was used. For loci with multiple genotyped SNPs, one was randomly selected for inclusion. Only accessions with unique multilocus genotypes across all markers were included and in cases where accessions were identical across loci, one accession was included in the analysis as the representative of that genotype. This was done to prevent biases in population structure estimation that might arise from the inclusion of replicates of the same accession, which are common in the stock center. Both programs were run three times across a range of K values starting at K = 1 and ending at K = 30 and the run with the median likelihood was used for analyses. In STRUCTURE, the correlated frequencies with admixture model was used. In InStruct, mode 2 was used, which infers population structure and selfing rates at the population level.
Calculation of haplotype sharing:
Haplotype sharing (K) was computed from a data matrix including all accessions and their genotypes at the background loci. As in Zhao et al. (2007), haplotype sharing was computed between every possible pairwise combination of accessions as the total number of haplotypes in common between the accessions divided by the total number of loci with present data for both individuals. This provides a measure of the proportion of loci that are identical in state between any pair of accessions.
Phenotyping:
Phenotype data used for association mapping with the natural accessions are from growth chamber experiments conducted at North Carolina State University's Phytotron facility and are previously published (Olsen et al. 2004) (see Table S5). Of the 475 accessions we genotyped, 275 had phenotype data we used in association analyses. The MAGIC lines and their construction are described elsewhere (Scarcelli et al. 2007; Kover et al. 2009). Importantly, 192 flowering time htSNPs, accounting for a subset of the htSNPs from 47 genes, have been genotyped in the MAGIC lines. The MAGIC lines are the result of seven generations of single seed inbreeding after the intercrossing phase. Growth chamber phenotyping of the MAGIC lines was done at New York University using EGC walk-in chambers under both long-day conditions (14-hr light: 10-hr dark) and short-day conditions (10-hr light: 14-hr dark) at 20°. Five individuals each for 360 MAGIC lines were grown in a randomized design in 72-cell growing flats. The flats were repositioned within the chamber every 7 days and watered by subirrigation every 4 days. We phenotyped days to flowering, which is measured as the number of julian days after which the primary inflorescence had extended >1 mm above the rosette, and rosette leaf number, which is the number of total rosette leaves on a plant at bolting and is frequently used as a surrogate for flowering time.
Association tests:
Two hundred seventy-five phenotyped accessions with nonredundant multilocus genotypes were used for association mapping. We used a previously described mixed model approach for conducting structured associations (Yu et al. 2006; Zhao et al. 2007). The model used was of the form
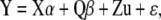 |
with Y a vector of phenotypes, X a vector of single locus genotypes, α a vector of fixed effects of the n − 1 genotype classes, Q a matrix of the K − 1 subpopulation ancestry estimates for each individual from STRUCTURE, β a vector of the fixed effects for each of the subpopulations, Z an identity matrix, u a matrix of random deviates due to genomewide relatedness (as inferred from K), and ɛ a vector of residual errors. PROC MIXED was used for all tests and was run in SAS v9.1.3. HtSNP effect measurements were conducted using a reduced structured association model, excluding the kinship matrix. For the MAGIC lines, one-way ANOVAs were conducted in JMP v5 to test whether htSNPs were associated with differences in flowering time across the lines. False discovery rate (FDR) analyses were conducted using QVALUE in R (Storey 2002; Storey and Tibshirani 2003).
RESULTS AND DISCUSSION
Identification and genotyping of htSNPs at flowering time genes and background loci:
A. thaliana typically exhibits strong linkage disequilibrium on the scale of ∼5–10 kb (Kim et al. 2007). To take advantage of this short-range disequilibrium for association mapping, we identified htSNPs representative of common haplotype structure at 51 candidate genes that we recently resequenced (see Figure 1 and Table S1). In all but a few cases, the entire coding region as well as 1 kb of the 5′-UTR and promoter, and 0.5 kb of downstream region was sequenced. Details of the levels and patterns of nucleotide variation at these flowering time genes are reported elsewhere (Flowers et al. 2009).
We also identified htSNPs in 319 background fragments that were previously resequenced (Nordborg et al. 2005). One hundred eighty-seven of these fragments were comprehensively genotyped in the same manner as the candidate genes; for the remaining fragments, only 1 htSNP was genotyped from each fragment. We successfully genotyped 957 htSNPs from 475 A. thaliana accessions at the candidate genes and the background loci.
Population structure in the genotyped accessions:
A. thaliana possesses extensive population structure that can confound genetic association studies (e.g., Zhao et al. 2007), and we attempted to identify population structure specific to our sample using both the program STRUCTURE (Pritchard et al. 2000; Falush et al. 2003) and the related program InStruct (Gao et al. 2007), which explicitly accounts for inbreeding while estimating population structure.
Runs of STRUCTURE and InStruct produced very different most likely K estimates, with K = 10 and K = 2 having the highest likelihoods for STRUCTURE and InStruct, respectively. This suggests, as has been reported elsewhere (Gao et al. 2007), that the inclusion of selfing in population structure estimation can have a dramatic effect on the determination of a most likely K value. Ancestry assignments of accessions to particular subpopulations, however, were very similar between the two methods (see Figure S2). Results from K = 2 corroborate previous findings of large-scale genetic differentiation between European and Asian A. thaliana accessions, with a region of admixture existing in Eastern Europe (Schmid et al. 2006). Subpopulations identified at K > 2 appear to differentiate subgroups of European ancestry (e.g., Portuguese-Spanish accessions, Scandinavian accessions), which constitute the bulk of our sample. Analysis of the extent of haplotype sharing between all pairs of accessions shows that despite clear population structure detectable via model-based approaches, most individuals share 30–60% of their alleles (see Figure S3).
Structured association mapping with flowering time SNPs:
Previous studies had shown that a mixed model analysis correcting for both population structure and pairwise kinship is the best, and we conducted an association analysis on the background SNPs at each locus (see materials and methods) to identify the best approach for our sample.
We examined variation in flowering time, a key life history trait in A. thaliana. The phenotype data used was days to flowering (FT) and rosette leaf number (RLN) in both long day (LD) and short day (SD) growth chamber conditions, measured for 275 accessions. All these flowering time traits were highly heritable, with broad sense heritabilities (H2), ranging from 0.49 to 0.7 in the accessions and from 0.33 to 0.65 in the MAGIC lines (Table S6).
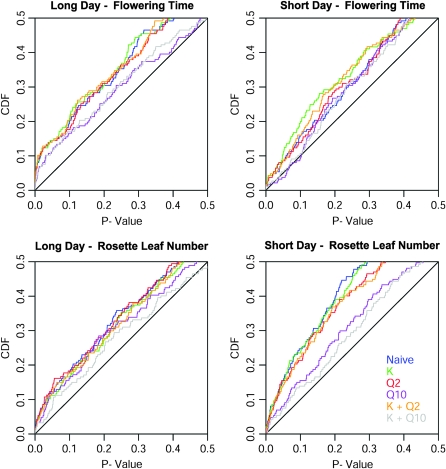
We found that a mixed model including the K haplotype sharing matrix (Yu et al. 2006; Zhao et al. 2007) and a population ancestry matrix Q from a STRUCTURE run of K = 10 (Yu et al. 2006; Zhao et al. 2007) performed best in reducing confounding population structure and relatedness bias, with the P-value distribution most closely resembling a uniform distribution (see Figure 2). On the basis of our results using Q matrices from STRUCTURE runs from K = 2 through K = 10 (results for intermediate K values are not shown), it appeared that using a Q matrix from a run of K = 9 or 10 was especially important to reducing the high rate of nominal significance. It should be noted, however, that this model (the K + Q10 model) does not completely eliminate the effects of population structure. Given these results, we ran association tests for all htSNPs using the K + Q10 mixed model, and found that between 29 and 42 flowering time htSNPs were nominally significant in any given trait/environment combination (for example rosette leaf number in short days, RLN-SD).
Figure 2.—
Cumulative density functions (cdfs) for the background loci using several alternative models. The naïve association is a one-way ANOVA, whereas the models including K (i.e., haplotype sharing) and/or Q (i.e., STRUCTURE ancestry estimates) are variants of the full model described in materials and methods. The axes are restricted to a maximum of 0.5 to facilitate comparison of the different models. The y = x line depicts the cdf of a uniform distribution. Results from Q matrices for intermediate K values are excluded from the plot for the purpose of clarity, and because they performed noticeably worse than the K = 10 matrix.
While these analyses identify a large number of flowering time gene htSNPs associated with either flowering time and/or rosette leaf number, these analyses have two problems. First, despite taking into consideration both population structure and pairwise kinship among our samples, the distributions of associations with background SNPs are still biased, indicating that the confounding effects of population stratification have not been eliminated. Second, we need to account for the multiple statistical tests used in our association analysis of flowering time SNPs.
To account for the bias in distributions that result from cryptic population structure, we use empirical rather than nominal significance thresholds. In this way, we focus only on candidate gene htSNPs whose nominal significance is in the 5% tail of the P-value distribution of the mixed model analysis for all SNPs. Using this empirical significance threshold, we find that 50 candidate gene htSNPs are in the 5% tail of all SNPs in at least one environment (see Figure 3). These htSNPs represent only 27 of the flowering time genes, due to multiple htSNPs in the same gene showing significant associations; FLC, GA1, and HOS1 each had four empirically significant htSNPs, while ELF5, FD, FES1, TFL2, and VIN3L each had three significant htSNPs.
Figure 3.—
Associations across all flowering and background SNPs. Results for the K + Q10 model at each genotyped SNP are plotted as −log (P-value) by physical position in the genome. Candidate gene htSNPs that are empirically significant are highlighted by light blue or yellow vertical lines. Empirical 5%-, Bonferroni 5%- and FDR 5%-corrected multiple-testing thresholds for significance are plotted by trait as blue, red, and green horizontal lines, respectively. These lines are not shown if they surpass the most significant locus for a trait.
Sixteen of these 27 genes were significant in at least two traits. CO, ELF5, and FES1 each had at least one htSNP associated with every trait. Three genes—GA1, GAI, and PHYD—had an htSNP that exhibited associations with three traits. As an internal control, we also tested FRI functionality for associations by using the genotypes of the accessions at the Columbia- and Landsberg erecta-type deletions as markers; these tests were all highly significant (P < 0.01).
The second problem we face is multiple testing, and we approach this issue in two ways. One method of adjusting for multiple tests is the Bonferroni correction, and using this traitwise correction we find that htSNPs in only two candidate genes—CO and GAI—are significant (see Figure 3). It is generally acknowledged, however, that the Bonferroni can be overly conservative, particularly in genomics studies where a large number of tests are undertaken. A standard approach is to estimate the false discovery rate (FDR), which allows one to estimate the proportion of significant tests that will be false positives by chance (Storey 2002; Storey and Tibshirani 2003). We estimate the number of htSNPs that are significant at FDR values of 0.05, 0.1, and 0.2 (see Table 1). Interestingly, no short-day trait was significant at these low FDR values. Only four htSNPs met a FDR of 0.05; these were in CO (2 htSNPs), GAI, and VIN3-L (see Figure 3). The number of significant flowering time htSNPs increases to 10 and 16, with FDR values of 0.1 and 0.2, respectively. In the latter case, we expect three to four false positives at the given FDR threshold.
TABLE 1.
Flowering time htSNP associations across multiple significance thresholds
| Number of flowering time htSNPs
|
||||
|---|---|---|---|---|
| Threshold | LD-FT | SD-FT | LD-RLN | SD-RLN |
| Nominal P ≤ 0.05 | 42 | 31 | 36 | 29 |
| Empirical P ≤ 0.05 | 22 | 24 | 23 | 20 |
| Bonferroni P ≤ 0.05 | 2 | 1 | 1 | 0 |
| FDR ≤ 0.05 | 4 | 0 | 1 | 0 |
| FDR ≤ 0.1 | 10 | 0 | 1 | 0 |
| FDR ≤ 0.2 | 16 | 0 | 1 | 0 |
For associations with FDR ≤ 0.1, we further examined the MAFs, allele effects, and percentage of phenotypic variance explained by the htSNPs (see Table 2). The associated htSNPs ranged in minor allele frequency from 0.01 to 0.41. Interestingly, GAI p358 had a minor allele frequency of 0.01 in the mapping panel, which was far different from its MAF of 0.12 in the original resequencing data. Analysis of this association suggests it is likely to be a false positive, driven by a small number of individuals possessing the minor allele and an individual within this group carrying the highest trait value of all accessions.
TABLE 2.
Information regarding htSNPs with associations at FDR ≤ 0.1
| Trait | HtSNP | Na | MAF | R2b | 2ac | 2a/σPd | Trait associations (P ≤ 0.01)e | P-value | Q-value |
|---|---|---|---|---|---|---|---|---|---|
| LD-FT | CO p347 | 265 | 0.41 | 0.06 | 3.62 | 0.56 | 3 | 0.00001 | 0.00187 |
| CO p795 | 255 | 0.26 | 0.09 | 5.32 | 0.78 | 3 | 0.00001 | 0.00187 | |
| GAI p358 | 215 | 0.01 | 0.12 | 24.1 | 3.53 | 3 | 0.00001 | 0.00187 | |
| VIN3-L p5026 | 159 | 0.07 | 0.09 | 13.24 | 1.94 | 1 | 0.0001 | 0.01555 | |
| FLC p6809 | 268 | 0.09 | 0.04 | 4.88 | 0.71 | 1 | 0.0008 | 0.07775 | |
| VIN3 p2942 | 270 | 0.14 | 0.04 | 4.12 | 0.6 | 1 | 0.001 | 0.07775 | |
| GI p5241 | 269 | 0.09 | 0.03 | 4.56 | 0.67 | 1 | 0.0012 | 0.07997 | |
| FLC p3312 | 263 | 0.3 | 0.04 | 3.28 | 0.48 | 1 | 0.0014 | 0.08708 | |
| FES1 p1223 | 267 | 0.39 | 0.03 | 2.84 | 0.42 | 4 | 0.0019 | 0.0933 | |
| FES1 p1177 | 270 | 0.4 | 0.03 | 2.8 | 0.41 | 2 | 0.0022 | 0.09736 | |
| LD-RLN | CO p795 | 255 | 0.26 | 0.02 | 1.14 | 0.34 | 3 | 0.00001 | 0.00428 |
Number of accessions with phenotype data that were also successfully genotyped.
The partial R2 for the htSNP effect in a model also including Q.
The difference between the two homozygous genotypes in the model also including Q.
The difference between the two homozygous genotypes scaled by the standard deviation of the phenotype.
The number of other traits that the SNP was associated with at the nominal P ≤ 0.01 level.
The other associations significant at an FDR ≤ 0.1 were all more plausible, as they all possessed larger numbers of individuals with the minor allele, making it less likely that they are due to outlier effects. The additive phenotypic difference between the homozygous genotypes (excluding GAI p358), ranged from 2.8 to 13.24 days for LD-FT for these significantly associated SNPs, and was 1.14 days for CO p795 in LD-RLN. In general, the detected associations had moderate effects, explaining between 2 and 9% of the phenotypic variance, with most associations explaining <5% of the variation in flowering time traits.
Association mapping in multiparent advanced generation intercross (MAGIC) lines:
We initially tried to determine whether we could replicate our results using the comparison of our candidate gene associations to quantitative trait loci from biparental recombinant inbred lines (RILs), as has become common in association studies in this species (Ehrenreich et al. 2007; Zhao et al. 2007). However, we found that no available RIL population segregates for more than a small fraction of the flowering time-associated htSNPs in our study. This was problematic and led us to try to replicate our associations in a set of MAGIC lines recently generated from the intercrossing of 19 different progenitors. These lines segregate for all common SNPs that were genotyped in the natural accessions (Scarcelli et al. 2007; Kover et al. 2009).
We genotyped 192 htSNPs from the flowering time genes in a set of 360 MAGIC lines, including 20 of the 50 htSNPs that appeared promising from the SNP-based association tests in the accessions (before correcting for multiple tests). These significant htSNPs were located in 14 flowering time genes (see Table 3). We also genotyped the two common loss-of-function deletions at FRI in the MAGIC lines. The MAGIC lines were phenotyped for the same traits as those analyzed in the natural accessions (i.e., LD-FT, LD-RLN, SD-FT, SD-RLN) and association results were compared between the two populations.
TABLE 3.
Comparison of nominal associations in accessions and MAGIC lines
| Accessions
|
MAGIC
|
|||||||
|---|---|---|---|---|---|---|---|---|
| HtSNP | LD-FT | SD-FT | LD-RLN | SD-RLN | LD-FT | SD-FT | LD-RLN | SD-RLN |
| ATMYB33 p119 | + | + | ||||||
| CO p347 | + | + | + | + | + | |||
| FES1 p1877 | + | + | + | |||||
| FLC p2775 and p3312 | + | + | + | + | + | |||
| FLC p6809 | + | |||||||
| FRI p725 | + | + | ||||||
| GA1 p7762 | + | + | + | + | ||||
| GA1 p8429 | + | + | + | |||||
| HOS1 p1176 and p5516 | + | |||||||
| LD p258 | + | |||||||
| PHYD p3094 | + | + | + | + | ||||
| PIE p898 | + | |||||||
| RGL2 p2115 | + | + | ||||||
| TFL2 p1199 | + | + | ||||||
| TFL2 p1346 | + | |||||||
| VIN3 p2942 | + | + | + | + | ||||
| VIN3-L 4961 | + | + | ||||||
| VIN3-L p5026 | + | + | ||||||
Plus (+) indicates an observed nominally significant association. HtSNPs in boldface were nominally associated in both populations for at least one trait. Positions correspond to the positions in the multiple sequence alignments in File S1. HtSNPs in the same gene that had identical patterns of association were collapsed into a single row.
Of the flowering time htSNPs that exhibited an association in the accessions and were genotyped in the MAGIC lines, seven htSNPs representing six of 32 associations (∼20%) had some level of corroboration between the two line sets (see Table 3). No htSNP that was genotyped in both sets of lines exhibited an identical pattern of association between the two populations. The replicated htSNPs occurred in CO, FLC (two SNPs), GA1 (two SNPs), PHYD, and VIN3. It should be noted that although the significant FRI htSNP was not associated with any trait in these data, direct testing on FRI loss-of-function deletions produced a significant result (P ≤ 0.01) for all traits and environments. These results give corroborative evidence for a subset of the discovered associations, suggesting that they may be biologically meaningful.
Of the other 172 flowering time htSNPs, we have identified 21 in 12 genes that were associated in the MAGIC mapping population (FDR ≤ 0.1) but did not show significant associations in accessions. From the viewpoint of the candidate gene association mapping in accessions, these may represent false negatives.
Candidate gene association mapping of flowering time in A. thaliana:
The search for quantitative trait genes (QTGs)in plants has been a central goal of plant biology in recent years, and association mapping has emerged as a major approach in the identification of these loci. In general, the rapid decay of linkage disequilibrium in A. thaliana suggests that association mapping should be a useful approach to localizing QTL to genomic regions that may span only a few genes (Kim et al. 2007), and this species has thus emerged as a platform to test methods for association mapping (Zhao et al. 2007).
Both genomewide (Zhao et al. 2007) and candidate gene association studies (Olsen et al. 2004; Stinchcombe et al. 2004) in this species have begun to identify genes for quantitative trait variation, but the challenges of association mapping in A. thaliana are well documented (Aranzana et al. 2005; Weigel and Nordborg 2005; Zhao et al. 2007). First, variation in most traits is correlated with the population structure that exists in this species, likely causing a large number of false positive genotype–phenotype correlations throughout the genome (Zhao et al. 2007), although it is possible to control for this stratification when conducting association tests (i.e., by using statistical methodologies that take into account different estimates of stratification) (e.g., Yu et al. 2006). Second, for complex traits that are likely to be influenced by numerous QTGs, confirming a number of associations simultaneously can be difficult. The use of multiple biparental RILs or F2 populations has become a common mode of cross-validation (Ehrenreich et al. 2007; Zhao et al. 2007) for moderate- to large-scale studies in this species, but methods to systematically replicate multiple associations detected via association mapping techniques remains a significant issue.
We use the wealth of genetic information on flowering time as a springboard to find which genes isolated by molecular genetic approaches may harbor common polymorphisms that contribute to natural variation in A. thaliana. As described in this study, it is clear that candidate gene association studies in this species (as is true for all association mapping analyses) are plagued by several issues that need to be addressed. First, despite attempts to correct for population structure, the distributions of associations among randomly selected background SNPs still display a bias that may arise from continued confounding by population stratification. This problem is mitigated to some extent by using empirical distributions to set significance thresholds, providing some assurance that population structure effects are minimized. Using this approach, we find that 50 htSNPs in 27 flowering time candidate genes show association across at least one trait/environment combination. In several instances, the same htSNP shows association across multiple traits (see Tables 2 and 3).
A second problem for structured association mapping techniques is that in controlling for population structure, we cull the signal of true genotype–phenotype association from loci that are highly stratified. Flowering time is known to exhibit geographic clines (Stinchcombe et al. 2004) and it is also known that the genetic variation in A. thaliana is strongly correlated with these same geographic axes (Nordborg et al. 2005). It is thus likely that some flowering time QTGs are strongly differentiated across subpopulations, due to local adaptation or other causes, and that these loci will evade detection by structured association mapping. The extent to which such false negatives will occur should vary across traits, with false negatives being more problematic for traits that exhibit strong population structure.
A third issue in association mapping studies is multiple testing. One way to deal with this problem is to employ a Bonferroni correction, and we find that after applying this method SNPs in 2 genes—the photoperiod pathway gene CO and the gibberellic acid regulatory protein GAI—remain significantly associated even after this conservative correction. It is clear, however, that a Bonferroni correction may be too strict a standard, and an alternative approach is simply to use the FDR in determining which htSNPs may be relevant (Storey 2002; Storey and Tibshirani 2003). Using a strict FDR of 0.05, we find four that are significant; one htSNP is in VIN3-L, while the others are in genes identified in the Bonferroni correction (CO and GAI). Moreover, the number of recognized significant associations may be increased as long as we are aware that a more liberal FDR means a greater number of false positives. In our study, a FDR of 0.1 identifies 10 htSNPs in 7 genes (with one htSNP possibly being a false positive) while an FDR of 0.2 yields 16 htSNPs in 10 genes (of which 3–4 htSNPs are likely false positives).
Another avenue to determine which significant SNPs are worthy of further consideration is to use replication in an independent mapping population. We study the degree to which we can replicate candidate gene association results by using a recently developed set of A. thaliana MAGIC lines derived from intercrossing 19 founder accessions (Scarcelli et al. 2007; Kover et al. 2009). We retest 20 of the 50 significant htSNPs found in 14 of 27 flowering time genes (uncorrected for multiple tests) and observe 7 htSNPs in 5 flowering time genes that were also significant in our MAGIC population. The agreement between the two experiments, however, was low and the MAGIC lines were able to replicate only ∼20% of associations observed in the natural accessions. This lack of concordance might be due to differences in power between the two studies arising from differences in allele frequencies between the accessions and the MAGIC lines. However, this possibility seems unlikely as these 20 htSNPs occur at similar frequencies in the two panels (Table S7).
It is, in a sense, heartening to find that ∼20% of our significantly associated htSNPs may actually be replicated in an independent recombinant inbred mapping population. These results, however, do point to the continued difficulties in replicating and validating association study results and the importance of identifying the reasons for these difficulties. There are several possible explanations for our failure to confirm many of the significantly associated SNPs from the candidate gene mapping of natural accessions: (1) Our detected associations are spurious, (2) we lack the statistical power to detect associations in both line sets, (3) the environments used for growing the accessions and the MAGIC lines were slightly different because these experiments were conducted at different locations, and it is possible that this difference could have had an effect on the genotype–phenotype associations present in each experiment, (4) the associations detected at flowering time loci in the accessions are in some cases due to linkage disequilibrium between flowering genes and causal, linked loci between which disequilibrium got disrupted during the creation of the MAGIC lines, and/or (5) lastly, as we have stated previously (Ehrenreich et al. 2007), the possibility that epistatic relationships that appear as additive effects in accessions due to historical population structure and selfing are disrupted during the construction of inbred mapping populations. The cause of the discrepancies is unclear at this point, but we feel this may simply reflect an intrinsically high false positive rate in association mapping in structured populations such as A. thaliana.
Obversely, we also appear to have a high false negative rate (∼12%) in that several SNPs are significantly associated in the MAGIC mapping lines but not in our structured association mapping panel. Unlike structured accession mapping using the accessions, we do not expect any confounding effect of population structure in the MAGIC lines. It is thus possible that these SNPs possess associations that we are unable to detect in structured association mapping because they are stratified and their signal is removed by the use of population structure covariates in our statistical models. We should note, however, that our genotyping of flowering time gene htSNPs is incomplete in the MAGIC lines, which prevents us from drawing definitive conclusions as to the asymmetry in mapping results we observe.
Determining the causes that contribute to the failure to confirm many of the significant results across both structured association and recombinant inbred MAGIC mapping will require larger-scale experiments that can allow a more direct comparison between mapping results from these different populations; these experiments are underway. Nevertheless, there are a handful of genes with htSNPs that survive either stringent statistical testing thresholds and/or replication criteria, and these provide insight into the extent to which known flowering time genes contribute to natural variation in this life history trait within A. thaliana. We can assume that htSNPs that are significant after Bonferroni correction, the stringent FDR of 0.05, and/or those that showed replicated associations in the MAGIC lines, have the strongest evidence for being biologically meaningful. Using these criteria, we have the strongest evidence for the gene CO, which encodes a Zn-finger transcription factor that mediates photoperiod-dependent flowering time in A. thaliana as well as other flowering plant species. Previous studies have implicated photoreceptor genes such as the cryptochrome CRY2 (El-Assal et al. 2001; Olsen et al. 2004) and phytochrome genes PHYA-PHYD (Aukerman et al. 1997; Maloof et al. 2001; Balasubramanian et al. 2006; Filiault et al. 2008), but this is the first time CO has been shown to be possibly involved in natural variation in flowering time.
We also have very good evidence for an additional five loci (VIN3-L, PHYD, FLC, VIN3, and GA1) as being potential flowering time QTGs based on the htSNP results, and these include photoperiod, vernalization, and gibberellic hormone pathway genes. We do not consider the significant GAI htSNP a good candidate, as its low frequency leads us to believe the association may be spurious. Nevertheless, if we count the six loci we have discussed as well as the FRI gene, whose deletions are known to affect flowering time (Johanson et al. 2000), we find that at least ∼4–14% of known genes in the network have moderate- to high-frequency polymorphisms that contribute to natural variation in flowering time traits in A. thaliana.
The cumulative evidence we present suggests that we have identified putative flowering time QTGs that are targets for further characterization and validation. It is noteworthy that all major pathways leading to flowering time—the photoperiod, vernalization, and gibberellic acid pathways—are represented among our genes with significant markers. These results suggest that the evolution of flowering time in this species results from the modulation of multiple pathways that are responsive to diverse environmental and hormonal cues. Additional research can validate the effects of these genes to determine which of them are actual QTGs, examine the evolutionary ecological effects of variation at these genes, and determine the molecular mechanisms that these natural alleles may affect.
Acknowledgments
We thank Johanna Schmitt, Steve Welch, Amity Wilczek, and members of the Purugganan lab for insight into this project or comments on this manuscript. The genotyping of the FRI deletion alleles in the MAGIC lines was done by Angela Stathos. I.M.E was supported by both a Department of Education Graduate Assistance in Areas of National Need Biotechnology Fellowship and a National Science Foundation (NSF) Graduate Research Fellowship. P.X.K. was supported by a grant from the Natural and Enviromental Research Council. M.D.P. was supported by grants from the Department of Defense and the NSF's Frontiers in Biological Research program.
Supporting information is available online at http://www.genetics.org/cgi/content/full/genetics.109.105189/DC1.
References
- Aranzana, M. J., S. Kim, K. Zhao, E. Bakker, M. Horton et al., 2005. Genome-wide association mapping in Arabidopsis identifies previously known flowering time and pathogen resistance genes. PLoS Genet. 1: e60. [DOI] [PMC free article] [PubMed]
- Aukerman, M., M. Hirschfeld, L. Wester, M. Weaver, T. Clack et al., 1997. A deletion in the PHYD gene of the Arabidopsis Wassilewskija ecotype defines a role for phytochrome D in red/far-red light sensing. Plant Cell 9: 1317–1326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balasubramanian, S., S. Sureshkumar, M. Agrawal, T. P Michael, C. Wessinger et al., 2006. The PHYTOCHROME C photoreceptor gene mediates natural variation in flowering and growth responses of Arabidopsis thaliana. Nat. Genet. 38: 711–715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bandaranayake, C. K., R. Koumproglou, X. Y. Wang, T. Wilkes and M. J. Kearsey, 2004. QTL analysis of morphological and developmental traits in the Ler x Cvi population of Arabidopsis thaliana. Euphytica 137: 361–371. [Google Scholar]
- Bäurle, I., and C. Dean, 2006. The timing of developmental transitions in plants. Cell 125: 655–664. [DOI] [PubMed] [Google Scholar]
- Caicedo, A. L., J. R. Stinchcombe, K. M. Olsen, J. Schmitt and M. D. Purugganan, 2004. Epistatic interaction between Arabidopsis FRI and FLC flowering time genes generates a latitudinal cline in a life history trait. Proc. Natl. Acad. Sci. USA 101: 15670–15675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlson, C. S., M. A. Eberle, M. J. Rieder, Q. Yi, L. Kruglyak et al., 2004. Selecting a maximally informative set of single-nucleotide polymorphisms for association analyses using linkage disequilibrium. Am. J. Hum. Genet. 74: 106–120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clarke, J. H., R. Mithen, J. K. M. Brown and C. Dean, 1995. QTL Analysis of flowering time in Arabidopsis thaliana. Mol. Gen. Genet. 248: 278–286. [DOI] [PubMed] [Google Scholar]
- Ehrenreich, I. M., P. A. Stafford and M. D. Purugganan, 2007. The genetic architecture of shoot branching in Arabidopsis thaliana: a comparative assessment of candidate gene associations vs. quantitative trait locus mapping. Genetics 176: 1223–1236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- El-Assal, S., C. Alonso-Blanco, A. J. Peeters, V. Raz and M. Koornneef, 2001. A QTL for flowering time in Arabidopsis reveals a novel allele of CRY2. Nat. Genet. 29: 435–440. [DOI] [PubMed] [Google Scholar]
- El-Lithy, M. E., E. J. M. Clerkx, G. J. Ruys, M. Koornneef and D. Vreugdenhil, 2004. Quantitative trait locus analysis of growth-related traits in a new Arabidopsis recombinant. Plant Phys. 135: 444–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engelmann, K. E., and M. D. Purugganan, 2006. The molecular evolutionary ecology of plant development: flowering time in Arabidopsis thaliana. Adv. Bot. Res. 44: 507–526. [Google Scholar]
- Falush, D., M. Stephens and J. K. Pritchard, 2003. Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics 164: 1567–1587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filiault, D. L., C. A. Wessinger, J. Dinneny, J. Lutes, J. O. Borevitz et al., 2008. Amino acid polymorphisms in Arabidopsis phytochrome B cause differential responses to light. Proc. Natl. Acad. Sci. USA 105: 3157–3162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flowers, J. M., Y. Hanzawa, M. C. Hall, R. C. Moore and M. D. Purugganan, 2009. Population genomics of the Arabidopsis thaliana flowering time gene network. Mol. Biol. Evol. (in press). [DOI] [PubMed]
- Gao, H., S. Williamson and C. D. Bustamante, 2007. A Markov chain Monte Carlo approach for joint inference of population structure and inbreeding rates from multilocus genotype data. Genetics 176: 1635–1651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzalez-Martinez, S. C., N. C. Wheeler, E. Ersoz, C. Nelson and D. B. Neale, 2007. Association genetics in Pinus taeda L. I. Wood property traits. Genetics 175: 399–409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirschhorn, J. N., and M. J. Daly, 2005. Genome-wide association studies for common diseases and complex traits. Nat. Rev. Genet. 6: 95–108. [DOI] [PubMed] [Google Scholar]
- Jansen, R. C., J. W. Vanooijen, P. Stam, C. Lister and C. Dean, 1995. Genotype-by-environment interaction in genetic mapping of multiple QTL. Theor. Appl. Genet. 91: 33–37. [DOI] [PubMed] [Google Scholar]
- Johanson, U., J. West, C. Lister, S. Michaels, R. Amasino et al., 2000. Molecular analysis of FRIGIDA, a major determinant of natural variation in Arabidopsis flowering time. Science 290: 344–347. [DOI] [PubMed] [Google Scholar]
- Juenger, T. E., J. K. McKay, N. Hausmann, J. J. B. Keurentjes, S. Sen et al., 2005. Identification and characterization of QTL underlying whole plant physiology in Arabidopsis thaliana: δ13C, stomatal conductance and transpiration efficiency. Plant Cell. Env. 28: 697–708. [Google Scholar]
- Kim, S., V. Plagnol, T. T. Hu, C. Toomajian, R. M. Clark et al., 2007. Recombination and linkage disequilibrium in Arabidopsis thaliana. Nat. Genet. 39: 1151–1155. [DOI] [PubMed] [Google Scholar]
- Komeda, Y., 2004. Genetic regulation of time to flower in Arabidopsis thaliana. Annu. Rev. Plant Biol. 55: 521–535. [DOI] [PubMed] [Google Scholar]
- Koornneef, M., C. Alonso-Blanco and D. Vreugdenhil, 2004. Naturally occurring genetic variation in Arabidopsis thaliana. Ann. Rev. Plant Biol. 55: 141–172. [DOI] [PubMed] [Google Scholar]
- Kover, P. X., W. Valdar, J. Trakalo, N. Scarcelli, I. M. Ehrenreich et al., 2009. A multiparent advanced generation inter-cross to fine-map quantitative traits in Arabidopsis thaliana. PLoS Genet. 5: e1000551. [DOI] [PMC free article] [PubMed]
- Kuittinen, H., M. J. Sillanpaa and O. Savolainen, 1997. Genetic basis of adaptation: flowering time in Arabidopsis thaliana. Theor. Appl. Genet. 95: 573–583. [Google Scholar]
- Maloof, J. N., J. O. Borevitz, T. Dabi, J. Lutes, R. B. Nehring et al., 2001. Natural variation in light sensitivity of Arabidopsis. Nat. Genet. 29: 441–446. [DOI] [PubMed] [Google Scholar]
- Mouradov, A., F. Cremer and G. Coupland, 2002. Control of flowering time: interacting pathways as a basis for diversity. Plant Cell 14: S111–S130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordborg, M., T. T. Hu, Y. Ishino, J. Jhaveri, C. Toomajian et al., 2005. The pattern of polymorphism in Arabidopsis thaliana. PLoS Biol. 3: e196. [DOI] [PMC free article] [PubMed]
- Olsen, K. M., S. S. Halldorsdottir, J. R. Stinchcombe, C. Weinig, J. Schmitt et al., 2004. Linkage disequilibrium mapping of Arabidopsis CRY2 flowering time alleles. Genetics 167: 1361–1369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard, J. K., M. Stephens and P. Donnelly, 2000. Inference of population structure using multilocus genotype data. Genetics 155: 945–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scarcelli, N., J. M. Cheverud, B. A. Schaal and P. X. Kover, 2007. Antagonistic pleiotropic effects reduce the potential adaptive value of the FRIGIDA locus. Proc. Natl. Acad. Sci. USA 104: 16986–16991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmid, K., O. Torjek, R. Meyer, H. Schmuths, M. H. Hoffmann et al., 2006. Evidence for a large-scale population structure of Arabidopsis thaliana from genome-wide single nucleotide polymorphism markers. Theor. Appl. Genet. 112: 1104–1114. [DOI] [PubMed] [Google Scholar]
- Simpson, G. G., and C. Dean, 2002. Arabidopsis, the Rosetta stone of flowering time? Science 296: 285–289. [DOI] [PubMed] [Google Scholar]
- Stinchcombe, J. R., C. Weinig, M. C. Ungerer, K. M. Olsen, C. Mays et al., 2004. A latitudinal cline in flowering time in Arabidopsis thaliana modulated by the flowering time gene FRIGIDA. Proc. Natl. Acad. Sci. USA 101: 4712–4717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storey, J. D. 2002. A direct approach to false discovery rates. J. R. Stat. Soc. Series B, 64: 479–498. [Google Scholar]
- Storey, J. D. and R. Tibshirani 2003. Statistical significance for genome-wide experiments. Proc. Natl. Acad. Sci. USA 100: 9440–9445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stratton, D. A., 1998. Reaction norm functions and QTL-environment interactions for flowering time in Arabidopsis thaliana. Heredity 81: 144–155. [DOI] [PubMed] [Google Scholar]
- Tabor, H. K., N. J. Risch and R. M. Myers, 2002. Candidate-gene approaches for studying complex genetic traits: practical considerations. Nat. Rev. Genet. 3: 1–7. [DOI] [PubMed] [Google Scholar]
- Thornsberry, J. M., M. M. Goodman, J. Doebley, S. Kresovich, D. Nielsen et al., 2001. Dwarf8 polymorphisms associate with variation in flowering time. Nat. Genet. 28: 286. [DOI] [PubMed] [Google Scholar]
- Ueda, H., J. M. M. Howson, L. Esposito, J, Heward, H. Snook et al., 2003. Association of the T-cell regulatory gene CTLA4 with susceptibility to autoimmune disease. Nature 423: 506–511. [DOI] [PubMed] [Google Scholar]
- Ungerer, M. C., S. Halldorsdottir, J. Modliszewski, T. F. C. Mackay and M. D. Purugganan, 2002. Quantitative trait loci for inflorescence development in Arabidopsis thaliana. Genetics 160: 1133–1151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ungerer, M. C., S. Halldorsdottir, M. D. Purugganan and T. F. C. Mackay, 2003. Genotype-environment interactions at quantitative trait loci affecting inflorescence development in Arabidopsis thaliana. Genetics 165: 353–365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaisee, C., K. Clement, E. Durand, S. Hercberg, B. Guy-Grand et al., 2000. Melanocortin-4 receptor mutations are a frequent and heterogenous cause of morbid obesity. J. Clin. Invest. 106: 253–262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Berloo, R., and P. Stam, 1999. Comparison between marker-assisted selection and phenotypical selection in a set of Arabidopsis thaliana recombinant inbred lines. Theor. Appl. Genet. 98: 113–118. [Google Scholar]
- Weber, A., R. M. Clark, L. Vaughn, J. D. J. Sanchez-Gonzalez, J. Yu et al., 2007. Major regulatory genes in maize contribute to standing variation in teosinte. Genetics 177: 2349–2359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber, A. L., W. H. Briggs, J. Rucker, B. M. Baltazar, J. D. J. Sanchez-Gonzalez et al., 2008. The genetic architecture of complex traits in teosinte (Zea mays ssp. parviglumis): new evidence from association mapping. Genetics 180: 1221–1232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weigel, D., and M. Nordborg, 2005. Natural variation in Arabidopsis: how do we find the causal genes? Plant Physiol. 138: 567–568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinig, C., M. C. Ungerer, L. A. Dorn, N. C. Kane, S. Halldorsdottir et al., 2002. Novel loci control variation in reproductive timing in Arabidopsis thaliana in natural environments. Genetics 162: 1875–1881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinig, C., L. A. Dorn, N. C. Kane, M. C. Ungerer, S. Halldorsdottir et al., 2003. Heterogeneous selection at specific loci in natural environments in Arabidopsis thaliana. Genetics 165: 321–329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werner, J. D., J. O. Borevitz, N. H. Uhlenhaut, J. R. Ecker, J. Chory et al., 2005. a FRIGIDA-independent variation in flowering time of natural Arabidopsis thaliana accessions. Genetics 170: 1197–1207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werner, J. D., J. O. Borevitz, N. Warthmann, G. T. Trainer, J. R. Ecker et al., 2005. b Quantitative trait locus mapping and DNA array hybridization identify an FLM deletion as a cause for natural flowering-time variation. Proc. Natl. Acad. Sci. USA 102: 2460–2465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson, L. M., S. R. Whitt, A. M. Ibanez, T. R. Rocheford, M. M. Goodman et al., 2004. Dissection of maize kernel composition and starch production by candidate gene association. Plant Cell 16: 2719–2733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu, J., G. Pressoir, W. H. Briggs, B. Vroh, M. Yamasaki et al., 2006. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat. Genet. 38: 203–208. [DOI] [PubMed] [Google Scholar]
- Zhao, K., M. J. Aranzana, S. Kim, C. Lister, C. Shindo et al., 2007. An Arabidopsis example of association mapping in structured samples. PLoS Genet. 3: e4. [DOI] [PMC free article] [PubMed] [Google Scholar]