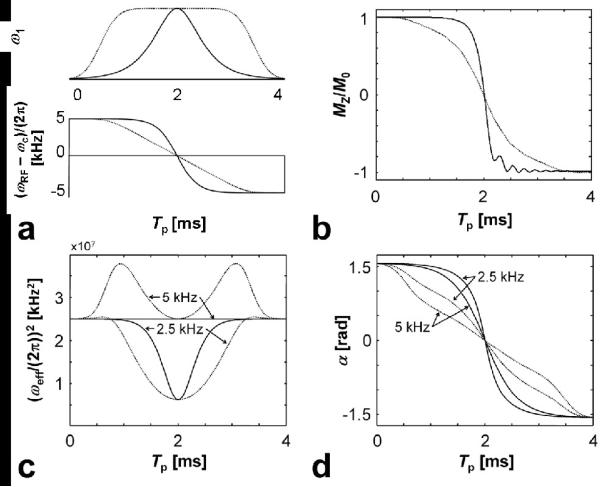
Figure 2.

Properties of adiabatic full passage (AFP) pulses, namely the hyperbolic secant HS1 (solid lines) and HS4 (dotted lines) pulses. a) amplitude and frequency modulation functions., with T_p = 4 ms, R-value = 40, corresponding to B = 10 kHz, ${\omega }_1^{\max }∕\left(2\pi \right)=2.5\mathrm{kHz}$; b) trajectories showing the inversion of the magnetization for the isochromat centered at the carrier frequency of the pulse. Note that during the AFP, the magnetization of each isochromat within the BW becomes inverted by the end of the pulse; c-d) evolution of α(t) and (ω_eff/(2π))² during the pulses. Since α(t) and ω_eff/(2π))² depend not only on the modulation functions but also on the pulse parameters, the cases corresponding to ${\omega }_1^{\max }∕\left(2\pi \right)=2.5\mathrm{kHz}$ and 5 kHz are presented. Note that when ${\omega }_1^{\max }∕\left(2\pi \right)=\mathrm{A}(\equiv BW∕2)$, i.e. when ${\omega }_1^{\max }∕\left(2\pi \right)=5\mathrm{kHz}$, then ω_eff/(2π))² during the HS1 pulse becomes time-independent. This is because the known trigonometric identity ω²_eff = A·[sech²(β(2t/T_p-1)) + tan²(β(2t/T_p-1))] = A.