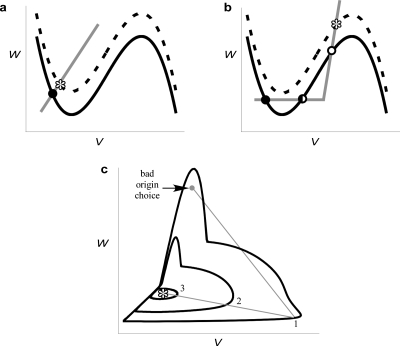
Figure 8.

State space dynamics. [(a) and (b)] Example nullclines for two-state variable systems. The fast variable nullcline (black) corresponds to dV∕dt=0 and the slow variable nullcline (gray) corresponds to dW∕dt=0. When the Laplacian term is zero (e.g., spatially homogenous state variable patterns) the fixed points of the system correspond to the intersection of the nullclines. For example, in excitable systems, there is a stable solution to the PDE [Eq. 4] that represents all sites at a “quiescent” state that corresponds to a stable fixed point (depicted as closed circles). Depending on the shape of the slow variable nullcline, there may be additional fixed points. For example, (b) depicts three intersections of the nullclines including a marginally stable fixed point (half-filled circle) and an unstable fixed point (open circle). The dashed lines indicate the effect of adding a constant value to the fast variable equation which corresponds to the dynamics at ${\stackrel{⃑}{u}}^{*}$. This addition causes a vertical shift in the fast variable nullcline and the result is depicted as a dashed line. This shift may act to slightly perturb the quiescent solution as in (a) or may act to fundamentally change the system fixed points as in (b), where the shift results in the elimination of two fixed points. (c) The “bad” choice of origin illustrates nonunique θ representation as indicated by the three intersection points of the outermost trajectory by the gray line originating at the origin.