Fig. (1).

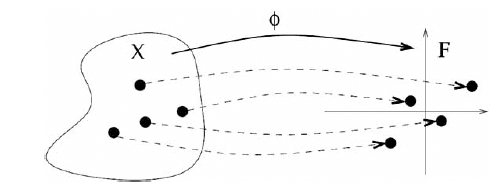
Defining a kernel over a space X, such as the space of all small molecules or the space of all proteins, is equivalent to embedding X in a vector space F of finite or infinite dimension through a mapping Φ:X → F.The kernel between two points in X is equal to the inner products of their images in F, as shown in (1).