Figure 2.

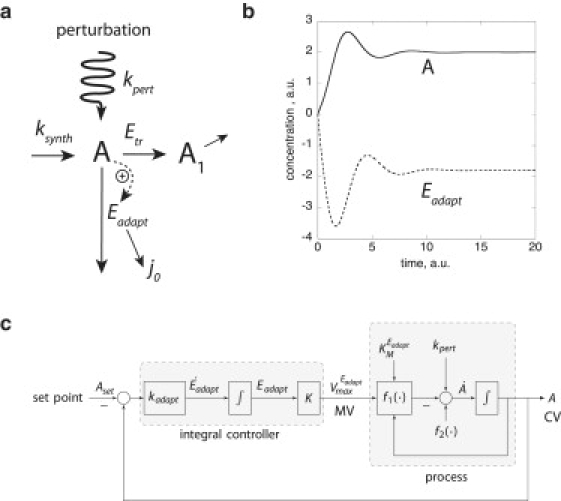
(a) Reaction scheme of system with rate Eqs. 1 and 2. Species A is formed by a zero-order process with rate constant k_synth and then transformed to the product A₁. Rate constant k_pert is related to a perturbing process (wavy line), which increases the level of A. To remove excess A, A is forming enzyme species E_adapt, which removes A with the flux $V_{\text{max}}^{E_{\text{adapt}}}A/\left(K_{\mathrm{M}}^{E_{\text{adapt}}}+A\right)$ (indicated by the vertical arrow). To get robust adaptation in A independent of k_pert, E_adapt is removed through a zero-order flux j₀ = k_adaptA_set. (b) Calculation showing that negative E_adapt concentrations may arise when A_set is regarded as a fixed setpoint. Initial concentrations of A and E_adapt are zero; k_adapt = 5, k_pert = k_synth = 0.5, $V_{\text{max}}^{E_{\text{adapt}}}=1$, $K_{\mathrm{M}}^{E_{\text{adapt}}}$ = 1, $V_{\text{max}}^{E_{\text{tr}}}$ = 110, $K_{\mathrm{M}}^{E_{\text{tr}}}$ = 100, and A_set = 2. Concentration and timescales are in arbitrary units (a.u.). (c) Scheme of the adaptive process shown in panel a containing the setpoint A_set, the integral controller and the process units. The controlled variable (CV) is A. Eqs. 1 and 2 are written as dA/dt = f₂(·) – f₁(·) + k_pert, dE_adapt/dt = k_adapt(A – A_set), respectively, with $f_1(·)=V_{\text{max}}^{E_{\text{adapt}}}A/\left(K_{\mathrm{M}}^{E_{\text{adapt}}}+A\right)$, $f_2(·)=k_{\text{synth}}-V_{\text{max}}^{E_{\text{tr}}}A/\left(K_{\mathrm{M}}^{E_{\text{tr}}}+A\right)$, and $V_{\text{max}}^{E_{\text{adapt}}}$ = K · E_adapt. K is the turnover number for E_adapt, i.e., $K=k_{\text{cat}}^{E_{\text{adapt}}}$. MV: manipulated variable.