Figure 6.

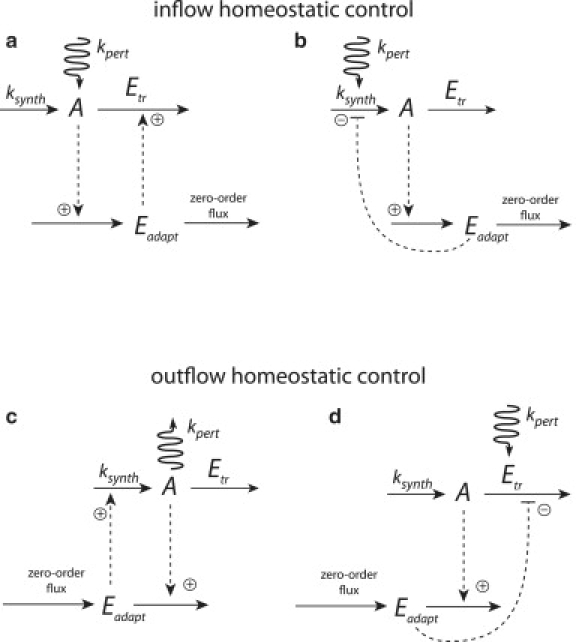
Homeostatic control motifs. Due to the kinetic restriction that concentrations need to be positive, two classes of homeostatic controllers arise: 1), inflow homeostatic controllers leading to homeostasis in the concentration of A for increasing (and moderate decreasing) perturbations in A (panels a and b); and 2), outflow homeostatic controllers leading to homeostasis in A for decreasing (and moderate increasing) perturbations in A (panels c and d). Rate equations with example parameter values are given in the Appendix. Note that many of the parameter values may be changed within certain limits (besides changing k_pert) without affecting the homeostasis. (a) Schematic representation of the two (inflow) homeostatic models shown in Fig. 3. Robust homeostasis is due to the zero-order kinetic removal of E_adapt. (b) Inflow homeostatic model where E_adapt inhibits the inflow of A through k_synth. To maintain homeostasis the perturbation needs to be applied to the same reaction channel as k_synth. The integral feedback is due to the zero-order removal of E_adapt and is not related to the physico-chemical negative feedback from E_adapt to (k_synth + k_pert). (c) Outflow homeostatic controller by removing E_adapt through A. (d) Outflow homeostatic controller by inhibiting E_tr through E_adapt. Similar to panel b, homeostasis is obtained when the perturbation increases the outflow of A through the same reaction channel that is used by enzyme E_tr.