Figure 1.

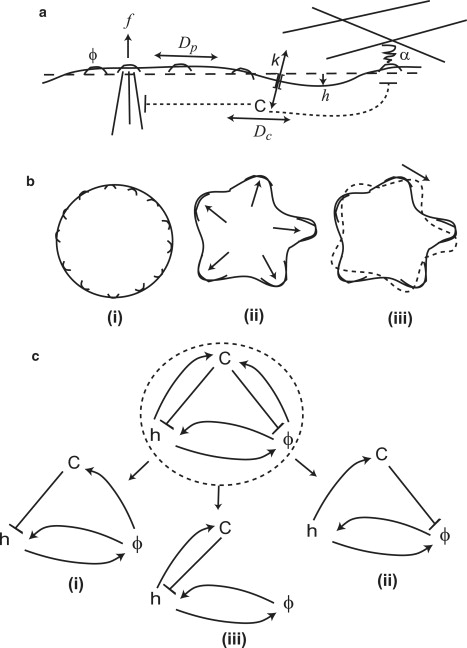
(a) Scheme of our model; one-dimensional flat membrane with local height deviation h and a concentration of membrane proteins (MP) ϕ that diffuse with coefficient D_p and activate actin polymerization of protrusive force $\tilde{f}$, and adhesion to external substrate α. The local calcium concentration C depends on the influx through channels and outflux through pumps, diffuses with coefficient D_c and inhibits the actin-driven force and adhesion (dashed lines). (b) The stable system (i) is uniform and mixed, whereas the Turing instability (ii) leads to stationary phase separation, and the wave-instability (iii) leads to oscillatory or propagating domains. (c) The overall feedbacks and coupling of our model (Eqs. 2–4) and the simpler subcases (i–iii) that give rise to wave instability.