Figure 1.
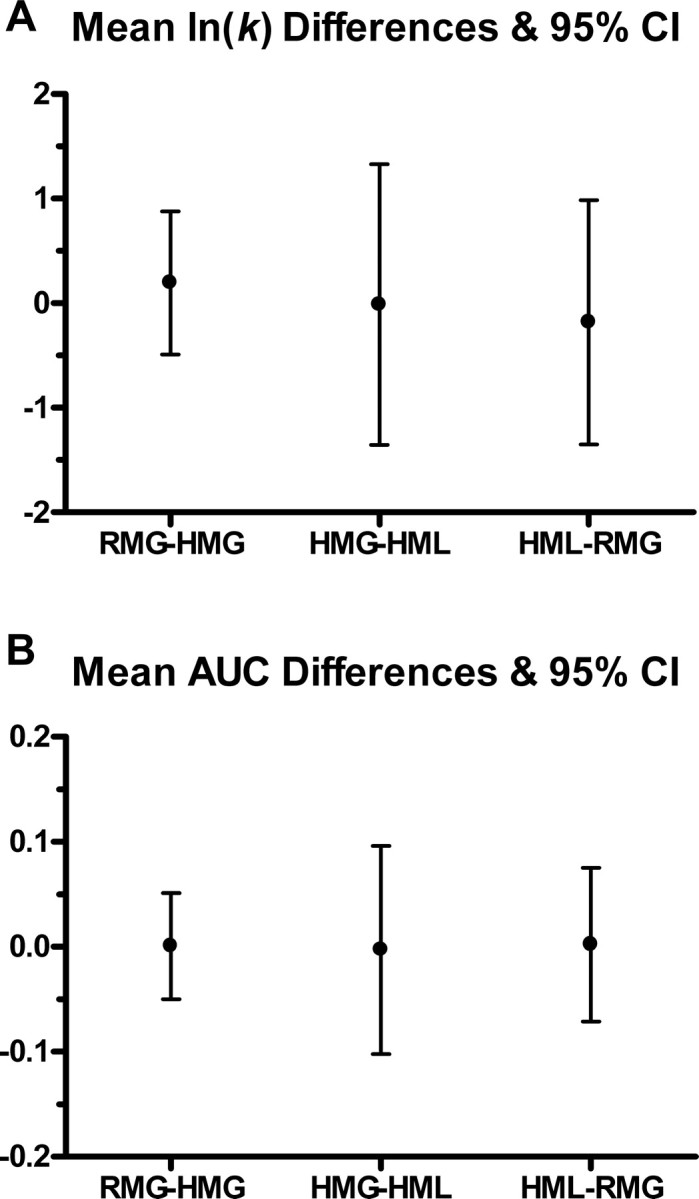
Indifference points for delays of 1, 7, 30, and 180 d were collected from each individual before scanning in each of three discounting conditions and were subsequently fitted to a hyperbolic curve using Mazur's (1987) nonlinear function. Estimated ks were then log transformed to address skewed distributions and then entered into a repeated-measures ANOVA to test for differences in discounting between the conditions. Within-subject differences between discounting conditions were determined not to be significant (F(2,28) = 0.21, p = 0.81): RMG–HMG = 0.196 ± 0.68, HMG–HML = −0.014 ± 1.34, and HML–RMG = −0.18 ± 1.17 (A). Indifference points were also used to calculate AUC measures which were subsequently used in a repeated-measures ANOVA to detect within-subject difference between discounting conditions. AUC allows for freedom from the theoretical framework of the hyperbolic discounting function and problems associated with estimated parameters (Myerson et al., 2001). Results indicate no statistically significant difference between average normalized AUC measures (F(2,28) = 0.00, p = 0.99) (B): RMG–HMG = 0.001 ± 0.05, HMG–HML = −0.003 ± 0.10, and HML–RMG = 0.002 ± 0.07.
