Cortical Correspondence with Probabilistic Fiber Connectivity

Abstract

This paper presents a novel method of optimizing point-based correspondence among populations of human cortical surfaces by combining structural cues with probabilistic connectivity maps. The proposed method establishes a tradeoff between an even sampling of the cortical surfaces (a low surface entropy) and the similarity of corresponding points across the population (a low ensemble entropy). The similarity metric, however, isn’t constrained to be just spatial proximity, but uses local sulcal depth measurements as well as probabilistic connectivity maps, computed from DWI scans via a stochastic tractography algorithm, to enhance the correspondence definition. We propose a novel method for projecting this fiber connectivity information on the cortical surface, using a surface evolution technique. Our cortical correspondence method does not require a spherical parameterization. Experimental results are presented, showing improved correspondence quality demonstrated by a cortical thickness analysis, as compared to correspondence methods using spatial metrics as the sole correspondence criterion.

1 Introduction

Measurements of cerebral topographical properties such as cortical thickness and curvature are of great interest for quantitative investigations of neural development and anatomic connectivity, both for healthy populations and for clinical studies. Group analysis of such cerebral properties requires the ability to compute corresponding points across a population of cortical surfaces. Consistent computation of corresponding points on the cortical surface (defined as the boundary between the white matter (WM) and gray matter (GM) surfaces) is a difficult task, given the highly convoluted geometry of the brain and the high variability of folding patterns across subjects. It should also be noted that no generic “ground truth” definition of dense correspondence exists for the cortex. The choice of particular correspondence metric must, therefore, be application-driven.

A variety of automated cortical correspondence computation algorithms have been proposed. The FreeSurfer system [1,2] provides an entire framework for the segmentation, surface reconstruction, topology correction, cortical flattening and spherical parameterization of the cortex. The correspondence across a population of cortical surfaces is established through the registration of their respective spherical representations with an average surface, based on an average convexity measure referred to as the sulcal depth, discussed in Section 3.3. Tosun et al. [3] estimate a multispectral optical flow warping procedure that aims to align the shape measure maps of an atlas and a subject brain’s normalized maps, based on the shape index and curvedness metrics.

A shortcoming of these methods is that they use an atlas or a template surface to which the other surfaces are aligned in a pair-wise manner. It has been shown that group-wise correspondence methods that consider the entire population at once rather than processing one surface at a time yield better statistical population models [4,5,6]. In one of the earliest such methods by Kotcheff and Taylor [7], each shape is represented as a point in 2N-dimensional space, with associated covariance Σ. The method minimizes information content across an ensemble via a cost function ${\Sigma }_k\log ({\lambda }_k+\alpha )$, where λ_k are the eigenvalues of Σ and α is a regularization term. The Minimum Description Length (MDL) method proposed by Davies et al. [8] hypothesizes that the simplest description of a population is the best; in this context, they measure simplicity by the length of the code to transmit the data as well as the model parameters. MDL implementations in 3D usually rely on spherical parameterizations of the surfaces, which must be obtained through a preprocessing step, such as the method proposed in [9], that relaxes a spherical parameterization onto the input mesh. In [10], we present a gradient descent optimization method for the MDL algorithm and explore using local curvature in addition to spatial locations in the MDL cost function.

An empirical study by Styner et al.[6] demonstrates that ensemble-based statistics improve correspondences relative to pure geometric regularization, and that MDL performance is virtually the same as that of (min log |Σ+αI|), as proposed in Kotcheff and Taylor’s methoddescribed above. This last observation is consistent with the well-known result from information theory: in general, MDL is equivalent to minimum entropy [11]. Cates et al. [12,13] propose a system exploring this property; their entropy-based particle correspondence framework is the underlying technique for the methodology presented in this paper and will be discussed in more detail in Sec. 3.

We present a method that extends the entropy-based particle framework to allow the usage of additional local information, called correspondence features throughout this manuscript, for computing correspondence. Specifically, we propose a novel method for integrating fiber connectivity information into the correspondence framework. Structural MRI scans show white matter homogeneously, such that it is impossible to infer the orientation of the fiber tracts within each voxel. The understanding of the WM structure, however, can be significantly improved by additional information on fiber tracts that can be extracted from diffusion weighted imaging (DWI) scans. One of the main contributions of this manuscript is a suitable mapping of the fiber tract structure to the cortical surface. Connectivity maps, which represent whether each voxel on the cortical surface is connected via fiber tracts to a given region of interest (ROI), is the proposed solution to this problem.

Various tractography algorithms have been proposed in recent years to extract fiber tract paths from DWI scans. Streamline tractography [14] generates tracts by following the direction of maximal diffusion at each voxel. While these methods have low computation costs and simplify the visualization of the extracted fiber tracts, they cannot deal with noisy input images, regions of high isotropy, or partial volume effect. In contrast, stochastic tractography methods [15,16,17] take the uncertainty of fiber orientations into account, and therefore yield results that are more suitable for our purposes, as discussed in Sec. 2.

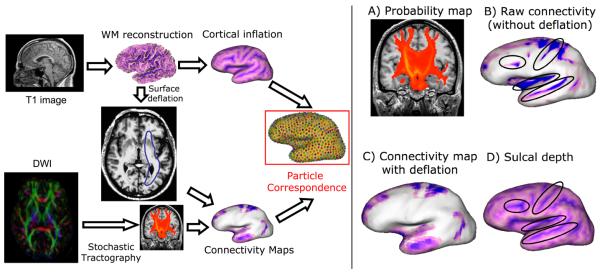
In the next section, a summary of our proposed approach is provided. Then, in Sec. 3, we discuss in detail the entropy-based particle correspondence framework and its extension to incorporate local correspondence features. Sec. 4 presents the two main novel contributions of this manuscript, namely, the methodology followed for projecting DWI-based connectivity information to the cortical surface and the surface deflation algorithm proposed for overcoming the problems associated with fiber tracking near the WM/GM boundary. We then define our evaluation criteria in Sec. 5 and present experimental results in Sec. 6. Fig.1 summarizes our pipeline.

Fig. 1.

Left, pipeline overview. We use T1 images to generate WM surfaces and inflated cortical surfaces, as well as local sulcal depth. Selected ROI’s and the DWI image are input to the stochastic tractography (ST) algorithm. WM surface deflated using proposed algorithm is used to construct connectivity maps on the surface from ST results. Inflated cortical surfaces and the connectivity maps are used to optimize correspondence. Right, impact of brain deflation algorithm on surface connectivity values. The stochastic tractography algorithm gives connectivity probabilities for the brainstem for this subject(A). The noisy tracking around temporal lobe is reflected on the connectivity map that uses simple averaging(B). The surface deflation method ignores the noisy signal and reflects a more accurate connectivity map(C). Note how strongly the averaging method depends on sulcal depth(D), illustrated in highlighted regions.

2 Methodology Overview

In this work, we are presenting a cortical correspondence system that incorporates various local functions of spatial coordinates. We choose to use a particle-based entropy minimizing system, as introduced by Cates et al.[12,13], for the correspondence computation in a population-based manner. Specifically, we use the extension to this methodology we presented in [5] that allows the use of correspondence features for establishing correspondence. These features are locally defined functions that provide additional information about the surface, such as curvature. This extension is critical for the application of the entropy-based particle correspondence framework to populations of cortical surfaces, as additional information sources can have significant impact on correspondence quality. Structural features such as sulcal depth and local curvature provide additional information about the geometry of the brain; DWI-based fiber connectivity features provide augmented knowledge about the white matter structure. Furthermore, given the highly folded and curved nature of the cortex surface, Euclidean distances measured in 3D space between points do not reflect the actual distance along the cortical sheet (e.g. in the case of two points lying on different banks of a sulcus); it therefore makes little sense to use spatial proximity as a standalone measure of correspondence strength.

The particle framework uses a point-based surface sampling to optimize surface correspondence in a population-based manner. Like-numbered samples, named particles, define correspondence across the population. The optimization consists of moving the particles along the surfaces in the direction of the gradient of an energy functional that strikes a balance between an even sampling of each surface (characterized by shape entropy) and a high spatial similarity of the corresponding samples across the population (ensemble entropy). Local measurements on the object surfaces, referred to as correspondence features, are incorporated into the ensemble entropy to provide a generalized correspondence definition.

One of the main contributions of this work is the use of fiber connectivity patterns for optimizing cortical correspondence. This is achieved by using connectivity of the cortex to various ROI’s as correspondence features. A stochastic tractography algorithm, described in Sec. 4.1, generates connectivity maps that represent the probability of each voxel being connected to these ROI’s. A separate feature channel is used for connectivity to each individual ROI.

There is, however, a major obstacle to using these connectivity maps for cortical correspondence: the connectivity probabilities typically decrease drastically near the WM/GM boundary, as the diffusion gets too isotropic and noisy near the surface. This effect is more emphasized at the ridges of the gyri (as opposed to the valleys of the sulci). Thus, the tractography values at the cortical boundary voxels are more of a function of local sulcal depth than of actual connectivity. A major contribution of this work is a method of computing the connectivity probability at the cortical surface using a surface deflation algorithm, as described in Sec. 4.2. This produces a new, smoother surface that follows the cortical boundary closely while leaving out the gyri. Then, the connectivity probability at each cortical voxel is defined as the connectivity probability value at the corresponding inner-surface voxel.

A major challenge in using the particle framework for solving the cortical correspondence problem is the highly convoluted geometry of the human cortex. In the current implementation, the particles are assumed to be living on the local tangent planes of the surfaces for computational efficiency purposes; highly convoluted surfaces present a challenge to this assumption due to the rapidly changing tangent planes. We solve this problem by defining an alternative domain to the problem, by ‘inflating’ the cortical surface. This results in much smoother surfaces. A one-to-one mapping between this surface and the original cortical surface is necessary, as the particles live on the inflated surface, whereas the correspondence features (such as the sulcal depth or the probabilistic connectivity) are only defined on the original surface. A set of automated tools distributed as part of the FreeSurfer [1,2] package are used for preprocessing the data as well as for the cortical inflation, as described in Sec. 3.3.

3 Entropy-Based Cortical Correspondence with Local Features

3.1 Entropy-Based Shape Correspondence

Entropy-Based Surface Sampling

In this work, we use a surface sampling technique, described in [13], using a discrete set of points called particles. These particles move away from each other under a repulsive force, while constrained to lie on the surface. The repulsive forces are weighted by a Gaussian function of inter-particle distance; interactions are therefore local for sufficiently small σ.

It is noteworthy that the current formulation computes Euclidean distance between particles, rather than the geodesic distance on the surface, for computational efficiency purposes. Thus, a sufficiently dense sampling is assumed, so that nearby particles lie in the tangent planes of the zero sets of a scalar function F which provides the implicit object surface. This is an important consideration for the application to the cortical surface; the highly convoluted surface challenges this assumption, and the distribution of particles may be affected by neighbors that are outside of the true manifold neighborhood. As discussed in Sec. 2, we overcome this problem by transforming the domain of the problem to a smoother one, obtained by cortex inflation.

Ensemble Entropy of Correspondence Positions

An ensemble ε is a collection of M surfaces, each with their own set of particles, i.e. ε = z¹, . . . , z^M. The ordering of the particles on each shape implies a correspondence among shapes, and thus we have a matrix of particle positions $P=x_j^k$, with particle positions along the rows and shapes across the columns. We model each surface $z^k\in {\Re }^{Nd}$ as an instance of a random variable Z (where N is the number of particles and d is the surface dimension), and propose to minimize the combined ensemble and shape cost function

$$Q=H\left(Z\right)-\sum _{k}H\left(P^k\right),$$ (1)

which favors a compact ensemble representation balanced against a uniform distribution of particles on each surface as discussed in the previous paragraph. The different entropies are commensurate so there is no need for ad-hoc weighting of the two function terms.

Given the low number of examples relative to the dimensionality of the space, we must impose some conditions in order to perform the density estimation. For this work we assume a normal distribution and model p(Z) parametrically using a Gaussian with covariance Σ. The entropy is then given by

$$H\left(Z\right)\approx \frac{1}{2}\log \mid \Sigma \mid =\frac{1}{2}\sum _{j=1}^{Nd}\log {\lambda }_j,$$ (2)

where λ₁, ..., λ_Nd are the eigenvalues of Σ.

Since, in practice, Σ will not have full rank, the covariance is estimated from the data, letting Y denote the matrix of points minus the sample mean for the ensemble, which gives Σ = (1/(M - 1))YY^T. The negative gradient -∂H/∂P gives a vector of updates for the entire system, which is recomputed-once per system update. This term is added to the shape-based updates described in the previous section to give the update of each particle.

3.2 Using Local Features for Improving Correspondence

In the case of computing entropy of vector-valued functions of the correspondence positions P, we now consider the more general case where $\tilde{P}=f\left(x_j^k\right)$, where $f:{\Re }^d\to {\Re }^q$, where d is the dimensionality of the surface and q is the dimension of f (number of correspondence features). $\tilde{Y}$ becomes a matrix of the function values at the particle points minus the means of those functions at the points, and we compute the general cost function simply as

$$\tilde{H}\left(\tilde{P}\right)=\log \mid \frac{1}{M-1}{\tilde{Y}}^T\tilde{Y},\mid .$$ (3)

Then, the gradient of $\tilde{H}$ with respect to each shape k can be computed using the chain rule, by introducing the Jacobian of the functional data for shape k.

3.3 Surface Reconstruction and Cortex Inflation

In this work, we use FreeSurfer for the cortical surface reconstruction as well as surface inflation. We initialize the FreeSurfer algorithm with the output of the atlas based tissue segmentation tool itkEMS, which uses an Expectation-Maximization approach to segment the major brain tissue classes and correct for intensity inhomogeneity using both T1 and T2 weighted images[18].

The inflation algorithm of FreeSurfer[1] provides a much smoother surface than the cortical surface while minimizing metric distortions. This is achieved via the optimization of an energy functional consisting of the weighted sum of a spring force that works towards ‘inflating’ the surface and a metric preservation term that ensures that as little metric distortion as possible is introduced. The inflation process is such that points that lie in convex regions move inwards while points in concave regions move outwards over time. Thus, the average convexity/concavity of the surface over a region, referred to as sulcal depth, can be computed as the integral of the normal movement of a point during inflation.

4 Using Probabilistic Fiber Connectivity for Cortical Correspondence

4.1 Stochastic Tractography

In this work, we use an open-source implementation of a modification of Friman’s stochastic tractography algorithm[15]. In this approach, fiber tracts are modeled as sequences of unit vectors whose orientation is determined by sampling a posterior probability distribution. The posterior distribution is given by a prior likelihood of the fiber orientation multiplied by the likelihood of the orientation given the DWI data. Friman uses a tensor model constrained to be linearly anisotropic to lower the computational cost of the algorithm; deviations from this distribution are modeled as uncertainty in the fiber orientation. At each step, the orientation of the previous vector in the sequence affects the prior, ensuring no backtracking occurs. The tracking stops when the tract reaches a voxel with a low posterior probability of belonging to the white matter. We use the output of the itkEMS algorithm described above, co-registered with the DWI data (by registering the T2-weighted image with the DWI baseline using an affine transformation with 15 dof’s), as the necessary soft WM segmentation input. The ROI’s are obtained from the FreeSurfer segmentation.

A high number of sample fibers are tracked from each voxel included in the input ROI; the probabilistic connectivity of a voxel to the ROI is defined as the ratio of fiber samples that travel through a voxel over the total number of samples. As described in the next section, the connectivity values on the WM/GM boundary are discarded, and the values at the corresponding deflated surface location are used instead, to compensate for the fading DWI signal at the boundary. Finally, to normalize for various effects such as number of voxels in the ROI’s and brain size, we perform a histogram equalization on the connectivity feature values read on the deflated surface, for each individual and for each ROI.

4.2 Surface Deflation for Connectivity Mapping

In order to get accurate readings of fiber connectivity probability values, an inner white matter surface with one-to-one correspondence to the WM/GM boundary is necessary. This surface should be not only sufficiently away from the boundary, but also without the convolutions caused by sulci and gyri. Without such a deflated surface, the probabilistic fiber connectivity values become heavily dependent on the local sulcal depth, yielding high connectivity values near sulci and low connectivity values near the gyri, as the fibers must be tracked a longer distance through the isotropic boundary region to reach the gyri (see Fig. 1). We propose a surface evolution method that evolves the WM surface by progressively smoothing out the gyri. To prevent the local sulcal depth from dominating the connectivity values, it’s important to have a surface that is not only sufficiently away from the WM-GM boundary but also much smoother. This is accomplished by a mean-curvature-based smoothing algorithm, described in [19,20]. This iterative method smoothes the surface mesh using a relaxation operator, such that the vertices are repositioned according to

$$V_i^{t+1}=(1-\lambda )V_i^t+\lambda {\stackrel{‒}{V}}_i^t,$$

where V_i is the position of the ith vertex, t is the number of iterations, λ ∈ [0, 1] is a smoothing parameter, and ${\stackrel{‒}{V}}_i$ is the average vertex position, which is the average position of neighboring triangle centers weighted by the triangle areas.

However, we alter this algorithm such that vertices located near the valleys of thesulci are fixed (by forcing the velocity λ to 0 at these vertices), which results in the smoothing of only the gyri, while keeping the rest of the mesh intact. The fixed locations are progressively released, to avoid creating singular points on the surface due to the hard constraints posed. The progressive relaxation is based on thresholding of the L₂ norm of the mean curvature H, defined as

$${\mid \mid H\mid \mid }_2=\sqrt{\frac{1}{4\pi }\int H^{2}dA}.$$

The vertices to be fixed initially are determined based on the sulcal depth. All positive local maxima of the sulcal depth are marked as fixed, and all vertices of the mesh that are located between already fixed locations are also fixed, in order to create merged surface patches rather than standalone points. It is preferable to start with too many fixed vertices rather than too few, as the progressive relaxation stage ensures no vertices remain fixed for more than necessary. Constraining the fixed points to positive sulcal depth values ensures vertices located on the gyri are free to move at all times, whereas the sulci can start moving only after the surrounding gyri have been smoothed out.

The progressive relaxation of the fixed locations is necessary to avoid any patches from remaining fixed indefinitely despite the fact that the rest of the mesh around it has sufficiently deflated. Once the fixed sulcal region becomes flat (detected by the mean curvature threshold), the zero-velocity constraint on the vertex is released, and the vertex is free to move.

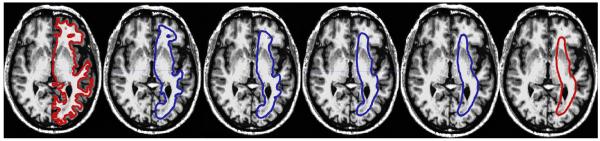
As a final step in the deflation, we shrink the entire surface inwards by about one voxel, to ensure that the vertices at the sulci move away from the WM/GM boundary. Without this shrinking step, the probabilistic connectivity values at the sulci and gyri would be treated differently, which would introduce unwanted bias by only moving the gyri away from the WM/GM boundary. Note that the shrinking has to be done in small increments to avoid introducing topological changes to the surface. Fig. 2 shows intermediate results of the surface deflation on an axial slice of the brain scan as well as the final scaling.

Fig. 2.

Brain deflation progress for one subject. The surface outline is shown in contrasting colors overlayed on an axial slice of the brain. The leftmost image shows the original WM surface, and the consequent images show the progress of the deflation at 1000 iteration intervals. The second rightmost surface is used for retrieving probabilistic connectivity images after a final scaling step, shown on the far right. Note the progressive smoothing of the gyri as the surrounding regions become flat, which relaxes the velocity constraint on these vertices.

5 Evaluation Criteria for Correspondence Quality

To compare the results of the various correspondence methods, evaluation metrics are needed. The choice of evaluation metrics is important since the definition of a “good” correspondence can greatly vary among different applications. In this work, we are using the well established generalization and specificity metrics[6], based on the cortical thickness and sulcal depth measures. It should be noted that sulcal depth based evaluation is biased, since sulcal depth is used for optimization both by FreeSurfer and partially by our method. Cortical thickness based metrics provide an unbiased evaluation. We also use the mean variance (averaged across the surface) of cortical thickness and sulcal depth given the various correspondence results as an additional evaluation criterion.

Given a statistical shape model, generalization is a measure of how well the model can describe unseen objects of the same class. The generalization ability G(M) is computed by performing a leave-one-out principal components analysis (PCA), reconstructing the left-out object, and averaging the reconstruction error for each object, where M is the number of shape eigenmodes used in reconstruction. A good model should exhibit low generalization values.

Specificity is a metric of how well the model fits the object class, in that it measures the distance between measurements in the training set and new measurements generated using the model. A specific model should only generate measurements similar to those in the training set. The specificity S(M) is computed via generating a large number of random measurement vectors (such as cortical thickness) from the model PCA shape space and comparing them to the measurement vectors in the training set.

6 Results and Discussion

We applied our methodology to a dataset of 9 healthy subjects with 1.5T DTI scans as well as structural MRI scans. The DTI scans had 60 gradient directions and 10 baselines, with b = 700s/mm² and (2mm)³ voxel size. Cortical surfaces were reconstructed via FreeSurfer from T1 images that have been corrected for bias via the itkEMS tool using both T1 and T2 scans. No manual interventions were made to the FreeSurfer pipeline. Only left hemispheres were used.

We compare three methods of correspondence computation: FreeSurfer, xyz-based particle system, and connectivity-based particle system. For the latter, we used probabilistic connectivity measurements to the corpus callosum, the brainstem and the left caudate, with the ROI segmentations provided by FreeSurfer. We also use sulcal depth as an additional feature channel. Each feature channel was weighted such that the variance of the features across the population would have a mean value of 1.0 across the surface. This is necessary to prevent features with large absolute values (such as spatial location, typically in the range [-128..128]) from dominating the features with small absolute values (such as connectivity probabilities, in the range [0..1]).

In general, we expect our method to produce improved correspondence over certain regions (for instance, the ones that are strongly identifiable by fiber tract connections to subcortical regions chosen as ROI’s) and smaller improvement in other regions where no relevant additional local information is provided. The goal of our approach is to improve local cortical correspondence in given regions by using relevant data. Note that it would be up to each individual application to define what regions are important for the given context, and what additional data can be used to improve the correspondence in these critical regions.

In particular, for this study, since we observed fiber connections to the temporal lobe from both the corpus callosum and the left caudate, we expect to see significantly improved correspondence in this region. Therefore, in addition to the cortical thickness variance averaged across the entire surface, we also report the same values computed over the temporal lobe only.

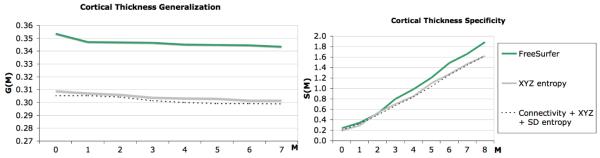
The results are summarized in Fig. 3. FreeSurfer yields a much tighter sulcal depth distribution than our method, which is to be expected as this is a biased evaluation metric. The sulcal depth based generalization and specificity plots (not shown) also show better results for FreeSurfer. However, the unbiased cortical thickness measurements show, as seen in Fig. 4, that the connectivity-based entropy system has better generalization and specificity properties, independent of the number of shape eigenmodes used (M). Our method also yields tighter cortical thickness distribution overall compared to both FreeSurfer and the spatial location based particle system. In particular, the correspondence quality was significantly enhanced in the temporal lobe, which appears to present a ‘problem area’ for the other two algorithms (as evidenced by higher than average cortical thickness variance). The incorporation of additional connectivity information clearly improves correspondence. Our results are also in agreement with the previous findings [4,5,6] that group-wise approaches tend to be more efficient than pair-wise correspondence optimization methods.

Fig. 3.

Average variances of cortical thickness and sulcal depth measurements across the whole cortical surface as well as across the temporal lobe, given different correspondence maps

Fig. 4.

Cortical thickness based generalization and specificity comparison. For both evaluation metrics, a lower value indicates a better correspondence. Therefore, we see that our method outperforms the other two algorithms regarding these two metrics.

7 Conclusion

We present a novel method that allows using data from diffusion weighted images along with structural MRI scans in a cortical correspondence setting. Our algorithm allows for the fiber connectivity information extracted from the DWI to be effectively projected on the cortical surface using a novel surface deflation technique. We then use our entropy-based dynamic particle framework to seamlessly integrate this information with geometrical cues, such as spatial location and sulcal depth, in order to improve cortical correspondence.

Our results illustrate the powerful generalizability of this technique: the user can improve the correspondence in all regions of the cortical surface, as long as strongly identifiable local features can be provided. Such local features can be extracted from structural images, DTI, or other imaging modalities such as magnetic resonance angiography (MRA). Future work includes exploring additional features to be used for this purpose as well as applying the technique to group analysis studies.