The Normalization Model of Attention

Abstract

Attention has been found to have a wide variety of effects on the responses of neurons in visual cortex. We describe a model of attention that exhibits each of these different forms of attentional modulation, depending on the stimulus conditions and the spread (or selectivity) of the attention field in the model. The model helps reconcile proposals that have been taken to represent alternative theories of attention. We argue that the variety and complexity of the results reported in the literature emerge from the variety of empirical protocols that were used, such that the results observed in any one experiment depended on the stimulus conditions and the subject’s attentional strategy, a notion that we define precisely in terms of the attention field in the model, but that has not typically been completely under experimental control.

Introduction

Attention has been known to play a central role in perception since the drawn of experimental psychology (James, 1890). Over the past 30 years, the neurophysiological basis of visual attention has become an active area of research, yielding an explosion of findings. Neuroscientists have utilized a variety of techniques (single-unit electrophysiology, electrical microstimulation, functional imaging, and visual-evoked potentials) to map the network of brain areas that mediate the allocation of attention (Corbetta and Shulman, 2002; Yantis and Serences, 2003) and to examine how attention modulates neuronal activity in visual cortex (Desimone and Duncan, 1995; Kastner and Ungerleider, 2000; Reynolds and Chelazzi, 2004). During the same period of time, the field of visual psychophysics has developed rigorous methods for measuring and characterizing the effects of attention on visual performance (Braun, 1998; Carrasco, 2006; Cavanagh and Alvarez, 2005; Sperling and Melchner, 1978; Verghese, 2001; Lu and Dosher, 2008).

We review the single-unit electrophysiology literature documenting the effects of attention on the responses of neurons in visual cortex, and we propose a computational model to unify the seemingly disparate variety of such effects. Some results are consistent with the appealingly simple proposal that attention increases neuronal responses multiplicatively by applying a fixed response gain factor (McAdams and Maunsell, 1999; Treue and Martinez-Trujillo, 1999), while others are more in keeping with a change in contrast gain (Li and Basso, 2008, Martinez-Trujillo and Treue, 2002; Reynolds et at., 2000) or with effects that are intermediate between response gain and contrast gain changes (Williford and Maunsell, 2006). Other studies have shown attention-dependent sharpening of neuronal tuning at the level of the individual neuron (Spitzer et al., 1988) or the neural population (Martinez-Trujillo and Treue, 2004). Still others have shown reductions in firing rate when attention was directed to a nonpreferred stimulus that was paired with a preferred stimulus also inside the receptive field (Moran and Desimone, 1985; Recanzone and Wurtz, 2000; Reynolds et al., 1999; Reynolds and Desimone, 2003). These different effects of attentional modulation have not previously been explained within the framework of a single computational model. We demonstrate here that a model of attention that incorporates divisive normalization (Heeger, 1992b) exhibits each of these different forms of attentional modulation, depending on the stimulus conditions and the spread (or selectivity) of the attentional feedback in the model.

In addition to unifying a range of experimental data within a common computational framework, the proposed model helps reconcile alternative theories of attention. Moran and Desimone (1985) proposed that attention operates by shrinking neuronal receptive fields around the attended stimulus. Desimone and Duncan (1995) proposed an alternative model, in which neurons representing different stimulus components compete and attention operates by biasing the competition in favor of neurons that encode the attended stimulus. It was later suggested that attention instead operates simply by scaling neuronal responses by a fixed gain factor (McAdams and Maunsell, 1999; Treue and Martinez-Trujillo, 1999). Treue and colleagues advanced the “feature-similarity gain principle,” that the gain factor depends on the match between a neuron’s stimulus selectivity and the features or locations being attended (Treue and Martinez-Trujillo, 1999; Martinez-Trujillo and Treue, 2004). Spitzer et al., 1988 proposed that attention sharpens neuronal tuning curves, and Martinez-Trujillo and Treue (2004) explained that sharpening is predicted by their “feature-similarity gain principle.” Finally, Reynolds et al., 2000 proposed that attention increases contrast gain. Indeed, the initial motivation for the model proposed here derived from the reported similarities between the effects of attention and contrast elevation on neuronal responses (Reynolds and Chelazzi, 2004; Reynolds et al., 1999,2000; Reynolds and Desimone, 2003).

The proposed normalization model of attention combines aspects of each of these proposals and exhibits all of these forms of attentional modulation. Thus, the various models outlined above are not mutually exclusive. Rather, they can all be expressed by a single, unifying computational principle. We propose that this computational principle endows the brain with the capacity to increase sensitivity to faint stimuli presented alone and to reduce the impact of task irrelevant distracters when multiple stimuli are presented. We argue that the ostensible variety and complexity of the results reported in the literature emerge from the variety of empirical protocols that were used, with the results observed in any one experiment depending on the stimulus conditions and the subject’s attentional strategy. Finally, we suggest that evolution may have co-opted previously existing normalization circuits in visual cortex, enabling attentional selection and its concomitant impact on behavioral performance.

The Normalization Model of Attention

The three basic components of the model are: the stimulation field, the suppressive field, and the attention field (a set of Matlab routines that constitute the model can be downloaded from the authors’ websites: http://www.snl-r.salk.edu/~reynolds/Normalization_Model_of_Attention/and http://www.cns.nyu.edu/heegerlab/). These components are described in detail below but we begin by providing an intuition for them. The responses of a population of neurons to a visual stimulus can be depicted as a “neural image” (Robson, 1980) in which the brightness at each image location corresponds to the response of one neuron. Figure 1 depicts such neural images representing each of the components of the model. In this simulation, two oriented grating stimuli were presented in the two halves of the visual field (i.e., in opposite hemifields), both with the same orientation. Neurons in visual cortex are highly selective for the spatial position of a visual stimulus, and for a particular combination of visual features (here, we use orientation as an example feature but other features or combinations of features could be used instead). The “stimulation field” of a neuron in the model characterizes its selectivity, both in terms of spatial position and orientation. The stimulation field is a theoretical concept that would be equivalent to a neuron’s receptive field only if there were neither suppression nor attention. Likewise, we use the term “stimulus drive” to represent what a neuron’s response would be due to the stimulation field alone, in the absence of suppression and attention. The response of a visual neuron to a preferred stimulus can be suppressed by the simultaneous presentation of nonpreferred stimuli. The “suppressive field” characterizes the spatial positions and features that contribute to this suppression. The suppressive field pools over a broader range of spatial locations and features (e.g., orientations) than the stimulation field. The suppression is divisive such that the stimulus drive from a preferred stimulus is normalized with respect to (divided by) the activity in other neurons that respond to the surrounding context. We use the term “suppressive drive” to represent the amount of suppression contributing to a neuron’s response for a particular stimulus and attentional state. The effect of attention is simulated in our model by taking the stimulus drive for the entire population of simulated neurons and multiplying it by an “attention field.” The attention field is specified in terms of its gain for each neuron in the population, i.e., in terms of its spatial and featural extents. The attention field is multiplied by the stimulus drive before normalization, so it affects both the stimulus drive and suppressive drive in determining the output firing rate of each simulated neuron.

Figure 1. Normalization Model of Attention.

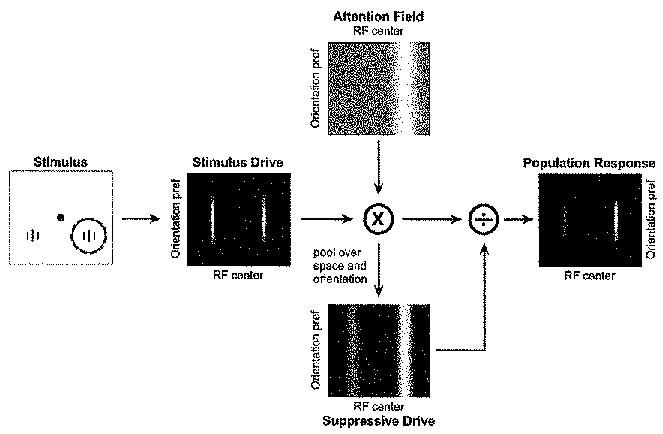
The stimulus drive is multiplied by the attention field and divided by the suppressive drive to yield the output firing rates. Left panel depicts the stimulus. A pair of vertically orientated gratings were presented as input to the model, identical in contrast, one in each hemifield. Central black dot, fixation point. Solid circle indicates the receptive field of a model neuron selective for vertical orientation and centered on the grating stimulus in the right hemifield. Dashed red circle indicates the attention field, which was centered on the stimulus on the right. Middle panel depicts the stimulus drive for a collection of neurons with different receptive field centers and orientation preferences. Neurons are organized according to their receptive field center (horizontal position) and preferred orientation (vertical position). Brightness at each location in the image corresponds to the stimulus drive to a single neuron. Top panel depicts the attention field when attending to the stimulus on the right (i,e., corresponding to the dashed red circle in She left panel). The attentional field is the strength of the attentional modulation as a function of receptive field center and orientation preference. Here, attentional gain varied as a function of stimulus position, without regard to orientation. Midgray indicates a value of 1 and white indicates a value greater than 1. The attention field is multiplied point-by-point with the stimulus drive. The suppressive drive (bottom panel) is computed from the product of the stimulus drive and the attention field, and then pooled over space and orientation. The panel on the right shows a neural image depicting the output firing rates of the population of neurons, computed by dividing the stimulus drive by the suppressive drive. The stimulus, stimulation field, suppressive field, and attention field all had Gaussian profiles in space and orientation.

The resulting simulated neural responses depend on the size of the stimulus (relative to the sizes of the stimulation field and suppressive field), the combination of features that make up the stimulus, the spatial extent of attention field, and the featural extent of the attention field. The core idea is that the attention field reshapes the distribution of activity across the population of neurons, shifting the balance between excitation and suppression. For example, consider the case (discussed in further detail below. Figure 4E) in which two stimuli are presented within a neuron’s receptive field, one moving in the model neuron’s preferred direction and the other in the nonpreferred (i.e., opposite) direction. Only the preferred direction contributes to the stimulus drive but both contribute to the suppressive drive such that the response of the neuron to the pair is less than it would be to the preferred direction on its own. Consider what happens when attending to the preferred direction. This multiplies the stimulus drive from the preferred direction stimulus in a manner that is equivalent to increasing its contrast. The suppression from the nonpreferred direction is now less effective because attention has shifted the balance of excitation and suppression in favor of the preferred direction, leading to a larger output firing rate. On the other hand, attending to the nonpreferred motion shifts the balance in favor of the nonpreferred stimulus, increasing its suppressive effect and leading to a smaller output firing rate.

Figure 4. Attentionat Modulation of Neuronal Contrast-Response Functions with Two Stimuli in the Receptive Field.

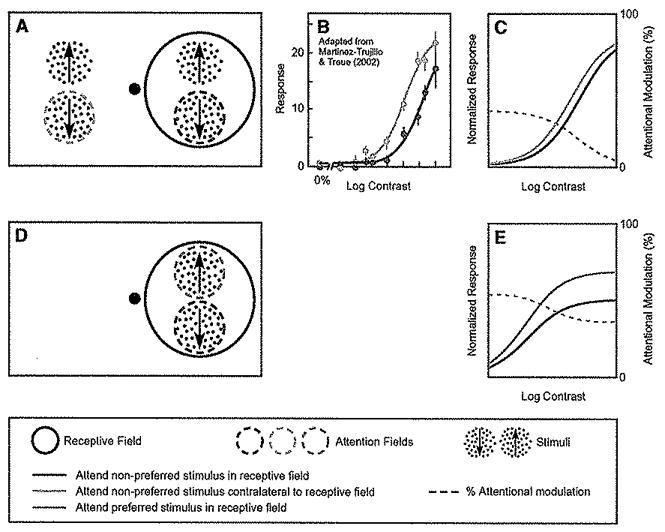
(A) Stimulus and task used by Martinez-Trujillo and Treue (2002) while recording in MT. The contrast of the preferred direction stimulus (indicated by the upward arrow) within the receptive field was systematically varied across trials, whereas the contrast of the nonpreferred stimulus (indicated by the downward arrow) was held fixed. The monkey was cued to attend either the nonpreferred stimulus in the receptive field (dashed red circle) or the stimulus in the opposite hemifield (dashed blue circle)

(B) Attention caused predominantly a change in contrast gain. Red curve and data points, responses as a function of contrast, when attention was directed to the nonpreferred stimulus in the receptive field. Blue curve and data points, responses to the Identical stimuli, when attending the opposite hemifield. Dashed gray curve, percentage increase in firing rate at each contrast.

(C)Model simulation exhibiting results similar to those observed experimentally.

(D) Complementary experiment with two stimuli placed within the receptive field, one preferred and the other nonpreferred. The contrasts of the two stimuli covaried (always identical to one another).

(E) Simulated neuronal responses were larger when attention was directed to the preferred-direction stimulus (green curve) than when it was directed to the nonpreferred stimulus (red curve). The effect of attention was approximated by a response gain change (multiplicative scaling). Simulation parameters were identical to those in (C) (Table 1).

The model is presented as a mathematical abstraction, without specifying the underlying biophysical mechanisms or neural circuitry. Although we list some possible mechanisms (see Discussion), detailing the biophysical mechanisms was very specifically not our goal. Indeed, we would argue that it is premature to follow a reductionist path toward characterizing the underlying mechanisms (especially without first demonstrating and testing the phenomenological validity of the model), and doing so could obscure the emergent simplicity of the phenomena (Laughlin, 2005). We use simulations to illustrate the qualitative properties of the model and its ability to account for patterns observed in experimental data. These are supplemented with mathematical derivations of limiting cases that clarify the reasons why the model exhibits these properties.

Stimulation Fields and Stimulus Drive

The stimulation field of a simulated neuron in our model is the range of spatial positions and orientations that can evoke an excitatory response. Consider a population of orientation-selective visual neurons (e.g., in visual cortical area V4), whose receptive fields cover the visual field. Each neuron can be characterized by its receptive field center and its orientation preference. We assume, for simplicity, that the response properties of these neurons are otherwise identical, that they ail have the same receptive field size and shape (i.e., ignoring cortical magnification) and identical orientation tuning curve bandwidths. Also for simplicity, we treat only one dimension of spatial position (e ., assuming that the neurons’ receptive fields are all centered along an arc of equal eccentricity). These simplifying assumptions are not strictly necessary but make it easier to describe the model. Figure 1 (middle panel) depicts an example of the stimulus drive for this simulated population of V4 neurons.

Suppressive Fields and Normalization

The suppressive field of a neuron in our model is the range of spatial positions and orientations that can suppress the response. Whereas the stimulus drive is assumed to be selective for feature and location, suppression is assumed to be largely nonspecific. As a result, a given stimulus can exert a suppressive effect on neurons tuned for other features or positions. This is consistent with data in V1, for example, where the responses to an optimally oriented stimulus are diminished by superimposing an orthogonal stimulus, that is ineffective in driving the cell when presented alone (Bauman and Bonds, 1991; Bonds, 1989; Carandini et al., 1997; Morrone et al., 1982). V1 neurons are likewise suppressed by stimuli at surrounding locations, extending beyond the stimulation field (Allman et al., 1985; Bair et al., 2003; Blakemore and Tobin, 1972; Cavanaugh et al., 2002a, 2002b; DeAngelis et al., 1994; Levitt and Lund, 1997; Nelson and Frost, 1985). Suppression can also be observed when a preferred and a nonpreferred stimulus are presented at separate locations within a neuron’s stimulation field (Reynolds and Desimone, 2003; Snowden et al., 1991). There is an extensive literature on such suppressive phenomena in V1 (for a review of the early literature, see Heeger, 1992b), in ventral stream areas V4 and IT (Miller et al., 1993; Missal et al., 1997; Reynolds et al., 1999; Richmond et al., 1983; Rolls and Tovee, 1995; Sato, 1989; Zoccolan et al., 2005), and in dorsal stream visual cortical areas MT and MST (Britten and Heuer, 1999; Recanzone et al., 1997; Treue et al., 2000).

The normalization model of visual cortical responses was introduced in the early 1990s to explain a variety of such suppressive phenomena evident in the response properties of V1 neurons (Albrecht and Geisler, 1991; Carandini and Heeger, 1994; Carandini et al., 1997; Heeger, 1991, 1992a, 1992b, 1993; Nestares and Heeger, 1997; Robson, 1988; Tolhurst and Heeger, 1997a, 1997b) and later extended to explain suppression in other visual cortical areas (Heeger et al., 1996; Simoncelli and Heeger, 1998). The normalization model posits that the stimulus drive is suppressed, effectively normalizing (dividing) the response of each neuron by the sum total stimulus drive across a population of neurons.

Normalization is computed by taking the stimulus drive (E) of each simulated neuron and dividing it by a constant (σ) plus the suppressive drive (S). The constant σ determines the contrast gain of the neuron’s response. The normalized responses are then subjected to a threshold (T), simulating the effect of spiking threshold, and the firing rate of the simulated neuron is taken to be proportional to the amount of response exceeding the threshold. This threshold model of spike generation, although oversimplified, is a reasonable approximation for the relationship between membrane potential fluctuation and firing rate (Anderson et al., 2000; Carandini, 2004a; Carandini and Ferster, 2000; Finn et al., 2007; Granit et al., 1963). The resulting firing rates (R) of the population of simulated neurons can be expressed as a function of the stimulus drive and suppressive drive:

$$\text{R}(\text{x},\theta )=\mid \text{E}(\text{x},\theta )/[\text{S}(\text{x},\theta )+\sigma ]{\mid }_{\text{T}},$$ (1)

where x and θ represent the receptive field centers and orientation preferences, respectively, of each neuron in the population, |·|_T indicates rectification with respect to the threshold T, and where S and σ are nonnegative. The suppression is pooled over spatial positions and orientations such that it can itself be expressed in terms of the stimulus drive. Specifically, for the simulations reported here, we computed the suppression from the stimulus drive (ignoring the effect of attention for the time being but see below), as an average over a range of receptive field centers and orientation preferences:

$$\text{S}(\text{x},\theta )=\text{s}(\text{x},\theta )\ast \text{E}(\text{x},\theta ),$$ (2)

where s(x, θ) is the suppressive field (i.e., the extent of pooling over space and orientation) and * is convolution. Figure 1 (bottom panel) shows an example of the suppressive drive. We have assumed for our simulations that the spatial pooling in the suppressive field is independent of orientation and vice versa (i.e., separable convolution), although that need not be the case. We have also assumed that the integral of s(x, θ) equals 1. The final normalized responses (i.e., the output firing rates) are also shown in Figure 1 (right panel).

The resulting normalized responses can be expressed in terms of stimulus contrast:

$$\begin{array}{c}\text{R}(\text{c};\text{x},\theta )=\mid \text{E}(\text{x},\theta ;\text{c})/[\text{s}(\text{x},\theta )\ast \text{E}(\text{x},\theta ;\text{c})+\sigma ]{\mid }_{\text{T}}\\ \text{r}(\text{c})=\alpha \text{c}/(\text{c}+\sigma ),\end{array}$$ (3)

where c is stimulus contrast and E(x, θ; c) is the stimulus drive of the population of neurons evoked by contrast c. For the case considered here in which the stimulus drive is a linear summation of the visual stimulus contrast, E(x, θ; c) is proportional to c. The contrast-response function, r(c) = R(c; x, θ), is the output firing rate as a function of contrast for a single neuron in the population with x and θ representing, respectively, its receptive field center and orientation preference, and with the stimulus centered in its receptive field. We use the simplified notation, r(c), instead of R(c; x, θ), because each neuron in the population exhibits a similar dependence on contrast, and to draw a distinction between the collected responses of a population of neurons represented by capital R and the responses of a single neuron represented by lower case r. The response gain, α, determines the maximum attainable response. Factors that affect α include the stimulus orientation and location relative to the preferred orientation and receptive field center of the simulated neuron. The contrast gain, σ, determines the contrast at which the response achieves half the maximum. The resulting neural responses saturate (level off) at high stimulus contrasts, due to normalization, regardless of whether the high contrast stimulus is preferred or nonpreferred (Heeger, 1991; Heeger, 1992b), in agreement with experimental results (Albrecht and Hamilton, 1982). That is, when the contrast is high (c ≫ σ), the responses are approximated by r(c) ≈ α. Depending on the choice of threshold, the rectification can approximate a power law such that c in the above equation gets replaced with cⁿ (Anderson et al., 2000; Finn et al., 2007). This yields a contrast-response function with a steeper slope at the rising part of the curve and more complete saturation at high contrasts. For the purposes of this paper, the simulations were performed with an exponent of 1 but higher exponents would be needed to fit electrophysiological measurements.

The balance between stimulus drive and suppressive drive in the normalization model depends on stimulus size. A large stimulus (e.g., an oriented grating pattern covering the entire visual field) fills both the stimulation and suppressive fields and hence evokes equal excitation and suppression (because the integral of s(x, θ) equals 1, as noted above). A small stimulus, on the other hand, can evoke a strong stimulus drive but a relatively weak suppressive drive. This can be expressed as a modification of Equation 3:

$$\text{r}(\text{c})=\alpha \text{c}/(\text{c}+\beta {\text{c}}_{\text{s}}+\sigma ),$$ (4)

where c is the contrast of a center stimulus, c_s is the contrast of a surround stimulus, and β is a scale factor (between 0 and 1) on the suppression from the surround stimulus. Making a stimulus smaller is equivalent to setting the surround contrast to zero which decreases the suppressive drive. Increasing the size of the stimulus by making c_s nonzero increases the suppression which decreases the output firing rate. As an aside, we note that this model predicts an interaction between contrast and stimulus size (Cavanaugh et al., 2002a), thereby explaining the observation that neurons prefer smaller stimuli at higher contrasts (Kapadia et al., 1999; Sceniak et al., 1999). We rely on an analogous shift in the balance between excitation and suppression to explain how attention can yield a change in either contrast gain or response gain depending on the stimulus size and the spatial extent of the attention field (see below).

Attention Fields and Attentional Gain

The effect of attention is simulated in our model by taking the stimulus drive across the population of neurons and multiplying it point-by-point by an attention field (Figure 1). In its simplest form, the attention field is 1 everywhere except for a small range of spatial positions and feature values where the attentional gain is greater than 1 (Figure 1, top panel). Its effect in our model is to multiply the stimulus drive, which is then inherited by the suppressive drive:

$$\text{R}(\text{x},\theta )=\mid [\text{A}(\text{x},\theta )\text{E}(\text{x},\theta )]/[\text{S}(\text{x},\theta )+\sigma ]{\mid }_{\text{T}}$$ (5)

$$\text{S}(\text{x},\theta )=\text{s}(\text{x},\theta )\ast [\text{A}(\text{x},\theta )\text{E}(\text{x},\theta )],$$ (6)

where A(x, θ) is the attention field. Applying the attention field in the model can yield either a change in response gain, a change in contrast gain, or a combination of the two, depending on the stimulus size and the extent of the attention field relative to the sizes of the stimulation and suppressive fields.

First, consider a case in which the stimulus is small and the attention field is large (Figure 2A). The responses of a model neuron can be approximated as:

$$\begin{array}{c}\text{R}(\text{c};\text{x},\theta )=\mid \gamma \text{E}(\text{x},\theta ;\text{c})/[\text{s}(\text{x},\theta )\ast (\gamma \text{E}(\text{x},\theta ;\text{c}))+\sigma ]{\mid }_{\text{T}}\\ \text{r}(\text{c})=\alpha (\gamma \text{c)}/(\gamma \text{c}+\sigma )\\ =\alpha \text{c}/(\text{c}+\sigma /\gamma ),\end{array}$$ (7)

where γ > 1 is the peak gain of the attention field, and the other symbols are defined above. The attention field A(x, θ) can be approximated by the constant γ in Equation 7 because the attention field is assumed to be large; this approximation would be exact if the attention field was constant for all x and θ. Under these conditions, the effect of attention is simply to multiply the stimulus drive by a constant, which predicts a pure change in contrast gain by a factor of γ. This appears as a leftward shift of the contrast-response function, plotting responses versus the logarithm of contrast (Figure 2A). In other words, the attentional modulation (percentage change in response when the stimulus is attended) is larger for contrasts corresponding to the rising portion of the neuron’s contrast-response function than for saturating contrasts (Figure 2A, dashed gray curve).

Figure 2. The Normalization Model of Attention Exhibits Qualitatively Different Forms of Attentional Modulation, Depending on the Stimulus Size and the Size of the Attention Field.

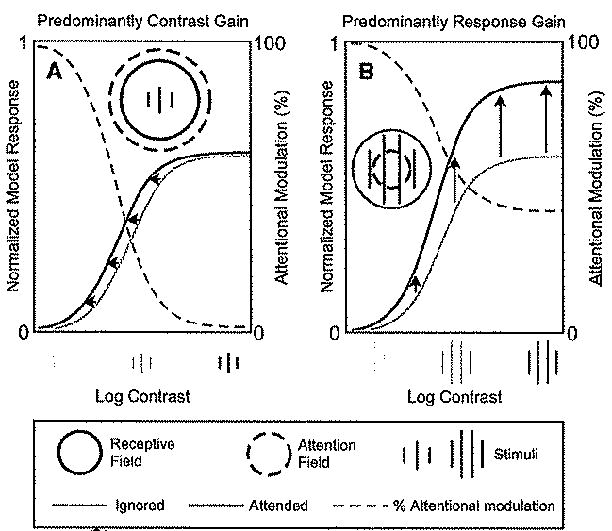
Each panel shows contrast-response functions for a simulated neuron, when attending to a stimulus within the neuron’s receptive field and when attending to a stimulus in the opposite hemifield.

(A) Contrast gain for small stimulus size and large attention field. Red curve, simulated responses as a function of contrast when the stimulus in the receptive field was attended. Blue curve, responses when attending toward the opposite hemifield. Attentional modulation is indicated by the dashed gray curve, which quantifies the percentage increase in the responses when the stimulus within the neuron’s receptive field was attended versus not. The stimulus was 0.6 times the size to the stimulation field and the attention field was six times the size of the stimulation field (not drawn to scale, see Table 1 for simulation parameters).

(B) Response gain for larger stimulus size and smaller attention field. In comparison to (A), the stimulus size was 5/3 larger (i.e., equal to the size of the stimulation field) and the attention field was 10 times smaller (i.e., about 2/3 the size of the stimulation field). All other model parameters were identical in both panels (Table 1).

Next, consider the case in which the stimulus is large (e.g., filling both the stimulation and suppressive fields) and the attention field is small relative to the suppressive field (Figure 2B). In this case, the attention field not only multiplies the stimulus drive but also changes the effective spatial spread of the stimulus drive akin to making the stimulus smaller. The responses of a model neuron, with the stimulus and the attention field centered on its receptive field, can be approximated as:

$$\text{r}(\text{c})=\alpha (\gamma \text{c})/(\gamma \text{c}+\beta \text{c}+\sigma ),$$ (8)

where γ > 1 is the peak gain of the attention field, 0 < β < 1 is a scale factor on the suppressive drive from the region surrounding the stimulation field (see Equation 4), and the surround contrast (c_s in Equation 4) equals the center contrast (c_s = c). The attentional gain, γ, is multiplied only by the center contrast because the attention field is small; this approximation would be exact if A(x, θ) = γ only for the neuron being recorded and 1 for all other receptive field centers and orientation preferences. For low contrasts (c ≪ σ), Equation 8 is approximated by r(c) ≈ α γ c/σ, such that increasing γ simply scales the predicted responses. For high contrasts (c ≫ σ), Equation 8 is approximated by r(c) ≈ α γ′, where γ′ = γ/(γ + β), which is independent of c because the responses saturate at high contrasts. But again, increasing γ predicts larger responses. Figure 2B shows a simulation result that approaches the limit of a pure response gain, using a relatively large stimulus and a small attention field. The contrast-response function is shifted upward (not leftward), and the attentional modulation is large across the full range of contrasts (Figure 2B, dashed gray curve). For the simulations in Figures 2A and 2B, only the stimulus size and the attention field size differed; all other model parameters were the same (Table 1).

Table 1.

Model Parameters

Figure Panel	Stimulus	Attention Field		Baseline
	Size	Size	Tuning Width (Deg)	Peak	Mod	Unmod
1	3	30	–	2
2A	3	30	–	2
2B	5	3	–	2
3C	5	30	–	2	X	X
3F	7	7	–	2	X
4C	5	5	20	5
4E	5	5	20	5
5C	10	10	–	2
6C	10	30	60*	2
7C	5	5	45*	5

Stimuli and attention fields varied across simulations, as listed in the table. Spatial sizes are in arbitrary units; only the relative values are meaningful For simulations with two or more stimuli, all had the same size. For all simulations, the size of the stimulation field was 5 and the size of the suppressive field was 20. Orientation and direction tuning curves were Gaussian functions; tuning widths are listed in degrees corresponding to the standard deviation of the Gaussian. For simulations of experiments in V4, involving oriented grating stimuli, the orientation tuning width of the stimulation field was 30° and the tuning width of the suppressive field was 180°. For simulations of experiments in MT/MST involving moving stimuli, these values were doubled to cover 360° of motion directions. A dash (−) for the attention field tuning width means that all orientations or directions were attended equally. An asterisk (*) for Figures 6C and 7C means that the attention field tuning width was as listed when attending the moving stimuli, but was unselective (all directions attended equally) when attention was directed to the fixation point. Baseline activity added to the stimulus drive was modulated by attention (marked by X under “Mod”). Baseline activity added after normalization was not modulated by attention (marked by X under “Unmod”).

A combination of response gain and contrast gain can also be realized by an appropriate choice of stimulus size and attention field size (see below, Figure 3F). Feature-based attention can give rise to analogous effects, depending on the number of different feature values (e.g., orientations) in the stimulus, and the featural extent of the attention field (i.e., the range of orientations attended) relative to that of the stimulation and suppressive fields (see below, Figure 4).

Figure 3. Attentional Modulation of Neuronal Contrast-Response Functions.

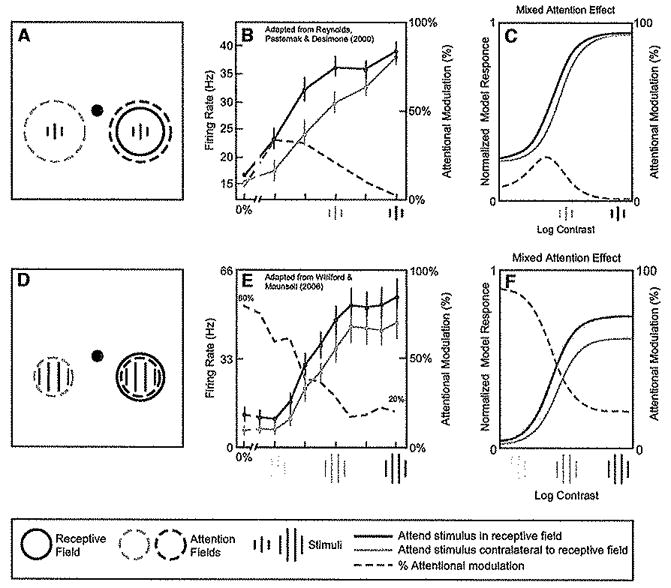
(A) Stimulus and task used by Reynolds et al. (2000) while recording neural activity in V4. Sequences of gratings were presented to the left and right visual fields, ons of which was positioned within the receptive field of the recorded neuron. Monkeys were cued to attend either to the stimulus sequence in the receptive field (dashed red circle) or the stimulus sequence in the opposite hemifield (dashed blue circle), to detect a target that appeared in the sequence.

(B) Attention caused the largest percentage increase in firing rates at low contrast (adapted from Reynolds et al., 2000). Red curve and data points, responses as a function of contrast, when attention was directed to stimuli in the receptive field. Blue curve and data points, responses to the identical stimuli when unattended. Dashed gray curve, percentage increase in firing rate at each contrast.

(C) Normalization model of attention can exhibit similar results. Stimuli, receptive fields, and attention fields are not drawn to scale; Simulation parameters are listed in Table 1.

(D) Stimulus and task used in a similar experiment by Williford and Maunsell (2006), also while recording in V4.

(E) Attention caused neither a pure contrast gain change nor a pure response gain change (adapted from Williford and Maunsell, 2006), Rather, the greatest percentage Increase in firing rates was at low contrasts (dashed gray curve), but with the largest absolute increase in firing rates at high contrasts {compare red and blue curves).

(F) Normalization model of attention can exhibit similar results. The simulation was identical to that in (C) except (1) the stimttius was larger and attention field was smaller and (2) additional baseline activity was added for (C) (see Table 1).

In principle, the attention field can have any number of possible distributions over space and feature dimensions, each corresponding to a different behavioral “strategy.” Both the spatial extent and the featural extent (range of orientations) of the attention field can vary depending on the stimulus and task. The attention field could also, in principle, be less than 1 for some spatial locations and orientations leading to suppression at unattended locations (although this is not necessary to account for attentional suppression, which is mediated naturally through the suppressive field). The attention field need not be unimodal; multiple peaks would simulate attending to multiple locations simultaneously (Cavanagh and Alvarez, 2005; McMains and Somers, 2004; Mitchell et al., 2007). The attention field can be narrow in space and broad in orientation (spatial attention), or it can instead be narrow in orientation and broad in space (feature-based attention). The spatial extent of the attention field is related to the spatial bias in the biased competition model of attention (Desimone and Duncan, 1995). It is also related to the “spotlight” (Posner et al., 1980) or “zoom lens” in descriptive models of attention (Eriksen and St. James, 1986; Eriksen and Yeh, 1985). The featural extent of the attention field is related to the feature bias in the biased competition model and to the “feature-similarity gain principle” that has been proposed as a model for the effects of feature-based attention (Boynton, 2005; Martinez-Trujillo and Treue, 2004; Treue and Martinez-Trujillo, 1999). However, the attention field differs from the feature-similarity gain principle, in that the effect of attention in our model does not directly alter firing rate by a scaling factor, being instead mediated through the normalization computation.

A Unified Account of Attentionai Modulation of the Contrast-Response Function

We begin by considering three studies that have measured the effect of attention as a function of contrast. Two of these were conducted in macaque area V4 with a single stimulus inside the receptive field (Reynolds et al., 2000; Williford and Maunsell, 2006). The third study (Martinez-Trujllio and Treue, 2002), which was conducted in macaque area MT with two stimuli in the receptive field, is discussed below, in the first of these studies (Reynolds et al., 2000), the monkey was cued to attend either to a sequence of grating stimuli within the receptive field, or on separate trials, to a location in the opposite hemifield (Figure 3A). The animal’s task was to detect a differently oriented target at the cued location. Figure 3B shows the average responses of 39 neurons that were modulated by attention, plotted as a function of contrast. Contrasts were selected for each neuron such that the lowest nonzero contrast was below the neuron’s contrast threshold, when attention was directed away from the receptive field stimulus, and the highest contrast tested was at or above saturating contrast. Consistent with the idea that attention changes contrast gain, this study found that there was a reduction in contrast threshold, only modest attention effects at high contrast, and large attention-dependent increases in firing rates at intermediate contrasts (Figure 3B, dashed gray curve).

Williford and Maunsell (2006) used a similar stimulus and task (Figure 3D) but found more substantial increases in firing rates at high contrasts (Figure 3E), A key subset of the data, shown in the figure, corresponded to those neurons with responses that saturated at high contrasts, because those neurons had the potential to distinguish between changes in contrast gain (for which the largest attention effects would be evident at intermediate contrasts) and response gain (for which the largest effects would be evident at the highest contrasts). Attention did not simply modulate contrast gain; there were substantial increases in firing rates at the highest contrasts. Nor were the data consistent with a pure response gain change, as attention did not have a fixed muitiplicative effect on firing rates across contrasts. Rather, the effect of attention was a monotonieally decreasing function of contrast, from ~80% at low contrasts to ~20% at high contrasts (Figure 3E, dashed gray curve).

How can these data, which differ from each other, be reconciled, and what are their implications for models of attention? Contrast gain and response gain are both properties of the normalization model of attention (Figures 2A and 2B, respectively). The model can also yield effects that are intermediate between contrast gain and response gain. The particular result obtained with the model depends on several factors, including the size of the stimulus and the size of the attention field, both relative to the sizes of the stimulation and suppressive fields. With a small stimulus and a large attention field, the model predicts results (Figure 3C) like those reported by Reynolds et al, (2000). By changing the size of the stimulus and the size of the attention field (such that both are roughly equal in size to the stimulation field), the model predictions (Figures 3F) are similar to the observations of Williford and Maunsell (2006). Therefore, the normalization model of attention is, in principle, consistent with the results from both of these experiments.

Although no attempt was made to fit the data, the model parameters were adjusted to produce simulation results in Figures 3C and 3F that resembled the experimental results. In particular, baseline activity was added to the model simulations. A small baseline was added to the stimulus drive, for both Figures 3C and 3F, assuming that attention modulates spontaneous activity from afferent neurons just as it is assumed to modulate stimulus-evoked activity. This resulted in an attention-dependent elevation in the baseline firing rates of the simulated neurons, as has been reported both in single-unit electrophysiology and fMRI studies (Chawla et al., 1999; Haenny et al., 1988; Kastner et al., 1999; Luck et al., 1997; Offert et al., 2008; Ress et al., 2000; Reynolds et al., 2000; Silver et al., 2007). For Figure 3C, an additional baseline response was added after normaiization, yielding a component of spontaneous activity that was not modulated by attention. Both of these components of baseline activity were small, but they were needed so that the simulations exhibited attentional modulation as a function of contrast (Figures 3C and 3F, dashed gray curves) like that observed in the experimental results (Figures 3B and 3E, dashed gray curves). Other than the stimulus size, attention field size, and the unmodulated component of the baseline activity, the rest of the simulation parameters were identical (Table 1).

These model simulations suggest that the experimental results might have differed in these two studies primarily because of differences in the stimulus and attention field sizes. In support of this suggestion, the stimulus sizes were different from one another in the two studies. Reynolds et al. (2000) used small (0.4° × 1.5°–2°) stimuli such that most of the contrast energy was concentrated with a small region of visual space and recorded from neurons with relatively large receptive fields (centered in peripheral regions of the visual field). Williford and Maunsell (2006) instead matched the stimulus sizes to the receptive fields, filling the classical receptive fields with grating patches. Therefore, their stimuli were larger, with respect to the receptive fields, than those used in the earlier study. We speculate that the attentional strategy may also have been different. In the Reynolds et al. study, monkeys maintained fixation throughout the trial and released a manual lever upon appearance of the target. The monkeys in Williford and Maunsell’s task were required to maintain fixation while planning an accurate saccade to the target. Given the evidence that the oculomotor system provides attentional feedback signals (Cavanaugh and Wurtz, 2004; Ekstrom et al., 2008; Moore and Armstrong, 2003; Moore and Fallah, 2001; Muller et al., 2005; Winkowski and Knudsen, 2008), the requirement to saccade accurately to the target in the Williford and Maunsell study might plausibly have caused the attention fields to be more narrowly focused in their study than in the Reynolds et al, study. Additional experiments will be needed to determine if these factors account for the observed differences, specifically designed to control the animal’s attentional strategy (i.e., the spatial extent of the attention field).

Attentional Modulation of the Contrast-Response Function with Two Stimuli in the Receptive Field

Martinez-Trujillo and Treue (2002) measured contrast-response functions in macaque area MT with two stimuli in the receptive field (Figure 4A). One stimulus moved in the preferred direction and the other moved in the nonpreferred (opposite) direction. The contrast of the preferred direction stimulus within the receptive field was systematically varied across trials, whereas the contrast of the nonpreferred stimulus was held fixed. There were also two stimuli placed at a symmetrical location in the opposite hemifield, with the same two directions of motion. The monkey’s task was to detect a change in speed or direction of one of the stimuli. The monkey was cued on half the trials to attend to the nonpreferred stimulus within the receptive field, while ignoring the other three stimuli. On other half, the monkey was cued to attend to the stimulus in the opposite hemifield moving in the same direction of motion as the nonpreferred stimulus. In other words, the contrast-response function of the preferred stimulus was measured under two attentional states, both of which involved attending to the nonpreferred direction of motion, either at a location within the receptive field or at a distant (opposite hemifield) location. Martinez-Trujillo and Treue (2002) reported predominantly a change in contrast gain (Figure 4B).

Similar results can be achieved with the normalization model of attention (Figure 4C). The reason for this is that attending to the nonpreferred stimulus increases only the suppressive drive. Because the contrast of the nonpreferred stimulus was fixed, this increase in suppressive drive is the same for all stimulus conditions. This is equivalent to adding a constant to the denominator, i.e., changing the contrast gain (see Supplemental Material available online for derivation).

The model exhibits a very different pattern of behavior if we slightly alter the stimuli and task as illustrated in Figure 4D. In this simulation, attention was directed to one of the two stimuli within the receptive field, either the preferred stimulus or the non-preferred stimulus. The contrasts of the preferred and nonpreferred stimuli covaried from trial to trial, so they were always identical to one another. Figure 4E shows the result of simulating this experiment; the contrast-response function when attending to the preferred stimulus (Figure 4E, green curve) was approximately a scaled copy of that observed when attention was instead directed to the nonpreferred stimulus (Figure 4E, red curve). The model predicts predominantly a response gain change under these conditions (see Supplemental Material for derivation) because attending to the preferred versus nonpreferred stimulus shifts the balance of excitation and suppression in a manner that is directly analogous to the effect of spatial attention with a large stimulus and small attention field (Figure 2B and Equation 8). Here, the stimulus is large in its featural extent (including opposite motion directions) instead of being large in space, and the attention field is small in its featural extent (focusing on one of the two motion directions) instead of being small in space. This prediction of the model could be tested by conducting both experiments and making within-cell comparisons of the effects of attention on contrast response functions.

Spatial Attention and Multiplicative Scaling of Neuronal Tuning Curves

One of the most well-studied forms of attentional modulation, which helped motivate the proposal that attention simply scales firing rates, is attention-dependent scaling of neuronai tuning. Motter (1993) recorded neuronal responses in macaque areas V1, V2, and V4 to stimuli that varied in orientation. He found that directing attention to the stimulus in the receptive field often increased neuronal firing rates and that this increase tended to be largest for stimuli presented near the peak of the neuron’s orientation tuning curve. In a now classic study, McAdams and Maunsell (1999) quantified this effect in area V4 using the experimental protocol illustrated in Figure 5A. On some trials, monkeys attended to a grating in the receptive field of the recorded neuron, to report whether two successive gratings were identical or differed in orientation by 90°. On other trials, attention was instead directed to a colored blob appearing in the opposite hemifield, to report whether successive stimuli differed in color. The grating orientation was varied from one trial to the next, to measure a full orientation-tuning curve for trials in which the grating was either attended or ignored. McAdams and Maunsell (1999) measured the neuron’s orientation tuning curve and examined how it changed with attention. Consistent with Motter’s earlier report, they found that attention scaled the orientation tuning curve, without changing its width (Figure 5B). Treue and Martinez-Trujillo (1999) found a similar result in area MT for direction tuning. This elegant experiment focused primarily on feature-based attention, as opposed to spatial attention, but they also quantified the effect of spatial attention after carefully controlling for any effects of feature-based attention, and found that spatial attention scaled neuronal tuning curves.

Figure 5. Spatial Attention Causes a Multiplicative Scaling of Tuning Curves.

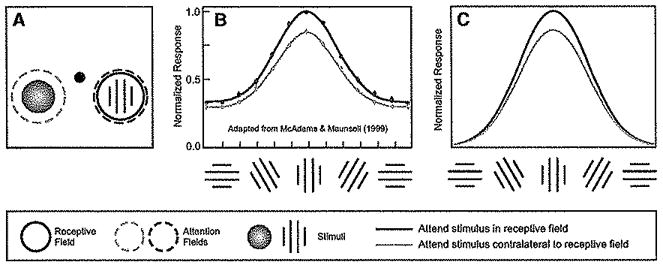
(A) Stimulus and task. On some trials, monkeys attended to the grating in the receptive field of the neuron being recorded (dashed red circle) to report whether two successive gratings were Identical or differed in orientation by 90°. On other trials, attention was instead directed to a colored blob appearing in the opposite hemifield (dashed blue circle) to report whether successive stimuli differed in color.

(B) Orientation tuning curves averaged across a population of V4 neurons, with and without attention (adapted from McAdams and Maunsell, 1999). These curves were obtained by fitting each neuron’s tuning curve with a Gaussian, shifting the neuron’s preferred orientation to align all tuning curves and then averaging the Gaussian fits. Red indicates orientation tuning when attention was directed to stimuli in she receptive field, to perform the orientation discrimination task. Blue, orientation tuning when attention was directed away from the receptive field to perform the color discrimination task. (C) Model simulation yielded similar results; multiplicative scaling of the tuning curve when spatial attention was directed to a stimulus in the receptive field. See Table 1 for simulation parameters.

The normalization model of attention accounts for this scaling naturally (Figure 5C). The normalization component of the model has, in fact, been used to account for an analogous finding, scaling of tuning curves with increasing contrast (Heeger, 1992b; Reynolds and Chelazzi, 2004). The attention field in this simulation was broad (unselective) for orientation, so the attentional gain depended only on spatial position (as in Figure 1, top panel). In addition, the suppressive field was broad in orientation. Because of this, the responses of the simulated neurons can be approximated as a product of two functions, one that depends on contrast (the contrast-response function) and the other that depends on orientation (the orientation tuning curve). Attending to stimuli in the receptive field produced a larger contrast gain but with no effect on the shape of the orientation turning curve, such that the simulated responses were a multiplicatively scaled copy of the orientation tuning curve (see Supplemental Material for derivation).

Feature-Based Attention and Nonmultiplicative Scaling of Neuronal Tuning

Spitzer, Desimone, and Moran (Spitzer et al., 1988) proposed that attention can alter the sharpness of orientation tuning. Monkeys were trained to perform an orientation discrimination task. Spitzer and colleagues recorded neuronal responses in macaque area V4 as monkeys performed two versions of the task: an easy version in which the animals had to discriminate large orientation differences (45°) and a hard version in which the orientation differences were smaller (22.5°). They found in the more difficult task that neuronal responses were larger, and that orientation tuning was narrower. McAdams and Maunsell (1999) noted that this finding was inconsistent with their observation that attention scales orientation tuning curves in V4.

However, a pair of studies conducted by Martinez-Trujillo and Treue suggests that this discrepancy may be attributable to differences in attentional strategy. In one study (Treue and Martinez-Trujillo, 1999), feature-based attention was matched across conditions and they found a multiplicative scaling of tuning. A subsequent study (Martinez-Trujillo and Treue, 2004) varied feature-based attention and concluded that attention increased the gain of neurons tuned for the attended direction of motion while decreasing the gain of neurons for which the attended direction was nonpreferred. They concluded that this sharpened the pattern of activity across the population of neurons with receptive fields centered on the stimulus. The experimental protocol is illustrated in Figure 6A. A pair of stimuli were presented simultaneously while recording responses of a neuron in visual cortical area MT. One of the stimuli was in the receptive field of the recorded neuron and the other was in the opposite hemifield. The two stimuli moved in the same direction on each trial, but this motion direction varied from trial to trial. Spatial attention was controlled by directing the monkey to attend on all trials away from the receptive field stimulus, either to the fixation point, or to the stimulus in the opposite hemifield from the receptive field. With spatial attention under control, the effect of manipulating feature-based attention was measured. On half the trials, feature-based attention was directed to a motion direction defined by the stimulus in the opposite hemifield, which matched the direction of motion inside the receptive field. On the other half, monkeys were cued to attend the fixation point, i.e., to ignore the direction of motion. Consistent with earlier reports of feature-based attention (Chelazzi et al., 1993, 1998; Haenny et al., 1988; Haenny and Schiller, 1988; Maunsell et al., 1991; Motter, 1994a, 1994b; Treue and Martinez-Trujillo, 1999), responses were elevated when feature-based attention was directed to a stimulus moving in the neuron’s preferred direction of motion and reduced when attention was directed to the opposite (nonpreferred) direction (Figure 6B).

Figure 6. Feature-Based Attention Can Cause a Sharpening of Tuning Curves.

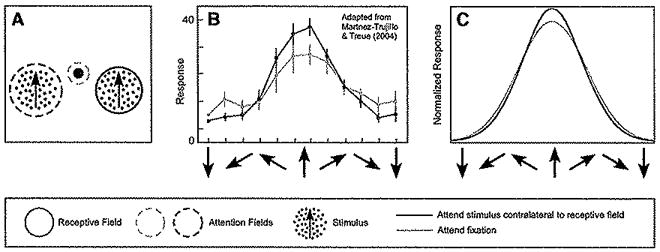
(A) Stimulus and task. A pair of stimuli were presented simultaneously while recording responses of a neuron in visual cortical area MT. One stimulus was in the receptive field of the recorded neuron and the other was in the opposite hemifield. The directions of the two stimuli were yoked. The monkey was cued to attend either to the fixation point (dashed blue circle), or to the stimulus in the opposite hemifield (dashed red circle) to detect a change in speed or direction. That is, spatial attention was always directed away from the receptive field, but feature-based attention was matched to the stimulus in the receptive field on half the trials.

(B) Feature-based attention caused a sharpening of motion direction tuning (adapted from Martinez-Trujillo and Treue, 2004). Blue, responses when attention was directed to the fixation point. Red, responses when attention was directed to the stimulus in the opposite hemifield.

(C) Model simulations yielded similar results. Blue, responses of a model neuron when the attention field was flat (equal) for all motion directions, and spatial attention was directed away from the model neuron’s receptive field. Red, responses when attention was again directed away from the simulated neuron’s receptive field but to the same direction of motion as the stimulus in the receptive field. See Table 1 for simulation parameters.

The model can exhibit a comparable increase in responses when attending the neuron’s preferred stimulus, and a reduction in responses when attending the opposite (nonpreferred) stimulus. This is illustrated in Figure 6C, which shows the pattern of activity across the population of neurons with receptive fields centered on the stimulus in the right hemifield but tuned to all different motion directions, or equivalently the tuning curve of one neuron in response to all different motion directions. To simulate attention to the fixation point, the attention field was selective for the location of the fixation point, but was unselective for motion direction. To simulate attention to the moving stimulus, feature-based attention was assumed to be spatially invariant, and spatial attention was assumed to be invariant to motion direction. This corresponded to a cross-shaped attention field, with a peak at the attended location extending over all motion directions and a superimposed peak at the attended motion direction that extended over all positions. With feature-based attention restricted to a direction of motion that matched that of the stimulus in the receptive field, tuning was narrower because the stimulus drive was multiplied by the attention field which was itself selective for motion direction (see Supplemental material for derivation).

The model thus offers a way to reconcile different conclusions that have been reached about whether attention simply scales firing rates or sharpens tuning curves. The predictions of the model depend on the attentional strategy that is used to perform a given task. A purely spatial attention strategy, in the model, corresponds to an attention field that is constant (flat) across feature dimensions (orientation, direction of motion, etc.) but selective for spatial position. This causes a simple scaling of tuning curves (Figure 5). A purely feature-based attention strategy corresponds to an attention field that is selective for a feature but not selective for spatial position. This causes a sharpening of tuning (Figure 6). These different attention strategies yield different results, underlining the importance of controlling task strategy, as was done in the two Treue and Martinez-Trujillo studies.

Attentional Modulation of Tuning Curves with Two Stimuli in the Receptive Field

If two stimuli appear simultaneously within a neuron’s receptive field the response to the pair is substantially stronger when attention is directed to the more preferred of the two stimuli, as compared to when the nonpreferred stimulus is attended. Moran and Desimone (1985) first reported this when recording in areas V1, V2, V4, and TEO. This finding was subsequently replicated in area MT (Treue and Martinez-Trujillo, 1999; Treue and Maunsell, 1996) and in V2 and V4 (Ghose and Maunsell, 2008; Luck et al., 1997; Reynolds et al., 1999).

Reynolds, Chelazzi and Desimone (Reynolds et al., 1999) proposed an early version of the normalization model of attention to account for their observations and conducted experiments to test a key prediction of the model. Consistent with the model, they found that when a preferred stimulus was paired with a non-preferred stimulus, the nonpreferred stimulus typically suppressed responses to the preferred stimulus. Critically, when attention was directed to the nonpreferred stimulus, this increased the suppression in a manner that was similar to that resulting from elevating the contrast of the nonpreferred stimulus. Reynolds and Desimone (2003) took this a step further by showing, also consistent with the predictions of normalization, that the magnitude of suppression increased with the contrast of the nonpreferred stimulus. Ghose and Maunsell (2008) carried out similar experiments that replicated and extended the core findings of Reynolds, Chelazzi, and Desimone (Reynolds et al., 1999), and proposed a similar normalization model to account for their findings.

Treue and Martinez-Trujillo conducted an elegant experiment that examined attentional modulation with two stimuli in the receptive field (Figure 7). One stimulus was a nonpreferred stimulus for the MT neuron that was being recorded. The other stimulus varied across the full range of motion directions and was thus typically the more preferred stimulus of the two. Attention was directed either to the fixation point or to one of the two stimuli in the receptive field (Figure 7A). Responses were smaller when attending the nonpreferred stimulus (Figure 7B, blue curve) relative to the neutral (attending fixation) condition (Figure 7B, yellow curve). Responses were larger when attention was directed to the stimulus that varied in its motion direction with the largest responses when the stimulus moved in the preferred direction (Figure 7B, red curve).

Figure 7. Attentional Modulation of Tuning when Two Stimuli Are Present within the Receptive Field.

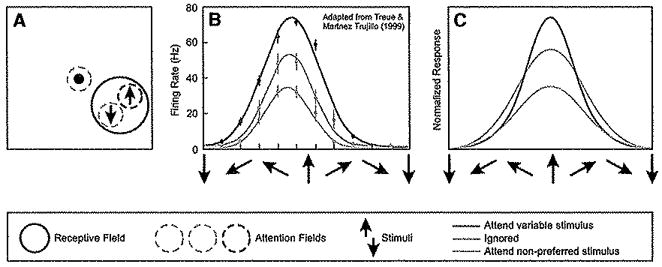
(A) Stimulus and task. A pair of stimuli was presented simultaneously while recording responses of a neuron in visual cortical area MT. Both stimuli were presented within the recorded neuron’s receptive field. One stimulus moved in the nonpreferred direction (indicated as downward), and the other varied in motion direction. Attention was directed either to the fixation point (dashed yellow circle) or to one of the two stimuli in the receptive field (dashed red and blue circles) to detect a change in speed or direction.

(B) Responses were larger when attending the variable direction stimulus (particularly when it moved in the preferred direction) and smaller when attending the nonpreferred stimulus (adapted from Treue and Martinez-Trujillo, 1999). Yellow, tuning (response as a function of the motion direction of the variable stimulus) when attention was directed to fixation. Blue, tuning when attention was directed to the nonpreferred stimulus. Red, tuning when attention was directed to the stimulus with variable motion direction.

(C) Responses of a model neuron. Yellow, simulated responses when the attention field was flat (equal) for all motion directions, and spatial attention was directed to the fixation point (i.e., away from the model neuron’s receptive field). Blue, simulated responses when the attention field was selective for the spatial location corresponding to the receptive field of the model neuron, and selective for the direction of motion opposite to that preferred by the model neuron. Feature-based attention was thus restricted to a nonpreferred direction of motion. Red, simulated responses when the attention field matched that of the variable stimulus, i.e., with a spatial selectivity corresponding to the receptive field and with a direction selectivity that varied with the stimulus motion direction. See Table 1 for simulation parameters.

The normalization model of attention exhibits a similar behavior (Figure 7C), under conditions designed to simulate those of the Treue and Martinez-Trujillo (1999) experiment. The responses of a model neuron can be approximated by assuming that the suppressive field was constant across all motion directions. Under this approximation, the model makes three predictions (see Supplemental Data for derivation). First, attending the nonpreferred stimulus should reduce the neuronal responses, as was observed experimentally. Second, attending the variable motion should increase the responses, also as observed. Third, the model predicts a sharpening of tuning when attending the variable motion direction. Such sharpening was observed in a later study (Martinez-Trujillo and Treue, 2004)—see Figure 6 above—but it was not reported by Treue and Martinez-Trujillo (1999). The model offers a possible way of reconciling the ostensible conflict in these results, because the degree of sharpening in the model depends on the width of the attention field. It was assumed to be relatively broad in the simulation appearing in Figure 7C, resulting in a modest sharpening of the tuning curve. This proposal could be tested by repeating both experiments together, making within-cell comparisons of the attentional effects when attending to a broad versus narrow range of features, with and without a suppressive stimulus in the receptive field, yielding sharpening of tuning only when the attention field is narrow.

Discussion

Attention has been reported to have a variety of effects on the responses of neurons in the macaque visual cortex. To account for these various effects, we have shown that a computational model, the normalization model of attention, exhibits each of these different forms of attentional modulation, depending on sensory conditions and task strategy (specifically, the size of the stimulus and the spread of the attention field, relative to the size of the receptive field and the width of the orientation/direction tuning curve). The proposed model combines Heeger’s normalization model of visual responses, with two hitherto distinct ideas: Treue’s “feature-similarity gain principle” that attentional gain depends on the match between a neuron’s selectivity and the attended spatial location and features (the multiplication in the numerator in the present model) and Reynolds’ suggestion that attention modulates the mechanisms that mediate contrast gain control (the multiplication in the denominator in the present model).

Relation to Other Models

The normalization model of attention is an extension of a model (Reynolds et al., 1999) that was initially suggested as a way of implementing biased competition (Desimone and Duncan, 1995) and predicted that attention would yield a shift in the contrast response function (Reynolds et al., 2000). Ghose and Maunsell (2008) introduced a similar model; their implementation of normalization, following Britten and Heuer (1999), included a parameter that enables it to behave like a winner-take-all operation, though Ghose and Maunsell concluded that the winner-take-all operation did not account well for their data. The present model differs from the models suggested by Reynolds et al. (1999) and Ghose and Maunsell (2008) in that we have incorporated a relatively narrow stimulation field and a broader suppressive field (Cavanaugh et al., 2002a, 2002b). Also, the present model incorporates feature-specific attentional modulation. The incorporation of feature-based attentional modulation in our model is similar to feature-selective biases assumed in the biased competition model (Duncan and Desimone) and the feature-similarity gain principle (Treue and Martinez-Trujillo, 1999), according to which neuronal responses are increased or decreased by a gain factor that depends on the match between the attended feature and the neuron’s preferred feature. A previous model combined the feature-similarity gain principle with normalization (Boynton, 2005), but there was a critical difference between that model and our current model. Boynton (2005) suggested that the neural responses were multiplied by the feature-similarity gain only after normalization whereas attention has its effect in our model before normalization. Incorporating the attentional gain before divisive suppression is what enabled the model to exhibit many of the variety of behaviors that we have demonstrated, including the transition from contrast gain to response gain with changes in stimulus size and attention field size. This also enabled the current model to exhibit attention-dependent response decreases under some circumstances, even though the gain of the attention field was always greater than or equal to one. An example is the sharpening of tuning curves demonstrated in Figure 6. Previous models (e.g., Boynton, 2005) resorted to using an attentional gain greater than one for the preferred feature value and less than one for feature values well away from the preferred. In our model, the suppression for flanking feature values arose naturally as a byproduct of normalization.

The model is also related to a number of more detailed models that have been proposed as biophysicaily plausible implementations of biased competition or the feature-similarity gain principle (Ardid et al., 2007; Deco and Rolls, 2005; Hamker and Zirnsak, 2006; Spratling and Johnson, 2004; Tiesinga et al., 2004). These more detailed models represent interesting alternative possible ways that the computations that define our model may be implemented in the brain (see below).

Predictions

The primary prediction of the model is that the effect of attention should systematically shift from response gain to contrast gain by appropriate manipulations of the stimulus size and attention field size. Testing this prediction will involve developing robust psychophysical procedures for controlling attention field size.

A second prediction of the model is that there be interactions between attention and surround suppression. Divisive normalization with a narrow stimulation field and a broader suppressive field has been used to account for contrast-dependent surround-suppression in macaque area V1 (Cavanaugh et al., 2002a, 2002b). Consequently, directing attention to a center stimulus should cause the neuronal responses to be driven more strongly by the center stimulus, thereby reducing the suppressive influence of “distractor” stimuli in the receptive field surround. Similarly, directing attention to a target in the suppressive region of the surround should magnify suppression, resulting in a diminished response to the distracter in the classical receptive field (Reynolds and Chelazzi, 2004).

A third model prediction is illustrated in Figure 4E. In that simulation, a preferred stimulus and a nonpreferred stimulus were presented simultaneously within the classical receptive field of the model neuron, and the contrasts of the two stimuli covaried to measure a contrast-response function for the pair of stimuli. The model predicts that the contrast-response function will be approximately multiplicatively scaled when directing attention to the preferred stimulus versus the nonpreferred stimulus. Thus, the attention effects are predicted to be strongest for the highest contrasts.

Depending on how normalization is implemented, the model predicts that attention may affect response latencies. Some versions of the normalization model have accounted for the reduction in latency that is observed with elevations in contrast (Carandini and Heeger, 1994; Carandini et al., 1997; Victor, 1987). In these implementations of normalization, contrast elevation reduces the time constant of the neural membrane (via shunting inhibition). If we were to incorporate such an implementation of normalization in the attention model, then this would lead to the prediction that attention should cause a measurable reduction in response latency. One previous study did not find evidence for this (Reynolds et al., 2000). However, a more recent study reported a trend in this direction (Lee et al., 2007).

Computational Benefits of Normalization

The present model adds attentionai selection to the wide variety of computational functions posited for normalization. Theoreticians have offered several (not mutually exclusive) rationales for normalization, including the proposal that it serves to limit the dynamic range of neural firing rates without changing the relative responses of different neurons in the population (Heeger, 1992b), to make the responses of a population of neurons normally distributed and statistically independent thereby making for a more efficient neural code (Schwartz and Simoncelli, 2001; Simoncelli and Olshausen, 2001; Wainwright et al., 2002; Wainwright and Simoncelli, 2000), to normalize the population response akin to normalizing a probability distribution thereby simplifying the decoding or “readout” of the neural population (Heeger and Simoncelli, 1993; Simoncelli, 2003; Simoncelli and Heeger, 1998) and for making neural representations invariant with respect to one or more stimulus dimensions (Heeger et al., 1996; Kouh and Poggio, 2008; Simoncelli and Heeger, 1998), Normalization of visual cortical responses is analogous to earlier models of retinal light adaptation (Sperling and Sondhi, 1968) and to models of contrast gain control in the retina and LGN (Baccus and Meister, 2002; Bonin et al., 2005; Kaplan et al., 1987; Mante et al., 2005; Shapley and Victor, 1978; Shapley and Victor, 1981). Normalization, therefore, has been proposed as a “canonical” cortical computation (Grossberg, 1973; Heeger et al., 1996; Kouh and Poggio, 2008).

Model Limitations

The model proposed here is a simplification of the computations actually carried out by cortical circuits. While it does offer a relatively simple way to account for a variety of neurophysiological data, it is also the case that model parameters not varied here could affect the qualitative behavior of the model. For example, we have for simplicity assumed that that the stimulation field, suppressive field, and attention field are smooth and concentric. Under this assumption, the behavior of the model shifts from contrast to response gain, depending only on the size of the stimulus and the attention field. But this simplifying ideal is an approximation to the more complex scenario that may hold for any given actual neuron. Other distributions could be envisioned, such as “bumpy” stimulation and suppressive fields, for which the ratio of excitation to inhibition at high contrasts would change depending on the shape of the stimulus and the (possibly multi-modal) shape of the attention field.

Attentional modulation has been shown to have temporal dynamics—attention has different effects on firing rates at different times—that are beyond the reach of the current model. For example, Reynolds, Pasternak and Desimone (Reynolds et al., 2000) found a complete lack of attentional modulation during the early transient part of the response evoked by the onset of a high contrast stimulus. In the interest of simplicity, we have focused on a feedforward implementation of normalization. However, normalization can be implemented through feedforward or feedback connections or a combination of the two. Implementations that rely on intracortical feedback (e.g., Heeger, 1993) produce transient responses at stimulus onset. Thus, while the feedforward model proposed here is attractive for its simplicity and explanatory power, a feedback implementation of normalization is likely needed to account for the temporal evolution of attentional modulation (note that the attention field is always assumed to be mediated by feedback from higher cortical areas; the issue here is whether the divisive suppression is implemented via feedforward or via recursive lateral and/or feedback connections). Spratling and Johnson (2004) proposed a model that includes a mechanism that is analogous to feedback normalization and found that it can account for the observation that attention has no effect during the onset transient.

Attention causes a marked reduction in the variability of the neuronal response, as indexed by the Fano factor (Mitchell et al., 2007). Thus, attention does not simply modulate the rate parameter of a homogeneous Poisson-like spiking process. Rather, in addition to modulating firing rates, attention also reduces fluctuations in firing rate that may represent a source of internal noise. These observations are not accounted for by the current model, but attention-dependent reduction in firing rate variability is a property of a model proposed by Tiesinga et al. (2004). The mechanism that they proposed for controlling response gain and firing rate variability involved synchrony of interconnected networks of inhibitory interneurons, which might be a possible mechanism for approximating divisive suppression in the normalization model.

In addition to changes in the firing rates of individual neurons, attention can also modulate the degree of temporal coherence across the neural population (Bichot et al., 2005; Fries et al., 2001; Steinmetz et al., 2000). Clues about the mechanisms that give rise to attention-dependent response synchronization come from studies conducted in anesthetized animals, showing that narrow spiking interneurons play a privileged role in response synchronization (Hasenstaub et al., 2005). Narrow spiking interneurons, which are inhibitory, may be responsible for both normalization and synchronization, as well as reductions in response variability (see preceding paragraph and also Tiesinga et al., 2004). Experiments distinguishing narrow and broad spiking neurons in primates as they perform attentionally demanding tasks hold the promise of elucidating the possible role of narrow spiking neurons in attentional modulation (Mitchell et al., 2007)

While we have considered spatial and feature-based forms of attentional selection, there is mounting evidence that attention can operate on more complex properties of stimuli, such as contours, surfaces, and whole objects (Gilbert and Sigman, 2007; Khoe et al., 2005; Mitchell et al., 2004; Qui et al, 2007; Schoenfeld et al., 2003; Valdes-Sosa et al., 2000). Attending to one feature of an object leads to the obligate selection of other features of the same object while drawing attention away from features of other objects. This type of selection thus depends critically on the neural mechanisms that mediate perceptual organization, that is, the integration of visual features into whole objects and the segmentation of visual features into separate objects. As we gain insight into the mechanisms that mediate perceptual organization, there may be opportunities for extending the current model, and we speculate that these effects may be quite naturally explained by the same neural computations cascaded across the hierarchy of visual cortical areas.

Descriptive, Computational, and Mechanistic Models

The fact that even a very simple computational model can exhibit a variety of different forms of attentional modulation underscores the limitations that are inherent in previous descriptive models of attention (contrast gain, response gain, sharpening of tuning curves), which are convenient shorthands for the different (and ostensibly conflicting) results that have been reported in the literature. A given profile of results that is consistent with one or another of these descriptive models does not necessarily rule out an alternative descriptive model, because the different descriptive models need not be incompatible with one another. We propose instead that the computational principles embodied in the normalization model of attention offer a more promising stepping stone for progress.

The normalization model offers a computational, not a mechanistic, characterization of attentional modulation in visual cortex. With this model in hand, one can proceed to assess the single-unit electrophysiological phenomena with greater experimental control over the stimuli (e.g., stimulus size) and attentional strategy (e.g., attention field size). One can also test predictions of the model at the level of large populations of neurons (e.g., as measured with optical imaging or functional magnetic resonance imaging) and at the level of behavioral performance (as measured psychophysically).

We remain agnostic as to the possible biophysical implementation of the attentional modulation, except to point out that biophysically plausible models of such multiplicative effects have been proposed (Abbott and Chance, 2005; Ardid et al., 2007; Chance et al., 2002; Doiron et al., 2001; Hahnloser et al., 2000; Hasenstaub et al., 2007; Marder and Calabrese, 1996; Mishra et al,, 2006; Mitchell and Silver, 2003; Murphy and Miller, 2003; Prescott and De Koninck, 2003; Salinas and Abbott, 1996; Salinas and Sejnowski, 2001; Sherman and Guillery, 1998; Shu et al., 2003; Spratling and Johnson, 2004; Tiesinga et al., 2004). In light of our limited ability, at present, to probe the individual elements of the actual biological circuit in a Hending animal, we view the simplicity of our proposal as a strength. Mechanistic models will become increasingly important as new approaches in systems neuroscience make it possible to gain deeper insight into underlying circuitry and cellular mechanisms.

Nor do we care, for the purposes of this paper, to specify the mechanism underlying the stimulus drive, that is, the mechanism by which neurons achieve their selectivity for orientation and spatial location. Selectivity has been characterized with linear summation (Adelson and Bergen, 1985; Heeger, 1992a, 1992b; Movshon et al., 1978a, 1978b), not unlike the original description by Hubel and Wiesel (1962) for how simple and complex cell responses in V1 might depend on inputs from the lateral geniculate nucleus. The biophysical mechanism for the linear summation might depend on a push-pull combination of synaptic excitation and inhibition (Ferster and Miller, 2000; Hirsch and Martinez, 2006).

Also, normalization itself can be implemented with a variety of biophysical mechanisms (for review, see Carandini, 2004b). It can be implemented either through feedforward {Carandini et al., 2002; Priebe and Ferster, 2008) or feedback connections (Carandini et al., 1997; Heeger, 1993) or a combination of the two. The differences between feedforward and feedback implementations are most evident in the transient activity immediately following stimulus onset (Bair et al., 2003). Here, however, we focus on steady-state responses. Shunting inhibition through lateral connections from other neurons in the cortical neighborhood has been proposed as one possible mechanism for normalization (Carandini and Heeger, 1994; Carandini et al., 1997; Kouh and Poggio, 2008). Feedforward synaptic depression has been shown to yield nearly identical behavior (Carandini et al., 2002). Other possible mechanisms include an increase in the overall synaptic conductance at high contrasts (Chance et al., 2002) or a decrease in noise at high contrasts which makes the cells less responsive because their membrane potential is less likely to cross threshold (Finn et al., 2007). Normalization might not have a single biophysical mechanism. It might instead emerge from a complex combination of a variety of mechanisms (Priebe and Ferster, 2008). Regardless of the mechanism(s), normalization appears to operate at multiple (perhaps ail) stages of the visual system.

To develop a mechanistic understanding the underlying circuitry will require steps to probe the elements of the circuit itself. It will be important to distinguish between the different types of neurons that make up visual cortical circuits while recording in attending animals. Such distinctions between cell types are regularly made in phylogenetically lower species, such as the rat, rabbit, and ferret (Buzsáki and Eidelberg, 1982; McCormick et al., 1985; Simons, 1978; Swadlow, 2003) and in acute nonhuman primate experiments (Disney et al., 2007; Joshi and Hawken, 2006; Nassi and Callaway, 2007), but rarely have different types of neurons been distinguished in behaving nonhuman primates (Constantinidis and Goldman-Rakic, 2002). Of particular relevance are reports that two classes of visual cortical neurons in macaque, defined by spike width, exhibited differential effects of attention (Mitchell et al., 2007; Chen et al., 2008). The two classes may correspond to morphologically and pharmacologically distinct cell types (the broad spiking class may be largely made up of pyramidal neurons, while the narrow spiking neurons are likely to be composed largely of GABAergic Parvalbumin-positive neurons with the morphology of basket cells and chandelier ceils). In addition to neuronal type, it will be helpful to determine whether attentional modulation differs by laminar position, to understand whether the effects of attention depend on where neurons project to and from in the cortical circuit (Callaway, 1998; Mehta et al., 2000). Another key emerging direction is research devoted to understanding subcellular mechanisms that may play important roles in attentional modulation. For example, while the glutamatergic inputs from higher cortical areas (e.g., frontal eye field, posterior parietal cortex) likely play an important role in attentional modulation of visual cortex, there is also evidence that cholinergic inputs from the basal forebrain may also be involved (Disney et al., 2007; Herrero, et al., 2008). Of particular interest will be to characterize how these various mechanisms relate to the computational principles that underlie the normalization model of attention.

The computational architecture of visual cortex is very similar from one area to another; the types, arrangements, and connections of cortical neurons are highly stereotyped (Douglas and Martin, 2007; Mountcastle, 1997). This suggests that each cortical area conducts calculations of the same form (e.g., linear summation, attentional modulation, divisive normalization, and spike threshold) at each stage of visual processing. Models of MT physiology, for example, posit that the greater selectivity and invariance exhibited by MT neurons in comparison to their V1 inputs derives from an appropriate linear summation of V1 inputs, coupled with normalization and spike threshold (Heeger et al., 1996; Simoncelli and Heeger, 1998). Models of ventral stream processing posit an analogous hierarchy of computations such that neurons in successive stages of processing exhibit selectivity for increasingly more complex combinations of certain visual features while also exhibiting increased invariance to other stimulus attributes (Riesenhuber and Poggio, 1999, 2002). We propose that attention likewise affects each stage of processing such that the attention fields are cascaded across the hierarchy of visual cortical areas, and the attentional effects are accumulated across the hierarchy. For the purposes of this paper, the simulations were performed with a single processing stage, but we believe that a full simulation with multiple stages of feature integration and attentional modulation would be needed to quantitatively fit electrophysiological measurements.