Abstract
A high-field electron paramagnetic resonance (HFEPR) study of oxalate decarboxylase (OxdC) is reported. OxdC breaks down oxalate to carbon dioxide and formate and possesses two distinct manganese(II) binding sites, referred to as site-1 and -2. The Mn(II) zero-field interaction was used to probe the electronic state of the metal ion and to examine chemical/mechanistic roles of each of the Mn(II) centers. High magnetic-fields were exploited not only to resolve the two sites, but also to measure accurately the Mn(II) zero-field parameters of each of the sites. The spectra exhibited surprisingly complex behavior as a function of pH. Six different species were identified based on their zero-field interactions, two corresponding to site-1 and four states to site-2. The assignments were verified using a mutant that only affected site-1. The speciation data determined from the HFEPR spectra for site -2 was consistent with a simple triprotic equilibrium model, while the pH dependence of site-1 could be described by a single pKa. This pH dependence was independent of the presence of the His-tag and of whether the preparations contained 1.2 or 1.6 Mn per subunit. Possible structures of the six species are proposed based on spectroscopic data from model complexes and existing protein crystallographic structures obtained at pH 8 are discussed. Although site-1 has been identified as the active site and no role has been assigned to site-2, the pronounced changes in the electronic structure of the latter and its pH behavior, which also matches the pH-dependent activity of this enzyme, suggests that even if the conversion of oxalate to formate is carried out at site-1, site-2 likely plays a catalytically relevant role.
Keywords: EPR, oxalate decarboxylase, manganese(II), high magnetic-field, metalloprotein
Introduction
Manganese in its divalent state, Mn(II), plays important roles in a number of biological processes such as bacterial virulence1,2, radioprotection3,4, oxidative stress5 and a number of other enzymatic processes (for example see 6). An effective technique for selectively detecting and probing the electronic state of Mn(II) ions in biological environments has been electron paramagnetic resonance (EPR) spectroscopy. However, conventional EPR has proven to be of limited value due to poor resolution and high spectral complexity. Recently, several experiments have been carried out using high magnetic-field high-frequency EPR (HFEPR)7–10 that suggest that this approach not only circumvents these two limitations, but also allows accurate measurement of the magnetic spin parameters of an Mn(II) ion from which valuable information about its electronic structure and interactions with the environment can be extracted.
The EPR spectrum of a Mn(II) ion is determined essentially by three interactions: the Zeeman, describing the interaction between the electronic spin and the external magnet fields; the hyperfine, arising from the magnetic interaction between the electronic-spin and nuclear-spin (I(55Mn)= 5/2) values; and two zero-field interactions, defined by the parameters D and E. The Zeeman and hyperfine interactions have been found to be essentially isotropic, described by the scalar values g and A respectively. The detailed descriptions of the three interactions and how they influence the Mn(II) EPR spectrum can be found elsewhere (pertinent details are also given in the supporting information). Figure 1 summarizes the relevant aspects of the Mn(II) HFEPR spectroscopy. When the applied magnetic field is sufficiently large so that the Zeeman interaction (gβB) is much larger than the zero-field interaction, as is the case in our measurements, the spectra become greatly simplified. Of the five formally allowed EPR transitions, there are two limiting cases that are particularly interesting. Near liquid helium temperatures, only the ms =−5/2 level is populated and the ms =−5/2↔−3/2 transition is the only significant contribution to the HFEPR spectrum. The center of the spectrum is determined by the Zeeman interaction (Bcenter=hν/gβ, where ν is the microwave frequency used to detect the spectrum) and the overall shape is defined purely by the zero-field interaction (Figure 1). For frozen protein samples in which Mn(II) centers are randomly orientated, the relative positions of these three “turning” points of the powder spectrum are determined by D and E and the relative disposition of these points define the algebraic sign of D. It is important to note that as long as the Zeeman interaction is much greater than the zero-field interaction, the shape of the HFEPR spectrum is independent of the microwave frequency used to detect the Mn(II) ions, that is the microwave frequency only defines the center of the spectrum.
Figure 1.
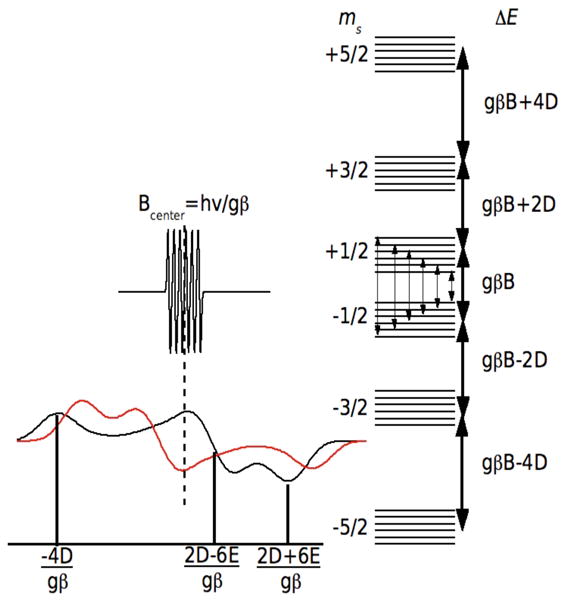
The EPR spectra (left) and energy levels (right) of a Mn(II) ion when the Zeeman interaction (gβB) is the dominant interaction. The energy diagram is for the case where E=0 and the heavy arrows denote the five formally allowed electronic spin transitions. The powder spectrum of the ms=−5/2 →−3/2 transition is shown for D < 0 (red) and D > 0 (black). The ms=−1/2 →1/2 spectrum and the associated electron-nuclear hyperfine transitions (fine arrows) are also shown. Both, the ms=−5/2 →−3/2 and ms=−1/2 →1/2 spectra are centered Bcenter=hν/gβ. The labeled field positions are relative to Bcenter.
The second limiting case is the spectrum of the ms =−1/2↔1/2 transition. We have already discussed the HFEPR spectroscopy of this transition in detail.11 It is best detected at elevated temperatures where the ms =−1/2 level is optimally populated (typically about 23 K at 10 T). This transition is unaffected by the zero-field interaction to first-order. For this reason, its spectrum is extremely intense and highly resolved with six sharp lines corresponding to the hyperfine transitions (Figure 1). However, like the spectrum of the ms =−5/2↔−3/2 transition it is centered at hν/gβ. The shape of each of these six resonances is influenced by higher-order contributions of the zero-field interaction, the second-order contribution being proportional to |D|/gβB. This means that unlike the ms =−5/2↔−3/2 transition, the shapes of each of the six hyperfine resonances depend on the microwave frequency used for detection. It is possible to extract the zero-field parameters from simulations of these line shapes.
The zero-field interaction is arguably the most interesting of these interactions. It arises from the spin-spin and spin-orbit interactions of the five unpaired Mn(II) electrons. Although, it has been long known that the zero-field interaction gives a measure of how much the Mn(II) environment departs from spherical symmetry 12, the details of how it depends on the molecular structure are not well understood. A number of quantitative, but essentially phenomenological, models of the Mn(II) zero-field interaction have been developed that have had varying degrees of success.13 However, none have proven to be completely reliable. Recently, there has been some success in calculating the Mn(II) zero-field interaction using ab initio quantum chemical methods.14,15 Such calculations hold the promise of a usable general theoretical framework.
In spite of the lack of detailed theoretical knowledge, there is growing experimental evidence that the Mn(II) zero-field interaction can be used as an effective chemical probe of the electronic state of the Mn(II) centers. Mn(II) containing superoxide dismutases (MnSODs) are highly structurally homologous and have identical primary ligands, yet can be readily discriminated by their zero-field interactions.11 This likely arises from the sensitivity of the Mn(II) zero-field interaction to electrostatic contributions from the surrounding protein environment well beyond the immediate ligands 11,16,17. Similarly, the Mn(II) zero-field interactions of closely related manganese terpyridine complexes have been found to correlate with their Mn3+/Mn2+ reduction potential demonstrating the sensitivity of the zero-field interaction to the subtle effects of electrostatics and bonding.18
We have exploited HFEPR and Mn(II) zero-field interactions to characterize the manganese binding in Oxalate decarboxylase (OxdC). This protein is found in a number of bacteria and fungi and breaks down oxalate to carbon dioxide and formate. In addition to the substrate, the processing of oxalate also requires dioxygen.19 Through what is thought to be a radical-based catalytic cycle involving electron transfer from the metal ion to the bound dioxygen, the oxalate molecule is heterolytically cleaved into the products.19,20 OxdC exists as a hexamer. Each monomeric subunit appears to have been formed from the fusion of two oxalate oxidase cupin domains, each having a mononuclear manganese binding-site with a coordination sphere similar to that of the oxidase. 21–23
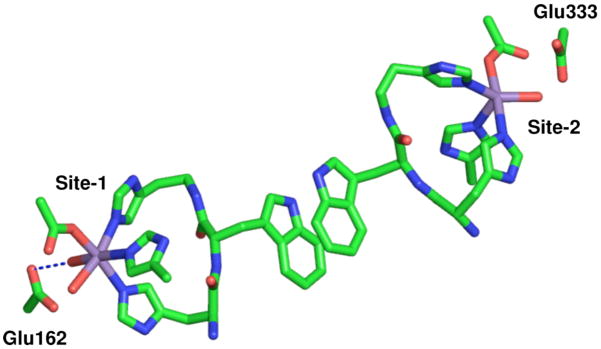
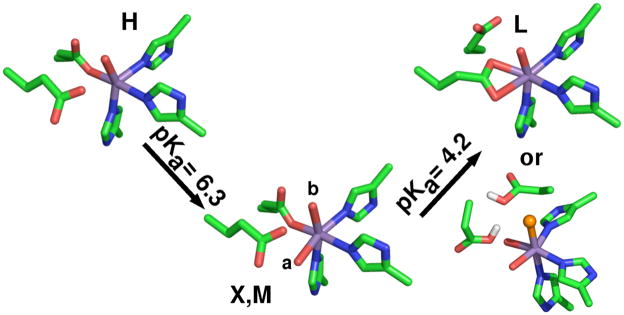
The N-terminal Mn(II) ion as found in the 1UW8 24 OxdC structure is six-coordinate with 3 histidines in a facial configuration, 1 glutamic acid and 2 water ligands with the glutamic acid ligand hydrogen-bonding one of the water molecules (Figure 2, from here on this site will be referred to as site-1). A number of experiments have demonstrated that this is the catalytic site.24–27 By contrast, the C-terminal Mn(II) ion (referred to as site-2) is five-coordinate in a square-pyramidal geometry and, like site-1, has three facially configured histidines and a water ligand that is also hydrogen-bonded to the glutamate residue that directly ligates the metal ion (Figure 2). The shortest distance between these sites is between those of adjacent monomers. Two other B. subtilis wild-type OxdC structures (1J58 28 and 1L3J 28,29) have been solved, in both cases a formate molecule binds site-1 and site-2 is six-coordinate with an additional water ligand. In all cases, the structures were obtained from crystals poised at pH 8. By contrast, it has been well established that OxdC only becomes maximally active well below pH 5. This means that although the crystallographic structures provide valuable information regarding the overall three-dimensional structure of OxdC there is no certainty as to the structure of the metal binding sites at the optimal pH. Moreover, these structures give little information about the electronic state of the manganese ions that could provide also important insights into chemical/mechanistic roles of the two manganese ions.
Figure 2.
The pH 8 structure of the two OxdC Mn(II) binding sites as found in the 1UW8 structure. The shortest distance between the sites is between sites on adjacent subunits of a trimer.
Specifically, the purpose of this study was to exploit the highly sensitive nature of the Mn(II) zero-field interaction to characterize the manganese-binding sites in two types of OxdC preparations: one having slightly higher than 1 Mn(II) per subunit of protein and a C-terminal His-tag used to facilitate purification (hereafter referred to as JIC-OxdC) and the other having closer to full metal content and no tag (hereafter referred to as UF-OxdC). Angerhofer and workers have examined the latter type using HFEPR.10 Although the UF-OxdC sample could be thought of as more ideal in terms of metal content and no tag, kinetic measurements present a complex picture with the His-tagged low metal occupancy version actually having a higher activity per Mn content (Table 1). The C-terminal His-tag appears to have little structural effect since the C-terminal end of the 2VO9 (His-tagged mutant) and 1UW8 (non-His-tagged wild-type) structures are virtually identical.24,25 However, one complication has been that all of the known structures were obtained from crystals having full metal occupancy despite being derived from preparations that did not, hence relating these crystallographic structures to kinetic measurements is not necessarily straightforward. This was one of the compelling reasons for using HFEPR. As will become evident in our description of the HFEPR study, not only did we find consistency between spectroscopy and crystal structures at high pH, but there was also clear evidence for complex pH-dependent changes in the structure.
Table 1.
The comparison of physical and enzymatic properties of the two studied B. subtilis OxdC preparations.
| JIC-OxdCa | UF-OxdCb | |
|---|---|---|
| Metal content | 1.2 Mn/subunit | 2.0 Mn/subunit |
| His-Tag | C-terminal | None |
| Quaternary Structure | Hexamer | Hexamer |
| Steady-state kinetic parameters | ||
| Vmax | 95 U/mg | 79 U/mg |
| 79 U/mg/Mn | 40 U/mg/Mn | |
| Km | 7 mM | 5 mM |
| kcat/Km | 11000 M−1s−1 | 11000 M−1s−1 |
| pKa associated with optimal activity | ~4.6 (see supporting information) | 4.2 |
Materials and Methods
Protein Preparation
Wild-type B. subtilis oxalate decarboxylase was expressed in Escherichia coli with a C-terminal His-tag (JIC-OxdC), purified using nickel affinity chromatography and treated with Chelex 20 resin (BioRad) to remove adventitious metal ions as described previously24 with modifications to the method of the induction of protein expression.25 Samples were additionally treated with 10 mM EDTA before buffer exchange into the final buffers using desalting columns followed by concentration using Amicon centrifugal devices (Millipore). The typical manganese contents were 1.2 Mn/subunit for the wild-type protein and 1.4 Mn/subunit for the mutant. HFEPR samples contained 300 mM NaCl, 50 mM buffer and 10% glycerol. Sample concentrations ranged from 100 to 570 μM/subunit. The reported pHs were those measured at 0°C immediately prior to flash freezing in liquid nitrogen. The pHs of a number of samples were also checked after the experiments. Citrate and acetate buffers were used for pHs between 4 and 6; MES buffer for pH 6.5; TRIS for pH between 7 and 9. Hexamethylenetetramine (HMTA) was used for pH 6.3 samples.
The isolation and purification of the non-His-tagged UF-OxdC was identical to those previously reported.20
High-field EPR spectrometer
The HFEPR spectrometer has been described in detail elsewhere.30 Field calibration was based on a Mn(II)-doped MgO standard sample (g=2.0010131) and the absolute error in field measurements was 1 G (0.1 mT) or 0.0001 in g.
Spectrum simulations
Simulations of the spectra of the ms=−1/2→1/2 transitions were carried out as previously described.11,32 The estimated error limits of the fitting procedure were ±0.06 GHz for the two zero-field parameters. Simulations of the 4 K spectra were based on standard second-order perturbation solutions to the spin Hamiltonian (Eq. 1). The dominant contribution to these spectra was from the ms=−5/2→−3/2 transition. The g- and hyperfine tensors were assumed to be isotropic. All six “allowed” transitions (Δms=1) were calculated. The amplitudes of the transitions were properly weighed to take into account the quantum mechanical transition probabilities as well as populations of the six levels as defined by Boltzmann’s equation. The isotropic g-values and hyperfine couplings obtained from the simulations are given in the supporting materials.
Molecular structures were generated using the program PyMOL (Delano Scientific LLC, www.pymol.org).
Results
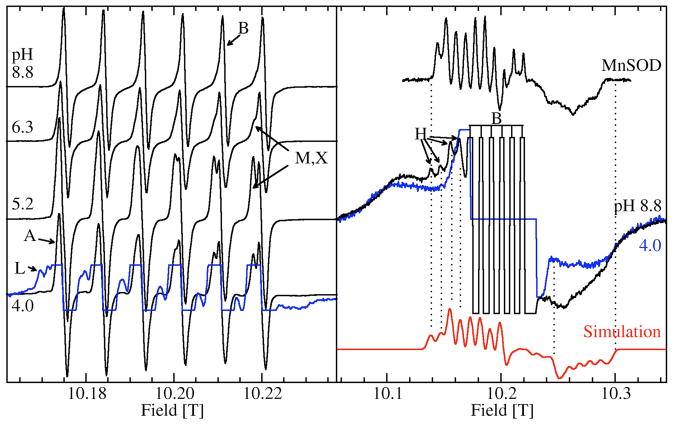
Figure 3 shows the 285 GHz EPR spectra of JIC-OxdC at various pH values. As will be discussed below, under identical conditions both the JIC- and UF-OxdC gave near identical results. It was readily apparent from these HFEPR spectra along with those obtained at 190 and 95 GHz (data not shown) that there were at least five distinct resonances, arising from the high, medium and low pH forms of site-2 designated H, M, L, respectively, and A and B for the acidic and basic pH forms of site-1 (Figures 3 and 4 and Table 2), the amplitudes of which were pH-dependent. As will be described below, there were probably a total of six distinct components. These resonances were readily resolvable based on the distinct zero-field interaction parameters of each of the corresponding Mn(II) centers. Measurements of the zero-field interactions parameters and the relative populations of each of the species were facilitated by the ability to acquire independently the spectra of the ms= −5/2→−3/2 (Figure 4) and −1/2→1/2 transitions (Figure 3) at multiple microwave frequencies. Figures 3 and 4 also show simulations of the various resonances and the zero-field parameters obtained from them are listed in Table 1. By following the changes in the zero-field interaction and intensities as a function of pH, we determined that resonances corresponding to H, L, and M arose from the site-2 Mn(II) and A and B from site-1, as elaborated below.
Figure 3.
The pH dependence of the 285 GHz 25 K Mn(II) EPR spectra of the ms=−1/2→1/2 transition of JIC-OxdC. The left panel shows narrow field range spectra of the six hyperfine resonances associated with A, B, M, X and L and a ×8 expanded spectrum (blue trace) of the pH 4.0 spectrum shows the more complex features of L. The right panel shows spectra of the pH 8.8 (black) and 4.0 (blue) samples obtained with a ×4 broader field sweep. The truncated six lines of the pH 8.8 spectrum correspond to the six lines seen in the corresponding spectrum on the left panel. Similar six-lines in the pH 4.0 spectrum have been suppressed for clarity. The broad underlying features common to both pHs are due to the ms=−5/2→−1/2 and ms=−3/2→−1/2 transitions. The four indicated left-most hyperfine features belong to H (black) and are not present at low pHs (blue). A simulation (red) based on these four features as well as the edge positions marked by the two dotted lines on the high-field side of the spectrum is also shown. For comparison, the spectrum of the ms=−1/2→1/2 transition of the pentacoordinated Mn(II) center in E. coli MnSOD is also shown.
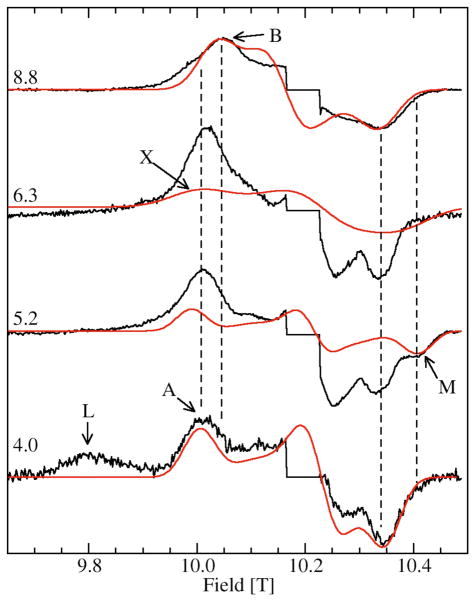
Figure 4.
The pH dependence of the ms=−5/2→−3/2 of the 285 GHz 4 K Mn(II) EPR spectra of JIC-OxdC. The sharp central six line features corresponding to the ms=−1/2→1/2 transitions have been suppressed. The red traces are the simulations of the features indicated, except for the simulation of L which is shown in Figure 5. The two vertical dashed lines between 10.00 and 10.05 T indicate the shift in field positions of the A and B components (see Figure 6) and the two between 10.35 and 10.45 T, the position of the shifted high-field edge of M relative to the other site-2 components.
Table 2.
The zero-field parameters of the different site-1 and -2 Mn(II) species of OxdC. Unless otherwise noted the parameters were determined from the 285 GHz 4 K (ms=−5/2→−3/2) data and refer to the wild-type protein.a
| Species | Zero-Field Parameters (in GHz) | Conditions | ||
|---|---|---|---|---|
| D | E | |||
| OxdC Site-1 | ||||
| B | −1.11 | 0.30 | pH 8.8, TRIS | |
| A | −1.35 | 0.23 | pH 4.0, citrate | |
| OxdC Site-2 | ||||
| Hb,c | 10.73 | 1.70 | pH 8.8, citrate, 25 K and 190 GHz | |
| Xd | 1.40 | 0.34 | pH 6 and pH 5, citrate, 95 GHz | |
| Mb | −1.50 | 0.45 | pH 5.2, citrate, 4 and 25 K | |
| L | 4.17 | 0.72 | pH 4.0, citrate, 25 K | |
| Lb | +5.06 | 0.25 | pH 4.0, citrate | |
| E. coli MnSOD (trigonal bipyramid) | 10.64 | 0.85 | ||
| E. coli MnSOD+azide complexc,e | 1.39 | 0.27 | ||
| E. coli MnSOD six-coordinatec,e | 1.44 | 0.27 | ||
| Mn(II) containing bacterial photosynthetic reaction centers b,d,g | 3.33 | 0.75 | ||
| Mn(II) doped in Bis(2-pyridylmethyl)amine Zn complex (six-coordinate) f | −7.09 | 0.10 | ||
| N-methyl-N,N′,N′-tris(2-pyridylmethyl)ethane-1,2-diamine Mn(II) complex (N5Cl) ligand set | +5.39 | 0.18 | ||
| N-methyl-N,N′,N′-tris(2-pyridylmethyl)propane-1,2-diamine Mn(II) complex (N5Cl) ligand set | +4.07 | 0.00 | ||
see supporting information for isotropic g and hyperfine coupling values.
verified with simulations of 190 GHz spectra (data not shown).
E and the absolute value of D determined from simulation of the center transition.
E and the absolute value of D determined from simulation of the center transitions of the 95 GHz difference spectrum of the pH 6 and pH 5 citrate buffered samples, only the absolute value of D was determined.
See text for details.
see ref. 33
High pH Spectra
The pH 8.8 HFEPR spectrum of JIC-OxdC was composed essentially of B and H (Figure 3). The relative amplitude of these components obtained from simulations ranged from 1:1 to 1:2, depending on the sample and simulation parameters used. The two distinct components were consistent with the pH 8.0 crystallographic structure (1UW8). Site-1 has been found to be six-coordinate with near octahedral geometry while site-2 had an unusual five-coordinate near square-pyramidal structure (Figure 2).24 The spectral width of the ms=−1/2→1/2 transitions of H was so large its characteristic resonances were not evident in the spectra obtained with the much narrower magnetic field range used to obtain the six-line spectrum of B (Figure 3, right panel). This indicated that the zero-field interaction of H was very large compared to B. It has been previously shown that the quantity |D|+E can be directly determined from the field positions of the low-field hyperfine features (indicated by the four arrows in Figure 3).11 The sum was 12.43 GHz. Simulations of the 285 and 190 GHz spectra yielded a D value of 10.7 GHz (Figure 3, as with all simulations of the center transition only the absolute value of D could be determined). This large value was similar to those of the trigonal-bipyramidal five-coordinate Mn(II) center in manganese superoxide dismutases (MnSODs) indicating that H corresponded to the high pH form of site-2 (Table 2).8,32 The E value of H (1.70 GHz) was significantly larger than those of MnSODs, possibly indicative of the nearly square-pyramidal structure of site-2 compared to the trigonal-bipyramidal geometry found in MnSODs. Component B zero-field parameters were entirely consistent with those of other six-coordinate pseudo-octahedral Mn(II) centers found in other proteins (Table 2); therefore, B was assigned to site-1. Between pH 7 and pH 5, there was a distinct shift in the spectrum of B. Below pH 5, the resonant field positions, and therefore the zero-field parameters, became constant. This low pH form of site-1, designated A, had a slightly larger D value, but was still consistent with a six-coordinate Mn(II) center.
Low pH Spectra
A more pronounced effect of decreasing pH was the rapid diminution of the amplitude of H. Below pH 6, it became undetectable. Below pH 5, there was a rapid rise of a new set of resonances that we designated L. In the ms=−5/2→−3/2 4 K spectra, the characteristic resonance for L was a broad 9.8 T feature (Figure 4). The corresponding ms=−1/2→1/2 transition resonances could also be readily seen in the ×8 expansion of the 25 K pH 4 spectrum (Figure 3, left panel). Several additional sharp resonances appeared to the low-field side of each of the six sharp site-1 resonances in addition to a broad resonance on the high-field edge. At pH 4, the simulations and double integrations of the HFEPR spectra showed that there were an equal number of Mn(II) centers corresponding to L and A. This further supported the assignment that component L arose from the low pH form of site-2. The contribution of A to the spectrum was very similar to that of B.
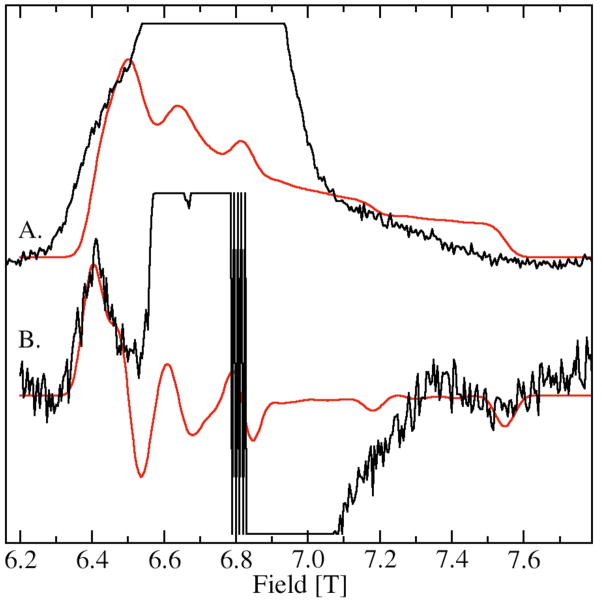
The zero-field interaction of L was considerably larger than that of A and B. This was apparent from the greatly down-field shifted 9.8 T resonance in the 285 GHz spectrum (Figure 4) and the equivalent 6.4 T resonance in the 190 GHz spectrum (Figure 5B). However, this low pH from of site-2 had a much smaller zero-field interaction than H, the high-pH form of site-2. The complete spectrum of the ms=−5/2→−3/2 transition of L was so wide that it was not possible to obtain all of it using 285 GHz microwaves, since it extended beyond 10.5 T, the field limit of our magnet. However using 190 GHz, it was possible to obtain the totality of the spectrum of the ms=−5/2→−3/2 transition of L (Figure 5). Its zero-field interaction was nearly axial with a positive D value of +5 GHz (Table 2). Although the low-field edge of the spectrum was well-defined, the high-field edge was considerably broader indicating that the zero-field interaction was anisotropically distributed, that is the zero-field interaction in L was significantly more distributed along the zero-field axis than along a direction perpendicular to it. “Fast-passage” spectra that had better signal-to-noise ratios confirmed the orientation-dependent disorder.34 The zero-field parameters obtained from the 190 and 285 GHz spectra of the ms=−5/2→−3/2 transition were different from those obtained from simulations of the 285 GHz spectra of the ms=−1/2→1/2 transition (Figure 3, left panel). There were two likely contributions to the discrepancy. This anisotropic distribution that is readily visible in the 190 GHz ms=−5/2→−3/2 spectrum is not completely accounted for in the simulation that assumes an independent Gaussian distribution in D and E. Another more significant contribution to the discrepancy is that the simulation of the ms=−1/2→1/2 transition requires not only fitting the positions, but also the shapes of the six sharp resonances. In this case, the shapes were partially obscured by the resonances from A leading to a greater uncertainty in the simulated values. This is a potential pitfall common to all strategies for determining the zero-field parameters from the ms=−1/2→1/2 spectra that have overlapping resonances. For these reasons, the zero-field parameters from the ms=−5/2→−3/2 spectrum were likely to be more reliable since values could be “read-off” and the fitting procedure was much more sensitive to positions of the edges rather than to the details of the line shape. In should be noted that the possibility that the zero-field interaction in this particular case was temperature dependent could not be discounted. The Mn(II) zero-field interaction of MnSOD shows a marked temperature dependence above 25 K.32
Figure 5.
The 190 GHz HFEPR spectrum of JIC-OxdC L obtained at pH 4, (A.) fast-passage (< 1G modulation and 3K) and (B.) normal conditions (20 G modulation and 4K). Simulations are in red. The simulation of the fast-passage spectrum is simply the integral of the simulation of spectrum B. Contributions from species A are truncated in spectra A and B.
Intermediate pH Spectra
At intermediate pH values, there was a different set of resonances apparent in the 25 and 4 K spectra, designated M (Figures 3, left panel and 4). It reached a maximum at about pH 5 and its contribution to the ms=−1/2→1/2 spectrum appeared as a progressive splitting of the six hyperfine lines with increasing magnetic-field (Figure 3, left panel) and in the ms=−5/2→−3/2 spectrum (Figure 4) as a distinct shoulder at 10.4 T (Figure 4). Evidently, the zero-field interaction of M was smaller than H or L, but slightly larger than site-1 A or B. Simulations confirmed this. M had D and E values of −1.50 and 0.45 GHz respectively (Table 2).
Construction of Speciation Curves
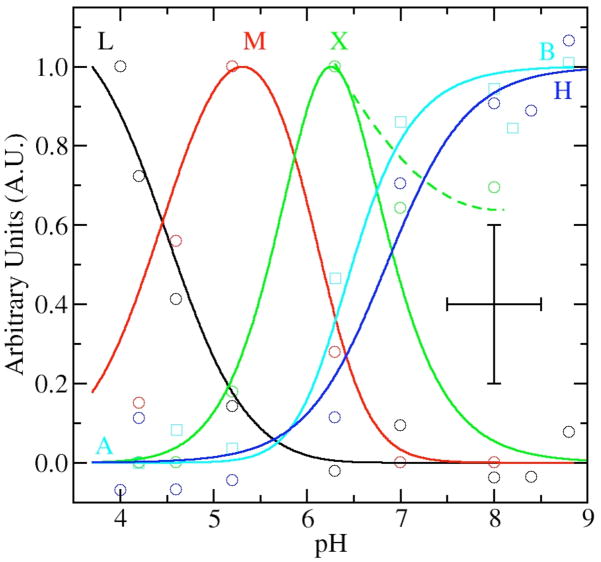
Having identified five distinct components of the HFEPR spectra, we proceeded to analyze and model their pH-dependence (Figure 6). The shift in field position of the site-1 resonances, components A and B (Figure 3), nicely followed a standard monoprotic titration curve with a pKa of 6.9 (Figure 6). The speciation data for components H, L and M were determined from the 25 K spectra by normalizing the amplitudes of resonances arising from these components against the intensity of six sharp lines of site-1 components (Figure 3). The contribution of M was also independently derived from the field position of the high-edge of the 4 K spectra (Figure 4). The speciation curves of M determined in this way had essentially the same pH-dependence as those determined using relative amplitudes. Given the quality of speciation data, no attempt was made to determine the quantities of L, M and H relative to each other and the data were separately and arbitrarily normalized to unity (Figure 6).
Figure 6.
The pH dependence of selected spectral features as a function of pH: the L component in the 4 K spectra (black circles); the 25 K H resonance (blue circles); the 4 K M component (red circles); X contribution from fits of both 25 and 4 K spectra (green circles); and the shift in field position of the site-1 ms=−5/2→−3/2 contribution (cyan circles, see Figure 4). The corresponding lines are from manual fits of the data using standard speciation equations for triprotic equilibria with pKas at 4.2, 6.2 and 6.3 for site-2 contributions and monoprotic equilibrium curve with a pKa of 6.9 for site-1. The dashed green line shows the trend of experimental X data at high pH. The data and speciation curves have been arbitrarily normalized to unit. The crossed bars give the estimated maximum error in the measurements.
It was possible to obtain rough estimates of the relative populations of site-1 and site-2 at low pH since the spectrum of the former remained constant below pH 6. At higher pHs, spectral contributions from ms=−5/2→−3/2 and ms=−3/2→−1/2, as well as ms=−1/2→1/2 transitions of B obscured the spectrum of the ms=−1/2→1/2 spectrum of H. This led to large uncertainty in the relative population, estimates of the ratio site-1 to site-2 ranged from 0.5:0.5 to 0.3:0.7. At low pHs, the spectra of site-1 and -2 were much more similar and determination of the relative populations more reliable. The estimates were based on the simulation of narrow ms=−1/2→1/2 spectrum of A which remained unchanged below pH 6. The double integral of the simulation was compared to that of the total experimental spectrum to obtain the ratio of site-1 to site-2. This was done over 5 different pHs and eight different samples varied from 0.3:0.7 to 0.4:0.6 (with a conservative error estimate of ±0.2), meaning that in the samples used in this study site-2 was slightly more populated. The ratio did not depend on either pH or the buffer used (see below).
Modeling of Speciation Data
For site-2, speciation curves based on diprotic equilibria require that M become maximum midway between the fall of H and rise of L. This was not the case. It appeared that the pH dependence of site-2 required at least three coupled acid-base equilibria to obtain adequate agreement with pKa values of 4.2, 5.7–6.2 and 6.3 (Figure 6). In our preliminary analysis of spectra, we found no spectroscopic signatures corresponding to the component that would have reached a maximum concentration at about pH 6 and hence we could not fix the middle pKa. Schematically, the pH relationship between the various components could be summarized by:
This triprotic equilibrium model predicted a second intermediate pH species in addition to component M. It became apparent that the pH-dependent variations in spectral features first assigned to component M did not vary uniformly and were not totally consistent with a single species. For example, scaled subtraction of the 4 K spectra obtained at pH 5 and 6 indicated excess intensity in the pH 6 spectra that was beyond predictions of the speciation curves. Simulation of the difference spectrum showed if this excess intensity was indeed due to X then its zero-field parameters were likely to be similar to those of M, but more distributed, that is the spectrum of X was broader and less resolved. Closer inspection of the 95 GHz spectra (see for example supporting information) of the center transitions led to the same conclusion. Taking the spectral contribution of component X into account also helped to explain the extended shoulders in the pH 6 to 9 spectra which we had initially assumed were due to extended distribution in zero-field parameters of site-1 at high pH (component B). If one assumed the assignment of X to be correct, then the data analysis indicated significant amounts of X even above pH 8.
Buffer Dependences
Since the transition from B to A was continuous over the three different buffers (from pH 9 to 6 in TRIS, pH 6 in MES and pH 5 and below in citrate) used to obtain the speciation curves, there was little reason to believe that the results strongly depended on the buffers used. This also appeared to hold true for site-2 since H, X, M and L changed in a relatively continuous and predictable manner. Spectra obtained in the pH 6–7 region using hexamethylenetetramine (HMTA) buffer yielded entirely consistent results with those obtained in MES and TRIS; that is, the relative quantities of H, X and M were the same as shown in Figure 6. Below pH 5.5, the zero-field interaction of L obtained using a 1,4-bis(hydroxyethyl) piperazine buffer was slightly different than in citrate. However the poor quality of the ms=−5/2→−3/2 spectrum (data not shown) due to protein stability problems in the piperazine buffer precluded a detailed analysis. By contrast, A appeared unchanged in this buffer.
Verification of Site Assignment
Measurements on the OxdC SENS161-4DSSN variant verified the site assignments of the various components. The mutation has been shown to affect only the environment of site-1 while keeping the structure of the primary ligand-sphere intact. Crystallographic studies have shown that in this mutant three water molecules replace the carboxylic acid side-chain of Glu162, the oxygen atom of one situated in the same position as the Glu162 carboxylate oxygen that shares a hydrogen bond with the water ligand of site-1. The position of the Asp161 carboxylate group introduced into the mutant was about 13 Å from the metal center. The structure of the site-1 ligand-sphere itself was unchanged by the mutation.25 As might be expected, the distinct ms=−1/2↔1/2 spectrum of site-2 H at high pH was unaffected by the mutation. Likewise, close examination of the HFEPR spectra of the ms=−5/2→−3/2 also indicated that M, X and L were also unchanged (Figure 7). The loss of the water-ligand/protein hydrogen-bond also did not have a significant effect on the characteristic pKa of site-1, but did have a strong effect on the Mn(II) zero-field interactions of A and B. In both cases, there was an inversion in the sign of the zero-field interaction (Table 2).
Figure 7.
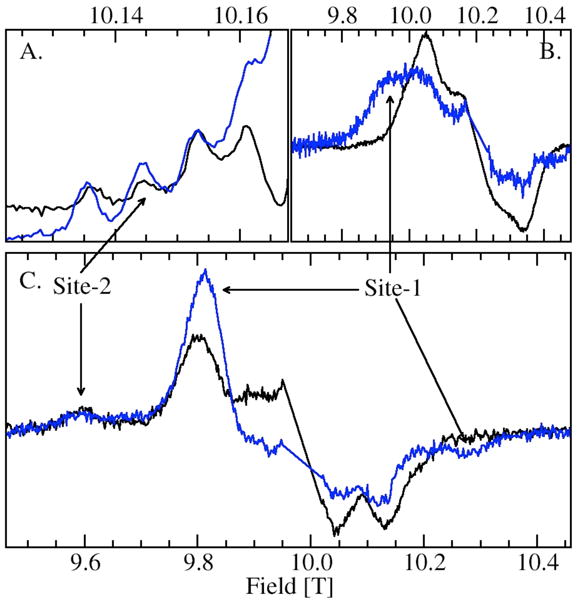
Comparison of the wild-type (black) and SENS161-4DSSN variant (blue) of JIC-OxdC: (A.) portion of the ms=−1/2→1/2 pH 8 HFEPR spectra showing the four hyperfine features corresponding to the five-coordinate site-2 Mn(II) center; (B.) ms=−5/2→−3/2 pH 8 spectrum of the site-1 region; (C.) ms=−5/2→−3/2 pH 4 (citrate) spectrum the spectra have normalized to site-2 feature at 9.6 T.
Comparison of the JIC- and UF-OxdC preparations
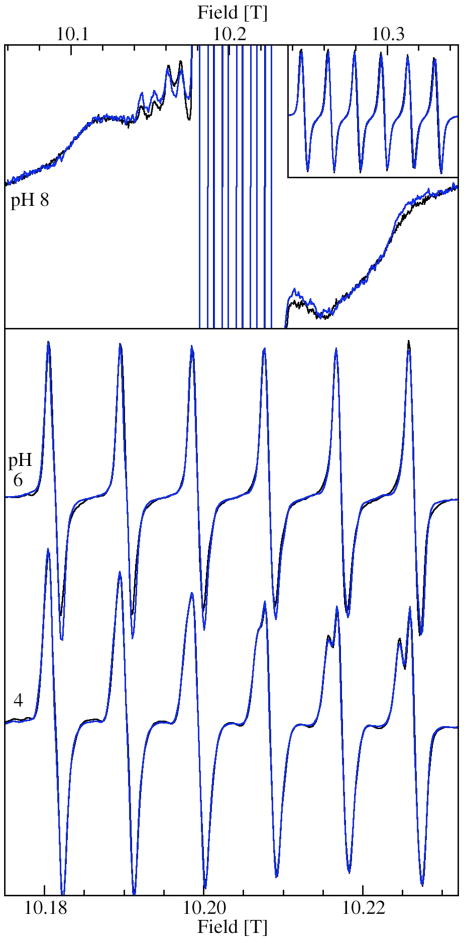
Identical pH-dependences were found in the samples of UF-OxdC (Figure 8), that is spectra were essentially identical at all pHs. Moreover, the relative amount of site-2 and site-1 were the same at pH 8 and 4. In the pH 8 spectrum, the broad underlying feature, as discussed above, arises mostly from the ms=−3/2→−1/2 spectrum of site-1, the contribution from site-2 being much broader and, hence, less intense. The resolved ms=−1/2→1/2 hyperfine features arising for site-2 in both JIC and UF preparations had the same relative intensity compared to the corresponding ms=−3/2→−1/2 features. At pH 4, ms=−1/2→1/2 spectrum was dominated by site-2 M(X) and site-1 A and their contribution was evidently the same in both JIC and UF-OxdC, since the spectra were identical. At pH 6, the ms=−5/2→−3/2 spectra of the two samples in HMTA buffer yielded the same spectra (data not shown). There were differences in the previously published ms=−1/2→1/2 spectra of the UF sample10 and of those shown in Figure 8. The spectra of initially isolated JIC samples were in fact identical to the former. However, buffer exchange or washing led in both UF and JIC cases to spectra shown in Figure 8. To test whether this was due to decoordination of specific or adventitious metal from the protein, a pH 6 UF sample in HMTA buffer that had the previously published spectrum was diluted to twice the volume with the same buffer containing 10 mM EDTA and reconcentrated to the original volume using ultrafiltration. No significant amounts of manganese ions were detected in the filtrate. Hence, there was no release of manganese from the protein. This was consistent with previous work which detected no free manganese after washing.10 However in our study, the spectrum of the washed reconcentrated protein was identical to those shown in Figure 8. Moreover aside from changes associated with pH, additional buffer exchanges and washings did not affect the spectra. A more detailed investigation is clearly needed. Nonetheless, it was evident that the JIC and UF-OxdC preparations behaved in an identical manner.
Figure 8.
Comparison of the ms=−1/2→1/2 HFEPR spectra of JIC (black) and UF-OxdC (blue): at pH 8, both in Tris (upper panel); pH 6 UF in HMTA and JIC in citrate; and pH 4 both in citrate (lower panel). The upper panel inset shows the site-1 portions of the spectra that have been truncated in the main panel.
Discussion
The JIC and UF samples were indistinguishable by HFEPR when prepared in the same manner. Despite having different Mn(II) contents (1.2 and 1.6 Mn/subunit, for JIC and UF samples respectively), the relative Mn(II) distribution between the two states appeared to be the same in both preparations at the three pHs where both samples were measured, in particular at pH 4 where OxdC is optimally active. This established that the His-tag used in the isolation of JIC-OxdC did not affect the HFEPR spectroscopy nor did it bind Mn(II) ions to any appreciable extent. The spectroscopic data also suggested that the higher metal content of the UF preparation was either lowered to that of the JIC preparation during buffer exchanges or all individual subunits containing Mn(II) had in fact both sites occupied. As describe above, it was unlikely that there was significant loss of manganese arising from washing or buffer exchanges. The distribution of manganese as determined from HFEPR measurements was roughly 0.6 ions in site-2 and 0.4 in site-1 and was the same for both preparations, independent of pH and unaffected by the SENS161-4DSSN mutation. The HFEPR spectra exhibited no sign of disorder or heterogeneity in the structure of the ligand-spheres of the two sites. The sharpness of resonances was comparable to other manganese binding proteins, such as MnSODs. The fact that pH dependent activities (see supporting information) were also nearly identical in both the UF and JIC samples strongly suggested that these two preparations were also biochemically very similar. A simple explanation for all these observations is that in both preparations all individual subunits containing Mn(II) had both sites occupied. More detailed spectroscopic work is required to establish this.
pH dependent structures
Since changes in the HFEPR spectra tracked changes in enzyme activity, it was likely that they reflected biochemically significant changes in the ligand-sphere. The HFEPR measurements showed unequivocally that the electronic structure of the site-2 in OxdC is able to take on at least three, if not four, distinct pH-dependent conformations. The large changes in not only the magnitude, but also the axiality of the Mn(II) zero-field interaction going from conformation H to M to L indicate changes in the geometry of the metal ion binding site (Scheme 1). As discussed in the introduction, the attribution of a particular set of Mn(II) zero-field parameters to a structure can only be qualitative. The exception was at high pH where crystallographic data was available.
Scheme 1.
The four pH-dependent structures of OxdC site-2. X and M differ by the position of the water ligand labeled a. Glu333 site-2 equivalent of Glu162 hydrogen-bonds the water in component X and M. The different proposals of component L: (upper) shows a bidentate glutamate or (lower) the glutamate ligand becomes protonated and is replaced by a chloride anion (orange).
The zero-field parameters of the high pH forms of the two sites, B and H, were entirely consistent with the six- and five-coordinate geometries of site-1 and site-2, respectively, that are seen in the pH 8 1UWA structure (Scheme 1). The values for H were the similar to those of centers in MnSODs that have same five ligands, but with geometry closer to a square-bipyramid. The zero-field interactions of the two sites at high pH differed by an order of magnitude. The nearly one order of magnitude smaller zero-field interaction of M (and X) compared to H likewise indicated that the coordination number of site-2 changed from 5 to 6 with a decrease in pH. Moreover, it appeared that at least in frozen solutions above pH 8, the five- (H) and six-coordinated (X) forms of site-2 might have both been present in equilibrium (Figure 6), similar to what has been encountered in MnSODs.16,32,35
The zero-field parameters, D~−1.4 and E~0.4 GHz, of X and M were very similar to those of six-coordinate Mn(II) of MnSODs with exogenous sixth ligands and, also, site-1 A and B (Table 2). In light of these similarities, it seemed likely that the structures of X and M resembled that of the pH 8 1J58 six-coordinate site-2 structure that had an additional water ligand compared to the 1UWA site-2. The difference in the zero-field interactions of X and M were small; hence, it was likely that they were structurally very similar. The spectral features of X were broader than those of M indicating that the zero-field parameters of the latter were more distributed. These observations suggest that the differences in X and M arose from small changes in protein electrostatic environment or the extent of disorder in the ligand sphere or both.
The site-2 zero-field interaction going from M to L underwent significant changes with the latter being considerably larger. The zero-field parameters were too small for a five-coordinate site, yet were certainly larger than those of component M and of the low-symmetry six-coordinate Mn(II) in manganese containing bacterial reaction center. Only the six-coordinate Mn(II) centers doped into bis(2-pyridylmethyl)amine complexes of Zn(II) (D= −7.1 GHz and E=0.1) was larger.33 The large D value of this doped center was likely due to the highly distorted geometry of the ligand spheres. Hence, one possibility was that L was highly distorted, for example as shown in Scheme 1 where Glu133 becomes a bidentate ligand at low pH. Chemically it is not clear what the driving force for such a rearrangement in the ligation would be. Recently, Hureau and coworkers have measured two synthetic six-coordinate Mn(II) complexes possessing a N5Cl donor set (Table 2). The larger of the two zero-field interactions was within 10% of that of L (Scheme 1). The manganese site in oxalate oxidase is thought to be able to bind chloride anions.36 It is worth noting that all OxdC samples possess large amounts of NaCl (200 to 500 mM) which was required to stabilize the high-concentrations of protein used. Hence, the large L zero-field may have resulted from chloride ligation (Scheme 1). Irrespective of the structure of L, its characteristic pKa of 4.6 closely matched the pH at which enzyme activity became optimal (pH 4.6, see supporting information). Although the pH dependence of the enzyme activity has been link to oxalate (pKa1=1.3 and pKa14.3)20, it may also be associated with the protein.
In contrast to site-2, A and B are likely to be very similar in structure. The small differences in their zero-field interactions likely represent subtle changes in the protein electrostatic environment rather than changes in the ligand sphere. As a point of comparison, it is possible to get slightly larger changes in the zero-field interaction by simply replacing the hydrogen-bond between Glu162 and a site-1 water ligand with a water-water hydrogen-bond, as is the case in the SENS161-4DSSN mutant (Figures 1 and 7). Nonetheless, since site-1 has been established as the site of catalytic activity24–27 and maximal enzyme activity is achieved only below pH 4.5 (see supporting information), it would appear that the low pH form of site-1, species A, is the most catalytically relevant. However, the fact that site-1 only undergoes subtle electronic structural changes with pH while site-2 most likely undergoes much larger modifications, even possibly changes in ligands, that correlate with activity suggests the possibility that the two manganese sites are not independent and influence each other.37
Application of HFEPR to Mn(II) centers in OxdC and in general
The use of both the ms=−1/2→1/2 and ms=−5/2→−3/2 spectra greatly facilitated our ability to assign and measure accurately zero-field interactions of the Mn(II) species in OxdC. Although the spectrum of the ms=−1/2→1/2 transition gave relatively sharp lines, the resolution was insufficient to unambiguously assign individual line-shape features, for example in the case where the spectrum of M overlaps with both A and B (Figure 3, left panel). The line-shape and resolution of the spectrum of the ms=−1/2→1/2 transition is determined by the second-order zero-field contributions. These contributions decrease with increasing observation frequency resulting in loss of resolution and the distinct zero-field line-shape. Although decreasing the observation frequency does increase the second-order zero-field contribution, this often leads to an increase in the complexity of the line-shapes. This can be readily seen in the richly complex spectrum of species H and also that of manganese superoxide dismutase.11 Hence in the presence of overlapping resonances, especially in cases where the relative contributions of specific components are unknown as is the case for site-2, spectra assignment purely based on the ms=−1/2→1/2 spectrum can be challenging no matter what frequency is used. By comparison, the spectrum of ms=−5/2→−3/2 does not depend on the observation frequency as long as it is much greater than the zero-field interaction and the shape of the spectrum can yield the zero-field parameters directly. However, the spectral resolution is low and problematic when there are multiple Mn(II) centers (Figure 4). The optimal method is to exploit both transitions and also their different dependence on observation frequency to achieve maximal information.
Supplementary Material
Acknowledgments
This work was supported in part by the Biotechnology and Biological Sciences Research Council with a Biochemistry and Cell Biology Committee studentship (to MRB) and a Core Strategic Grant to the John Innes Centre. JG gratefully acknowledges the Alexander von Humboldt foundation for a Feodor Lynen research fellowship; VLP, the NIH (GM39406) for support and LCT and CH, the CEA for postdoctoral positions. We also thank Nigel Richards and Mario Moral (University of Florida) for supplying samples of untagged, wild type OxDC. Their work is supported by the NIH (DK61666).
Footnotes
Enzyme activity as a function of pH; Resonant field equations governing the powder spectra shown in Figure 2; 95 GHz data; isotropic hyperfine and g-values; and complete citations for reference 29 and 38. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Papp-Wallace KM, Maguire ME. Annu Rev Microbiol. 2006;60:187. doi: 10.1146/annurev.micro.60.080805.142149. [DOI] [PubMed] [Google Scholar]
- 2.Zaharik ML, Finlay BB. Front Biosci. 2004;9:1035. doi: 10.2741/1317. [DOI] [PubMed] [Google Scholar]
- 3.Daly MJ, Gaidamakova EK, Matrosova VY, Vasilenko A, Zhai M, Venkateswaran A, Hess M, Omelchenko MV, Kostandarithes HM, Makarova KS, Wackett LP, Fredrickson JK, Ghosal D. Science. 2004;306:1025. doi: 10.1126/science.1103185. [DOI] [PubMed] [Google Scholar]
- 4.Culotta VC, Yang M, O’Halloran TV. Biochim Biophys Acta. 2006;1763:747. doi: 10.1016/j.bbamcr.2006.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tseng HJ, Srikhanta Y, McEwan AG, Jennings MP. Mol Microbiol. 2001;40:1175. doi: 10.1046/j.1365-2958.2001.02460.x. [DOI] [PubMed] [Google Scholar]
- 6.Holyoak T, Sullivan SM, Nowak T. Biochemistry. 2006;45:8254. doi: 10.1021/bi060269g. [DOI] [PubMed] [Google Scholar]
- 7.Gaffney BJ, Su C, Oliw EH. Appl Magn Reson. 2001;21:413. doi: 10.1007/bf03162417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Un S, Dorlet P, Voyard G, Tabares LC, Cortez N. J Am Chem Soc. 2001;123:10123. doi: 10.1021/ja016258m. [DOI] [PubMed] [Google Scholar]
- 9.Goldfarb D, Narasimhulu KV, Carmieli R. Magn Reson Chem. 2005;43:S40. doi: 10.1002/mrc.1668. [DOI] [PubMed] [Google Scholar]
- 10.Angerhofer A, Moomaw EW, Garcia-Rubio I, Ozarowski A, Krzystek J, Weber RT, Richards NG. J Phys Chem B. 2007;111:5043. doi: 10.1021/jp0715326. [DOI] [PubMed] [Google Scholar]
- 11.Un S, Tabares LC, Cortez N, Hiraoka BY, Yamakura F. J Am Chem Soc. 2004;126:2720. doi: 10.1021/ja036503x. [DOI] [PubMed] [Google Scholar]
- 12.Chakravarty AS. J Chem Phys. 1963;39:1004. [Google Scholar]
- 13.Newman DJ, Urban W. Adv Phys. 1975;24:793. [Google Scholar]
- 14.Carmieli R, Larsen TM, Reed GH, Zein S, Neese F, Goldfarb D. J Am Chem Soc. 2007;129:4240. doi: 10.1021/ja066124e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Duboc C, Phoeung T, Zein S, Pecaut J, Collomb MN, Neese F. Inorg Chem. 2007;46:4905. doi: 10.1021/ic062384l. [DOI] [PubMed] [Google Scholar]
- 16.Tabares LC, Cortez N, Hiraoka BY, Yamakura F, Un S. Biochemistry. 2006;45:1919. doi: 10.1021/bi051947m. [DOI] [PubMed] [Google Scholar]
- 17.Tabares LC, Cortez N, Un S. Biochemistry. 2007;46:9320. doi: 10.1021/bi700438j. [DOI] [PubMed] [Google Scholar]
- 18.Gätjens J, Sjodin M, Pecoraro VL, Un S. J Am Chem Soc. 2007;129:13825. doi: 10.1021/ja076024o. [DOI] [PubMed] [Google Scholar]
- 19.Tanner A, Bowater L, Fairhurst SA, Bornemann S. J Biol Chem. 2001;276:43627. doi: 10.1074/jbc.M107202200. [DOI] [PubMed] [Google Scholar]
- 20.Reinhardt LA, Svedruzic D, Chang CH, Cleland WW, Richards NGJ. J Am Chem Soc. 2003;125:1244. doi: 10.1021/ja0286977. [DOI] [PubMed] [Google Scholar]
- 21.Dunwell JM. Biotechnol Genet Eng Rev. 1998;15:1. doi: 10.1080/02648725.1998.10647950. [DOI] [PubMed] [Google Scholar]
- 22.Dunwell JM, Khuri S, Gane PJ. Microbiol Mol Biol Rev. 2000;64:153. doi: 10.1128/mmbr.64.1.153-179.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dunwell JM, Purvis A, Khuri S. Phytochemistry. 2004;65:7. doi: 10.1016/j.phytochem.2003.08.016. [DOI] [PubMed] [Google Scholar]
- 24.Just VJ, Stevenson CE, Bowater L, Tanner A, Lawson DM, Bornemann S. J Biol Chem. 2004;279:19867. doi: 10.1074/jbc.M313820200. [DOI] [PubMed] [Google Scholar]
- 25.Burrell MR, Just VJ, Bowater L, Fairhurst SA, Requena L, Lawson DM, Bornemann SB. Biochemistry. 2007;46:12327. doi: 10.1021/bi700947s. [DOI] [PubMed] [Google Scholar]
- 26.Just VJ, Burrell MR, Bowater L, McRobbie I, Stevenson CEM, Lawson DM, Bornemann S. Biochem J. 2007;407:397. doi: 10.1042/BJ20070708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Svedruzic D, Liu Y, Reinhardt LA, Wroclawska E, Cleland WW, Richards NGJ. Arch Biochem Biophys. 2007;464:36. doi: 10.1016/j.abb.2007.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Anand R, Dorrestein PC, Kinsland C, Begley TP, Ealick SE. Biochemistry. 2002;41:7659. doi: 10.1021/bi0200965. [DOI] [PubMed] [Google Scholar]
- 29.Schwarzenbacher R, et al. Proteins. 2004;56:392. [Google Scholar]
- 30.Un S, Dorlet P, Rutherford AW. Appl Mag Res. 2001;21:341. [Google Scholar]
- 31.Burghaus O, Plato M, Rohrer M, Moebius K, MacMillan F, Lubitz W. J Phys Chem. 1993;97:7639. [Google Scholar]
- 32.Tabares LC, Cortez N, Agalidis I, Un S. J Am Chem Soc. 2005;127:6039. doi: 10.1021/ja047007r. [DOI] [PubMed] [Google Scholar]
- 33.Glerup J, Goodson PA, Hodgson DJ, Michelsen K, Nielsen KM, Weihe H. Inorg Chem. 1992;31:4611. [Google Scholar]
- 34.Smoukov SK, Telser J, Bernat BA, Rife CL, Armstrong RN, Hoffman BM. J Am Chem Soc. 2002;124:2318. doi: 10.1021/ja012480f. [DOI] [PubMed] [Google Scholar]
- 35.Borgstahl GEO, Pokross M, Chehab R, Sekher A, Snell EH. J Mol Biol. 2000;296:951. doi: 10.1006/jmbi.1999.3506. [DOI] [PubMed] [Google Scholar]
- 36.Whittaker MM, Whittaker JW. J Biol Inorg Chem. 2002;7:136. doi: 10.1007/s007750100281. [DOI] [PubMed] [Google Scholar]
- 37.Recent work on the Mn-dependence of activity is consistent with the hypothesis that both sites are capable of catalyzing the decarboxylation reaction. (Richards, personal communication).
- 38.Frisch MJ, et al. Gaussian 03, Revision B.05. 2003 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.