Skip to main content
PMC home page
Plant Physiology logoLink to Plant Physiology
. 2009 Oct;151(2):949–954. doi: 10.1104/pp.109.138305

New Insights into the Mechanisms of Water-Stress-Induced Cavitation in Conifers

Hervé Cochard 1,*, Teemu Hölttä 1, Stéphane Herbette 1, Sylvain Delzon 1, Maurizio Mencuccini 1
PMCID: PMC2754640  PMID: 19641033

Abstract

Cavitation resistance is a key parameter to understand tree drought tolerance but little is known about the mechanisms of air entry into xylem conduits. For conifers three mechanisms have been proposed: (1) a rupture of pit margo microfibrils, (2) a displacement of the pit torus from its normal sealing position over the pit aperture, and (3) a rupture of an air-water menisci in a pore of the pit margo. In this article, we report experimental results on three coniferous species suggesting additional mechanisms. First, when xylem segments were injected with a fluid at a pressure sufficient to aspirate pit tori and well above the pressure for cavitation induction we failed to detect the increase in sample conductance that should have been caused by torus displacement from blocking the pit aperture or by membrane rupture. Second, by injecting xylem samples with different surfactant solutions, we found a linear relation between sample vulnerability to cavitation and fluid surface tension. This suggests that cavitation in conifers could also be provoked by the capillary failure of an air-water meniscus in coherence with the prediction of Young-Laplace's equation. Within the bordered pit membrane, the exact position of this capillary seeding is unknown. The possible Achilles' heel could be the seal between tori and pit walls or holes in the torus. The mechanism of water-stress-induced cavitation in conifers could then be relatively similar to the one currently proposed for angiosperms.

Since few decades of research on the deciphering of tree drought tolerance, experimental evidence has been accumulated on a key process (i.e. the xylem cavitation) to understand plant physiology, ecology, and chorology (Ewers et al., 1997; Hacke and Sperry, 2001; Tyree and Zimmermann, 2002). For trees, cavitation is involved in diebacks caused by extreme drought or freeze events (Cox and Malcolm, 1997; Brodribb and Cochard, 2009). In the 21st century, these extreme events may be exacerbated by climate change in ecosystems. Thus it is crucial to decipher the molecular mechanisms and to identify tree genome parts involved in the cavitation process to select candidate tree genotypes to future environmental conditions. The deciphering of cavitation mechanisms in trees is an essential step to identify candidate genes involved in this physiological process. However, these mechanisms remain astonishingly difficult to understand because experimental facts do not always corroborate the current paradigms. We have recently proposed a new hypothesis for freezing-induced cavitation in angiosperms (Lemoine et al., 1999) and conifers (Mayr et al., 2007). The aim of this study was to provide further insights into the mechanism of water-stress-induced cavitation in conifers.

The cavitation in trees is not caused by homogeneous nucleation in the bulk of the sap (Pickard, 1981; Tyree and Sperry, 1989). Indeed, water has a very high tensile strength (Caupin and Herbert, 2006) and homogeneous nucleation occurs only at a pressure much more negative than pressures typically measured in trees, even at low temperature (Cochard et al., 2007a). The current consensus is that cavitation occurs at the interface between the sap and the conduit walls in agreement with the air-seeding hypothesis (Crombie et al., 1985; Sperry and Tyree, 1988; Cochard et al., 1992; Tyree and Zimmermann, 2002). Cavitation spreads when an air bubble is aspirated from one conduit to another, most probably at the level of pits where the porosity in the wall is the highest.

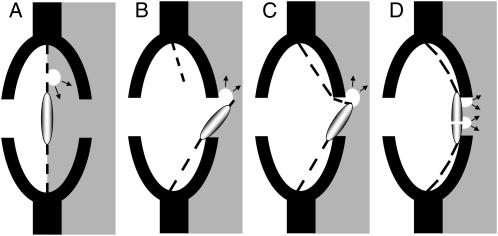
Pits in conifers look like microscopic trampolines with a central thickening (torus) surrounded by a web-like structure (margo) of microfibril strands. It has long been recognized that these pits behave as valves preventing the spreading of air into adjacent tracheids (Bailey, 1916). Sperry and Tyree (1990) were probably the first to propose a mechanism for the air-seeding hypothesis in conifers. Their experiments suggested that air seeding could form when the tori become displaced from their normal sealing position over the pit apertures. Theoretically, cavitation could then occur by elastic stretching of the margo (margo stretch seeding; Fig. 1C) or by rupture of the microfibril strands (margo rupture seeding; Fig. 1B; Hacke et al., 2004; Domec et al., 2006). According to these hypotheses, cavitation in conifers should be a function of margo mechanical properties. An experiment to test it is to inject stems with fluids under high pressure and to record changes in hydraulic conductance (Sperry and Tyree, 1990). However, in latewood tracheids, air seeding may also occur by capillary rupture of air-water menisci through pores in the pit margo (Domec and Gartner, 2002; margo capillary seeding; Fig. 1A). Direct observation of the structure of margo with a scanning microscope allows predictions of the threshold pressure causing this capillary rupture.

Figure 1.

Figure 1.

Open in a new tab

Hypothetic mechanisms of air seeding through a conifer pit membrane: margo capillary seeding (A), margo rupture seeding (B), margo stretch seeding (C), and capillary seeding at seal level between the torus and the pit wall or through a pore in the torus (D). The capillary-rupture mechanism (D) is supported by experiments conducted in this study.

We recently proposed an alternative mechanism for air seeding in conifers (Cochard, 2006). Considering that both the torus surface and the inner wall of the pit chamber are probably not perfectly smooth, the seal formed by the aspirated torus is likely to be slightly porous. In theory, air seeding could then be caused by the capillary rupture of air/water menisci located between the torus and pit wall aperture (Fig. 1D; seal capillary seeding). If the pit torus is porous, a torus capillary seeding may also be considered. Cavitation would then be a function of the seal or torus porosity and, a priori, less influenced by margo flexibility. According to the Young-Laplace equation for capillary rupture, one should expect a linear relationship between surface tension and air-seed pressure under this hypothesis. Similarly, the slope of the vulnerability curve should be inversely proportional to surface tension. This assumes that surface tension has no effect on membrane mechanics and hence air seeding by rupture or stretch seeding.

The aim of this study was to provide experimental assessments for the different possible mechanisms proposed for cavitation in conifers. We analyzed the structure of pit margo to assess the margo capillary-seeding mechanism. We manipulated sap surface tension to test the validity of the capillary-seeding hypothesis. Finally, injected segments under high pressure have been used to test margo stretch-seeding and rupture-seeding hypotheses.

RESULTS

Pit Wall Anatomy

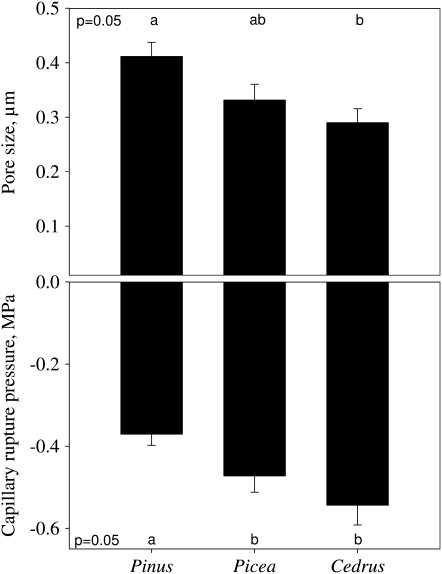
The pits of three species were the typical structure of conifers. Pit margo was porous and pores between the microfibrils were similar across species, although significantly larger in Pinus than in Cedrus (Fig. 2A). The estimated capillary rupture pressure of unaspirated margo averaged −0.5 MPa across species and was significantly less negative in Pinus (Fig. 2B). The resolution of our scanning electron microscopy (SEM) did not enable us to detect pores in the pit tori.

Figure 2.

Figure 2.

Open in a new tab

Average pore radius in the pit margo of three conifer species (top section). The corresponding capillary rupture pressure is shown on the bottom section. For all species, the capillary rupture pressure is much less negative than the actual measured pressure, indicating that cavitation was not caused by a rupture of a meniscus located in the pit margo. Error bars indicate the se.

Effects of Surface Tension on Xylem Cavitation

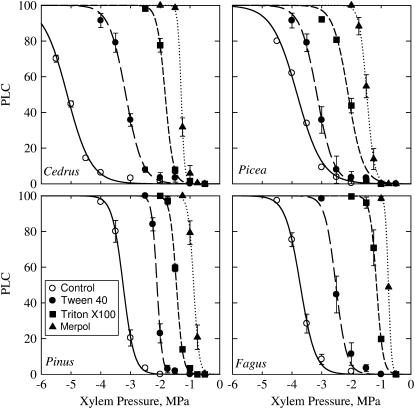
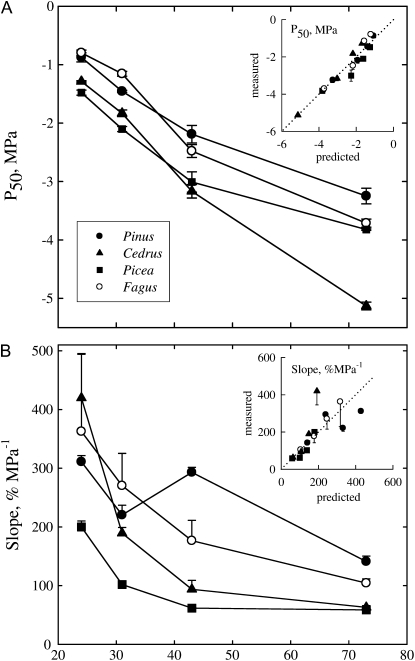
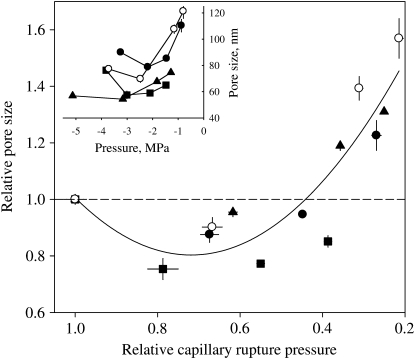
Reducing sap surface tension by addition of different surfactants strongly influenced the xylem vulnerability to cavitation in a similar fashion for analyzed species including Fagus (Fig. 3). Surfactants with lower surface tension strongly increased xylem vulnerability, which results in less-negative P50 values and steeper slopes. For each species, a significant (r2 > 0.9, P < 0.0001) linear relationship was found between P50 values and sap surface tension (Fig. 4A). Slopes of vulnerability curves were inversely proportional to surface tension (Fig. 4B). Assuming that surface tension alone determined the changes in P50 of injected samples with the different solutions, and using the samples with the reference ionic solution to estimate the critical pore radius for P50, we computed the theoretical P50 (Fig. 4A, inset) and slope values (Fig. 4B, inset) according to Equation 4. The predicted and actual values did not differ significantly (P > 0.72 paired Student's t test). This finding suggests that contact angle α in Equation 4 was probably constant across surfactants. According to Equation 4, we computed for each species and surfactants the mean pore size corresponding to each P50 value (Fig. 5). For all species, pore size tended to decrease first with increasing P50 values but sharply increased for the highest cavitation pressures (corresponding to the lowest surface tensions).

Figure 3.

Figure 3.

Open in a new tab

Effects of different surfactant on the xylem vulnerability curves of four tree species. The presence of surfactant in the xylem sap strongly increased xylem vulnerability for both coniferous and angiosperm species. Error bars indicate the se. Lines are best sigmoid fits.

Figure 4.

Figure 4.

Open in a new tab

Effect of sap surface tension on the xylem pressure provoking 50% loss of xylem conductance (A) and on the slope of the vulnerability curve at P50 for four tree species (B). Lowering water surface tension with different surfactants strongly increased both P50 and slope parameters for all species. The insets in A and B show the correlations between the measured P50 and slope values and the values predicted from a reduction of water surface tension alone according to Young-Laplace capillary equation. Error bars represent 1 se.

Figure 5.

Figure 5.

Open in a new tab

Relative and absolute (inset) variations of air-seeding pore sizes computed when cavitation pressure was modulated by manipulating surface tension. The pore size was derived from the Young-Laplace capillary equations for the different P50 values on four species (different symbols, same as in Fig. 4). Error bars indicate the se.

Effects of Surface Tension on Pit Wall Mechanics

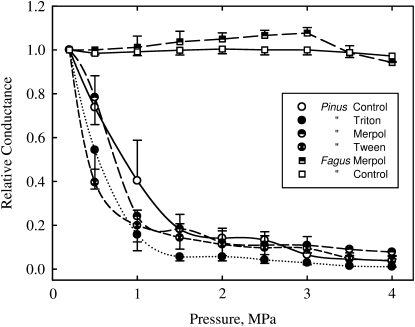
The hydraulic conductance of injected Pinus segments with the reference ionic solution was strongly reduced when fluid pressure was increased from 0 to +4 MPa (Fig. 6). Eighty percent loss of conductance was observed at +1.5 MPa. Further loss of conductance was only measured for pressures above +2.5 MPa. At +4 MPa sample conductance was reduced by 96% of its initial value. Samples treated with different surfactants behaved similarly, but the drop of conductivity from 0 to 1.0 MPa tended to be greater than for controls. However, no correlation was found between the relative conductance at 0.5 and 1 MPa and the P50 values determined in the previous experiment for Pinus (data not shown). Never a recovery in conductance at high pressure gradients was observed. By contrast, the hydraulic conductance of Fagus segments treated with the reference ionic solution or Merpol remained constant for pressures in the range of 0 to +4 MPa (Fig. 6).

Figure 6.

Figure 6.

Open in a new tab

Relative variations of xylem hydraulic conductance with increasing fluid pressure. Pinus and Fagus samples were perfused with water (white symbols) or different surfactant solutions. Error bars indicates the se.

DISCUSSION

Some mechanisms have been proposed to explain the entry of air through the coniferous pits. These hypotheses are illustrated in Figure 1. This study provides more insight into the validity of these mechanisms. In conifers, the anatomy of the xylem conduits can vary substantially within a ring, with earlywood tracheids having larger lumens and thinner walls than latewood ones. Similarly, the tracheids in reaction wood have a very peculiar anatomy. The vulnerability to cavitation can vary significantly for these different structures (Sperry and Tyree, 1990; Mayr and Cochard, 2003) and it is likely that the cavitation mechanism also differs between them (Domec and Gartner, 2002). Because the hydraulic conductivity of latewood and reaction wood tracheids is normally very low, our vulnerability curves should predominantly indicate the vulnerability of the large earlywood tracheids (Dalla-Salda et al., 2009). Hence, the tested mechanisms in our experiments are only relevant for the cavitation of earlywood tracheids.

The expected scenarios for air seeding in conifers can be classified according to their physical mechanisms. The pit margo rupture-seeding (Fig. 1B) and stretch-seeding (Fig. 1C) hypotheses are predominantly determined by the structural mechanics of the pits, i.e. the mechanical properties of the microfibril strands in the pit margo. By contrast, the pit margo (Fig. 1A) and pit torus capillary-seeding (Fig. 1D) mechanisms are determined by the failure to constrain the movement of the gas-liquid meniscus from one conduit to another, i.e. the porosity of these structures. In this study we have conducted different experiments to test these mechanisms.

Sperry and Tyree (1990) have suggested that cavitation-inducing tensions may be a function of pit membrane flexibility, more vulnerable species having more flexible membranes. Under this hypothesis, we should have observed a correlation between membrane flexibility and sap surface tension. Surfactants can impact the rheological properties of cellulosic fibers (Swerin, 1998; Amelina et al., 2000) and surface tension did modify membrane flexibility in Pinus as indicated by the greater drop in conductivity in the high pressure injection experiment (Fig. 6). However, membrane flexibility was not correlated with surface tension and pit vulnerability to cavitation in our study. Furthermore, if cavitation was caused by the rupture of the microfibril strands or by elastic stretching, allowing the tori to be pulled out through the pit apertures, we should have expected an increase in sample hydraulic conductance for fluid pressure above the cavitation pressure. This was hypothesized because the mechanical force exerted by the fluid under positive pressure on the pit membrane has the same in magnitude as the force generated when the sap has the opposite negative pressure. Our results obtained by injecting samples with pure water or with a low surface tension fluid did not confirm this hypothesis. However, our experiments were conducted on samples much longer than tracheid lengths that may have hindered the expected increase in conductance. Altogether, our results suggest that pit structural mechanics was probably not the main determinant of earlywood tracheid cavitation for the coniferous species. However, additional observations on more species and with more sophisticated techniques are clearly needed to confirm this point.

In a second set of experiments, we have analyzed the effect of sap surface tension on xylem cavitation. According to the Young-Laplace equation, surface tension should strongly impact the mechanisms involving a capillary rupture. Decreasing surface tension may also impact the stretch-seeding mechanism if surfactants decreased the coefficient of friction between the aspirated membranes (Osterberg, 2000; Salmi et al., 2007). However, the striking correlations between the parameters of vulnerability curves and their predictions from the Young-Laplace equation corroborate the hypothesis of the capillarity rupture as a mechanism for the penetration of air through the pits of coniferous species. A number of studies have reported an effect on surface tension on cavitation pressure for angiosperm species (Crombie et al., 1985; Sperry and Tyree, 1988; Choat et al., 2004) but to our knowledge, this is the first evidence for gymnosperms. The exact localization of the meniscus that may rupture and cause the entry of air into the tracheid remains speculative. A passage of air through the pores of pit margo would be consistent with this mechanism. However, the large size of pores in the pit margo predicts a seeding pressure much less negative than the one actually measured. This hypothesis can then be rejected, in agreement with previous conclusions (Sperry and Tyree, 1990). Moreover, Domec et al. (2006) reported for Pseudostuga menziesii that torus aspiration always occurs at a much higher pressure (less negative) than the pressure causing air seeding through pores in the membrane. Therefore, the porosity of the margo is probably small enough to seal the torus against the pit wall when tracheids cavitate (Hacke et al., 2004; Domec et al., 2006). Once this sealing has occurred, the porosity of the seal is no longer determined by the structure of the pit margo but by (1) the contact between the torus and the pit wall and (2) the porosity of torus itself. The contact surface between the pit wall and the torus often appears rugose or granular under scanning microscopy observations (Jansen et al., 2008). The porosity might be substantial and a capillary rupture at this level is a likely hypothesis. In addition, Jansen et al. (2008) have recently reported the presence of tiny pores in the tori of one conifer species. Theoretically, air seeding could also occur through these pores but the existence of such pores in other coniferous species has not yet been documented. Seal and torus capillary seeding could potentially be differentiated by analyzing how capillary pore sizes and cavitation pressures vary with surface tension. The pore size at the contact surface between the pit wall and the torus probably decreases when the force exerted on the torus increases. Hence, it is expected to find a monotonous decrease in porosity with more negative cavitation pressures. If cavitation occurs by air seeding through pores in the tori, the situation is probably more complex. Aspirated tori can be seen that has porous discs with finite thickness that undergo bending and stretching deformations when xylem pressures decrease. Lowering xylem pressures probably bends the torus, which implies that the convex side stretches, but the concave side of the disc (where air-water menisci are located) is compressed. Under more pulling forces caused by more negative sap pressures, the whole torus may start to stretch on both sides. If this scenario is correct pore size should not vary monotonously with cavitation pressures but should first decrease and then decrease with increasing pressures. The results shown in Figure 5 tend to support this hypothesis.

In conclusion, our results support a capillary failure mechanism for water-stress-induced cavitation in conifers. However, our results cannot absolutely rule out a role of surface tension in promoting rupture or stretch seeding via alterations of membrane mechanics. The mechanism could then be rather similar to the mechanism proposed for angiosperms. Under this hypothesis, the porosity of torus or seal between the torus and the inner pit chamber wall would be the Achilles' heel of the sap transport system. Analyses of pit structures in conifers are under way to validate these hypotheses.

MATERIALS AND METHODS

Plant Material

Experiments were conducted on tree species planted in the King's Buildings campus, Edinburgh University (Edinburgh, United Kingdom). Three conifers (Pinus sylvestris, Picea sitchensis, and Cedrus atlantica) were selected to cover a large range of cavitation resistance (Cochard, 2006). As a control, we also conducted experiments on one angiosperm tree (Fagus sylvatica) with moderate resistance to cavitation (Lemoine et al., 2002). Shoots were collected from sun-exposed branches of mature trees. To minimize possible intraspecific variations, all shoots were sampled on one tree for each species. Shoots were collected in the morning and analyzed during the same day. In the laboratory, 0.28-m-long samples were cut under tap water from the main shoot axis. For conifers, the bark was stripped off at each extremity. Sample diameter ranged from 5 to 9 mm.

Effects of Surface Tension on Xylem Cavitation

Xylem cavitation was assessed with the Cavitron technique (Cochard, 2002; Cochard et al., 2005), a technique derived from the centrifuge method of Alder et al. (1997). The technique uses the centrifugal force to increase the water tension in a xylem segment and, at the same time, measures the decrease of its hydraulic conductance. The curve of percentage loss of xylem conductance (PLC) versus xylem water tension indicates the sample vulnerability to cavitation.

Control samples were vacuum infiltrated with a reference ionic solution of 10 mm KCl and 1 mm CaCl2 in deionized ultrapure water. For experimental samples, different nonionic surfactants were added to this ionic solution. We selected three surfactants (Tween 40, Triton X-100, Merpol) to obtain a range of surface tension. The solutions (0.5% v/v) were above the critical micelle concentration. The surface tension of the different solutions was measured by the du Noüy platinum ring method using a torsion balance tensiometer (White Electric Instrument Co.). Surface tension ranged from 73 mN/m for the ionic solution to 24 mN/m for Merpol. Tween 40 and Triton X-100 were intermediate (43 and 31 mN/m, respectively). Samples were infiltrated until at least 5 mL had injected through the segments. This represented at least twice the total segment water content. Abundant bubble formation at the outlet of the segments was another indication that the solutions had completely displaced the sap in the conduit lumens.

Vulnerability curves were determined for three different samples for each treatment. During centrifugation, samples were injected with the same fluid as the one used to infiltrate them. Xylem pressure (P) was first set to a reference pressure (−0.5 MPa) and the sample maximal conductance (Kmax) was determined. The xylem pressure was then set to a more negative pressure and the new sample conductance K was determined again. The sample percent loss of conductance was then computed as PLC = 100 × (1 − K/Kmax). The procedure was repeated for more negative pressures (with −0.25 or −0.5 MPa step increments depending on segment vulnerability) until PLC reached at least 95%. Rotor velocity was monitored with an electronic tachymeter (10 rpm resolution) and xylem pressure was adjusted at approximately ±0.02 MPa. Following Pammenter and Vander Willigen (1998) and Cochard et al. (2007b), a sigmoid function was fitted to each curve:

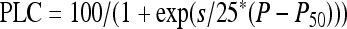graphic file with name M1.gif (1)

where P50 is the pressure causing 50 PLC and s is a slope parameter. P50 and s values were averaged for each treatment and t tests were used to compare treatments.

Pit Wall Mechanics

We tested whether sap surface tension affected pit wall mechanical properties by injecting, under varying pressure gradients, 0.28-m-long segments with the same solutions used in the previous experiment. Experiments were conducted on P. sylvestris and F. sylvatica was used as a control species.

Segments were first infiltrated with the different solutions as described before. The terminal end of each segment was then inserted in a pressure chamber positioned upside down and filled with the same solution. The solution was contained in a plastic reservoir fitted directly to the pressure chamber rubber seal. With this setup, less than 5 mm of the terminal sample end was in contact with the solution inside the chamber and no pressurized air was in contact with the sample. A water-filled tubing was fitted to the proximal sample end and connected to an analytical balance to measure the water flow F through the sample. The air pressure in the chamber was first adjusted to a pressure P equal to +0.2 MPa. The segment conductance K was then computed as:

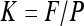graphic file with name M2.gif (2)

The pressure P in the chamber was then increased stepwise up to +4 MPa. Between each step, the pressure was increased slowly (typically at 5 kPa s−1) to minimize the variation in pressure gradient along the segment. At each step, the pressure was maintained constant until the water flow through the sample stabilized. Sample conductance was then computed following Equation 2.

Pit Wall Anatomy

Pit wall anatomy was assessed with a SEM microscope (model SEM 505, Philips) on sections obtained from control segments of previous experiments. Five-millimeter-long samples were split in half longitudinally with a razor blade and one axial surface was refreshed with a sliding microtome. The samples were dehydrated during 48 h in an oven and coated with evaporated gold under high vacuum. Thousands of pits were present on the sample cut surface, and a large number of them were sectioned in half, thus exposing their pit wall. For each species, we selected pits located in the earlywood and measured the long (r1) and short (r2) radius of the three biggest pores for four different pits. The capillary radius (r) of the pore was computed as:

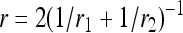graphic file with name M3.gif (3)

Following Young-Laplace equation, the capillary rupture pressure (Pm) of the margo is given by:

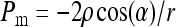graphic file with name M4.gif (4)

with ρ the surface tension of the water (73 mN/m) and α the contact angle between the meniscus and the pore. We assumed α = 0 for all the surfactants.

Acknowledgments

We are very grateful to David G. Biron for revising our manuscript.

The author responsible for distribution of materials integral to the findings presented in this article in accordance with the policy described in the Instructions for Authors (www.plantphysiol.org) is: Herve Cochard (cochard@clermont.inra.fr).

References

  1. Alder NN, Pockman WT, Sperry JS, Nuismer S (1997) Use of centrifugal force in the study of xylem cavitation. J Exp Bot 48: 665–674 [Google Scholar]
  2. Amelina EA, Shchukin ED, Parfenova AM, Pelekh VV, Vidensky IV, Bessonov AI, Aranovich G, Donohue M (2000) Effect of cationic polyelectrolyte and surfactant on cohesion and friction in contacts between cellulose fibers. Colloids Surf A Physicochem Eng Asp 167: 215–227 [Google Scholar]
  3. Bailey IW (1916) The structure of the bordered pits of conifers and its bearing upon the tension hypothesis of the ascent of sap in plants. Bot Gaz 62: 133–142 [Google Scholar]
  4. Brodribb T, Cochard H (2009) Hydraulic failure defines the recovery and point of death in water-stressed conifers. Plant Physiol 149: 575–584 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Caupin F, Herbert E (2006) Cavitation in water: a review. C R Phys 7: 1000–1017 [Google Scholar]
  6. Choat B, Jansen S, Zwieniecki MA, Smets E, Holbrook M (2004) Changes in pit membrane porosity due to deflection and stretching: the role of vestured pits. J Exp Bot 55: 1569–1575 [DOI] [PubMed] [Google Scholar]
  7. Cochard H (2002) A technique for measuring xylem hydraulic conductance under high negative pressures. Plant Cell Environ 25: 815–819 [Google Scholar]
  8. Cochard H (2006) Cavitation in trees. C R Phys 7: 1018–1026 [Google Scholar]
  9. Cochard H, Barigah T, Herbert E, Caupin F (2007. a) Cavitation in plants at low temperature: is sap transport limited by the tensile strength of water as expected from Briggs' z-tube experiment? New Phytol 173: 571–575 [DOI] [PubMed] [Google Scholar]
  10. Cochard H, Casella E, Mencuccini M (2007. b) Xylem vulnerability to cavitation varies among poplar and willow clones and correlates with yield. Tree Physiol 27: 1761–1767 [DOI] [PubMed] [Google Scholar]
  11. Cochard H, Cruiziat P, Tyree MT (1992) Use of positive pressures to establish vulnerability curves: further support for the air-seeding hypothesis and implications for pressure-volume analysis. Plant Physiol 100: 205–209 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Cochard H, Damour G, Bodet C, Tharwat I, Poirier M, Améglio T (2005) Evaluation of a new centrifuge technique for rapid generation of xylem vulnerability curves. Physiol Plant 124: 410–418 [Google Scholar]
  13. Cox RM, Malcolm JW (1997) Effects of duration of a simulated winter thaw on dieback and xylem conductivity of Betula papyrifera. Tree Physiol 17: 389–396 [DOI] [PubMed] [Google Scholar]
  14. Crombie DS, Milburn JA, Hipkins MF (1985) Maximum sustainable xylem sap tensions in Rhododendron and other species. Planta 163: 27–33 [DOI] [PubMed] [Google Scholar]
  15. Dalla-Salda G, Martinezmeier A, Cochard H, Rozenberg P (2009) Variation of wood density and hydraulic properties of Douglas-fir (Pseudotsuga menziesii (mirb.) Franco) clones related to a heat and drought wave in France. For Ecol Manag 257: 182–189 [Google Scholar]
  16. Domec JC, Gartner BL (2002) How do water transport and water storage differ in coniferous earlywood and latewood? J Exp Bot 53: 2369–2379 [DOI] [PubMed] [Google Scholar]
  17. Domec JC, Lachenbruch BL, Meinzer FC (2006) Bordered pit structure and function determine spatial patterns of air-seeding thresholds in xylem of Douglas-fir (Pseudotsuga menziesii; Pinaceae) trees. Am J Bot 93: 1588–1600 [DOI] [PubMed] [Google Scholar]
  18. Ewers FW, Cochard H, Tyree MT (1997) A survey of root pressures in vines of a tropical lowland forest. Oecologia 110: 191–196 [DOI] [PubMed] [Google Scholar]
  19. Hacke UG, Sperry JS (2001) Functional and ecological xylem anatomy. Perspect Plant Ecol Evol Syst 4: 97–115 [Google Scholar]
  20. Hacke UG, Sperry JS, Pittermann J (2004) Analysis of circular bordered pit function. ii. Gymnosperm tracheids with torus-margo pit membranes. Am J Bot 91: 386–400 [DOI] [PubMed] [Google Scholar]
  21. Jansen S, Pletsers A, Sano Y (2008) The effect of preparation techniques on SEM-imaging of pit membranes. IAWA J 29: 161–178 [Google Scholar]
  22. Lemoine D, Cochard H, Granier A (2002) Within crown variation in hydraulic architecture in beech (Fagus sylvatica L.): evidence for a stomatal control of embolism. Ann Sci 59: 19–27 [Google Scholar]
  23. Lemoine D, Granier A, Cochard H (1999) Mechanism of freeze-induced embolism in Fagus sylvatica L. Trees (Berl) 13: 206–210 [Google Scholar]
  24. Mayr S, Cochard H (2003) A new method for vulnerability analysis of small xylem areas reveals that compression wood of Norway spruce has lower hydraulic safety than opposite wood. Plant Cell Environ 26: 1365–1371 [Google Scholar]
  25. Mayr S, Cochard H, Ameglio T, Kikuta SB (2007) Embolism formation during freezing in the wood of Picea abies. Plant Physiol 143: 60–67 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Osterberg M (2000) The effect of a cationic polyelectrolyte on the forces between two cellulose surfaces and between one cellulose and one mineral surface. J Colloid Interface Sci 229: 620–627 [DOI] [PubMed] [Google Scholar]
  27. Pammenter NW, Vander Willigen C (1998) A mathematical and statistical analysis of the curves illustrating vulnerability of xylem to cavitation. Tree Physiol 18: 589–593 [DOI] [PubMed] [Google Scholar]
  28. Pickard WF (1981) The ascent of sap in plants. Prog Biophys Mol Biol 37: 181–229 [Google Scholar]
  29. Salmi J, Osterberg M, Laine J (2007) The effect of cationic polyelectrolyte complexes on interactions between cellulose surfaces. Colloids Surf A Physicochem Eng Asp 297: 122–130 [Google Scholar]
  30. Sperry JS, Tyree MT (1988) Mechanisms of water stress-induced xylem embolism. Plant Physiol 88: 581–587 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Sperry JS, Tyree MT (1990) Water-stress-induced xylem embolism in three species of conifers. Plant Cell Environ 13: 427–436 [Google Scholar]
  32. Swerin A (1998) Rheological properties of cellulosic fibre suspensions flocculated by cationic polyacrylamides. Colloids Surf A Physicochem Eng Asp 133: 279–294 [Google Scholar]
  33. Tyree MT, Sperry JS (1989) Vulnerability of xylem to cavitation and embolism. Annu Rev Plant Physiol Plant Mol Biol 40: 19–38 [Google Scholar]
  34. Tyree MT, Zimmermann M (2002) Xylem Structure and the Ascent of Sap, Ed 2. Springer-Verlag, Berlin

Articles from Plant Physiology are provided here courtesy of Oxford University Press

RESOURCES