A method to generate equivalent energy spectra and filtration models based on measurement for multidetector CT Monte Carlo dosimetry simulations

Abstract

The purpose of this study was to present a method for generating x-ray source models for performing Monte Carlo (MC) radiation dosimetry simulations of multidetector row CT (MDCT) scanners. These so-called “equivalent” source models consist of an energy spectrum and filtration description that are generated based wholly on the measured values and can be used in place of proprietary manufacturer’s data for scanner-specific MDCT MC simulations. Required measurements include the half value layers (HVL₁ and HVL₂) and the bowtie profile (exposure values across the fan beam) for the MDCT scanner of interest. Using these measured values, a method was described (a) to numerically construct a spectrum with the calculated HVLs approximately equal to those measured (equivalent spectrum) and then (b) to determine a filtration scheme (equivalent filter) that attenuates the equivalent spectrum in a similar fashion as the actual filtration attenuates the actual x-ray beam, as measured by the bowtie profile measurements. Using this method, two types of equivalent source models were generated: One using a spectrum based on both HVL₁ and HVL₂ measurements and its corresponding filtration scheme and the second consisting of a spectrum based only on the measured HVL₁ and its corresponding filtration scheme. Finally, a third type of source model was built based on the spectrum and filtration data provided by the scanner’s manufacturer. MC simulations using each of these three source model types were evaluated by comparing the accuracy of multiple CT dose index (CTDI) simulations to measured CTDI values for 64-slice scanners from the four major MDCT manufacturers. Comprehensive evaluations were carried out for each scanner using each kVp and bowtie filter combination available. CTDI experiments were performed for both head (16 cm in diameter) and body (32 cm in diameter) CTDI phantoms using both central and peripheral measurement positions. Both equivalent source model types result in simulations with an average root mean square (RMS) error between the measured and simulated values of approximately 5% across all scanner and bowtie filter combinations, all kVps, both phantom sizes, and both measurement positions, while data provided from the manufacturers gave an average RMS error of approximately 12% pooled across all conditions. While there was no statistically significant difference between the two types of equivalent source models, both of these model types were shown to be statistically significantly different from the source model based on manufacturer’s data. These results demonstrate that an equivalent source model based only on measured values can be used in place of manufacturer’s data for Monte Carlo simulations for MDCT dosimetry.

INTRODUCTION

The use of multidetector row CT (MDCT) imaging is escalating, resulting in a considerable increase in the contribution from CT scans to the estimated collective radiation dose from medical procedures.^{1, 2, 3} In order to understand and quantify the risk associated with MDCT examinations, efforts have been made to more accurately determine the radiation dose to individual radiosensitive organs, which are important quantities used to calculate metrics such as effective dose^{4, 5} and cancer risk.^{6, 7, 8}

Monte Carlo (MC) radiation transport packages designed to simulate specific scanner makes and models have become a popular method to calculate organ dose from MDCT.⁹ MC codes are typically coupled to computational anthropomorphic phantoms that model patient anatomy of varying shapes and sizes for both genders and a range of ages.¹⁰ Multiple groups adopted this approach and developed MC simulation software to investigate organ dose from various MDCT scanning protocols to adult patients, pediatric patients, and even to estimate fetal dose.^{11, 12, 13, 14, 15}

An accurate MDCT MC simulation typically requires a detailed description of the scanner under investigation, including specifications of the photon energy spectrum, the bowtie and inherent filtration design, and the geometry of the scanner (e.g., focal spot to isocenter distance, fan angle, z-axis collimation, and cone angle settings). It is usually possible to ascertain the necessary geometry from documentation of scanner specifications. However, scanner-specific source descriptions that include filtration designs and spectra are typically proprietary, so vendor cooperation through nondisclosure agreements (or equivalent) has been required to obtain this information. While in some cases published generalized tungsten anode energy spectra, either from empirically measured or theoretical models, have been used in MC simulations,¹⁶ there is no such published data on the design of bowtie and inherent filtration, which may vary considerably from scanner to scanner. As a consequence, MDCT MC dosimetry simulations have been performed by a limited number of researchers who normally can only investigate a small subset of existing scanners for which they have obtained confidential information to build their source models.

In order to overcome such restrictions, the purpose of this work is to introduce a method to construct source models that only requires physical measurements and calculations. The goal of this method is to generate an “equivalent” source model that consists of two parts. The first part is an equivalent energy spectrum, defined as “an idealized energy spectrum that results in identical attenuation properties as the actual spectrum of a given x-ray tube.”¹⁷ The second part is an equivalent filter description, defined as an idealized filter that attenuates the equivalent spectrum in the same manner that the actual filter attenuates the actual spectrum (including bowtie filtration and its variation across the fan angle). Such an approach obviates the need for obtaining proprietary information and allows the generation of source models to characterize any given scanner. Since this method is designed to require only measured data taken from the scanner of interest, it should result in more accurate scanner-specific MC dosimetry simulations compared to those that use generic source models.

In this study we will first present the scanner measurements and calculations necessary to generate equivalent source models. Then, the predictive accuracy of equivalent source model MDCT MC simulations will be assessed by comparing the results of multiple CT dose index (CTDI) simulations performed using equivalent source models with a previously presented MC software package¹¹ to physically measured CTDI values. Finally, equivalent source model simulations will be evaluated relative to conventional manufacturer-based source model simulations, first by comparing the accuracy of CTDI simulations using each type of source model and then through an analysis of variance to determine if these source models produce statistically different simulation results.

MATERIALS AND METHODS

CT scanner models

The CT scanners

To investigate the robustness of the proposed method, 64-slice CT scanners from four major CT scanner manufacturers were included in this study: The LightSpeed VCT (General Electric Medical Systems, Waukesha, WI), SOMATOM Sensation 64 (Siemens Medical Solutions, Inc, Forcheim, Germany), Philips Brilliance CT 64 (Philips Medical Systems, Cleveland, Ohio), and Toshiba Aquilion 64 (Toshiba Medical Systems, Inc., Otawara-shi, Japan). Each of these is a third generation, multidetector row CT scanner that supports multiple nominal beam collimation settings as well as multiple beam energies. Each scanner is equipped with x-ray beam filtration that includes from one to three bowtie filter combinations. For this study each different scanner and bowtie filter combination was assessed separately (the GE LightSpeed VCT has three bowtie filter settings, the Toshiba Aquilion 64 has two, while the Siemens Sensation 64 and Philips Brilliance 64 each has one, resulting in seven unique scanner∕bowtie filter combinations). Each of the scanner∕bowtie filter combinations was randomly assigned a reference letter, either A, B, C, D, E, F, or G and will be referred to by their assigned letter from this point on.

Source models based on manufacturer-provided information

Data describing the x-ray source for each scanner described in Sec. 2A1 were obtained from the manufacturers under a nondisclosure agreement. Each manufacturer provided a description of the x-ray energy spectra representing the relative number of photons at each energy level for each available kVp setting. Additionally, they provided specifications of scanner filtration by specifying the dimensions and materials of all available bowtie filters as well as the design of any other inherent filtration. The scanner geometry necessary for the MC simulations, namely, the focal spot to isocenter distance and fan angle, was also obtained directly from the manufacturers; however, this information is usually available in user manuals or specification sheets included in the CT scanner documentation.

Measurements to generate equivalent source models

Overview of physical measurements used to generate equivalent source models

The scanner measurements required in this method are generally not part of routine medical physics measurements for CT but can be performed reasonably quickly and efficiently with commonly used equipment. It should be noted that some scanners must be put into service mode because these measurements are performed with a nonrotating (parked) gantry. For each scanner∕bowtie filter combination, two types of measurements were obtained: (a) First and second half value layers (HVL₁ and HVL₂) and (b) bowtie filter attenuation profiles. Each requires a set of exposure measurements, which were performed with a standard 100 mm pencil ionization chamber (ion chamber) and calibrated electrometer.

Half value layer measurements

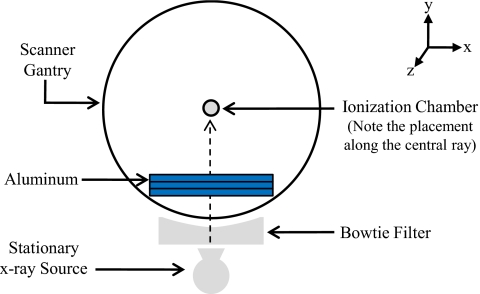
The method used to measure MDCT HVLs is similar to standard HVL measurements used for conventional radiograph machines. The gantry was parked so that the x-ray tube remained stationary at the 6 o’clock position. The ion chamber was fixed along the central ray (directly above the stationary x-ray tube), ensuring that the table was not in the x-ray beam path, at a distance above the source sufficient to establish good measurement geometry (for all measurements the ion chamber was positioned at or above the scanner isocenter). An initial exposure value was taken using a particular kVp, mA s, and collimation setting. Additional exposure measurements were obtained using the same settings, adding thin slabs (0.5–2.0 mm) of type 1100 alloy aluminum in the beam path until the resulting exposure was less than half the initial value to obtain the HVL₁ and less than a quarter of the initial value to obtain the HVL₂. The experimental setup is illustrated in Fig. 1. For scanner∕bowtie filter combination A–G, measurements were performed to determine the HVL₁ and HVL₂ for all available beam energies.

Figure 1.

Diagram of HVL measurement set up.

Bowtie profile measurements

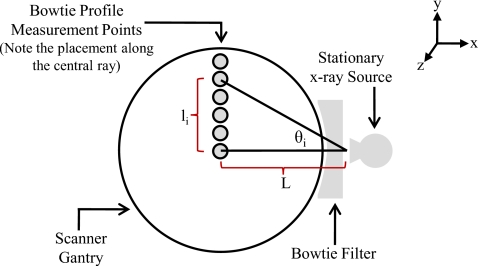
Bowtie profile measurements were performed to characterize the attenuation of the actual spectrum across the fan beam due to the scanner’s bowtie and inherent filtration. The gantry was parked so that the x-ray tube was fixed at the 3 o’clock position. The ion chamber was clamped to a ring stand, which was placed so that the active portion of the chamber was not directly above the patient table. The table was adjusted so that the ion chamber was initially centered at the scanner isocenter. Using 120 kVp, 300 mA s, and a fixed collimation setting (a single beam energy, tube current, and collimation was sufficient for this method), exposure measurements were incrementally obtained by moving the table in 5–10 mm intervals in the +y direction in order to profile the exposure attenuation from the upper half of the bowtie filter. A diagram of this setup is shown in Fig. 2. Because the range of the table’s vertical motion was usually insufficient to sample the entire upper half of the fan beam, the necessary data were acquired by (1) initially clamping the ion chamber to the base of the ring stand, then (2) incrementing the table position vertically to its limit, then (3) sliding the chamber a known vertical distance in the +y direction along the ring stand and lowering the table by the same distance, and finally (4) continuing the vertical table incrementation in the +y direction until the entire upper half of the axial plane (i.e., the half fan angle) was sampled. It is assumed that the attenuation profile in the axial plane is symmetric about the central ray (θ_i=0 in Fig. 2), so only measuring the upper half of the bowtie’s attenuation is sufficient.

Figure 2.

Diagram of bowtie profile measurements of attenuation across the fan beam.

The value of the angle for a given measurement, θ_i in Fig. 2, was calculated using the manufacturer-provided focal spot to isocenter distance L- and the vertical distance the ion chamber was moved from isocenter l_i,

$${\theta }_i={\tan }^{-1}(l_i∕L).$$ (1)

This procedure was carried out to obtain bowtie profile measurements for scanner∕bowtie filter combination A–G using the scan protocol described above.

Computational methods to generate the equivalent source models

Overview of equivalent spectrum generation algorithm

The goal of the first part of the source generation algorithm is to produce an equivalent spectrum for a given scanner, bowtie filter setting, and beam energy characterized by HVLs similar to those physically measured. This approach does not assume prior knowledge of the scanner’s actual spectrum or filtration scheme. Three inputs are necessary for this algorithm: (a) The HVL measurements for the scanner of interest, (b) an initially soft (low average energy and therefore small HVL) tungsten anode x-ray energy spectrum, and (c) an arbitrarily defined description of the material and central ray thickness of a corresponding equivalent bowtie filter (which will remain constant throughout this process). Specifically, this approach assumes an equivalent bowtie filter composed of aluminum with a central ray thickness of 0.5 mm. While this may not be the actual material or central ray thickness for any actual bowtie filter, this assumption will be shown to be reasonably robust for this methodology. The general algorithm is outlined in this section and details are provided in subsequent sections.

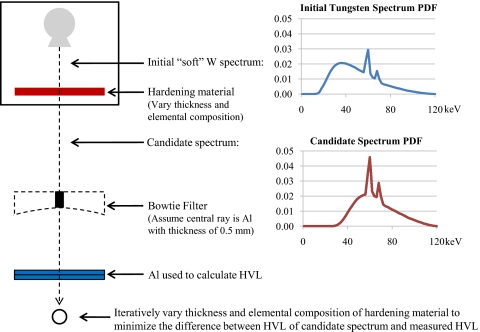
The following steps, illustrated in Fig. 3, are used to obtain the equivalent spectrum: (1) The input soft tungsten anode spectrum [represented by the upper probability density function (PDF) in Fig. 3] is transmitted through a very thin, uniform sheet of an arbitrarily defined “hardening” material and the number of remaining x-ray photons at each energy is calculated, assuming exponential attenuation, producing a “candidate” spectrum (represented by the lower PDF in Fig. 3), (2) then the spectrum resulting from transmitting the candidate spectrum through the central ray of the bowtie is calculated and the associated KERMA in air is subsequently computed by summing the product of the energy fluence and the mass energy-absorption coefficient for air over all energies, (3) next the spectrum resulting from transmitting the candidate spectrum through the central ray of the bowtie plus a very thin, uniform sheet of aluminum is calculated and the KERMA in air is again computed, and (4) then step (3) is repeated while incrementally increasing the thickness of aluminum by 1.0 μm until the calculated KERMA in air is a factor of 2 and then a factor of 4 less than the initial KERMA in air obtained in step (2). Since KERMA in air is directly proportional to exposure, these thicknesses of aluminum represent the HVL₁ and HVL₂ of the candidate spectrum. Steps (1)–(4) are repeated while incrementally increasing the thickness of the hardening material (thus increasing the HVLs of the candidate spectrum) by 10.0 μm until the difference between the candidate spectrum’s calculated HVLs and the measured values is minimized. Since this method assumes that the exact material and design of the filtration are unknown, the entire process is repeated using various hardening materials that are often used in scanner construction, namely, aluminum, graphite, lead, and titanium. The candidate spectrum with calculated HVLs that best match the measured HVLs, regardless of the hardening material type, is deemed the equivalent spectrum.

Figure 3.

Illustration of method for generating equivalent spectrum from measured HVL.

The initial tungsten spectrum referred to in step (1) was obtained using Boone and Seibert’s tungsten anode spectral model using interpolating polynomials (TASMIPs).¹⁸ Siewerdsen et al. created SPEKTR, a MATLAB (the MathWorks, Natick, MA) tool that allows a user to obtain TASMIP spectra with an energy resolution of 1.0 keV from the TASMIP library while specifying the beam energy (kVp), percent voltage ripple, and any beam filtration.¹⁹ For each kVp setting available on the scanners described in Sec. 2A1, a soft tungsten spectrum was obtained via the SPEKTR tool using no added filtration and 25% voltage ripple. In each instance, this created an initial spectrum with sufficiently low average beam energy and thus initial HVLs that are less than any of the measured HVLs. The exponential attenuation and KERMA in air calculations were performed using the photon mass attenuation coefficients (μ∕ρ) and mass energy-absorption coefficients (μ_en∕ρ) for air, reported by Hubbell and Seltzer,²⁰ respectively.

Equivalent spectrum generation algorithm using both HVL₁ and HVL₂

The HVL₂ is the highest order descriptor of a particular x-ray beam obtained in the measurements described in Sec. 2B2, so equivalent spectra were first generated to match the measured HVL₂ values. Specifically, the algorithm described in the previous section was carried out to produce candidate spectra for each hardening material type which had calculated HVL₂ values approximately equal to the measured HVL₂ values. For each specific hardening material and thickness that yields the best estimate of HVL₂, the HVL₁ was also calculated. The equivalent spectrum was chosen as the candidate spectrum that both matched HVL₂ and simultaneously had a calculated HVL₁ that best matched the measured HVL₁. For scanner∕bowtie filter combination A–G, the equivalent spectra were generated using HVL₁ and HVL₂ measurements for all available beam energies using routines coded in MATLAB. Source models using spectrum resulting from this algorithm will be denoted as the HVL₁&HVL₂ source models.

Equivalent spectrum generation algorithm using only HVL₁

Another set of equivalent spectra was generated in a manner similar to that described in Sec. 2C2 with the exception that only the measured HVL₁ was considered. These alternative forms of equivalent spectra allowed us to investigate the necessity of measuring the HVL₂, which can be cumbersome. Again, the algorithm described in Sec. 2C1 was carried out to produce a candidate spectrum for each of the hardening material types, but in this case the spectrum was generated so that its calculated HVL₁ approximately matched the measured HVL₁. The equivalent spectrum was then determined by simply selecting the candidate spectrum whose calculated HVL₁ had the best agreement with the measured value. For scanner∕bowtie filter combination A–G, the equivalent spectra were generated using only HVL₁ values for all available beam energies using routines coded in MATLAB. Source models using spectrum resulting from this algorithm will be denoted as the HVL₁ source models.

Equivalent bowtie filter generation algorithm

The second part of the source generation algorithm is performed after acquiring an equivalent spectrum. The goal of this part is to obtain a description of an equivalent bowtie filter (filtration path length as a function of θ in Fig. 2) that attenuates the equivalent spectrum in the same manner that the actual bowtie filter attenuates the actual x-ray beam across the entire fan angle. For this part of the algorithm, the following inputs are necessary: (a) The equivalent spectrum (generated using the methods described in either Sec. 2C2 or Sec. 2C3) for the scanner∕bowtie filter combination and beam energy of interest, and (b) the bowtie profile measurements made for the same scanner∕bowtie filter combination. As stated in Sec. 2C1, the equivalent bowtie material is arbitrarily defined to be aluminum with a central ray thickness of 0.5 mm.

Again utilizing the fact that exposure is directly proportional to KERMA in air, the equivalent path length of aluminum for a given bowtie profile measurement angle θ_i is generated from the following steps: (1) Using the bowtie profile measurement data, the ratio of the measured exposure at θ_i to the measured central ray exposure is computed: (2) then the equivalent spectrum is numerically transmitted through the center portion of the equivalent bowtie, again assuming an exponential attenuation, and the subsequent KERMA in air is calculated, as described in Sec. 2C1: (3) next the equivalent spectrum is transmitted through a very thin, uniform sheet of aluminum and the subsequent KERMA in air is calculated; (4) then the ratio of the KERMA in air obtained in step (3) to the KERMA in air from step (2) is computed: and (5) steps (3) and (4) are repeated while incrementally increasing the thickness of aluminum by 1.0 μm until the difference between the values obtained in step (1) (measured exposure ratio) and step (4) (calculated exposure ratio) is minimized. The resulting thickness of aluminum is deemed the equivalent path length for θ_i. This process is repeated for each measurement angle sampled in the bowtie profile measurements producing the equivalent bowtie filter description.

The method to iteratively determine the aluminum bowtie filter path length for each measured angle was implemented using routines coded in MATLAB. This algorithm was carried out using each of the equivalent spectra generated in Secs. 2C2, 2C3. The result was a complete set of equivalent source models (e.g., spectrum and bowtie description) based on both HVL₁ and HVL₂ measurements (HVL₁&HVL₂ models) as well as a complete set of equivalent source models based solely on HVL₁ measurements (HVL₁ models) for each scanner∕bowtie filter combination A–G at each available beam energy.

Overview of the Monte Carlo method

Monte Carlo simulations

All simulations were performed using the MCNPX (MCNP eXtended version 2.6.d) Monte Carlo code.^{21, 22} Simulations were performed using only photons with a low-energy cutoff of 1 keV. The photon transport model does not explicitly create photoelectrons but instead assumes that all deposited energies are absorbed at the photon interaction site resulting in a condition of charged particle equilibrium (CPE). Under the assumption of CPE, collision KERMA is equal to the absorbed dose. So for each simulated photon, the absorbed dose to the volume of interest in the phantom was calculated by tallying the photon energy fluence and converting to collision KERMA, again using the mass energy-absorption coefficients obtained by Hubbell and Seltzer.²⁰

Modeling of the CT source

As described in previous publications,^{10, 11} modifications were made to the standard MCNP source code to model the possible x-ray source positions, photon energies, and initial photon trajectories of various CT scan protocols. Since standard CTDI₁₀₀ measurements were being simulated, this work only utilized single axial scans. The longitudinal beam width is modeled using the full width at half maximum (FWHM) value of the radiation beam profile obtained from OSL measurements made for each collimation setting on each scanner (as opposed to the nominal collimation value). The energy of each simulated photon is obtained by sampling the energy spectrum for the scanner of interest. Attenuation due to scanner filtration is modeled by first looking up the filter material and path length corresponding to the trajectory of the photon from the filtration description. Then, the resulting attenuation is calculated using the photon mass attenuation coefficients and applied as a MCNP source weight factor.

CTDI₁₀₀ phantom and pencil ion chamber model

Conventional CTDI₁₀₀ experiments using the standard head (16 cm in diameter) and body (32 cm in diameter) phantoms were used for validation and comparison purposes.²³ These phantoms are polymethylmethacylate (PMMA) cylinders that are 15 cm in length. They both have five sockets that will accept a PMMA insert or the ion chamber, one at the center and four 1 cm below the phantom surface, each 90° apart from its neighbor. The phantoms, inserts, and the ion chamber were all simulated using standard MCNP geometry and material descriptions. The ion chamber was explicitly modeled as two concentric cylinders, with a 1.6 mm thick outside cylindrical shell consisting of C552 to model the chamber wall and an inner cylinder of air that is 3.4 cm in diameter and 10 cm in length to represent the active portion of the chamber.

CTDI₁₀₀ simulation and measurement experiments

Using a particular scanner∕bowtie filter combination and beam energy, a series of CTDI₁₀₀ measurements (in mGy∕mA s) were obtained at both the center and periphery (12 o’clock) positions for both CTDI phantoms. Analogous CTDI₁₀₀ simulations were performed using three different source model types: Those based on information provided by the manufacturer described in Sec. 2A2, the HVL₁ equivalent source models described in Sec. 2C3, and the HVL₁&HVL₂ equivalent source models described in Sec. 2C2. MCNP tally results are reported in mGy∕source particle, so normalization factors calculated from air scan measurements (CTDI₁₀₀ in air in mGy∕mA s) and corresponding air simulations (in mGy∕source particle) were applied to obtain simulated CTDI₁₀₀ values in units of mGy∕mA s, as described by DeMarco et al.¹⁰

CTDI_100,center and CTDI_{100,periphery} measurements and simulations were performed for scanner∕bowtie filter combinations A–G at each available beam energy. The possible kVp settings varied among the scanner manufacturers. Four of the scanner∕bowtie filter combinations (A, C, E, and G) allow 80, 100, 120, or 140 kVp scans, two (B and F) allow 80, 100, 120, or 135 kVp scans, and the last (D) allows 80, 120, or 140 kVp scans. This resulted in 108 unique possible measurement conditions (6 scanner∕bowtie combinations×4 kVp settings×2 phantoms×2 positions+1 scanner∕bowtie combination×3 kVp settings×2 phantoms×2 positions). All 108 conditions were simulated using both equivalent source model types. Only 120 kVp source specifications were supplied by the manufacturer of scanner∕bowtie filter combination D so only 100 of the measurement conditions could be simulated using the manufacturer-based source models (noting that direct comparisons to simulations utilizing manufacturer’s data could only be done at 120 kVp for this particular combination).

Each CTDI₁₀₀ measurement and corresponding simulation was performed using one available nominal collimation, which also varied among scanner manufacturers. Depending on the manufacturer, the nominal collimation value used for each experiment was one of the following: 4×5 mm (20 mm) with a FWHM of 21.5 mm, 20×1.2 mm (24 mm) with a FWHM of 27.9 mm, 4×8 mm (32 mm) with a FWHM of 36.9 mm, or 64×0.625 mm (40 mm) with a FWHM of 43.7 mm.

Evaluation of the source models

Comparison of CTDI simulations to measured results

The results of the CTDI₁₀₀ simulations using each of the three source model types described above were separately compared to the analogous measured CTDI₁₀₀ values. The percent error between each simulation and measurement result was calculated to evaluate the accuracy of the simulations performed with each individual source model type. Then, for each source model type, the root mean square (RMS) of the percent error values were calculated across all kVp values for each scanner∕bowtie filter combination using the results of both the center and 12:00 measurement positions on both the head and body CTDI phantoms. These RMS values serve as metrics to independently evaluate the predictive accuracy of the three source model types for each individual scanner∕bowtie filter combination.

Comparison of equivalent and manufacturer source models

The percent agreement between simulated and measured CTDI₁₀₀ results were used to compare the performance of the different source model types under investigation based on (a) a scanner∕bowtie filter combination basis and (b) pooling all scanner∕bowtie filter combinations. Part (b) of this analysis provides a metric to determine if simulations using source models based on manufacturer-provided data, HVL₁ equivalent source models, or HVL₁&HVL₂ equivalent source models have the best overall performance in terms of accurately predicting the measured CTDI₁₀₀ value.

Analysis of variance (ANOVA) tests were performed to determine whether the three types of source models produce simulation results that are statistically different from each other. First, all results underwent log transformation to satisfy the normality assumption in the ANOVA test. ANOVA methods were then used to compare the results from the three source model types, taking into account the seven scanner∕bowtie categories, all kVp’s, both sized phantoms, and both chamber positions. If there was a significant difference between the results for a given scanner∕bowtie filter combination for the different source model types, pairwise tests were used to compare the three methods on a stratified scanner∕bowtie filter combination basis. For each stratified scanner∕bowtie category, ANOVA analyses were used to compare the three types of source models. A Bonferroni adjustment was used as postestimation of multiple comparisons if there was a significant difference among the three methods.

Finally, another analysis was used to determine whether the overall performance of the three source model types were statistically similar to each other at varying levels of the desired accuracy. To do this, a categorical variable was used, which was the level of agreement between the measured and simulated results with values as follows: 1—indicating outstanding agreement of within +∕−1%, 2—representing excellent agreement of greater than +∕−1% but within +∕−2%, 3—representing very good agreement of greater than +∕−2% but within +∕−5%, 4—representing good agreement of greater than +∕−5% but within +∕−10%, and 5—representing agreement that is greater than +∕−10%. For various agreement thresholds, a generalized estimating equation (GEE) population-averaged model was performed to compare the accuracy of the simulations employing the three source model types using compound correlation structure as levels of agreement (i.e., 1%, 2%, 5%, and 10%) in binomial family with logit link. Furthermore, multivariate logistic was performed at each level of agreement to compare the individual source model simulation results. This analysis reveals whether each type of source model produces statistically different simulation results from those produced by the other types of source models for a specific level of predictive accuracy; therefore, the results will determine the level of accuracy at which the HVL₁ models provide statistically different simulation results than the HVL₁&HVL₂ source models. This will help to answer the question of whether HVL₁ and HVL₂ measurements are both necessary when employing the proposed equivalent model source model generation method.

RESULTS

The measured HVLs (HVL₁ and HVL₂) described in Sec. 2B2 are presented in Tables 1, 2, respectively. These values include measurements for each of the seven scanner∕bowtie combinations at each of the available beam energies. The mean value is presented along with a summary of the minimum and maximum HVLs to illustrate the range for a given beam energy value across different scanner∕bowtie filter combinations.

Table 1.

Measured first half value layer (HVL₁) in mm Al for each scanner∕bowtie combination at each available beam energy.

Beam energy (kVp)	Scanner∕bowtie filter combination							Mean	Minimum	Maximum
	A	B	C	D	E	F	G
80	6.00	4.66	5.44	6.35	4.46	3.49	4.46	4.98	4.46	6.35
100	7.40	5.84	6.63	⋯	5.61	4.47	5.56	5.92	4.47	7.40
120	8.50	7.05	7.77	8.93	6.59	5.45	6.61	7.27	5.45	8.93
135	⋯	7.87	⋯	⋯	⋯	6.10	⋯	6.99	6.10	7.87
140	9.50	⋯	8.75	9.83	7.57	⋯	7.57	8.64	7.57	9.83

Table 2.

Measured second half value layer (HVL₂) in mm Al for each scanner∕bowtie combination at each available beam energy.

Beam energy (kVp)	Scanner∕bowtie filter combination							Mean	Minimum	Maximum
	A	B	C	D	E	F	G
80	13.30	10.99	12.20	13.69	10.63	8.35	10.66	11.40	8.35	13.69
100	16.20	13.49	15.18	⋯	13.16	10.70	13.23	13.66	19.70	16.20
120	18.80	15.52	17.04	19.63	15.97	13.59	16.06	16.66	13.59	18.80
135	⋯	17.25	⋯	⋯	⋯	14.74	⋯	16.00	14.74	17.25
140	21.00	⋯	19.83	21.96	18.29	⋯	17.76	19.77	17.76	21.00

The results for each of the CTDI₁₀₀ measurement and simulation experiments described in Sec. 2F are presented for each scanner∕bowtie filter combination in Tables S1–S7, which can be found online at http:∕/www.medphys.org∕SupplementalMaterials.asp. These tables also display the percent difference between each measurement and the corresponding simulation for the three source model types. The agreement between simulation and measurement was within 10% for 103 out of the 108 experiments using HVL₁&HVL₂ source models. Similarly, agreements were within 10% for 102 out of the 108 experiments using HVL₁ source models. Only 49 out of the 100 simulations using manufacturer-based source models were within 10% of the analogous measurement. For the HVL₁&HVL₂ and the HVL₁ methods, the only beam energy setting for which simulations and measurements disagreed by >10% was 80 kVp. The RMS of the percent error value across all beam energies, both CTDI phantoms, and both measurement positions for simulations using each type of source model is shown in Table 3 for each scanner∕bowtie filter combination. For five out of the seven scanner∕bowtie filter combinations (A, C, D, E, and G), the source models obtained using the HVL₁&HVL₂ method resulted in smaller RMS values than did the other two source models. For combination B and F simulations, the HVL₁ method’s source models had the smallest associated RMS value. The bottom row of Table 3 displays the mean RMS value across all scanner∕bowtie filter combination for each source model. This pooled RMS value for HVL₁&HVL₂ method is slightly less than that of the HVL₁ method and substantially less than that of the manufacturer-based source model simulations.

Table 3.

RMS error for each scanner∕bowtie combination as well as pooled across all scanner∕bowtie combinations.

Scanner∕bowtie combination	Manufacturer-based source model	HVL1 source model	HVL1&HVL2 sourcemodel
A	5.50	5.38	4.14
B	10.62	6.25	7.18
C	12.60	5.39	4.02
D	2.56	2.76	2.52
E	11.83	4.31	3.80
F	20.18	7.40	7.72
G	9.51	3.89	3.37
Pooled	12.50	5.34	5.11

The results of the ANOVA test described in Sec. 2G2 are summarized in Table 4. Combination A and D showed no significant difference between any of the source model types. The remaining combinations did show significant difference; thus the results of each individual source model type were compared to each other on a stratified scanner∕bowtie category basis. For these analyses, Bonferroni adjusted p values were used for the comparisons. For each combination (B, C, E, F, and G), the source models based on manufacturer-provided data produced significantly different results than either the HVL₁ or HVL₁&HVL₂ equivalent source models, while the HVL₁ method’s results were not significantly different than those of the HVL₁&HVL₂ method.

Table 4.

ANOVA analysis results. If significant differences were found among the three methods, the pairwise ANOVA results are shown individually. Bonferroni adjustment was used as postestimation of multiple comparisons if there was significant difference among the methods.

Scanner∕bowtie combination	Manufacturer- provided vs HVL1	Manufacturer- provided vs HVL1&HVL2	HVL1 vs HVL1&HVL2
A	Not differentp=0.1738
B	Differentp<0.0001	Differentp<0.0001	Not differentp=0.1000
C	Differentp<0.0001	Differentp<0.0001	Not differentp=0.6500
D	Not differentp=0.7379
E	Differentp<0.0001	Differentp<0.0001	Not differentp=0.1421
F	Differentp<0.0001	Differentp<0.0001	Not differentp=0.8533
G	Differentp<0.0001	Differentp<0.0001	Not differentp=0.6363

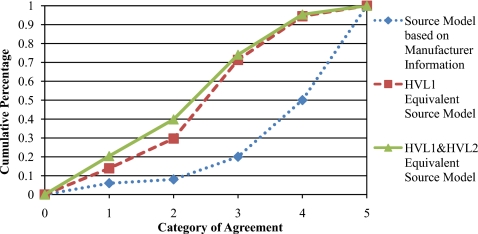
A plot of the number of cases at each level of agreement curves described in Sec. 2G2 is shown in Fig. 4. The five categorical variables used in this analysis (1–5)represent absolute levels of agreement between simulation and measurement with values of <1%, <2%, <5%, <10%, and >10%, respectively. For each source model, the plot shows the cumulative percentage of total simulations that fall into each level of agreement category. The GEE population-averaged model performed to compare the three methods discussed in Sec. 2G2 resulted in four p values <0.05, indicating there are overall differences among the three source model types. The multivariate logistic analyses performed to separately compare each of the source model types with each other at each individual level of agreement revealed that the manufacturer-based source models produced significantly different results, at each categorical level of agreement, from both the HVL₁ source models (all p values <0.0001) and the HVL₁&HVL₂ source models (all p values <0.0001). The HVL₁ and HVL₁&HVL₂ source model comparisons resulted in p values, indicating no significant difference between the two methods for all levels of agreement (p=0.1976 for 1%, 0.1003 for 2%, 0.6284 for 5%, and 0.7405 for 10% agreement).

Figure 4.

The cumulative percentage of CTDI₁₀₀ simulations that are characterized by the level agreement with measured CTDI₁₀₀ values specified by each category: (1:⩽±1% 2:>±1% but ⩽±2% 3:>±2% but⩽±5% 4:>±5% but ⩽±10% 5:>±10%).

DISCUSSION

The goal of this study was to present a method to obtain CT scanner source models based only on the measured values and validate their use for MC dosimetry simulations. These source models partially consist of an equivalent x-ray spectrum generated to match measured HVLs. A method to obtain HVLs was described, which requires parking the scanner gantry, which may require the scanner to be switched into service mode. Alternative techniques to measure HVLs for CT scanners, which do not require a stationary source, have been proposed but typically require special equipment.^{24, 25} The second part of the proposed source model is an equivalent filtration description that is generated to attenuate the equivalent spectrum across the fan angle in the same manner that the actual filtration attenuates the actual spectrum, as measured by the bowtie profile measurements.

Two different types of equivalent source models, those based only on HVL₁ measurements and those based on both HVL₁ and HVL₂ measurements, along with manufacturer-provided source models were evaluated in this study. Validation experiments were performed by assessing the accuracy of multiple CTDI₁₀₀ simulations using all three source model types for each of the available beam energies on the scanner∕bowtie filter combinations described in Sec. 2. Inspection of Tables S1–S7 shows that simulation results agreed with measurements to within 10% for 103 out of the 108 (95.4%) and 104 out of the 108 (96.3%) experiments performed using the HVL₁ and HVL₁&HVL₂ source models, respectively. Simulations utilizing manufacturer-based source models only achieved agreement of ⩽10% for 49 out of the 100 simulations. Thus, assuming an acceptable agreement level of 10%, it is apparent that simulations using the equivalent source models attained the necessary accuracy for validation much more frequently than simulations using source models based on manufacturer’s data.

The RMS of the percent error values reported at the bottom rows of Tables S1–S7 and summarized in Table 3 serves as a metric to compare the simulation accuracy for a particular source model on a scanner∕bowtie combination basis. Analyzing the RMS value across all beam energies (and across both CTDI phantoms and measurement positions) provides a thorough evaluation of a source model’s overall performance for a particular scanner∕bowtie filter combination. The HVL₁&HVL₂ source model simulations resulted in better predictive accuracy (smaller RMS percent error values) than the other two types of source models for five out of the seven scanner∕bowtie filter combinations, while the HVL₁ source models simulations had a lower RMS value for the remaining two combinations. It should be noted that for some scanner∕bowtie filter combinations, similar performance was observed between all three source model types (i.e., combination A and D) and some combinations resulted in substantial differences between the manufacturer source models and the equivalent source models (i.e., combination B, C, E, F, and G). However, for all combinations the two equivalent source model types had relatively small differences in their predictive accuracy.

The pooled RMS values across all scanner∕bowtie filter combinations presented at the bottom row of Table 3 indicate that the overall performance, on a whole, of the HVL₁&HVL₂ was slightly better than that of the HVL₁ source model and that both of the equivalent source models were superior to the source models based on manufacturer-provided data. Both of the equivalent source types had associated mean RMS values across all combinations <6% (5.34% and 5.11% for the HVL₁ and HVL₁&HVL₂ source models, respectively), while the manufacturer-based source model simulations exceeded 10% (12.50%).

Tables S2 and S6 illustrate that for scanner∕bowtie filter combination B and F, the 80 kVp CTDI percent error values are relatively large for the equivalent source models (these simulations accounted for most of the equivalent source simulations that did not meet the 10% difference metric). One reason for this might be that, for diagnostic energy ranges, exposure is approximately proportional to the square of the kVp (when keeping the tube current fixed). As a result, if the mA s setting for 80 kVp HVL and bowtie profile measurements are too low, the exposure values may have inherent error from quantum noise due to insufficient tube output. This is especially true for source models generated based partly on HVL₂ since the large amount of aluminum filtration used to obtain the necessary exposure values significantly reduces the number of photons detected by the ion chamber. This hypothesis could not be immediately tested due the limited accessibility of the scanners employed for this study; however, additional work should be done to investigate the effect of the tube current setting on 80 kVp equivalent source simulation results and possibly determine a minimum mA s threshold setting to obtain simulation results with the desired accuracy level. This could be especially relevant for estimating dose to pediatric patients, where 80 kVp scans are more commonly used.

The CTDI percent error values shown in Table S4 for scanner∕bowtie filter combination D reveal that the manufacturer-based source models resulted in a relatively small RMS value (2.56%) compared to the other scanner∕bowtie filter combinations. As noted in Sec. 2 for this scanner∕bowtie filter combination, it was only possible to evaluate 120 kVp manufacturer-based source model simulations; therefore, the reported RMS value only takes one beam energy setting into account. It is unclear whether a full data set from the manufacturer would improve or worsen the RMS value. However, the lack of available data suggests another advantage to using the equivalent source method. Since the proposed method is based strictly on measurements, it is possible to obtain source models for any kVp and bowtie filter combination available on the scanner of interest.

The ANOVA analyses performed on a scanner∕bowtie filter combination basis showed that for five out of the seven scanner∕bowtie filter combinations, both the HVL₁ and HVL₁&HVL₂ equivalent source model simulations produced significantly different results than did the manufacturer-based source model simulations in terms of predictive accuracy. Since it has already been established that the equivalent source model simulations were more accurate in predicting measured CTDI values, this analysis demonstrates that there is a statistically proven benefit to using either the HVL₁ or HVL₁&HVL₂ equivalent source methods rather than manufacturer-based source models. In the other two cases (combination A and D), the manufacturer-provided data proved to produce simulation accuracy that was statistically similar to the equivalent source simulations.

Finally, the overall performance of the three types of source models were statistically compared by utilizing categorical variables, indicating level of agreement between simulated and measured values. These analyses allowed comparisons to be made at individual levels of accuracy. The results showed that at each assigned level of agreement (<1%, <2%, <5%, and <10%), the equivalent source model simulations significantly outperformed the manufacturer-based source model simulations. Comparisons of the HVL₁&HVL₂ method with the HVL₁ method proved that there is no statistical difference between the two types of equivalent source models at any level of agreement. This suggests that, for any desired level of accuracy, it is not necessary to measure HVL₂, which can be a time consuming, cumbersome task.

In order to encourage the use of this method, the goal of this study was to present a simple, heuristic approach to generating equivalent source models rather than proposing more sophisticated optimization algorithms. It is possible that applying stricter requirements when generating the equivalent spectra, such as requiring the candidate spectrum optimization function to simultaneously take into account both HVL₁ and HVL₂ measurements, might result in simulations with greater accuracy. It should also be noted that while a numerical spectrum generation algorithm was presented in this work, a well-validated analytical method exists to determine spectra from the measured attenuation curves via the Laplace transform.^{26, 27} Improved results might also be obtained by using some optimal combination of material types for the equivalent bowtie filter or hardening materials. Further exploration of such alternative source model generation techniques should be encouraged; however, the easy-to-implement method proposed in this work has been shown to result in accurate and robust simulations across an extremely wide range of validation experiments. To encourage further investigations, a full set of required measurement data (HVLs and bowtie profile) and the resulting equivalent source models (HVL₁ and HVL₁&HVL₂) for one scanner∕bowtie filter combination has been made available at http:∕/medqia.org∕∼mcnitt∕Equivalent_Source∕.

The use of equivalent source models generated by the proposed method has considerable advantages over the use of manufacturer-provided data. In addition to obviating the need to obtain confidential information via some type of nondisclosure agreement, this method produced simulation results that more accurately matched physical measurements. Data supplied by the manufacturer are usually provided for a specific combination of x-ray tube, bowtie filter, and even software version for a particular scanner. Subsequent models of the same scanner may not feature the same combination of attributes (e.g., different software version and different x-ray tube) and thus any previously supplied data may not exactly characterize the actual scanner being evaluated. These apparently minor differences are very difficult to discern and could partly explain why the manufacturer-based models did not perform as well as the equivalent source models. On the other hand, equivalent source models are based on scanner-specific measurements. Since any scanner modifications may alter the HVL and∕or bowtie profile measurements, the equivalent source method will naturally factor them into the resulting source models accordingly.

In this study we have described a novel method to generate source models using only measured values for MDCT MC dosimetry simulations and have demonstrated their ability to produce highly accurate simulations over a wide range of scanners and bowtie filter combinations. These equivalent source models consist of unique spectrum and filtration combinations based on scanner-specific measurements, which might seem to imply that equivalent source model simulations apply only to the particular scanner on which measurements were obtained. The generalizability of these equivalent source models will be investigated in future studies that will focus on the range of measurement values for scanners of the same make and model (small measurement variations would result in similar equivalent source models and thus similar dosimetry simulations) and variations in dose characteristics of scanners of different makes and models. The latter of these studies will specifically involve performing equivalent source model simulations to estimate organ doses from a wide range of commercially available scanners for a number of different patient models in order to determine the optimal means for calculating and reporting CT dose values.