Detection of genomic islands via segmental genome heterogeneity

Abstract

While the recognition of genomic islands can be a powerful mechanism for identifying genes that distinguish related bacteria, few methods have been developed to identify them specifically. Rather, identification of islands often begins with cataloging individual genes likely to have been recently introduced into the genome; regions with many putative alien genes are then examined for other features suggestive of recent acquisition of a large genomic region. When few phylogenetic relatives are available, the identification of alien genes relies on their atypical features relative to the bulk of the genes in the genome. The weakness of these ‘bottom–up’ approaches lies in the difficulty in identifying robustly those genes which are atypical, or phylogenetically restricted, due to recent foreign ancestry. Herein, we apply an alternative ‘top–down’ approach where bacterial genomes are recursively divided into progressively smaller regions, each with uniform composition. In this way, large chromosomal regions with atypical features are identified with high confidence due to the simultaneous analysis of multiple genes. This approach is based on a generalized divergence measure to quantify the compositional difference between segments in a hypothesis-testing framework. We tested the proposed genome island prediction algorithm on both artificial chimeric genomes and genuine bacterial genomes.

INTRODUCTION

Bacteria are arguably the most diverse and versatile organisms on the planet, exploiting every imaginable habitat and rapidly responding to physiological challenge and to ecological change. Since the industrial revolution, bacteria have increased their resistance to antibiotics, developed tolerance to caustic solvents and materials, gained the ability to degrade artificially synthesized substances, learned to flourish when attached to novel surfaces and have escaped our efforts to banish their pathogenic varieties. Such remarkable abilities to adapt belie the constraints of intra-genomic mutational processes, which are limited in their capacity to effect change because they alter existing genetic material in a slow, step-wise fashion. However, bacteria also experience frequent saltational evolution whereby genes for novel metabolic processes are introduced from unrelated individuals via horizontal gene transfer (HGT). In contrast to mutation, the expansion of a cell's physiological capabilities via gene acquisition provides potentially large numbers of fully functional, evolutionarily vetted genes which can then cooperate to confer complex metabolic functions. As a result, bacteria may experience very rapid and dramatic changes in ecological abilities after gaining genes, which allow for the degradation of new food sources, or the synthesis of new metabolites, or the attachment to and invasion of host tissues.

Since the first genome sequence became available, it has been clear that acquisition of novel DNA is a common mechanism for bacterial evolution (1), and that the genomes of all free-living bacteria are littered with large numbers of recently-acquired genes (2). A primary agent of rapid genomic change is the genomic island, a group of tens to hundreds of genes whose products may cooperate to confer complex functions to the recipient cells (3). Among the first classes of genomic islands to be described were pathogenicity islands, so named because virulence genes in many organisms were not only physically clustered in the chromosome but also bore signs of recent acquisition such as unusual nucleotide composition (4). For example, the pathogenic Escherichia coli serovar O157:H7 has hundreds of recently introduced genes organized into several large islands that are not found in non-pathogenic strains of E. coli (5). When comparing related taxa, it becomes clear that genomic islands encode functions associated with complex changes in ecological niche (3). Because they mediate the simultaneous introduction of tens or hundreds of genes, genomic islands provide a pathway for the acquisition of very complex traits, which require the action of many gene products, potentially initiating large changes in physiological repertoire. Therefore, the identification of genomic islands provides insight into the evolutionary events which distinguish closely related, but ecologically distinct, taxa.

Despite the central role of genomic islands in modulating bacterial evolution, methods for their identification leave much room for improvement. Two approaches are common. First, a phylogenetic approach relies on the identification of a large region of DNA which is absent from the genomes of close relatives. For example, pathogenicity islands in Salmonella enterica serovar Typhi are missing from the genomes of other strains of Salmonella (6,7). Yet, this approach has the drawback of requiring genome sequences from multiple relatives of the bacterium of interest. Even with several genomes available, the polarity of changes in gene inventory may not be clear: was a genomic island gained, or did a large deletion occur? In addition, the presence of multiple paralogs confounds the ability to identify genes lacking true orthologs.

In contrast, parametric approaches may identify genes in bacterial genomes that have unusual sequence characteristics—such as atypical nucleotide composition, dinucleotide frequencies or codon usage bias—relative to the bulk of the genes in a genome. Often, such genes bear atypical features because they were recently introduced from genomes which have experienced different sets of directional mutation pressures (8–10). Here, individual genes are categorized as likely to be native or likely to be alien. A region of the chromosome with large numbers of potentially alien genes may then be labeled as a putative genomic island. One can then look for features (such as the presence of an integrase, a linked tRNA gene functioning as a phage attachment site, or the presence of direct repeats flanking the genomic island), which are associated with some genomic islands and also implicate recent gene acquisition (3,4). While parametric approaches do not rely on genome comparisons, they suffer from the limitations of ‘bottom–up’' methods, which must first identify individual genes as being atypical. In addition, groups of weakly atypical alien genes often escape detection as false negatives. Moreover, there is no systematic way of determining if the putative groups of atypical genes are actually similar to each other, as one would predict if their atypical features reflect a common ancestry in a foreign genome.

To circumvent the problems of the ‘bottom–up’ approaches, we propose a ‘top–down’ method for the robust identification of genomic islands which avoids the identification of individual atypical genes. Rather than identifying alien genes and grouping them into islands, we divide the genome into successively smaller regions, each with distinct composition, using a recursive segmentation procedure (11,12). At the core of the segmentation model is a newly developed, robust and highly sensitive divergence measure to quantify the compositional difference between genome sequences: a generalized version of the Jensen–Shannon divergence measure. This measure has been shown to be highly accurate in detecting atypical genes (13). Unlike ‘bottom-up’ measures which rely on arbitrary comparison thresholds and are limited by the information contained within individual coding regions, our ‘top–down’ method is robust in the identification of large, multi-gene chromosomal segments, and does so within a statistical hypothesis testing framework. After delineating the compositionally distinct segments, the atypicality of a segment is measured with respect to the average genome composition. Genomic islands can be identified as one or more successive, atypical segments. Thus, the genomic islands are detected with precision, and their mosaic organizational structure is revealed.

MATERIALS AND METHODS

Genome sequences

The complete genome sequences of Archaeoglobus fulgidus, Bacillus subtilis, Citrobacter koseri ATCC BAA-895, Deinococcus radiodurans R1, E. coli CFT073, E. coli W3110, E. coli MG1655, Escherichia fergusonii ATCC 35469, Haemophilus influenzae Rd, Klebsiella pneumoniae 342, Mesorhizobium loti, Methanocaldococcus jannaschii, Neisseria gonorrhoeae, Ralstonia solanacearum, S. enterica subsp. enterica serovar Choleraesuis str. SC-B67, S. enterica subsp. enterica serovar Dublin str. CT_02021853, Salmonella typhimurium LT2, S. enterica subsp. enterica serovar Typhi str. CT18, S. enterica subsp. arizonae serovar 62:z4,z23, S. enterica subsp. enterica serovar Gallinarum str. 287/91, Shigella flexneri, Sinorhizobium meliloti, Synechocystis PCC6803, Thermotoga maritima and Vibrio parahaemolyticus were obtained from GenBank. Protein-coding, tRNA and tmRNA genes were extracted using the coordinates provided in the annotation.

Artificial genomes

Artificial genomes for assessing the parametric methods for atypical gene detection were constructed as described previously (14). Briefly, the artificial genomes were constructed using generalized hidden Markov models. First, the core of a genome representing the mutational bias of the ancestral (native) genes was extracted using a gene clustering method based on the Akaike Information Criterion. Genic variability in the core genome was partitioned as distinct classes of similar genes using a k-means clustering algorithm based on the Kullback–Leibler divergence measure. Gene models trained on these gene classes were incorporated in the framework of a generalized hidden Markov model to generate an artificial counterpart of a genuine genome. The artificial genome provides a reservoir for initiating gene transfers.

We constructed artificial genomes of the prokaryotes A. fulgidus DSM4304, B. subtilis 168, D. radiodurans R1 chromosome I, E. coli MG1655, H. influenzae Rd KW20, M. jannaschii DSM2661, N. gonorrheae FA1090, R. solanacearum GMI1000, S. enterica Typhi, S. meliloti 1021, Synechocystis sp. PCC6803 and T. maritima MSB8. Chimeric artificial genomes were constructed as the mosaic sets of genes sampled from different artificial genomes placed in an artificial E. coli genomic backbone.

Unique S. enterica Typhi CT18 genes

Genes unique to the S. enterica serovar CT18 genome were detected as those not found in the genomes of related enteric bacteria (no significant homologues as revealed by pariwise BLAST), including E. coli CFT073, E. coli W3110, E. fergusonii ATCC 35469, C. koseri ATCC BAA-895 and K. pneumoniae 342. Genes likely to be ancestral to the CT18 genome are those that detected homologues with >70% protein similarity more than one of those taxa; ambiguous genes had homologs in only one of those taxa. Genes smaller than 400 nt were not included in this analysis.

Divergence measures

To assess the compositional difference between two or more genes or sequence segments, we first obtained the generalization of the standard Jensen–Shannon divergence measure denoted D(p₁,p₂) between two probability distributions p₁ and p₂,

1

where 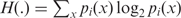is the Shannon entropy function.

When applied to DNA sequences, the distributions p₁(x) and p₂(x) generally represent relative frequencies of occurrence of nucleotides in each sequence. Therefore, they capture only the nucleotide composition of the sequence but not the order of occurrence of nucleotides. Thus, the above formulation assumes that the nucleotides at each position are independently and identically distributed. To account for correlations in the occurrence of nucleotides, we obtained a Markovian form of the JSD that will be appropriate for sequences assumed to be generated by Markov sources of arbitrary order (Supplementary Data). The standard JSD then becomes a special case of the Markov version when the model order is zero. The Markovian Jensen–Shannon divergence (MJSD) of order m is defined as (15),

2

where H^m(.) is the conditional entropy function:

3

Here, z denotes the sequence of m nucleotides preceding nucleotide x, p_j(x,z) is the joint probability of x, z and p_j(x | z) is the conditional probability of x given z.

Weight factors π₁ = l₁/L and π₂ = l₂/L, L = l₁ + l₂ (11) were assigned to the corresponding subsequences S₁ and S₂ of length l₁ and l₂. Substituting in the above expression for the MJSD leads to

4

where H^m(S₁) and H^m(S₂) are the Markov entropies for the subsequences S₁ and S₂, and H^m(S) is the Markov entropy for the sequence S obtained by concatenating S₁ and S₂.

Another way of correcting for short-range correlations is to convert a sequence of nucleotides into a sequence of ‘overlapping’ oligonucleotides and then compute the Jensen–Shannon divergence; we term this measure Jensen–Shannon divergence oligonucleotide (JSDO).

Statistical significance of D^m and D_max^m

For an observed value of D^m, the significance value is the probability P(D^m ≤ x). For m = 0, Grosse et al. (11) obtained the analytic probability distribution of D^m,

5

where χ_d² is the chi-square distribution function with d = k-1 degrees of freedom, k is the alphabet size. We show that for any m > 0 the probability distribution P(D^m ≤ x) also follows a χ_d² distribution with d = k^m(k-1) degrees of freedom (Supplementary Data). To assess the statistical significance of D_max^m, the maximum divergence value obtained at a sequence position, we obtained, similar to the m = 0 case, a combined analytic-numerical approximation of the probability distribution,

6

The values of the parameters β and N_eff were found by fitting empirical distributions to the above analytic expression, obtained via Monte Carlo simulations (Supplementary Data). As for m = 0 case (11), we found that N_eff is linearly related to log N and β is effectively a constant function independent of N for m = 1 and m = 2.

The recursive segmentation algorithm

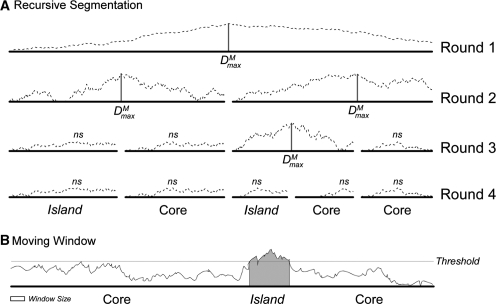
There is a long history of the recursive segmentation method that employs standard Jensen–Shannon (JS) divergence as a measure of compositional difference between two sequences (11,12,16–19). Here, we describe briefly our modified recursive segmentation procedure, where we replace JSD with MJSD as a measure of divergence [see also ref. (15)]. To segment a single sequence string S, we compute D^m for every position along a sequence. If the maximum value, D_max^m, is large enough to be considered statistically significant, then the position where the maximum was found is considered a segmentation point (Figure 1A). The sequence is split at the segmentation point and the two resulting subsequences are candidates for further segmentation. If D_max^m is not statistically significant, no segmentation is carried out. This recursive procedure (Figure 1) is referred to as the top–down MJSD segmentation method in the text below.

Figure 1.

Schematic representation of recursive segmentation and moving-window methods for island detection. (A) The recursive segmentation technique. The dashed line shows the value of MJSD, D^m, across each possible split location. If D_max^m is statistically significant, the sequence is segmented at that point, represented by a vertical bar. In this example, four splits are made resulting in five segments; values of D_max^m that are not significant are denoted as ns. Comparison of segments to the genome as a whole shows two segments are islands and three represent the core genome. (B) The moving-window technique. Values are calculated for windows of a specified size; windows with values over a predetermined threshold are identified as atypical and annotated as an island (gray region). Here, there is insufficient signal for the 5′ region to be marked as a putative island, resulting in a false negative.

Determination of atypical character of a genome segment

After a genome is fragmented into homogeneous domains by the recursive segmentation method, the atypicality of each domain is measured with respect to the genome. We define the atypicality score for a domain as the probability of getting the divergence value or less in random sequences,

7

Here, D^m denotes the MJSD between the domain in question and the entire genome. If AS is greater than an established threshold, the domain is deemed atypical.

The Wn Covariance measure for assessing atypicality

Covariance can also be used as a measure of atypicality (20). The atypicality of a gene, g, with respect to the genome, G, is assessed through the covariance measure,

8

where f_k(s) is the normalized frequency of word or oligomer k, and t is the number of all possible distinct oligomers (Tsirigos,A., personal communication). If the value of cov(g,G) is less than an established threshold, gene g is deemed atypical. This method is referred to as Wn, where n denotes the size of the words (or oligomers) used; note that t = 4ⁿ.

Window methods

Previous methods typically use a windowing approach whereby multiple genes are examined in a window of fixed length. The position of this window is moved over a genome, and consecutive windows with unusual compositional character are labeled as genomic islands (Figure 1B). For comparative purposes, we implemented a moving-window method where the MJSD measure is used to assess the atypicality of sequence within a sliding window against the genome as a whole. We term this approach the bottom up MJSD–window method. Our proposed prediction algorithm was also compared to a recently introduced window-based method IVOM (6). Unlike the Wn method which uses n-mer frequencies with n fixed, IVOM combines the frequencies of all size n-mers, n = 1 to 8, in the framework of an interpolated Markov model. Here, the Kullback–Leibler divergence is used to quantify the compositional difference between a region within a window and the whole genome. If this difference is larger than an established threshold, the window is deemed atypical. The consecutive atypical windows define the ‘raw’ genomic islands whose boundaries are refined using a hidden Markov model in a post-processing step to determine the change points.

Accuracy assessment of the parametric methods

The accuracy of the parametric methods was assessed by obtaining the ROC curve, which is the plot of true positive rate (fraction of the positives correctly identified by a method) as a function of false-positive rate (fraction of the negatives that are incorrectly identified as positives by a method). Area under this curve (AUC) defines a measure of accuracy: the higher the AUC, the higher the accuracy.

RESULTS

Here, we present the method for identification of genomic islands in five steps: (i) developing a metric for measuring compositional differences between segments; (ii) assessing the efficacy of this method in identifying segment boundaries; (iii) developing a method for recursive segmentation of genomes into compositionally distinct segments; (iv) assessing the method for identifying genomic islands in both artificial and genuine bacterial genomes; and (v) comparing the ‘top–down’ approach to ‘bottom–up’ methods.

Identifying alien genes

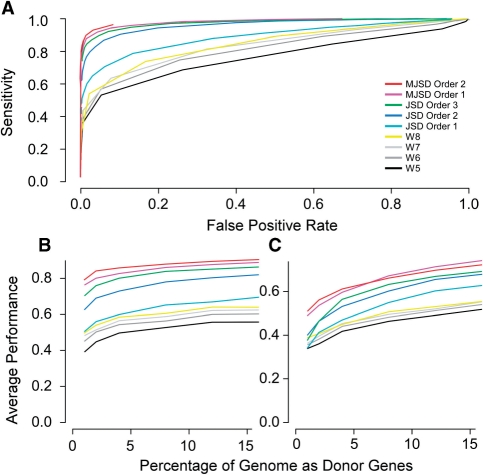
As with all parametric methods, we must quantify the difference between two regions or classes of DNA and determine if those differences are significant. To accomplish this, we generalized the Jensen–Shannon divergence to account for correlated evolution by incorporating Markov models of sequences in place of an i.i.d. model in the divergence measure (see ‘Materials and Methods’ section). We tested our measures by attempting to identify atypical genes within artificial chimeric genomes, which mimic the sequence properties of the genuine genomes on which they are modeled (14). As the ‘evolutionary’ histories of genes in these genomes are known precisely, they serve as valid test beds for parametric methods of atypical gene detection. Artificial chimeric genomes were first constructed with a core of genes modeled from the E. coli genome; alien genes were incorporated randomly from artificial genomes modeled on ten diverse donor genomes (see ‘Materials and Methods’ section). We measured the atypicality of a gene with respect to the genome using JSDO and MJSD with model orders 1 and 2 (Figure 2); the performance of Wn was also assessed for comparison. Standard JSD and JSDO methods have earlier been shown to outperform other parametric methods (13), which are not shown for clarity. The MJSD method outperformed the JSDO and Wn methods irrespective of the amount of acquired genes (Figure 2). The first-order MJSD measure examines the order of occurrence of two nucleotides, and it outperformed the JSDO method using dinucleotide composition as the discriminant criterion. Similarly, second-order MJSD outperformed JSDO using trinucleotide composition as the discriminant criterion. All methods—including the zeroth order MJSD (equivalently, standard JSD using the nucleotide composition)—outperformed the octanucleotide-based Wn method.

Figure 2.

ROC curves for MJSD, JSD and Wn methods for detecting atypical genes. (A) Detecting atypical genes in an artificial E. coli genome with 16% donor genes. (B) Detection of the N% highest atypicality values in an artificial E. coli core. (C). Detection of the N% highest atypicality values in a genuine E. coli core, where N denotes the percent donor genes.

The performance of the methods was also evaluated by examining the percentage of true alien genes occupying the N% highest atypicality score values, where N% is the percentage of total genes that the recipient genome acquired from the donor organisms (Figure 2B and C). To minimize the effects of pre-existing alien genes, we took two approaches. First, we simulated transfer from artificial donor genomes to an E. coli artificial core genome as described above (Figure 2B). Second, we simulated transfer from genuine donor genomes into a genuine E. coli core genome (Figure 2C) that was created using Akaike information criterion based gene clustering (14,21). The relative performance of the parametric methods on these test genomes (Figure 2C) was similar to the trend observed with artificial chimeric genomes (Figure 2B). All results suggest that the MJSD metric is superior to other metrics in identifying atypical sequences. Therefore, we implemented MJSD as the metric to discriminate between typical and atypical regions of the genome.

Identifying segment boundaries

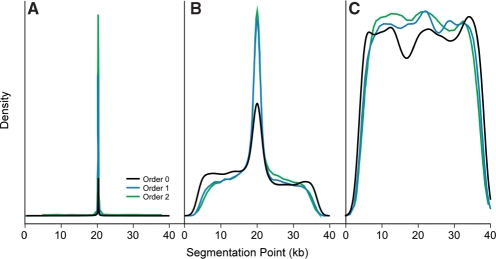
Existing methods that identify genomic islands first identify atypical genes. However, improperly annotated genes are often compositionally unusual, thereby confounding parametric methods for the identification of alien genes. Therefore, we propose to abandon gene annotations and divide chromosomes into segments without regard to gene boundaries. For this approach to be effective, the MJSD metric must be able to identify the boundary between two compositionally distinct regions of DNA without first identifying gene boundaries or using coding frame information to interpret compositional patterns. To evaluate our metric, we joined two DNA sequences of the same length from different bacterial genomes; the MJSD segmentation procedure was then applied to find the join point. If the segmentation algorithm were reliable, it would consistently report optimal segmentation at the midpoint of a sufficiently long chimeric sequence construct.

The correct segmentation point is clearly identified when the two sequences being concatenated are sufficiently long and have originated from phylogenetically distant species. For example, the boundary between 20-kb regions of S. enterica and M. loti are clearly identified to within ∼10 bases even without identifying the borders of the underlying genes (Figure 3A). Higher-order MJSD algorithms perform better at placing the segmentation closer to the sequence midpoint. Segment boundaries were poorly identified when the segments were small, owing to lack of sufficient information. Boundaries between segments smaller than 5–10 kb are not found reliably (data not shown); therefore, this method is limited to the identification of large segments encoding more than ∼5–10 genes. This range encompasses the vast majority of described genomic islands (22) and is confirmed by the discovery of various-sized genomic islands in the artificial chimeric genomes (Tables 1 and 2; Supplementary Table 4).

Figure 3.

Assessing segment boundaries. Two 20-kb fragments are joined and the MJSD algorithm is used to locate the segmentation point. The frequency of finding the segmentation point (location of D_max^m) among 10 000 replicates is plotted as a function of its position on the catenated fragment. (A) Salmonella fragments concatenated with Mesorhizobium fragments. (B) Salmonella fragments concatenated with E. coli fragments. (C) Contiguous fragments of the Salmonella genome.

Table 1.

Accuracy comparison of the top–down and bottom–up (1KB window) MJSD methods (averaged over 50 artificial genomes)

Genes per island	Cutoff
	50			75			90			95
	Top– down AUC	Bottom–up AUC	MJSD percent*	Top– down AUC	Bottom–up AUC	MJSD percent	Top– down AUC	Bottom–up AUC	MJSD percent	Top– down AUC	Bottom–up AUC	MJSD percent
Ten donor genomes
3	0.736	0.966	0.00	0.735	0.927	0.06	0.733	0.823	0.26	0.730	0.724	0.52
6	0.829	0.977	0.08	0.826	0.947	0.18	0.825	0.891	0.38	0.821	0.820	0.60
9	0.909	0.979	0.24	0.908	0.950	0.40	0.905	0.906	0.54	0.902	0.857	0.76
12	0.959	0.981	0.66	0.958	0.955	0.72	0.956	0.929	0.88	0.953	0.891	0.88
15	0.986	0.976	0.88	0.985	0.950	0.90	0.982	0.912	0.90	0.980	0.869	0.98
Salmonella donor genome
3	0.572	0.678	0.20	0.571	0.486	0.74	0.567	0.377	1.00	0.564	0.350	1.00
6	0.640	0.709	0.40	0.633	0.496	0.78	0.626	0.328	0.94	0.621	0.288	0.98
9	0.669	0.698	0.40	0.661	0.475	0.92	0.653	0.301	1.00	0.641	0.237	1.00
12	0.728	0.681	0.60	0.714	0.463	0.92	0.701	0.305	0.98	0.693	0.221	1.00
15	0.780	0.691	0.78	0.774	0.469	0.98	0.753	0.302	0.98	0.749	0.227	1.00

*Percentage of genomes where MJSD top–down outperforms MJSD bottom–up.

Table 2.

Accuracy of the MJSD and IVOM methods (averaged over 50 artificial genomes)

Genes per island	Cutoff
	50			75			90			95
	MJSD AUC	IVOM AUC	MJSD percent*	MJSD AUC	IVOM AUC	MJSD percent	MJSD AUC	IVOM AUC	MJSD percent	MJSD AUC	IVOM AUC	MJSD percent
Ten donor genomes
3	0.736	0.966	02	0.735	0.953	02	0.733	0.917	10	0.730	0.895	12
6	0.829	0.984	02	0.826	0.968	14	0.825	0.940	22	0.821	0.914	28
9	0.909	0.991	20	0.908	0.983	24	0.905	0.964	30	0.902	0.945	30
12	0.959	0.994	52	0.958	0.986	62	0.956	0.968	60	0.953	0.951	66
15	0.986	0.992	76	0.985	0.980	82	0.982	0.966	86	0.980	0.951	84
18	0.978	0.994	54	0.975	0.984	58	0.970	0.967	72	0.959	0.956	66
25	0.987	0.994	52	0.982	0.988	50	0.976	0.976	68	0.972	0.961	76
35	0.991	0.992	68	0.986	0.983	68	0.980	0.967	76	0.976	0.959	74
50	0.992	0.993	52	0.989	0.986	64	0.985	0.974	76	0.974	0.961	64
Salmonella donor genome
3	0.565	0.717	21	0.564	0.658	25	0.560	0.608	38	0.557	0.587	42
6	0.640	0.851	14	0.633	0.708	42	0.626	0.615	60	0.621	0.590	60
9	0.669	0.859	10	0.661	0.756	30	0.653	0.636	60	0.641	0.585	66
12	0.728	0.872	20	0.714	0.756	42	0.701	0.617	58	0.693	0.565	68
15	0.780	0.889	30	0.774	0.767	58	0.753	0.614	82	0.749	0.566	86
18	0.718	0.911	02	0.698	0.795	22	0.671	0.646	54	0.649	0.582	72
25	0.770	0.915	10	0.734	0.814	30	0.691	0.662	60	0.673	0.576	76
35	0.871	0.912	32	0.822	0.805	60	0.771	0.626	94	0.748	0.563	96
50	0.919	0.912	62	0.879	0.809	85	0.819	0.652	94	0.781	0.538	96

*Percentage of genomes where MJSD outperforms IVOM.

As expected, segmentation was less effective when the two sequences arose from the same genome or from the genomes of phylogenetically proximal organisms (Figure 3B). The few boundaries faithfully detected represent sampling of disparate sections of the genome(s), at least one of which may have been introduced by horizontal gene transfer and thus bears atypical character. In contrast, when contiguous segments are examined—here, the two segments are adjacent in the S. enterica genome—we saw no assignment of segment boundaries, as evidenced by a near uniformity in the segmentation distribution (Figure 3C). This shows that the segmentation method is not simply biased toward reporting the central position as a segmentation point. For a quantitative assessment, we obtained the upper and lower 90% confidence boundaries for the true location corresponding to D_max^m. As expected, the size of the confidence interval is highly correlated with both the genome level differences and the size of the segments (Supplementary Figure 3). Therefore, we conclude that the MJSD metric is robust in identifying segment boundaries within DNA sequences without regard to gene boundaries.

Identifying island boundaries in artificial chimeric genomes

The algorithm begins by dividing the chromosome into two segments which have a statistically significant maximum difference in sequence properties (see ‘Materials and Methods’ section, Supplementary Data for details on significance testing); each segment is recursively divided until all segments are deemed uniform. As the ancestry of genes in genuine genomes is not known with certainty, we evaluated the performance of the recursive, binary segmentation method by using it to find boundaries of islands in artificial chimeric genomes (see ‘Materials and Methods’ section for details on their construction). We compared recursive segmentation to a moving-window approach; as a control, we also examined the results of segmentation performed by randomly placing breakpoints in genomic sequences. Moving-window methods are widely used because they are relatively easy to implement and readily interpretable; this approach has been implemented for genomic island detection by the IVOM method (6). Their major drawback is their sensitivity to the window size: islands are poorly detected when they are smaller than the window size, yet smaller windows render less predictive power to the method. Furthermore, this approach is inherently unable to delineate the boundaries between compositionally distinct regions.

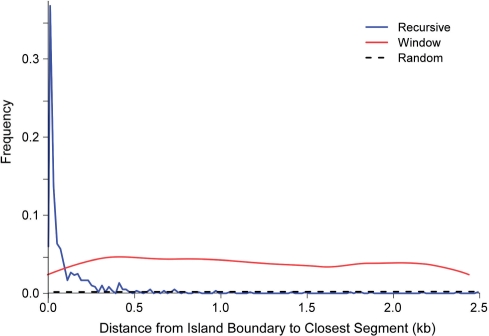
The distribution of closest segmentation distance from the island boundary is plotted in Figure 4. We transferred islands composed of 15 genes from 10 possible artificial genomes into the artificial E. coli core backbone genome; we simulated six horizontal transfers in 50 chimeric genomes. For the moving-window method, there is a uniform distribution of endpoints within the interval (0, window_size/2) because an island boundary will be located randomly within a window. In contrast, the recursive segmentation method places breakpoints within 250 bp of the island boundaries more than 80% of the time and outperforms a 5-kb window 92% of the time. To obtain similar accuracy to the recursive method, we would need to use a sliding window of size 80 bp; since the power of moving-window methods diminish with decreasing window size, this would undermine its capabilities. Both recursive and window methods outperform the control algorithm, where segment boundaries are placed at random within the sequence. We conclude that the recursive method is better suited to delineating genomic island boundaries.

Figure 4.

Distributions of island boundary distance to closest segment. The ‘random segmentation’ randomly cuts the genome into the same number of segments as the recursive segmentation algorithm. The window algorithm divides the genome into 930 fragments, whereas the recursive algorithm divides the genome into (on average) 101 fragments.

Detecting genomic islands in chimeric artificial genomes

We compared the top–down recursive segmentation to a moving-window approach using the same atypicality scoring metric (AS) and to the IVOM method. To estimate accuracy, we constructed chimeric genomes with islands transferred from 10 artificial genomes into an artificial E. coli genomic backbone. Various numbers of genes (3, 6, 9, 12, 15, 18, 25, 35 or 50) were contained within each island and a total of six islands were inserted into each artificial genome. This was repeated 50 times for each island size, resulting in 450 in silico chimeric genomes being constructed. In addition, we repeated this process by inserting regions from an artificial S. enterica genome into an artificial E. coli genome. As S. enterica is closely related, and compositionally similar, to E. coli, the task of identifying the genomic islands originated from Salmonella should be more difficult.

The accuracy of the methods in identifying the genomic islands was assessed by computing the area under the ROC curve (AUC, see ‘Materials and Methods’ section); AUC = 1 denotes a perfect classification while AUC = 0.5 (area under the diagonal line) denotes a random classification. A comparison of the MJSD and IVOM methods is summarized in Table 1 and an example is shown in Figure 5. Data are shown for different sizes of genomic islands and for different fractions of the genomic island required to be identified (termed ‘cutoff’). For instance, the cutoff used in Figure 5 is 90%, meaning that if an island of size 20 kb has <18 kb labeled as alien, it is considered a false negative. In contrast, the false-positive rate is still given in terms of nucleotides incorrectly labeled as foreign. When gene-based methods are used, 90% of an island region is defined as 90% of the nucleotides in genes in the island region.

Figure 5.

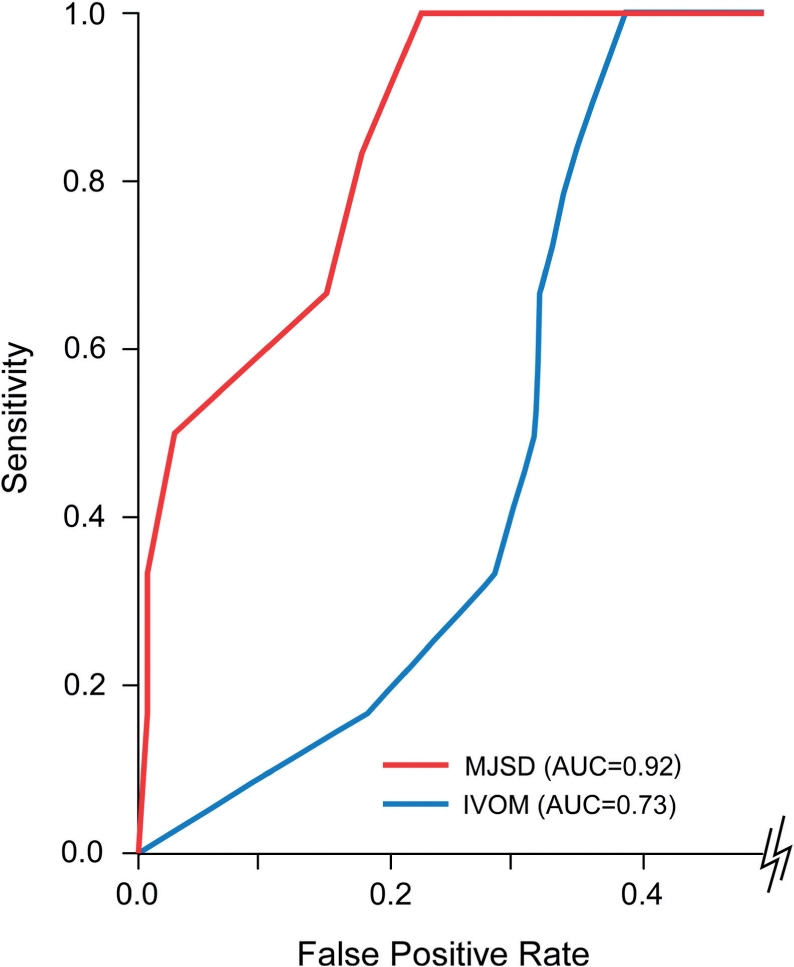
An ROC curve comparing the IVOM and MJSD methods on a single artificial chimeric genome. The cutoff for declaring an island as found is 90% and the six genomic islands encompass 50 genes each.

The top–down, recursive segmentation algorithm identifies genomic islands better than bottom–up method when the size of the island was sufficiently large (Table 1; Supplementary Table 4). As expected, this observation becomes more pronounced for genomic islands originating from an artificial Salmonella genome in an artificial E. coli genome due to the similarity of the genome nucleotide distributions. Short, weakly atypical alien regions could not be detected accurately by the recursive method and thus windowing is better equipped for detecting very small islands (three to nine genes); however, the simultaneous analysis of numerous, adjacent genes allowed the top–down approach to better locate large genomic islands. These results support our premise that analysis of large genomic regions allows the robust detection of genomic islands from compositionally similar donors.

Both the recursive MJSD and IVOM methods perform well in identifying islands; however, MJSD outperforms IVOM in identifying genomic islands with more than 12 genes at higher cutoffs (Table 2). That is, MJSD does better when we require larger fraction of an island to be predicted correctly. This performance was also seen when an artificial Salmonella genome is the sole donor, though both methods found fewer island-borne genes. Here MJSD outperforms IVOM at higher cutoffs even when a genomic island contains only six genes. For very large genomic islands, MJSD outperforms IVOM at any cutoff (Table 2). In addition, as the size of the island increases, the superiority of the MJSD method outweighs the advantages of the interpolated octamer frequencies of IVOM. Therefore, we conclude that the MJSD metric is effective in identifying large genomic islands, outperforming the most effective existing methods.

Identification of genomic islands in S. enterica Typhi CT18

While artificial genomes provide a valuable test bed, the genomic islands they contain are constructed according to a limited set of rules. To examine the behavior of the MJSD recursion method when applied to genuine genomes, we analyzed the S. enterica Typhi CT18 genome, which has been explored extensively for the presence of genomic islands (6,7). This process has been facilitated by the numerous genome sequences from different serovars of Salmonella, which provide an unusually rich resource for the phylogenetic identification of recently acquired genes. There are currently 17 annotated pathogenicity islands in Salmonella genomes, and 13 of these are thought to be present and active in S. enterica Typhi CT18 (6). In addition, this strain has multiple bacteriophage insertions and two other islands not previously noted (23–25), leading to 21 large regions that are of reliably foreign origin (Supplementary Table 3).

We applied the MJSD top–down algorithm and two bottom–up MJSD algorithms (MJSD-window and MJSD-gene, using genes in place of windows) to identify genomic islands in the S. enterica Typhi CT18 genome (Figure 6A). For comparison, we used the IVOM algorithm, which was reported to be highly accurate on this genome (6). We define an island to be found when a given percentage of its nucleotides have been classified as horizontally transferred. FPR results are shown in Table 3 for various cutoffs. Of the three cutoffs shown, only 40% and 60% give reasonable values for FPR (0.09–0.21); the 80% cutoff is shown to illustrate the large jump in FPR observed when higher cutoffs are used. While these figures may seem low, detecting 40–60% of the island in an initial analysis is useful in focusing further efforts to refine its boundaries. This is particularly true since the false-positive rate is fairly low.

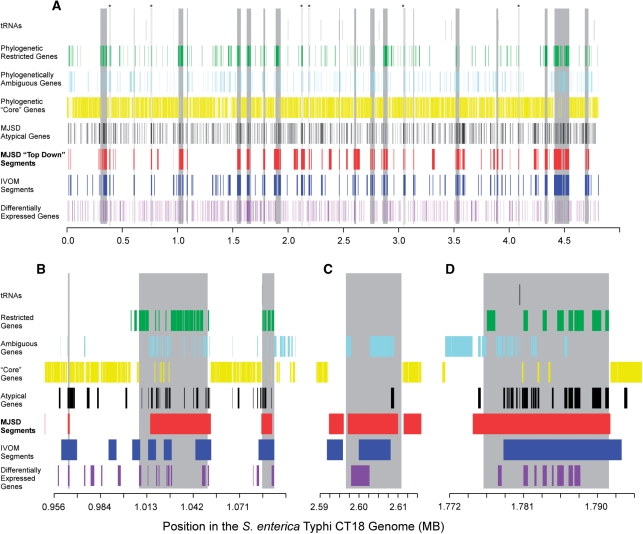
Figure 6.

Predictions made by the top–down and gene-based MJSD, IVOM, and phylogenetic methods. Known and novel islands are shown as vertical gray bars. Genes restricted to the Salmonella genome and those found in related genomes (‘core’ genes) were detected by BLAST similarities (see ‘Materials and Methods’ section). Differentially expressed genes are those upregulated during pathogenesis (26). (A) The entire genome of S. enterica Typhi CT18 showing previously described islands (Supplementary Table 3). (B) A region of the genome that demonstrates the ability of top–down MJSD to accurately capture island boundaries and identify novel regions of varying sizes. The two known islands and a likely non-functional islet (the small region near 965 kb) are accurately detected. (C) The CS54 island's boundaries are best defined using top–down MJSD. (D) An island composed of an integrase gene and known virulence genes is delineated by both the MJSD and IVOM methods; borders are approximated.

Table 3.

The false-positive rates (FPRs) for the MJSD and IVOM methods in detecting known islands in the Salmonella enterica Typhi CT18 genome

	Cutoffa
	40	40	60	60	80	80
Method	Allb	All-1	All	All-1	All	All-1
MJSD	9.5	8.8	17.3	14.5	51.4	39.5
IVOM	11.4	10.3	21.3	15.7	80.3	37.1

^aCutoff value to determine when an island is found.

^bAll: all islands are found; All-1: all but one island are found.

When we require all islands to be found at a 40% cutoff, we find that IVOM has an 11.4% FPR, while MJSD (alpha = 0.01, segmentation model order = 1, atypicality assessment model order = 2) has a false-positive rate (FPR) of 9.5%, a 14% improvement. (Whereas the published IVOM method uses a change point optimization to help determine the precise start and end of an island, we use a modified implementation that allows a tradeoff between sensitivity and FPR. When the original optimizations are used, we find that one insertion is missed at an FPR of 13.1%.) Furthermore, out of the 605 kb of DNA encoded by islands, IVOM detects only 446 kb (non-optimized) or 451 kb (optimized), whereas top–down MJSD detects 477 kb. Thus, even though the islands are deemed ‘identified’ by IVOM, more of each the island is found (on average) by top–down MJSD. The non-recursive MJSD algorithms also underperformed the recursive version. MJSD-window resulted in a FPR of 39% and MJSD-gene false-positive rate was 40.5%, further validating our top–down approach.

‘False’ positives in identifying S. enterica Typhi islands

The false-positive rates discussed above are certainly inflated, since many locations likely correspond to horizontally transferred regions that are not formally recognized as pathogenicity islands or bacteriophages. As examples, six regions are encircled in Figure 6A and noted with asterisks. Each region corresponds to an atypical segment identified by both the MJSD top–down and IVOM algorithms; each region also shows an excess of individually atypical genes. From a phylogenetic standpoint, each segment has few or no ‘core’ genes shared with related taxa and each contains several genes unique to that island. Therefore, these regions carry many of the hallmarks of recently acquired regions.

Microarray data support the position that many ‘false positives’ are actually pathogenicity islands. At least 630 CT18 genes are upregulated during at least one phase of pathogenesis (26), and 103 of these reside in known genomic islands (statistically significant association with known genomic islands, P < 0.02, Fisher's exact test). Of the 103 known island harbored genes, 82 have significant MJSD scores (AS ≥ 0.999), giving an estimate of sensitivity to be 80%. Of the other differentially expressed genes not yet associated with known pathogenicity islands, we found 70 such genes in 30 putative island regions (Supplementary Figure 4), which contain a total of 383 kb, or 7.8% of the total genome in addition to known existing islands.

Detecting genomic islands in genuine genomes

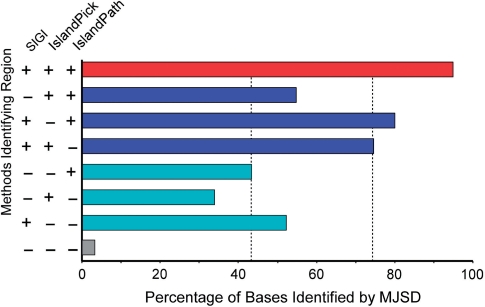
The analysis of the Salmonella serovar Typhi genome suggests that the MJSD segmentation approach accurately detects genomic islands in genuine genomes. To assess the performance of the method on other genomes, we downloaded from IslandViewer (27) the locations of genomic islands identified by SIGI-HMM (28), IslandPick (29) and IslandPath-DIMOB (30) in publicly available genomes. Genomes were chosen for analysis where (a) at least 20 kb of DNA was classified as island by two of the three methods, (b) at least 20 kb of DNA was classified as island by all three methods and (c) this represented at least 40% of the total DNA classified as island by any of the methods; a total of 20 genomes were selected (Supplementary Table 6). Islands were then identified by MJSD using conservative thresholds. MJSD robustly identified as islands (97% of bases) regions that were previously classified as such by all three methods (red bar in Figure 7). For regions identified by two of the three previous methods (that is, missed by SIGI, IslandPick or IslandPath, but detected by the other two), between 54% and 83% (average of 74%) of bases were identified as island by MJSD (blue bars in Figure 7). This lower number reflects the weaker atypical character of these regions and/or the misclassification of native DNA as island. If the region was identified by only one method, MJSD was even less likely to classify it as island (cyan bars in Figure 7) and very little DNA was classified as an island that was deemed native by the three previous methods (gray bar in Figure 7). This shows the potential of the MJSD method in consistently and robustly detecting putative genomic islands in genuine genomes.

Figure 7.

Performance of MJSD in predicting previously identified genomic islands among 20 bacterial genomes. Islands were identified by SIGI-HMM (28), IslandPick (29) and IslandPath-DIMOB (30). The accuracy in identifying islands reported by one, two or all the above three methods is assessed by obtaining the percentage islands’ nucleotides correctly labeled as island by the MJSD method. Dashed lines represent mean values.

Algorithm efficiency

The top–down, MJSD recursive algorithm is computationally efficient on bench-top computers, being suitable for routine analysis of large-sized genomes or automated assessment of library sequences. On our machines, the MJSD algorithm completes a single genome in a matter of minutes whereas the IVOM algorithm requires 1 to 2 h.

DISCUSSION

Complementarity of parametric approaches

Previous approaches for delineating genomic islands in bacterial genomes have focused either on individual genes or on small regions within fixed-size windows. For example, the Wn program assesses the atypicality of genes individually or collectively within a moving window of fixed number of genes (20,31). The IVOM method attempts to enhance its discriminative power by using a sophisticated variable-order (interpolated) model in place of fixed-order model used in Wn (6). These moving-window methods have shown promising results yet suffer from the vagaries of bottom–up approaches. Our method does not replace the bottom–up parametric methods; rather, it addresses their inherent weakness in localizing large laterally transferred genomic regions, and so should be used in concert with existing methods. The top–down approach intrinsic to the recursive segmentation procedure assesses the compositional characteristics of large transferred regions directly. As expected, the top–down method excelled at identifying large islands and bottom–up approaches performed better in identifying smaller islands (Table 1). In addition, our top–down approach performed better in identifying large islands at more stringent cutoffs.

Complementarity of phylogenetic and parametric approaches

Phylogenetic methods are often considered to be the most reliable methods for detecting laterally acquired genes. Genomic regions with limited phylogenetic distributions—that is, genes absent from the organism's close relatives—are considered to have been acquired horizontally. The success of such methods clearly depends on the breadth and depth of the sequence database, but even with a rich set of genomes for comparison the phylogenetic approach cannot identify genomic islands unambiguously. First, phylogenetic discordance often results from gene loss in multiple lineages, leading to false predictions of islands. This problem is further exacerbated by rapidly evolving genes, which confound ortholog identification. Second, paralogs are often misidentified as orthologs, preventing the identification of large genomic islands since it appears that broadly shared genes appear in regions otherwise bearing genome-specific genes. Therefore, genes found frequently in genomic islands will often have homologs in related genomes, obscuring the phylogenetic signal and confounding the identification of the genomic island. For example, well-established islands in the Salmonella serovar Typhi genome were populated with false ‘core’ genes with homologs found in most or all related taxa (Figure 6B). Thus, sets of core genes include clear island-borne loci, such as those encoding bacteriophage integrases. Parametric methods can complement the phylogenetic approaches in the identification of genomic islands beyond those cases when closely related genomes are lacking.

An integrated strategy for detecting genomic islands

The synergy of the phylogenetic, bottom–up parametric and top–down parametric approaches provide for more robust identification of genomic islands than afforded by any single approach. For example, six strong candidates are indicated with asterisks in Figure 6A. For many other regions, phylogenetic data are compelling but not conclusive. The islands are not uniformly populated with genes unique to Salmonella, as many of the island-born genes have homologues in related genomes. The bottom–up methods detected only a few of the constituent genes as sufficiently atypical to be deemed foreign. The top–down MJSD method provides the complementary assessment that the genes in each island are sufficiently different from the flanking regions—and sufficiently similar to each other—that they are placed into a putative island. The predictions of the IVOM approach are more fragmented that the MJSD approach, and do not identify the end points as accurately. However, the sum of all data—the lack of core genes, presence of many unique genes, presence of strongly atypical genes and overall atypicality of the genomic segment with defined boundaries—together point to the presence of a large genomic island (Figure 6).

Other uses of the generalized Jensen–Shannon divergence

Generalization of the Jensen–Shannon divergence measure improved the performance of our method significantly. The generalization consisted of capturing short-range correlations within symbolic sequences by assuming that a symbolic sequence is generated by a source of arbitrary Markov order m. Although we have focused here on application of the generalized measure to the detection of genomic islands, the use of the generalized measure in place of the conventional JSD measure will likely improve other algorithms used in genome annotation; these algorithms include, but are not limited to, the delineation of coding and noncoding regions (16), detection of isochores, CpG islands and complex repeats (19), gene clustering (13) and protein profile–profile comparison (32).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

The US National Science Foundation (grants EMT 0523643 and FIBR 0527023 to A.R.) and the US National Institutes of Health (grant GM078092 to J.G.L.). Funding for open access charge: Keck Graduate Institute of Applied Life Sciences.

Conflict of interest statement. None declared.