Rational modulation of conformational fluctuations in adenylate kinase reveals a local unfolding mechanism for allostery and functional adaptation in proteins

Abstract

Elucidating the complex interplay between protein structure and dynamics is a prerequisite to an understanding of both function and adaptation in proteins. Unfortunately, it has been difficult to experimentally decouple these effects because it is challenging to rationally design mutations that will either affect the structure but not the dynamics, or that will affect the dynamics but not the structure. Here we adopt a mutation approach that is based on a thermal adaptation strategy observed in nature, and we use it to study the binding interaction of Escherichia coli adenylate kinase (AK). We rationally design several single-site, surface-exposed glycine mutations to selectively perturb the excited state conformational repertoire, leaving the ground-state X-ray crystallographic structure unaffected. The results not only demonstrate that the conformational ensemble of AK is significantly populated by a locally unfolded state that is depopulated upon binding, but also that the excited-state conformational ensemble can be manipulated through mutation, independent of perturbations of the ground-state structures. The implications of these results are twofold. First, they indicate that it is possible to rationally design dynamic allosteric mutations, which do not propagate through a pathway of structural distortions connecting the mutated and the functional sites. Secondly and equally as important, the results reveal a general strategy for thermal adaptation that allows enzymes to modulate binding affinity by controlling the amount of local unfolding in the native-state ensemble. These findings open new avenues for rational protein design and fundamentally illuminate the role of local unfolding in function and adaptation.

The existence of conformational fluctuations (i.e., dynamics) in proteins has been known for decades (1), and the importance of these fluctuations to such biological processes as molecular recognition, catalysis, and allostery has increasingly been appreciated (2–4). The emergence of dynamics as a prerequisite to function suggests that in addition to structural requirements, such as shape and chemical complementarity, function imposes requirements for flexibility (i.e., the ability to undergo fluctuations) as well. Indeed, the biological functions of proteins can be viewed as arising from a complex interplay between protein structure and fluctuations, and to decipher the import of these related properties experimental strategies are needed that will decouple the structural and dynamic contributions.

Here we investigate conformational fluctuations and their impact on the binding reaction of Escherichia coli adenylate kinase (AK), an enzyme that catalyzes the reversible conversion of AMP and ATP to ADP. Our approach in this study is to investigate a natural adaptation strategy to maintain protein flexibility in cold-adapted enzymes. Flexibility appears to be a property that has been conserved throughout the process of thermal adaptation in proteins (5). Namely, in characterizing the sequence differences between lactate dehydrogenase (LDH) variants of notothenoid fish that have adapted to survive in different sea temperatures, Somero and colleagues (6) noted that cold-adapted enzymes incorporated more glycine (Gly) residues and hypothesized that such substitutions are used to modulate the K_m by altering the flexibility of the native state. More specifically, by increasing the population and number (degeneracy) of states that do not bind the substrate, an increase in K_m could be effected (6). It is our hypothesis that locally unfolded states may be the adaptively important states in question and that Gly substitutions in proteins serve to maintain the proper balance of these locally unfolded states at lower temperatures. Furthermore, we propose that such mutations can affect functional changes by selectively modulating the properties of minor excited (i.e., locally unfolded) states, which can be viewed as excursions from the ground- (fully folded) state.

Based on this thermal adaptation strategy, we targeted several surface-exposed valine (Val) residues that are distant from the active site for mutation to Gly. We show that the effects of these mutations are to increase temperature-dependent fluctuations in the native-state ensemble, although they leave the ground-state structure unaffected. Despite the absence of ground-state structural perturbations, the effect of the mutations on the temperature dependence of binding affinity of AK were substantial. In addition to revealing a previously unreported locally unfolded state that is populated at a level of 5% in the native-state ensemble of WT AK, these results reveal that mutations distal from the active site can be rationally applied to proteins, such that the binding affinity is affected not through structural changes, but by modulating the conformational fluctuations. Further, these results reveal that a single surface mutation to Gly can shift the adaptive temperature by as much as 10° C without changing the structure of the bound complex, a result that has broad implications for the rational design of enzymes with altered functional properties.

Results and Discussion

Dynamics-Directed Mutation Strategy.

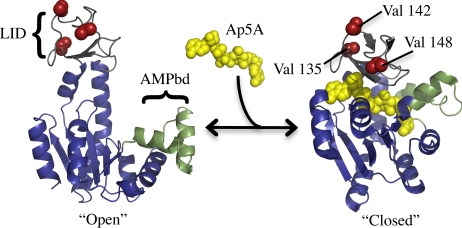
AK has been used as a model system to study enzyme function/dynamic relationships using a variety of experimental and computational approaches (2, 7–9). The protein has two small structural appendages commonly referred to as the “LID” and “AMP-binding” domains (Fig. 1), which have been demonstrated to be highly dynamic on a wide range of time scales (2, 7, 8), undergoing large spatial changes (10, 11) and dynamic dampening upon ligand binding (7). The goal of our experimental strategy is to selectively probe the conformational manifold of states that contribute to the dynamics of the LID domain, in search of states that are both similar to local unfolding and relevant to substrate binding. To accomplish this objective, we have carefully chosen mutations that should promote locally unfolded states (12) without disturbing the structural properties of the fully folded ground state.

Fig. 1.

Mutation strategy applied to adenylate kinase. Structure of “Open” [i.e., Apo-AK; (PDB ID 4AKE) (11)] and “Closed” [i.e., complex of AK and the nonhydrolysable bisubstrate analogue inhibitor P¹,P⁵-Di(adenosine) pentaphosphate (Ap5A); PDB ID 1AKE (10)] states of AK. LID is shown in gray. The “LID domain,” as defined by Shapiro et al. (7). AMPbd is shown in green. The “AMP binding domain” (7). Red spheres, selected mutation sites.

Three Val to Gly mutations at surface-exposed positions in the LID domain were selected. Such mutations are expected to increase the conformational entropy associated with unfolding the mutated region of the protein, if indeed locally unfolded states are relevant. The β-branched amino acid Val (as well as isoleucine) is known to have relatively small increases in conformational entropy upon unfolding, as steric collisions of the bulky side chain limit conformational degrees of freedom upon unfolding (13). The absence of a side chain in Gly, on the other hand, results in a comparatively large increase in the conformation entropy of unfolding (13). As such, Val–Gly mutations should, in principle, promote the probability of locally unfolded states by increasing the entropy associated with local unfolding (13).

We have defined several criteria for selecting mutation sites in AK, such that the effects should be manifested exclusively in the conformational entropy, as described above, rather than in a perturbation of the structure of the fully folded state of the protein. The criteria areas follows: (i) the side chains of the mutated residues should be highly surface-exposed, involving few to no intramolecular contacts, (ii) the side chain should contain no important moieties, such as charged or highly polar groups, that could contribute to long-range interactions, and (iii) the mutated sites (i.e., the deleted Val side chains) should be spatially distant (>8 Å) from the active site, thus making no contact with the ligand. As no stabilizing contacts within the native fold or between the protein and ligand will be perturbed by such a mutation, little or no effect should be seen to the ground-state unbound structure or the structure of the bound complex. Three positions were selected in the LID domain of AK, which satisfy the above three criteria: v142g, v148g, and v135g (red spheres in Fig. 1).

Distal Mutations Propagate to the Binding Site.

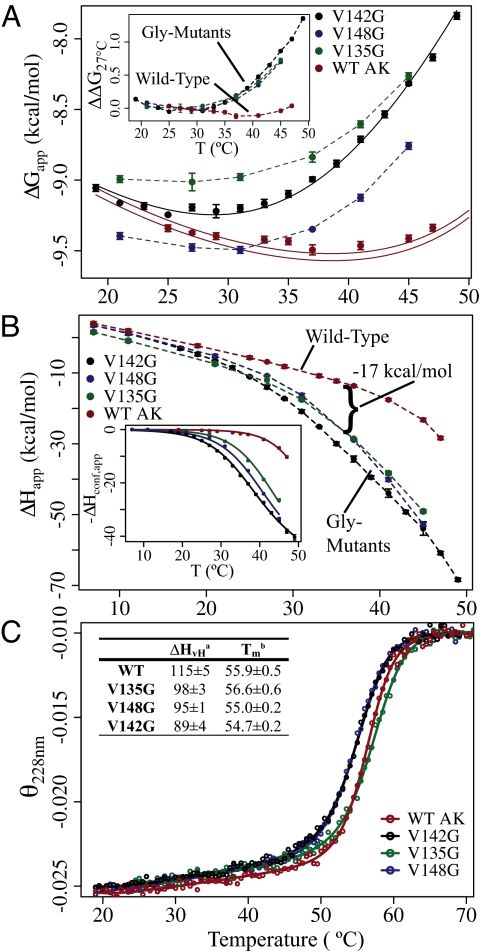
To ascertain the impact of the surface-exposed Gly substitutions, isothermal titration calorimetry (ITC) was used to measure the binding of AK to the bisubstrate analog, P¹,P⁵-Di(adenosine-5′) pentaphosphate (Ap5A). The Ap5A–AK complex has been previously shown to be an excellent model of the (ternary) substrate bound state (10, 14), and is ideally suited for calorimetric analysis. Although the mutations are quite remote from the binding site, they all cause dramatic changes in the temperature-dependent thermodynamics of inhibitor binding. At 37° C and above, all mutations decreased binding affinity (Fig. 2A), while effecting large increases in the favorable enthalpy of binding (Fig. 2B). Interestingly, the temperature dependence of the binding affinities are similar for all of the mutants and different from the WT (Fig. 2A Inset), consistent with the hypothesis that the mutations are effecting these changes through a similar mechanism. This finding is also supported by the similarity in the enthalpy of binding of each mutant (Fig. 2B). Surprisingly, thermal unfolding experiments using circular dichroism (CD) reveal only minimal changes in the T_m of the protein (Fig. 2C), although the apparent (i.e., van't Hoff) enthalpy of global unfolding, ΔH_vH, is significantly reduced in the mutants (Fig. 2C Inset). The origin of these effects is discussed in more detail below.

Fig. 2.

Distal mutations affect the thermodynamics of binding and folding. (A) Apparent free energy (ΔG_app) of binding. The solid black line shows the fitted curve for the v142g ΔG data. The solid red lines represent the prediction of WT data based on the fitting of ΔH_conf,app. Lines represent the prediction, plus and minus the average standard error of determining ΔG_app. (Inset) Change in ΔG_app for each protein, with temperature, referenced from 27° C. ΔΔG_{27° C}(Temp) = ΔG(Temp) − ΔG(27° C). (B) Apparent enthalpy of binding (ΔH_app) Ap5A. (Inset) Corrected data and fitting functions representing −ΔH_conf,app (Eq. 2a). (C) Representative circular dichrosim thermal unfolding experiments (deg·cm²/dmol·res). Denatured state signals are normalized. Lines are fitting functions for a two-state thermodynamic model. (Table) Thermodynamic parameters determined from the two-state fits: a, van't Hoff enthalpy (kcal/mol) (at T_m); b, transition midpoint temperature (°C).

The ITC results suggest that the binding reaction is coupled to a conformational equilibrium that is modulated by the mutations. Accounting for this equilibrium, the association reaction can be written in terms of a “binding incompetent” (BI) state, that has little or no affinity for the ligand, which is in equilibrium with a “binding competent” (BC) high-affinity state, and that the addition of ligand promotes the population of the BC state through mass action (15). In such a case, the apparent free energy consists of two terms,

where the first term represents the intrinsic free energy of interaction between the BC state and the ligand, and the second term accounts for the apparent contribution of the conformational equilibrium between the BI and BC states to the free energy (see SI Appendix). Similarly, the binding enthalpy has two terms.

The conformational term, ΔH_conf,app, can be used to directly fit the ITC data (Fig. 2B Inset) for the thermodynamic parameters governing the conformational equilibrium (i.e., T_m,conf, ΔC_p,conf, and ΔH_conf) (see SI Appendix). Two noteworthy aspects of the calorimetric data emerge. First, the enthalpy difference between the BI and BC states is significant (ΔH_conf (35.1° C) = 33 ± 1 kcal/mol), amounting to what would be expected for the enthalpy of unfolding of the entire LID domain (as described in Mutational Effects Promote Local Unfolding). Secondly, the data obtained for all of the proteins can be fit with a common ΔC_p,conf [660 ± 70 cal/(mol*K)] and ΔH_conf (see above), each protein differing only in the fitted T_m,conf, the midpoint temperature for the BC to BI state transition. Furthermore, the effect of the mutation to Gly on T_m,conf is quite large, shifting the local unfolding transition midpoint from 52.5 ± 0.1° C (WT) to as low as 35.1 ± 0.3°C (v142g).

In terms of the presented model and analysis, the significance of these calorimetric results is threefold. First, the fact that only the T_m,conf differs between each protein indicates that the Gly mutations have indeed selectively increased the entropy of the BI state, consistent with the assertion that the mutational effects are primarily manifested as increases in the conformational degeneracy of a locally unfolded state. Secondly, by strong inference the results suggest that the thermodynamic and conformational character of the BI state is common to the WT and all three Gly mutants. Thirdly, the data indicate that the transition between the BI and the BC state is a highly cooperative “two-state” process. This point is supported by the demonstration that the van't Hoff and calorimetric enthalpy changes for the local unfolding transitions are equal (see SI Appendix) (16). We also note that the parameters obtained from an analysis of the binding enthalpies quantitatively reproduce the binding affinity for the WT protein as demonstrated for v142g (solid lines in Fig. 2A), further corroborating our model and analysis.

Structural Mapping of Mutational Effects.

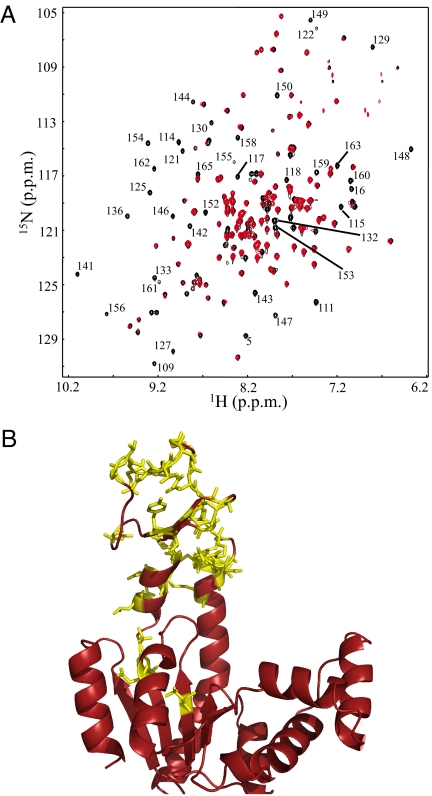
To obtain a site-resolved view of the mutational effects, ¹H-¹⁵N HSQC NMR spectra were gathered at 33° C for the WT and v142g proteins (Fig. 3A). As is evident, a large number of resonances clearly seen in the WT spectra have no measurable intensity in the v142g spectrum. No new peaks appear concomitant to this loss, indicating that the resonances for residues affected by the BC to BI transition are severely broadened because of a chemical exchange process.

Fig. 3.

Mutational effects propagate to entire LID domain. (A) ¹H-¹⁵N HSQC spectra of WT (black) and v142g (red) AK at 33° C. Labels are provided for all residues that were assignable from published values (29), and have measurable intensity in the WT spectrum, but no measurable intensity in v142g. (B) The same residues (labeled in Fig. 3A) are shown in yellow with “sticks,” projected on the open conformation of AK (PDB ID 4AKE) (11).

Of note, all but two of the broadened and assignable residues are included in a contiguous chain, from residue 109 to 165 (Fig. 3B), consistent with the mutation at position 142 affecting a large region including, but not limited to, the LID domain. Qualitatively similar results are observed for mutations at positions 135 and 148 as well. We also note that not all residues experiencing chemical exchange need be directly involved in the BI–BC transition. Clearly, conformational processes can affect neighboring amides. In summary, the NMR data demonstrate that the mutations to the LID domain appear to bring about a cooperative conformational process that is consistent with the large enthalpy (ΔH_conf,app) observed by ITC.

Mutational Effects Propagate in the Absence of Structural Changes.

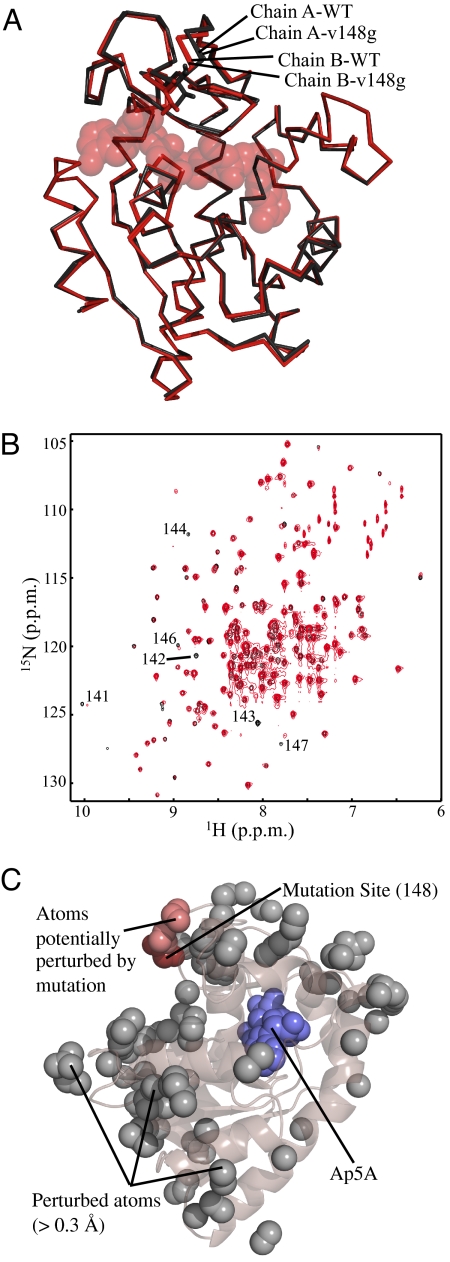
To determine whether the effects of the Val–Gly mutations were to the conformational manifold in the excited states of AK or to the ground-state structures, X-ray crystallography was performed on the Ap5A bound complex. WT and v148g crystallize in the same space group (P2₁2₁2) and asymmetric unit (ASU), and therefore merit detailed comparison. The WT and v148g crystals diffracted to 2.0 Å, (see Table S2 in the SI Appendix for crystallographic statistics). As expected, the v148g mutation causes minimal, if any, discernable perturbation to the compact fold of AK in the bound state (Fig. 4A). AK crystallizes with two molecules in the asymmetric unit, with discernable structural differences between the two. The all-atom RMSD values between the WT and mutant proteins that occupy the same location in the ASU are small (≈0.2 Å), and less than the value calculated between the two copies in the same ASU (≈0.4 Å) (see Table S3 in the SI Appendix). The comparison shows that the impact of the mutations cannot be reconciled in the context of structural differences between the WT and the mutants. Indeed, the results reveal that the effects of crystal packing far exceed any effects of the mutation on the ground-state structure of the bound complex.

Fig. 4.

Surface Gly mutations in LID conserve ground-state structure. (A) Alignment of the reported crystal structures of WT and v148g AK. Shown in red are chains (WT and v148g) from position A within the asymmetric unit. Shown in black are chains from position B within the asymmetric unit. (B) ¹H-¹⁵N HSQC spectra of WT (black) and v142g (red) AK at 21° C, which suppress local unfolding within the LID region. Enhanced contrast is used for v142g to allow visualization of peaks with decreased intensity, most likely because of exchange broadening. Available assignments are provided for resonances with differences at this temperature. (C) Analysis of structural perturbations effected by mutation. The gray spheres represent all atoms that move >0.3 Å from the WT to mutant structure in both copies within the ASU. The dark red spheres show the mutation site (position 148). The light red spheres show all perturbed atoms (gray) that can be connected to the mutation site by a continuous chain (< 6 Å per step) of other perturbed atoms. Blue spheres, Ap5A.

To further investigate the hypothesis that the mutational effects were to the excited-state repertoire, and not the ground-state structures, NMR chemical shifts (v142g) were again analyzed, but at low temperature (21° C), where the BI state is minimal. The overlaid spectra are shown in Fig. 4B. This comparison demonstrates that the chemical shift of very few residues are perturbed at this temperature, suggesting that the structure of the unbound or “open” state is strikingly similar for the WT and v142g proteins at this temperature. The few perturbed residues are generally in close sequence proximity to the mutated residue. In short, structural analysis by NMR and X-ray crystallography strongly suggests that the mutations increase the probability of a set of thermodynamically distinct excited states and do not affect the ground-state structure of the free or ligand-bound protein.

Both the crystal structure solved for liganded v148g and the chemical shifts of unbound v142g reinforce the concept that allosteric mutational effects cannot be reconciled in the context of the structural changes, or in terms of a pathway of structural distortion between the mutated site and the active site. This finding is demonstrated by the analysis of the X-ray data (Fig. 4C), where all structural perturbations >0.3 Å are identified (gray spheres in Fig. 4C). Within this set of perturbed atoms, the network of all interacting (i.e., <6 Å) partners (light red spheres in Fig. 4C) extending from the mutated site (dark red spheres in Fig. 4C) is small, and does not approach the binding site. The importance of this result cannot be overstated. Although it is clear that mutations or bindings to allosteric systems may manifest themselves as structural perturbations, the results presented here argue directly against an exclusively mechanical interpretation of energy propagation and reinforces the view that the dynamic contribution to allosteric effects (3, 17, 18), is not only critical, but can also be rationally modulated.

Mutational Effects Promote Local Unfolding.

As noted, the mutation strategy implemented here is designed to increase the probability of excited states while leaving the structures of the ground states unaffected. The results and analysis thus far indicate that the mutational effects are manifested as expected. But the question remains, how similar is the BI state to a locally unfolded state, wherein those residues that are affected by the mutation (from Fig. 3) are unfolded, with the remaining part of the structure being folded?

To address this question, we used the COREX algorithm (19), which uses the high-resolution structure as a template, and a long-standing surface area-based parameterization of unfolding energetics to predict the ΔH and ΔC_p of unfolding of different regions of the protein structure. If the BI state were indeed a locally unfolded state, a reasonable model based on the NMR data (Fig. 3) would be to assume that residues 110–164 are unfolded in the BI state. By using COREX, the predicted thermodynamics of unfolding this region (PDB ID 4AKE) were calculated and compared with the experimentally determined values (Table 1). The agreement is excellent. Surprisingly, the thermodynamic parameters estimated for global unfolding of v142g (Fig. 2C) also match the COREX-predicted values for unfolding the remaining residues, 1–109 and 165–214. Because the difference in T_ms of the local and global unfolding transitions are greatest for the v142g mutant, the two-state model for global unfolding (as applied to the CD data; Fig. 2C) represents a valid approximation.

Table 1.

Experimental and predicted thermodynamics of local and global unfolding

Parameter	T(°C)	Local*		Global†		Sum‡
		ITC§	Corex‖	CD¶	Corex‖	Experimentally Determined**	Corex‖
ΔH (kcal/mol)	35.1	33 ± 1	32.7	(34 ± 9§§)‡‡	40.6	67 ± 10§§	73.3
	54.7	(46.3 ± 2.2§§)††	46.5	89 ± 4	88.2	135 ± 6.2§§	134.6
ΔCp [kcal/(mol*K)]	—	0.66 ± 0.06	0.7	2.8 ± 0.2	2.4	3.5 ± 0.26§§	3.1

Values after all ± represent experimental 95% confidence intervals.

*^,†,‡Experimental and computational measures of possible unfolding reactions. Residues: *110–164, ^†1–109 and 165–214, ^‡1–214.

^§,¶Experimental parameters estimates from ITC (Fig. 2B Inset) and CD (of v142 g) (Fig. 2C), respectively.

^‖Values calculated by using the COREX energy function and PDB ID 4AKE. Confidence is generally ±10%.

**Sum of enthalpy and heat capacity for the BI–BC transition (ITC) and the native–denatured transition (CD).

^††Calculated as ΔH_local(35.1) + ΔCp_local (54.7–35.1).

^‡‡Calculated as ΔH_global(54.7) + ΔCp_global(35.1–54.7).

^§§Propagated 95% confidence interval.

Two important results emerge from the agreement between experimental and predicted values. First, the ΔH and ΔC_p predicted by COREX are directly calculated from expected changes in solvent-exposed surface area (19). Therefore, in terms of changes in solvent exposure, the BC–BI transition appears to be indistinguishable from a local unfolding of residues 110–164. Second, the fact that the sum of the heat of the BC–BI and the native–denatured-state transitions equal the total enthalpy expected for unfolding all residues, suggests that fluctuation to the BI state is the dominant local unfolding process in the unbound native-state ensemble.

A New View of the Native State Ensemble of Apo-AK.

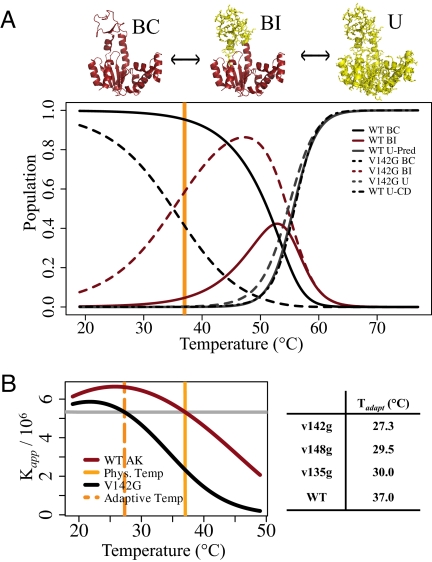
Recent computational studies suggest that the transition between the open and closed states of AK is more complex than a simple two-state process (20, 21), a conclusion supported by the current results. Combining the parameter estimates gained from ITC and CD experiments, a three-state model for unliganded AK emerges, involving the fully folded BC state, the BI state with a locally unfolded region, and the fully unfolded (U) state. The populations of all states in this system are plotted as a function of temperature for WT and v142g AK in Fig. 5A (see also SI Appendix). From this plot, we see that the BI state is highly populated under strongly native conditions, 30–40° C. In WT AK, the BI state is ≈5% populated at 37° C, which is the optimal growing temperature for E. coli. Control experiments indicate that the BC–BI equilibrium is relatively insensitive to variation in pH (7–8), ionic strength, and magnesium concentration, supporting the conclusion that the presence of this state is robust with respect to experimental conditions.

Fig. 5.

Gly mutations lower adaptive temperature by redistributing the AK ensemble. (A) Populations are calculated from the BI/BC (K_conf) equilibrium estimated from the ITC data, and the Unfolded/BI (K_unf) equilibrium estimated from the CD unfolding experiments on v142g (the reasonability of this approximation is seen in this plot, from the high probability of the BI state at 47° C, before the global unfolding transition). Therefore, the partition function for the system is Q = 1 + K_conf + K_conf ·K_unf. The probability of BC, BI and unfolded (U) states are calculated by 1/Q, K_conf/Q, and K_conf ·K_unf/Q, respectively. The dot-dashed line shows the population of the U state for WT as calculated directly from the CD unfolding parameter estimates (see Fig. 2C Table). The orange line marks the optimal growing temperature for E. coli. (B) Plot of the apparent binding affinity (K_app) for Ap5A, calculated from the ITC data fitting (Fig. 2 A and B). The dashed orange line marks the temperature where K_app is equal for v142g and WT (37° C), i.e., the new surrogate homeostatic temperature of v142g. (Table) Surrogate homeostatic temperatures, T_adap, calculated for all mutants. K_app,mut(T_adapt) = K_app,wt(37° C).

Importantly, this simulation demonstrates how evidence of the BI population in the WT AK native state is manifested in the WT CD unfolding data. The probability of the unfolded state as estimated from CD (dot-dashed line Fig. 5A), is plotted along with the unfolded state probabilities predicted by the three-state model (solid-gray line in Fig. 5A). The agreement of the two curves is clear. This finding demonstrates that the presence of the BI population explains the apparent differences (Fig. 2C Inset) in the thermodynamics (using a two-state model) of unfolding for the WT and mutant proteins. Also of note, the prevalence of the local unfolding in the LID domain, even for the WT protein, provides mechanistic insight into why sequence changes within the LID, not the hinge or core regions, were found to be mostly responsible for adaptations of the kinetic properties of AK from Bacillus sp. (22).

Implications for Molecular Adaptation.

Enzymes adapted to different environments must maintain both the properties of the catalytic site, which allow for catalysis and molecular recognition of the substrate, and also alter kinetic parameters such as K_m and k_cat. Many studies have demonstrated that a common adaptive strategy is to change regions of structure that are outside of the active site, with the integrity of the active site remaining highly to perfectly conserved (5, 23, 24). In the case of cold temperature adaptation, the promotion of conformational flexibility seems to be the key target of adaptive mutations (6, 25). In particular, Somero and colleagues (6) have hypothesized that the decreased substrate affinity of some cold-adapted enzymes is a result of the highly flexible native state exploring nonbinding conformations. Our results demonstrate how changing the properties of nonbinding (BI) excited states, rather than perturbing the structure of the fully folded ground state, can mediate this type of adaptive change. To see this more clearly, we plot the fitted apparent association constant (K_app) of inhibitor binding for the WT and v142g proteins as a function of temperature (Fig. 5B). By using K_app as a surrogate adaptive endpoint and 37° C as our original homeostatic temperature, we see that the v142g mutation reduces the surrogate homeostatic temperature [K_app,mut(T_adaptive) = K_app,wt(37° C)], by ≈10° C (see SI Appendix). Thus, a significant adaptive change can be mediated by this mechanism via a single point mutation. We note that this result and adaptive mechanism are generalizable to any protein–ligand binding reaction with similar thermodynamic features.

The importance of this adaptation strategy is twofold. First, the change in binding occurs in the absence of structural changes in the active site or structural core of the protein. Instead, the affinity is modulated by changing dynamic fluctuations of the protein structure. To date, structure-based protein design strategies have been based largely on static representations of the protein and ligand (26). The results presented here reveal a strategy for rational adaptation/design that targets the fluctuations rather than the structure. The fact that all three mutations produced similar effects suggests that this approach can be robustly applied, although the approach awaits further study on a wide range of systems. Second, the promotion of BI states among the many interconverting members of the native ensemble (i.e., flexibility), as proposed by Somero and colleagues (6), is directly confirmed to be a useful strategy for the adaptive modulation of binding affinity. By extension, the counterintuitive functional utility of radical conformational excursions to highly disordered, loss of function states is clearly demonstrated. Finally, it should be noted that although the current study investigates only the effects of the mutations on K_app, Somero and colleagues (6) hypothesized that k_cat can also be affected by flexibility-altering mutations. The validity of this hypothesis with respect to AK is currently under investigation.

Conclusions

The results presented here reveal that a structure-preserving mutation approach, which is based on an adaptation strategy seen in enzymes from cold-adapted organisms, has allowed us to selectively increase the probability of a locally unfolded state of AK, without changing the structural properties of the native fold. Because there is no accompanying structural change, these results demonstrate directly that perturbations (e.g., mutations or binding of allosteric ligands) can propagate to functional sites in the absence of a pathway of structural distortion linking the sites. Instead, these results reveal the importance of local conformational fluctuations in determining and maintaining function in proteins. Moreover, the striking agreement of the structural and energetic features of this locally unfolded state between the WT and the three Gly mutants of AK is suggestive of a robust mechanism in which the same effect (i.e., stabilizing or destabilizing a locally unfolded state) can be facilitated by mutations at numerous sites. The implication is that design principles can be independently applied to the dynamic fluctuations of a protein without affecting structure significantly.

Materials and Methods

Protein Expression, Purification and Mutagenesis.

The protein was expressed in HMS174 with the pEAK91 plasmid (27) and purified as previously described (28). Mutagenesis was performed with the Quick Change kit, obtained from Stratagene. Mutations were confirmed by sequencing and mass spectroscopy.

ITC and CD.

ITC experiments were performed on a MicroCal VP-ITC. Data were fit by using a single-site binding model. Heats of dilution were determined by overtitration when possible, or from ligand–buffer titration experiments. Experimental conditions were 0.04 mM AK, 60 mM Pipes, 1 mM EDTA, 7.85 pH, and 7–49° C. Data analysis details are included in the SI Appendix. CD experiments were performed under identical buffer conditions with 4 μM AK. The CD was monitored at 228 nm, temperature was increased 1° C/min. Reversibility of folding was ≈90% for all proteins. Fitted parameters are based on 4–5 repeat experiments.

Crystallography.

Crystals were grown by the sitting drop method, in conditions similar to those previously reported (10). Protein was 20–45 mg/mL with ≈2 mM Ap5A in 50 mM Mes, pH 6.7, 1 mM EDTA. Precipitant solutions in the above buffer were 3% wt/vol PEG 2K with 1.8–2.3 M ammonium sulfate, pH 7.0–7.3. In 50% precipitant solution, crystals grew in 24–48 h, with a 0.5 mL precipitant reservoir. Crystals were cryoprotected in Paratone. Data were processed by using HKL2000 (HKL). Phases were determined by molecular replacement by using PHASER and PDB ID 1AKE as a probe (10). Initial refinement was performed with COOT and Refmac. Further refinement was performed by using PHENIX. Optimal R-free was achieved by using TLS refinement with 10 translation libration screw units per protein chain. See SI Appendix for refinement statistics.

NMR.

¹⁵N labeled AK was prepared by using Cambridge Isotopes Bio-Express media, and purifying as above. Experimental conditions were identical to ITC conditions, with 2 mM EDTA and ≈1.0 mM AK concentration. All experiments were performed on a Varian 800 MHz spectrometer. Partial assignments were made from previously published values (29).