Testing in semiparametric models with interaction, with applications to gene-environment interactions

Summary

Motivated from the problem of testing for genetic effects on complex traits in the presence of gene-environment interaction, we develop score tests in general semiparametric regression problems that involves Tukey style 1 degree-of-freedom form of interaction between parametrically and non-parametrically modelled covariates. We find that the score test in this type of model, as recently developed by Chatterjee and co-workers in the fully parametric setting, is biased and requires undersmoothing to be valid in the presence of non-parametric components. Moreover, in the presence of repeated outcomes, the asymptotic distribution of the score test depends on the estimation of functions which are defined as solutions of integral equations, making implementation difficult and computationally taxing. We develop profiled score statistics which are unbiased and asymptotically efficient and can be performed by using standard bandwidth selection methods. In addition, to overcome the difficulty of solving functional equations, we give easy interpretations of the target functions, which in turn allow us to develop estimation procedures that can be easily implemented by using standard computational methods. We present simulation studies to evaluate type I error and power of the method proposed compared with a naive test that does not consider interaction. Finally, we illustrate our methodology by analysing data from a case-control study of colorectal adenoma that was designed to investigate the association between colorectal adenoma and the candidate gene NAT2 in relation to smoking history.

1. Introduction

Modern genetic association studies often focus on discovery of susceptibility loci, i.e. identification of genetic variants that are associated with the trait under study. The risks of multifactorial traits, such as cancer, however, are determined by complex interactions between genetic and environmental exposures and the chance for discovery of the underlying susceptibility genes can be substantially reduced if the possibility of heterogeneity in genetic effects due to interactions is ignored. Thus, in recent years, there has been increasing attention in omnibus testing of genetic main effects and gene-environment or gene-gene interactions for detection of susceptibility genes for complex traits. Clearly, tests of association incorporating interactions require larger degrees of freedom than those which are based only on main effects. When the number of extra degrees of freedom required is relatively small, recent studies have shown that the omnibus tests can be a robust and powerful approach for detecting genetic association irrespectively of whether certain specific forms of interactions are present or not (Chatterjee et al., 2006; Kraft et al., 2007). However, if the required number of degrees of freedom is large, then the omnibus tests can have poor power. Thus parsimonious modelling of gene-gene and gene-environment interactions should be considered for construction of powerful omnibus tests.

Chatterjee et al. (2006) proposed the use of a Tukey style 1 degree-of-freedom model for interaction for testing the genetic association of a disease with a set of genetic variants, such as tagging single nucleotide polymorphisms (SNPs) in a candidage gene, that may potentially interact with another set of genetic variants or/and with one or more environmental exposures. SNPs represent a natural genetic variability at high density in the human genome. A genetic locus corresponding to an SNP has two possible alleles (states), namely the normal and the variant. The SNP-genotype data for a subject can have three possible values and are often coded numerically as the number of variant alleles that the subject carries on the pair of homologous chromosomes that are inherited from his or her parents.

In this paper, we shall consider extending the work of Chatterjee et al. (2006) focusing on the problem of gene-environment interaction. Thus, for example, if D denotes the binary indicator of a disease outcome, X denotes a ‘design matrix’ that is associated with a set of genetic variants G, Z denotes the desig matrix that is associated with an environmental exposure of interest and S denotes a set of additional cofactors, such as age and sex, then the risk of the disease can be modelled by using Tukey’s form of gene-environment interaction as

$$\mathrm{pr}(D=1\mid X,S,Z,\gamma )=H(X^{\mathrm{T}}{\beta }_0+S^{\mathrm{T}}{\eta }_0+Z^{\mathrm{T}}{\theta }_0+\gamma X^{\mathrm{T}}{\beta }_0{Z}^{\mathrm{T}}{\theta }_0),$$ (1)

where H(·) is the logistic distribution function. Unlike in the standard logistic regression model where potentially a separate interaction parameter is allowed between each pair of design elements of the genetic and environmental factors, in model (1), a single parameter (γ) is used to capture interactions. Moreover, in model (1), the omnibus null hypothesis of interest can be simply stated as β₀=0 under which both genetic main effects and gene-environment interactions disappear from the model. A complication, however, is that, under β₀=0, the parameter γ also disappears from the model and hence is not identifiable from the data. Nevertheless, Chatterjee et al. (2006) noticed that, for each fixed value of γ, model (1) can be used to construct a valid score test for β₀=0. They proposed to use maxima of such score statistics over a range of the parameter γ as the final test statistics for testing β₀=0. They observed that the score test has particular computational advantages, because under the null hypothesis model (1) reduces to a standard logistic regression model involving only main effects of Z and S.

In this paper, we extend the work by Chatterjee et al. (2006) in two novel ways. First, we consider modelling complex effects of continuous environmental exposures by using non-parametric regression models. The problem is particularly motivated by the fact that modern molecular epidemiologic studies often involve measurement of environmental exposures through continuous biomarkers, the relationships of which with the disease can be highly complex and non-linear. Thus for exmaple in the logistic context, we might consider the model

$$\mathrm{pr}(D=1\mid X,S,Z,\gamma )=H\{X^{\mathrm{T}}{\beta }_0+S^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z\right)+\gamma X^{\mathrm{T}}{\beta }_0\left(Z\right)+\gamma X^{\mathrm{T}}{\beta }_0{\theta }_0\left(Z\right)\},$$ (2)

where θ₀(·) is an unknown function. Second, we consider general semiparametric models with possible repeated measures (Lin and Carroll, 2006), where the effects are given through terms roughly of the form on the right-hand side of model (2). In particular, we assume that, for each subject or cluster i, there are j=1,. . . , J observations (Y_ij, X_ij, S_ij, Z_ij). We write Ỹ_i=(Y_i1, . . . ,, Y_iJ) and work with a criterion function

$$\mathcal{L}\{\tilde{Y},{\nu }_1,\dots ,{\nu }_J,{\zeta }_0\},\text{with}{\nu }_j=X_j^{\mathrm{T}}{\beta }_0\{1+\gamma {\theta }_0\left(Z_j\right)\}+S_j^{\mathrm{T}}{\eta }_0,$$ (3)

where a criterion function could mean either an actual likelihood function, a composite likelihood function, i.e. one that is a likelihood function for a reduced set of data, or a working independence likelihood function. In particular, criterion functions have scores in the parameters (β₀, η₀, ζ₀, θ₀) that have mean 0 given appropriate subcomponents of ${(X_j,S_j{Z}_j)}_{j=1}^J$. The case of no repeated measures as in model (1) occurs when J=1.

Our interest is in testing for the hypothesis of the form H₀ : β₀=0. As in Chatterjee et al. (2006), it is natural to use a score testing approach to this problem to avoid numerical difficulty that is associated with parameter estimation under general models of the form (1) and (2). In particular, we note that estimation of γ in these models can be numerically unstable because of lack of identifiability of this parameter under β₀=0. This also means that γ cannot be consistently estimated at contiguous alternatives. In practice, even in fully parametric models, this lack of identifiability means that estimating γ is numerically instable, leading to non-convergence if its range is not restricted.

Following Chatterjee et al. (2006), we propose to perform score-type tests for eadh value of γ and then to maximize these tests over an interval of γ-values, and to use numerical devices to create levels of significance. It is possible to create the score statistic directly, and to apply the asymptotic expansions that were developed by Lin and Carroll (2006) to analyse these statistics. However, two problems arise.

1. The first problem is that the direct score statistic requires undersmoothing for the non-parametric estimation of θ₀(·) in expression (3). By modifying the directly calculated score statistic in a suitable manner using a profile argument, we shall show how to create test statistics that lose no local power yet allow regular smoothing, such as cross-validation.

2. The second problem to overcome is that, in the repeated measures case that J>1, the distribution of the profile score statistic depends on random variables that are formed as solutions to integral equations. Rather than go about this problem directly and solve the integral equation, which would be extremely difficult, we show that the crucial terms can be estimated by using nothing more than the Gaussian repeated measures algorithm of Wang (2003); see also Lin et al. (2004) for a non-iterative solution and Huggins (2006) for another simple computational device.

Thus, we shall develop a test statistic that is straightforward to compute and does not require undersmoothing, and the method also allows a simple implementation when the score test is maximized over a range for γ.

Our methodology is easiest to understand in the non-repeated measures case that J=1, and we take this up in Section 2. The repeated measures case is described in Section 3. Section 4 gives the results of a simulation study. Here we find that our maximized tests lose little power when there is no interaction and can gain great power advantages over a main effects test when there are interactions. Section 5 illustrates an application of the proposed method for omnibus testing of the effects genetic variants in the NAT2 gene and their interactions with the number of years since stopping smoking on the risk of colorectal adenoma by using a case-control study that was conducted with the prostate, lung, colorectal and ovaraian cancer screening trial (Hayes et al., 2000).

We close this section with a few remarks about identifiability. The models that we study are examples of a problem where γ is a nuisance parameter and, under the null hypothesis (5) that β₀=0, the nuisance parameter is unidentified. Model (1) is of course reminiscent of Tukey’s 1 degree-of-freedom test for interaction (Tukey, 1949). However, unlike in that context, in our problem the parameter γ is a nuisance parameter and is not of primary interest. The method of Chatterjee et al. (2006) is more closely akin to the basic suggestion in Davies (1987), namely to fix the nuisance parameter, to compute an appropriate test statistic and then to maximize that test statistic over a range of values for the nuisance parameter. Thus, one way to think about our testing procedure is as the appropriate, efficient (both computationally and in terms of power) way of implementing the basic approach of Davies (1987) in our context, while taking care to eliminate the concerns of undersmoothing and solution of integral equations that arise from a less targeted approach.

2. Testing without repeated measures

2.1. Data and notation

The data consist of a response Y, parametrically modelled covariates S and X, the latter possibly interacting with a non-parametrically modelled covariate Z. We consider a general log-likelihood or criterion function

$$\mathcal{L}[Y,S^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z\right)+X^{\mathrm{T}}{\beta }_0\{1+\gamma {\theta }_0\left(Z\right)\},{\zeta }_0],$$ (4)

where β₀ and η₀ are the main effects, θ₀(·) is an unknown function, γ is the interaction effect and ζ₀ are nuisance parameters. In this section, we are interested in testing the parametric hypothesis

$$H_0:{\beta }_0=0.$$ (5)

As described in Section 1, Chatterjee et al. (2006) addressed a similar problem for a fully parameteric model where Z is also modelled parametrically. They used a score-based testing procedure to test H₀. We generalize their idea for the general semiparametric model that is given in expression (4). We describe below the major steps to derive the test statistic for testing hypothesis (5).

In what follows, we use a simple subscripting convention for derivatives of the log-likelihood. Thus, with (•), we set

$$\begin{array}{c}\hfill {\mathcal{L}}_{\theta }\left(•\right)=(\partial ∕\partial \nu )\mathcal{L}\{Y,S^{\mathrm{T}}\eta +\nu +X^{\mathrm{T}}\beta (1+\gamma \nu ),\zeta \}{\mid }_{\nu =\theta \left(Z\right)},\hfill \\ \hfill {\mathcal{L}}_{\theta \theta }\left(•\right)=({\partial }^2∕\partial {\nu }^2)\lambda \{Y,S^{\mathrm{T}}\zeta +\nu +X^{\mathrm{T}}\beta (1+\gamma \nu ),\zeta \}{\mid }_{\nu =\theta \left(Z\right)},\hfill \\ \hfill {\mathcal{L}}_{\zeta }\left(•\right)=(\partial ∕\partial \zeta )\mathcal{L}\{Y,S^{\mathrm{T}}\eta +\nu +X^{\mathrm{T}}\beta (1+\gamma \nu ),\zeta \}{\mid }_{\nu =\theta \left(Z\right)},\hfill \\ \hfill {\mathcal{L}}_{\theta \zeta }\left(•\right)=(\partial ∕\partial \zeta ){\mathcal{L}}_{\theta }\{Y,S^{\mathrm{T}}\eta +\nu +X^{\mathrm{T}}\beta (1+\gamma \nu ),\zeta \}{\mid }_{\nu =\theta \left(Z\right)},\hfill \end{array}$$

etc. Thus, in an abuse of notation we do not indicate in the notation that these partial derivatives do not depend on the parameters and covariates only via S^Tη(Z)+X^Tβ{1+γ θ(Z)}.

2.2. Estimation of parameters under the null hypothesis

Here we show how to estimate the parameters and the function at the null hypothesis.

The strength of score tests is that we fit the model under the null hypothesis. Under the null hypothesis, the log-likelihood or criterion function for the model is written as $\mathcal{L}\{Y,S^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z\right),{\zeta }_0\}$, a standard form that is easy to handle. The log-likelihood under the alternative is much more difficult to deal with numerically because of the interaction.

By definition of a log-likelihood or criterion function, at the null hypothesis,

$$0=E[{\mathcal{L}}_{\theta }\{Y,S^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z\right),{\zeta }_0\}\mid X,S,Z].$$ (6)

The first step of the process is to estimate the function θ₀(·) for any fixed value of δ=δ*=(η*ζ*). We shall use kernel methods because of their convenient theory, bu this step can be modified in practice by using any smoother. The resulting estimate is denoted as θ^(· ,δ*). Let K(·) be a smooth symmetric density function with bounded support, let h be a bandwidth and let K_h (z)=h^-1 K(z/h). Define ϕ_k=∫ Z^k K(z) dz and G_h (z)=(1, z/h)^T. We follow Lin and Carroll (2006) to estimate the parameters under hypothesis H₀: for any fixed value of δ=δ*, estimate θ₀(z) by solving the local likelihood equation

$$0=n^{-1}\sum _{i=1}^n{K}_h(Z_i-z)G_h(Z_i-z){\mathcal{L}}_{\theta }\{Y_i,S_i^{\mathrm{T}}{\eta }^{\ast }+{\alpha }_0+{\alpha }_1(Z_i-z),{\zeta }^{\ast }\},$$

for α^₀ and set θ^(z, δ*).

The second step in the process is now smoothing method independent. To estimate δ₀=(η₀,ζ₀) maximize in δ the function

$$n^{-1}\sum _{i=1}^n\mathcal{L}\{Y_i,S_i^{\mathrm{T}}\eta +\widehat{\theta }(Z_i,\delta ),\zeta \},$$

the so-called profile method, which solves

$$\begin{array}{c}\hfill 0=n^{-1}\sum _{i=1}^n\{S_i+{\widehat{\theta }}_{\eta }(Z_i,\delta )\}{\mathcal{L}}_{\theta }\{Y_i,S_i^{\mathrm{T}}\eta +\widehat{\theta }(Z_i,\delta ),\zeta \},\hfill \\ \hfill 0=n^{-1}\sum _{i=1}^n[{\mathcal{L}}_{\zeta }\{Y_i,S_i^{\mathrm{T}}\eta +\widehat{\theta }(Z_i,\delta ),\zeta \}+{\widehat{\theta }}_{\zeta }(Z_i,\delta ){\mathcal{L}}_{\theta }\{Y_i,S_i^{\mathrm{T}}\eta +\widehat{\theta }(Z_i,\delta ),\zeta \}],\hfill \end{array}$$

where θ^η(Z_i, δ) and θ^ζ(Z_i, δ) are the derivatives of θ^(Z_i, δ) with respect to η or ζ respectively. Call the resulting estimate δ^.

2.3. The score function and asymptotic theory

2.3.1. Derivation

One approach to developing a score statistic is to fix the function θ(·), to derive the score statistic and then to plug in estimates of nuisance parameters and the function θ(·). This does not work well because the function estimate itself needs profiling, and indeed this approach requires undersmoothing for its validity.

In contrast, our test statistic is a particular implementation of the profiled log-likelihood or criterion function, which is derived as follows. In general, the log-likelihood function for an observation is $\mathcal{L}\{Y,S^{\mathrm{T}}\eta +X^{\mathrm{T}}\beta +\theta \left(Z\right)+\gamma X^{\mathrm{T}}\beta \theta \left(Z\right),\zeta \}$. Recall that δ(η, ζ). For given (β, δ), let θ(Z, β, δ) be the profile function that solves

$$E[{\mathcal{L}}_{\theta }\{Y,S^{\mathrm{T}}\eta +X^{\mathrm{T}}\beta +\theta (Z,\beta ,\delta )+\gamma X^{\mathrm{T}}\beta \theta (Z,\beta ,\delta ),\delta \}\mid Z]=0.$$ (7)

Define X̃_pro=X{1+γ θ(Z,0,δ)}+θ_β(Z,0,β), where θ_β(Z,β,β)=(∂/∂ β)θ(Z, β, δ). The profiled log-likelihood is $\mathcal{L}\{Y,S^{\mathrm{T}}\eta +X^{\mathrm{T}}\beta +\theta (Z,\beta ,\delta )+\gamma X^{\mathrm{T}}\beta \theta (Z,\beta ,\delta ),\zeta \}$. Differentiating it with respect to β and evaluating at the null hypothesis β=0, the profiled (efficient) score is easily seen to be ${\tilde{X}}_{\mathrm{pro}}{\mathcal{L}}_{\theta }\{Y,S^{\mathrm{T}}\eta +\theta (Z,0,\delta ),\zeta \}$.

In addition, differentiating equation (7) with respect to β=0 and evaluating it at β=0 and δ=δ₀ shows that X̃_pro={1+γθ₀(Z)} X̃, where

$$\tilde{X}=X-E[X{\mathcal{L}}_{\theta \theta }\{Y,S^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z\right),{\zeta }_0\}\mid Z]∕E[{\mathcal{L}}_{\theta \theta }\{Y,S^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z\right),{\zeta }_0\}\mid Z].$$

We thus propose the following profiled score statistic for β₀:

$${\mathcal{T}}_{n,\mathrm{pro}}\left(\gamma \right)=n^{-1∕2}\sum _{i=1}^n\{1+\gamma \widehat{\theta }(Z_i,\widehat{\delta })\}{\tilde{X}}_{i,\mathrm{est}}{\mathcal{L}}_{\theta }\{Y_i,S_i^{\mathrm{T}}\widehat{\eta }+\widehat{\theta }(Z_i,\widehat{\delta }),\widehat{\zeta }\},$$ (8)

where X̃_{i, est} is an estimated version of X̃_i, with the terms to be estimated in X̃ obtained by separate non-parametric regressions in the numerator and denominator. The normalization by n^-1/2 is conveient for the asymptotic theory.

2.3.2. Theoretical results

Let ${\delta }_0={({\eta }_0^{\mathrm{T}},{\zeta }_0^{\mathrm{T}})}^{\mathrm{T}}$ and make the definitions

$$\begin{array}{c}\hfill {\theta }_{\delta }(z_0,{\delta }_0)=-E[{\mathcal{L}}_{\theta \delta }\{Y,S^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z\right),{\zeta }_0\}\mid Z=z_0]∕E[{\mathcal{L}}_{\theta \theta }\{Y,S^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z\right),{\zeta }_0\}\mid Z=z_0],\hfill \\ \hfill ∊={\mathcal{L}}_{\delta }\{Y,S^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z\right),{\zeta }_0\}+{\theta }_{\delta }(Z,{\delta }_0){\mathcal{L}}_{\theta }\{Y,S^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z\right),{\zeta }_0\},\hfill \\ \hfill \mathcal{M}=-E\left(∊{∊}^{\mathrm{T}}\right),\hfill \\ \hfill \mathcal{N}=E\left(X\{1+\gamma {\theta }_0\left(Z\right)\}{[{\mathcal{L}}_{\theta \delta }\{Y,S^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z\right),{\zeta }_0\}+{\mathcal{L}}_{\theta \theta }\{Y,S^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z\right),{\zeta }_0\}{\theta }_{\delta }(Z,{\delta }_0)]}^{\mathrm{T}}\right),\hfill \\ \hfill \Psi \left(\gamma \right)=\{1+\gamma {\theta }_0\left(Z\right)\}\tilde{X}{\mathcal{L}}_{\theta }\{Y,S^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z\right),{\zeta }_0\}-{\mathcal{NM}}^{-1}∊.\hfill \end{array}$$

The main result of this section justifying our methodology is stated below. Technically, a precise argument requires little more than that the linear expansions for the parametric and non-parametric parts that are given in Lin and Carroll (2006) hold to order o_p(n^-1/2), the latter uniformly.

Result 1

Suppose that we are testing for H₀:β₀=0. Assume that h α n^-α with 1/3 ≤ α ≤ 1/5. Then, for any fixed γ, the score function for β₀ can be written as

$${\mathcal{T}}_{n,\mathrm{pro}}\left(\gamma \right)=n^{-1∕2}\sum _{i=1}^n{\Psi }_i\left(\gamma \right)+o_p\left(1\right).$$

In addition, assume that, for any γ₁ and γ₂, $\nu ({\gamma }_1,{\gamma }_2)=E\left\{\Psi \left({\gamma }_1\right){\Psi }^{\mathrm{T}}\left({\gamma }_2\right)\right\}$ is finite. Then, under the hypothesis that β=0 ${\mathcal{T}}_{n,\mathrm{pro}}\left(\gamma \right)$ as a function of γ ∈ [L, R] converges weakly to a Gaussian process $\mathcal{W}\left(\gamma \right)$ with mean 0 and covariance function $\nu ({\gamma }_1,{\gamma }_2)$.

Remark 1

There are two methods that can be used to estimate the covariance matrix of the estimated score.

1. First, suppose as in logistic regression that there are no nuisance parameters ζ₀, and that $\mathcal{L}(\cdot )$ is a log-likelihood function and not a general criterion function. Then we can write ${\Psi }_i\left(\gamma \right)={\Psi }_i^{\ast }\left(\gamma \right){\mathcal{L}}_{\theta }\{Y_i,S_i^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z_i\right)\}$ with ${\Psi }_i^{\ast }\left(\gamma \right)=\{1+\gamma {\theta }_0\left(Z_i\right)\}{\tilde{X}}_i-{\mathcal{NM}}^{-1}{\tilde{S}}_i$, where

   $$\tilde{S}=S-E[S{\mathcal{L}}_{\theta \theta }\{Y,S^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z\right)\}\mid Z]∕E[{\mathcal{L}}_{\theta \theta }\{Y,S^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z\right)\}\mid Z].$$

   Let ${\widehat{\Psi }}_i^{\ast }\left(\gamma \right)$ be the estimated version of ${\Psi }_i^{\ast }\left(\gamma \right)$ This estimated version requires the definition of X̃_i, S̃_i and additional non-parametric regressions, which are easily accomplished via kernel or spline methods. Further, let ${\mathcal{I}}_{\theta ,\text{null}}\{S_i^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z_i\right)\}$ be the conditional information matrix for θ under the null model. Then we estimate the covariance matrix of ${\mathcal{T}}_n\left(\gamma \right)$

   $${\mathcal{I}}_{{\beta }_{0,n}}\left(\gamma \right)=n^{-1}\sum _{i=1}^n{\mathcal{I}}_{\theta ,\text{null}}\{S_i^{\mathrm{T}}\widehat{\eta }+\widehat{\theta }(Z_i,\widehat{\eta })\}{\widehat{\Psi }}_i^{\ast }\left(\gamma \right){\widehat{\Psi }}_i^{\ast }{\left(\gamma \right)}^{\mathrm{T}}.$$

2. In general, ${\mathcal{I}}_{{\beta }_0,n}\left(\gamma \right)$ can be estimated as the sample covariance matrix of the terms Ψ̂_i(γ), the estimated version of Ψ_i(γ). In likelihood problems, simplifications arise becuase we can compute the covariance matrix of Ψ (·) given (X, Z, S) by using Fisher information calculations.

Remark 2

The validity and unbiasedness of the profiled score statistic primarily depend on the use of x̃. In simpler models, such as the Gaussian model, x̃=X - E(X|Z) is simply the residual of a non-parametric Gaussian regression of each component of X on Z. In general, x̃ can be thought of as the residual of a weighted non-parametric Gaussian regression of each component of X on Z, where the error variance for weighting is taken to be $-1∕{\mathcal{L}}_{\theta \theta }(\cdot )$. This interpretation enables us to construct estimates of x̃ with considerable ease in many cases, especially in the presence of repeated measurements; see Section 3 for details.

2.4. The test statistic and its implementation

Here we define our test statistic and show how to implement it in practice to compute critical values.

The score test statistic, for a fixed value of γ, is then given by ${\mathcal{T}}_{n,\mathrm{pro}}{\left(\gamma \right)}^{\mathrm{T}}{\mathcal{I}}_{{\beta }_{0,n}}^{-1}\left(\gamma \right){\mathcal{T}}_{n,\mathrm{pro}}\left(\gamma \right)$. We compute the final test statistic as

$${\mathcal{T}}_n^{\ast }=\underset{L\le \gamma \le R}{\max }\left\{{\mathcal{T}}_{n,\mathrm{pro}}^{\mathrm{T}}\left(\gamma \right){\mathcal{I}}_{{\beta }_{0,n}}^{-1}\left(\gamma \right){\mathcal{T}}_{n,\mathrm{pro}}\left(\gamma \right)\right\},$$

Where L and R are prespecified lower and upper bounds of γ. Our approach is also related to adaptive tests that have been developed for non-parametric alternatives of functions with unknown smoothness; see for example Horowitz and Spokoiny (2001).

To implement the test, we need to simulate the null distribution of ${\mathcal{T}}_n^{\ast }$ and to obtain the desired critical values. Oure method avoids the need to determine critical values for the maximum of a function of a Gaussian process. Using result 1 we can generate realizations from the limiting distribution of the score statistic as

$$T_0\left(\gamma \right)=n^{-1∕2}\sum _{i=1}^n{\widehat{\Psi }}_i\left(\gamma \right){\mathcal{Z}}_i,$$

where Ψ̂(γ) is Ψ(γ) evaluated at δ^ and θ^(z, δ ^) and ${\mathcal{Z}}_1$, . . ., ${\mathcal{Z}}_n$, are standard normal random variates which are drawn independently of the data. The null distribution of ${\mathcal{T}}_n^{\ast }$ is then simulated by generating ${\mathcal{T}}_0^{\ast }={\max }_{L\le \gamma \le R}\left\{T_0{\left(\gamma \right)}^{\mathrm{T}}{\mathcal{I}}_{{\beta }_{0,n}}^{-1}\left(\gamma \right)T_0\left(\gamma \right)\right\}$ repeatedly. This methods is the semiparametric version of a method that was discussed by Lin and Zou (2004) and Chatterjee et al. (2006).

3. General interaction model with repeated measures

3.1. Data and notation

In this section we generalize the ideas that were presented earlier to the case when repeated measures are present in the data. Repeated measures models can arise from various fields of research, e.g. matched case-control studies, finance and epidemiology. The key feature of these models is that the non-parametric function is evaluated for each of the repeated measurements. Lin and Carroll (2006) developed kernel-based estimation procedures and investigated asymptotic properties of the estimators in general semiparametric regression problems. We shall use their results and methodology in our context.

In this section we set out the notation to be used.

For simplicity only, we suppose that there are J repeated measurements for each individual. Only obvious notational changes are requires for the more general case. Specifically, we consider a log-likelihood or criterion function

$$\mathcal{L}\{\tilde{Y},{\nu }_1({\beta }_0,{\theta }_0,{\eta }_0),\dots ,{\nu }_J({\beta }_0,{\theta }_0,{\eta }_0),{\zeta }_0\},$$

Where ${\nu }_j({\beta }_0,{\theta }_0,{\eta }_0)=X_j^{\mathrm{T}}{\beta }_0\{1+\gamma {\theta }_0\left(Z_j\right)\}+{\theta }_0\left(Z_j\right)+S_j^{\mathrm{T}}{\eta }_0$ γ is the common interaction parameter for each of the repeated measurements and ζ0 is the collection of all the nuisance parameters. Then, with a slight abuse of notation in the first formula below,

$$\begin{array}{c}\hfill E[\partial \mathcal{L}\{\tilde{Y},{\nu }_1({\beta }_0,{\theta }_0,{\eta }_0),\dots ,{\nu }_J({\beta }_0,{\theta }_0,{\eta }_0),{\zeta }_0\}∕\partial {\theta }_0\left(Z_k\right)\mid {(X_j,Z_j,S_j)}_{j=1}^J]=0,\hfill \\ \hfill E[\partial \mathcal{L}\{\tilde{Y},{\nu }_1({\beta }_0,{\theta }_0,{\eta }_0),\dots ,{\nu }_J({\beta }_0,{\theta }_0,{\eta }_0),{\zeta }_0\}∕\partial (\beta ,\eta ,\zeta )\mid {(X_j,Z_j,S_j)}_{j=1}^J]=0;\hfill \end{array}$$

see Lin and Carroll (2006) for more discussion. In Section 3.6, we describe methods for the partially linear model when working independence among the errors is used, and hence weaker conditioning assumptions are required.

Letting •={Ỹ, ν₁ (β,θ,η),. . . ,, ν_J(β, θ, ν),. . . ,, ν_J(β,θ, ζ}, we define terms ${\mathcal{L}}_{j\theta }\left(•\right)$, ${\mathcal{L}}_{jk\theta }\left(•\right)$, ${\mathcal{L}}_{\zeta }\left(•\right)$ and ${\mathcal{L}}_{j\theta \zeta }\left(•\right)$ in the same way as described in Section 2.1. Thus, for example,

$$\begin{array}{cc}\hfill {\mathcal{L}}_{j\theta }\left(•\right)=& \frac{\partial }{\partial {\nu }_j}\mathcal{L}[\tilde{Y},S_1^{\mathrm{T}}\eta +\theta \left(Z_1\right)+X_1^{\mathrm{T}}\beta \{1+\gamma \theta \left(Z_1\right)\},\dots ,S_j^{\mathrm{T}}\eta +{\nu }_j+X_j^{\mathrm{T}}\beta (1+\gamma {\nu }_j),\dots ,\hfill \\ \hfill & {S_J^{\mathrm{T}}\eta +\theta \left(Z_J\right)+X_J^{\mathrm{T}}\beta \{1+\gamma \theta \left(Z_J\right)\},\zeta ]}_{{\nu }_j=\theta \left(Z_j\right)},\hfill \\ \hfill {\mathcal{L}}_{jk\theta }\left(•\right)=& \frac{{\partial }^2}{\partial {\nu }_j\partial {\nu }_k}\mathcal{L}[\tilde{Y},S_1^{\mathrm{T}}\eta +\theta \left(Z_1\right)+X_1^{\mathrm{T}}\beta \{1+\gamma \theta \left(Z_1\right)\},\dots ,S_j^{\mathrm{T}}\eta +{\nu }_j+X_j^{\mathrm{T}}\beta (1+\gamma {\nu }_j),\dots ,\hfill \\ \hfill & {S_k^{\mathrm{T}}\eta +{\nu }_k+X_k^{\mathrm{T}}\beta (1+\gamma {\nu }_k),\dots ,S_J^{\mathrm{T}}\eta +\theta \left(Z_J\right)+X_J^{\mathrm{T}}\beta \{1+\gamma \theta \left(Z_J\right)\},\zeta ]}_{{\nu }_j=\theta \left(Z_k\right)}\dots .\hfill \end{array}$$

3.2. Estimation under the null model

In this section, we display the method for estimation of parameters and the function θ(·), at the null hypothesis.

Under the null hypothesis, the criterion function is given by

$$\mathcal{L}\{\tilde{Y},{\theta }_0\left(Z_1\right)+S_1^{\mathrm{T}}{\eta }_0,\dots ,{\theta }_0\left(Z_J\right)+S_J^{\mathrm{T}}{\eta }_0,{\zeta }_0\}.$$

Let δ=(η, ζ). We estimate θ₀· and δ₀ under the null model by using methodology that was proposed in Lin and Carroll (2006): for any fixed δ=δ*=(η*, ζ*), estimate θ₀(z) by solving for (α0,α1)

$$\begin{array}{cc}\hfill 0=& \sum _{i=1}^n\sum _{j=1}^J{K}_h(Z_{ij}-z)G(Z_{ij}-z){\mathcal{L}}_{j\theta }\{{\tilde{Y}}_i,\widehat{\theta }(Z_{i1},{\delta }^{\ast })+S_{i1}^{\mathrm{T}}{\eta }^{\ast },\dots ,{\alpha }_0+{\alpha }_1(Z_{ij}-z)∕h\hfill \\ \hfill & +S_{ij}^{\mathrm{T}}{\eta }^{\ast },\dots ,\widehat{\theta }(Z_{iJ},{\delta }^{\ast })+S_{iJ}^{\mathrm{T}}{\eta }^{\ast },{\zeta }^{\ast }\},\hfill \end{array}$$

and setting θ^(z,δ*) Next, estimate δ by maximizing

$$\sum _{i=1}^n\mathcal{L}\{{\tilde{Y}}_i,\widehat{\theta }(Z_{i1},\delta )+S_{i1}^{\mathrm{T}},\dots ,\widehat{\theta }(Z_{iJ},\delta )+S_{iJ}^{\mathrm{T}}\eta ,\zeta \}$$

with respect to δ. This can be accomplished by implementing a profiling algorithm as in Lin and Carroll (2006)

3.3. The score function and asymptotic theory

3.3.1. Derivation of the profile score

As we have seen in Section 2.3, our test statistic will be based on the score function of a profiled log-likelihood. In this section, we derive the profiled log-likelihood and the score function, but here the repeated measures aspect makes the calculations less transparent and indeed leads to real issues of implementation. Let f_j(z) be the marginal density of Z_j. Again, for any (β, δ), we define θ(z, β, δ) by the repeated measures version of equation (7), namely the solution to the equation

$$\begin{array}{cc}\hfill 0=& \sum _{j=1}^J{f}_j\left(z\right)E[{\mathcal{L}}_{j\theta }\{\tilde{Y},X_1^{\mathrm{T}}\beta \{1+\gamma \theta (Z_1,\beta ,\delta )\}+\theta (Z_1,\beta ,\delta )+S_1^{\mathrm{T}}\eta ,\dots ,\hfill \\ \hfill & X_J^{\mathrm{T}}\beta \{1+\gamma \theta (Z_J,\beta ,\delta )\}+\theta (Z_J,\beta ,\delta )+S_J^{\mathrm{T}}\eta ,\zeta \}\mid Z_j=z].\hfill \end{array}$$ (9)

Defining ${\omega }_j(\beta ,\theta ,\delta )=X_j^{\mathrm{T}}\beta \{1+\gamma \theta (Z_j,\beta ,\delta )\}+\theta (Z_j,\beta ,\delta )+S_j^{\mathrm{T}}\eta$, the profiled log-likelihood function is $\mathcal{L}\{\tilde{Y},{\omega }_1(\beta ,\theta ,\delta ),\dots ,{\omega }_J(\beta ,\theta ,\delta ),\zeta \}$. Let ${\mathcal{L}}_{j\theta \beta }\{\tilde{Y},{\omega }_1(\beta ,\theta ,\delta ),\dots ,{\omega }_J(\beta ,\theta ,\delta ),\zeta \}$ and ${\mathcal{L}}_{jk\theta }\{\tilde{Y},{\omega }_1(\beta ,\theta ,\delta ),\dots ,{\omega }_J(\beta ,\theta ,\delta ),\zeta \}$ be the derivatives of ${\mathcal{L}}_{j\theta }\{\tilde{Y},{\omega }_1(\beta ,\theta ,\delta ),\dots ,{\omega }_J(\beta ,\theta ,\delta ),\zeta \}$ with respect to β and θ(Z_k, β, δ) respectively. Differentiating and setting β=0, the profiled score becomes

$$\sum _{j=1}^J[\{1+\gamma \theta (Z_j,0,\delta )\}{X}_j+{\theta }_{\beta }(Z_j,0,\delta ,\gamma )]{\mathcal{L}}_{j\theta }\{\tilde{Y},{\omega }_1(0,\theta ,\delta ),\dots ,{\omega }_J(0,\theta ,\delta ),\zeta \},$$

where, by differentiating equation (9) with respect to β and solving θ_β(z, β, δ, γ) is the solution of the functional integral equation

$$\begin{array}{cc}\hfill 0& =\sum _{j=1}^J{f}_j\left(z\right)E[{\mathcal{L}}_{j\theta \beta }\{\tilde{Y},{\omega }_1(\beta ,\theta ,\delta ),\dots ,{\omega }_J(\beta ,\theta ,\delta ),\zeta \}+\sum _{k=1}^J{\mathcal{L}}_{jk\theta }\{\tilde{Y},{\omega }_1(\beta ,\theta ,\delta ),\dots ,{\omega }_J(\beta ,\theta ,\delta ),{\zeta }_0\}\hfill \\ \hfill & \times {\theta }_{\beta }(Z_k,\beta ,\delta ,\gamma )\mid Z_j=z].\hfill \end{array}$$ (10)

Then, for any fixed value of γ, the profiled score function for β₀ evaluated at β₀=0, β₀=β^ and θ(z)=θ^(z,δ^) is given by

$$\begin{array}{cc}\hfill {{\mathcal{T}}_n}_{\mathrm{pro}}\left(\gamma \right)=& n^{-1∕2}\sum _{i=1}^n\sum _{j=1}^J[\{1+\gamma \widehat{\theta }(Z_{ij},\widehat{\delta })\}{X}_{ij}+{\widehat{\theta }}_{\beta }(Z_{ij},0,\widehat{\delta },\gamma )]{\mathcal{L}}_{j\theta }\{\tilde{Y},\tilde{\theta }(Z_{i1},\widehat{\delta })\hfill \\ \hfill & +S_{i1}^T\widehat{\eta },\dots ,\widehat{\theta }(Z_{ij},\widehat{\delta })+S_{iJ}^{\mathrm{T}}\widehat{\eta },\widehat{\zeta }\}\hfill \end{array}$$

3.3.2. Asymptotic theory

Denote (•)={Ỹ, ω₁ (β₀, θ₀, δ₀),. . . , ω_J(β₀, θ₀, δ₀) and denote (•_i) to be (•) evaluated at the ith observation. Do all calculations at the null model β₀=0. Define θ_δ(z,δ₀) such that

$$0=\sum _{j=1}^J{f}_j\left(z\right)E\{{\mathcal{L}}_{j\theta \delta }\left(•\right)+\sum _{k=1}^J{\theta }_{\delta }(Z_k,{\delta }_0){\mathcal{L}}_{jk\theta }\left(•\right)\mid Z_j=z\}.$$

Further define

$$\begin{array}{c}\hfill {\mathcal{M}}_1=-\mathrm{cov}\{{\mathcal{L}}_{\delta }\left(•\right)+\sum _{j=1}^J{\mathcal{L}}_{j\theta }\left(•\right){\theta }_{\delta }(Z_j,{\delta }_0)\},\hfill \\ \hfill {\mathcal{M}}_{2}E\left[\sum _{j=1}^J\{1+\gamma {\theta }_0\left(Z_j\right)\}{X}_j{\{{\mathcal{L}}_{j\theta \delta }\left(•\right)+\sum _{k=1}^J{\theta }_{\delta }(Z_k,{\delta }_0){\mathcal{L}}_{jk\theta }\left(•\right)\}}^{\mathrm{T}}\right],\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\Psi }_i\left(\gamma \right)=& \sum _{j=1}^J[X_{ij}\{1+\gamma {\theta }_0\left(Z_{ij}\right)\}+{\theta }_{\beta }(Z_{ij},0,{\delta }_0,\gamma )]{\mathcal{L}}_{j\theta }\left({•}_i\right)\hfill \\ \hfill & -{\mathcal{M}}_2{\mathcal{M}}_1^{-1}\{{\mathcal{L}}_{\theta }\left({•}_i\right)+\sum _{j=1}^J{\mathcal{L}}_{j\theta }\left({•}_i\right){\theta }_{\delta }(Z_{ij},{\delta }_0)\}.\hfill \end{array}$$

Then we have the following result.

Result 2

Suppose that we are interested in testing H₀ : β₀=0. Assume that h α n^-α where 1/3 ≤ α ≤ 1/5. Then, for any fixed γ, the score function for β₀ can be written as

$${\mathcal{T}}_{n,\mathrm{pro}}\left(\gamma \right)=n^{-1∕2}\sum _{i=1}^n{\Psi }_i\left(\gamma \right)+o_p\left(n^{-1∕2}\right).$$

In addition, assume that, for any γ₁ and γ₂ $\mathcal{V}({\gamma }_1,{\gamma }_2)=E\left\{\Psi {\left({\gamma }_2\right)}^{\mathrm{T}}\right\}$ is finite. Then, under the hypothesis that β₀=0, ${\mathcal{T}}_{n,\mathrm{pro}}\left(\gamma \right)$ as a function of γ ∈ [L, R] converges weakly to a Gaussian process $\mathcal{W}\left(\gamma \right)$ with mean 0 and covariance function V(γ1, γ2).

Using result 2, we construct the test statistic and the critical values in the obvious analogy with Sections 2.3 and 2.4. To implement this in practice though, we must solve the integral equations for θ_β(·_ and θ_δ(·), which is very difficult to do. In the next section, we show how to estimate these quantities without directly solving the integral equations.

3.4. Computation of θ_β(·) and θ_δ(·)

The main difficulty in performing the score test is that, for each γ, we must compute θ^_β (z,0,δ₀, γ) and θ^_β (z, 0, δ₀), the former of which is the solution of integral equation (10), making implementation difficult. In this section we show that θ_β(z, 0, δ₀, γ) can be viewed as a regression function and hence can be computed via a non-parametric Gaussian repeated measures regression, which is easily computed and for which the exact solution is known; see Huggins (2006) and Lin et al. (2004). The result can be stated as follows: details are in Appendix A.

Result 3

Define Q_ij =-X_ij{1+γθ₀(Z_ij)}. Let V_i be the J × J matrix with elements ν^ijk. Then θ_β (z, 0, δ₀, γ) is identified as the formal solution of the Gaussian repeated measures problem that was solved by Wang (2003) and Huggins (2006) with ‘responses’ being the components of Q_ij and the inverse of the covariance matrix being V_i

The algorithm for estimating θ_β(·) now is quite simple. Define Q̂_ij=-{1+γθ^(Z_ij,δ^). Then we construct each component of θ^_β(z,0,β^,γ) by performing a non-parametric repeated measures regression under the null model with β=0, with the response being the appropriate component of Q^_ij and the inverse of the covariance matrix being V̂_i=(ν^^ijk), where ${\widehat{\nu }}^{ijk}=-{\mathcal{L}}_{jk\theta }\{{\tilde{Y}}_i,\widehat{\theta }(Z_{i1},\widehat{\delta })+S_{il}^{\mathrm{T}}\widehat{\eta },\dots ,\widehat{\theta }(Z_{iJ},\widehat{\delta })+S_{iJ}^{\mathrm{T}}\widehat{\eta },\widehat{\zeta }\}$ and θ^(z,δ^) is computed under the null model with β₀=0.

We can estimate θ_δ(·) in a similar manner. We do this componentwise. Let ${\mathcal{L}}_{j\theta \delta ,l}\left(•\right)$ denote the lth component of ${\widehat{\theta }}_{\beta }(z,0,\widehat{\delta },\gamma )$, and similarly for θ_δ,l(·). Define ${(R_l^{i1},\dots ,R_{iJ}^l)}^T=-V_i^{-1}{\{{\mathcal{L}}_{i1\theta \delta ,l}\left(•\right),\dots ,{\mathcal{L}}_{iJ\theta ,l\left(•\right)}\}}^{\mathrm{T}}$. Then θ_δ,l(·) can be thought of as the Gaussian repeated measures regression of $R_{ij}^l$ on Z_ij pretending that the inverse of the covariance matrix for the ith cluster is V_i. In practice, we construct θ^_δ,l(·) by using ${\widehat{R}}_{ij}^l$ and ${\widehat{V}}_i^{-1}$.

3.5. Special case: partially linear repeated measurement model

In this section we consider the partially linear Gaussian model as an example to demonstrate our methodology. Specifically, we consider the model

$$Y_{ij}=X_{ij}^{\mathrm{T}}{\beta }_0\{1+\gamma {\theta }_0\left(Z_{ij}\right)\}+{\theta }_0\left(Z_{ij}\right)+S_{ij}^T{\eta }_0+{\epsilon }_{ij},$$

where ${\tilde{\epsilon }}_i=({\epsilon }_{i1},\dots ,{\epsilon }_{iJ})$ has an N(0, Σ) distribution. We want to test for H₀: β₀=0. The asymptotic theory is not affected by estimation of Σ, so here we assume that it is known.

Let Σ=(σ_jk)_{j,k=1,. . . ,,J} and Σ^-1=V=(v^jk). Then the log-likelihood function is given by

$$\mathcal{L}=-\frac{1}{2}\sum _{q=1}^J\sum _{l=1}^J{\nu }^{q1}(Y_q-{\mu }_q)(Y_l-{\mu }_l),$$

where ${\mu }_j=X_j^{\mathrm{T}}{\beta }_0\{1+\gamma {\theta }_0\left(Z_j\right)\}+{\theta }_0\left(Z_j\right)+S_j^T{\eta }_0$. Now we observe that, when β₀=0,

$$\begin{array}{c}\hfill {\mathcal{L}}_{j\theta }\left(•\right)=\sum _{l=1}^J{\nu }^{jl}(Y_l-{\mu }_l),\hfill \\ \hfill {\mathcal{L}}_{j\theta \beta }\left(•\right)=\gamma X_j\sum _{l=1}^J{\nu }_{jl}(Y_l-\mu l)-\sum _{l=1}^J{\nu }^{jl}{X}_l\{1+\gamma {\theta }_0\left(Z_l\right)\},\hfill \\ \hfill {\mathcal{L}}_{jk\theta }\left(•\right)=-{\nu }^{jk}.\hfill \end{array}$$

For β₀=0, θ_β (z, 0, η0, γ) solves

$$0=\sum _{j=1}^J{f}_j\left(z\right)E(\sum _{k=1}^J{\nu }^{jk}[X_k\{1+\gamma {\theta }_0\left(Z_k\right)\}+{\theta }_{\beta }\left(Z_k\right),0,{\eta }_0,\gamma ]\mid Z_j=z).$$ (11)

Hence the profiled score function is given by

$$\begin{array}{cc}\hfill {\mathcal{T}}_{n,\mathrm{pro}}\left(\gamma \right)=& n^{-1∕2}\sum _{i=1}^n\sum _{j=1}^J\sum _{k=1}^J{\nu }^{jk}[\{1+\gamma \widehat{\theta }(Z_{ij},\widehat{\eta })\}{X}_{ij}+{\widehat{\theta }}_{\beta }(Z_{ij},0,\widehat{\eta },\gamma )]\hfill \\ \hfill & \times \{Y_{ik}-\widehat{\theta }(Z_{ik},\widehat{\eta })-S_{ik}^{\mathrm{T}}\widehat{\eta }\}.\hfill \end{array}$$

Now we can construct the score test by using result 2.

Remark 3

Referring to Section 3.4, we observe that estimation of θ_β(·) becomes much simpler in this case. Using the fact that ${\mathcal{L}}_{jk\theta }\left(•\right)=-{\nu }^{jk}$, we can construct θ^_β(·) by performing a non-parametric componentwise Gaussian repeated measures regression of Q̂_k=-{1+γ θ^(Z_k,ν^) on Z_k pretending that the error covariance matrix is Σ, where β₀=0 is computed under the null model with β₀=0. Similarly, we can estimate θ_η(·) by performing a non-parametric Gaussian repeated measures regression of -S_ij on Z_ij by using Σ as the error covariance matrix.

3.6. Testing under working independence

In practice, often working independence is used to simplify the computations in the presence of repeated measures. In this set-up, we pretend that there is no correlation among the data. In our context, this leads to the assumption that σ_jk=0 for j ≠ k, and we work with the criterion function

$${\mathcal{L}}^{WI}=-\frac{1}{2}\sum _{j=1}^J{\sigma }_{jj}^{-1}{(Y_j-{\mu }_j)}^2,$$

where ${\mu }_j=X_j^{\mathrm{T}}{\beta }_0\{1+\gamma {\theta }_0\left(Z_j\right)\}+{\theta }_0\left(Z_j\right)+S_j^{\mathrm{T}}\eta 0$. The use of this criterion function simplifies the calculations to a great extent. For any generic random variable W, define ${\tilde{W}}_j=W_j-m_Z^W\left(Z_j\right)$ with

$$m_Z^W\left(z\right)=\sum _{j=1}^J{\sigma }_{jj}^{-1}{f}_j\left(z\right)E(W_j\mid Z_j=z)∕\sum _{j=1}^J{\sigma }_{jj}^{-1}{f}_j\left(z\right).$$

Under the hypothesis that H₀: β₀=0, we then observe that now θ_β(·) and θ_η(·) have closed form expressions:

$$\begin{array}{c}\hfill {\theta }_{\beta }(z,0,{\eta }_0,\gamma )=-\{1+\gamma {\theta }_0\left(z\right)\}{m}_Z^X\left(z\right),\hfill \\ \hfill {\theta }_{\eta }(z,{\eta }_0)=-m_Z^S\left(z\right).\hfill \end{array}$$

The profiled score statistic is given by

$${\mathcal{T}}_{n,\mathrm{pro}}^{\mathrm{WI}}\left(\gamma \right)=n^{-1∕2}\sum _{i=1}^n\sum _{j=1}^J{\sigma }_{jj}^{-1}\{1+\gamma \widehat{\theta }(Z_{ij},\widehat{n})\}{\tilde{X}}_{ij,\mathrm{est}}\{Y_{ij}-\widehat{\theta }(Z_{ij},\widehat{\eta })-S_{ij}^{\mathrm{T}}\widehat{\eta }\},$$

where ${\tilde{X}}_{ij,\mathrm{est}}=X_{ij}-{\widehat{m}}_Z^X\left(Z_{ij}\right)$. We can compute ${\widehat{m}}_Z^X\left(z\right)$ by running a componentwise Gaussian repeated measures regression on X_ij and Z_ij by using the working independence set-up.

Further define

$$\begin{array}{c}\hfill {\mathcal{M}}_1=-\mathrm{cov}\left[\sum _{j=1}^J{\sigma }_{jj}^{-1}{\tilde{S}}_j\{Y_j-{\theta }_0\left(Z_j\right)-S_j^{\mathrm{T}}{\eta }_0\}\right],\hfill \\ \hfill {\mathcal{M}}_2=-E\left[\sum _{j=1}^J{\sigma }_{jj}^{-1}\{1+\gamma {\theta }_0\left(Z_j\right)\}{X}_j{\tilde{S}}_j^{\mathrm{T}}\right].\hfill \end{array}$$

Result 2 then translates to the following result.

Result 4

Assume that h α n^-α where 1/3 ≤ α ≤ 1/5. Then, under the assumption of working independence,

$${\mathcal{T}}_{n,\mathrm{pro}}^{\mathrm{WI}}\left(\gamma \right)=n^{-1∕2}\sum _{i=1}^n\sum _{j=1}^J{\sigma }_{jj}^{-1}[\{1+\gamma {\theta }_0\left(Z_{ij}\right)\}{\tilde{X}}_{ij}+{\mathcal{M}}_2{\mathcal{M}}_1^{-1}{\tilde{S}}_{ij}]\{Y_{ij}-{\theta }_0\left(Z_{ij}\right)-S_{ij}^{\mathrm{T}}{\eta }_0\}+o_p\left(1\right).$$

Define ${\Psi }_{ij}^{\ast }\left(\gamma \right)=\{1+\gamma {\theta }_0\left(Z_{ij}\right)\}{\tilde{X}}_{ij}+{\mathcal{M}}_2{\mathcal{M}}_1^{-1}{\tilde{S}}_{ij}$ and let ${\widehat{\Psi }}_{ij}^{\ast }\left(\gamma \right)$ (γ) be the sample version. Under the null hypothesis, we estimate the covariance matrix of ${\mathcal{T}}_{n,\mathrm{pro}}^{WI}$ by

$${\mathcal{I}}_{{\beta }_0,n}^{\mathrm{WI}}=n^{-1}\sum _{i=1}^n\sum _{j=1}^J{\sigma }_{jj}^{-1}{\widehat{\Psi }}_{ij}^{\ast }\left(\gamma \right){\widehat{\Psi }}_{ij}^{\ast }{\left(\gamma \right)}^{\mathrm{T}}.$$

The score statistic, maximized over γ, is then given by

$${\mathcal{T}}_n^{\ast }=\underset{\gamma \in [L,R]}{\max }\left\{{\mathcal{T}}_{n,\mathrm{pro}}^{\mathrm{WI}}{\left(\gamma \right)}^{\mathrm{T}}{\left({\mathcal{I}}_{{\beta }_0,n}^{\mathrm{WI}}\right)}^{-1}{\mathcal{T}}_{n,\mathrm{pro}}^{\mathrm{WI}}\left(\gamma \right)\right\}.$$

Using lemma 4 in Appendix A, we can now implement the score test by using the technique that was described in Section 2.4. We start by generating

$${\mathcal{T}}_0^{\mathrm{WI}}\left(\gamma \right)=n^{-1∕2}\sum _{i=1}^n\sum _{j=1}^J{\sigma }_{jj}^{-1}{\widehat{\Psi }}_{ij}^{\ast }\left(\gamma \right){\mathcal{Z}}_{ij},$$

where ${\mathcal{Z}}_i={(Z_{i1},\dots ,Z_{iJ})}^{\mathrm{T}}$, i=1, . . . ,, n, are independent random vectors that are generated from an N(0,Σ̂) distribution. We can form Σ̂ as the sample covariance matrix of the residuals $\{Y_{ij}-\widehat{\theta }(Z_{ij},\widehat{\eta })-S_{ij}^{\mathrm{T}}\widehat{\eta }\}$. The null distribution of ${\mathcal{T}}_n^{\ast }$ is then simulated by repeatedly generating

$${\mathcal{T}}_0^{\ast }=\underset{\gamma \in [L,R]}{\max }\left\{{\mathcal{T}}_0^{\mathrm{WI}}{\left(\gamma \right)}^{\mathrm{T}}{\left({\mathcal{I}}_{{\beta }_0,n}^{\mathrm{WI}}\right)}^{-1}{\mathcal{T}}_0^{\mathrm{WI}}\left(\gamma \right)\right\}.$$

Remark 4

We reiterate that one needs to estimate ${\widehat{m}}_Z^X\left(Z_{ij}\right)$ and ${\widehat{m}}_Z^S\left(Z_{ij}\right)$ to implement the score test. These quantities can be easily estimated by performing componentwise Gaussian repeated measures regressions of X_ij and S_ij on Z_ij by using the working independence set-up.

4. Simulations

4.1. Testing without repeated measures

For the simulation for the test for β₀=0, we used the following conventions. We used 31 values of γ in the range [-3, 3]. The variable Z=Uniform[-2, 2], whereas the function θ₀ (z)=sin (2z) is distinctly non-linear. In keeping with our data example, the sample size was n=1400.

We generated X in three ways:

1. as a bivariate standard normal random variable;

2. X=(X₁, X₂) where X₁=Bernoulli(0.6) and X₂=N(0, 1);

3. as two dummy variables. Thus, we first generated a standard normal random variable r, and X₁=I(r < -0.4) and X₂=I(r>0.4).

We set β₀=c(1, 1)^T, where we set c=0.0, 0.01, . . . ,, 0.15 for power calculations. The true value of γ was varied: γ_true=0,1,2. We ran simulations both with and without additional covariates S: in the former case, we set S to be generated from a univariate N(0, 1) distribution and used η0=1.

For each scenario, we ran 1000 simulated data sets. To estimate the level of significance, we applied the method in Section 2.4 with 1500 replications. The Epanechnikov kernel was used to carry out the computation. We used different bandwidths of the form h=κ std(Z)n^-1/5 with various values of κ ranging from 0.5 to 2. The results are very similar in each of those cases and hence we report the results for κ=1 only. The results are displayed in Figs 1-3. There three main conclusions are clear.

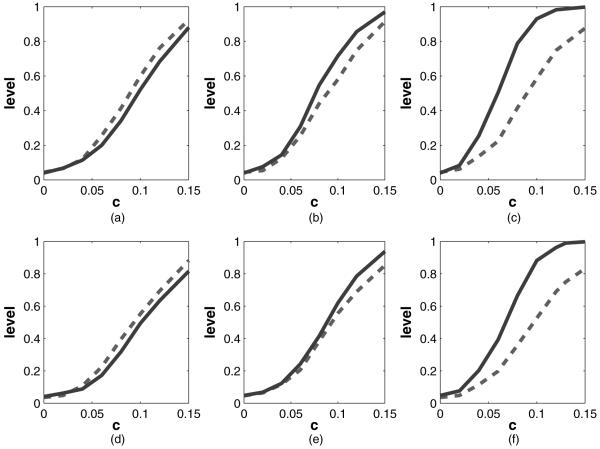
Fig. 1.

Results of the simulation for testing whether β=0 as described in Section 4.1 by using kernel-based calculations (here X is a bivariate standard normal random variable; , our method; - - -, naive test, value of c and the vertical axis plots the corresponding power): (a) γ_true=0, without S; (b) γ_true=1, without S; (c) γ_true=2, without S; (d) γ_true=0, with S; (e) γ_true=1, with S; (f) γ_true=2, with S

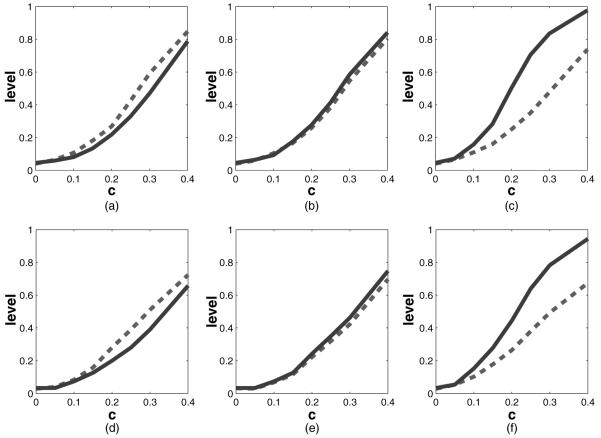
Fig. 3.

Results of the simulation for testing whether β=0 as described in Section 4.1 by using kernel-based calculations (here X=(X₁, X₂) is two dummy variables; thus, we first generated a standard normal random variable r, and X₁=I(r < -0.4) and X₂=I(r < 0.4);, our method;-------, naive test, which assumes γ=0; the true value that was used was β=c(1, 1)^T; the horizontal axis plots the value of c and the vertical axis plots the corresponding power): (a) γ_true=0, without S; (b) γ_true=1, without S; (c) γ_true=2, without S; (d) γ_true=0, with S; (e) γ_true=1, with S; (f) γ_true=2, with S

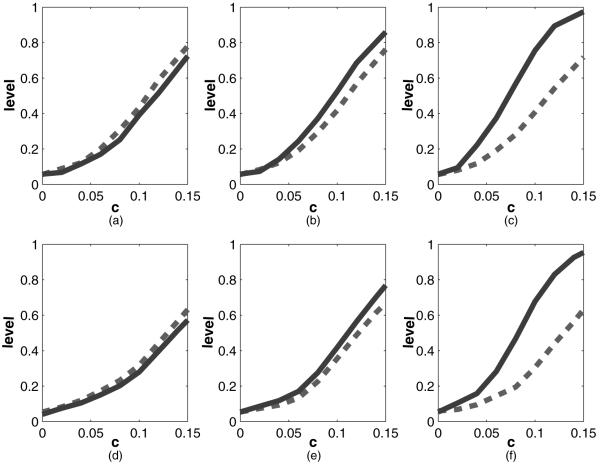
1. The test level of our method is near nominal, being 0.051 without S and 0.057 with S in the model.

2. For the main effects model with γ_true=0, our maximized score-type test loses only modest power compared with the efficient (in this case) main effects score test.

3. When there are interactions, our methods greatly dominate the main effects score test as γ_true increases.

For comparison, we repeated the simulation by using penalized B-spline regression, using a second-order B-spline with 10 basis functions and with a second-order difference penalty. The smoothing parameter was chosen by generalized cross-validation. The results were very similar to those obtained for kenrnel methods. The near equivalence of kernel and spline methods here is no surprise, since there is evidence in Gaussian cases that smoothing splines are equivalent to kernel methods (Silverman, 1984; Lin et al., 2004). Recently, Li and Ruppert (2008) showed that penalized B-spline regression is also asymptotically equivalent to kernel regression methods in the Gaussian case.

4.2. Testing with repeated measures

We use the following set-up for our simulations for testing β₀=0. We generate samples from the partially linear gaussian repeated measures model: for i=1, . . . , n and j=1, . . . , J,

$$Y_{ij}=X_{ij}^{\mathrm{T}}{\beta }_0+{\theta }_0\left(Z_{ij}\right)(1+\gamma X_{ij}^{\mathrm{T}}{\beta }_0)+{\epsilon }_{ij},$$

with n=200 and J=3, where we take the true value of the parameter to be β₀=c(1, -1)^T and set c=0.001, . . . , 0.06 for power calculation. We set τ₀(z)=sin (2z) to be the true function. We generated X from the standard bivariate normal distribution and Z from the Uniform[-2, 2] distribution. The error vectors (ε1, . . . , εJ)^T are generated from a multivariate normal distribution with covariance matrix σ=I + 0.6 (11^T - I).

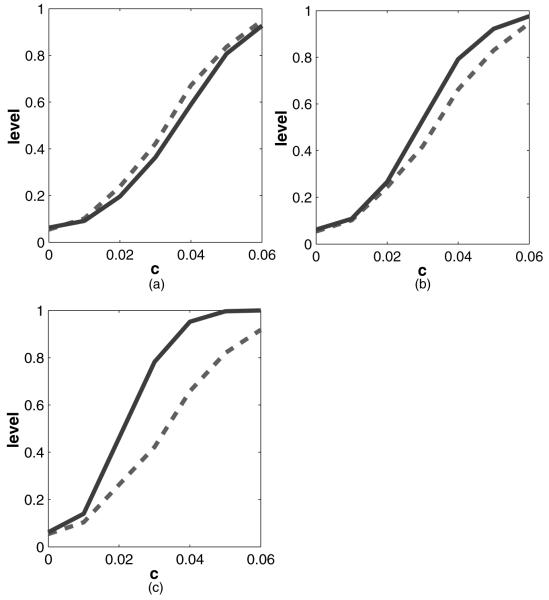
We use 11 values of γ in [0, 2] to compute the test statistic. The true values of γ that are used to generate the data are taken to be γ_true=0, 1, 2. As in the previous simulation, we use the Epanechnikov kernel with bandwidth h=κ std (Z)n^-1/5 where the value of κ ranged from 0.5 to 2. In this case also, we observe that the results are very similar for each of the choices of bandwidth and hence we report the results for κ=1. We generate 1000 data sets for each case and for each data set we apply our method by using 1000 replications. The results are given in Fig. 4. The level of our test is 0.051, which is very close to the nominal level of 0.05. It is evident that, although our test loses very little power when γ_true=0, it achieves great power gain in the presence of interaction as seen in cases where γ_true=1, 2.

Fig. 4.

Results of the simulation for testing whether β₀=0, as described in Section 4.2 by using kernel-based calculations (, our method; - - -, naive test which assumes γ=0; the true value that was used was β=c(1, -1)T; the horizontal axis plots the value of c and the veritcal axis plots the corresponding power): (a) γ_true=0; (b) γ_true=1; (c) γ_true=2

We redid the simulation by using B-splines with 10 basis functions where the penalty parameter is estimated at the null model by using generalized cross-validation. The results are nearly identical of Fig. 4, as we would expect in the Gaussian case.

5. Data analysis

Chatterjee et al. (2006) illustrated application of their methodology by using a case-control study for investigation of association between colorectal adenoma, a precursor of colorectal cancer, and NAT2, a candidate gene that is known to play an important role in detoxification of certain aromatic carcinogens in cigarette smoke. The study involved about 700 cases and 700 controls who were genotyped for six known functional polymorphisms related to NAT2 acetylation activity. The genotype data were used to construct diploytpe information, i.e. the pair of haplotypes that the subjects carried along their pair of homologous chromosomes. The frequency distribution of these diplotypes and associated acetylation phenotypes are shown in Table 4 of Chatterjee et al. (2006). In principle, the diplotypes are not observed directly and we can only assign diplotypes on the basis of the unphased genotype data. However, in many instances such as this example, when we have tightly linked SNPs, the phase ambiguity is often minimal, i.e. we can assign a very large proportion (greater than 95%) of the subjects a specific diplotype with a very high probability (greater than 0.95). In such cases, it is esier just to remove those few people for whom the diplotypes are more uncertain and to assume that for the rest of the people the diplotypes are known. In our data set. we removed a small number of people whose haplotypes were quite uncertain.

Chatterjee et al. (2006) considered an omnibus test that can account for interaction of NAT2 history with smoling history, defined as ever, former or never smokers. We consider a similar application involving NAT2 diplotypes but model the effect of CIG_STOP (years since stopping smoking) in a continuous fashion with non-parametric regression among smokers. Because of a few high leverage values, we censored CIG_STOP at 45. In our analysis, the cofactor S included gender and three indicator dummy variables for age level: between 60 and 65 years, between 65 and 70 years and more than 70 years. For modelling the effect of NAT2 diplotypes, we considered a series of 14 different analyses where in the kth analysis we compare the risk that is associated with the k (k=1, . . . ,, 14) most common diplotypes in reference to the rest, with the associated design matrix X_k being defined by k corresponding dummy variables. To account for non-smokers in this analysis, we defined δ to be the indicator of smoking (ever versus never) and considered the following model:

$$\mathrm{pr}(D=1\mid X,S,Z)=H\{(1-\delta ){\beta }_0+S^{\mathrm{T}}{\beta }_1+X^{\mathrm{T}}{\beta }_2+\delta \theta \left(Z\right)+\gamma \delta X^{\mathrm{T}}{\beta }_2\theta \left(Z\right)\}.$$ (12)

Modifying our methods to handle this slightly more complex model is straightforward: details are available from the authors.

Table 1 compares results of the proposed method for testing β₂=0 on the basis of model (12) with those for a test for only the corresponding main effects of the diplotypes, ignoring NAT2-smoking interaction, i.e. assuming γ=0. We observe that, in each analysis, stronger evidence of association is seen in our new test. For example, when the 12 most common diplotypes were used, our method had a level of significance of 0.036 versus a level of significance of 0.214 for the main-effect-based test. Interestingly, when all 14 common diplotypes are used, the level of significance of the test proposed was 0.066, which is quite close to that for the test that was used by Chatterjee et al. (2006), also using all the 14 diplotypes, but accounting for interaction with the categorical smoking history variable defined as never, former or current smoker.

Table 1.

Levels of significance (p-values) of the test for genetic effects in a regression model in which Z is years since stopping smoking^†

Diplotype	Results for our method		Results for γ=0
	Test	p-value	Test	p-value
1	11.4	0.001	3.3	0.066
2	13.9	0.003	5.7	0.055
3	16.6	0.002	9.8	0.016
4	16.7	0.007	9.8	0.041
5	19.5	0.007	11.3	0.045
6	19.7	0.017	11.4	0.087
7	20.0	0.021	12.3	0.098
8	21.3	0.025	13.1	0.111
9	24.1	0.015	14.2	0.116
10	25.2	0.016	15.3	0.120
11	25.2	0.027	15.4	0.180
12	25.6	0.036	15.4	0.214
13	25.9	0.055	15.8	0.262
14	26.7	0.066	16.6	0.279

^†Age category and gender were modelled additively and parametrically. The analysis is done for the most common diplotype, the most common two diplotypes, and so on. The non-parametric regression was done by using penalized order 2 B-splines with 10 segments, with penalization done via generalized cross-validation.

6. Discussion

We have developed methodology for an efficient score test for genetic effect in general semiparametric models that can account for gene-environment interaction with non-parametrically specified environmental effects. The procedure proposed allows for repeated measurements.

We proposed a profiled score statistic which can be performed by using standard bandwidth selection procedures. We also found that these profiled score tests are efficient.

The main difficulty of performing the score test is that one must estimate a function which itself is a solution of an integral equation that is difficult to solve. In the case of repeatedly measured data, the solution generally does not a closed form expression and hence some sort of numerical procedure is required for estimation. In this paper, we overcome this problem by developing an easily implementable estimation procedure which does not involve solving integral equations and can be performed easily via standard software. The key idea lies in the fact that the target functions, based on their estimating equations, can be interpreted as Gaussian repeated measures regressions.

Simulations that were presented in the paper show that the score tests proposed maintain the desired type I error level, indicating that the asymptotic approximations work well for studies such as ours. Moreover, both simulation studies and the data example indicate that the score test proposed taking account of the interaction can achieve higher statistical power than naive tests which ignore interaction altogether. Future research areas of interest include extension of the score test to account for the interaction of the genetic factors with several different, but biologically related, environmental factors, such as different biomarkers for a nutrient, simultaneously. In principle, the score test can be extended by using generalized additive models to account for the effect of several different continuous exposures. Further theoretical development, however, is needed to establish the asymptotic theory for such procedures.

Fig. 2.

Results of the simulation for testing whether β=0 as described in Section 4.1 by using kernel-based calculations (here X=(X₁, X₂) where X₁=Bernoulli (0.6) and X₂=N(0, 1);, our method;-------, naive test, which assumes γ=0; the true value that was used was β=c(1, 1)^T; the horizontal axis plots the value of c and the vertical axis plots the corresponding power): (a) γ_true=0, without S; (b) γ_true=1, without S; (c) γ_true=2, without S; (d) γ_true=0, with S; (e) γ_true=1, with S; (f) γ_true=2, with S

Appendix A: Argument for result 1

For simplicity of notation, here we consider only the case that there are no nuisance parameters ζ₀. The more general case is a simple extension.

To prove the results, we rely on several technical conditions that for brevity we do not state here explicitly. These conditions are well known and standard in smoothing theory. Refer to Claeskens and Van Keilegom (2003), Claeskens and Carroll (2007) and Lin and Carroll (2006) among many others for the details of these assumptions. As stated just before result 1, we require that the linear expansions for the parametric and non-parametric parts that were given in Lin and Carroll (2006) hold to order o_p (n^-1/2); the latter uniformly.

A.1. Expansion of ${\mathcal{T}}_n\left(\gamma \right)$

Let θ^(j) (·) be the jth derivative of θ(·) with respect to z₀. Let f_z(z₀) be the density function of Z. Make the definitions

$$\begin{array}{c}\hfill \Omega \left(z_0\right)=E[{\mathcal{L}}_{\theta \theta }\{Y,S^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z\right)\}\mid Z=z_0],\hfill \\ \hfill {\theta }_{\eta }(z_0,{\eta }_0)=-E[S{\mathcal{L}}_{\theta \theta }\{Y,S^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z\right)\}\mid Z=z_0]∕\Omega \left(z_0\right).\hfill \end{array}$$

Note that $S_i+{\theta }_{\eta }(Z_i,{\eta }_0)={\tilde{S}}_i$, and recall that

$$\mathcal{M}=-\mathrm{cov}\left[\{S+{\theta }_{\eta }(Z,{\eta }_0)\}{\mathcal{L}}_{\theta }\{Y,S^{\mathrm{T}}{\eta }_0+\theta \left(Z\right)\}\right].$$

Then using Lin and Carroll (2006) we have that, uniformly in z₀,

$$\begin{array}{cc}\hfill \widehat{\theta }(Z_0,{\eta }_0)-{\theta }_0(Z_0,{\eta }_0)=& -n^{-1}\sum _{i=1}^n{K}_h(Z_i-z_0){\mathcal{L}}_{\theta }\{Y_i{S}_i^T{\eta }_0+{\theta }_0\left(Z_i\right)\}∕f_Z\left(z_0\right)\Omega \left(z_0\right)+({\varphi }_2{h}^2∕2){\theta }_0^{\left(2\right)}\left(z_0\right)\hfill \\ \hfill & +O_p\{h^4+\log \left(n\right)\left(n\right)∕nh\},\hfill \end{array}$$ (13)

$$\widehat{\eta }-{\eta }_0=-{\mathcal{M}}^{-1}{n}^{-1}\sum _{i=1}^n{\tilde{S}}_i{\mathcal{L}}_{\theta }\{Y_i{S}_i^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z_i\right)\}+o_p\left(n^{-1∕2}\right).$$ (14)

The score statistic for β is, via Taylor series,

$$\begin{array}{cc}\hfill {\mathcal{T}}_{n,\mathrm{pro}}\left(\gamma \right)=& n^{-1∕2}\sum _{i=1}^n\{1+{\gamma }^{{\theta }_0}\left(Z_i\right)\}{\tilde{X}}_i\mathcal{L}\{Y_i,S_i^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z_i\right)\}+n^{-1∕2}\sum _{i=1}^n{\mathcal{S}}_{1i}\left(\gamma \right)\left\{\widehat{\theta }(Z_i-{\theta }_0\left(Z_i\right))\right\}\hfill \\ \hfill +& n^{-1∕2}\sum _{i=1}^n{\mathcal{S}}_{2i}\left(\gamma \right)(\widehat{\eta }-{\eta }_0)+o_p\left(1\right)\hfill \\ \hfill =& A_{1n}+A_{2n}+A_{3n}+o_p\left(1\right)\hfill \end{array}$$

where

$$\begin{array}{c}\hfill {\mathcal{S}}_{1i}\left(\gamma \right)={\tilde{X}}_i[\gamma {\mathcal{L}}_{\theta }\{Y_i,S_i^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z_i\right)\}+\{1+\gamma {\theta }_0\left(Z_i\right)\}{\mathcal{L}}_{\theta \theta }\{Y_i,S_i^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z_i\right)\}]\hfill \\ \hfill {\mathcal{S}}_{2i}\left(\gamma \right)=\gamma {\theta }_{\eta }\left(Z_i\right){\tilde{X}}_i{\mathcal{L}}_{\theta }\{Y_i,S_i^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z_i\right)\}+\{1+\gamma {\theta }_0\left(Z_i\right)\}{\tilde{X}}_i{\tilde{S}}_i^T{\mathcal{L}}_{\theta \theta }\{Y_i,S_i^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z_i\right)\}.\hfill \end{array}$$

By definition of X̃, it is easy to see that, to order o_p(1),

$$A_{2n}=-n^{-1∕2}\sum _{i=1}^n{\mathcal{L}}_{\theta }\{Y_i,S_i^T{\eta }_0+{\theta }_0\left(Z_i\right)\}E\{{\mathcal{S}}_{1i}\left(\gamma \right)\mid Z_i\}∕\Omega \left(Z_i\right)=0,$$

where we have used equations (6) and (13). Also, using equation (14) and the definition of $\mathcal{N}$ we obtain

$$A_{3n}=-\mathcal{N}{\mathcal{M}}^{-1}{n}^{-1∕2}\sum _{i=1}^n{\tilde{S}}_i{\mathcal{L}}_{\theta }\{Y_i{S}^{\mathrm{T}}{\eta }_0+{\theta }_0\left(Z_i\right)\}+o_p\left(1\right).$$

The result now follows by collecting all ther terms. It is readily seen that the expansion is uniform in γ∈[L, R].

A.2. Weak convergence

Weak convergence is trivial. Examining the form of the test statistic ${\mathcal{T}}_{n,\mathrm{pro}}\left(\gamma \right)$ in equation (8), we see that it is linear in γ and can be written as U_n + γV_n, where (U_n, V_n) are jointly asymptotically normally distributed.

Appendix B: Argument for result 2

Define

$$\Omega \left(z\right)=\sum _{j=1}^J{f}_j\left(z\right)E\{{\mathcal{L}}_{jj\theta }(\cdot )\mid Z_j=z\}$$

and

$$\begin{array}{c}\hfill \mathcal{A}(B,Z_1,Z_2)=\sum _{j=1}^J\sum _{k\ne j=1}^J{f}_j\left(z_1\right)E\{{\mathcal{L}}_{jk\theta }(\cdot )B(Z_k,z_2)∕\Omega \left(Z_k\right)\mid Z_j=z_1\},\hfill \\ \hfill Q(Z_1,Z_2)=\sum _{j=1}^J\sum _{k\ne j=1}^J{f}_{jk}(z_1,z_2)E\{{\mathcal{L}}_{jk\theta }(\cdot )\mid Z_j=z_1,Z_k=z_2\}∕\Omega \left(Z_2\right),\hfill \end{array}$$

where f_j(z) is the density of Z_j and f_jk(z₁, z₂) is the bivariate density of (Z_j, Z_k), which are assumed to have bounded support and are positive on the support. Let $\mathcal{G}(z_1,z_2)$ be the solution to

$$\mathcal{G}(z_1,z_2)=Q(z_1,z_2)-\mathcal{A}(\mathcal{G},z_1,z_2).$$

Using the results of Lin and Carroll (2006) we obtain that, uniformly in z,

$$\begin{array}{cc}\hfill \widehat{\theta }(z,{\eta }_0)-{\theta }_0\left(z\right)=& (\varphi h^2∕2)b\left(z\right)-n^{-1}\sum _{i=1}^n\sum _{j=1}^n{K}_h(Z_{ij}-z){\mathcal{L}}_{ij\theta }\left(•\right)∕\Omega \left(z\right)+n^{-1}\sum _{i=1}^n\sum _{j=1}^n{\mathcal{L}}_{ij\theta }\left(•\right)\mathcal{G}(z,Z_{ij})∕\Omega \left(z\right)\hfill \\ \hfill & +o_p\{h^4+\log \left(n\right)nh\},\hfill \end{array}$$ (15)

$$\widehat{\eta }-{\eta }_0=-{\mathcal{M}}_1^{-1}{n}^{-1}\sum _{i=1}^n\sum _{j=1}^n\{S_{ij}+{\theta }_n(Z_{ij},{\eta }_0)\}{\mathcal{L}}_{ij}\left(•\right)+o_p\left(n^{-1∕2}\right).$$ (16)

Define

$$\begin{array}{c}\hfill {\mathcal{T}}_{k,n}\left(\gamma \right)=\sum _{j=1}^J[X_j\{1+\gamma {\theta }_0\left(Z_j\right)\}+{\theta }_{\beta }(Z_j,0,{\eta }_0,\gamma )]{\mathcal{L}}_{jk\theta }(\cdot ),\hfill \\ \hfill {\mathcal{T}}_{\eta ,n}\left(\gamma \right)=\sum _{j=1}^J\sum _{k=1}^J[X_j\{1+\gamma {\theta }_0\left(Z_j\right)\}+{\theta }_{\beta }(Z_j,0,{\eta }_0,\gamma )]{(S_k+{\theta }_{\eta }(Z_k,{\eta }_0))}^{\mathrm{T}}{\mathcal{L}}_{jk\theta }(\cdot ).\hfill \end{array}$$

It is easily shown that

$$\begin{array}{cc}\hfill {\mathcal{T}}_{n,\mathrm{pro}}\left(\gamma \right)=& n^{-1∕2}\sum _{i=1}^n\sum _{j=1}^J[X_{ij}\{1+\gamma {\theta }_0\left(Z_{ij}\right)\}+{\theta }_{\beta }(Z_{ij},0,{\eta }_0,\gamma )]{\mathcal{L}}_{ij\theta }(\cdot )+n^{-1∕2}\sum _{i=1}^n{\mathcal{T}}_{i\eta ,n}\left(\gamma \right)(\widehat{\eta }-{\eta }_0)\hfill \\ \hfill +& n^{-1∕2}\sum _{i=1}^n\sum _{j=1}^J{\mathcal{T}}_{ik,n}\left(\gamma \right)\{\widehat{\theta }(Z_{ij},{\eta }_0)-{\theta }_0\left(Z_{ik}\right)\}+n^{-1∕2}\sum _{i=1}^n\sum _{j=1}^J{\mathcal{L}}_{ij\theta }(\cdot )\{{\widehat{\theta }}_{\beta }(Z_{ij},0,\widehat{\eta },\gamma )-{\theta }_{\beta }(Z_{ij},0,{\eta }_0,\gamma )\}\hfill \\ \hfill +& o_p\left(1\right).\hfill \end{array}$$

Using equation (16) and the fact that $E\left\{{\mathcal{T}}_{\eta ,n}\left(\gamma \right)\right\}={\mathcal{M}}_2$, it is easy to see that

$$n^{-1∕2}\sum _{i=1}^n{\mathcal{T}}_{i\eta ,n}^{\mathrm{T}}\left(\gamma \right)(\widehat{\eta }-{\eta }_0)=-{\mathcal{M}}_2{\mathcal{M}}_1^{-1}{n}^{-1∕2}\sum _{i=1}^n\sum _{j=1}^J\{S_{ij}+{\theta }_{\eta }(Z_{ij},{\eta }_0)\}{\mathcal{L}}_{ij\theta }\left(•\right)+o_p\left(1\right).$$

Next, using equation (15), we now derive that, up to terms of o_p (1),

$$\begin{array}{cc}\hfill n^{-1∕2}\sum _{i=1}^n\sum _{k=1}^J{\mathcal{T}}_{ik,n}\left(\gamma \right)\{\widehat{\theta }(Z_{ik},{\eta }_0)-{\theta }_0\left(Z_{ik}\right)\}& =-n^{-1∕2}\sum _{i=1}^n\sum _{k=1}^J{\mathcal{T}}_{ik,n}\left(\gamma \right)\{n^{-1}\sum _{r=1}^n\sum _{j=1}^J{K}_h(Z_{rj}-Z_{ik}){\mathcal{L}}_{rj\theta }(\cdot )∕\Omega \left(Z_{ik}\right)\}\hfill \\ \hfill & +n^{-1∕2}\sum _{i=1}^n\sum _{j=1}^n{\mathcal{T}}_{ik,n}\left(\gamma \right)\{n^{-1}\sum _{r=1}^n\sum _{j=1}^J{\mathcal{L}}_{rj\theta }(\cdot )\mathcal{G}(Z_{ik},Z_{rj})∕\Omega \left(Z_{ik}\right)\}\hfill \\ \hfill & =n^{-1∕2}\sum _{r=1}^n\sum _{j=1}^J{\mathcal{L}}_{rj\theta }(\cdot )\{C_1\left(Z_{rj}\right)+C_2\left(Z_{rj}\right)\},\hfill \end{array}$$

where we define

$$\begin{array}{c}\hfill C_1(z,\gamma )=-\sum _{k=1}^J{f}_k\left(z\right)E\{{\mathcal{T}}_{ik},n\left(\gamma \right)\mid Z_k=z\}\Omega \left(z\right),\hfill \\ \hfill C_2(z,\gamma )=E[\sum _{k=1}^{J}E\{{\mathcal{T}}_{ik,n}\left(\gamma \right)\mid Z_k\}\mathcal{G}(Z_k,z)∕\Omega \left(Z_k\right)].\hfill \end{array}$$

We now note that

$$\sum _{k=1}^J{f}_k\left(z\right)E\{{\mathcal{T}}_{ik,n}\left(\gamma \right)\mid Z_k=z\}=0$$

by deifnition of θ_β(·) with β₀=0 and hence C₁ (z, γ)=C₂ (z, γ)=0.

Finally, we recognize that θ^_β(·) is the repeated measures regression of Q_ij on Z_ij and hence yields an asymptotic expansion similar to equation (15). Together with the fact that $E\{{\mathcal{L}}_{j\theta }(\cdot )\mid X,S,Z\}=0$, it is now straightforward to show that the fourth term in the expansion of ${\mathcal{T}}_{n,\mathrm{pro}}\left(\gamma \right)=o_p\left(1\right)$ completing the proof.

Appendix C: Argument for result 3

Under the null hypothesis, θ_β(z, 0, δ₀, γ) solves

$$0=\sum _{j=1}^J{f}_j\left(z\right)E(\sum _{k=1}^J[X_k\{1+\gamma {\theta }_0\left(z_k\right)\}+{\theta }_{\beta }(Z_k,0,{\delta }_0,\gamma )]{\mathcal{L}}_{jk\theta }\left(•\right)\mid Z_j=z).$$ (17)

Recall that K_h (z)=h^-1 K(z/h) and G_h (z)=(1,z/h)^T. Consider the problem of solving, for |{m(z), m⁽¹⁾ (z)|},

$$0=n^{-1}\sum _{i=1}^n\sum _{j=1}^J{K}_h(Z_{ij}-z)G(Z_{ij}-z)[\sum _{k\ne j=1}^J{\nu }^{ijk}\{Q_{ik}-m\left(Z_{ik}\right)\}+{\nu }^{ijj}{Q}_{ij}-{\nu }^{ijj}G{(Z_{ij}-z)}^{\mathrm{T}}{(m\left(z\right),m^{\left(1\right)}\left(z\right))}^{\mathrm{T}}]$$

where ${\nu }^{ijk}=-{\mathcal{L}}_{ijk\theta }\left(•\right)$ Define

$$F_n\left(z\right)=n^{-1}\sum _{i=1}^n\sum _{j=1}^J{\nu }^{ijj}{K}_h(z_{ij}-z)G{(z_{ij}-z)}^{\mathrm{T}}.$$

The solution then satisfies

$$F_n\left(z\right){(m\left(z\right),m^{\left(1\right)}\left(z\right))}^{\mathrm{T}}=n^{-1}\sum _{i=1}^n\sum _{j=1}^n{K}_h(Z_{ij}-z)[\sum _{k\ne j=1}^J{\nu }^{ijk}\{Q_{ik}-m\left(Z_{ik}\right)\}+{\nu }^{ijj}{Q}_{ij}].$$

Note that

$$F_n\left(z\right)=\sum _{j=1}^{J}E({\nu }^{ij}\mid Z_j=z)\left(\begin{array}{cc}\hfill f_j\left(z\right)\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\varphi }_2\hfill \end{array}\right)+o_p\left(1\right),$$

Where ϕ₂=∫ z²k(z) dz. Hence, taking the limit of both sides we obtain that m(z) satisfies

$$\sum _{j=1}^{J}E({\nu }^{jj}\mid Z_j=z)f_j\left(z\right)m\left(z\right)=\sum _{j=1}^J{f}_j\left(z\right)\sum _{k\ne j=1}^{J}E[{\nu }^{jk}\{Q_k-m\left(Z_k\right)\}\mid Z_j=z]+\sum _{j=1}^J{f}_j\left(z\right)E({\nu }^{jj}{Q}_j\mid Z_j=z),$$

which is identical to equation (17) with m(z)=θ_β(z,0,δ₀,γ). This completes the argument.