A method comparison study of timeline followback and ecological momentary assessment of daily cigarette consumption

Abstract

Introduction:

Uncertainty exists about how best to measure daily cigarette consumption. Two common measures are timeline followback (TLFB), which involves structured, prompted recall, and ecological momentary assessment (EMA), which involves recording consumption, as it occurs, on a handheld electronic device.

Methods:

We evaluated the agreement between TLFB and EMA measures collected for 14 days prior to the target quit date from 236 smokers in a smoking cessation program. We performed a Bland–Altman analysis to assess agreement of TLFB and EMA using a regression-based model that allows for a nonuniform difference between methods and limits of agreement that can vary with the number of cigarettes smoked.

Results:

For pairs of measurements taken on the same smoker, TLFB counts were on average 3.2 cigarettes higher than EMA counts; this difference increased for larger numbers of cigarettes. Using a model that allows for variable limits of agreement, the width of the 95% interval ranged from 8.7 to 61.8 cigarettes, with an average of 26.4 cigarettes. Variation between the methods increased substantially for larger cigarette counts, leading to wider limits and poorer agreement for heavy smokers.

Discussion:

Throughout the measurement range, the estimated limits of agreement were far wider than the limits of clinical significance, defined a priori to be 20% of the number of cigarettes smoked. We conclude that TLFB and EMA cannot be considered equivalent for the assessment of daily cigarette consumption, especially for heavy smokers.

Introduction

Smoking cessation studies routinely record daily cigarette consumption. Apart from its obvious face value, daily consumption is important as a measure of dependence (e.g., Chaiton, Cohen, McDonald, & Bondy, 2007), as a predictor of future cessation (Hughes & Carpenter, 2006), as an index of exposure to smoking-related toxins, as a risk factor for postcessation health outcomes (Duarte, Luiz, & Paschoal, 2008; Hastie, Haw, & Pell, 2008), as a key dimension of the natural history of smoking (Yong, Borland, Hyland, & Siahpush, 2008), and as a measure of the economic cost of smoking. Thus, failure to record consumption accurately may cause bias and inefficiency in estimates of its effects on a range of outcomes, and it is imperative that the methods used to assess it be accurate and clearly understood.

An individual's cigarette consumption is typically recorded as a fixed quantity estimated by global self-report, both in epidemiological surveys and in clinical studies (e.g., Cokkinides, Ward, Jemal, & Thun, 2005; Shiffman, Brockwell, Pillitteri, & Gitchell, 2008; Shiffman, Dresler, et al., 2002). Because consumption may vary from day to day and measures may be needed to assess the effects of interventions (Hanson, Zylla, Allen, Li, & Hatsukami, 2008; Shiffman, Ferguson, & Strahs, 2009) or the natural history of smoking (Yong et al., 2008), more precise methods have been developed to assess daily smoking rate. One approach is the timeline followback (TLFB), which asks subjects to retrospectively report daily cigarette consumption over some period of time (Lewis-Esquerre et al., 2005; Toll, Cooney, McKee, & O'Malley, 2005). One concern about TLFB is that it relies on the subject's recollection and therefore is subject to recall error (Bradburn, Rips, & Shevell, 1987; Hammersley, 1994; Shiffman, Stone, & Hufford, 2008).

An alternative approach, known as ecological momentary assessment (EMA; Shiffman, Stone, & Hufford, 2008; Stone & Shiffman, 1994), avoids recall by having smokers record each cigarette as they smoke it. In a typical implementation, smokers use a handheld computer to log a time-stamped record for each cigarette (e.g., Shiffman, 2009).

Shiffman (2009) compared EMA and TLFB measures of daily smoking over a 2-week period. EMA estimates of consumption were higher on about one third of days but overall averaged 2–3 cigarettes/day lower than TLFB. The two estimates correlated well at the subject level but only modestly (β = 0.29) across days within subjects. Shiffman attributed much of the discrepancy to heaping, or the tendency to round values to even multiples of 10; 43% of the daily TLFB values had zero as the final digit. Comparisons with biochemical markers of smoking suggested that the EMA cigarette counts might be more valid. Levels of carbon monoxide, a biochemical residue of smoking, correlated better with EMA-reported smoking than with TLFB, especially in relation to across-time variation in subjects’ cigarette consumption.

In this paper, we extend Shiffman's correlational and mean difference analyses, using the Bland and Altman (1986) approach (Altman & Bland, 1983), to evaluate the level of agreement between EMA and TLFB measures and to determine how agreement varies with consumption. The Bland–Altman approach consists of a range of statistical techniques for assessing the agreement between two methods of measurement. The starting point of such an analysis is a plot of the difference between two measurement methods against their average in order to determine whether the methods are interchangeable as well as to gauge any systematic bias. The observed level of agreement is then compared with a clinical standard of agreement determined a priori. This goes beyond the correlational analysis reported by Shiffman (2009), which tests the strength of the association between two measures without evaluating their agreement. Recent innovations to the basic approach account for the possibility of repeated measurements or additional sources of variability in the data (Bland and Altman, 1999, 2007).

Methods

Data source

We used data collected and previously analyzed by Shiffman (2009; Shiffman, Gwaltney, et al., 2002). Participants were 236 smokers (≥10 cigarettes/day for 2 years or more) who enrolled in a smoking cessation research study. For 16 days prior to a designated quit date, participants were directed to smoke as normal and to log each cigarette on an electronic diary (ED) just before smoking it. On four to five smoking occasions per day, selected at random by the ED, the device administered an assessment. Each evening, participants also had an opportunity to report any cigarettes that they had failed to log. These amounted to 3.8% (SD = 5.3%) of the total daily entries. The ED also audibly prompted participants at four to five randomly selected times per day when they were not smoking; participants responded to 91% of such prompts within the 2 min allowed, indicating that they were carrying and attending to the device. On Days 3, 8, and 15, participants returned to the clinic and completed a TLFB questionnaire indicating how many cigarettes they had smoked on each day since the last assessment. The questionnaire was in the form of a calendar; that is, the form presented subjects with a matrix consisting of seven columns labeled with the days of the week and rows representing weeks. The calendar included markings for any holidays that fell within the recall period, and subjects were encouraged to fill in personal milestones (e.g., birthdays, weddings, activities) as aids to recall.

The analysis focused on 14 days (Days 2–15, eliminating the incomplete Day 1 and Day 16, the last day before quitting) and included only person-days on which cigarette counts were recorded by both TLFB and EMA. We excluded from the analysis 27 person-days during which the EDs malfunctioned and counts may have been inaccurate. There remained a total of 3,159 measurements performed by TLFB and EMA on 236 subjects. On average, 13.5 days per subject (out of a possible 14) were available for analysis. Postquit measurements taken after this 14-day period represent a distinct set of smoking conditions, with subjects working to achieve and maintain abstinence, and were therefore not included in this analysis, which focuses on ongoing ad libitum smoking.

Data analyses

We performed a Bland and Altman (1986) analysis to evaluate agreement between TLFB and EMA (Altman & Bland, 1983). The key to such an analysis is a plot of the difference between the two measures for each person-day (TLFB − EMA) against the average of the two measures ((TLFB + EMA)/2). Because the true cigarette count is not known, the average of the two measurements serves as its proxy. From these basic summaries, one can calculate two indices of agreement: the average bias and 95% limits of agreement. The average bias is the mean of the difference between methods and represents how much one method over- or underestimates the other. The limits of agreement form an interval in which 95% of the differences between the two measurement methods are expected to fall; in the simplest case, they are computed as two SDs above and below the average bias. The width of the interval of agreement determines how well the two measures agree; namely, a smaller range suggests better agreement.

When there are repeated measurements per subject, there is typically correlation within individuals and consequently the simple method for calculating limits of agreement produces limits that are too narrow. To account for this, one can calculate limits of agreement using the modified Bland and Altman (1999, 2007) method for repeated measurements. As in the basic Bland–Altman method, the repeated measures model assumes that the average difference and the variability of differences are constant throughout the range of measurement. Bland and Altman suggest that if these assumptions are not met, one should use a two-stage regression approach for calculating the average difference and limits of agreement. First, to calculate the mean difference, one performs a simple linear regression of the difference between TLFB and EMA on the average (A) of the two measurements. Next, the absolute values of the residuals from the first regression are regressed on A, and the two regression equations are combined to form the 95% limits of agreement. As is the case with all the Bland–Altman methods, this relies on the assumption that the differences are normally distributed.

We obtained valid, correlation-adjusted SEs and 95% CIs for the limits of agreement using a nonparametric bootstrap method (functions boot() and boot.ci() in the boot package of R version 2.7.1; R Development Core Team, 2008). The 236 participants were sampled with replacement 1,000 times. Pointwise 95% CIs were calculated over the range of cigarette consumption based on the 2.5 and 97.5 percentiles of the resampling distribution for the limits of agreement.

Finally, we compared observed limits of agreement with predetermined limits of clinical significance to assess the agreement between TLFB and EMA. Because the regression-based Bland–Altman method allows the limits of agreement to vary according to the average of the two methods of measurement, the limits of clinical significance were defined similarly to be 20% of the average.

Results

Cigarette consumption

A summary of the data is displayed in Table 1. The daily cigarette counts capture a wide range of smoking behaviors, ranging from abstinence to 85 and 74 cigarettes/day for TLFB and EMA, respectively. The mean, median, and quartiles were slightly higher for TLFB than for EMA, suggesting a possible systematic difference between the methods.

Table 1.

Summary of daily cigarette counts obtained by TLFB and EMA

Method	Minimum	First quartile	Median	Third quartile	Maximum	M	SD
TLFB	0	18	22	30	85	24.84	10.84
EMA	0	15	21	28	74	22.14	10.14

Note. TLFB = timeline followback; EMA = ecological momentary assessment.

Analysis

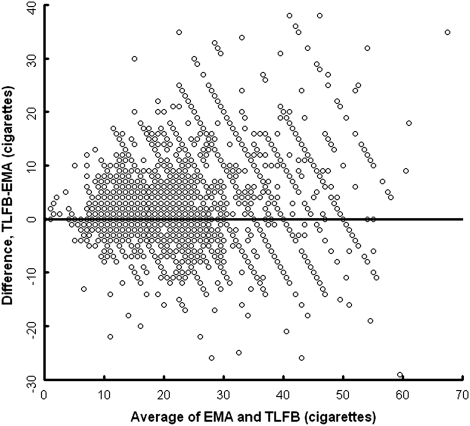
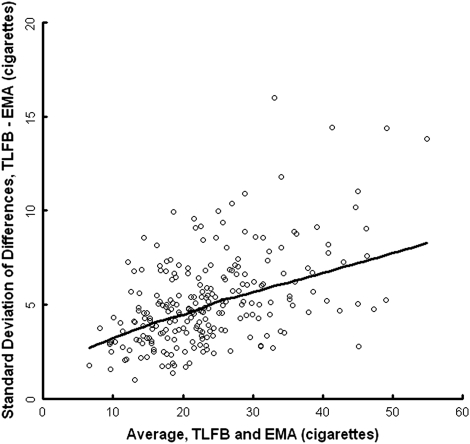
Figure 1 displays a plot of the difference between measurements against their average. The repeated measures Bland–Altman model assumes implicitly that both the mean bias and the variability of the differences are constant throughout the range of measurement. Inspection of Figure 1, however, suggests a possible relationship between the differences and the magnitude of the average measurements that would violate both assumptions. A Spearman rank correlation coefficient of .3 between the absolute differences and the averages confirms that the average size of the differences varies across the range of measurement. Figure 2 assesses the assumption of constant variance by comparing the SD of differences between TLFB and EMA against the average of the two measurements. There is a clear positive association between the variability of the differences and the magnitude of the average measurement. In other words, on days marked by higher cigarette consumption, there was greater disagreement between EMA and TLFB. By implication, heavier smokers would demonstrate greater discrepancy between the two sources. Because both the assumptions of the repeated measures Bland–Altman method appear to be violated, we employed the regression-based Bland–Altman method that allows for nonuniform differences and nonconstant variance.

Figure 1.

Bland–Altman plot for the difference between methods and the average of methods. The solid line indicates the line of agreement representing no bias.

Figure 2.

Scatter plot of the SD of differences between timeline followback and ecological momentary assessment for each subject against the mean of both methods of measurement. The Spearman rank correlation between the absolute value of the differences and the average is .3. The solid line is a loess smooth.

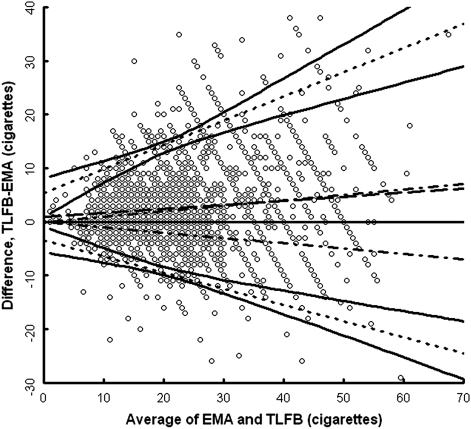
We fit the model for nonuniform differences with nonconstant SD in stages. In the first stage, we regressed the differences on the averages, which led to an intercept of .9 with a statistically significant slope of 0.1, t(3157) = 5.67, p < .001. This regression line represents the bias of TLFB over EMA and implies that for every 10-cigarette increase in the average of TLFB and EMA, the difference between the two measurements increases by one cigarette. Furthermore, the direction of the bias indicates that TLFB measurements are slightly higher than EMA measurements for the same replicate pair; on average, TLFB estimates were 3.2 cigarettes higher than EMA data. In the second stage, we determined the limits of agreement by regressing the absolute value of the residuals from the first stage on the average of TLFB and EMA, leading to a significant association, F(1,3157) = 318, p < .001. The estimated intercept was 1.8, t(3157) = 8.14, p < .001, and the estimated slope was 0.2, t(3157) = 17.83, p < .001. This regression line was combined with the mean difference to form the 95% limits of agreement, as shown in Figure 3. The width of this interval ranges from 8.7 to 61.8 cigarettes with an average of 26.4 cigarettes and increases for higher values of cigarette consumption. Viewed as a percentage of the average of TLFB and EMA, the limits of agreement are greater than the predetermined 20% standard of clinical agreement throughout the range of measurement. For example, the width of the limits of agreement is 118.9% of the average of TLFB and EMA for the commonly reported value of 20 cigarettes and 104.4% for 30 cigarettes. The 95% CI for the limits of agreement is two cigarettes wide for the most commonly reported count (20 cigarettes) and widens at the lower and upper ends of the range of average cigarette counts.

Figure 3.

Bland–Altman plot for the difference between methods and the average of methods. The solid line indicates the line of agreement representing no bias, and the dashed line represents the mean bias. The dotted lines correspond to the 95% limits of agreement and are surrounded by pointwise 95% CIs. The dot-dashed lines are the a priori limits of clinical significance. The limits of agreement and mean bias were obtained by the Bland–Altman approach for nonconstant variance and nonuniform difference.

The Shapiro–Wilk test of normality for the differences between TLFB and EMA was significant (W = 0.96, p < .001). However, Bland and Altman (1999) indicate that because approximately 95% of observations are often within two SDs of the mean even for nonnormal distributions, this assumption is not crucial to the analysis. In our data, 93.5% of the observations fall within the estimated limits of agreement.

A notable feature of the Bland–Altman plots in Figures 1 and 3 are the parallel diagonal ridges extending from the upper left to the lower right of the graph, most pronounced at the higher end of the range of cigarette counts. Each ridge corresponds to a single value of TLFB (as in regression residual plots; see Searle, 1988). Thus, these lines represent artifacts of data heaping, which is more pronounced in TLFB because of the tendency of subjects to report daily consumption as multiples of 10 and 20 cigarettes. EMA data display no such artifacts.

Discussion

We examined agreement between TLFB-assessed and EMA-assessed daily cigarette consumption, using a variant of the Bland–Altman method that accommodates a nonuniform difference between methods of measurements and a nonconstant variance in that difference over the range of measurement. TLFB cigarette counts were higher than EMA on average at every level of consumption, with the gap increasing with the number of cigarettes consumed. The estimated slope for this relationship was small but significantly different from zero, suggesting that the nonuniform difference model is more appropriate for these data than the standard Bland–Altman model.

The Bland–Altman analysis also allowed us to compute the limits of agreement, that is, a prediction interval in which 95% of the differences between TLFB and EMA in future measurements will fall. However, the standard Bland–Altman method, as well as the modification for repeated measures, assumes that the differences are constant across the range of cigarette consumption, while the data suggest that the differences grow wider as cigarette consumption increases. Indeed, the regression-based analysis employed here indicates that the difference between TLFB and EMA is smaller for low cigarette counts than for high cigarette counts. This is not unexpected because cigarette counts on days of heavy smoking should be harder to remember on TLFB and also harder to record faithfully on EMA.

Bland and Altman emphasize that the evaluation of agreement between methods of measurement should have a clinical, rather than purely statistical, basis. We defined a clinically significant difference, a priori, to be 20% of the true cigarette count as approximated by the average of the two methods of measurement. Figure 3 shows that the differences between TLFB and EMA very often exceed this limit, indicating that TLFB and EMA are not, as a practical matter, substitutable for each other. This suggests that one must exercise circumspection when using either method, particularly with heavier smokers. Based on correlations with biochemical indicators (Shiffman, 2009), EMA data appear to be more accurate, but the wide discrepancies at higher average estimated smoking rates also suggest that smokers may fail to record all their cigarettes on days of heavy smoking, possibly biasing EMA estimates downward.

The pattern of diagonal ridges in the Bland–Altman plots (Figures 1 and 3) reflects the discreteness of the data; specifically, there is one ridge for each TLFB value in the data set. Because TLFB observations are commonly “heaped” at multiples of 10 cigarettes (>40%, compared with the 10% expected under accurate recording), the ridges corresponding to these observations are prominent. The parallel lines are more pronounced for higher cigarette counts because these counts are more likely to be rounded off to the nearest multiple of 10. Such behavior appears in numerous self-reported outcome variables (Heitjan & Rubin, 1990), including self-reported cigarette counts (Wang & Heitjan, 2008). Because cigarettes are sold in packs of 20, it is plausible that actual smoking is concentrated at multiples of 20. However, Klesges, Debon, and Ray (1995) found no such heaping in the distribution of the nicotine by-product cotinine, suggesting that the heaping is a bias in self-report rather than an actual feature of smoking behavior.

There are limitations to the statistical methodologies employed in this analysis. The regression-based Bland–Altman method employed here does not account for the longitudinal nature of the data; on the other hand, both the standard and repeated measures Bland–Altman methods fail to account for the nonuniform differences and nonconstant variance present in these data. As a rule, accounting for replicate measures widens the limits of agreement by a small amount (Bland & Altman, 1999). In this example, where the limits of agreement are already unacceptably wide, failure to adjust for within-subject correlation is not a significant shortcoming, as it would only widen the limits further. More importantly, we believe that limits of agreement that vary with the magnitude of the measurement (Figure 3) better capture the essence of the relationship between EMA and TLFB than limits that are constant throughout the range of measurement. Future work is necessary to develop analysis methodology that simultaneously accommodates repeated measures, nonuniform differences, and nonconstant variance.

Additional limitations arise from the nature of self-reported cigarette counts. As indicated above, TLFB is subject to heaping error that the currently available analysis methodologies do not address. Although EMA appears to eliminate heaping, it is not a perfect method. It still relies on subject cooperation and compliance to capture smoking episodes and may miss cigarettes that smokers fail to record. Because there is no “gold standard” reference method for daily cigarette self-report, comparisons must be made to the average of TLFB and EMA. By default, equal weights are given to each method, whereas the biochemical data suggest that EMA estimates are likely closer to the truth.

Additionally, our analyses use TLFB data covering a relatively short recall period during contemporaneous self-monitoring by EMA and are not necessarily generalizable to TLFB data collected in a typical setting. In this case, participants were asked to recall smoking behavior over a 1- to 7-day period for TLFB measurements, whereas in practice, recall periods can span a month or more. In regard to the contemporaneous EMA monitoring, Shiffman (2009) found that monitored TLFB measures averaged 1.5 cigarettes/day lower than baseline TLFB measures recorded prior to monitoring. Furthermore, 52% of participants reported smoking the same number of cigarettes every day of recall during premonitoring TLFB as compared with only 3% of the monitored TLFB reports. Additionally, heaping was more pronounced during the premonitoring period when 64.3% of TLFB measures were rounded at 10, as compared with 42.8% during the monitoring period. Although it is possible that the participants altered their smoking behavior during the monitoring period, it seems more likely that the regular prompting of EMA caused them to be more attentive to cigarette consumption. Thus, the lack of agreement we found between TLFB and EMA measurements may be even more pronounced for unmonitored TLFB.

Because the true cigarette counts remain unknown, it is impossible, on the basis of these data alone, to say how accurate either method is. On average, TLFB gives higher daily cigarette consumption than EMA. Importantly, on one third of days, EMA estimates are higher than TLFB, indicating that the discrepancy cannot consistently be due to failure to record cigarettes on EMA. Without a gold standard, it is unclear to what extent TLFB overreports or EMA underreports smoking; it is even possible that both methods are biased in the same direction. By comparing the two methods as we have done, however, one can assess the agreement between them. Our analysis demonstrates that the agreement is generally poor and becomes worse for increasing cigarette counts.

What are the implications for smoking research? The current practice of asking smokers for a global estimate of their daily cigarette consumption yields the highest level of heaping (Shiffman, 2009) and thus is likely to contain substantial error. However, such data may serve adequately for gross comparisons among subjects. When there is a need to assess consumption more precisely and, particularly, when the research focuses on changes in consumption, better methods may be needed. Based on associations with cotinine and carbon monoxide, EMA methods appear to be more accurate (Shiffman, 2009). However, the current analysis suggests that self-reported heavy smokers may fail to record many cigarettes (or exaggerate their smoking on recall), suggesting some caution in the use of both EMA and TLFB. Averaging of data from the two methods may yield the most robust estimates. In any case, investigators should be aware that EMA and TLFB data yield divergent estimates, especially for heavy smokers.

Funding

USPHS: National Cancer Institute (CA116723); National Institute on Drug Abuse (DA06084).

Declaration of Interests

Saul Shiffman is a founder of invivodata, inc., which provides electronic diaries for research.