Abstract
When faced with choices between two sources of reward, animals can rapidly adjust their rates of responding to each so that overall reinforcement increases. Herrnstein's ‘matching law’ provides a simple description of the equilibrium state of this choice allocation process: animals reallocate behavior so that relative rates of responding equal, or match, the relative rates of reinforcement obtained for each response. Herrnstein and colleagues proposed ‘melioration’ as a dynamical process for achieving this equilibrium, but left details of its operation unspecified. Here we examine a way of filling in the details that links the decision-making and operant-conditioning literatures and extends choice-proportion predictions into predictions about inter-response times. Our approach implements melioration in an adaptive version of the drift-diffusion model (DDM), which is widely used in decision-making research to account for response-time distributions. When the drift parameter of the DDM is 0 and its threshold parameters are inversely proportional to reward rates, its choice proportions dynamically track a state of exact matching. A DDM with fixed thresholds and drift that is determined by differences in reward rates can produce similar, but not identical, results. We examine choice probability and inter-response time predictions of these models, separately and in combination, and possible implications for brain organization provided by neural network implementations of them. Results suggest that melioration and matching may derive from synapses that estimate reward rates by a process of leaky integration, and that link together the input and output stages of a two-stage stimulus-response mechanism.
Keywords: drift-diffusion, decision making, melioration, matching, operant conditioning, instrumental conditioning, reward rate, reinforcement learning, neural network
1. Introduction
For much of the twentieth century, psychological research on choice and simple decision making was typically carried out within one of two separate traditions. One is the behaviorist tradition, emerging from the work of Thorndike and Pavlov and exemplified by operant conditioning experiments with animals (e.g., Ferster & Skinner, 1957), including the variable interval (VI) and variable ratio (VR) tasks that we examine in this article. The other tradition, while also focused quantitatively on simple behavior, can be categorized as cognitivist: its emphasis is on internal, physical processes that transduce stimuli into responses, and on behavioral techniques for making inferences about them. This style of research originated in the mid-1800s in the work of Donders, and is exemplified by choice-reaction time experiments with humans (e.g., Posner, 1978), among other approaches.
Today the boundaries between these traditions are less well defined. From one side, mechanistic models of internal processes have achieved growing acceptance from contemporary behaviorists (e.g., Staddon, 2001). From the other side, there is a growing appreciation for the role of reinforcement in human cognition (e.g., Bogacz, Brown, Moehlis, Holmes, & Cohen, 2006; Busemeyer & Townsend, 1993). Here we propose a theoretical step toward tightening the connection between these traditions. This step links models of choice based on the content of a perceptual stimulus (as in simple decision making experiments) with models of choice based on a history of reinforcement (as in operant conditioning experiments). It thereby provides a potential explanation of response time (RT) and inter-response time (IRT) data in operant conditioning, and the development of response biases in simple decision making. As we show, behavioral results in both the conditioning and decision making literatures are consistent with the predictions of the model we propose to link these traditions.
Specifically, we prove that a classic behaviorist model of dynamic choice reallocation — ‘melioration’ (Herrnstein, 1982; Herrnstein & Prelec, 1991; Herrnstein & Vaughan, 1980; Vaughan, 1981) — can be implemented by a classic cognitive model of two-alternative choice-reaction time — the drift-diffusion model (Ratcliff, 1978), hereafter referred to as the DDM — under natural assumptions about the way in which reinforcement affects the parameters of the DDM. Melioration predicts that at equilibrium, behavior satisfies the well-known ‘matching law’ (Herrnstein, 1961). This states that relative choice proportions equal, or match, the relative rates of the reinforcement actually obtained in an experiment:
| (1) |
Here Bi represents the rate at which responses of type i are emitted, and Ri represents the rate of reinforcement, or reward, earned from these responses (we will use the terms ‘reinforcement’ and ‘reward’ interchangeably).
The DDM and variants of it can in turn be implemented in neural networks (Bogacz et al., 2006; Gold & Shadlen, 2001; Smith & Ratcliff, 2004; Usher & McClelland, 2001), and we show that parameter-adaptation by reinforcement can be carried out by simple physical mechanisms — leaky integrators — in such networks. Furthermore, while it is relatively abstract compared to more biophysically detailed alternatives, our simple neural network model gains analytical tractability by formally approximating the DDM, while at the same time maintaining a reasonable, first-order approximation of neural population activity (as in the influential model of Wilson & Cowan, 1972). It therefore provides an additional, formal point of contact between psychological theories, on the one hand, and neuroscientific theories about the physical basis of choice and decision making, on the other.
In what follows, we show how melioration emerges as a consequence of placing an adaptive form of the DDM in a virtual ‘Skinner box’, or operant conditioning chamber, in order to perform a concurrent variable ratio (VR) or variable interval (VI) task. In these tasks, an animal faces two response mechanisms (typically lighted keys or levers). In both tasks, once a reward becomes available, a response is then required to obtain it, but ordinarily no ‘Go’ signal indicates this availability. In a VR task, rewards are made available for responses after a variable number of preceding responses; each response is therefore rewarded with a constant probability, regardless of the inter-response duration. To model a VR task mathematically, time can therefore be discretized into a sequence consisting of the moments at which responses occur. In a VI task, in contrast, rewards become available only after a time interval of varying duration has elapsed since the previous reward-collection, and this availability does not depend on the amount of any responding that may have occurred since that collection. Modeling VI tasks therefore requires a representation of time that is continuous rather than discrete. Finally, ‘concurrent’ tasks involve two or more response mechanisms with independent reward schedules. Each of these may be a VR or VI schedule, or one of a number of other schedule-types; the particular combination used is then identified as, for example, a VR-VR, VI-VI, or VR-VI schedule.
Having shown how an adaptive DDM can implement melioration, we then develop a neural implementation of this model that can be used to make predictions about firing rates and synaptic strengths in a model of brain circuits underlying choice and simple decision making.
In the Discussion, we address the relationship of this model to other neural models of melioration and matching, and we propose a possible mapping of the model onto the brain. We conclude by addressing the prospects for extending the current model to tasks involving more than two concurrent responses.
2. Results
2.1. Choice proportions of the adaptive DDM
Exact melioration and matching occur for one model in a family of adaptive choice models based on the DDM; for the other models in this family, close approximations to matching can be obtained.
The model family that we analyze uses the experience-based or feedback-driven learning approach of the adaptive DDM in Simen, Cohen, and Holmes (2006). This adaptive model was designed to learn to approximate optimal decision-making parameters (specifically, response thresholds) of the DDM in a two-alternative decision making context (discussed in Bogacz et al., 2006). In an operant conditioning context, and with a slight change to its method of threshold adaptation, the expected behavior of this model (Model 1) is equivalent to melioration, which leads to matching at equilibrium (i.e., a state in which choice proportions are essentially unchanging). Model 1 makes choices probabilistically, and as a function of the relative reward rate (Ri/(R1 + R2)) earned for each of the two alternatives (this quantity is sometimes referred to as ‘fractional income’, e.g., Sugrue, Corrado, & Newsome, 2004).
We also include in this family another model (Model 2) that adapts a different DDM parameter (drift). This model is discussed in Bogacz, McClure, Li, Cohen, and Montague (2007). Although it cannot achieve exact matching (Loewenstein & Seung, 2006), this model provides an account of another important function that is widely used in reinforcement learning (Sutton & Barto, 1998) to determine choice probabilities: the ‘softmax’ or logistic function of the difference in reward rates earned from the two alternatives. We address this model because behavioral evidence abounds for both types of choice function, and because the adaptive DDM may be a single mechanism that can account for both.
The rest of the model family consists of parameterized blends of these two extremes. These blended models adapt thresholds and drift simultaneously in response to reward rates (the proportional weighting of each of these parameters defines the model space spanning the range between Model 1 and Model 2).
We begin our discussion of choice proportions with Model 1, which implements melioration and achieves matching exactly via threshold adaptation. We then move on to the alternative that adapts drift, and finally to models that blend the two approaches.
2.1.1. Model 1: the threshold-adaptive, zero-drift diffusion model
In order to determine the effects of parameter adaptation on the behavior of Model 1 (or any other model in the adaptive DDM family), we make use of known, analytical expressions for its expected error proportions and decision times in the context of decision making tasks.
In a decision-making task, the response time of the DDM is determined by the time it takes after the onset of a stimulus for a drift-diffusion process to reach an upper or lower threshold (±z; see Fig. 1). A drift-diffusion process is a random walk with infinitesimally small time steps that can be defined formally (Gardiner, 2004) by the following stochastic differential equation (SDE):
| (2) |
See Fig. 1 for an interpretation of the drift parameter A and the noise parameter c. As the distance between thresholds and starting point increases, response time increases. At the same time, accuracy increases, because it is less likely that random fluctuations will push the diffusion process across the threshold corresponding to the wrong response to the current perceptual stimulus.
Figure 1.
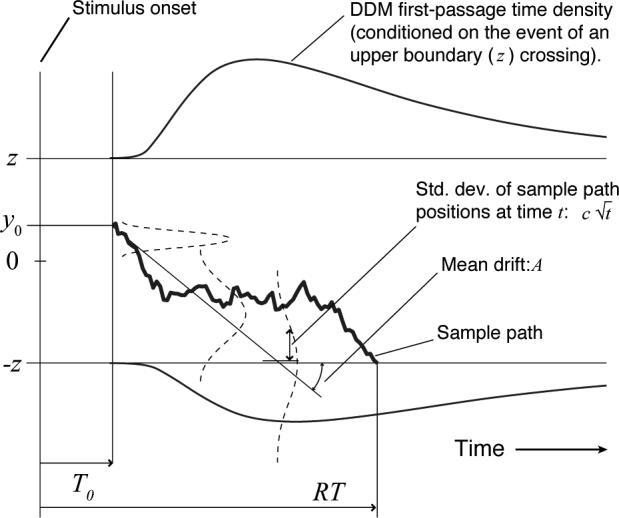
Parameters, first-passage density and sample path for the extended drift-diffusion model (DDM). The leftmost point of the horizontal, time axis is the time at which stimulus onset occurs. In this example, the drift, which models the effect of a perceptual stimulus, is downward with rate A; y0 is the starting point of the diffusion process. The sample path is an individual random walk in continuous time; the distribution of an ensemble of such paths is shown by the dashed Gaussians that expand vertically as time progresses. Response time distributions are equivalent to the distributions of first-passage times shown as ex-Gaussian-shaped curves above the upper and below the lower threshold (T0 is depicted here as elapsing before the random walk begins, but this is only for simplicity — a component of T0 should follow the first-passage to encode motor latency.)
The expected proportion of errors (denoted 〈ER〉) and the expected decision time (denoted 〈DT〉) are described by the following analytic expressions (Busemeyer & Townsend, 1992; cf. Bogacz et al., 2006 and Gardiner, 2004):
| (3) |
| (4) |
Varying the drift (A), thresholds (±z) and starting point (y0) produces adaptive performance.
Model 1 is a variation on the model in Simen et al. (2006). The latter model achieves an approximately reward-maximizing speed-accuracy tradeoff (SAT) in a large class of simple decision making tasks. It does this by setting the absolute value of both thresholds equal to an affine function of the overall reward rate R earned from either response: z = zmax – w · R. Its basic operating principle is that as R increases, thresholds decrease, so that the diffusion process reaches a threshold more quickly (speed increases), but is also more likely to cross the wrong threshold (accuracy decreases).
The current model, Model 1, sets thresholds to be inversely proportional to reward rates. This inverse proportionality produces SAT-adjustment properties similar to those of the affine function used in Simen et al. (2006). Model 1 also generalizes the symmetric threshold-setting algorithm defined in that article to allow for independent adaptation of the two thresholds (we denote their values as θ1, corresponding to the upper threshold, +z, and θ2, corresponding to the lower threshold, −z) based on independent estimates of the reward rate earned for each response (denoted R1 and R2 respectively):
| (5) |
This asymmetric threshold adaptation is equivalent to adapting thresholds ±z symmetrically while simultaneously adapting the starting point y0; however, picking the convention that the starting point is always 0 makes notation more compact. Eqs. 3-4 can then be interpreted by substituting (θ1 + θ2)/2 for z, and (θ2 – θ1)/2 for y0. We refer to Model 1 as the threshold-adaptive DDM.
In order for an analysis of response times and choice probabilities based on the DDM to be exact, however, we cannot allow the threshold to change during the course of a single decision. A threshold that grows during decision making will produce different expected response times and probabilities that are difficult to derive analytically. In order to make exact analytical use of the DDM, the model updates the thresholds according to Eq. 5 only at the moment of each response:
| (6) |
Thereafter, they remain fixed until the next response. Simulations suggest that using Eq. 5 directly without this change-and-hold updating produces very similar results.
2.1.2. Reward rate estimation
In order to use reinforcement history to control its threshold parameters, the model must have a mechanism for estimating the rate of reward earned for each type of response (we will refer to the two response types in a two-alternative task — e.g., a left vs. a right lever press — as response 1 and response 2). The model computes the estimate Ri of reward earned for response i by the ‘leaky integrator’ system defined in Eq. 7:
| (7) |
The time-solution of Eq. 7, Ri(t), is obtained by convolving the impulse-response function of a low-pass, resistor-capacitor (RC) filter (a decaying exponential) with the input reward stream, ri(t) (Oppenheim & Willsky, 1996). If rewards are punctate and intermittent, then they can be represented by a reward stream ri(t) which is a sum of Diracdelta impulse functions (sometimes referred to as ‘stick functions’). Eq. 7 is a continuous-time generalization of the following difference equation, which defines Ri as an exponentially weighted moving average of the input ri(n) (where n indexes time steps of size Δt; n can also be used to index only the times at which responses are emitted):
| (8) |
This is a common approach to reward rate estimation in psychological models (e.g., Killeen, 1994). The extreme rapidity with which animals are able to adapt nearly optimally to changing reinforcement contingencies (e.g., Gallistel, Mark, King, & Latham, 2001), and near-optimal fitted values of τ in Sugrue et al. (2004), suggest that animals must also have a mechanism for optimizing τR or α as well (e.g., the multiple time scales model of Staddon & Higa, 1996).
We take a continuous-time approach (Eq. 7) in order to account for animal abilities in variable interval (VI) tasks (and for simplicity, we leave τR fixed). In these tasks, the reward rate in time (rather than the proportion of rewarded responses) must be known in order to adapt properly.1
2.1.2. Matching by the threshold-adaptive, zero-drift diffusion model
We now describe what happens when the threshold-adaptive diffusion model (Model 1) is applied to a typical task in the instrumental or operant conditioning tradition. One such task is a concurrent VI-VI task, in which there is usually not a signal to discriminate, and no ‘Go’ signal or cue to respond.2
A natural application of the DDM to this design involves setting the drift term to 0: no sensory evidence is available from the environment for which a response will produce reward. Instead, only reinforcement history is available to guide behavior. We refer to the DDM with drift identically 0 as a zero-drift diffusion model.
As we show in Appendix B, the choice probabilities are as follows for a zero-drift diffusion model with starting point equal to 0, and thresholds θ1 and θ2 of possibly differing absolute values:
| (9) |
Substituting ξ/Ri for θi gives the following:
| (10) |
When decision making is iterated repeatedly with a mean response rate b, the rate Bi of behavior i equals Pi · b. Eq. 10 is then equivalent to the matching law (Eq. 1) for two-response tasks.
If we ignore response times and simply examine choice sequences, we note that the adaptive diffusion model is equivalent to a biased coin-flipping procedure, or Bernoulli process, for selecting responses (at least whenever it is in a steady state in which relative response rates are constant for some time period). For that reason, the adaptive diffusion model predicts that the lengths of runs in which only one of the two responses is emitted will be distributed approximately as a geometric random variable — this is a feature of its behavior that is commonly used to distinguish coin-flipping models that account for matching from others that match by some other means. Geometrically distributed run lengths frequently occur in experiments in which a changeover delay (COD) or other penalty is given for switching from one response to the other (e.g., Corrado et al., 2005) whereas run lengths are non-geometric when CODs are absent (e.g., Lau & Glimcher, 2005). Indeed, without such penalties, matching itself is usually violated. This result suggests that, in addition to the account we give here of choice by reinforcement-biased coin-flipping, some theoretical account must eventually be given for an apparently prepotent tendency toward response-alternation that competes with the biasing effects of reinforcement. Such an account, however, is beyond the scope of our current analysis.
2.1.3. Melioration by the threshold-adaptive, zero-drift diffusion model
Melioration itself arises from Model 1 automatically. Loosely speaking, melioration (Herrnstein, 1982; Herrnstein & Prelec, 1991; Herrnstein & Vaughan, 1980; Vaughan, 1981) is any process whereby an increase in obtained reward for one response leads to a greater frequency of that response. (The formal definition of melioration and a proof based on Eq. 10 that Model 1 implements melioration are given in Appendix A.)
Because an increase in reward rate for one response brings its threshold closer to the DDM starting point, the model dynamically reallocates choice proportions so that the more rewarding response is selected with higher probability, and thus relatively more frequently, in such a way that exact matching occurs at equilibrium. Importantly, though, the model's overall response rate must also be known before anything can be said about the absolute frequency of each type of response.
2.1.4. Difficulties faced by Model 1
In fact, without some additional model component for controlling response rates, the zero-drift diffusion model with thresholds set by Eq. 5 and — critically — reward rates estimated by Eq. 7 produces a response-rate that inevitably collapses to 0 at some point. This occurs because at least one and possibly both of the two thresholds moves away from the starting point after every response (because one or both of the reward rate estimates must decrease at every moment). This slows responding, which in turn reduces the rate of reward in a VR or VI task, in a vicious circle that ultimately results in the complete cessation of responding. We discuss why this result is inevitable in section 2.2.
One way to resolve this problem is to enforce a constant rate of responding. This can be achieved by renormalizing both thresholds after each response so that their sum is always equal to a constant K (i.e., divide the current value for θi (call it ) by the sum of current values and multiply by the sum of old values (θ1 + θ2) = K to get the new value ; as a result, ).
Some form of renormalization is therefore promising as a solution to response-rate collapse. However, since inter-response times and response rates are variable features of behavior that we seek to explain by the use of the DDM, we can not assume constant response rates. Instead we use a different renormalization scheme, outlined in section 2.2.7, that is based on a second drift-diffusion process operating in parallel with the choice process. This parallel process effectively times intervals (Simen, 2008) and adaptively enforces a minimum overall response rate (B1 + B2).
It is worth noting that an even simpler solution exists which can account for RT data in many tasks, but which is unable to handle traditional VI schedules. Rather than basing thresholds on reward rates, this solution sets thresholds inversely proportional to the expected reward magnitude for each response, computed by Eq. 8, as for example in Bogacz et al. (2007) and Montague and Berns (2002). In this case, reward rates do not decrease toward 0 (and thresholds do not increase toward infinity) at every moment other than when a reward is received. Instead, a threshold only increases when its corresponding response earns less than what is expected, and complete cessation of responding never occurs except on an extinction schedule — that is, a schedule in which rewards are omitted on every response.
Nevertheless, peculiarities in the RT and IRT predictions of Model 1 (discussed in Section 2.2) and the need to consider VI schedules for generality lead us next to consider a second approach to adaptive behavior by the DDM.
2.1.5. Model 2: the drift-adaptive, fixed-threshold DDM
Adapting drift on the basis of reward rates is another way to achieve choice reallocation, and this approach has antecedents in psychology (Busemeyer & Townsend, 1993) and behavioral neuroscience (Yang et al., 2005). A drift-adaptation approach does not generally achieve exact matching, but it also does not suffer the same sort of response rate collapse as the threshold-adaptive diffusion model.
Bogacz et al. (2007) investigated drift adaptation rather than threshold adaptation in a drift-diffusion model of human performance in an economic game similar to a concurrent VR-VR experiment (Egelman, Person, & Montague, 1998; Montague & Berns, 2002). They noted that when drift is determined by the difference in expected value for each response (i.e., A in Eqs. 3-4 equals γ · (R1 – R2)), and when the input stimulus equally favors both responses, then choice probability is given by a sigmoid function of the difference in expected value (specifically, a logistic function equal to 1 – 〈ER〉, with 〈ER〉 defined by Eq. 3 with y0 = 0). They further note that this choice probability rule is identical to the ‘softmax’ function typically used for probabilistic action selection in reinforcement learning (Sutton & Barto, 1998). For this model, the choice proportion ratio is as follows:
| (11) |
Eq. 11 can approximate the strict matching law as long as R1/(R1 + R2) is not too close to 0 or 1, and the model's trial-by-trial performance is qualitatively similar to melioration as defined by Herrnstein and Vaughan (1980) (cf. Montague & Berns, 2002 and Soltani & Wang, 2006). Corrado et al. (2005) also find evidence for a better fit to monkey behavioral data using a sigmoid function of reward rate differences than was found in fits of a choice function based on the ratio of reward rates (as in Sugrue et al., 2004).
In order to get the close fits that are sometimes observed experimentally (Davison & McCarthy, 1988; Williams, 1988) between data and the predictions of the strict matching law over the total possible range of relative reward rate values (R1/(R1 + R2)) ranging from 0 to 1, a DDM-derived logistic choice function (as in Eq. 3) requires the right balance between expected reward difference (proportional to A), noise (c) and fixed threshold z. For any given data set for which strict matching appears to hold, a parameter set can be found so that a logistic function of reward rate differences fits the data fairly well. However, for a different data set with a different range of reward rates that also accords with strict matching (e.g., a condition in the same experiment that doubles or halves the reward magnitues for both responses), the same threshold and noise values cannot produce a good fit. When choice proportions are plotted as a function of relative reward rates (as in Fig. 3E), the same logistic function will overmatch3 if reward magnitudes for each response are boosted. The sigmoid in that case will become too steep at its inflection point to approximate the identity line predicted by matching. Thus, empirical results in the literature suggest that in order for sigmoid choice functions derived from the DDM to fit data generally, either thresholds or noise must be adapted as well as drift.
Figure 3.
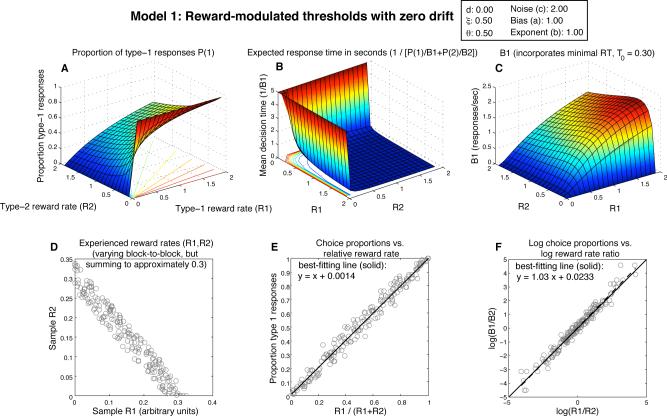
Expected behavior of Model 1, the zero-drift diffusion model (drift=0) with threshold adaptation (θi = ξ/Ri). A) Surface shows expected proportion of 1-responses as a function jointly of reward rate for 1-responses (R1) and reward rate for 2-responses (R2); radial lines in the R1,R2 plane show contours of constant choice probability. B) Expected response time as a function of R1 and R2; this 3D plot is rotated relative to panels A and C to make the shape of the surface more easily discernible; since its height goes to infinity, it is also truncated to 5 sec. C) Expected 1-response rate (B1) as a function of R1,R2 (notice the collapse to 0 along both the R1 and R2 axes). D) Scatterplot of random R1,R2 pairs, representing blocks of 100 responses in which those reward rates were obtained. E) Scatterplot showing expected choice proportions plotted vs. relative reward rate in those blocks of responses; the best-fitting line (solid) is superimposed, and its equation is displayed. Matching predicts a slope of 1 and intercept of 0 (dashed line). F) Choice ratio B1/B2 plotted vs. the reward ratio R1/R2 on a log-log scale, which is frequently used for highlighting generalized matching behavior. Predicted behavior is plotted as a dashed line; best-fitting line is solid.
We have demonstrated that the threshold-adaptive, zero-drift diffusion model predicts the strict matching law.4 Furthermore, the drift-adaptive, fixed-threshold DDM predicts the sigmoid choice function for which some researchers have found evidence (e.g., Lau & Glimcher, 2005 and Corrado et al., 2005). On the basis of implausible IRT predictions of either model in isolation (discussed in the next section), we will argue that simultaneously adapting both drift and thresholds in response to changing reward rate estimates is the most sensible modeling approach.
We now turn to the other major feature of behavior that the DDM is used to explain in decision making research — response times. These predictions may be used to predict response rate and inter-response times in operant conditioning tasks.
2.2 Decision times and inter-response times
We have shown that the DDM can implement biased coinflipping as a temporally extended stochastic process. As was shown in Bogacz et al. (2006) and Usher and McClelland (2001), a simple stochastic neural network can in turn implement diffusion processes (see section 2.5). Thus, to the extent that neural networks stand as plausible models of brain circuits, the preceding results suggest progress in mapping the abstract coin-flipping stages of several models onto the brain (for example, the models of Corrado et al., 2005; Daw, O'Doherty, Dayan, Seymour, & Dolan, 2006; Lau & Glimcher, 2005; Montague & Berns, 2002).
However, the real strength of the DDM in decision-making research has been its ability to provide a principled account for the full shape of RT distributions in a variety of decision making experiments involving humans and non-human primates (Smith & Ratcliff, 2004). Since we propose to model performance in typical VR and VI conditioning tasks (tasks in which no signal to respond is given) by restarting the DDM from 0 after every response, the same first-passage time distributions of the DDM serve as IRT predictions without any modifications (cf. a similar approach in Blough, 2004). These IRT predictions must be addressed before an adaptive DDM can be considered a plausible behavioral model of operant conditioning data.
2.2.1. Slower responding for less rewarding responses
The adaptive DDM discussed in section 2.1 predicts slower responding when a response is chosen that has recently been less rewarding than the alternative (either because rewards for that response have been small when the response was made, or because that response has been made only infrequently). This is true regardless of whether drift or threshold or both of these are adapted. In the case of threshold adaptation alone (Model 1), the less rewarded response will have a threshold that is on average farther from the starting point than the threshold for the more rewarded response; a zero-drift diffusion process therefore takes more time to reach the more distant threshold. The same holds for a model in which thresholds are equidistant, but drift is nonzero (Model 2); in that case, drift toward one threshold will produce faster responses of that type than the alternative. These qualitative predictions are implied by Eq. 4 when reward-modulated thresholds and/or drift are substituted.
2.2.2. Absolute rates of responding
Beyond predicting relative response rates, the DDM predicts absolute IRTs and absolute rates of responding. In fact, the adaptive DDM with threshold modulation and zero drift (Model 1) predicts a variant of the absolute response-rate phenomenon known as ‘Herrnstein's hyperbola’ when we make the same assumptions as Herrnstein and colleagues. Herrnstein's hyperbola (De Villiers & Herrnstein, 1976) is a hyperbolic function that describes response rate as a function of earned reward rate (R1) in a variety of single-schedule tasks (those in which there is only a single response alternative):
| (12) |
Here Re is the ‘extraneous’ rate of reward earned from all other behaviors besides the behavior of interest (for example, Re may represent the reward the animal obtains from grooming behaviors in an experiment that focuses on lever-pressing rates as B1). The constant k represents the sum of all behaviors in which the subject engages during the experiment (both the experimental response and all other behaviors). This result derives from the matching law (Eq. 1) as long as Re is assumed to be constant (De Villiers & Herrnstein, 1976). In fact, however, the constant k assumption does not appear to be widely accepted by researchers in animal behavior, because of variations that appear to depend on satiety and other experimental factors (Davison & McCarthy, 1988; Williams, 1988). Furthermore, assuming a constant rate of reward Re earned from inherently rewarding behavior extraneous to the task seems implausible. Nevertheless, Eq. 12 can be successfully fit to data from a wide range of experiments, and when we make the same assumptions, the adaptive-threshold, zero-drift diffusion model (Model 1) produces a very similar equation for B1, with one interesting deviation.
In order to model single-schedule performance with the DDM, we assume that the upper threshold, θ1, corresponds to response 1, and that the lower threshold, which we now call θe, corresponds to choosing some other response (e.g., grooming), the total rate of reward for which is Re. The mean decision time of the zero-drift diffusion model is the following (see Eq. 34 in Appendix C):
| (13) |
T0 represents the assumption of an unavoidable sensory-motor latency that must be added to the decision time of Eq. 34 in order to give a response time; T0 may itself be assumed to be a random variable, typically modeled as uniformly distributed and with variance that is small relative to that of decision times (at least in the typical decision making experiment; cf. Ratcliff & Tuerlinckx, 2002).
It will also be useful to note the following relationship between the rate of behavior i and the rate of overall behavior, which is proved in Appendix D:
| (14) |
That is, the expected rate of the ith response is the probability of choosing the ith response, times the expected rate of responses of any kind.
Substituting Eq. 9 and Eq. 13 into Eq. 14 gives the following:
| (15) |
Except for the final term in the denominator, this is identical to Eq. 12. Furthermore, k in DeVilliers and Herrnstein's formula — which is intended to represent the rate of all behavior in total — corresponds in Eq. 15 to the inverse of the residual latency T0, and this is indeed the least upper bound on the rate of behavior that can be produced by the model (holding Re fixed and taking R1 to infinity). Thus the threshold-adaptive DDM (Model 1) provides nearly the same account for approximately hyperbolic single-schedule responding as the matching law (as long as R1 and Re are not too small, and under the problematic assumption of constant Re — we examine the consequences of abandoning this assumption in section 2.2.4).
2.2.3. Choice and IRT predictions combined
Now we are in a position to examine the combined choice proportion and IRT/response-rate predictions of the adaptive DDM, to see how they compare to the choice-proportion predictions of the strict and generalized matching laws, and to the response-rate predictions of the strict matching law in single-schedule tasks. Fig. 3 shows the expected proportion of 1-responses for the threshold-adaptive, zero-drift diffusion model in panel A, the expected decision time for either type of response (without the contribution of the residual latency T0) in panel B, and the expected rate of 1-responses, B1, in panel C. Taking slices through the surface in panel C by holding R2 fixed and letting R1 range from 0 to infinity produces the quasi-hyperbolic functions of R1 defined by Eq. 15. All surfaces are shown as functions defined for pairs of earned reward rates, R1 and R2 (R2 may be interpreted as extraneous reward (Re) in a single-schedule task, or as the reward rate for 2-responses in a concurrent task).
Panel D shows a uniform sampling of reward rate pairs that might be earned in many blocks of an experiment in which the overall rate of reward is kept roughly constant by the experimenter, but in which one response may be made more rewarding than the other (as in Corrado et al., 2005); each scatterplot point represents a single block. Each point in panels E and F shows the proportion of 1-responses in a block of 100 responses from the choice probability function in panel A. The two reward rates ‘experienced’ in each 100-response sample correspond to one of the 200 points in the R1,R2 plane plotted in panel D. Panel E plots 1-response proportion against the relative reward rate for 1-responses; points falling on the diagonal from (0,0) to (1,1) adhere to the strict matching law. Panel F plots the same data, but in terms of behavior ratios vs. reward ratios, on a log-log scale; points falling on any straight line in this plane adhere to the generalized matching law (Baum, 1974). Note that Herrnstein's hyperbola would produce a B1 surface in panel C that would look identical in shape to the surface in panel A — thus, it is the values of B1 corresponding to values of R2 near 0 that disrupt the equivalence of the threshold-adaptive DDM and the predictions of the matching law.
2.2.4. Response-rate collapse in Model 1
The response rates of Model 1 and Model 2 are determined by the decision time of the DDM. If we do not renormalize thresholds, then we can abandon the implausible assumption of constant response times made in section 2.1.4. We can also abandon the implausible assumption of constant Re, made in section 2.2.2, by modeling rewards for extraneous behavior as we would in a two-choice task: whenever the lower threshold θe is crossed, extraneous behavior is performed and Re either increases or decreases.
However, when we do this, Model 1 produces a catastrophic outcome: response rates on both alternatives ultimately diminish to 0. This occurs because as Ri approaches 0, θi approaches infinity (by Eq. 5). Eq. 13 then implies that RT also goes to infinity as long as does not approach 0 (i.e., as long as Rj has some finite maximum). In fact, both R1 and Re have finite maxima, because the residual latency T0 ensures that both B1 and Be are finite (and rewards are contingent upon behavior). Thus θ1 and θe are bounded below at values greater than 0. At the same time, reward rates for either behavior can be arbitrarily close to 0, so that θ1 and θe (and therefore RT) are unbounded above.
In VR-VR tasks, in fact, one response winds up being selected exclusively by Model 1, just as it would be by melioration per se. This leads to a reward rate of zero for that response, and therefore, by the argument just given, complete catatonia. Similar problems occur in VI-VI tasks even when both options have been chosen in the last few trials, because an unrewarded choice threshold accelerates when it increases, but decelerates when it decreases. This follows from our use of a reward-rate estimation process (Eq. 7) that changes continuously in time.
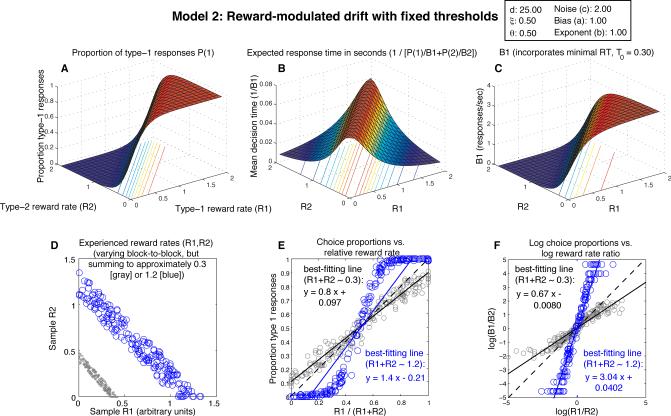
2.2.5. Reward magnitude-independent response rates in Model 2
The drift-adaptive, fixed-threshold model (Model 2) does not have this problem in the regime of exclusive choice; when drift strongly favors one response over the other, the favored response is made so much more rapidly than the less preferred that overall response time is finite (see Fig. 4B). Holding thresholds constant and adapting only drift instead produces the converse problem of much larger response times near a 1:1 ratio of the two response types (which is the ratio expected when drift is near 0). Furthermore, expected response rates are equal for all points on the line R1 = R2, even (0,0). Near the origin, though, the response rate of any plausible model should go to 0 or at least decrease, since no reward is being earned. Functionally, this is a less severe problem than the response-rate collapse produced by Model 1, since Eq. 13 shows that a zero-drift model always has a finite expected response time if thresholds are finite (note that the B1 surface is above 0 everywhere along the R1 axis in Fig. 4C). This response-rate pattern is nevertheless quite implausible, given the widespread finding that response rate increases as reward rate increases. Furthermore, the IRT near R1 ≈ R2 grows arbitrarily large as thresholds grow large (or noise grows small).
Figure 4.
Expected behavior of Model 2, the fixed-threshold diffusion model with drift adaptation (drift = d · (R1 – R2), with drift coefficient d = 25, and threshold θi = 0.5). Notice the implausibly high response rate at (R1,R2) = (0,0) in panels B and C, a point where no responding should be expected. Furthermore, while a reasonable approximation to strict matching is observed in Panel E for relative reward rates near 0.5 and summed reward rates near 0.3 as in Fig. 3 (gray scatterplots), keeping other parameter values the same while doubling reward rates in panel D (so that the rates obtained for responses 1 and 2 sum to approximately 0.6) produces overmatching (not shown); quadrupling rewards leads to extreme overmatching (blue scatterplots in D, E, and F). In contrast, Model 1's behavior approximates strict matching for all reward rate combinations.
Therefore, in order for Model 2 to achieve reasonable response times near a 1:1 behavioral allocation where drift A is near 0 (i.e., R1 ≈ R2), Eq. 4 may require thresholds to be small, or noise to be large, or both. If noise is large and thresholds are small, however, then the overall response rate is high (and IRT is small) for all combinations of reinforcement history (R1,R2). Also, substituting small thresholds or large noise into Eq. 3 produces a shallow sigmoid that can result in undermatching behavior5 in experiments with approximately a fixed level of total reward (corresponding, for example, to the scatterplot of reward rate pairs in panel D of Figs. 3-5). Thus, for Model 2, either overall response rate is uniformly very high regardless of reinforcement history, or dramatic slowdowns in response rate occur near a 1:1 behavioral allocation.
Figure 5.
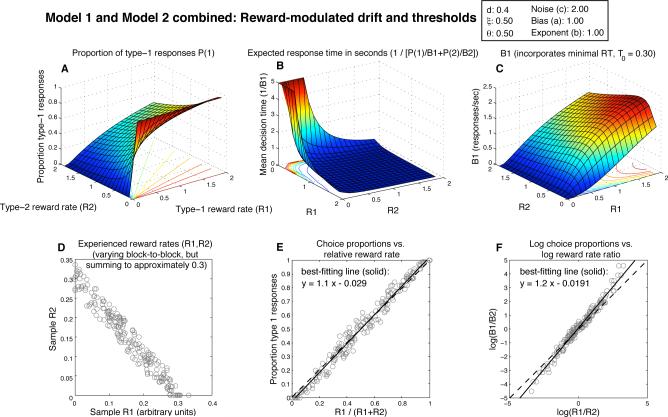
Expected behavior of a combination of Model 1 and Model 2, the DDM with both threshold and drift adaptation (drift = d · (R1 – R2), θi = ξ/Ri, with d = 0.4, and θi = 0.5). Note the rotation once again of the plot in panel B relative to panel A and C, and its truncation to 5 sec. As with Model 1 alone, the absolute magnitude of obtained reward rates has little effect on the quality of the approximation to strict matching.
2.2.6. Model 1 and Model 2 combined
Combining threshold and drift adaptation can mitigate these IRT problems, just as combining them may be necessary in order to fit choice proportions. As shown in Fig. 5, overall response rate is low and IRT is high near (R1,R2) = (0,0) (panel B), which is consistent with the observation that animals cease responding in extinction (that is, when rewards are no longer given for responses). Also, B1 is greater than 0 when R2 = 0 and R1 > 0 (panel C). This too is closer to what is seen empirically, and to what is predicted by the matching law under the assumption of constant reward for extraneous behavior.
The surfaces in Fig. 5 B and C are somewhat deceptive, though: they are based on expected DT as predicted by Eq. 4, and this equation assumes a fixed threshold and drift. In order for these surfaces to provide useful descriptions of the system's behavior, the point (R1,R2) must change slowly enough that the average response rate over multiple responses converges to nearly its expected value. An argument based on iterated maps then shows that the system will in fact reach an equilibrium somewhere (with the particular equilibrium response rates depending on the reward schedule) so that these figures are still useful. The problem is that this equilibrium can easily occur at (R1,R2) = (0,0) as thresholds increase over multiple trials. Even worse, a reward rate estimate can collapse to nearly 0 (with the value of its corresponding threshold on the next trial exploding to infinity) within the course of a single, long response, and such long responses are bound to occur eventually, even if they are rare.
2.2.7. Threshold renormalization
We propose a threshold renormalization process that solves both problems: it prevents single-trial threshold blowups, and, across multiple trials, it breaks the system out of the vicious circle in which lower reward rates lead to lower response rates, which lead in turn to still lower reward rates in VI and VR tasks. This approach uses an adaptive, drift-diffusion-based interval timer, defined by the following SDE, to bound response times:
| (16) |
This diffusion process begins at 0 after every response and has a positive drift that is proportional to the current reward rate being earned from all responses (R = R1 + R2), plus a positive constant ζ that ensures a minimum rate of responding. With a single fixed threshold K > 0, the first-passage-time distribution of this system is the Wald, or inverse Gaussian, distribution, with expected time K/(R+ζ) and variance Kc2/(R + ζ)3 (Luce, 1986).
Whenever an upper-limit IRT duration encoded by the timer has elapsed without a response, the timer triggers a rapid potentiation of both reward rate estimates: both estimates are multiplied by a quantity that grows rapidly on the time scale of an individual response time. This potentiation increases, and thresholds concomitantly decrease, until one response threshold hits the choice diffusion process at its current position. At this point, both the choice drift-diffusion process and the timer start over again and race each other to their respective thresholds. Thus, the choice diffusion process frequently triggers a response before the IRT-limit has elapsed on the next trial. This model component solves the threshold-instability problem, but it is modular and separable; it may be possible by some method currently unknown to us to renormalize thresholds without it.
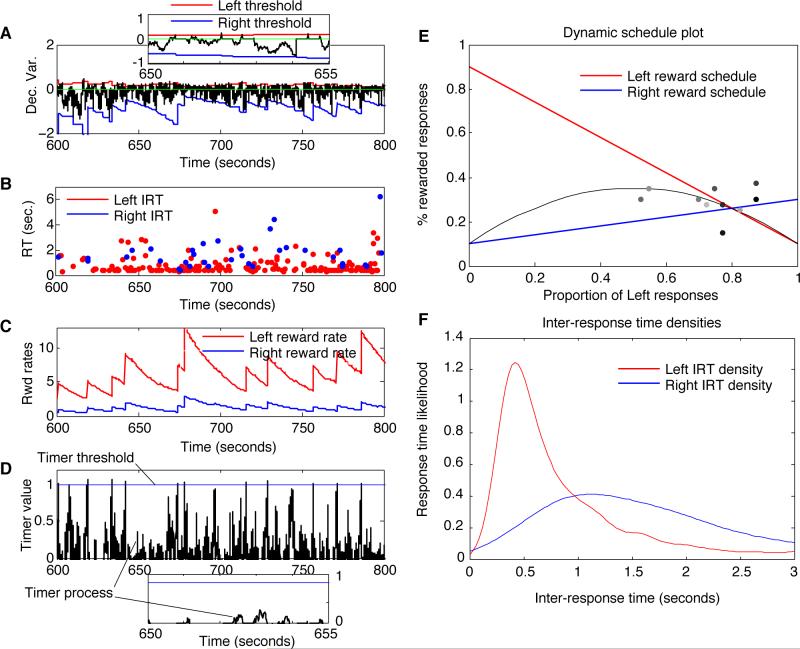
2.2.8. Model performance in a dynamic VR task
Fig. 6 shows the entire system at work in real time on a dynamic, concurrent VR-VR task. This task is prototypical of economic game tasks performed by humans (e.g. ‘the Harvard Game’, Herrnstein, 1997, and Egelman et al., 1998). It is a classic example of dynamic reinforcement contingencies that depend on a subject's previous response history (e.g., Herrnstein & Prelec, 1991). One parameterization of this task is depicted graphically in panel E. There, the horizontal axis represents the percentage of leftward responses made by a subject in the last n trials (in this case, the typical value of 40), in a task involving left and right button pressing (the percentage of rightward responses is 100 minus this value). The vertical axis represents the expected percentage of responses that are rewarded with a unit of reward (variants of this scheme involve basing either the magnitude of the reward, the delay to reward delivery, or the interval between rewards in a concurrent VI-VI task, on response history). The solid, descending straight line plots the reward percentage for leftward responses as a function of past response history; the ascending, dashed line plots the reward percentage for rightward responses. The curved dashed line represents the expected value obtained at a given allocation of behavior.
Figure 6.
Melioration by an adaptive-threshold, zero-drift diffusion model in a dynamic, VR-VR task (with threshold explosion controlled by a drift-diffusion timer). A) The diffusion process over the course of many responses. The trajectory of the decision variable is in black, causing Left responses whenever it intersects the upper threshold in red, and Right responses when it intersects the bottom threshold in blue. At each response, it resets to 0 and begins to drift and diffuse again. A 5-sec window is magnified in the inset. B) The plot of inter-response times (IRTs) in seconds. At points where the IRTs jump to a large value, the system is in danger of response-rate collapse (which is prevented by the expiration of a drift-diffusion response timer). C) The two reward rate estimates over time; large jumps indicated potentiation occurring because the response timer elapsed. D) The ‘decision’ variable of the DDM timer, in black, and a fixed threshold in blue. Whenever the timer hits threshold, a weight renormalization takes place. This occurs for three out of the six responses occurring in the magnified, twenty-second window shown in the inset. E) The reward schedules for Left responses (red) and Right responses (blue) as a function of response proportions in the preceding 40 trials (expected reward is in grey). Dots show choice proportion and reward proportion on the previous 40 trials, plotted once every 40 trials; light dots represent points near the beginning of the simulation, while dark dots represent points near the end. F) The IRT distribution for Left (red) and Right (blue) responses — Right IRTs were on average much longer than those for the more preferred Left responses.
In this figure, Model 1 was simulated to illustrate the effect of the adaptive interval timer (since Model 1 is the most susceptible to response-rate collapse) and to show how close to the system is able to come to strict matching (since only Model 1 produces exactly the right response proportions to achieve strict matching). Panel A shows the choice drift-diffusion process iterated repeatedly within boundaries defined by upper and lower thresholds, which are in turn defined by the two reward rate estimates in panel C. Individual response times generated by the model are plotted at the time of their occurrence in panel B, and the Gaussian kernel-smoothed empirical densities of response times for left and right responses are shown in panel F; these densities display the pronounced RT/IRT difference between more and less preferred responses that can develop for some parameterizations of the model. Panel E superimposes a scatterplot of a sequence of leftward response proportions (horizontal coordinate) and the corresponding reward earned (vertical coordinate) on consecutive blocks of 40 responses, in the task defined by the dynamic VR-VR schedules given by the straight lines; points occurring closer to the end of the simulation are darker. Thus the system quickly moves to the matching point (the intersection of the two schedule lines, which is the only possible equilibrium point for a strict meliorator), but then moves around it in a noisy fashion. This noisy behavior results from computing response proportions inside a short time window, making it difficult to distinguish Model 1 from Model 2 (Bogacz et al., 2007) and related models (e.g., Montague & Berns, 2002; Sakai & Fukai, 2008; Soltani & Wang, 2006) in this task.
2.3 Neural network implementation
The adaptive drift-diffusion model can be implemented by a simple, stochastic neural network. Here we build on key results from a proof of this correspondence in Bogacz et al. (2006). We use these results to show that drift adaptation is achieved by changing a set of weights linking stimulus-encoding units to response-preparation units. These latter units prepare responses by integrating sensory information and competing with other units preparing alternative responses. We refer to these weights as stimulus-response (SR) weights. We then show that threshold adaptation is achieved by adapting a second set of weights linking response-preparation units to response-trigger units — we refer to these as response-outcome (RO) weights (highlighting the fact that these weights are modulated in response to outcomes of behavior, regardless of the current stimulus).6
2.3.1 Neural network assumptions
The neural DDM implementation of Bogacz et al. (2006) and Usher and McClelland (2001) rests on a simple leaky integrator model of average activity in populations of neurons (cf. Gerstner, 1999; Shadlen & Newsome, 1998; Wong & Wang, 2006). A single quantity, Vi(t), stands for a time-averaged rate of action potential firing by all units in population i (action potentials themselves are not modeled). In the same manner as the reward rate estimator of Eq. 7 (but with a much faster time constant), this time-average is presumed to be computed by the synapses and membrane of receiving neurons acting as leaky integrators applied to input spikes. Reverberation within an interconnected population is then presumed to lead to an effective time constant for the entire population that is much larger than those of its constituent components (Robinson, 1989; Seung, Lee, Reis, & Tank, 2000).
Each unit in the network is defined by the following system of SDEs, which, aside from its stochastic component, is fairly standard in artificial neural network modeling (Hertz, Krogh, & Palmer, 1991):
| (17) |
| (18) |
Eq. 17 states that momentary input to unit i is computed as a weighted sum of momentary outputs (Vj) from other units. This output is corrupted by adding Gaussian white noise (dWij/dt),7 representing the noise in synaptic transmission between units. This internally generated noise may be large or small relative to the environmental noise that is received from the sensory periphery; for our purposes, all that matters is that there are uncorrelated sources of white noise in the system. For simplicity, we weight the noise by a constant coefficient c, rather than potentiating it by the connection strength wij. Weight-dependent potentiation seems at least as plausible as a constant coefficient and would cause the noise amplitude in a receiving unit to depend on the firing rates of units projecting to it — we do not yet know how such state-dependent noise would affect our results.
This converging, noisy input is then low-pass filtered by the unit to reduce the noise — that is, the unit's leaky integration behavior causes it to attenuate, or filter out, high frequencies (Oppenheim & Willsky, 1996). As in Eq. 7, the unit in Eq. 17 computes the continuous-time equivalent of an exponentially weighted average, with smaller τi producing steeper time-discounting; dividing through by τi shows that smaller τi also produces less attenuation of noise. Thus xi(t) represents a time-average of its net input that trades off noise attenuation against the ability to pass high-frequency input signals.
This time-averaged value is then squashed by a logistic sigmoid function (Eq. 18), to capture the notion that firing rates in neurons are bounded below by 0 and above by some maximum firing rate — we will exploit this gradual saturation effect in constructing response triggers. Finally, amplification or attenuation of the outputs of a unit are then implemented by the interconnection strengths wij.
In what follows, we will further assume that some units operate mainly in the approximately linear range of the logistic centered around its inflection point (cf. Cohen, Dunbar, & McClelland, 1990); in those cases, a linearized approximation to the above equations is appropriate. When linearized, Eqs. 17-18 can be combined into a single, linear, SDE commonly known as an Ornstein-Uhlenbeck (OU) process:
| (19) |
(Note that without the negative feedback term – yi, Eq. 19 is a drift-diffusion process.) Here, Ii represents the net input to unit i, and dWi refers to a Wiener process that is the net result of summed noise in the inputs (as long as the noise in these inputs is uncorrelated, this summing produces another Wiener process, but with larger variance). Units of this type were used in the DDM-implementation of Bogacz et al. (2006), but for our purposes, saturating nonlinearities in some units will be critical features of the model.
2.3.2 Implementation of the drift-diffusion model
Stochastic neural network models have been related to random walk and sequential sampling models of decision making (including the DDM) by a number of researchers (e.g., Bogacz et al., 2006; Gold & Shadlen, 2002; Roe, Buse-meyer, & Townsend, 2001; Smith & Ratcliff, 2004; Usher & McClelland, 2001; Wang, 2002).
For a standard two-alternative decision making task — in which each trial has one correct and one error response — one unit acts as an integrator of evidence in favor of one hypothesis about the correct response, and the other as an integrator for the other hypothesis. Mutual inhibition creates competition between the integrators, such that increased activation in one retards the growth or leads to a decrease of activation in the other (thereby forming a ‘neuron-antineuron’ pair). By using activations to represent ‘preference’ rather than ‘evidence’, however, the same model can be applied to operant conditioning tasks.
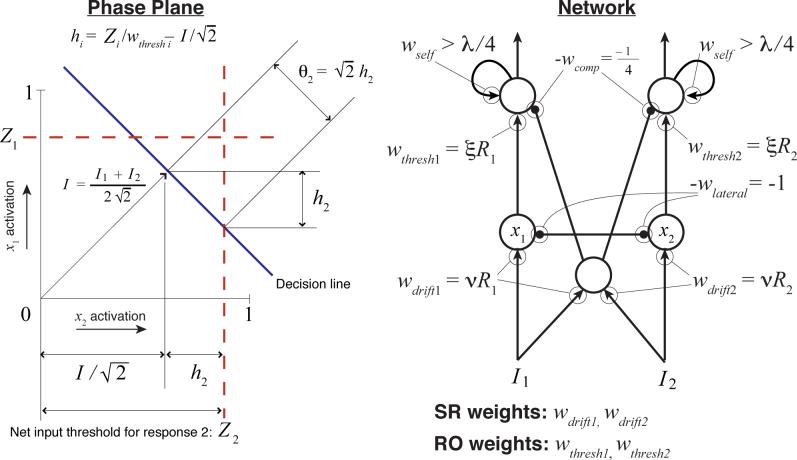
A network of this type can be defined by a system of two SDEs describing the activity of the two integrators over time. The state of the system can then be plotted as a point in a two-dimensional space called the phase-plane. These SDEs in turn can be reduced to a single SDE (Grossberg, 1988; Seung, 2003) which, when properly parameterized, or balanced (i.e., wlateral in Fig. 7 equals 1), is identical to the DDM (Bogacz et al., 2006). This single SDE describes how the difference in activation between the two accumulators, xd, changes over time. If the input to the first accumulator is I1, and the input to the second is I2, then the SDE is:
| (20) |
This equation describes how the state of the system moves along a line through the phase-plane that Bogacz et al. (2006) refer to as the decision line. The system rapidly approaches this line from the origin, and then drifts and diffuses along it until reaching a point at which one unit is sufficiently active to trigger its corresponding response.8
Figure 7.
Threshold modulation for the drift-diffusion model. On the left is a phase-plane for integrator activation. Assuming that the network is balanced and that thep integrators are leaky enough, then reductions of the trigger-unit thresholds (Z1 and Z2) by size Δ are equivalent to reductions of size √2Δ along the decision line. To ensure that thresholds are not reduced below 0 on the decision line (the point where the ray from the origin intersects the decision line), a compensating term must be added to the triggering thresholds. Note that if integrator activity is bounded above by 1, then unlike the DDM itself, an absolute threshold value Zi > 1 implies a total inability to produce response i. The network on the right depicts units governed by Eqs. 17-18 as circles; positive interconnection weights wij are depicted as arrowheads, and negative weights as small, solid circles; labels next to the arrowheads/circles identify the value of each weight. Eq. 19 is a suitable approximation for the leaky integrator units at the bottom of the network (they are assumed to remain in the linear range of their activation functions), but bistability (and therefore nonlinearity) are essential aspects of the threshold-readout units at the top. White noise is added to the output of any unit after weighting by a connection strength. The network depiction shows the weights that are modulated by reward, along with the diffuse inhibition necessary to add the compensating factor to the thresholds; for simplicity, it does not show units that would be necessary to carry out threshold renormalization by occasionally multiplying both RO weights by a large constant.
Bogacz et al. (2006) also showed (effectively) that a small time constant τd in a balanced model leads to tight clustering of the two-dimensional process around the attracting decision line. When tight clustering occurs, we can ignore fluctuations away from the decision line and think of the system as simply drifting and diffusing along it. A simple geometric argument (see Fig. 7) then shows that in the case of small τ, absolute thresholds applied to individual integrator outputs translate into thresholds qi for the drift-diffusion process implemented by xd as follows:
| (21) |
Here, Zi is an absolute firing rate threshold applied to unit i (we will address a possible physical mechanism for threshold ‘readout’ below). Thus, any change to Zi leads to corresponding changes in θi. This fact provides the basis for implementing the threshold adaptation procedure of Model 1, discussed below.
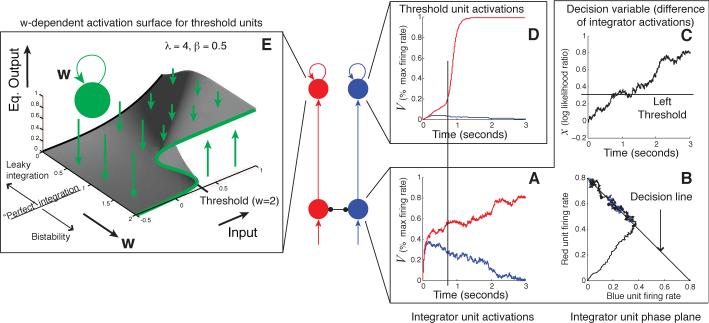
Fig. 8A shows an example of the evolution of a balanced system over time. After stimulus onset in a decision making task — or after reset to the origin following the previous response in a VR or VI task without a ‘Go’ signal — the system state (y1,y2) approaches the attracting decision line. Slower, diffusive behavior occurs along this line, and as long as the thresholds are stationary, the process will ultimately cross one of them with probability 1. Projection of the state (y1,y2) onto the decision line yields the net accumulated evidence x(t), which approximates the DDM as shown in Fig. 8C.
Figure 8.
A two-stage neural network implementing a decision process. The first layer (bottom red and blue units) implements the preference-weighing diffusion process: the two units’ activations are plotted in the box A; these activations are then shown in the phase plane in box B, which depicts the predicted attracting line for the two-dimensional process; box C shows the difference between these activations over time, forming a one-dimensional random walk. The second, bistable layer of units implements response triggers that apply thresholds to this accumulated preference. Self-excitation w creates bistability by transforming the sigmoid activation function from the black curve at the left of the activation surface plot on the left into the green function on the right. The resulting activity is approximately digital, with rates between 0 and 1 occurring only transiently at the time of a threshold crossing.
2.3.3 Drift adjustment by SR weights
As in the stochastic neural network models already mentioned, as well as in (Grossberg, 1971, 1982; Grossberg & Gutowski, 1987), reward-modulated stimulus-response mappings are presumed to be encoded by the input weights labelled ‘SR’ in Fig. 7. For typical VI and VR experimental designs, we have assumed that there is only a single stimulus that is continuously present. Thus, for simplicity, we set the pre-weighted input to each integrator unit to 1 throughout the course of a simulated experiment (inputs can be toggled between 1 and 0 to model cued-response experiments). After each response, we set each SR weight proportional to the current estimate of reward rate for the corresponding response. Inputs to each unit thus equal nRi(tL), where tL is the time of the previous response, so that drift is given by the following:
| (22) |
Again, we have assumed adaptation of Ri(t) in continuous time by Eq. 7, but discrete updating of the weight based on the current Ri value at the time of each response, as in Eq. 6. This approach ensures stationary drift rates during a single response, which is necessary in order for Eqs. 3-4 specifying expected choice proportions and response times to be exact. Nevertheless, these results are still approximately correct even if we continuously adapt the weights, as long as reward rate estimates do not change too rapidly during the preparation of individual responses. In this respect, weights as well as units have the exponential decay property of a capacitor or leaky integrator, which is a feature of a number of synaptic plasticity models (Hertz et al., 1991).
2.3.4 Threshold adjustment by RO weights
A threshold can be implemented by a low-pass filter unit with a sigmoidal activation function if the unit's output is fed back into itself through a sufficiently strong recurrent connection wii (i.e., wii > λ/4 in Eq. 18). As in the model of Wilson and Cowan (1972), such units develop bistability and hysteresis as self-excitation is increased (see Fig. 8E). In contrast, linear units become unstable and blow up to infinity when self-excitation is strong enough; a squashing function, however, traps such an explosive process against a ceiling.
Because of this behavior, strongly self-exciting units can function as threshold-crossing detectors and response-triggers: below a critical level of input, their output is near 0 (i.e., the value of approximately 0.3 labeled ‘Threshold’ on the Input axis in Fig. 8E); above the critical input level, output jumps like an action potential, to nearly the highest possible value. Once activated, a threshold unit then displays hysteresis, remaining at a high output level for some period of time even if inputs decrease.
Response-trigger units therefore implement energy barriers that accumulated evidence or preference must surmount in order to generate a punctate response. This is ideal behavior for a circuit element that makes an all-or-none decision about whether to initiate a sequence of muscle contractions. The activation of such a response-trigger varies continuously, as we should expect from any plausible model of a physical mechanism. Nevertheless, at all times other than when input signals have recently exceeded threshold, response-trigger outputs are far from the levels needed to contract muscles. Furthermore, this hysteresis property can be used to control the emission of ‘packets’ of multiple, rapid responses, rather than the individual responses on which we have so far focused attention: as long as a trigger's output is high, a fast oscillator can be toggled on by the response-trigger output to produce high-rate responding. Such packets of high-rate responding are often observed in conditioning experiments (e.g., Church, Meck, & Gibbon, 1994).
These properties are important for a physical implementation of thresholds. For ease of analysis, though, thresholds can still be modeled with sufficient accuracy to predict behavior as simple step functions. The critical level of input necessary to cause a response-trigger unit to transition between the low- and high-activation states (about 0.3 in Fig. 8E) can be considered to be a simple threshold applied to integrator outputs. This fact makes threshold adaptation easy to understand: from the perspective of an integrator unit (one of the bottom units in the network diagrams of Fig. 7 and Fig. 8), this threshold Z is reduced by m if an amount m of additional excitation is supplied to the threshold unit on top of the excitation provided by the integrator. Similarly, if the excitatory weight connecting an integrator to a threshold unit with threshold Z is multiplied by γ, then the effective threshold for the integrator becomes Z/γ.
Therefore, by multiplying the RO weights by an estimate of reward rate for the corresponding response, Ri, our threshold adaptation algorithm can be directly implemented. The only remaining issue stems from the fact that the effective DDM threshold θi is an affine function of the absolute firing rate threshold Z (Eq. 21). In order to make θi inversely proportional to Ri, we must cancel the additive term by adding (I1 +I2)/4. We can do this simply by inhibiting the response-trigger units by exactly this amount. This need to cancel motivates our use of a collector of diffuse, excitatory input to provide pooled inhibition to both response triggers (see the middle unit in the network of Fig. 7). Bogacz and Gurney (2007) similarly used diffuse, pooled inhibition to generalize a neural implementation of the DDM to an asymptotically optimal statistical test for more than two decision making alternatives; Frank (2006) used pooled inhibition to implement inhibitory control; and Wang (2002) used it simply to implement a biologically realistic form of lateral inhibition between strictly excitatory units.
3. Discussion
We have analyzed an implementation of melioration by an adaptive drift-diffusion model. Adaptation is achieved by estimating the rate of reward earned for a response through a process of leaky integration of reward impulses; reward rate estimates then weight the input signals to a choice process implemented by a competitive neural network with a bistable output layer. Weighting signals by reward-rate amounts to adapting the threshold (Model 1) and drift (Model 2) of the DDM, which is implemented by the neural choice network when the network's lateral, inhibitory weights balance the ‘leakiness’ of the leaky integration in its input layer (Bogacz et al., 2006). Diffusive noise in processing then leads to random behavior that can serve the purpose of exploration.
Our attempt to blend operant conditioning theory and cognitive reaction time theory has historical antecedents in the work of researchers in the behaviorist tradition (Davison & Tustin, 1978; Davison & McCarthy, 1988; Nevin, Jenkins, Whittaker, & Yarensky, 1982) who have linked operant conditioning principles with signal detection theory (SDT; Green & Swets, 1966). Indeed, SDT is ripe for such an interpretation, given its reliance on incentive structures to investigate humans’ low-level signal processing capabilities. Our work is part of a natural extension of that approach into decision making that takes place over time, producing RT/IRT data which is not normally considered in SDT.
In addition to serving as a bridge between melioration and a possible neural implementation, the adaptive DDM makes quantitative predictions about inter-response times as well as choice probabilities in operant conditioning experiments with animal subjects, and economic game experiments with human subjects. Response times and inter-response times are a valuable dependent variable in such tasks that can help to elucidate the mechanisms underlying choice. Indeed, although choice-RT and IRT data in concurrent tasks seem to have received less attention than response proportions in the animal behavior literature, RT and IRT data have occasionally been used to distinguish between alternative models of operant conditioning (e.g., Blough, 2004; Davison, 2004). Data from both of these articles included long-tailed RT/IRT distributions that appear log-normal or ex-Gaussian — approximately the shape predicted by the DDM. Blough (2004) specifically fit RT distributions with a DDM and found better evidence for adaptation of drift as a function of reward rate rather than of threshold. In addition, monkey RT data and neural firing rate data from the motion discrimination, reaction-time experiment of Roitman and Shadlen (2002) have been taken to support both the DDM and neural integrators of the type we have discussed as models of decision making (cf. Gold & Shadlen, 2001).
In a replication of the human economic game experiment of Egelman et al. (1998) and Montague and Berns (2002), Bogacz et al. (2007) found clear evidence of an RT effect as a function of an enforced delay between opportunities to respond. As the delay interval grew, mean RT also grew. For delays of 0 msec, 750 msec and 2000 msec, average inter-choice times (including the enforced delay) were 766 msec, 1761 msec and 3240 msec respectively. This corresponds to average RTs of 766 msec, 1011 msec, and 1240 msec respectively. This is a profound effect on RT by an independent variable — enforced inter-trial delay — that had no obvious effect on relative reward rates or observed choice probabilities, and is therefore completely outside the scope of models of behavioral reallocation such as melioration. Bogacz et al. (2007) gave a compelling account of choice probabilities in this task in terms of a drift-adaptive DDM with reward rates updated only after each response,9 but fits of that model did not take RT data into account and produced parameters for which RTs must be greater than those observed. When we examined the performance of a threshold-adaptive, zero-drift diffusion model with similarly discrete reward-rate updates in this task,10 it achieved fast enough RTs but exhibited a tendency toward exclusive preference for one or the other response that was not observed in the data. Thus, it seems likely that combining threshold and drift adaptation and/or including an adaptive timing mechanism would give a significantly better fit to choice and RT data taken together. In addition, the delay-dependent RT results of Bogacz et al. (2007) appear to call for a version of the adaptive DDM in which internal estimates of reward rate decay during the delay period (as in Eq. 7) and concomitantly, drift decreases and/or thresholds increase.
Both the adaptive-drift and adaptive-threshold versions of the DDM predict that RTs and IRTs must be longer for the less preferred choice in a two-choice task, and this qualitative relationship is seen in both animal and human behavioral data (Blough, 2004; Busemeyer & Townsend, 1993; Petrusic & Jamieson, 1978). We take these and other behavioral results as strong evidence that adaptive random walk models may provide an account of dynamical choice behavior on a trial-by-trial level that is furthermore explicit in the following sense: as an SDE, it specifies the state of the choice process from moment to moment.
This explicit character of diffusion-implemented melioration lends itself naturally to theorizing about the physical mechanisms underlying choice. In addition to efforts in theoretical behaviorism, much recent empirical and theoretical work in neuroeconomics has been devoted to understanding these mechanisms. In particular, a variety of explicitly neural models of choice in response to changing reward contingencies have been proposed (e.g., Grossberg & Gutowski, 1987; Montague & Berns, 2002; Soltani & Wang, 2006). Most share a common structure: input weights leading into a competitive network are modified in response to reward inputs, leading to choice probabilities that are a logistic/softmax or otherwise sigmoidal function of the difference between input weight strengths (and thus of the difference between expected reward values). A key distinction of the neurally implemented threshold-adaptive DDM (Model 1) is that it includes reward-modulated weights at a later, output stage of processing in the network, and can thereby formally achieve exact matching. In its location of reward-modulated synaptic weights, this model is structurally similar to the more abstract neural model in Loewenstein and Seung (2006), whose synaptic strengths are modified by a more general (but probably more slowly changing) process that acts to reduce the covariance of reward and response, and which can also achieve exact matching in tasks not involving continuous time (VI tasks, for example, do not appear to be within the scope of this covariance-reduction rule).
When choice proportions in empirical data do not clearly distinguish between input-stage and output-stage models, the best way to distinguish them (or to identify the relative contributions of input and output weights) may be to fit both choice and RT/IRT data simultaneously.
3.1. Mapping on to neuroanatomy
The model family that we have presented provides a generic template for reward-modulated decision making circuits in the brain. By positing that connection strengths are equivalent to reward-rate estimators, the model represents a theoretical view of synapses at the sensory-motor interface as leaky integrators of reward impulses. An alternative view is one in which population firing rates, rather than synaptic strengths, represent these integrated impulses (e.g., firing rates directly observed in monkey anterior cingulate cortex, Seo & Lee, 2007, and perhaps indirectly in a host of human brain imaging experiments, Rushworth, Walton, Kennerley, & Bannerman, 2004). Under the assumptions of Eq. 17, this alternative view seems more consistent with the affine threshold transformation of Simen et al. (2006) than the multiplicative weight adaptation of Models 1 and 2; however, if firing rate representations can act multiplicatively rather than additively on decision-making circuits, then a synaptic weight and a population firing-rate become functionally equivalent.
In any case, diffuse transmission of reward impulses is central to both approaches. The prominent role of the basal ganglia in reward processing and action initiation therefore suggests that reward-modulated sensory-motor connections may map onto routes through these subcortical structures. Bogacz and Gurney (2007) and Frank (2006) hypothesize that the subthalamic nucleus in the basal ganglia controls responding by supplying diffuse inhibition to all response units, and Lo and Wang (2006) also attribute control functionality to the basal ganglia in a model of saccade thresholds. Given that both the excitatory and inhibitory paths in Fig. 7 must be potentiated by reward, we speculate that the excitatory and inhibitory pathways in our model may map onto cortex and the basal ganglia as follows: SR weights correspond to cortico-cortical connections (consistent with reward-modulated firing rates observed in monkey lateral intraparietal cortex, e.g., Platt & Glimcher, 1999); RO weights correspond to direct-pathway cortico-striatal connections; and compensatory weights correspond to excitation of the indirect pathway through the basal ganglia (Alexander, De-Long, & Strick, 1986). The mapping we propose assumes that the direct pathway through the basal ganglia is parallel and segregated, but that the indirect pathway is not. Alternatively, the subthalamic nucleus may play a diffuse inhibition role here that is analagous to that proposed in Bogacz and Gurney (2007) or Frank (2006).
The multi-stage architecture of this brain circuitry lends itself to multiple-layer models. However, splitting into multiple layers and using integrator-to-threshold weights are also functionally necessary in our model, because threshold behavior (bistability and hysteresis) cannot be obtained from the drift-diffusion process itself — and without nonlinear energy barriers, any buildup of activation in decision units would produce proportional, premature movement in response actuators such as eye or finger muscles. In contrast, other neural models lump both integration and threshold functionality into a single layer of bistable units. For each response, these models implement a nonlinear stochastic process with an initially small drift, followed by a rapid increase in drift after reaching a critical activation level (e.g., Soltani & Wang, 2006; Wong & Wang, 2006). Analytical RT predictions for such models are not currently known, and it may be possible to approximate such systems with idealized two-layer models for which analytically tractable RT predictions exist. However, we were originally motivated to split the system into two layers — rather than to lump the integration and threshold functions into one layer — by the results of Bogacz et al. (2006), who argued for starting-point/threshold modulations without drift modulation in certain decision making tasks in order to maximize reward. See other arguments in favor of splitting over lumping in Schall (2004). Nevertheless, lumping layers together clearly cannot be ruled out, and a single-layer model seems more economical in resources and more parsimonious in parameters than a two-layer model.
In general, the additional layer in our model might earn its keep in at least two ways:
It might help to earn greater reward: using extra degrees of freedom may allow a closer approach to exact matching than is possible with single-layer models that produce a sigmoid choice probability function (e.g. Montague & Berns, 2002; Soltani & Wang, 2006). Strict matching amounts to balancing the rate of returns on competing behaviors precisely, and this often leads to near-maximization in contexts with diminishing marginal returns (Williams, 1988). Sigmoid choice functions can only approximate this precise balance.
If the two layers of weights have different time scales of adaptation, it might alleviate the problem of multiple time scales in which a stimulus (e.g., the look, sound or smell of a Skinner box) predicts an average reward level that changes slowly over time, whereas specific response-outcome contingencies within that environment might change rapidly. Furthermore, if SR mappings are difficult to learn, then it might be easier to preserve them in the face of rapidly changing RO contingencies if those contingencies are encoded in a second set of RO weights with greater plasticity.
An experiment that could help to distinguish between multiple-stage and single-stage models would be one in which reinforcement was contingent on a stimulus-response mapping (e.g., the colored-light/saccade-target pairing in Corrado et al., 2005 and Lau & Glimcher, 2005), but in which the stimulus was correlated with the response. For example, the frequency with which the better-rewarded red target appeared at, say, 0° of visual angle, as opposed to 180° , could be manipulated. Suppose that red has recently appeared at 0° many times, and has frequently been chosen and rewarded. Now red appears at 180°. If a bias toward 0° saccades persists, then that might be interpreted as evidence for an RO encoding separate from an SR encoding, whereas absence of bias would be evidence against it.
3.2. Stochastic behavior
We have presented a model that is fundamentally stochastic. However, it seems perfectly reasonable to assume, on the contrary, that fully deterministic processes underlie choice behavior, and that the research goal of linking psychological and neuroscientific approaches to the study of decision making is best served by deterministic theoretical models. We are agnostic on this point: stochastic models may serve merely as useful compressions of vastly elaborate deterministic processes into a few, simple, stochastic differential equations (consider the enormous value of statistical mechanical concepts like temperature and pressure, even within the classical, deterministic physics of the eighteenth century); or the stochastic aspect of our model may represent behavioral-level effects of fundamental quantum randomness at the level of synapses (discussed, e.g., in Glimcher, 2005). It is clear though that random behavior can indeed be adaptive, since much of life involves competition between agents that are capable of modeling each other's intentions; game theoretic results indicate that random behavior is optimal in many such circumstances (Nash, 1950; Von Neumann & Morgenstern, 1944). See recent accounts of behavior that, in accord with these results, is indistinguishable from truly stochastic performance (Barraclough, Conroy, & Lee, 2004; Busemeyer & Townsend, 1993; Neuringer, Jensen, & Piff, 2007) and a review of these in Glimcher (2005), as well as arguments based on parallels between the Darwinian evolution of organisms and the mutation and selection of behaviors within an organism (e.g., Staddon, 2001).
We note also that the concept of internally-generated noise is consistent with theories that specifically address the tradeoff between the exploration of new behaviors and the exploitation of old, successful behaviors. These theories (Aston-Jones & Cohen, 2005; Cohen, McClure, & Yu, 2007; McClure, Gilzenrat, & Cohen, 2006) address the tradeoff in terms of brain mechanisms and neuromodulators. With more noise comes a greater chance of choosing options that have not been recently rewarded; indeed, without some means of trying new behaviors, operant reward contingencies can never be discovered in the first place. According to one theory of the functional role of norepinephrine (NE) in the brain (Aston-Jones & Cohen, 2005), NE transmission causes a receiving neuron to steepen its firing-rate/input (FI) curve in the approximately linear region of the curve. In the case of units with a sigmoid activation function, gain increases can serve to lower effective response thresholds (Cohen et al., 1990) and improve performance in a chain of linked units (Servan-Schreiber, Printz, & Cohen, 1990). Gain increases in linear units with noisy inputs also lead to greater noise in a unit's outputs, so that a mechanism for noise amplification may arise from the action of NE on cortical neurons. A complementary mechanism for noise reduction is an inescapable consequence of leaky integration, which is frequently hypothesized as a function of populations of neurons (Shadlen & Newsome, 1998; Usher & McClelland, 2001).
In fact, matching and melioration amount to making a very specific exploration/exploitation tradeoff that approximately maximizes reward in a variety of experimental paradigms (Williams, 1988). A corollary of the matching law is that animals allocate their investments in behavior (e.g., lever presses or keypecks per second) in such a way that the returns on those investments (e.g., food pellets earned per keypeck) are equal:
| (23) |
This property makes melioration particularly well suited to environments in which reward contingencies are dynamic, and this is always the case when there are diminishing returns for persistent behavior (e.g., foraging in a location with finite resources). In the exploration/exploitation tradeoff specified by matching, more rewarding responses are produced more frequently, but less rewarding responses are also sampled with a frequency proportionate to their expected value, so that unexpected increases in their value can be detected. What the additional parameters of the adaptive DDM allow is a range of similar tradeoffs that provide the same responsiveness to dynamic contingencies, and that include matching as a special case.
It is worth noting, however, that in many specific tasks, matching and melioration do not produce optimal performance. Fig. 6E is a case in point. Here, melioration's equilibrium choice allocation of roughly 80% Left responses — the matching point at the intersection of the two reward schedule lines — produces a lower expected reward percentage than what could be obtained with 50% Left responses. Indeed, this property of melioration makes it suitable as a theory of behavior that is usually adaptive, but that also includes such obviously suboptimal patterns as addiction (Herrnstein & Prelec, 1991, 1997).
We have shown that diffusive noise in a neural network is sufficient to produce implementations of classic models of conditioning and simple decision making that have been used to explain a wealth of behavioral data, and increasingly, neurophysiological data. Given that noise is potentially so useful, that it is in plentiful supply in the form of thermal energy in the brain, and that the mechanisms needed to amplify and attenuate it can be so simple, we speculate that properly generating, managing and using ‘noise’ may be a central feature of brain function.
3.3 More than two alternatives
The analytical expressions that we have used for the choice probability and response time of the DDM (Eqs. 3-4) are known only for two-alternative tasks; choice probabilities and expected response times (hence response rates) in tasks involving three or more alternatives are solutions of partial differential equations for which there appear to be no known, closed form solutions (Gardiner, 2004). We have numerically simulated three and four dimensional diffusion processes with 0 drift and thresholds inversely proportional to reward rates. Such processes are again the abstract equivalent of processing in a leaky competing accumulator network with more than two channels (McMillen & Holmes, 2006). Interestingly, in dimensions three and greater, exact matching does not seem to be the equilibrium state even for the adaptive-threshold, zero-drift diffusion model (Model 1), which produces exact matching in two dimensions. Instead, overmatching appears to be the inevitable result: choices producing more than the average amount of reward are selected with a frequency that is greater than predicted, and choices producing less than the average are less frequently selected.
However, the generality of the matching law implied by Eq. 1 for arbitrary numbers of response alternatives is questionable, since experiments with animals involving three or more responses appear to be rare (indeed, even in two-alternative tasks, violations of the strict matching law are frequent enough to motivate the use of the generalized matching law). At the very least, they are vastly outnumbered by studies involving only two responses (note the absence of references to such work in comprehensive reviews such as Davison & McCarthy, 1988, Herrnstein, 1997 and Williams, 1988). Simulations therefore suggest that, in addition to making quantitative RT and IRT predictions in operant conditioning tasks, the threshold-adaptive, zero-drift diffusion model makes a novel prediction about choice probabilities in a task design that is not well-explored: namely, that at equilibrium, overmatching should universally be the case in tasks with three or more responses.
A multi-alternative circuit of the type we have investigated can also be used to model behavior in an economic game task that has been investigated with human subjects — the n-armed bandit task. Daw et al. (2006) examined brain activity and behavior in such a task, and found that the optimal Kalman filter-based model for that task did not fit the data well — an optimal approach to reducing uncertainty about unexplored options was not observed. Once again, however, a softmax function was found to fit behavior better than the alternative choice models investigated, a result that is consistent with a diffusion model of choice. Our hope is that an n-channel version of the model we have proposed may help to explain behavior in such tasks as an n-dimensional melioration process, with an exploration/exploitation tradeoff driven largely by a process that effectively compares recent rates of return for each option. Such a model would continue to combine the abilities of classic theoretical models from the behaviorist and cognitive traditions to explain choice probabilities and response times, and of neural models to account for electrophysiological recording and imaging data from the brain.
4. Experimental Procedures
Simulations of all SDEs in the paper were done with Euler-Maruyama method (Gardiner, 2004):
| (24) |
Our choice of Δt was sufficiently small that, in most cases, at least a hundred time steps occurred for each threshold crossing of the DDM (when Δt grows larger than this, the approximation develops a considerable deviation from the behavior of the continuous process).
Figure 2.
Two examples of rate estimates in response to a regularly paced sequence of input pulses (here shown as finite-width rectangles). On the left, input pulses are widely spaced. The dashed line plots the actual rate of the pulses in pulses per second. On the right, a higher rate of pulses leads to a higher estimate, which oscillates around the true rate parameter (the dashed line). The results for two different time constants — τR = 10sec, bold; τR = 75sec, thin — are shown in both plots.
Acknowledgments
This work was supported by the National Institutes of Health through a Conte Center for Neuroscience Research grant (MH062196) and a postdoctoral NRSA training fellowship to Patrick Simen (MH080524). We also benefitted from discussion with collaborators supported by a Department of Defense Multi-disciplinary Research Program of the University Research Initiative (MURI-15). We thank an anonymous reviewer for deriving Eq.11.
Appendix A Equivalence of discrete-time system to melioration
Formally, melioration is defined in terms of a cost function, RD, that an animal always seeks to minimize by reallocating behavior (Herrnstein, 1982):
| (25) |
Here, ti is the proportion of some total time of an experiment, T , during which only behavior i is performed (0 < ti < 1). In a strictly two-alternative task, t1 = 1 – t2. Herrnstein and colleagues defined melioration in terms of proportions of time and assumed that the rate of behavior Bi (in, e.g., responses/sec) was proportional to ti, the time allocated to behavior i (in seconds): Bi = biti. Thus Eq. 25 can be reframed easily as follows:
| (26) |
Herrnstein and Vaughan (1980) described melioration verbally as involving the following: whenever RD > 0, increase t1 (which reduces R1/t1 and brings RD closer to 0). Similarly, whenever RD < 0, increase t2 (which amounts to reducing t1 since t1 + t2 = 1). This verbal statement can be formalized as a simple proportional feedback control law that attempts to minimize |RD|:
| (27) |
This differential equation can be easily transformed into a discrete-time difference equation that updates average behavioral allocations (by changing thresholds) in a punctate manner:
| (28) |
Here we show that the threshold renormalization scheme used to ensure constant response rates in section 2.1.4 produces behavior that is formally equivalent to melioration:
| (29) |
| (30) |
| (31) |
This is equivalent to saying that if RD > 0, then increase t1.
Appendix B First-passage probabilities for Model 1
Eq. 3, repeated here, gives the probability of a first-passage through the lower threshold of the DDM:
The first-passage probability of the diffusion model with zero drift (Model 1) is the limit of 〈ER〉 as the drift term A goes to 0:
Applying L'Hopital's rule gives the following:
| (32) |
We proposed a variable translation that set the starting point to 0 for every response, and moved thresholds (θi) independently of each other:
This translation along with Eq. 32 implies that the probabilities for first-passage through the upper threshold (Pθ1) and through the lower threshold (Pθ2) are:
| (33) |
Appendix C Expected first-passage time for Model 1
The expected decision time of the zero-drift diffusion model (Model 1) is obtained by computing a Taylor series expansion of Eq. 4, which gives the average decision time for the DDM, and then once again letting A go to 0:
Replacing the hyperbolic tangent function with an expression in terms of exponentials gives the following:
Now we treat the two terms in this sum separately, considering each as a function of A and taking their Taylor expansions up to second order terms:
Term 2 equals:
The limit of Term 1 as A goes to 0 is z2/c2. The limit of Term 2 as A goes to 0 is –y0/c2. This implies:
After changing variables, this gives:
| (34) |
Appendix D Individual response rate is proportional to overall response rate
The following variables denote all the relevant quantities:
RTi = expected RT for response i (decision time + T0, sec);
bi = local rate of behavior i (responses/sec) = 1/RTi;
ti = proportion of time T devoted to behavior i (unitless);
Bi = global rate of behavior i (responses/sec) = ti · bi;
T = total time in experiment (sec).
Overall response rate, , is the harmonic mean of the two individual response rates:
| (35) |
n · P(i) · RTi = ti · T is the expected amount of time devoted to behavior i.
n · = expected size of T after n responses.
The proportion of time T allocated to behavior i is given by the following approximation:
| (36) |
This in turn implies the following:
| (37) |
Footnotes
In contrast, some problematic assumptions are required before discrete-time schemes (Eq. 8) can be applied to VI tasks. These attempt to estimate reward rates in continuous time by making only discrete adjustments to an expected reward magnitude estimate after each response. To account for absolute time, then, they must assume that responses occur at a constant rate, or that in between observed responses comes a regularly paced stream of unobserved responses (as in, e.g., Bush & Mosteller, 1951). Rather than make such assumptions from the start, we have chosen to see how far we can get without them.
Although see, for example, Corrado, Sugrue, Seung, & New-some, 2005 and Lau & Glimcher, 2005 for recent applications of a constant-probability form of VI-VI design in which signal discrimination and cued responding do occur.
‘Overmatching’ is said to occur when a slight relative reward advantage results in a larger relative choice frequency than is predicted by the matching law (Davison & McCarthy, 1988).
The same argument shows that raising reward impulses to a power and multiplying one of them by a constant furthermore predicts the following generalized matching law (Baum, 1974), which is a more robust description of a wider range of behavioral data (at the cost of two additional parameters): B1/B2 = a · (R1/R2)b.
That is, relative choice frequency is less than what matching predicts for the response earning a higher rate of reward.
The IRT timer that we used to renormalize weights in Fig. 6 can also be implemented in a neural network, and its rate can be adapted by tuning a single weight (Simen, 2008).
Since dW/dt is in some sense an abuse of notation, we will use the standard SDE notation in which dW appears by itself and is interpreted in terms of the Ito calculus (Gardiner, 2004).
When wlateral does not equal 1 and the accumulator network is unbalanced, the system implements an OU process as in Eq. 19. OU models of decision making are also prominent in the response-time literature (Usher & McClelland, 2001). If the lateral inhibition is less than 1, then the feedback coefficient multiplied by yi is negative, as in Eq. 19, and the expected value of the process approaches an asymptotic value (if lateral inhibition is 0, then the model approximates a race model, e.g., Vickers, 1970). If the lateral inhibition is greater than 1, then the feedback coefficient (call it a), is positive, and the process tends to blow up to positive or negative infinity. In both cases, if the drift term (I in Eq.19) is 0, then the choice probability function is a scaled error function (erf), or cumulative Gaussian (Bogacz et al., 2006; Moehlis, Brown, Bogacz, Holmes, & Cohen, 2004), and the choice proportion ratio is: . A cumulative Gaussian is a sigmoid function much like the logistic, and with α > 0, the explosiveness of the process tends to mitigate (though not eliminate) the threshold blowup problem faced by Model 1 (this problem is worsened with a stable OU process, α < 0). This partial solution is equivalent to thresholds that collapse toward 0 over time (e.g., Ditterich, 2006). Thus, the more general class of OU models are also promising as implementations of approximate melioration.
Importantly, their model also included an accumulating eligibility trace (Sutton & Barto, 1998), which is a method for crediting a part of each reward to every response, in proportion to the relative rate of that response.
We also included an eligibility trace in these simulations.
References
- Alexander GE, DeLong MR, Strick PL. Parallel organization of functionally segregated circuits linking basal ganglia and cortex. Annual Review of Neuroscience. 1986;9:357–381. doi: 10.1146/annurev.ne.09.030186.002041. [DOI] [PubMed] [Google Scholar]
- Aston-Jones G, Cohen JD. An integrative theory of locus coeruleus-norepinephrine function: adaptive gain and optimal performance. Annual Review of Neuroscience. 2005;28:403–450. doi: 10.1146/annurev.neuro.28.061604.135709. [DOI] [PubMed] [Google Scholar]
- Barraclough DJ, Conroy ML, Lee D. Prefrontal cortex and decision making in a mixed-strategy game. Nature Neuroscience. 2004;7(4):404–410. doi: 10.1038/nn1209. [DOI] [PubMed] [Google Scholar]
- Baum WA. On two types of deviation from the matching law: bias and undermatching. Journal of the Experimental Analysis of Behavior. 1974 July;22(1):231–242. doi: 10.1901/jeab.1974.22-231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blough D. Reaction time signatures of discriminative processes: differential effects of stimulus similarity and incentive. Learning and Behavior. 2004;32(2):157–172. doi: 10.3758/bf03196017. [DOI] [PubMed] [Google Scholar]
- Bogacz R, Brown E, Moehlis J, Holmes P, Cohen JD. The physics of optimal decision making: a formal analysis of models of performance in two-alternative forced choice tasks. Psychological Review. 2006;113(4):700–765. doi: 10.1037/0033-295X.113.4.700. [DOI] [PubMed] [Google Scholar]
- Bogacz R, Gurney K. The basal ganglia and cortex implement optimal decision making between alternative actions. Neural Computation. 2007;19:442–477. doi: 10.1162/neco.2007.19.2.442. [DOI] [PubMed] [Google Scholar]
- Bogacz R, McClure SM, Li J, Cohen JD, Montague PR. Short-term memory traces for action bias in human reinforcement learning. Brain Research. 2007;1153:111–121. doi: 10.1016/j.brainres.2007.03.057. [DOI] [PubMed] [Google Scholar]
- Busemeyer JR, Townsend JT. Fundamental derivations from decision field theory. Mathematical Social Sciences. 1992;23(3):255–282. [Google Scholar]
- Busemeyer JR, Townsend JT. Decision field theory: a dynamic-cognitive approach to decision making in an uncertain environment. Psychological Review. 1993;100(3):432–459. doi: 10.1037/0033-295x.100.3.432. [DOI] [PubMed] [Google Scholar]
- Bush RR, Mosteller F. A mathematical model for simple learning. Psychological Review. 1951;58(5):313–323. doi: 10.1037/h0054388. [DOI] [PubMed] [Google Scholar]
- Church R, Meck W, Gibbon J. Application of scalar timing theory to individual trials. Journal of Experimental Psychology: Animal Behavior Processes. 1994;20:135–155. doi: 10.1037//0097-7403.20.2.135. [DOI] [PubMed] [Google Scholar]
- Cohen JD, Dunbar K, McClelland JL. On the control of automatic processes: a parallel distributed processing account of the stroop effect. Psychological Review. 1990;97(3):332–361. doi: 10.1037/0033-295x.97.3.332. [DOI] [PubMed] [Google Scholar]
- Cohen JD, McClure SM, Yu AJ. Should I stay or should I go? How the human brain manages the trade-off between exploitation and exploration. Philosophical Transactions of the Royal Society B. 2007;362:933–942. doi: 10.1098/rstb.2007.2098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corrado GS, Sugrue LP, Seung HS, Newsome WT. Linear-nonlinear-poisson models of primate choice dynamics. Journal of the Experimental Analysis of Behavior. 2005;84(3):581–617. doi: 10.1901/jeab.2005.23-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davison M. Interresponse times and the structure of choice. Behavioral Processes. 2004;66:173–187. doi: 10.1016/j.beproc.2004.03.003. [DOI] [PubMed] [Google Scholar]
- Davison M, McCarthy D. The matching law: a research review. Lawrence Erlbaum Associates; Hillsdale, N.J.: 1988. [Google Scholar]
- Davison M, Tustin RD. The relation between the generalized matching law and signal-detection theory. Journal of the Experimental Analysis of Behavior. 1978;29:331–336. doi: 10.1901/jeab.1978.29-331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daw ND, O'Doherty JP, Dayan P, Seymour B, Dolan RJ. Cortical substrates for exploratory decisions in humans. Nature. 2006;441:876–879. doi: 10.1038/nature04766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Villiers PA, Herrnstein RJ. Toward a law of response strength. Psychological Bulletin. 1976;83(6):1131–1153. [Google Scholar]
- Ditterich J. Stochastic models of decisions about motion direction: behavior and physiology. Neural Networks. 2006;19:981–1012. doi: 10.1016/j.neunet.2006.05.042. [DOI] [PubMed] [Google Scholar]
- Egelman DM, Person C, Montague PR. A computational role for dopamine delivery in human decision making. Journal of Cognitive Neuroscience. 1998;10(5):623–630. doi: 10.1162/089892998563022. [DOI] [PubMed] [Google Scholar]
- Ferster CB, Skinner BF. Schedules of reinforcement. Appleton-Century-Crofts; New York: 1957. [Google Scholar]
- Frank MJ. Hold your horses: A dynamic computational role for the subthalamic nucleus in decision making. Neural Networks. 2006 October;19(8):1120–1136. doi: 10.1016/j.neunet.2006.03.006. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Mark TA, King A, Latham P. The rat approximates an ideal detector of changes in rates of reward: implications for the Law of Effect. Journal of Experimental Psychology: Animal Behavior Processes. 2001;27:354–372. doi: 10.1037//0097-7403.27.4.354. [DOI] [PubMed] [Google Scholar]
- Gardiner CW. Handbook of stochastic methods. Third ed. Springer-Verlag; New York, NY: 2004. [Google Scholar]
- Gerstner W. Population dynamics of spiking neurons: fast transients, asynchronous states, and locking. Neural Computation. 1999;12:43–89. doi: 10.1162/089976600300015899. [DOI] [PubMed] [Google Scholar]
- Glimcher PW. Indeterminacy in brain and behavior. Annual Review of Psychology. 2005;56:25–56. doi: 10.1146/annurev.psych.55.090902.141429. [DOI] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN. Neural computations that underlie decisions about sensory stimuli. Trends in Cognitive Science. 2001;5(1):10–16. doi: 10.1016/s1364-6613(00)01567-9. [DOI] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN. Banburismus and the brain: decoding the relationship between sensory stimuli, decisions, and reward. Neuron. 2002;36(2):299–308. doi: 10.1016/s0896-6273(02)00971-6. [DOI] [PubMed] [Google Scholar]
- Green DM, Swets JA. Signal detection theory and psychophysics. Wiley; New York: 1966. [Google Scholar]
- Grossberg S. On the dynamics of operant conditioning. Journal of Theoretical Biology. 1971;33:225–255. doi: 10.1016/0022-5193(71)90064-6. [DOI] [PubMed] [Google Scholar]
- Grossberg S. A psychophysiological theory of reinforcement, drive, motivation and attention. Journal of Theoretical Neurobiology. 1982;1:286–369. [Google Scholar]
- Grossberg S. Nonlinear neural networks: principles, mechanisms, and architectures. Neural Networks. 1988;1:17–61. [Google Scholar]
- Grossberg S, Gutowski W. Neural dynamics of decision making under risk: affective balance and cognitive-emotional interactions. Psychological Review. 1987;94(3):300–318. [PubMed] [Google Scholar]
- Herrnstein RJ. Relative and absolute strength of responses as a function of frequency of reinforcement. Journal of the Experimental Analysis of Behavior. 1961;4:267–272. doi: 10.1901/jeab.1961.4-267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrnstein RJ. Melioration as behavioral dynamism. In: Commons ML, Herrnstein RJ, Rachlin H, editors. Quantitative analyses of behavior. Vol. II: Matching and maximizing accounts. Ballinger; Cambridge, MA: 1982. [Google Scholar]
- Herrnstein RJ. In: The matching law: papers in psychology and economics. Rachlin H, Laibson DI, editors. Harvard University Press; Cambridge, MA: 1997. [Google Scholar]
- Herrnstein RJ, Prelec D. Melioration: a theory of distributed choice. Journal of Economic Perspectives. 1991;5:137–156. [Google Scholar]
- Herrnstein RJ, Prelec D. A theory of addiction. In: Rachlin H, Laibson DI, editors. The matching law: papers in psychology and economics. Russell Sage Foundation and Harvard University Press; Cambridge, MA: 1997. pp. 160–187. [Google Scholar]
- Herrnstein RJ, Vaughan WJ. Melioration and behavioral allocation. In: Staddon J, editor. Limits to action: The allocation of individual behavior. Academic Press; New York: 1980. [Google Scholar]
- Hertz J, Krogh A, Palmer RG. Introduction to the theory of neural computation. 1. Addison Wesley; Redwood City, CA: 1991. (Vol. Lecture Notes Volumes) [Google Scholar]
- Killeen PR. Principles of reinforcement. Behavioral and Brain Sciences. 1994;17(1):105–172. [Google Scholar]
- Lau B, Glimcher PW. Dynamic response-by-response models of matching behavior in rhesus monkeys. Journal of the Experimental Analysis of Behavior. 2005 November;84(3):555–579. doi: 10.1901/jeab.2005.110-04. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lo C-C, Wang X-J. Cortico-basal ganglia circuit mechanism for a decision threshold in reaction time tasks. Nature Neuroscience. 2006;9(7):956–963. doi: 10.1038/nn1722. [DOI] [PubMed] [Google Scholar]
- Loewenstein Y, Seung HS. Operant matching is a generic outcome of synaptic plasticity based on the covariance between reward and neural activity. Proceedings of the National Academy of Sciences U S A. 2006 October;103(41):15224–15229. doi: 10.1073/pnas.0505220103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luce RD. Response times: their role in inferring elementary mental organization. Oxford University Press; New York: 1986. [Google Scholar]
- McClure SM, Gilzenrat MS, Cohen JD. An exploration-exploitation model based on norepinephrine and dopamine activity. In: Weiss Y, Scholkopf B, Platt J, editors. Advances in neural information processing. Vol. 18. MIT Press; Cambridge, MA: 2006. pp. 867–874. [Google Scholar]
- McMillen T, Holmes P. The dynamics of choice among multiple alternatives. Journal of Mathematical Psychology. 2006;50:30–57. [Google Scholar]
- Moehlis J, Brown E, Bogacz R, Holmes P, Cohen JD. Optimizing reward rate in two alternative choice tasks: mathematical formalism. Center for the Study of Brain, Mind and Behavior, Princeton University; 2004. (Tech. Rep. No. 04−01) [Google Scholar]
- Montague PR, Berns GS. Neural economics and the biological substrates of valuation. Neuron. 2002 October;36:265–284. doi: 10.1016/s0896-6273(02)00974-1. [DOI] [PubMed] [Google Scholar]
- Nash J. Equilibrium points in n-person games. Proceedings of the National Academy of Sciences U S A. 1950;36:48–49. doi: 10.1073/pnas.36.1.48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuringer A, Jensen G, Piff P. Stochastic matching and the voluntary nature of choice. Journal of the Experimental Analysis of Behavior. 2007;88:1–28. doi: 10.1901/jeab.2007.65-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevin JA, Jenkins P, Whittaker S, Yarensky P. Reinforcement contingencies and signal detection. Journal of the Experimental Analysis of Behavior. 1982;37:65–79. doi: 10.1901/jeab.1982.37-65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oppenheim AV, Willsky AS. Signals and systems. Second ed. Prentice Hall; New York, NY: 1996. [Google Scholar]
- Petrusic WM, Jamieson DG. Relation between probability of preferential choice and time to choose changes with practice. Journal of Experimental Psychology: Human Perception and Performance. 1978;4(3):471–482. [Google Scholar]
- Platt ML, Glimcher PW. Neural correlates of decision variables in parietal cortex. Nature. 1999;400:6741, 233–238. doi: 10.1038/22268. [DOI] [PubMed] [Google Scholar]
- Posner MI. Chronometric explorations of mind. Lawrence Erlbaum Associates; Hillsdale, N.J.: 1978. [Google Scholar]
- Ratcliff R. A theory of memory retrieval. Psychological Review. 1978;85:59–108. [Google Scholar]
- Ratcliff R, Tuerlinckx F. Estimating parameters of the diffusion model: approaches to dealing with contaminant reaction times and parameter variability. Psychonomic Bulletin and Review. 2002;9(3):438–481. doi: 10.3758/bf03196302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson DA. Integrating with neurons. Annual Review of Neuroscience. 1989;12:33–45. doi: 10.1146/annurev.ne.12.030189.000341. [DOI] [PubMed] [Google Scholar]
- Roe RM, Busemeyer JR, Townsend JT. Multialter-native decision field theory: a dynamic connectionist model of decision making. Psychological Review. 2001;108(2):370–392. doi: 10.1037/0033-295x.108.2.370. [DOI] [PubMed] [Google Scholar]
- Roitman JD, Shadlen MN. Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. Journal of Neuroscience. 2002;22:21, 9475–9489. doi: 10.1523/JNEUROSCI.22-21-09475.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rushworth MFS, Walton ME, Kennerley SW, Banner-man DM. Action sets and decisions in the medial prefrontal cortex. Trends in Cognitive Science. 2004;8(9):410–417. doi: 10.1016/j.tics.2004.07.009. [DOI] [PubMed] [Google Scholar]
- Sakai Y, Fukai T. The actor-critic learning is behind the matching law: matching versus optimal behaviors. Neural Computation. 2008;20:227–251. doi: 10.1162/neco.2008.20.1.227. [DOI] [PubMed] [Google Scholar]
- Schall JD. On building a bridge between brain and behavior. Annual Review of Psychology. 2004;55:23–50. doi: 10.1146/annurev.psych.55.090902.141907. [DOI] [PubMed] [Google Scholar]
- Seo H, Lee D. Temporal filtering of reward signals in the dorsal anterior cingulate cortex during a mixed-strategy game. Journal of Neuroscience. 2007;27(31):8366–8377. doi: 10.1523/JNEUROSCI.2369-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Servan-Schreiber D, Printz H, Cohen JD. A network model of catecholamine effects: gain, signal-to-noise ratio, and behavior. Science. 1990 August;249:892–895. doi: 10.1126/science.2392679. [DOI] [PubMed] [Google Scholar]
- Seung HS. Amplification, attenuation and integration. In: Arbib MA, editor. The handbook of brain theory and neural networks. MIT Press; Cambridge, MA: 2003. pp. 94–97. [Google Scholar]
- Seung HS, Lee DD, Reis BY, Tank DW. The autapse: a simple illustration of short-term analog memory storage by tuned synaptic feedback. Journal of Computational Neuro-science. 2000;9:171–185. doi: 10.1023/a:1008971908649. [DOI] [PubMed] [Google Scholar]
- Shadlen MN, Newsome WT. The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. Journal of Neuroscience. 1998;18(10):3870–3896. doi: 10.1523/JNEUROSCI.18-10-03870.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simen P. Ramping, ramping everywhere: an overlooked model of interval timing. COSYNE abstracts. 2008 [Google Scholar]
- Simen P, Cohen JD, Holmes P. Rapid decision threshold modulation by reward rate in a neural network. Neural Networks. 2006;19:1013–1026. doi: 10.1016/j.neunet.2006.05.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith PL, Ratcliff R. Psychology and neurobiology of simple decisions. Trends in Neuroscience. 2004;27:161–168. doi: 10.1016/j.tins.2004.01.006. [DOI] [PubMed] [Google Scholar]
- Soltani A, Wang XJ. A biophysically based neural model of matching law behavior: melioration by stochastic synapses. Journal of Neuroscience. 2006;26(14):3731–3744. doi: 10.1523/JNEUROSCI.5159-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Staddon JER. The new behaviorism. Psychology Press; Philadelphia, PA: 2001. [Google Scholar]
- Staddon JER, Higa J. Multiple time scales in simple habituation. Psychological Review. 1996;103:720–733. doi: 10.1037/0033-295x.103.4.720. [DOI] [PubMed] [Google Scholar]
- Sugrue LP, Corrado GS, Newsome WT. Matching behavior and the representation of value in the parietal cortex. Science. 2004;304:1782–1787. doi: 10.1126/science.1094765. [DOI] [PubMed] [Google Scholar]
- Sutton RS, Barto AG. Reinforcement learning. MIT Press; Cambridge, MA: 1998. [Google Scholar]
- Usher M, McClelland JL. The time course of perceptual choice: the leaky, competing accumulator model. Psychological Review. 2001;108(3):550–592. doi: 10.1037/0033-295x.108.3.550. [DOI] [PubMed] [Google Scholar]
- Vaughan WJ. Melioration, matching, and maximization. Journal of the Experimental Analysis of Behavior. 1981 September;36(2):141–149. doi: 10.1901/jeab.1981.36-141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vickers D. Evidence for an accumulator model of psychophysical discrimination. Ergonomics. 1970;13:37–58. doi: 10.1080/00140137008931117. [DOI] [PubMed] [Google Scholar]
- Von Neumann JV, Morgenstern O. Theory of games and economic behavior. Princeton University Press; Princeton, N.J.: 1944. [Google Scholar]
- Wang XJ. Probabilistic decision making by slow reverberation in cortical circuits. Neuron. 2002;36(5):955–968. doi: 10.1016/s0896-6273(02)01092-9. [DOI] [PubMed] [Google Scholar]
- Williams BA. Reinforcement, choice, and response strength. In: Atkinson RC, Herrnstein RJ, Lindzey G, Luce RD, editors. Stevens’ handbook of experimental psychology: Vol. 2. learning and cognition. Vol. 2. Wiley; New York: 1988. pp. 167–244. [Google Scholar]
- Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophysical Journal. 1972;12:1–24. doi: 10.1016/S0006-3495(72)86068-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong KF, Wang XJ. A recurrent network mechanism of time integration in perceptual decisions. Journal of Neuroscience. 2006;26(4):1314–1328. doi: 10.1523/JNEUROSCI.3733-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang T, Hanks T, Mazurek ME, McKinley M, Palmer J, Shadlen MN. Incorporating prior probability into decision-making in the face of uncertain reliability of evidence. Society for Neuroscience abstracts. 2005 [Google Scholar]