Theoretical Calculation of Electronic Circular Dichroism of a Hexahydroxydiphenoyl-containing Flavanone Glycoside

Abstract

Time-dependent density functional theory (TDDFT) was employed for theoretical calculation of electronic circular dichroism (ECD) of a hexahydroxydiphenoyl (HHDP)-containing flavanone glycoside, mattucinol-7-O-[4″,6″-O-(aS)-hexahydroxydiphenoyl]-β-d-glucopyranoside (2). It identified the roles of the (2S)-flavanone and (aS)-HHDP moieties in generating the ECD spectrum of 2, and provided theoretical evidence for the empirical ECD rules applicable to monomeric flavanones and HHDP-containing compounds. The experimentally observed high-amplitude positive Cotton effect (CE) around 240 nm in 2 is derived from the (aS)-HHDP chromophore, while the low-amplitude negative CE in the 260–300 nm region is contributed by both the (aS)-HHDP and (2S)-flavanone moieties. The “linker” glucosyl moiety has little effect on the overall ECD. It appears that the respective chromophores in 2 contribute additively to the overall ECD and the empirical rules are applicable for configurational assignment. However, if an (aR)-HHDP chromophore is present as shown in mattucinol-7-O-[4″,6″-O-(aR)-hexahydroxydiphenoyl]-β-d-glucopyranoside (3), the dominant role of the (aR)-HHDP and interaction between the (aR)-HHDP and (2S)-flavanone moieties to its overall ECD may be confusing when applying the empirical rules to experimental ECD interpretation. Thus, theoretical calculation of the ECD that quantifies the contributions and interactions of different chromophores is essential for the assignment of the absolute configuration of such molecules.

After investigating a large number of chiroptically active flavonoids, Gaffield¹ concluded that flavanones of 2S configuration and dihydroflavonols of 2R,3R configuration exhibit a positive Cotton effect (CE) due to the n→π* transition (~330 nm) and a negative CE in the π→π* region (~ 280–290 nm) of their electronic circular dichroism spectra (ECD). This empirical rule has become the general tool to define the absolute configuration of naturally occurring chiral monomeric flavanones and dihydroflavonols because of its simplicity, sensitivity, and reliability.² The method requires less than 1 mg of the sample, and the sample non-destructiveness further emphasizes its advantage in natural products chemistry.

The hexahydroxydiphenoyl (HHDP) moiety is an essential stereogenic element of ellagitannins, a group of natural products widely distributed in plants. It is the precursor to ellagic acid produced by enzyme-catalyzed lactonization of the former in plants or in vitro hydrolysis of HHDP-containing compounds. HHDP occurs generally as the aS-isomer in natural products, and less often as the aR-enantiomer.³ Okuda et al. reported that (aS)-HHDP produced a high-amplitude positive CE around 235 nm and two less intense negative CEs around 265 nm and 280 nm in the experimental ECD spectra of ellagitannins.⁴ The significant positive CE around 235 nm is diagnostic for the (aS)-HHDP chromophore and this empirical rule has also been employed to determine the absolute configuration of alternative HHDP-containing compounds.^5,6

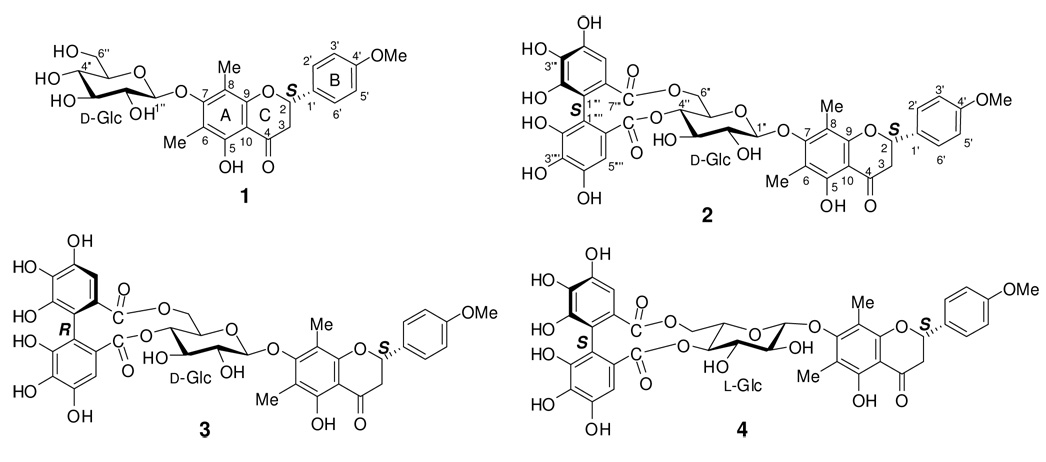
An important issue is whether these empirical rules are still applicable to natural products with mixed chromophores. There is no doubt that the experimentally observed ECD for such compounds is contributed by multiple chromophores. However, it is unknown how the interacting chromophores influence the overall ECD. With the advent of theoretical calculation of ECD by several methods,^7–12 it is possible to comprehend the principles regarding the generation of the ECD of a chiral organic compound. Our recent study¹⁰ has demonstrated that time dependent density functional theory (TDDBT) at the B3LYP/6–31G** level is a powerful method for calculating the ECD of flavonoids. The current study attempts to gain a fundamental understanding of the aforementioned HHDP/flavanone empirical rules at the molecular basis by theoretical calculation of the ECD of mattucinol-7-O-[4′,6″-O-(aS)-HHDP]-β-d-glucopyranoside (2), a natural product isolated from Miconia myriantha Bentham (Melastomataceae).⁶ Composed of flavanone, β-d-glucopyranosyl, and (aS)-HHDP structural moieties, this relatively bulky molecule is considered to be an ideal model to examine the roles of the three structural moieties in generating its overall ECD. To facilitate the conformational analysis and understanding of the theoretically calculated ECD of the title compound (2), we first performed conformational analysis and ECD calculation of mattucinol-7-O-β-d-glucopyranoside (1). Based on the optimized geometries of 2, we then calculated the ECD of 2 and two alternative structures by replacing the (aS)-HHDP and d-glucopyranosyl moieties with their antipodes, respectively, namely mattucinol-7-O-[4″,6″-O-(aR)-hexahydroxydiphenoyl]-β-d-glucopyranoside (3) and mattucinol-7-O-[4″,6″-O-(aS)-hexahydroxy-diphenoyl]-β-l-glucopyranoside (4).

Results and Discussion

ECD of Mattucinol-7-O-β-d-glucopyranoside (1)

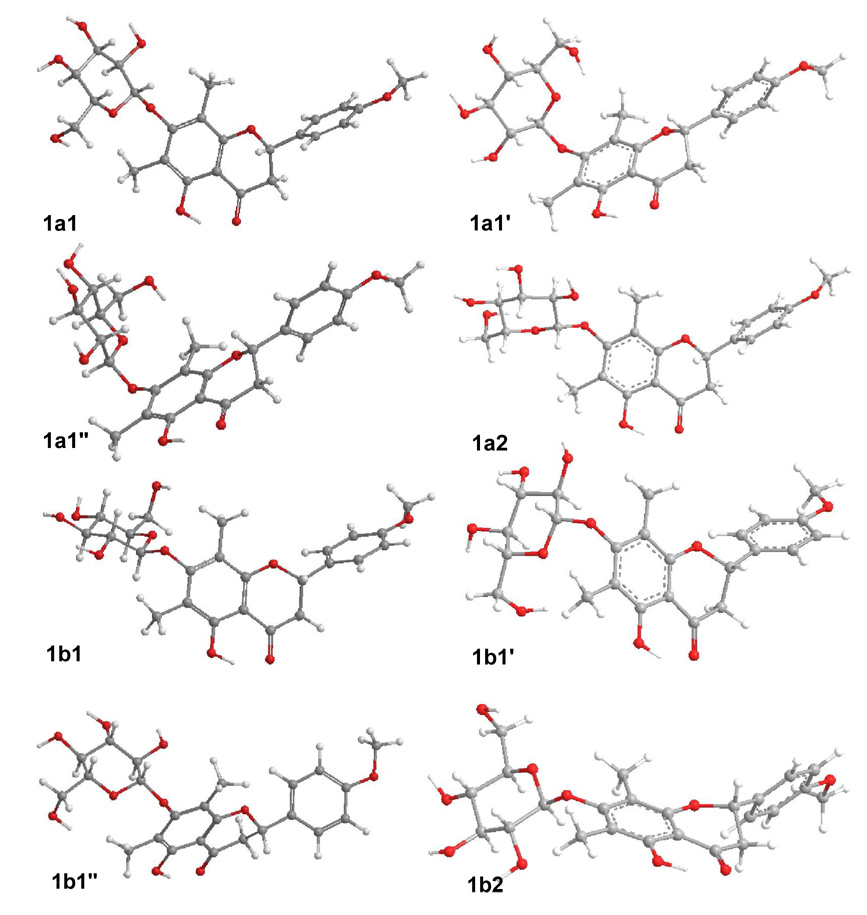
The initial conformational search for 1 was based on free rotation about the C2-C1′ C1″-O(C7), and (C1″)O-C7 single bonds. Our previous study¹⁰ and X-ray crystallographic data¹³ indicated that for similar flavanones, the B-ring was almost perpendicular to the A/C-ring plane in the optimized geometries or crystal structures. Thus, the orientation of the B-ring in compound 1 was set similarly for the starting conformation. Then, the DFT method at B3LYP/6–31G** level was performed to scan the potential energy surface of the conformers by rotating the glucosyl moiety about the C1″-O(C7) and (C1″)O-C7 bonds to locate the stable points (Figure S1, Supporting Information), affording 12 conformers 1a1, 1a1′ 1a1″ 1a2, 1a2′1a2″ 1b1, 1b1′ 1b1″ 1b2, 1b2′ and 1b2″ Further optimizations at B3LYP/6–31G** level relocated the eight stable conformers la1, 1a1′ 1a1″, 1a2, 1b1, 1b1′ 1b1″ and 1b2, as shown in Figure 2. The resulting relative energies (ΔE) and free energies (ΔG) are listed in Table 1.

Figure 2.

Optimized geometries of compound 1 at the B3LYP/6–31G** level in the gas phase.

Table 1.

Conformational Analysis of Compound 1 in the Gas Phase and in MeOH solution

	in gas phase												in MeOH
species
	Δ Ea	PE%b	ΔEc	PE%d	ΔGe	PG%f	ΔElbsg	PElbs%h	ΔEpwi	PEpw%j	ΔEsk	PEs%l
1a1	0.15	37.0	0.18	37.6	0.35	33.4	0.11	41.6	0.15	36.4	0.12	32.4
1a1′	4.22	0.0	4.43	0.0	4.94	0.0	4.77	0.0	4.31	0.0	1.66	2.4
1a1″	4.69	0.0	4.56	0.0	4.36	0.0	5.17	0.0	4.96	0.0	2.43	0.7
1a2	0.93	9.9	1.20	6.8	1.67	3.6	1.33	5.3	0.89	10.6	0.72	11.9
1b1	0.00	47.5	0.0	51.3	0.00	60.0	0.00	50.1	0.00	47.2	0.00	40.0
1b1′	3.98	0.1	4.18	0.0	4.74	0.0	4.53	0.0	4.05	0.1	1.45	3.4
1b1″	3.98	0.1	4.05	0.1	4.36	0.0	4.55	0.0	4.24	0.0	4.69	0.0
1b2	1.29	5.4	1.51	4.0	1.79	2.9	1.65	3.1	1.25	5.7	0.87	9.2

^a,c,eRelative energy, relative energy with ZPE, and relative Gibbs free energy, respectively (kcal/mol).

^b,d,fConformational distribution calculated by using the respective parameters above at the B3LYP/6–31G** level in the gas phase.

^g,hRelative energy (kcal/mol) and conformational distribution at the B3LYP/6–311++G**//B3LYP/6–31G** level, respectively.

^i,jRelative energy (kcal/mol) and conformational distribution at the B3PW91/6–31G**//B3LYP/6–31G** level, respectively.

^k,lRelative energy (kcal/mol) and conformational distribution at the B3LYP-SCRF/6–31G**//B3LYP/6–31G** level with COSMO model in MeOH solution, respectively.

For all conformers of 1, the atoms in the A- and C-rings (except C2) and their attached substituents are coplanar. The OMe-4′ group is coplanar with the B-ring and the latter ring is almost perpendicular to the A/C-ring plane. The glucosyl moiety is located above the A/C-ring plane in the 1a series but below this plane in the 1b series. Important dihedral angles in these conformers are listed in Table 2. It is evident that the Cl″- C2″ and (C1″)O-C7 bonds are in an anti orientation about the C1″- O(C7) bond in 1a1, 1a2, 1b1 and 1b2, implying that they are in extended conformations with the glucosyl moiety away from the A/C-ring plane. For conformers 1a1′ 1a1″, 1b1″ and 1b1″ in which the two bonds are in a gauche orientation, the glucosyl moiety is close to the A/C-ring plane in a crowded conformation. The results of conformational analysis of these conformers are shown in Table 2. Conformers 1a1, 1a2, 1b1 and 1b2 have distributions of 33.4%, 3.6%, 60.0% and 2.9%, respectively, by ΔG, accounting for almost 100% in the gas phase, contributions of the remaining four conformers towards the conformational itinerary being insignificant.

Table 2.

Important Dihedral Angles in Conformers of 1 (degrees).

	1a1	1a1′	1a1″	1a2	1b1	1b1′	1b1″	1b2
C1″-O-C7-C6	102	96	107	56	−79	−89	−79	−126
C2″-C1′-O-C7	164	−80	−20	119	163	−80	−23	118
O1-C2- C1′- C2″	−43	−43	−43	−43	−40	−38	−40	−43

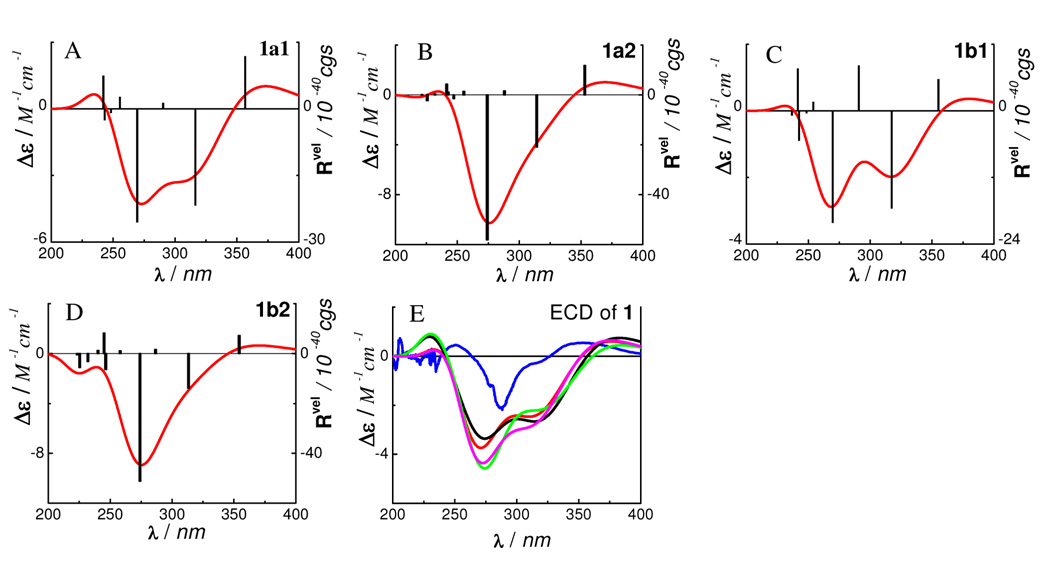
Based on the above conformational analysis, we calculated the ECD of conformers 1a1, 1a2, 1b1 and 1b2 in the gas phase by TDDFT at the B3LYP/6–31G** level. The calculated transitions, related rotatory strengths, and oscillator strengths of the two major conformers 1a1 and 1b1 are shown in Table 3. The simulated ECD curves of the four conformers as well as the weighted and experimental⁶ ECD spectra of 1 are shown in Figure 3. The calculated negative rotatory strengths at 269 and 316 nm in 1a1 and those at 270 and 317 nm in 1b1 may contribute to the experimentally observed high-amplitude negative CE at 282 nm and a negative CE around 320 nm (shoulder), while the calculated positive rotatory strengths at 357 nm in 1a1 and 355 nm in 1b1 may be associated with the experimentally observed positive CE at 350 nm. In addition, the positive rotatory strengths at 242 nm in both 1a1 and 1b1 may contribute to the experimentally observed low-amplitude positive CE 250 nm.

Table 3.

Key Transitions and Related Rotatory and Oscillator Strengths of Conformers 1a1 and 1b1 at the B3LYP/6–31G** Level in the Gas Phase

species	transition	ΔEa (eV)	λb (nm)	fc	Rveld	Rlene
	126→127	3.48	357	0.064	11.8	12.7
	125→127	3.92	316	0.013	−21.8	−23.1
1a1	122→127	4.27	290	0.008	1.4	−0.1
	124→127	4.60	269	0.234	−25.6	−23.7
	126→129	5.10	243	0.014	−2.6	−3.0
	125→128	5.12	242	0.024	7.5	4.8
	126→127	3.49	355	0.066	5.7	4.5
	125→127	3.91	317	0.012	−17.6	−18.9
1b1	122→127	4.26	291	0.005	8.2	6.9
	124→127	4.60	270	0.234	−20.2	−21.8
	125→128	5.11	242	0.019	−5.40	−7.43
	126→129	5.13	242	0.019	7.64	7.46

^aExcitation energy.

^bWavelength.

^cOscillator strength.

^dRotatory strength in velocity form (10⁻⁴⁰ cgs).

^eRotatory strength in length form (10⁻⁴⁰ cgs).

Figure 3.

Calculated ECD spectra of 1 in the gas phase at the B3LYP/6–31G** level (AD D), and its experimental and weighted ECD (E: experimental in MeOH; at the B3LYP/6–31G** level in the gas phase; at the B3LYP/6–311++G**//B3LYP/6–31G** level in the gas phase; at the B3PW91/6–31G**//B3LYP/6–31G** level in the gas phase; at the B3LYP-SCRF/6–31G**//B3LYP/6–31G** level with COSMO in MeOH).

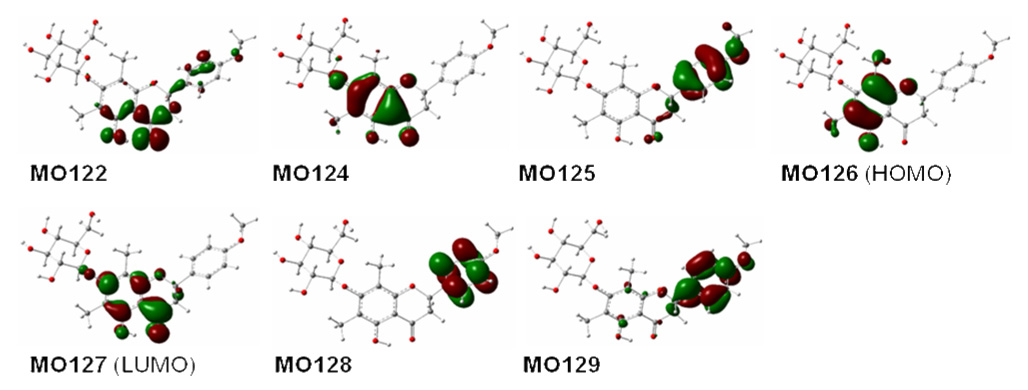
Molecular orbitals (MO) involved in the key transitions for the ECD of 1b1 are shown in Figure 4. The major negative rotatory strength at 270 nm is contributed by the electronic transition from MO124 involving a delocalized ${}_{11}{}^{14}\pi$ bonding (a fourteen-electron π system involving eleven atoms) orbital of the acetophenone unit in the flavanone moiety to its corresponding unoccupied MO127 (LUMO). In turn, the negative rotatory strength at 317 nm may be attributed to the electronic transfer from MO125 involving a delocalized ${}_7{}^8\pi$ bonding orbital of the B-ring in the flavanone moiety to MO127. The positive rotatory strength at 355 nm derives from the transition from MO126 (HOMO), involving a delocalized ${}_{11}{}^{14}\pi$ bonding orbital on the A/C-ring system without the participation of the n-electrons of the carbonyl group, to MO127. These results are consistent with our previous study that demonstrated the same molecular orbital transitions in production of the ECD of the simple flavanone, pinocembrin, although the resulting wavelengths from MO125 to MO127 and from MO126 to MO127 are different due to the utilization of different basis sets and the substitution effects on the B-ring (317 and 350 nm in 1b1 versus 301 and 317 nm in pinocembrin, respectively)¹⁰. It should be emphasized that our results support the classic interpretation that the diagnostic CE around 280–290 nm for flavanones are resulting from the π → π* transition of the acetophenone moiety. However, another diagnostic CE around 330 nm (less intense) for flavanones is derived from the electronic transition from MO126 (HOMO) to MO127 (LUMO), thus denouncing the classical interpretation that this CE is due to the acetophenone n→π* transition.¹

Figure 4.

Molecular orbitals involved in the key transitions in ECD of 1b1 at the B3LYP/6–31G** level in the gas phase.

Our previous study indicated that the B3LYP-SCRF method using the COSMO model was critical in acquiring appropriate ECD for the heptahydroxybiflavonoid, morelloflavone.¹⁰ In the current study we also performed the ECD calculation at B3LYP-SCRF/6–31G**//B3LYP/6–31G** level in MeOH solution (dielectric constant ɛ = 32.63) with the COSMO model for comparison. The effect of a larger basis set on the ECD of 1 in the gas phase was examined at B3LYP/6–311++G**//B3LYP/6- 31Q** level. The B3PW91/6–31G**//B3LYP/6–31G** method was also employed to calculate the ECD of 1. The conformational distributions of individual conformers at different levels are shown in Table 1. Overall, the calculated ECD curves at the above levels were similar and consistent with the experimental spectrum (Figure 3 and Figure S6–8). These results support our previous study that DFT (B3LYP) represents a feasible method for calculating/predicting the ECD of monomeric flavonoids.⁶

ECD of Mattucinol-7-O-[4′,6″-O-(aS)-hexahydroxydiphenoyl]-β-d-glucopyranoside (2)

The experimental ECD of 2 showed a high-amplitude positive CE around 240 nm, a low-amplitude negative CE in the 260–300 nm region, and a minor positive CE around 350 nm as shown in Figure 6E. Consideration of the additive ECD contribution of the HHDP and flavanone structural moieties in conjunction with the empirical rules (vide supra), the former was assigned aS and the latter 2S configuration.⁶ Our theoretical calculation of the ECD of 2 was based on this assumption.

Figure 6.

Calculated ECD spectra of 2 in the gas phase at B3LYP/6–31G** level (A → D), and its experimental and weighted ECD in MeOH (E: experimental in MeOH; at the B3LYP/6–31G** level in the gas phase; at the B3LYP/6–311++G**//B3LYP/6–31G** level in the gas phase; at the B3PW91/6–31G**//B3LYP/6–31G** level in the gas phase; at the B3LYP-SCRF/6–31G**//B3LYP/6–31G** level with COSMO in MeOH).

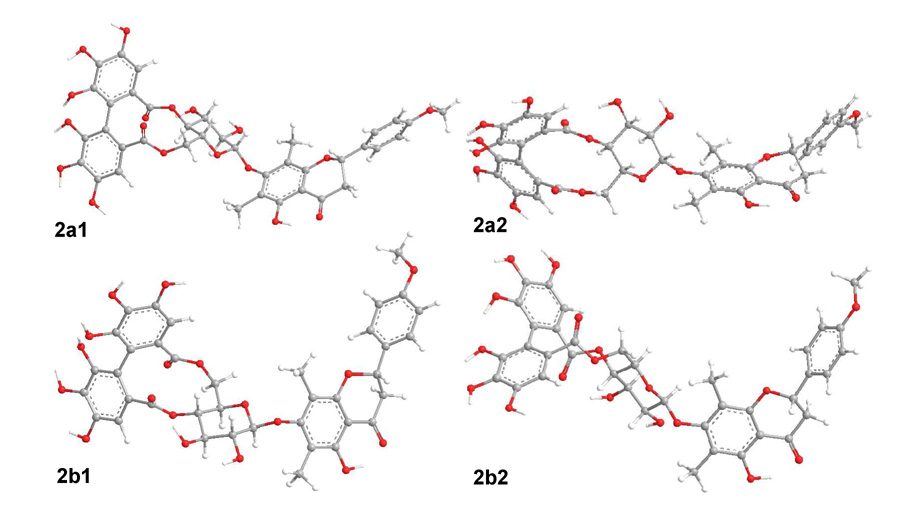
The optimized geometries of compound 1 provided a sound basis for the conformational analysis of compound 2. Once the (aS)-HHDP group is attached to the β-d-glucopyranosyl moiety, the conformational flexibility of the two structural moieties is limited thus simplifying the geometry optimization. Compound 2, like 1, would also give eight conformers by rotating the flavanone moiety about the (C1″)O-C7 and C1″-O(C7) bonds (Figure S3 and Table S8). However, only four conformers 2a1 (52.1%), 2a2 (2.8%), 2b1 (43.0%) and 2b2 (2.0%) were obtained with significant distributions at the B3LYP/6–31G** level by Gibbs free energy in the gas phase in which the flavanone and glucosyl moieties adopt conformations similar to 1a1, 1a2, 1b1 and 1b2, respectively (Figure 5). The dihedral angle C2′″-C1′″-C1″″-C2″″ of the (aS)-HHDP moiety in these conformers is 57°. Other key dihedral angles of the four conformers are shown in Table 4.

Figure 5.

Major conformers of optimized geometries of compound 2 at the B3LYP/6–31G** level in the gas phase.

Table 4.

Important Dihedral Angles in Conformers of 2 (degrees).

	2a1	2a2	2b1	2b2
C1″-O-C7-C6	104	57	−75	−126
C2″-C1″-O-C7	162	120	162	118
O1-C2-C1′-C2′	−43	−40	−42	−42
C2″′C1″′C1″″-C2″″	57	57	57	57
C1″′-C6″′-C7″′-O(C6″)	−139	−139	−139	−139
C1″″- C6″″- C7″″-O(C4″)	−125	−125	−125	−125

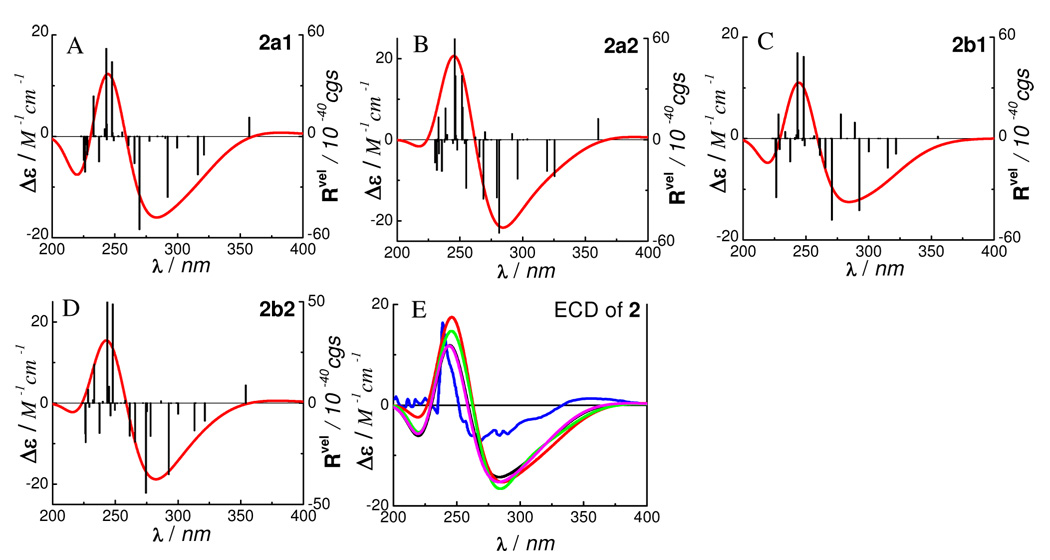
The ECD calculations of conformers 2a1, 2a2, 2b1 and 2b2 were carried out by the TDDFT method at the B3LYP/6–31G** level in the gas phase. The transitions, related rotatory strengths, and oscillator strengths of one major conformer, 2a1, are shown in Table 5. The simulated ECD of the four conformers and their weighted ECD are shown in Figure 6. The calculated and experimental ECD are in good agreement. The experimentally observed positive CE at 240 nm in 2 may result from the two high-amplitude positive rotatory strengths around 245 nm in the four conformers, while the low-amplitude negative CEs from 260–300 nm are contributed by a series of negative rotatory strengths, e.g., at 266, 270, 292, 316, and 321 nm in 2a1. The low-amplitude positive CE around 350 nm may be contributed mainly by the positive rotatory strength at 357 nm in 2a1 since the positive rotatory strength at 355 nm in another major conformer 2b1 is negligible and the contributions from the two minor conformers 2a2 and 2b2 would be very small.

Table 5.

Key Transitions and Oscillator and Rotatory Strengths of Conformer 2a1 at the B3LYP/6–31G** Level in the GasPhase.

transition	ΔEa(eV)	λb(nm)	fc	Rve1d	R1ene
203→204	3.47	357	0.063	11.2	13.3
202→205	3.86	321	0.044	−11.0	−19.2
201→204	3.92	316	0.013	−22.6	−24.3
202→206	4.24	292	0.075	−35.9	−39.9
199→204	4.60	270	0.277	−55.0	−56.8
197→205	4.67	266	0.019	−16.0	−17.9
198→206	4.98	249	0.035	−2.5	−12.7
202→208	5.00	248	0.088	44.0	44.8
197→206	5.10	243	0.038	51.8	56.6
192→205	5.22	237	0.014	−15.0	−17.7
200→208	5.32	233	0.149	23.7	39.0
190→206	5.480	226.3	0.017	−20.9	−21.9
194→205	5.483	226.1	0.012	−15.3	−15.3
191→204	5.50	225	0.012	−14.0	−13.6

^aExcitation energy.

^bWavelength.

^cOscillator strength.

^dRotatory strength in velocity form (10⁻⁴⁰ cgs).

^eRotatory strength in length form (10⁻⁴⁰ cgs).

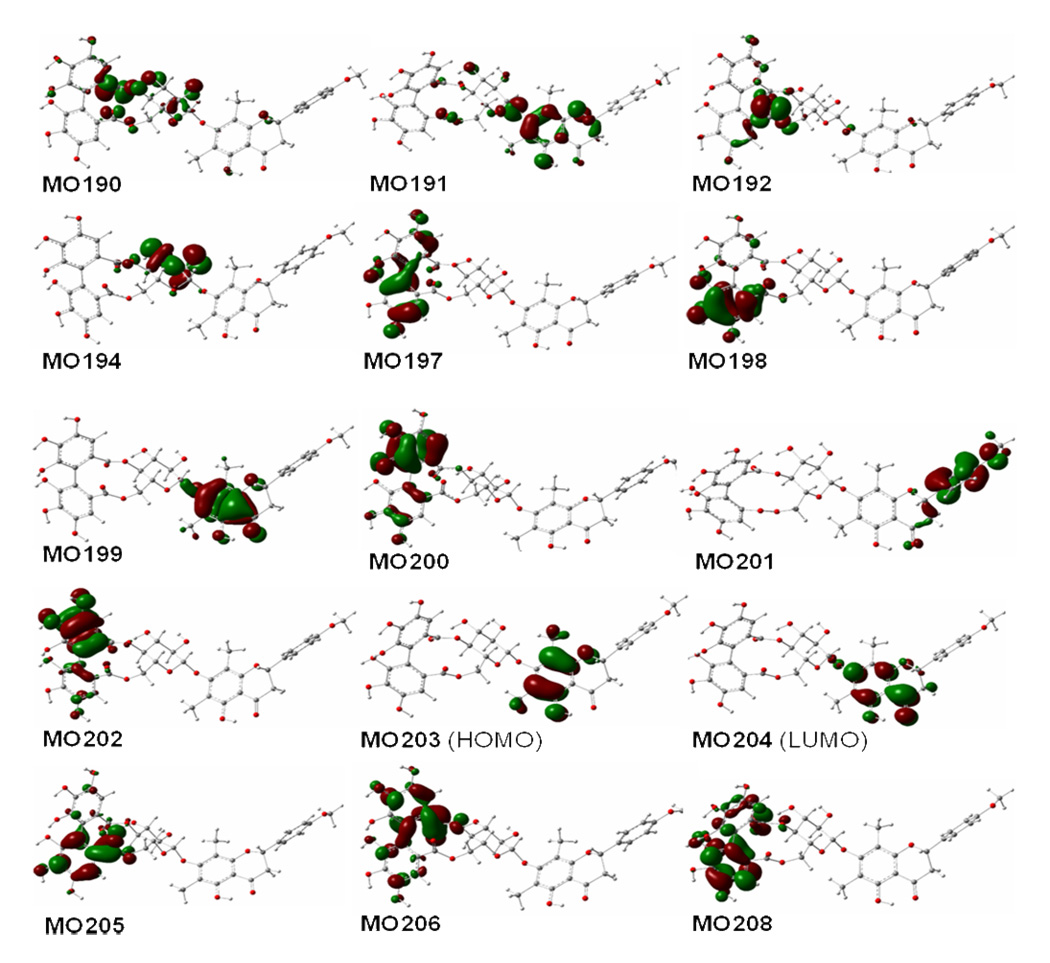
Analysis of the molecular orbitals of conformer 2a1 (Figure 7) involved in the contributions to the aforementioned rotatory strengths, reveals the roles of the (aS)-HHDP and (2S)-flavanone moieties in generating the overall ECD of this molecule. The (aS)-HHDP moiety not only generates the two strong positive rotatory strengths at 243 nm (MO197 to MO206) and 248 nm (MO202 to MO208) but also three strong negative rotatory strengths at 266 nm (MO197 to MO206), 292 nm (MO202 to MO206), and 321 nm (MO202 to MO205). The latter three negative rotatory strengths synergize the two negative rotatory strengths from the (2S)-flavanone moiety at 270 nm (MO 199 to MO204) and 316 nm (MO201 to MO204) contributing a broad CE in the 260–300 nm region. The positive rotatory strength at 357 nm (MO203 to MO204) of the (2S)-flavanone moiety represents the contribution of the diagnostic CE at the longer wavelength. In this case, it appears that the two chromophores have simple additive effects to the overall ECD and the original configurational assignment of 2 based on the empirical rules is thus confirmed.

Figure 7.

Molecular orbitals involved in key transitions generating ECD spectrum of 2a1 at the B3LYP/6–31G** level in the gas phase.

To examine the reliability of the ECD calculation of 2 at the B3LYP/6–31G** level, single point energies of each conformer were calculated at the B3LYP/6–311++G**//B3LYP/6–31G** level in the gas phase, at B3LYP-SCRF/6–31G**//B3LYP/6–31G** level with the COSMO model in MeOH, and at the B3PW91/6–31G**//B3LYP/6–31G** level in the gas phase. The conformational distributions of individual conformers at different levels are shown in Table S8. Minor changes for conformational distributions of conformers 2a1:2a2:2b1:2b2 were observed among the three levels, changing to 47.6:2.3:48.5:1.5%, 37.3:8.9:45.1:8.5%, and 45.2:8.2:45.1:8.5%, respectively (Table S8). However, the calculated ECD spectra of each conformer at the above three levels (Figure 6E and Figures S10–12) were largely similar to the ones obtained by B3LYP/6–31G** in the gas phase. For example, the transitions for conformer 2a1 at 357, 321, 316, 300, 292, 270, and 266 nm calculated at the B3LYP/6–31G** level in the gas phase are slightly shifted to 365, 325, 321, 303, 296, 275, and 269 nm at the B3LYP/6–311++G**//B3LYP/6–31G** level in the gas phase, to 358, 327, 315, 300, 292, 280, and 274 nm at the B3LYP-SCRF/6–31G**//B3LYP/6–31G** level with COSMO model in methanol, and to 357, 320, 316, 300, 291, 269, and 265 nm at the B3PW91/6–31G**//B3LYP/6–31G** level in the gas phase. Again, this indicates that the DFT with the modest basis set B3LYP/6–31G** would be a sufficient method for theoretical ECD calculation of flavonoids, in particular for dealing with relatively bulky naturally occurring compounds.

ECD of Mattucinol-7-O-[4″,6″-O-(aR)-hexahydroxydiphenoyl]-β-d-glucopyranoside (3)

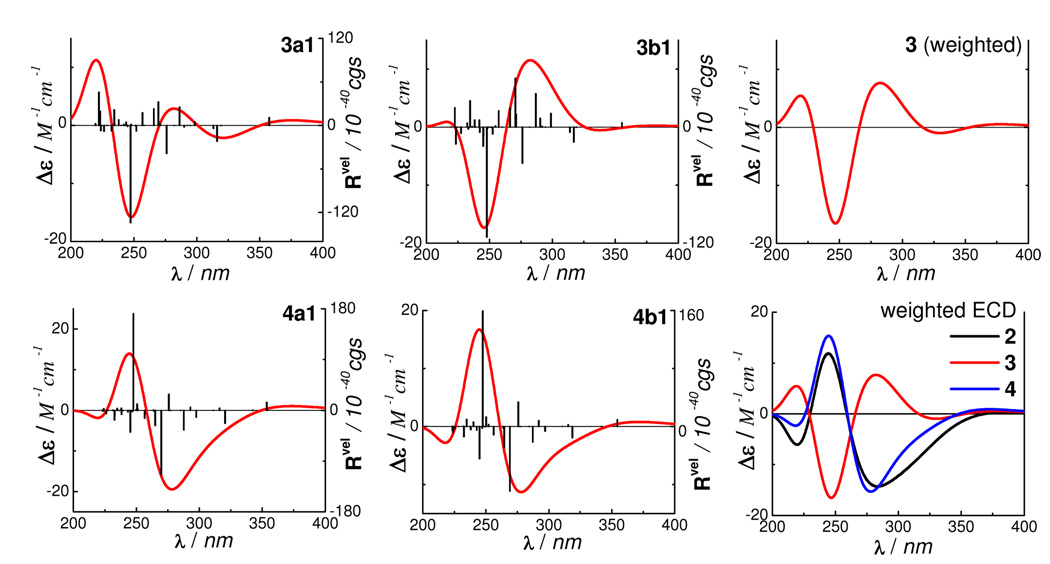
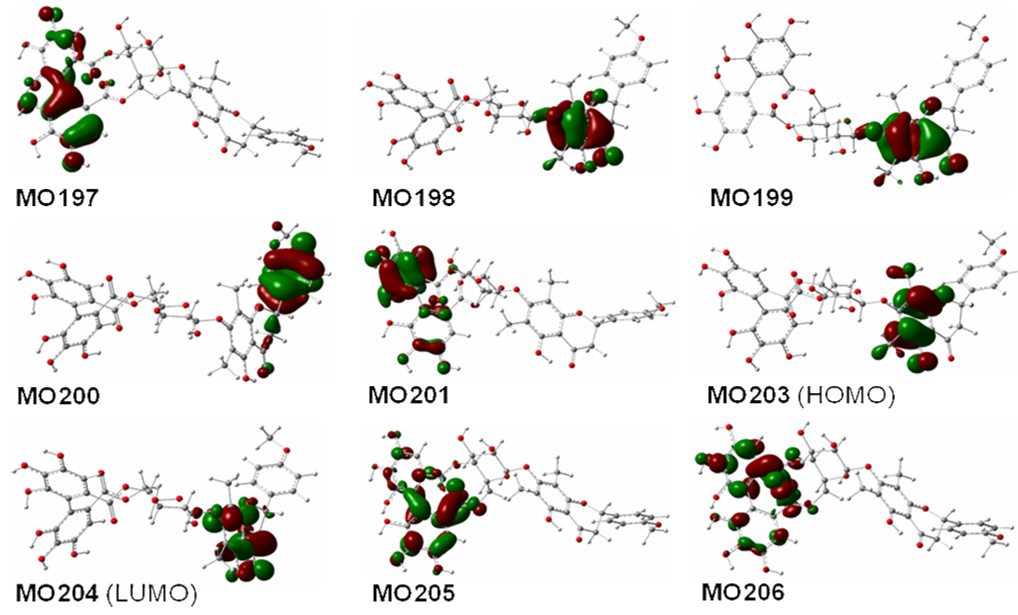
Next, we assessed the applicability of this method to the hypothetical compound 3 with (aR)-HHDP and (2S)- flavanone moieties. The geometry optimization of 3 was based on compound 2 and, thus, it would practically possess only four conformers that make significant contributions to the ECD. Since two among the four conformers are minor and their contributions to the overall ECD are negligible as evident in 1 and 2, only two conformers 3a1 and 3b1 corresponding to the two major conformers 2a1 and 2b1 (with distributions >95% by Gibbs free energy in the gas phase) of compound 2 were considered to provide a general conceptual indication for this purpose. Conformational analysis using these two conformers at the B3LYP/6–31G** level in the gas phase afforded a 44.9:55.1% ratio for 3a1:3b1. The calculated ECD of the two conformers by TDDFT at the same level and the weighted ECD are shown in Figure 8. As expected, the major rotatory strengths around 240 nm from the (aR)-HHDP moiety in 3a1 and 3b1 (Table 6) were reversed compared to conformers 2a1 and 2b1. Conformer 3b1 displays a high-amplitude negative rotatory strength at 248 nm. The major rotatory strength at 270 nm of the (2S)-flavavone moiety in 2a1 also reverses with a positive sign at 271 nm (from MO198 to MO204, Figure 9) in 3b1, with the signs of the characteristic rotatory strengths at 317 nm (MO200 to MO204) and 354 nm (MO202 to MO204) remaining the same as in 2a1. The electronic interaction between the (2S)-flavanone and (aR)-HHDP moieties also produces two positive rotatory strengths at 257 and 266 nm (MO 199 to MO206 and MO205, respectively). The only negative rotatory strength in the 260–300 nm region is at 276 nm resulting from the electronic transition (MO201 to MO206) within the HHDP moiety. As a result, an overall broad positive CE was generated in the 260–300 nm region of 3b1. Assuming the experimental and calculated ECDs of compound 3 to be similar, an erroneous 2R configuration may be assigned for the flavanone moiety based on the empirical rule requiring a positive CE in the 260–300 nm region. The complex interaction between chromophores in chiral molecules of this class clearly precludes ECD interpretation by simple empirical rules.

Figure 8.

Calculated ECD of compounds 2–4 by TDDFT at the B3LYP/6–31G** level in the gas phase.

Table 6.

Key Transitions and Oscillator Strengths and Rotatory Strengths of Conformer 3b1 of Compound 3 at the B3LYP/6–31G** Level in the Gas Phase.

transition	ΔEa(eV)	λb(nm)	fc	Rve1d	R1ene
203→204	3.49	355	0.068	4.59	−2.06
200→204	3.91	317	0.013	−15.3	−16.9
202→206	4.15	299	0.062	14.2	18.6
201→205	4.32	287	0.058	34.5	37.1
201→206	4.49	276	0.119	−37.3	−41.8
199→204	4.57	271	0.026	13.5	13.9
198→204	4.58	271	0.219	50.3	50.0
199→205	4.65	266	0.047	19.5	21.6
199→206	4.82	257	0.099	17.0	15.4
197→206	5.00	248	0.048	−113.5	−122.7
198→205	5.06	245	0.071	−19.6	−18.9
193→206	5.28	235	0.022	27.2	35.0
190→204	5.45	227	0.002	−6.3	−4.8
202→210	5.55	223.5	0.072	−17.5	−15.0
193→205	5.57	222.6	0.131	20.2	19.4

^aExcitation energy.

^bWavelength.

^cOscillator strength.

^dRotator ystrength in velocity form (10 ⁻⁴⁰cgs).

^eRotatory strength in length form (10⁻⁴⁰cgs).

Figure 9.

Molecular orbitals involved in key transitions generating ECD spectrum of 3b1 at the B3LYP/6–31G** level in the gas phase.

ECD of Mattucinol-7-O-[4″,6″-O-(aS)-hexahydroxydiphenoyl]-β-l-glucopyranoside (4)

It is reasonably conceived that the glucosyl moiety would have little effect on the ECD of chiral flavanones or dihydroflavonols in the 200–400 nm region, although the β-d-glucopyranosyl moiety is reported to induce minor negative CEs in phenolic glycosides.¹ This is evidenced by our theoretical calculation of the ECD of mattucinol-7-O-β-l-glucopyranoside, which showed an almost identical ECD to that of mattucinol-7-O-β-d-glucopyranoside (1) (Figure S9). Next, we assessed the influence of the configuration of the glucosyl moiety on the ECD of a relatively rigid molecule like 2. Thus, the β-d-glucopyranosyl unit in 2 was replaced with a β-l-glucopyranosyl moiety in the hypothetical mattucinol-7-O-[4″,6″-O-(aS)-hexahydroxydiphenoyl]-β-l-glucopyranoside (4). Similar to the treatment for compound 3, the geometry optimization of 4 was based on compound 2 and only two conformers 4a1 and 4b1 corresponding to the two major conformers 2a1 and 2b1 were used for conformational analysis at the B3LYP/6–31G** level in the gas phase, affording a ratio of 49.2:50.8%. The calculated ECD of the two conformers by TDDFT at the same level and the weighted ECD are shown in Figure 8. The signs of the major rotatory strengths from the (aS)-HHDP and (2S)-flavanone moieties remain the same as in 2 (refer to Figure S13 and Table S21 for key molecular orbitals and the transitions generating the ECD of 4, respectively). Overall, the calculated ECD spectra of 4 and 2 are similar, indicating that the absolute configuration of the glucopyranosyl unit has little effect on their ECD.

In conclusion, this study has identified the roles of the respective chromophores of an HHDP-containing flavanone glycoside in generating its ECD spectrum. The results indicated that the established empirical rules for HHDP and flavanone chromophores need to be used circumspectively when applied to complex natural products of this class with multiple chromophores. Theoretical calculation of the ECD that quantifies the contributions and interactions of the different chromophores is essential for defining the absolute configuration of such molecules.

Experimental Section

General Experimental Procedures

Experimental ECD spectra were recorded on a JASCO J-715 spectrometer in MeOH. The detailed methods and instrumentation employed for the isolation and structure identification of compounds are described in a previous paper.⁶

Compounds

Mattucinol-7-O-β-d-glucopyranoside (1) and mattucinol-7-O-[4″,6″-O-(aS)- hexahydroxydiphenoyl]-β-d-glucopyranoside (2) were isolated from the plant Miconia myriantha Bentham (Melastomataceae).⁶

Methods of Calculations

All calculations were performed at 298K by the GaussianO3 program package.¹⁴ DFT method was employed to scan the potential energy surface (PES) at B3LYP/6–31G** level to identify conformers of compound 1. Ground-state geometries were optimized at the B3LYP/6–31G** level, total energies of individual conformers were obtained and vibrational analysis was done to confirm these minima. Conformational structures of compounds 2–4 were built according to the optimized geometries of compound 1. TDDFT at the same level was employed to calculate excitation energy (in nm) and rotatory strength R in dipole velocity (R_vel) and dipole length R_len) forms. The calculated rotatory strengths were simulated into an ECD curve by using the Gaussian function:

$$\mathrm{\Delta }\in \left(E\right)=\frac{1}{2.297\times {10}^{-39}}\frac{1}{\sqrt{2\pi \sigma }}{{\displaystyle \sum _i^A\mathrm{\Delta }{E}_i{R}_i{e}^{-\left[\left(E-\mathrm{\Delta }{E}_i\right)/\left(2\sigma \right)\right]}}}^2$$

where σ is the width of the band at 1/e height and ΔE_i and R_i are the excitation energies and rotatory strengths for transition i, respectively. σ = 0.20eV and R_vel were used.

The “Self-Consistent Reaction Field” method (SCRF) with “COnductor-like continuum Solvent MOdel” (COSMO) was employed to perform the ECD calculation of major conformers of compounds 1 and 2 in MeOH solution at B3LYP-SCRF/6–31G**//B3LYP/6–31G** level.^15–17 In addition, the ECD calculations of major conformers of compounds 1 and 2 were carried out at B3LYP/6–311++G**//B3LYP/6–31G** and B3PW91/6–31G**//B3LYP/6–31G** levels.

Supplementary Material

1_si_001. Supporting Information Available.

Detailed computational calculating data of compounds 1–4. This information is available free from the Internet at http://pubs.acs.org.

Figure 1.

Structures of compounds 1–4.