Table 2.

Centrality measures used in this study

Centrality	Formula	Description
In degree	Cu = kin(u)	Number of connections into node u
Out degree	Cu = kout(u)	Number of connections out from node u
Sphere degree	Cu = kout(u) + ∑w∩u kout(w); w is any neighbor of u.	Number of nodes at 1 or 2 connections from node u
Clustering coefficient		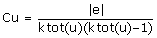The fraction of connections between the neighbors of node u
1/Clustering coefficient
Eccentricity	Cu = max{dist(u, w): w ∈ V}	The distance between node u and the most distant node in the net.
1/Eccentricity	Cu = 1/max{dist(u, w): w ∈ V}
Average distance		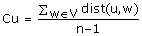Average distance of node u to the rest of nodes in the net
Closeness		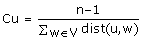Inverse of average distance
Katz		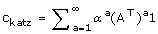A node has a larger ckatz value while more paths reach it.
KatzR		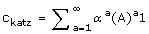A node has a larger ckatz value while more paths leave the node.
PageRank	cPR = d P cPR + ((1 - d) 1)	The centrality of a node depends on its incoming connections and the relative connectivity of these connections
PageRankR	cPR = d PT cPR + ((1 - d) 1)	The centrality of a node depends on its outcoming connections and the relative connectivity of these connections
Integration		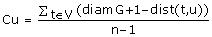The easiness of reaching node u from any other node
Radiality		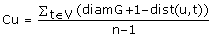The easiness of reaching any node from node u
SP-betweenness		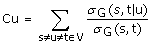The fraction of shortest paths inside the network, which utilize node u

In the table, kin(u), kout(u) and ktot(u) refer to the incoming, outgoing and total number of edges of node u. diamG refers to the diameter of the graph and dist(u, v) stands for the distance between nodes u and v. In clustering coefficient, |e| stands for the observed paths between the neighbours of a node. In Katz A is the adjacency matrix and α a damping factor. In PageRank d is a damping factor and P the transition matrix. In the formula for shortest path (SP) betweenness σ_G denotes the number of shortest path from s to t. For a more detailed description of these centralities, please read [17].