Abstract
In this work I develop and apply a theoretical method for calculating effective electronic couplings (or transfer integrals) between redox sites involved in hole or electron transfer reactions. The resulting methodology is a refinement and a generalization of a recently developed approach for transfer integral evaluation. In fact, it holds for any overlap between the charge-localized states used to represent charge transfer (CT) processes in the two-state model. The presented theoretical and computational analyses show that the prototype approach is recovered for sufficiently small overlaps. The method does not involve any empirical parameter. It allows a complete multielectron description, therefore including electronic relaxation effects. Furthermore, its theoretical formulation holds at any value of the given reaction coordinate and yields a formula for the evaluation of the vertical excitation energy (i.e., the energy difference between the adiabatic ground and first-excited electronic states) that rests on the same physical quantities used in transfer integral calculation. In this paper the theoretical approach is applied to CT in B-DNA base dimers within the framework of Density Functional Theory (DFT), although it can be implemented in other computational schemes. The results of this work, as compared with previous Hartree–Fock (HF) and post-HF evaluations, support the applicability of the current implementation of the method to larger π-stacked arrays, where post-HF approaches are computationally unfeasible.
INTRODUCTION
Recent years have seen a proliferation of experimental and theoretical studies of charge transfer (CT) processes in biological systems, with the aim of exploiting their intrinsic functions, toward the development of molecular electronics.1, 2, 3 In particular, CT through DNA π-stacks attracted increasing attention because of its possible implications for nanoelectronics4, 5, 6 and its biological importance in the processes of oxidative damage to DNA and the pertinent repair strategies.7, 8, 9 Despite the recent progress in DNA nanostructuring, DNA-based molecular electronics continues to be a challenging issue, since most of the chemicophysical properties of charge transport through DNA chains are still unclear, with disparate experimental evidence ranging from insulating10 to conductive behavior11 in different measurement conditions. Thereby, careful theoretical analyses of CT processes in DNA systems are required in order to understand the disparate experimental data and to make predictions useful to guide future experiments and applications. In this perspective, a crucial role is played by reliable calculations of the physical quantities governing the elementary CT steps.
The electrical conductance of single molecules is strictly related to the inherent electron transfer (ET) rate,12 which in general depends on the effective electronic coupling between the charge donor and acceptor groups.13 Within the framework of Markus’ ET theory, the rate constant is given by13, 14, 15
| (1) |
In Eq. 1, k is the electronic transmission coefficient, which is proportional to the mean-square transfer integral in the nonadiabatic regime16 (i.e., for weak electronic coupling), ν is an effective frequency for the nuclear motion along the reaction coordinate, λ is the reorganization energy, ΔG0 is the reaction free energy, kB is Boltzmann’s constant, and T is the temperature. λ is the only relevant parameter in the nuclear factor for self-exchange reactions, where ΔG0 is zero. The importance of this parameter for hole transfer along DNA chains (which corresponds to ET in the opposite direction, and is the mainly studied CT process in DNA, both experimentally4, 17, 18, 19, 20 and theoretically21, 22, 23, 24, 25, 26, 27) has been recently clarified,28 while in this work the attention is focused on the other relevant parameter, i.e., the transfer integral.
Indeed, I propose a theoretical method for transfer integral calculation in a much more general context than CT in DNA. Then I consider a hybrid-Density Functional Theory (hybrid-DFT) implementation of the method, which, in particular, appears quite suitable to study CT processes through DNA nucleobase stacks. In fact, in DNA systems, CT essentially proceeds through the π-stacked bases,29, 30 while the direct effect of the backbone on the effective electronic couplings between the donor and acceptor bases is negligible.22, 31 Since guanine (G) is the most easily oxidized nucleobase,32 it is a stepping stone for the hole transfer in both natural and synthetic DNA. Indeed, the hole transfer has been proposed to occur via a multihopping mechanism that involves both guanines and adenines,23, 33, 34 the latter being the main charge carriers between distant guanines. Direct G-hopping is expected to occur through short adenine-thymine (T) bridges (up to three to four Watson–Crick base pairs), via coherent superexchange, which becomes an elementary ET process in the case of adjacent G bases. For long bridges, the excess charge is carried by the intervening bases, after thermally induced endothermic hole excitation to an intermediate adenine. Recent experiments indicate that the incoherent mechanism for long-range CT processes can be either hopping of localized charges20 or polaron diffusive motion.35 In any case, CT essentially depends on two parameters: the site energies, corresponding to the localization of the excess charge on a single base or base pair, and the effective electronic coupling.36 Their values can be strongly affected by the fluctuations of the DNA structure (e.g., see Ref. 36 and references therein), but this is not a subject of this methodological work.
Disparate approaches have been developed for accurate transfer integral calculations in various redox biosystems.25, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49 In particular, valuable transfer integral calculations on stacked DNA bases mainly rest on Koopmans’ theorem,50 the single-particle picture, and the two-state model. Cogent tests of these approximations are desirable.30 In this respect, a significant contribution has been recently given by post-HF calculations on dimers and trimers of stacked DNA bases26 with the complete active space self-consistent field (CASSCF) approach and its second-order perturbation formulation, i.e., CAS-PT2. However, the high computational cost of those approaches limits their applicability to small DNA π-stacks and restricts the size of the manageable active spaces, although the latter issue can been at least partially addressed by means of the multistate formulation MS-PT2.26 Thus, an accurate correlated method for transfer integral evaluation in a wider range of DNA base stacks is desirable. This does not diminish the importance of the mentioned post-HF approaches, which helps in understanding the physics of crucial DNA segments through the analysis of the pertinent results and their fruitful comparison with the results from other accurate approaches.
A valid alternative approach to transfer integral evaluation in DNA stacks consists in the use of a DFT scheme with a suitable hybrid exchange-correlation (XC) functional. Similarly to the XC functionals of pure DFT, hybrid XC functionals cover both nondynamic and dynamic electron correlation effects, but improve on exchange delocalization effects, therefore increasing the relative impact of dynamic electron correlation. Moreover, hybrid functionals tend to correct for self-interaction errors, i.e., the unphysical electron self-interaction energy coming from the approximations in any DFT functional. Indeed, hybrid functionals mostly perform better than self-interaction corrected DFT and correcting their residual self-interaction errors does not necessarily improve their description of molecular properties.51
In this work I present an ab initio method to calculate transfer integrals within the diabatic picture of ET. It is implemented in a hybrid-DFT scheme, though the theoretical approach is amenable to other computational schemes, including post-HF calculations. It is a generalization of the method developed in Ref. 48, insofar as it can be used with diabatic states (which characterize the electron localization before and after the ET process) characterized by large overlaps. This circumstance is especially useful when the valence electron charge on relatively close electron donor and acceptor sites is localized by means of constrained DFT (CDFT).
The formal derivation of the formula for transfer integral evaluation and its substantial connection to the formula developed in Ref. 48 are presented in Sec. 2A. Its hybrid-DFT implementation, with and without use of the diabatic electronic states from CDFT, is described in Sec. 2B. Finally, in Sec. 3 the computational-theoretical method is employed for a full-electron calculation of the effective electronic coupling in two single-stranded dimers of flanking B-DNA nucleobases: GT and GG. Convergence and accuracy of the calculations are widely tested and compared to previous results in the literature.
The theoretical development in Sec. 2A yields also a formula [see Eqs. 5, 12] to calculate the excitation energies of the adiabatic CT states in terms of quantities pertaining to the diabatic states. Its performance is compared against previous multiconfiguration calculations.26 This full-electron method, in conjunction with the use of a suitable hybrid XC functional, is proposed as a valid alternative to post-HF methods, time-dependent DFT, which tends to underestimate the excitation energies of CT states,52 and approaches43, 46 based on Koopmans’ theorem, which show the opposite trend.26
THEORETICAL AND COMPUTATIONAL METHODS
Wave function overlap method for transfer integral evaluation
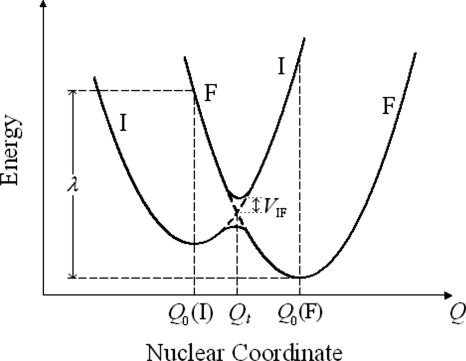
Within the two-state model, the ground-state vector of a system can be written as ∣ψ⟩=a∣ψI⟩+b∣ψF⟩, where ψI and ψF denote the reactant and product wave functions, respectively, which are introduced in the diabatic picture of the ET process. In these (diabatic or localized) electronic states the valence charge is localized on the donor and acceptor group, respectively, at any value of the reaction coordinate Q (Ref. 53) (see Fig. 1). The energy profile of the adiabatic ground and first excited electronic states shows a splitting at the transition state coordinate Qt, where the diabatic states come to degeneracy, so that both the conservation of energy and the Franck–Condon principle54 are rigorously satisfied in the electron transition from a diabatic surface to the other and the corresponding Franck–Condon factor takes its maximum value. Note that, strictly speaking, Fig. 1 depicts the free energy profile corresponding to a suitably defined reaction coordinate. The separation ΔEv of the adiabatic curves at Qt gives a measure of the effective electronic coupling VIF between ∣ψI⟩ and ∣ψF⟩ [see Eq. 5]. This splitting can be obtained starting from the secular equation
| (2) |
where λ is the generic energy eigenvalue, HII=⟨ψI∣H∣ψI⟩, HFF=⟨ψF∣H∣ψF⟩, HIF=⟨ψI∣H∣ψF⟩, and SIF=⟨ψI∣ψF⟩. The eigenvalues of Eq. 2 can be written in the implicit form
| (3) |
where ΔEIF=EI−EF≡HII−HFF is the energy difference, at the given nuclear configuration, between the ET initial (I) and final (F) diabatic states. Moreover, by using the explicit expressions of E+ and E− from Eq. 2, i.e.,
| (4) |
the vertical excitation energy can be written as
| (5) |
[so that ΔEv=2VIF at Q=Qt, where EI=EF (Ref. 55)], where
| (6) |
is the electron transfer matrix element or effective electronic coupling or transfer integral. In general, its value can depend on Q, as explicitly shown in Eq. 6. After insertion of the ground-state energy E≡E− from Eq. 3 into the diagonal terms of Eq. 2, the eigenvalue equations for the components of ∣ψ⟩ take the form
| (7) |
where the symbol UIF has been used for the quantity implicitly defined by
| (8) |
and a and b are related to the overlap integrals A≡⟨ψI∣ψ⟩=a+bSIF and B≡⟨ψF∣ψ⟩=b+aSIF by the linear relations
| (9) |
From Eq. 7 the two following expressions are obtained:
| (10) |
| (11) |
Finally, the insertion of Eqs. 10, 11 into Eq. 8 and its comparison with Eq. 6 gives
where Eq. 9 has been exploited to obtain the last expression. Note that the factor σ depends on SIF also implicitly, through the a and b parameters. Equation 12 holds whichever the value of the overlap SIF between the reactant and product states, and of the reaction coordinate Q. On the other hand, when the Condon approximation (which consists in neglecting the dependence of VIF all along the Q axis) is not satisfied, a meaningful value of VIF(Q) to be inserted into the expression of the ET rate constant has to be obtained close enough to Qt, i.e., in the proximity of the crossing seam point of Fig. 1. If the system is exactly at Qt, where ΔEIF=0 and a=b, then both the numerator and the denominator in the formula for UIF vanish. However, UIF and thus VIF has an eliminable discontinuity at Q=Qt (see Appendix0), and shows the correct behavior for Q approaching Qt, as directly shown by Eq. 5 for ΔEIF=0. Thereby, if VIF is sensitive to a given nuclear motion, it can be calculated by means of Eq. 12 within the regime of configurations surrounding Qt, where the Condon approximation is satisfied (see also next subsection). Afterwards, the vertical excitation energy at the given coordinate Q is obtained from Eq. 5.
Figure 1.
Cross section of the energy profile for the initial electronic state I and the final electronic state F of a typical ET reaction. The solid curves represent the adiabatic states, while the dashed lines describe the diabatic states. Q0(I) and Q0(F) denote the equilibrium nuclear coordinates of I and F, respectively. Qt is the transition state coordinate, corresponding to the lowest energy on the crossing seam surface. The reorganization energy λ is also indicated.
In Ref. 48 the effective electronic coupling has been obtained in the approximate UIF form, which lacks of the large-overlap corrective factor σ. Equation 12 provides an improvement on the method of Ref. 48. In fact, it can be applied to significantly wider classes of systems, including covalently bridged redox systems, where CDFT can be used to obtain the CT diabatic states and large SIF values are generally involved. Equation 11 has been used for transfer integral evaluation in various systems of interest to biochemistry and nanoelectronics. From the comparison with Eq. 12 it is clear that Eq. 11 can be used, in terms of either a and b or A and B, whenever SIF is much smaller than the quantity 2ab or 2AB. Under this condition, also the term can be neglected. Since the quantity a2+b2 is of the order of unity, neglecting the factor σ(a,b,SIF) in Eq. 12a amounts to a relative error approximately equal to SIF∕(2ab). Indeed, in various systems 2ab is of the order of magnitude of unity, so that the condition SIF=o(1) is sufficient for the use of Eq. 11.56 On the other hand, Eq. 12, which holds irrespective of the SIF value insofar as the two-state approximation is applicable, can also be used in cases where the diabatic states are characterized by a large overlap (e.g., this can be the case for close redox sites linked by a covalent bridge). The applicability and extension of Eq. 12 beyond the two-state model are the subject of future investigation, while a three-state analysis of Eq. 11 in the limit of negligible SIF has been presented in Ref. 48.
Note that the square modulus of the ground-state vector is given by ⟨ψ∣ψ⟩=a2+b2+2abSIF for real and normalized diabatic state vectors. The last term gives a measure of the overlap population57 between the two redox groups. Thus, a2+b2≠1, i.e., the coefficients a and b cannot be represented as sine and cosine of any angle. This means that, for a nonzero overlap SIF, the diabatic states cannot be obtained, at any coordinate, by rotation of the ground and first-excited adiabatic states (see also the expressions of a and b in the Appendix0). Some insights in the physical meaning of VIF(Q) are gained by considering the orthogonal transformation
| (13) |
in the more pictorial though simplified single-orbital picture, not used anywhere else in this work. Under the constraint that and are orthogonal, by fixing an overall phase factor and normalizing, the following delocalized electronic states are obtained:
| (14) |
They represent the adiabatic states when the system is at the transition state coordinate, which is always the case for systems like, e.g., the hydrogen molecule ion (see Ref. 57, p. 568). Out of Qt, the donor and acceptor groups are off resonance and the wave functions in Eq. 14 are not eigenfunctions of the Hamiltonian operator. Nevertheless, such wave functions can be analytically defined through Eq. 14 at every value of the reaction coordinate and describe a bondinglike (ϕbond) and an antibondinglike (ϕanti) orbitals. In fact, ∣ϕbond(r)∣2 and ∣ϕanti(r)∣2, which measure the corresponding electron charge densities at the coordinate r, are given by57
| (15a) |
| (15b) |
so that the valence electron charge partially concentrates in the region between the redox groups for the bondinglike wave function, while it lies more outside of the intervening region for the antibondinglike one. For example, in a diatomic molecule SIF∕(1+SIF) would be the fraction of an electron moved from each atomic orbital into the overlap region and twice this quantity is named the overlap population after Mulliken.58 If the valence charge moves from the distribution described by ∣ϕbond(r)∣2 to ∣ϕanti(r)∣2, at a given value Q of the reaction coordinate, the energy of the system changes by the quantity
| (16) |
as can be immediately derived from Eq. 14 and the definition of VIF(Q). In conclusion, the interpretation of Eq. 14 within the formalism of the ET theory readily leads to Eq. 16. The latter transparently shows that VIF(Q) gives the effective electronic coupling at any Q, which causes the energy splitting between the antibonding-like and bonding-like distributions of the valence electron charge, hence the energy gain in the latter.
System definition, diabatic states, and hybrid-DFT implementation of the method
Systems. The above theory is applied to the intrastrand hole transfer in the nucleobase stacks GT and GG from regular B-DNA. The GT stack offers a paradigmatic case, useful to test the performance of the proposed theoretical method for transfer integral evaluation and the limits of Eq. 11 as compared with the more general Eq. 12. In fact, previous calculations25, 26 indicate that GT is the base stack with the largest intrastrand charge transfer integral and a correspondingly large value of SIF.25 The importance of the GG system is clear from the introduction, where the major role of G in hole transfer along DNA has been elucidated. For both systems, since CT essentially proceeds through the nucleobases,22, 31 the sugar-phosphate backbone has been excluded from the presented single-point calculations. The computational implementation of Eqs. 11, 12 depends on the choice of the diabatic electronic states. In this work I consider the two recipes detailed below, whose performances are compared in Sec. 3.
Tensor product (TP) diabatic states. The systems under study, each consisting of two stacked B-DNA nucleobases, can be easily separated in a donor group D (i.e., one of the two nucleobases), where the hole is initially localized, and an acceptor group A that receives the transferring hole. Thereby, the initial and final electronic states can be conveniently defined as ∣ψI⟩=∣D+⟩∣A⟩ and ∣ψF⟩=∣D⟩∣A+⟩, respectively, where the charge localized on each nucleobase is explicitly indicated. In other words, the diabatic states are obtained as TPs of reference states for the isolated D and A groups in the initial and final oxidization states. All the required wave functions are built as single Slater determinants of the lowest-lying occupied spin orbitals. The feasibility of this procedure, also in relation to the spin contamination problem,59 has been discussed in Ref. 48. The A, B, and SIF quantities are directly obtained by exploiting the ET module in the NWCHEM computational chemistry package.60 The ET module is not used otherwise. The a and b coefficients are then obtained from Eq. 9. The energy difference between the diabatic states, i.e., ΔEIF, is computed as
| (17) |
In Eq. 17, ED+, EA+, ED, and EA are the ground-state DFT energies of the isolated subsystems in the specified charge states. They are directly provided by the self-consistent field DFT calculations of the ground states of the isolated donor and acceptor groups in the indicated oxidization states. WD+−A and WD−A+ denote the interaction energies between the D and A groups in the initial and final diabatic states, respectively. They are evaluated as energies of electrostatic interaction by using restraint electrostatic potential (RESP) charges that fit the quantum mechanical electrostatic potential on a specified grid. This is performed through the ESP module in the NWCHEM program,60 using a hyperbolic restraining of the partial atomic charges. After suitable testing, the maximum distance between a grid point and any of the atomic centers was set at the value 0.5 nm, against the default value of 0.3 nm, for a stricter fitting procedure. To the same aim, a grid spacing of 0.008 nm has been used against a default value of 0.05 nm.
CDFT diabatic states. The localized electronic states ∣ψI⟩=∣D+,A⟩ and ∣ψF⟩=∣D,A+⟩ are obtained from CDFT (Ref. 49) self-consistent field calculations on the overall system. As shown in Ref. 49, CDFT essentially consists in finding an effective external potential that, once added to the Hamiltonian, gives the electronic state of lowest energy satisfying a specific density constraint. In the present context, a unit positive charge is localized in the donor (acceptor) group for the initial (final) diabatic state. ΔEIF is directly given by the difference between the CDFT energies EI and EF. Hence, the approximations incidental to the partition in Eq. 17 and its evaluation are avoided and can be tested. All the CDFT calculations were performed with the Löwdin population scheme, while the Becke scheme turned out not to be feasible for the systems under study and the employed hybrid-DFT scheme.
Hybrid-DFT implementation. The electronic quantities required by the above two recipes are derived from spin-unrestricted hybrid-DFT calculations, using the NWCHEM package.60 The Becke half-and-half (here denoted BHH) hybrid XC functional61 is employed. It comprises Hartree–Fock exchange (which is essentially equal to the exact Kohn–Sham exchange61), Slater exchange, and PW91-LDA correlation. It derives from the rigorous adiabatic connection formula for the XC energy of Kohn–Sham DFT (Ref. 62) after linear interpolation of the interelectronic coupling-strength parameter, which switches on the Coulomb repulsion between electrons. Thus, BHH, as compared with other hybrid functionals, rests on a clear theoretical basis, without empirical choice for the amount of exact exchange. Moreover, in recent works the half-and-half choice has been successfully applied to the study of various properties of many π-stacked aromatic complexes, producing results in good agreement with high-quality post-HF calculations and experimental data.63, 64, 65, 66, 67 In this paper I propose the implementation of Eq. 12 in a hybrid DFT scheme with the BHH XC functional as a reliable approach to evaluation of the transfer integrals and the corresponding excitation energies in DNA stacks. The computational approach can also be applied to π-stacked systems of prohibitive size for the more expensive post-HF calculations. Moreover, it is worth noting that Eq. 12 can be used in whichever DFT scheme that is suitable for a given CT system and can be implemented in different computational schemes.
COMPUTATIONAL RESULTS AND DISCUSSION
In this section, I present calculations of the transfer integrals in the GG and GT single-stranded base dimers from B-DNA, using both the new method of Eq. 12 and the prototype approach48 in Eq. 11. The results from Eq. 12 are compared with those from Eq. 11, thus appreciating the advantages of the new methodology. Moreover, a comparison with the results from other methods is afforded, in order to test the performance of the hybrid-DFT implementation of Eq. 12 against the results from different methods on the DNA systems under consideration. This comparison is useful also in the light of future implementations of Eq. 12 in diverse computational schemes.
Effective electronic coupling in the GT dimer
My results for the effective electronic coupling and the excitation energy in the GT system, using both the TP and CDFT diabatic states and diverse atomic basis sets, are presented in the top panel of Table 1. The other two panels report, for comparison, results obtained by other authors with different theoretical and computational setups.
Table 1.
Upper panel: Relevant quantities for the 5′-GT-3′ base stack from regular B-DNA (the DFT values of this work use the BHH hybrid functional; coordinates are taken from Ref. 26), calculated in this work using both the TP and CDFT diabatic states, and different atomic basis sets. All the energy quantities are given in eV. The vertical excitation energy ΔEv and the transfer integral VIF are computed through the rightmost term of Eqs. 5, 12, respectively. The approximate estimates of the transfer integral by means of Eq. 11, using both the and parameters, and the quantities 2ab and SIF are also tabulated for the TP states. Center panel: the values of HIF, VIF, and SIF from Ref. 25 are reported for comparison. Bottom panel: HF and post-HF values of ΔEv, VIF, and the transition dipole moment μ12 (in a.u.) from Ref. 26.
| Method | ΔEv | VIF | ∣SIF∣ | ∣2ab∣ | ΔEv CDFT | VIF CDFT | ∣SIF CDFT∣ | ||
|---|---|---|---|---|---|---|---|---|---|
| This work | |||||||||
| 6-31g* | 1.335 | 0.140 | 0.012 | 0.195 | 0.132 | 0.149 | 1.300 | 0.135 | 0.053 |
| 6-31g** | 1.332 | 0.141 | 0.012 | 0.197 | 0.133 | 0.150 | 1.298 | 0.135 | 0.053 |
| 6-311g** | 1.334 | 0.132 | 0.015 | 0.181 | 0.122 | 0.142 | 1.317 | 0.128 | 0.064 |
| 6-311g**∕6-311++g** | 1.318 | 0.132 | 0.018 | 0.180 | 0.121 | 0.144 | 1.348 | 0.133 | 0.133 |
| 6-31++g** | 1.291 | 0.134 | 0.017 | 0.189 | 0.124 | 0.145 | |||
| 6-311++g** | 1.295 | 0.130 | 0.018 | 0.181 | 0.119 | 0.142 | |||
| 6-311++g(3df,3pd) | 1.297 | 0.127 | 0.017 | 0.176 | 0.116 | 0.138 | |||
| cc-pVDZ | 1.354 | 0.132 | 0.014 | 0.179 | 0.123 | 0.141 | 1.339 | 0.125 | 0.058 |
| cc-pVTZ | 1.326 | 0.129 | 0.016 | 0.176 | 0.118 | 0.140 | 1.311 | 0.126 | 0.070 |
| aug-cc-pVDZ | 1.290 | 0.129 | 0.017 | 0.180 | 0.118 | 0.140 | |||
| aug-cc-pVTZ | 1.298 | 0.126 | 0.017 | 0.174 | 0.115 | 0.137 | |||
| TZVP | 1.312 | 0.132 | 0.018 | 0.180 | 0.120 | 0.143 | 1.247 | 0.144 | 0.097 |
| Reference 25 | VIF(HIF) | ∣SIF∣ | |||||||
| DFT, FO, TZ2P | 0.141(0.334) | 0.023 | |||||||
| Reference 26 | ΔEv | VIF | μ12 (a.u.) | ||||||
| GMH-KTA∕6-31g* | 1.574 | 0.137 | 0.548 | ||||||
| CASSCF(7,8) | 1.799 | 0.098 | 0.340 | ||||||
| CASSCF(11,12) | 1.415 | 0.097 | 0.424 | ||||||
| CAS-PT2(11,12) | 1.175 | 0.081 | |||||||
Performance of the method and comparison with the prototype method of Eq. 11. The two-state approximation turns out to be well satisfied by the two types of diabatic states for both the systems studied in this work. This is quantified through the modulus of the ground state vector, N=⟨ψ∣ψ⟩1∕2, as obtained from its expression in terms of the diabatic states, i.e., ∣ψ⟩=a∣ψI⟩+b∣ψF⟩. In fact, I obtain values of N ranging from 0.992 to more than 0.999 with different computational setups.
Basis set effects are tested. They are relatively small. Yet, a decrease in the vertical excitation energy, ΔEv, after introduction of diffuse functions can be appreciated. The basis sets of highest quality [i.e., the largest Pople-style basis set, 6-311++g(3df,3pd),68 and Dunning’s correlation consistent polarized valence triple-zeta basis set, aug-cc-pVTZ (Ref. 69)] used in this work produce essentially identical results. I reckon them as the best values, reported in bold in the table.
In Table 1 the performance of the refined Eq. 12 is compared, for disparate basis sets, with that of Eq. 11 (which depends only implicitly on SIF, through parameters a and b), as expressed in terms of either a and b or A and B. There is a very good convergence of both the effective electronic couplings and the vertical excitation energies with respect to the basis set, once the latter has a triple-zeta quality and includes diffuse functions. As for the effective electronic couplings, UIF(a,b,ΔEIF) and UIF(A,B,ΔEIF) (i.e., and , respectively, in the shorthand notation of the tables) systematically give lower and upper approximations to VIF, respectively. The relative errors due the use of Eq. 11 are always less than 10%, essentially reflecting the values of the corresponding ratios SIF∕(2ab) [see Eq. 12]. On the other hand, the CDFT diabatic states show 2ab values comparable to the ones for the TP states, against a much larger overlap, which prevents the use of Eq. 11. For example, with the TZVP basis set, the two values and are obtained, while VIF CDFT=0.144 eV. Note that all the ΔEv and VIF values from TP and CDFT diabatic states agree up to the second significant digit, except for the TZVP estimates, which show slightly larger differences.
The CDFT diabatic states do not allow the use of basis sets with many diffuse functions. Nevertheless, the latter can be included for the crucial atoms; e.g., I report a calculation at the mixed 6-311g**∕6-311++g** level of the basis set, where diffuse functions were added to the atoms involved in the charge distributions of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), which are usually the most important orbitals in the single-particle picture of a CT process. As shown by the table, the mixed basis set gives good estimates of both ΔEv and VIF in spite of the very large value of SIF, thus further promoting the use of CDFT diabatic states in Eq. 12.
Among the basis sets allowing the use of both the TP and CDFT states, the best overall performance is yielded by the cc-pVTZ basis set.69 It gives very consistent estimates of ΔEv and VIF, and thus of ΔEIF, from the two sets of diabatic states (e.g., the two values of ΔEIF agree within ∼1%), which validates the use of Eq. 17. Hence, ΔEIF is essentially given by the different electrostatic interactions between the D and A groups once the valence charge is differently localized. This is a consequence of the fact that, as in other stacked DNA nucleobase dimers,30 donor and acceptor are not symmetry equivalent and are off resonance. Note that the cc-pVTZ values using the CDFT diabatic electronic states are close to the best estimates using the 6-311++g(3df,3pd) and aug-cc-pVTZ basis sets in conjunction with the TP diabatic states. Moreover, also other basis sets allowed by the CDFT states, such as 6-311g** and cc-pVDZ, show good performances compared to the best estimates.
In general, while the CDFT diabatic states offer a more straightforward computational implementation of Eq. 12, the TP states allow use of more accurate setups for the self-consistent field calculations. In fact, CDFT computation is hardly feasible (or even unfeasible) in the presence of atomic basis sets with many diffuse functions. Moreover, the CDFT diabatic states are characterized by a significantly larger overlap than the corresponding TP ones (see Table 1). Their definition reaches the largest uncertainties for quite close redox sites and depends on the population scheme used in setting the charge constraints.49 Nevertheless, the above results support their use by showing that they allow a satisfactory computational accuracy for the study of CT in DNA π-stacks. In fact, Eq. 12 yields accurate results also using CDFT diabatic states with large overlaps, which are obtained in many biochemical systems (e.g., the GT base pair under study) and are not manageable with Eq. 11. CDFT states can be a valuable choice in the DFT implementation of Eq. 12 and become essential in DFT studies of CT systems where a covalent bridge between donor and acceptor has to be considered.
Comparison with other methods. As shown in Table 1, my best estimates of transfer integral and vertical excitation energy (in bold in the table) are smaller than the one-electron values obtained within the framework of the generalized Mulliken–Hush (GMH)39 method as implemented in Ref. 26, where HF theory and Koopmans’ theorem50 approximation (KTA) are used. The discrepancy is significant for ΔEv. As confirmed by the results using the CDFT states, this discrepancy cannot be attributed to the approximations involved in the calculation of ΔEIF by means of Eq. 17. In fact, the latter turns out to work quite well for the non-symmetry-equivalent and well-separated D and A groups considered in this work. While the reasons for the above discrepancy are not further investigated in this work, it is worth noting that the implementations of Eq. 12 presented in Sec. 2B do not resort to the one-electron and KTA approximations. Rather, they use full-electron calculations, thus including relaxation effects.
Importantly, the ΔEv estimates by this work are midway between the post-HF results of Ref. 26 using the largest active space (i.e., 11 electrons within 12 π-orbitals). The ΔEv value from CASSCF(11,12) is larger than my DFT estimates with basis sets of disparate accuracy. Such a circumstance supports the theoretical-computational method proposed in this work, because CASSCF has a well-known tendency to overestimate the excitation energies in many physical contexts.70, 71, 72, 73, 74 On the converse, the ΔEv value from CAS-PT2(11,12) is smaller than the DFT values of this work. Note that CAS-PT2 tends to underestimate vertical excitation energies,71, 74, 75, 76 which can be corrected by employing a suitable value of an empirical level shift parameter,71, 76 though a residual appreciable underestimation of ΔEv can be obtained.71 Therefore, the comparison with the present results depends on the effectiveness of the level shift parameter used in Ref. 26. Moreover, also the here employed hybrid-DFT scheme can suffer from computational errors, due to the approximate character of the adopted (as well as of any currently available) XC functional. At last, the results from both this work and Ref. 26 should be tested against desired experimental data that allow a direct and accurate comparison with theory. In any case, the best values of ΔEv provided by this work and Ref. 26 differ by less than 10% and thus identify a relatively narrow probable range for the true excitation energy. In fact their agreement is within the computational errors. In particular, changes in the CAS-PT2 excitation energies by ∼0.1–0.3 eV can be usually expected by applying the empirical shift parameter.76
A different scenario comes out for the transfer integrals. The VIF best values of this work, i.e., 0.127 and 0.126 eV at the BHH∕6-311++g(3df,3pd) and BHH∕aug-cc-pVTZ computational levels, respectively, are significantly larger than the multireference values in Ref. 26 and ∼10% smaller than the DFT and HF estimates from Refs. 25, 26, respectively. The discrepancy with the HF estimate in Ref. 26 becomes negligible when the same basis set is used. In fact, at the 6-31g* level, I obtain a VIF value of 0.135 eV (0.140 eV) using the CDFT (TP) states, against the HF value of 0.137 eV from Ref. 26. This seems to indicate that the slight discrepancies between the two works are essentially a basis set effect. However, this explanation is not satisfactory by jointly considering the following points: (i) the HF evaluations of both VIF and ΔEv depend only weakly on the basis set.21, 30, 44 (ii) The estimates of the vertical excitation energy by the two works show an appreciable discrepancy even if the same 6-31g* basis set is used. (iii) VIF and ΔEv are strictly related, as shown by Eq. 5 or, within the GMH approach, by the equation39
| (18) |
where μ12 is the transition dipole moment connecting the two adiabatic states in the CT transition, and μ1−μ2 is the difference between the respective dipole moments. Hence, the discrepancies between the results from the two works have to be at least partially ascribed to inherently different approximations. For example, on the one hand, μ12 depends on the charge distribution in the CT fragments, which is calculated without accounting of electron correlation in the HF approach; on the other hand, the hybrid-DFT approach includes electron correlation, but may be affected by residual electron self-interaction, which is expected to be more effective when the 6-31g* basis set or smaller basis sets are used, as they do not yield an accurate enough description of the electron correlation.
The significant discrepancy with the VIF values from multireference calculations corresponds to a larger degree of charge localization in the latter. The current data do not allow to establish which of the two methods yield a better description of the correct charge distribution in the system under study. In fact, multireference approaches are also not exempt from shortcomings, such as the following ones: (i) They include the electron correlation only in the active space. (ii) In order to achieve quantitative accuracy, they generally need empirical decisions in the choice and handling of the active orbitals.59, 77 (iii) Large basis sets that are affordable in the hybrid-DFT approach (e.g., see the data in Table 1), as well as in other DFT computational schemes,25 are often excessively expensive or unfeasible for post-HF methods such as CASSCF or CAS-PT2. (iv) The convergence with respect to the active space can be hardly achieved for relatively large systems. In fact, with reference to the last point, the comparison of the transfer integral estimates by my approach and the multireference calculations in Ref. 26 is complicated by the fact that the data reported in the Table III of Ref. 26 do not provide us with enough information about the achievement of the convergence with respect to the active space, while the use of larger active spaces is still unfeasible. In particular, the CAS-PT2(11,12) electronic couplings use the CASSCF(11,12) transition dipole moments26 and the latter show a large increase in passing from the (7,8) to the (11,12) active space. Thus, a further increase with the size of the active space would lead to VIF estimates closer to the best value in this work and to the GMH-KTA value in the same Ref. 26.
My estimates of VIF employing basis sets of triple-zeta quality are systematically lower by about 10% than the value of 0.141 eV from Ref. 25, which makes use of the triple-zeta double-polarization TZ2P basis set in ADF.78 This value is obtained in two steps: (i) HIF is calculated with a DFT fragment-orbital (FO) approach, exploiting the HOMOs on the individual bases; (ii) VIF is derived from the Löwdin transformation79VIF=HIF−SIF(HII+HFF)∕2. The resulting values of HIF and VIF are very different, due to the large value of SIF. Indeed, the evaluations of VIF exploiting the Löwdin transformation are very sensitive to the value of the overlap between the diabatic states. As a numerical example, if SIF is endowed with a computational error of 0.001, i.e., SIF=0.023±0.001, the corresponding range of VIF, calculated according to Ref. 25, is 0.133–0.149 eV. For comparison, if the SIF estimate of this work at the TZVP level80 is affected by the same absolute error, SIF=0.023±0.001 (which, indeed, would mean an even larger relative error on the overlap), then the corresponding VIF value from Eq. 12 is in the quite small relative range of 0.131–0.132 eV. This is an important point if the best choice of the diabatic states for a given system leads to a nonzero overlap. Then, small errors in the SIF value coming from the approximations of the physical model and∕or the computation (e.g., a nonsufficiently large atomic basis set) can lead to significant errors in the derivation of the transfer integral from HIF and the Löwdin transformation (or, equivalently, the secular equation). This issue becomes even more critical when multielectron calculations are performed, because then the relation between HIF and VIF involves the delicate numerical difference of two energy quantities much larger than their difference. Moreover, it is related to the general problem of the definition of the diabatic states,49, 81 which is magnified for large overlaps.
In the above respect, the theoretical method defined by Eq. 12 offers as a valuable approach to transfer integral calculations, irrespective of the overlap between the employed diabatic states, insofar as they provide a good vector basis for the two-state model. Furthermore, note that Eq. 12 can also be implemented in the FO approach of Ref. 25.
At last, the refined theoretical method presented in this work, combined with appropriate hybrid-DFT setups, permits a reliable use of the CDFT diabatic states even when the corresponding SIF is so large to prevent the use of the previously employed48, 82, 83, 84 Eq. 11. Nevertheless, the latter remains an efficient tool for transfer integral evaluation in many CT systems, where donor and acceptor can be separated, so that the TP states can be used, or they are far enough (in long-range ET) that CDFT states with suitably small overlap can be obtained. I wish to stress that the CDFT approach of Ref. 49 affords a “natural” construction of the CT diabatic states. It exploits the idea85 that, by an appropriate choice of the external potential, DFT allows to achieve the lowest energy state of a system with an arbitrary density constraint. The approach developed in Ref. 49 provides a direct and self-consistent accomplishment of that idea. Another valuable method to localize the valence charge consists in the introduction of a suitable penalty functional that imposes an energy cost to electronic states with fractional occupation of the ion centers.86 Indeed, Eq. 12 is amenable to both these approaches to charge localization in DFT schemes. Moreover, it can be implemented in computational schemes other than DFT, where different localization methods are adopted.
Effective electronic coupling in the GG dimer
The results for the effective electronic coupling and the adiabatic excitation energy in the GG system from Eqs. 12, 5, respectively, are reported in the top panel of Table 2. Previous results by other authors are reported in the following panels.
Table 2.
Upper panel: Adiabatic excitation energy (ΔEv), effective electronic coupling (VIF), overlap between the diabatic electronic states (SIF), approximate estimates of VIF from Eq. 11 with both the (Ref. 87) and coefficients, for a GG base stack from regular B-DNA, calculated in this work using the BHH functional. Second panel: Values of VIF, HIF (in parentheses), and SIF from Ref. 25 reported for comparison. Third panel: VIF and HIF (in parentheses) values from Ref. 88. Bottom panel: HF and post-HF values of ΔEv, VIF, and transition dipole moment μ12 (in a.u.) from Ref. 26. Coordinates are taken from Ref. 26.
| Method | ΔEv | VIF | ∣SIF∣ | ||
|---|---|---|---|---|---|
| This work | |||||
| 6-311++g(3df,3pd) | 0.427 | 0.067 | 0.008 | 0.065 | 0.069 |
| aug-cc-pVTZ | 0.427 | 0.067 | 0.007 | 0.065 | 0.069 |
| TZVP | 0.447 | 0.078 | 0.008 | 0.076 | 0.079 |
| TZVP, CDFT | 0.461 | 0.081 | 0.052 | 0.069 | 0.093 |
| Reference 25 | VIF(HIF) | ∣SIF∣ | |||
| DFT, FO, TZ2P | 0.053(0.119) | 0.008 | |||
| Reference 88 | VIF(HIF) | ||||
| SCC-DFTB | 0.061(0.087) | ||||
| Reference 26 | ΔEv | VIF | μ12 (a.u.) | ||
| GMH-KTA∕6-31g* | 0.472 | 0.083 | 1.120 | ||
| CASSCF(7,8) | 0.414 | 0.067 | 1.015 | ||
| CASSCF(11,12) | 0.370 | 0.049 | 0.819 | ||
| CAS-PT2(11,12) | 0.392 | 0.051 | |||
Performance of the method and comparison with the prototype method of Eq. 11. As compared with the GT system, the GG stack has a smaller transfer integral and a correspondingly smaller SIF for both the sets of diabatic states. This allows accurate estimates of the effective electronic coupling from Eq. 11, hence of ΔEv from Eq. 5, using the TP states; e.g., the transfer integrals from Eq. 11 (Ref. 87) and Eq. 12 using the TZVP basis set differ by ∼3%. On the other hand, the accuracy of Eq. 11 using the CDFT states, though significantly improved as compared with the GT system, is still relatively low. In fact, the TZVP basis set leads to the values and , while VIF CDFT=0.081 eV. Note also that the TZVP basis set, lacking of the diffuse functions, appears to provide a less accurate description of the valence charge distribution in the GG stack than the other two basis sets. On the contrary, the results using the largest basis sets, which are reported in the first two rows of the table, are essentially identical.
Comparison with other methods. The best values in Table 2 show good matching with the corresponding results from CASSCF(7,8) calculations,26 yielding a close value of the vertical excitation energy and the same effective electronic coupling, within the accuracy afforded in Table 2. For the GG system the multireference results do not show a monotonic trend by improving the level of the calculation. Within the CASSCF scheme, the appreciable decrease in ΔEv with the size of the active space points to the need for a larger active space. On the other hand, the CAS-PT2 calculations include the multistate formulation MS-PT2,26 therefore improving the description of both static and dynamic electron correlation. The increase in ΔEv in passing from CASSCF(11,12) to CAS-PT2(11,12) stresses the importance of electron correlation effects (note, however, that μ12 is not recalculated at the CAS-PT2 level). In fact, the DFT and post-HF approaches considered in Table 2 give values of both ΔEv and VIF consistently lower than the reported HF calculations. Therefore, the estimate of the average transfer integral in a GG system through methods not properly including electron correlation can be affected by appreciable systematic errors. Instead, the hybrid-DFT implementation of Eq. 12 yields a feasible and accurate method for evaluating the average transfer integral. Furthermore, it offers a high ratio between quality of the results and computational cost, as it rests on a few quantities easily derived from self-consistent field calculations. Indeed, its approximate formulation of Eq. 11, whose computational cost is the same as for Eq. 12, has been already applied in combination with MD to relatively large quantum systems (up to 142 atoms)83 and in conjunction with Car–Parrinello MD (Ref. 89) to the thorny ferrous-ferric redox system.84 In both cases the TP diabatic states were characterized by suitably small overlaps, allowing a careful use of Eq. 11 (see also note in Ref. 56).
My VIF values at the BHH∕6-311++g(3df,3pd) and aug-cc-pVTZ levels are close to a recent estimate from Ref. 88, which employs the same approach as in Ref. 25 except for the use of the approximate self-consistent-charge density functional tight-binding (SCC-DFTB) method rather than full DFT as in Ref. 25. The estimates of VIF from Refs. 25, 88 show a moderate relative difference, while the respective values of HIF, hence of the gap between HIF and VIF, differ significantly, which can depend on the use of the Löwdin transformation and∕or on the different levels of the corresponding calculations (e.g., a not full correction of the tendency of the DFTB approach to yield an excessive localization of the net charge in electronic systems involving π-orbitals90). Anyway, my best value for VIF falls in the gap between the estimates of HIF and VIF from both Refs. 25, 88 and is larger than both the reported VIF values. This agrees with the fact that the exact value of VIF can only be increased by the quadratic terms in SIF neglected by the Löwdin transformation, although the relative magnitudes of my estimate of VIF and the two reported DFT values25, 88 can be determined by other relevant features of the different theoretical approaches, as in the case of the GT nucleobase stack.
CONCLUSIONS
I formulate a theoretical method for transfer integral and vertical excitation energy calculation, which is closely related to a method recently appeared in the literature48 and extends its applicability to broader classes of redox systems. The current formulation uses the two-state model, as described by the secular Eq. 2, without any further approximation. In particular, the limitations for the overlap between the diabatic states imposed in Ref. 48 are removed by the theoretical treatment of this work. The use of a given couple of diabatic states is limited only by its intrinsic quality as a set of localized electronic states able to accomplish the two-state model. Furthermore, the multistate theory of Ref. 48 suggests that Eq. 12 may have a good performance also beyond that approximation. This is the subject of a future study, while the two-state condition is well satisfied by the DNA nucleobase stacks considered in this work, as well as by many other molecular systems of interest to biochemistry and molecular electronics.
Both Eqs. 11, 12 have been presently implemented in (hybrid-)DFT schemes, although they involve a few electronic quantities which can be easily derived also from other computational schemes. The choice in this work rests on the fact that, in spite of the approximations incidental to any available XC functional, DFT or hybrid-DFT computational schemes offer the best compromise between accuracy and feasibility for the study of disparate biochemical contexts,91 because they include electron correlation and are manageable also in relatively large systems. An important methodological advantage of Eq. 12 relative to Eq. 11 consists in its general applicability with CDFT or otherwise localized electronic states which are characterized by a significantly larger overlap than the TP states. In previous works,48, 82, 83, 84, 87 Eq. 11 has been used in conjunction with TP diabatic states, whose construction has been allowed by the absence of covalent bridges participating in the relevant ET processes. However, this equation cannot be applied with suitable accuracy to CT systems where donor and acceptor cannot be separated and the overlap between the appropriate localized states is relatively large, so that the use of Eq. 12 becomes essential. Moreover, for the CT systems where both equations can be used, Eq. 12 is anyway more accurate than Eq. 11 at the same computational cost, as here shown on DNA stacks.
Equation 12, as well as Eq. 11, allows to calculate directly the transfer integral, VIF, without passing for the evaluation of the electronic coupling, HIF, and the subsequent use of the Löwdin transformation, or the construction of orthogonal CT diabatic states. This offers methodological simplification, which also favors the accuracy of the proposed theoretical-computational approach. In more general terms, the easy applicability of Eq. 12 in many computational schemes and without further approximations, as well as the fact that it avoids excited state computations, make it the main theoretical achievement of this work.
The refined theoretical method to calculate transfer integrals and CT excitation energies comes from an analytical derivation, different from the one in Ref. 48, which allows to overcome the limitations of Eq. 11. Yet, it rests on a few electronic structure properties directly derived from self-consistent field calculations. In this work, the performance of a hybrid-DFT implementation of Eq. 12 is tested against previous DFT, HF, and post-HF calculations, on the paradigmatic GG and GT base stacks from regular DNA. The discrepancies between the results from different works are appreciable, though unimportant in various cases. In fact, all the discussed methods appear to be valuable approaches to the study of CT processes through DNA π-stacks. On the other hand, Eq. 12 offers a method which is not subject to approximations used in the previous literature, except for the two-state model, and preserves its intrinsic theoretical validity irrespective of the specific physical system and the chosen computational scheme. Moreover, future implementations of Eq. 12 in different many-electron models can yield fruitful investigation of the electron correlation effects and thus of the limitations of the one-electron picture.
ACKNOWLEDGMENTS
I wish to thank Michael L. Klein, Rosa Di Felice, Stefano Corni, Ben Levine, Russel DeVane, Daniele Varsano, Elisa Molinari, Patrick H.-L. Sit, and Janel Lavezzo for helpful discussions. This work has been funded by the NIH, Grant No. GM 067689. Computing time was provided by CMM (University of Pennsylvania, Philadelphia, PA).
APPENDIX: BEHAVIOR OF EQ. 12 AT Qt
In this appendix I show that UIF, hence VIF, has only an eliminable discontinuity at Q=Qt. Solving Eq. 7 under the condition ⟨ψ∣ψ⟩=a2+b2+2abSIF=1, the following expressions are obtained:
| (A1) |
where and s≡sign(UIF). The ratio ∣ΔEIF∕(a2−b2)∣, whose evaluation is critical near Q=Qt, is given by
| (A2) |
Therefore, at the transition state coordinate Qt, where ΔEIF=0 and ΔEv0≡2∣UIF∣, the above ratio takes the finite value ΔEv0(Qt)[1−s(Qt)SIF(Qt)]. Moreover,
| (A3) |
so that
| (A4) |
I conclude, consistently with Ref. 48, that the approximate expressions of the transfer integral and the vertical excitation energy are also correctly related at Q=Qt.
References
- Nitzan A., Annu. Rev. Phys. Chem. 52, 681 (2001). 10.1146/annurev.physchem.52.1.681 [DOI] [PubMed] [Google Scholar]
- Aviram A., Ratner M., and Mujica V., Molecular Electronics II. Annals of the New York Academy of Sciences (The New York Academy of Sciences, New York, 2002), Vol. 960. [Google Scholar]
- Maruccio G., Biasco A., Visconti P., Bramanti A., Pompa P. P., Calabi F., Cingolani R., Rinaldi R., Corni S., Di Felice R., and Molinari E., Adv. Mater. (Weinheim, Ger.) 17, 816 (2005). 10.1002/adma.200400628 [DOI] [Google Scholar]
- Endres R. G., Cox D. L., and Singh R. R. P., Rev. Mod. Phys. 76, 195 (2004). 10.1103/RevModPhys.76.195 [DOI] [Google Scholar]
- Porath D., Cuniberti G., and Di Felice R., Top. Curr. Chem. 237, 183 (2004). [Google Scholar]
- Zwolak M. and Di Ventra M., Rev. Mod. Phys. 80, 141 (2008). 10.1103/RevModPhys.80.141 [DOI] [Google Scholar]
- Heller A., Faraday Discuss. 116, 1 (2000). 10.1039/b006196o [DOI] [PubMed] [Google Scholar]
- Boon E. M., Livingston A. L., Chmiel N. H., David S. S., and Barton J. K., Proc. Natl. Acad. Sci. U.S.A. 100, 12543 (2003). 10.1073/pnas.2035257100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holman M. R., Ito T., and Rokita S. E., J. Am. Chem. Soc. 129, 6 (2007). 10.1021/ja0668365 [DOI] [PubMed] [Google Scholar]
- Braun E., Eichen Y., Sivan U., and Ben-Yoseph G., Nature (London) 391, 775 (1998) 10.1038/35826 [DOI] [PubMed] [Google Scholar]; de Pablo P. J., Moreno-Herrero F., Colchero J., Gómez-Herrero J., Herrero P., Baró A. M., Ordejón P., Soler J. M., and Artacho E., Phys. Rev. Lett. 85, 4992 (2000) 10.1103/PhysRevLett.85.4992 [DOI] [PubMed] [Google Scholar]; Storm A. J., van Noort J., de Vries S., and Dekker C., Appl. Phys. Lett. 79, 3881 (2001) 10.1063/1.1421086 [DOI] [Google Scholar]; Gomez-Navarro C., Moreno-Herrero F., de Pablo P. J., Colchero J., Gómez-Herrero J., and Baró A. M., Proc. Natl. Acad. Sci. U.S.A. 99, 8484 (2002). 10.1073/pnas.122610899 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Porath D., Bezryadin A., De Vries S., and Dekker C., Nature (London) 403, 635 (2000) 10.1038/35001029 [DOI] [PubMed] [Google Scholar]; Xu B., Zhang P., Li X., and Tao N., Nano Lett. 4, 1105 (2004) 10.1021/nl0494295 [DOI] [Google Scholar]; Van Zalinge H., Schiffrin D. J., Bates A. D., Haiss W., Ulstrup J., and Nichols R. J., ChemPhysChem 7, 94 (2006) 10.1002/cphc.200500413 [DOI] [PubMed] [Google Scholar]; Kang N., Erbe A., and Scheer E., New J. Phys. 10, 023030 (2008). 10.1088/1367-2630/10/2/023030 [DOI] [Google Scholar]
- Nitzan A., J. Phys. Chem. A 105, 2677 (2001) 10.1021/jp003884h [DOI] [Google Scholar]; Nitzan A. and Ratner M. A., Science 300, 1384 (2003) 10.1126/science.1081572 [DOI] [PubMed] [Google Scholar]; Berlin Y. A. and Ratner M. A., Radiat. Phys. Chem. 74, 124 (2005). [Google Scholar]
- Marcus R. A. and Sutin N., Biochim. Biophys. Acta 811, 265 (1985). [Google Scholar]
- Eyring H., J. Chem. Phys. 3, 107 (1935) 10.1063/1.1749604 [DOI] [Google Scholar]; Eyring H., Chem. Rev. (Washington, D.C.) 17, 65 (1935). 10.1021/cr60056a006 [DOI] [Google Scholar]
- Kuznetsov A. M. and Ulstrup J., Electron Transfer in Chemistry and Biology (Wiley, New York, 1999). [Google Scholar]
- Landau L. D., Phys. Z. Sowjetunion 1, 88 (1932) [Google Scholar]; Landau L. D., Phys. Z. Sowjetunion 2, 46 (1932) [Google Scholar]; Zener C., Proc. R. Soc. London, Ser. A 137, 696 (1932) 10.1098/rspa.1932.0165 [DOI] [Google Scholar]; Zener C., Proc. R. Soc. London, Ser. A 140, 660 (1933). 10.1098/rspa.1933.0095 [DOI] [Google Scholar]
- Schuster G. B., Acc. Chem. Res. 33, 253 (2000). 10.1021/ar980059z [DOI] [PubMed] [Google Scholar]
- Giese B., Acc. Chem. Res. 33, 631 (2000). 10.1021/ar990040b [DOI] [PubMed] [Google Scholar]
- O’Neill M. A. and Barton J. K., Top. Curr. Chem. 236, 67 (2004). [Google Scholar]
- Bixon M., Giese B., Wessely S., Langenbacher T., Michel-Beyerle M. E., and Jortner J. J., Proc. Natl. Acad. Sci. U.S.A. 96, 11713 (1999). 10.1073/pnas.96.21.11713 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voityuk A. A., Jortner J., Bixon M., and Rösch N., J. Chem. Phys. 114, 5614 (2001). 10.1063/1.1352035 [DOI] [Google Scholar]
- Tong G. S. M., Kurnikov I. V., and Beratan D. N., J. Phys. Chem. B 106, 2381 (2002). 10.1021/jp013387g [DOI] [Google Scholar]
- Jortner J., Bixon M., Voityuk A. A., and Rösch N., J. Phys. Chem. A 106, 7599 (2002). 10.1021/jp014232b [DOI] [Google Scholar]
- Berlin Y. A., Kurnikov I. V., Beratan D. N., Ratner M. A., and Burin A. L., Top. Curr. Chem. 237, 1 (2004). [Google Scholar]
- Senthilkumar K., Grozema F. C., Fonseca Guerra C., Bickelhaupt F. M., Lewis F. D., Berlin Y. A., Ratner M. A., and Siebbeles L. D. A., J. Am. Chem. Soc. 127, 14894 (2005). 10.1021/ja054257e [DOI] [PubMed] [Google Scholar]
- Blancafort L. and Voityuk A. A., J. Phys. Chem. A 110, 6426 (2006). 10.1021/jp061184s [DOI] [PubMed] [Google Scholar]
- Ivanova A., Shushkov P., and Rösch N., J. Phys. Chem. A 112, 7106 (2008). 10.1021/jp8031513 [DOI] [PubMed] [Google Scholar]
- Kubař T. and Elstner M., J. Phys. Chem. B 113, 5653 (2009). 10.1021/jp901888r [DOI] [PubMed] [Google Scholar]
- Delaney S. and Barton J. K., J. Org. Chem. 68, 6475 (2003). 10.1021/jo030095y [DOI] [PubMed] [Google Scholar]
- Rösch N. and Voityuk A. A., Top. Curr. Chem. 237, 37 (2004). [Google Scholar]
- Priyadarshy S., Risser S. M., and Beratan D. N., J. Phys. Chem. 100, 17678 (1996). 10.1021/jp961731h [DOI] [Google Scholar]
- Steenken S. and Jovanovic S. V., J. Am. Chem. Soc. 119, 617 (1997). 10.1021/ja962255b [DOI] [Google Scholar]
- Giese B., Amaudrut J., Köhler A. -K., Spormann M., and Wessely S., Nature (London) 412, 318 (2001). 10.1038/35085542 [DOI] [PubMed] [Google Scholar]
- Nakatani K., Dohno C., and Saito I., J. Am. Chem. Soc. 121, 10854 (1999). 10.1021/ja9920213 [DOI] [Google Scholar]
- Conwell E. M., Bloch S. M., Mclaughlin P. M., and Basko D. M., J. Am. Chem. Soc. 129, 9175 (2007). 10.1021/ja0691472 [DOI] [PubMed] [Google Scholar]
- Grozema F. C., Tonzani S., Berlin Y. A., Schatz G. C., Siebbles L. D. A., and Ratner M. A., J. Am. Chem. Soc. 130, 5157 (2008). 10.1021/ja078162j [DOI] [PubMed] [Google Scholar]
- Farazdel A., Dupuis M., Clementi E., and Aviram A., J. Am. Chem. Soc. 112, 4206 (1990). 10.1021/ja00167a016 [DOI] [Google Scholar]
- Zhang L. Y., Friesner R. A., and Murphy R. B., J. Chem. Phys. 107, 450 (1997). 10.1063/1.474406 [DOI] [Google Scholar]
- Cave R. J. and Newton M. D., Chem. Phys. Lett. 249, 15 (1996) 10.1016/0009-2614(95)01310-5 [DOI] [Google Scholar]; Cave R. J. and Newton M. D., J. Chem. Phys. 106, 9213 (1997). 10.1063/1.474023 [DOI] [Google Scholar]
- Skourtis S. S. and Beratan D. N., Adv. Chem. Phys. 106, 377 (1999). 10.1002/9780470141656.ch8 [DOI] [Google Scholar]
- Regan J. J. and Onuchic J. N., Adv. Chem. Phys. 107, 497 (1999). 10.1002/9780470141663.ch9 [DOI] [Google Scholar]
- Prezhdo O. V., Kindt J. T., and Tully J. C., J. Chem. Phys. 111, 7818 (1999). 10.1063/1.480117 [DOI] [Google Scholar]
- Voityuk A., Rösch N., Bixon M., and Jortner J., J. Phys. Chem. B 104, 9740 (2000). 10.1021/jp001109w [DOI] [Google Scholar]
- Voityuk A. A. and Rösch N., J. Chem. Phys. 117, 5607 (2002). 10.1063/1.1502255 [DOI] [Google Scholar]
- Zheng X. H. and Stuchebrukhov A. A., J. Phys. Chem. B 107, 9579 (2003). 10.1021/jp022316u [DOI] [Google Scholar]
- Prytkova T. R., Kurnikov I. V., and Beratan D. N., J. Phys. Chem. B 109, 1618 (2005). 10.1021/jp0457491 [DOI] [PubMed] [Google Scholar]
- Nishioka H., Kimura A., Yamato T., Kawatsu T., and Kakitani T., J. Phys. Chem. B 109, 1978 (2005). 10.1021/jp046282x [DOI] [PubMed] [Google Scholar]
- Migliore A., Corni S., Di Felice R., and Molinari E., J. Chem. Phys. 124, 064501 (2006). 10.1063/1.2166233 [DOI] [PubMed] [Google Scholar]
- Wu Q. and Van Voorhis T., Phys. Rev. A 72, 024502 (2005) 10.1103/PhysRevA.72.024502 [DOI] [Google Scholar]; Wu Q. and Van Voorhis T., J. Chem. Phys. 125, 164105 (2006). 10.1063/1.2360263 [DOI] [PubMed] [Google Scholar]
- Koopmans T., Physica 1, 104 (1934). 10.1016/S0031-8914(34)90011-2 [DOI] [Google Scholar]
- Cremer D., Mol. Phys. 99, 1899 (2001). 10.1080/00268970110083564 [DOI] [Google Scholar]
- Dreuw A., Weisman J. L., and Head-Gordon M., J. Chem. Phys. 119, 2943 (2003). 10.1063/1.1590951 [DOI] [Google Scholar]
- Nakamura H. and Truhlar D. G., J. Chem. Phys. 115, 10353 (2001). 10.1063/1.1412879 [DOI] [Google Scholar]
- Franck J., Trans. Faraday Soc. 21, 536 (1926) 10.1039/tf9262100536; [DOI] [Google Scholar]; Condon E. U., Phys. Rev. 28, 1182 (1926). 10.1103/PhysRev.28.1182 [DOI] [Google Scholar]
- For a discussion on the relation among crossing of the diabatic energy surfaces, transfer integral, and minimum adiabatic energy splitting when other electronic states can intervene and an effective two-state model can be introduced, I refer to other works, e.g., Newton M. D., Chem. Rev. (Washington, D.C.) 91, 767 (1991) (and references therein). 10.1021/cr00005a007 [DOI] [Google Scholar]
- In Ref. , Eq. was used to study the distance dependence of the transfer integral in a small model of a blue copper azurin dimer. Table I therein shows that, as the distance between the pertinent redox sites is increased, the quantity 2ab passes from values comparable with unity to values smaller than 10−2. On the other hand, supporting calculations yielded values of SIF smaller than 10−4. This allowed a safe use of Eq. , although the theoretical development of Ref. cannot appreciate an exact upper limit for SIF, except for the necessary condition SIF=o(1).
- Weissbluth M., Atoms and Molecules (Academic, New York, 1978). [Google Scholar]
- Mulliken R. S., J. Chem. Phys. 23, 1833 (1955). 10.1063/1.1740588 [DOI] [Google Scholar]
- Koch W. and Holthausen M. C., A Chemist’s Guide to Density Functional Theory (Wiley, New York, 2000). [Google Scholar]
- Bylaska E. J., de Jong W. A., Govind N., Kowalski K., Straatsma T. P., Valiev M., Wang D., Apra E., Windus T. L., Hammond J., Nichols P., Hirata S., Hackler M. T., Zhao Y., Fan P. -D., Harrison R. J., Dupuis M., Smith D. M. A., Nieplocha J., Tipparaju V., Krishnan M., Wu Q., Van Voorhis T., Auer A. A., Nooijen M., Brown E., Cisneros G., Fann G. I., Fruchtl H., Garza J., Hirao K., Kendall R., Nichols J. A., Tsemekhman K., Wolinski K., Anchell J., Bernholdt D., Borowski P., Clark T., Clerc D., Dachsel H., Deegan M., Dyall K., Elwood D., Glendening E., Gutowski M., Hess A., Jaffe J., Johnson B., Ju J., Kobayashi R., Kutteh R., Lin Z., Littlefield R., Long X., Meng B., Nakajima T., Niu S., Pollack L., Rosing M., Sandrone G., Stave M., Taylor H., Thomas G., van Lenthe J., Wong A., and Zhang Z., NWChem, A Computational Chemistry Package for Parallel Computers, Version 5.1 (Pacific Northwest National Laboratory, Richland, WA, 2007); [Google Scholar]; Kendall R. A., Apra E., Bernholdt D. E., Bylaska E. J., Dupuis M., Fann G. I., Harrison R. J., Ju J., Nichols J. A., Nieplocha J., Straatsma T. P., Windus T. L., and Wong A. T., Comput. Phys. Commun. 128, 260 (2000). 10.1016/S0010-4655(00)00065-5 [DOI] [Google Scholar]
- Becke A. D., J. Chem. Phys. 98, 1372 (1993). 10.1063/1.464304 [DOI] [Google Scholar]
- Harris J. and Jones R. O., J. Phys. F: Met. Phys. 4, 1170 (1974) 10.1088/0305-4608/4/8/013 [DOI] [Google Scholar]; Gunnarsson O. and Lundqvist B. I., Phys. Rev. B 13, 4274 (1976) 10.1103/PhysRevB.13.4274 [DOI] [Google Scholar]; Langreth D. C., and Perdew J. P., Phys. Rev. B 15, 2884 (1977) 10.1103/PhysRevB.15.2884 [DOI] [Google Scholar]; Harris J., Phys. Rev. A 29, 1648 (1984). 10.1103/PhysRevA.29.1648 [DOI] [Google Scholar]
- Liao M., Lu Y., and Scheiner S., J. Comput. Chem. 24, 623 (2003). 10.1002/jcc.10226 [DOI] [PubMed] [Google Scholar]
- Waller M. P., Robertazzi A., Platts J. A., Hibbs D. E., and Williams P. A., J. Comput. Chem. 27, 491 (2006). 10.1002/jcc.20363 [DOI] [PubMed] [Google Scholar]
- Robertazzi A. and Platts J. A., J. Phys. Chem. A 110, 3992 (2006). 10.1021/jp056626z [DOI] [PubMed] [Google Scholar]
- Anderson J. A. and Tschumper G. S., J. Phys. Chem. A 110, 7268 (2006). 10.1021/jp0613889 [DOI] [PubMed] [Google Scholar]
- Miura M., Aoki Y., and Champagne B., J. Chem. Phys. 127, 084103 (2007). 10.1063/1.2761886 [DOI] [PubMed] [Google Scholar]
- Frisch M. J., Pople J. A., and Binkley J. S., J. Chem. Phys. 80, 3265 (1984). 10.1063/1.447079 [DOI] [Google Scholar]
- T. H.Dunning, Jr., J. Chem. Phys. 90, 1007 (1989). 10.1063/1.456153 [DOI] [Google Scholar]
- Kawashima Y., Nakayama K., Nakan H., and Hirao K., Chem. Phys. Lett. 267, 82 (1997). 10.1016/S0009-2614(97)00084-5 [DOI] [Google Scholar]
- Kühn O., Hachey M. R. D., Rohmer M. M., and Daniel C., Chem. Phys. Lett. 322, 199 (2000). 10.1016/S0009-2614(00)00394-8 [DOI] [Google Scholar]
- Ding W. -J., Fang W. -H., and Liu R. -Z., Chem. Phys. Lett. 369, 570 (2003). 10.1016/S0009-2614(03)00006-X [DOI] [Google Scholar]
- Zhang L., Peslherbe G. H., and Muchall H. M., Photochem. Photobiol. 82, 324 (2006). 10.1562/2005-07-08-RA-605 [DOI] [PubMed] [Google Scholar]
- González-Vázquez J. and González L., Chem. Phys. 349, 287 (2008). 10.1016/j.chemphys.2008.01.043 [DOI] [Google Scholar]
- Grimme S. and Waletze M., Phys. Chem. Chem. Phys. 2, 2075 (2000). 10.1039/b000177p [DOI] [Google Scholar]
- Schreiber M., Silva-Junior M. R., Sauer S. P. A., and Thiel W., J. Chem. Phys. 128, 134110 (2008). 10.1063/1.2889385 [DOI] [PubMed] [Google Scholar]
- Jensen F., Introduction to Computational Chemistry, 2nd ed. (Wiley, Chichester, 2007), pp. 153–159. [Google Scholar]
- Snijders J. G., Vernooijs P., and Baerends E. J., At. Data Nucl. Data Tables 26, 483 (1981). 10.1016/0092-640X(81)90004-8 [DOI] [Google Scholar]
- Löwdin P. O., J. Chem. Phys. 18, 365 (1950). 10.1063/1.1747632 [DOI] [Google Scholar]
- Note that TZVP is not a double-polarization basis set, but this is not relevant to the comparison.
- Stuchebrukhov A. A., J. Chem. Phys. 118, 7898 (2003). 10.1063/1.1563616 [DOI] [Google Scholar]
- Migliore A., Corni S., Di Felice R., and Molinari E., J. Phys. Chem. B 110, 23796 (2006). 10.1021/jp064690q [DOI] [PubMed] [Google Scholar]
- Migliore A., Corni S., Di Felice R., and Molinari E., J. Phys. Chem. B 111, 3774 (2007). 10.1021/jp068773i [DOI] [PubMed] [Google Scholar]
- Migliore A., Sit P. H.-L., and Klein M. L., J. Chem. Theory Comput. 5, 307 (2009). 10.1021/ct800340v [DOI] [PubMed] [Google Scholar]
- Dederichs P. H., Blügel S., Zeller R., and Akai H., Phys. Rev. Lett. 53, 2512 (1984). 10.1103/PhysRevLett.53.2512 [DOI] [PubMed] [Google Scholar]
- Sit P. H.-L., Cococcioni M., and Marzari N., Phys. Rev. Lett. 97, 028303 (2006). 10.1103/PhysRevLett.97.028303 [DOI] [PubMed] [Google Scholar]
- Migliore A., Corni S., Varsano D., Klein M. L., and Di Felice R., J. Phys. Chem. B 113, 9402 (2009). 10.1021/jp904295q [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubař T., Woiczikowski P. B., Cuniberti G., and Elstner M., J. Phys. Chem. B 112, 7937 (2008). 10.1021/jp801486d [DOI] [PubMed] [Google Scholar]
- Car R. and Parrinello M., Phys. Rev. Lett. 55, 2471 (1985). 10.1103/PhysRevLett.55.2471 [DOI] [PubMed] [Google Scholar]
- Niehaus T. A., Di Carlo A., and Frauenheim Th., Org. Electron. 5, 167 (2004). 10.1016/j.orgel.2003.11.001 [DOI] [Google Scholar]
- Nowak M. J., Lapinski L., Kwiatkowski J. S., and Leszczynski J., in Computational Chemistry: Reviews of Current Trends, edited by Leszczynski J. (World Scientific, Singapore, 1997), Vol. 2, pp. 140–216. [Google Scholar]