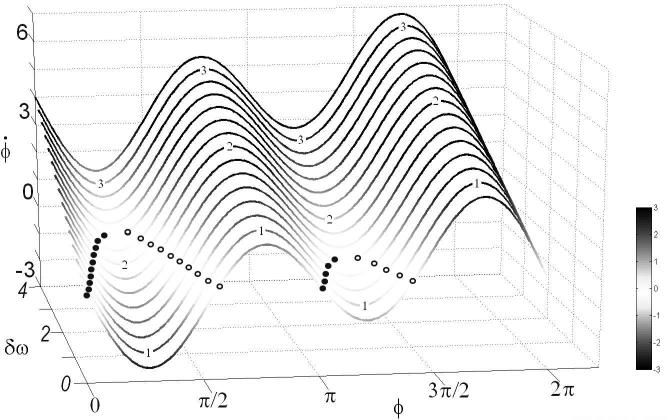
FIGURE 2.

Elementary coordination law (Eq. 1). Surface formed by a family of flows of the coordination variable ϕ (in radians) for increasing values of δω between 0 and 4. For this example, the coupling is fixed: a = 1 and b = 1. When $\stackrel{.}{\varphi }$ reaches zero (flow line becoming white), the system ceases to change and fixed point behavior is observed. Note that the fixed points here refer to emergent collective states produced by nonlinearly coupled elements. Stable and unstable fixed points at the intersection of the flow lines with the isoplane $\stackrel{.}{\varphi }$ = 0 are represented as filled and open circles, respectively. To illustrate the different regimes of the system, three representative lines labeled 1 to 3 fix δω at increasing values. Following the flow line 1 from left to right, two stable fixed points (filled circles) and two unstable fixed points (open circles) exist. This flow belongs to the multistable (here bistable) regime. Following line 2 from left to right, one pair of stable and unstable fixed points is met on the left, but notice the complete disappearance of fixed point behavior on the right side of the figure. That is, a qualitative change (bifurcation; phase transition) has occurred due to the loss of stability of the coordination state near antiphase, π rad. The flow now belongs to the monostable regime. Following line 3 from left to right, no stable or unstable fixed points exist yet coordination has not completely disappeared. This flow corresponds to the metastable regime, a subtle blend of coupling and intrinsic differences between the rhythmic elements in which behavior is neither completely ordered (synchronized) nor completely disordered (desynchronized).