Abstract
We describe a technique to simultaneously estimate a local neural fiber model and trace out its path. Existing techniques estimate the local fiber orientation at each voxel independently so there is no running knowledge of confidence in the estimated fiber model. We formulate fiber tracking as recursive estimation: at each step of tracing the fiber, the current estimate is guided by the previous. To do this we model the signal as a mixture of Gaussian tensors and perform tractography within a filter framework. Starting from a seed point, each fiber is traced to its termination using an unscented Kalman filter to simultaneously fit the local model and propagate in the most consistent direction. Despite the presence of noise and uncertainty, this provides a causal estimate of the local structure at each point along the fiber. Synthetic experiments demonstrate that this approach reduces signal reconstruction error and significantly improves the angular resolution at crossings and branchings. In vivo experiments confirm the ability to trace out fibers in areas known to contain such crossing and branching while providing inherent path regularization.
1 Introduction
The advent of diffusion weighted magnetic resonance imaging has provided the opportunity for non-invasive investigation of neural architecture. Using this imaging technique, neuroscientists want to ask how neurons originating from one region connect to other regions, or how strong those connections may be. For such studies, the quality of the results relies heavily on the chosen fiber representation and the method of reconstructing pathways.
To begin studying the microstructure of fibers, we need a model to interpret the diffusion weighted signal. Such models fall broadly into two categories: parametric and nonparametric. One of the simplest parametric models is the diffusion tensor which describes a Gaussian estimate of the diffusion orientation and strength at each voxel [1, 2]. While robust, this model can be inadequate in cases of mixed fiber presence or more complex orientations [3, 4]. To handle more complex diffusion patterns, various parametric models have been introduced: weighted mixtures [5, 6, 7, 8], higher order tensors [9], directional functions [10, 11, 12], and diffusion oriented transforms [13].
Nonparametric models often provide more information about the diffusion pattern. Instead of estimating a discrete number of fibers as in parametric models, nonparametric techniques estimate an oriented distribution function (ODF) describing an arbitrary configuration of fibers. For this estimation, Tuch [14] introduced Q-ball imaging to numerically compute the ODF using the Funk-Radon transform. The use of spherical harmonics simplified the computation with an analytic form [15, 16, 17] and spherical ridgelets further reduced the coefficients required [18]. Recently, Poupon et al. [19] demonstrated online direct estimation of single-tensor and harmonic coefficients using a linear Kalman filter. Another approach to producing an ODF is to assume a model for the signal response of a single-fiber and use spherical deconvolution [20, 21, 22, 11, 23]. A good review of both parametric and nonparametric models can be found in [24, 25].
Based on these models, several techniques attempt to reconstruct pathways. Deterministic tractography involves directly following the diffusion pathways. In the single tensor model, this means simply following the principal diffusion direction [26], while multi-tensor models often include techniques for determining the number of fibers present or when pathways branch [27, 7, 28, 29]. Kalman and particle filters have been used with single tensor streamline tractography [30, 31, 32], but these are used for path regularization and not to estimate the underlying fiber model. Another approach to regularizing single tensor tractography uses a moving least squares estimate weighted with the previous tensor [33]. While this present study focuses on deterministic techniques, probabilistic methods have been developed to form connections by diffusing out a connectivity map according to the ODF [34, 35, 36, 37].
While parametric methods directly describe the principal diffusion directions, interpreting the ODFs from model independent representations typically involves determining the number and orientation of principal diffusion directions present [38, 39, 20]. For example, Bloy et al. [40] find them as maxima on the surface of a high-order tensor; Descoteaux et al. [25] deconvolve with a sharpening kernel before extracting maxima; and Schultz et al. [41] decompose a high-order tensor into a mixture of rank-1 tensors. Ramirez et al. [42] provide a quantitative comparison of several such techniques.
1.1 Our contributions
Of the approaches listed above, almost all fit the model at each voxel independent of other voxels. In this paper, we describe a method to estimate the model parameters and perform tractography simultaneously within a causal filter. In this way, the estimation at each position builds upon the previous estimates along the fiber.
To begin estimating within a finite dimensional filter, we model the diffusion signal using a simple weighted mixture of two Gaussian tensors [5, 6, 43]. This enables estimation directly from the raw signal data without separate preprocessing or regularization steps. Because the signal reconstruction is nonlinear, we use the unscented Kalman filter to perform model estimation and then propagate in the most consistent direction. Using causal estimation in this way yields inherent path regularization, low signal reconstruction error, and accurate fiber resolution at crossing angles not found with independent optimization. We further note that the approach presented here generalizes to arbitrary fiber model with finite dimensional parameter space, and since the estimation is inherently smooth, it does not require arbitrary termination criteria such as curvature.
2 Approach
The main idea of our approach is to trace the local fiber orientations using the estimation at previous positions to guide estimation at the current position. In a loop, the Kalman filter estimates the model at the current position, moves a step in that direction, and then begins estimation again. Recursive estimation in this manner greatly improves the accuracy of resolving individual orientations and yields inherently smooth tracts despite the presence of noise and uncertainty.
Section 2.1 provides the necessary background on modeling the measurement signal using tensors and defines the specific two-fiber model employed in this study. Then, Section 2.2 describes how this model can be estimated using an unscented Kalman filter.
2.1 Modeling local fiber orientations
In diffusion weighted imaging, image contrast is related to the strength of water diffusion, and our goal is to accurately relate these signals to an underlying model of fiber orientation. At each image voxel, diffusion is measured along a set of distinct gradients, (on the unit sphere), producing the corresponding signal, . For voxels containing a mixed diffusion pattern, a general weighted formulation is written as,
| (1) |
where s0 is a baseline signal intensity, b is an acquisition-specific constant, wj are convex weights, and Dj is a tensor representing a diffusion pattern [6, 7].
From that general mixture model, we choose a restricted form with two equally-weighted tensors. This choice is guided by several previous studies. Behrens et al. [37] showed that at a b-value of 1000 the maximum number of detectable fibers is two. Several other studies have also found two tensors to be sufficient [6, 7, 38, 8]. Using this as a practical guideline, we chose a mixture of two Gaussians for a fiber model. Also, we assume the shape of each tensor to be ellipsoidal, i.e. there is one dominant principal diffusion direction m with eigenvalue λ1 and the remaining orthonormal directions have equal eigenvalues λ2 = λ3 (as in [44, 43, 8, 11]). Last, following the study of [38], we assume an equal combination (50%-50%) of the two tensors. While the effect of this second choice appears to have little to no effect on experiments, we have yet to quantify any potential loss in accuracy. These assumptions leave us with the following model used in this study:
| (2) |
where D1, D2 are each expressible as, D = λ1mmT + λ2 (ppT + qqT), with forming an orthonormal basis aligned to the principal diffusion direction m. The free model parameters are then m1, λ11, λ21, m2, λ12, and λ22.
2.2 Estimating the fiber model
Given the measured signal at a particular voxel, we want to estimate the underlying model parameters that explain this signal. As in streamline tractography, we treat the fiber as the trajectory of a particle which we trace out. At each step, we examine the measured signal at that position, estimate the underlying model parameters, and propagate forward in the most consistent direction.
To use a state-space filter for estimating the model parameters, we need the application-specific definition of four filter components:
The system state (x): the model parameters
The state transition (f[·]): how the model changes as we trace the fiber
The observation (h[·]): how the signal appears given a particular state
The measurement (y): the actual signal obtained from the scanner
For our state, we directly use the model parameters for the two-tensor model in Eq. 2:
| (3) |
where and . For the state transition we assume identity dynamics; the local fiber configuration does not undergo drastic change from one position to the next. Our observation is the signal reconstruction, y = s = [s1, ..., sn]T using si from Eq. 2, and our measurement is the actual signal interpolated at the current position.
Since the signal reconstruction using tensors is a nonlinear processes, we employ an unscented Kalman filter to perform estimation. Similar to classical linear Kalman filtering, the unscented version seeks to reconcile the predicted state of the system with the measured state and addresses the fact that those two processes–prediction and measurement–may be nonlinear or unknown. It does this in two phases: first it uses the system transition model to predict the next state and observation, and then it uses the new measurement to correct this state estimate. In what follows, we present the algorithmic application of the filter. For more thorough treatments, see [45, 46].
Suppose the system of interest is at time t and we have a Gaussian estimate of its current state with mean, , and covariance, . Prediction begins with the formation of a set sample states with associated convex weights, , spread around the current state. We use the covariance, Pt, to distribute this set deterministically:
| (4) |
where [A]i denotes the ith column of matrix A and κ is an adjustable scaling parameter. Next, this set is propagated through the state transition function, , to obtain a new predicted sample set: . Since in this study we assume the fiber configuration does not change, we may write this as, xt+1|t = f[xt] = xt. These are then used to calculate the predicted system mean state, , and covariance, , where Q is the injected process noise bias. This procedure comprises the unscented transform used to estimate the behavior of a nonlinear function: spread sample points based on your current uncertainty, propagate those samples using your transform function, and measure the spread of those transformed samples.
To obtain the predicted observation, we again apply the unscented transform this time using the predicted states, Xt+1|t, to estimate what we expect observe from the measurement of each state: . Keep in mind that for this study, our observation is the signal reconstruction from Eq. 2, and the measurement itself is looking at the diffusion-weighted signal, s, interpolated at the current position. From these, we obtain the predicted set of observations, , and may calculate its mean, , and covariance, where R is the injected measurement noise bias. The cross correlation between the state and observation is given as: .
As is done in the classic linear Kalman filter, the final step is to use the Kalman gain, , to correct our prediction system mean and covariance,
| (5) |
| (6) |
where is the actual signal measurement taken at this time.
To summarize the proposed technique, we are using the unscented Kalman filter to estimate the two-tensor model parameters. Tractography involves maintaining for each fiber its model parameter state, covariance, and position. At each iteration of the algorithm, we predict the new state which in this case is simply identity: xt+1|t = xt. Our actual measurement yt in Eq. 5 is to look at the diffusion-weighted signal, s, recorded by the scanner at this position. At subvoxel positions we interpolate directly on the diffusion-weighted images. With these, we step through the equations above to find the new estimated model parameters, xt+1. Last, we move a small step in the most consistent principal diffusion direction, either m1 or m2, and then repeat the process from that new location.
3 Experiments
We first use experiments with synthetic data to validate our technique against ground truth. We confirm that our approach accurately estimates the true underlying signal and reliably recognizes crossing fibers over a broad range of angles. Comparing against two alternative multi-fiber optimization techniques, we find the filtered approach gives consistently superior results (Section 3.1). Next, we perform tractography through crossing fiber fields and qualitatively examine the underlying orientations and branchings (Section 3.2). Lastly, we examine a real dataset to demonstrate how causal estimation is able to pick up fibers and branchings known to exist in vivo yet absent using other techniques (Section 3.3).
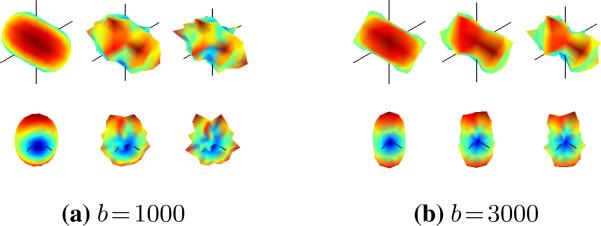
Following the experimental method of generating synthetic data found in [22, 25, 41], we used the average eigenvalues of the 300 voxels with highest fractional anisotropy (FA) in our real data set: {1200, 100, 100} μm2/msec (FA=0.91). We generated synthetic MR signals according to Eq. 2 using these eigenvalues to form an anisotropic tensor at both b = 1000 and b = 3000 using 81 gradient directions uniformly spread on the hemisphere. Two levels of Rician noise was introduced: relatively little noise which we call “clean” (σ = 0.1, SN≈ 5 dB) and significant noise which we call “dirty” (σ = 0.2, SNR≈ 10 dB). To get an idea of this level of noise, Fig. 1 visualizes a sample voxel with two fibers at a 60° angle.
Fig. 1.
Synthetic two-fiber voxel signal at a 60° angle (black wires indicate axes) showing the qualitative level of noise introduced. Each column shows the same signal from two viewpoints. Noise levels are pure (ground truth, no noise), “clean” (minimal noise), and “dirty” (heavy noise) (left to right in each group).
Throughout the experiments, we make comparisons against three alternative techniques. First, we use the same two-tensor model from Section 2.1 with a variant matching pursuit for brute force, dictionary-based optimization [47]. In our implementation, we simply project against a dictionary populated with the same pure two-tensor signals used to generate the synthetic data only oriented at 341 directions on the hemisphere, thus any error is due to the method's sensitivity to noise and discretization. Further, this is in effect the theoretical limit on performance for independent optimization techniques. This approach highlights the effect of using the same model but changing the optimization technique to one that treats each voxel independently. Second, we use spherical harmonics for modeling [22] and fiber-ODF sharpening for peak detection as described in [25] (order l = 8, regularization L = 0.006). This provides a comparison with an independently estimated, model-free representation. Note that this technique is very similar to spherical deconvolution. We will often refer to this method as “sharpened spherical harmonics”. Last, when performing tractography on real data, we use single-tensor streamline tractography as a baseline1.
3.1 Signal reconstruction and angular resolution
While the independent optimization techniques can be run on individually generated voxels, care must be taken in constructing reasonable scenarios to test the causal filter. For this purpose, we constructed a 2D field through which to navigate (see Fig. 4a). In the middle is one long fiber pathway where the filter begins estimating a single tensor but then runs into a field of voxels with two crossed fibers at a fixed angle. In this crossing region we calculated error statistics. Similarly, we computed the angular error over this region using both sharpened spherical harmonics and matching pursuit. We generated several similar fields, each at a different fixed angle. By varying the size of the crossing region or the number of fibers run, we ensured that each technique performed at least 500 estimations.
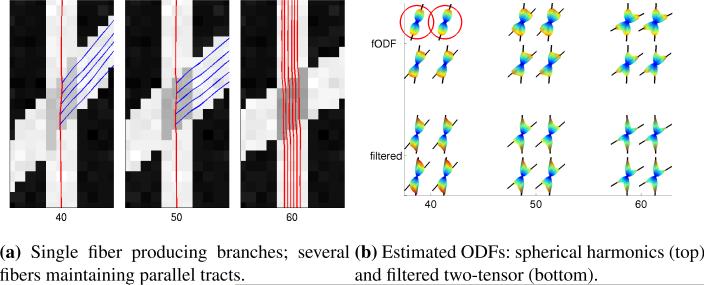
Fig. 4.
Closeup of the estimated ODFs of several neighboring voxels estimated within the crossing region at fixed angles: 40°, 50°, 60°. Notice that spherical harmonics (top row) show an angular bias and have trouble finding both axes at 40° (circled).
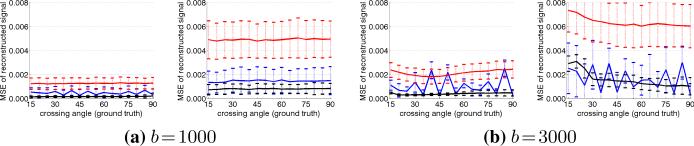
In the first experiment, we look at signal reconstruction error. We calculate the mean squared error of the reconstructed signal, s, against the ground truth signal,ŝ (pure, no noise): ∥s – ŝ∥2/∥ŝ∥2. Fig. 2 shows the results of using the proposed filter, matching pursuit, and spherical harmonics. Over each technique's 500+ estimations, the trend-lines indicate the mean error while the bars indicate one standard deviation. Spherical harmonics (red) appear to produce a smooth fit to the given noisy data. Matching pursuit (blue), despite having a dictionary filled only with the correct eigenvalues, shows the effect of discretization and sensitivity to noise. This experiment demonstrates that the proposed filter (black) accurately and reliably estimates the true underlying signal.
Fig. 2.
Mean squared error (MSE) between reconstructed signal and ground truth signal at various crossing angles. Notice how the increased noise has little effect on the filter (black) compared to using matching pursuit (blue) or spherical harmonics (red). Each subfigure shows both the clean and dirty experiments (left, right).
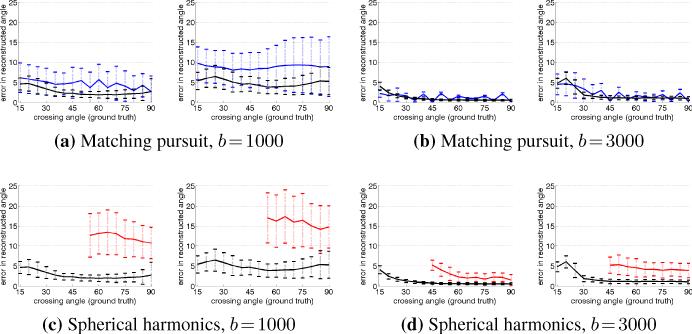
In the second experiment, we looked at the error in angular resolution by comparing the filtered approach to matching pursuit and sharpened spherical harmonics. Matching pursuit again shows the effects of noise and discretization. Consistent with the results reported in [25, 17], spherical harmonics are generally unable to detect and resolve angles below 50° for b = 1000 or below 40° for b = 3000. Fig. 3c and Fig. 3d confirm this, respectively. This experiment demonstrates that for b = 1000, the filtered approach consistently resolves angles down to 20-30° with 5° error compared to independent optimization which fails to reliably resolve below 60° with as much as 15° error. For b = 3000, the filtered approach consistently resolves down to 20-30° with 2-3° error compared to independent optimization which cannot resolve below 50° with 5° error.
Fig. 3.
Average angle error at various crossing angles comparing all three techniques: matching pursuit (blue), sharpened spherical harmonics (red), and the proposed filter (black). The filter provides stable and consistent estimation compared to either alternative technique. Each subfigure shows both the clean and dirty experiments (left, right).
3.2 Synthetic tractography
Having verified the technique's accuracy, we now turn to the resulting tractography. Fig. 4a shows a synthetic crossing fiber field at three fixed angles: 40°, 50°, 60° (b = 3000, noisy). From the bottom, we start several fibers that propagate upward where they encounter the crossing region. In Fig. 4b, we take a closer look at several neighboring sample voxels estimated within that crossing region, and we show the ODFs reconstructed using sharpened spherical harmonics and the proposed filter. As expected, at 40°, using spherical harmonics often only reports a single angle (circled). Further, a closer examination of the reported axes shows the bias toward a single averaged axis as reported in [38, 41]. In contrast, the filtered results are consistent and accurate. For illustration, the 40° and 50° fields in Fig. 4a show how detected branchings may be followed.
3.3 Tractography on real data
We tested our approach on a real human brain scan of 51 diffusion weighted images with voxel size of 1.66 × 1.66 × 1.7 mm3 and b = 900 s/mm2.
In this study, we focus on fibers originating in the corpus callosum. Specifically, we trace out the lateral transcallosal fibers that run through the corpus callosum out to the lateral gyri. It is known that single-tensor streamline tractography only traces out the dominant pathways forming the U-shaped callosal radiation (Fig. 5a and Fig. 6a). Several studies document this phenomena, among them the works of Descoteaux et al. [25] and Schultz et al. [41] have side-by-side comparisons. These fibers have been reported in using diffusion spectrum imaging [27], probabilistic tractography [11, 48, 25] and more recently with tensor decomposition [41].
Fig. 5.
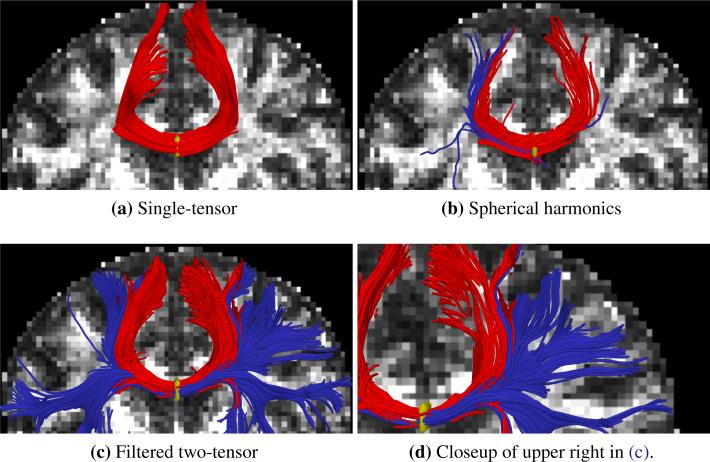
Filtered tractography (c),(d) picks up many fiber paths consistent with the underlying structures. Both single-tensor streamline (a) and sharpened spherical harmonics (b) are unable to find the majority of these pathways. Seed region indicated in yellow.
Fig. 6.
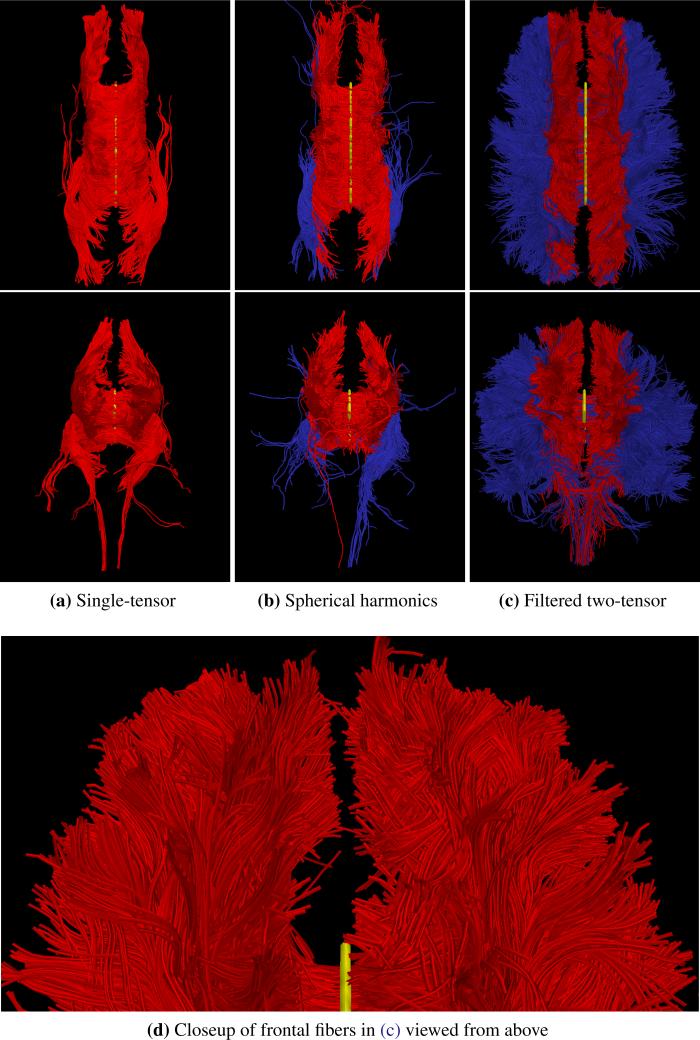
Tracing fibers originating from the center of the entire corpus callosum with views from above (top row) and front-to-back (bottom). The proposed filtered tractography (c) is able to find many of the lateral projections (blue) while single-tensor (a) is unable to find any and few are found with sharpened spherical harmonics (b). Seed region indicated in yellow.
In this study, we focus on two basic experiments: looking at the tracts surrounding a single coronal slice and all tracts passing through the corpus callosum. We seed each algorithm multiple times in the voxels at the intersection of the mid-sagital plane and the corpus callosum. To explore the branchings found using our technique, we considered a position as a branch point if we found a 5° -40° separation between the two tensors, both having FA≥0.15. Similarly, with sharpened spherical harmonics, we considered it a branch if we find a second maxima over the same range. While thresholds are somewhat arbitrary, we found little qualitative difference in adjusting these values.
For the first experiment, Fig. 5 shows tracts originating from within a few voxels intersecting a particular coronal slice. For a reference backdrop, we use a coronal slice showing FA intensity placed a few voxels behind the seeded coronal position. Keeping in mind that these fibers are intersecting or are in front of the image plane, this roughly shows how the fibers navigate the areas of high anisotropy (bright regions). Similar to the results in [25, 41], Fig. 5b shows that spherical harmonics only pick up a few fibers intersecting the U-shaped callosal radiata. In contrast, our proposed algorithm traces out many pathways consistent with the apparent anatomy. To emphasize transcallosal tracts, we color as blue those fibers exiting a corridor of ±22 mm around the mid-sagittal plane. Fig. 5d provides a closer inspection of Fig. 5c where, to emphasize the underlying anatomy influencing the fibers, we use the actual coronal slice passing through the voxels used to seed this run.
For the second experiment, Fig. 6 shows a view of the whole brain to highlight the overall difference between the three methods. Here again we emphasize with blue the transcallosal fibers found using the proposed filter. Fig. 6d provides a closeup of the frontal lobe from above to show the various pathways infiltrating the gyri.
4 Conclusions
Studies involving deterministic tractography rely on the underlying model estimated at each voxel as well as the reconstructed pathways. In this work, we demonstrated that using a causal filter provides robust estimates of much higher accuracy than independent estimation techniques. While the model we employed has been used previously in various forms, we primarily focused on the optimization technique used to estimate that model. Framing that estimation within a recursive filter allowed us to apply a standard technique for nonlinear estimation. We believe that exploring both alternative models and filtering techniques will provide more accurate and comprehensive information about neural pathways and ultimately enhance non-invasive diagnosis and treatment of brain disease.
Footnotes
J.G. Malcolm and Y. Rathi contributed equally to this work.
Using the freely available Slicer 2.7 (http://www.slicer.org).
References
- 1.Basser P, Jones D. Diffusion-tensor MRI: theory, experimental design and data analysis - A technical review. NMR in Biomedicine. 2002;25:456–467. doi: 10.1002/nbm.783. [DOI] [PubMed] [Google Scholar]
- 2.Behrens T, Woolrich M, Jenkinson M, Johansen-Berg H, Nunes R, Clare S, Matthews P, Brady J, Smith S. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magnetic Resonance in Medicine. 2003;50:1077–1088. doi: 10.1002/mrm.10609. [DOI] [PubMed] [Google Scholar]
- 3.Alexander D, Barker G, Arridge S. Detection and modeling of non-Gaussian apparent diffusion coefficient profiles in human brain data. Magnetic Resonance in Medicine. 2002;48:331–340. doi: 10.1002/mrm.10209. [DOI] [PubMed] [Google Scholar]
- 4.Frank L. Characterization of anisotropy in high angular resolution diffusion-weighted MRI. Magnetic Resonance in Medicine. 2002;47:1083–1099. doi: 10.1002/mrm.10156. [DOI] [PubMed] [Google Scholar]
- 5.Alexander A, Hasan K, Tsuruda J, Parker D. Analysis of partial volume effects in diffusion-tensor MRI. Magnetic Resonance in Medicine. 2001;45:770–780. doi: 10.1002/mrm.1105. [DOI] [PubMed] [Google Scholar]
- 6.Tuch D, Reese T, Wiegell M, Makris N, Belliveau J, Wedeen V. High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magnetic Resonance in Medicine. 2002;48:577–582. doi: 10.1002/mrm.10268. [DOI] [PubMed] [Google Scholar]
- 7.Kreher B, Schneider J, Mader I, Martin E, Hennig J, Il'yasov K. Multitensor approach for analysis and tracking of complex fiber configurations. Magnetic Resonance in Medicine. 2005;54:1216–1225. doi: 10.1002/mrm.20670. [DOI] [PubMed] [Google Scholar]
- 8.Peled S, Friman O, Jolesz F, Westin CF. Geometrically constrained two-tensor model for crossing tracts in DWI. Magnetic Resonance in Medicine. 2006;24(9):1263–1270. doi: 10.1016/j.mri.2006.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hlawitschka M, Scheuermann G. Visualization. 2005. HOT-lines: Tracking lines in higher order tensor fields. pp. 27–34. [Google Scholar]
- 10.McGraw T, Vemuri B, Yezierski B, Mareci T. Int. Symp. on Biomedical Imaging. 2006. Von Mises-Fisher mixture model of the diffusion ODF. pp. 65–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kaden E, Knøsche T, Anwander A. Parametric spherical deconvolution: Inferring anatomical connectivity using diffusion MR imaging. NeuroImage. 2007;37:474–488. doi: 10.1016/j.neuroimage.2007.05.012. [DOI] [PubMed] [Google Scholar]
- 12.Rathi Y, Michailovich O, Shenton M, Bouix S. Directional functions for orientation distribution estimation. Medical Image Analysis. 2009 doi: 10.1016/j.media.2009.01.004. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Özarslan E, Shepherd T, Vemuri B, Blackband S, Mareci T. Resolution of complex tissue microarchitecture using the diffusion orientation transform. NeuroImage. 2006;31(3) doi: 10.1016/j.neuroimage.2006.01.024. [DOI] [PubMed] [Google Scholar]
- 14.Tuch D. Q-ball imaging. Magnetic Resonance in Medicine. 2004;52:1358–1372. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]
- 15.Anderson A. Measurement of fiber orientation distributions using high angular resolution diffusion imaging. Magnetic Resonance in Medicine. 2005;54(5):1194–1206. doi: 10.1002/mrm.20667. [DOI] [PubMed] [Google Scholar]
- 16.Hess C, Mukherjee P, Han E, Xu D, Vigneron D. Q-ball reconstruction of multimodal fiber orientations using the spherical harmonic basis. Magnetic Resonance in Medicine. 2006;56:104–117. doi: 10.1002/mrm.20931. [DOI] [PubMed] [Google Scholar]
- 17.Descoteaux M, Angelino E, Fitzgibbons S, Deriche R. Regularized, fast, and robust analytical Q-ball imaging. Magnetic Resonance in Medicine. 2007;58:497–510. doi: 10.1002/mrm.21277. [DOI] [PubMed] [Google Scholar]
- 18.Michailovich O, Rathi Y. Int. Symp. on Biomedical Imaging. 2008. On approximation of orientation distributions by means of spherical ridgelets. pp. 939–942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Poupon C, Roche A, Dubois J, Mangin JF, Poupon F. Real-time MR diffusion tensor and Q-ball imaging using Kalman filtering. Medical Image Analysis. 2008;12(5):527–534. doi: 10.1016/j.media.2008.06.004. [DOI] [PubMed] [Google Scholar]
- 20.Jian B, Vemuri B. A unified computational framework for deconvolution to reconstruct multiple fibers from diffusion weighted MRI. Trans. on Medical Imaging. 2007;26(11):1464–1471. doi: 10.1109/TMI.2007.907552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jansons K, Alexander D. Persistent angular structure: New insights from diffusion MRI data. Inverse Problems. 2003;19:1031–1046. doi: 10.1007/978-3-540-45087-0_56. [DOI] [PubMed] [Google Scholar]
- 22.Tournier JD, Calamante F, Gadian D, Connelly A. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. NeuroImage. 2004;23:1176–1185. doi: 10.1016/j.neuroimage.2004.07.037. [DOI] [PubMed] [Google Scholar]
- 23.Kumar R, Barmpoutis A, Vemuri B, Carney P, Mareci T. MMBIA. 2008. Multi-fiber reconstruction from DW-MRI using a continuous mixture of von Mises-Fisher distributions. pp. 1–8. [DOI] [PubMed] [Google Scholar]
- 24.Alexander D. Multiple-fiber reconstruction algorithms for diffusion MRI. Annals of the New York Academy of Sciences. 2005;1046 doi: 10.1196/annals.1340.018. [DOI] [PubMed] [Google Scholar]
- 25.Descoteaux M, Deriche R, Anwander A. Deterministic and probabilistic Q-ball tractography: from diffusion to sharp fiber distributions. 2007. Technical Report 6273, INRIA.
- 26.Basser P, Pajevic S, Pierpaoli C, Duda J, Aldroubi A. In vivo fiber tractography using DT-MRI data. Magnetic Resonance in Medicine. 2000;44:625–632. doi: 10.1002/1522-2594(200010)44:4<625::aid-mrm17>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- 27.Hagmann P, Reese T, Tseng WY, Meuli R, Thiran JP, Wedeen V. Int. Symp. on Magnetic Resonance in Medicine. 2004. Diffusion spectrum imaging tractography in complex cerebral white matter: An investigation of the centrum semiovale. p. 623. [Google Scholar]
- 28.Guo W, Zeng Q, Chen Y, Liu Y. Int. Symp. on Biomedical Imaging. 2006. Using multiple tensor deflection to reconstruct white matter fiber traces with branching. pp. 69–72. [Google Scholar]
- 29.Qazi A, Radmanesh A, O'Donnell L, Kindlmann G, Peled S, Whalen S, Westin CF, Golby A. Resolving crossings in the corticospinal tract by two-tensor streamline tractography: Method and clinical assessment using fMRI. NeuroImage. 2008 doi: 10.1016/j.neuroimage.2008.06.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gössl C, Fahrmeir L, Putz B, Auer L, Auer D. Fiber tracking from DTI using linear state space models: Detectability of the pyramidal tract. NeuroImage. 2002;16:378–388. doi: 10.1006/nimg.2002.1055. [DOI] [PubMed] [Google Scholar]
- 31.Björnemo M, Brun A, Kikinis R, Westin CF. MICCAI. 2002. Regularized stochastic white matter tractography using diffusion tensor MRI. pp. 435–442. [Google Scholar]
- 32.Zhang F, Goodlett C, Hancock E, Gerig G. MICCAI. 2007. Probabilistic fiber tracking using particle filtering. pp. 144–152. [DOI] [PubMed] [Google Scholar]
- 33.Zhukov L, Barr A. Visualization. 2002. Oriented tensor reconstruction: Tracing neural pathways from diffusion tensor MRI. pp. 387–394. [Google Scholar]
- 34.Parker G, Alexander D. Information Processing in Medical Imaging. 2003. Probabilistic Monte Carlo based mapping of cerebral connections utilizing whole-brain crossing fiber information. pp. 684–696. [DOI] [PubMed] [Google Scholar]
- 35.Campbell JW, Siddiqi K, Rymar V, Sadikot A, Pike G. Flow-based fiber tracking with diffusion tensor and Q-ball data: Validation and comparison to principal diffusion direction techniques. NeuroImage. 2005;27(4):725–736. doi: 10.1016/j.neuroimage.2005.05.014. [DOI] [PubMed] [Google Scholar]
- 36.Hosey T, Williams G, Ansorge R. Inference of multiple fiber orientations in high angular resolution diffusion imaging. Magnetic Resonance in Medicine. 2005;54:1480–1489. doi: 10.1002/mrm.20723. [DOI] [PubMed] [Google Scholar]
- 37.Behrens T, Johansen-Berg H, Jbabdi S, Rushworth M, Woolrich M. Probabilistic diffusion tractography with multiple fibre orientations: What can we gain? NeuroImage. 2007;34:144–155. doi: 10.1016/j.neuroimage.2006.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zhan W, Yang Y. How accurately can the diffusion profiles indicate multiple fiber orientations? A study on general fiber crossings in diffusion MRI. J. of Magnetic Resonance. 2006;183:193–202. doi: 10.1016/j.jmr.2006.08.005. [DOI] [PubMed] [Google Scholar]
- 39.Seunarine K, Cook P, Hall M, Embleton K, Parker G, Alexander D. MMBIA. 2007. Exploiting peak anisotropy for tracking through complex structures. pp. 1–8. [Google Scholar]
- 40.Bloy L, Verma R. MICCAI. 2008. On computing the underlying fiber directions from the diffusion orientation distribution function. pp. 1–8. [DOI] [PubMed] [Google Scholar]
- 41.Schultz T, Seidel H. Estimating crossing fibers: A tensor decomposition approach. Trans. on Visualization and Computer Graphics. 2008;14(6):1635–1642. doi: 10.1109/TVCG.2008.128. [DOI] [PubMed] [Google Scholar]
- 42.Ramirez-Manzanares A, Cook P, Gee J. MICCAI. 2008. A comparison of methods for recovering intra-voxel white matter fiber architecture from clinical diffusion imaging scans. pp. 305–312. [DOI] [PubMed] [Google Scholar]
- 43.Friman O, Farnebäck G, Westin CF. A Bayesian approach for stochastic white matter tractography. Trans. on Medical Imaging. 2006;25(8):965–978. doi: 10.1109/tmi.2006.877093. [DOI] [PubMed] [Google Scholar]
- 44.Parker G, Alexander D. Probabilistic anatomical connectivity derived from the microscopic persistent angular structure of cerebral tissue. Phil. Trans. R. Soc. B. 2005;360:893–902. doi: 10.1098/rstb.2005.1639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Julier S, Uhlmann J. Unscented filtering and nonlinear estimation. IEEE. 2004;92(3):401–422. [Google Scholar]
- 46.van der Merwe R, Wan E. Workshop on Advances in Machine Learning. 2003. Sigma-point Kalman filters for probabilistic inference in dynamic state-space models. [Google Scholar]
- 47.Mallat S, Zhang Z. Matching pursuits with time-frequency dictionaries. Trans. on Signal Processing. 1993;41:3397–2415. [Google Scholar]
- 48.Anwander A, Descoteaux M, Deriche R. Human Brain Mapping. 2007. Probabilistic Q-Ball tractography solves crossings of the callosal fibers. p. 342. [Google Scholar]