Abstract
2H spin relaxation NMR experiments to study the dynamics of deuterated backbone α-positions, Dα, are developed. To date, solution-state 2H relaxation measurements in proteins have been confined to side-chain deuterons - primarily 13CH2D or 13CHD2 methyl groups. It is shown that quantification of 2H relaxation rates at Dα backbone positions and the derivation of associated order parameters of Cα-Dα bond vector motions in small [U-15N,13C,2H]-labeled proteins is feasible with reasonable accuracy. The utility of the developed methodology is demonstrated on a pair of proteins - ubiquitin (8.5 kDa) at 10°C, 27°C, and 40°C, and a variant of GB1 (6.5 kDa) at 22°C. In both proteins, the Dα-derived parameters of the global rotational diffusion tensor are in good agreement with those obtained from 15N relaxation rates. Semi-quantitative solution state NMR measurements yield an average value of the quadrupolar coupling constant, QCC, for Dα sites in proteins equal to 174 kHz. Using the uniform value of QCC for all Dα sites, we show that Cα-Dα bond vectors are motionally distinct from the backbone amide N-H bond vectors, with 2H-derived squared order parameters of Cα-Dα bond vector motions, S2 CαDα, on average slightly higher than their N-H amides counterparts, S2 NH. For ubiquitin, the 2H-derived backbone mobility compares well with that found in a 1-μs molecular dynamics simulation.
Introduction
It is becoming increasingly apparent that protein function is oftentimes predicated upon the character and amplitudes of motions undergone by protein structures - that is molecular dynamics.1–4 As a result, the past decade has witnessed an up-surge in the development of both experimental and theoretical approaches for studying motional processes in proteins on a variety of time scales. NMR spectroscopy is a particularly powerful experimental method for studying dynamics in proteins because it provides site-specific information that covers a wide range of motional time scales.5–12 The amide 15N nuclei are the most commonly used spin probes of backbone motions in proteins, and 15N-based NMR relaxation studies of fast dynamics at backbone 15N-1H amide positions of small- to medium-sized proteins are now largely routine.5,13
The popularity of 15N as a nuclear spin probe of motional processes in backbones of proteins stems from the ease and affordability of selective incorporation of 15N into backbone amide positions (without concomitant 13C-labeling of neighboring nuclear sites) as well as high sensitivity of 15N relaxation measurements.5,13 The rates of decay of 15N magnetization in amide moieties is expressed as the sum of dipolar (15N-1H) and 15N chemical shielding anisotropy (CSA) contributions.5,13,14 Quantitative interpretation of conventional 15N NMR relaxation data in terms of microdynamic characteristics of fast (pico- to nanosecond) motions requires, however, prior knowledge of a number of parameters, such as (i) exact 15N-1H bond lengths, (ii) amide 15N CSA values, and (iii) contributions to the relaxation rates due to chemical exchange, Rex, that, in principle, should be quantified independently. Although 15N relaxation rates in small- to medium-sized proteins can be usually measured with high accuracy, the uncertainties in any or all of the above parameters leads to ambiguities in the obtained measures of backbone order expressed as generalized order parameters (amplitudes) of N-H bond vector fluctuations, SNH.15,16 That is why significant efforts have been dedicated recently to development of NMR methodology that would provide `exchange-free' and `CSA-free' amide 15N relaxation data in proteins.17,18
In search of a `cleaner' spin probe of backbone order in protein molecules, we designed 2H-based spin relaxation experiments for the studies of dynamics at deuterated backbone α-positions, Dα. Deuterium relaxation is dominated by a strong and local quadrupolar interaction,19 and the knowledge of only a single parameter, the anisotropy of 2H quadrupolar tensor or quadrupolar coupling constant (QCC), is needed to quantitatively describe Dα 2H relaxation data in terms of order parameters of Cα-Dα bond motions, SCαDα. Since the seminal introduction of deuterium relaxation measurements to the field of protein NMR by Kay and co-workers,20 deuterium has been recognized as a particularly favorable probe for the studies of dynamics. Millet et al.21 and Skrynnikov et al.22 have demonstrated the utility of deuterium spin probes of side-chain dynamics by the measurement of five relaxation rates per deuteron in 13CH2D methyl groups of a 6.5-kDa protein L. The motional properties of 13CHD methylene positions in N-terminal drk SH3 domain have been studied by 2H relaxation.23 Comparisons of 2H-derived and 13C-derived methyl three-fold axis order parameters (S2 axis) in proteins have been provided.24,25 To date, however, 2H relaxation measurements in proteins have been confined to side-chain deuterons, primarily methyl groups of the 13CH2D20,21,26,27 or 13CHD227,28 variety. We show that the availability of increasingly sensitive NMR instrumentation allows the quantification of 2H relaxation rates at Dα positions of protein backbones as well as the associated order parameters of Cα-Dα bond vector motions in small [U-15N,13C,2H]-labeled protein molecules.
The developed NMR methodology has been applied to a pair of small proteins - an 8.5-kDa ubiquitin at three temperatures and a variant of a 6.5-kDa protein GB1. The parameters of the global molecular reorientation can be reproduced using Dα 2H R2/R1 ratios, with the extracted diffusion tensors in good agreement with those derived from 15N data in both proteins. Relying on a number of previous solid-state NMR measurements and our own semi-quantitative solution state results we propose the use of a uniform QCC value of 174 kHz for Dα sites in proteins. Using this QCC value, it is shown that Cα-Dα bond vectors are motionally distinct from the backbone amide N-H bond vectors. In particular, 2H-derived S2CαDα values are similar to, but are on average slightly higher than their 15N-derived S2NH counterparts. Importantly, Dα rates can sample protein backbone motions that are inaccessible through 15N relaxation measurements. Although for sensitivity reasons the developed methodology is expected to be limited to small protein molecules, a number of advantages of using 2H relaxation of Dα sites turn it into a useful complement to the existing array of NMR techniques for quantitative studies of motional order in proteins.
Materials and Methods
NMR Samples
The following isotopically labeled samples of wild-type human ubiquitin and a variant of GB1 protein have been used in this work: (i) [U-15N]-labeled (both proteins), (ii) [U-15N,13C,2H]-labeled (both proteins), and (iii) a mixture of [U-15N,13C,2H]-labeled and [U-15N,13C]-labeled GB1. The deuterated samples of both proteins have been obtained using [U-15N,13C]-glucose as the main carbon source in the 99.9% D2O-based E.coli media. Since carbon α positions are completely deuterated in proteins obtained using D2O as the solvent in bacterial medium,29,30 residual protonation of some aliphatic and aromatic sites is of no consequence for the present study. All samples of GB1 have been obtained using a co-expression vector where the sequence of GB1 serves as a removable tag, resulting in the addition of seven residues (-Ser-Ser-Gly-Leu-Val-Pro-Arg) to the C-terminus of the protein.
The [U-15N,13C,2H]- and [U-15N]-labeled NMR samples of human ubiquitin were 3.2 mM and 1.0 mM in protein concentration, respectively, and were dissolved in a 20 mM 90% H2O/10% D2O sodium phosphate buffer (pH 6.8) containing 0.03% NaN3 and a cocktail of protease inhibitors. The [U-15N,13C,2H]- and [U-15N]-labeled samples of GB1 were 5.8 mM and 1.2 mM in protein concentration, respectively, and were dissolved in a 25 mM 90% H2O/10% D2O sodium phosphate buffer (pH 6.5) containing 50 mM NaCl, 0.03% NaN3 and a cocktail of protease inhibitors. A third sample of GB1 contained a mixture of the [U-15N,13C,2H]- and [U-15N,13C]-labeled protein in the approximate ratio of 4.5:1 (final concentrations of [U-15N,13C,2H]- and [U-15N,13C]-GB1 of 4.5 and 1 mM, respectively), and was dissolved in a 25 mM 90% H2O/10% D2O sodium phosphate buffer (pH 6.5) as above to enable the measurements of Dα quadrupolar splittings and 1DCα-Hα residual dipolar couplings (RDCs) in the same protein solution (see below).
Experimental NMR pulse sequence details
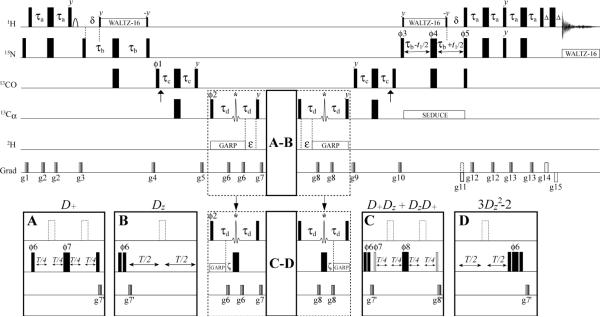
Figure 1 shows the pulse-schemes that have been designed for the measurements of RQ(D+), RQ(Dz), RQ(D+Dz+DzD+), RQ(3Dz2−2) at Dα sites of deuterated proteins. The scheme derives from a gradient sensitivity enhanced HN(COCA) experiment31 and involves additional magnetization transfers to and from Dα nuclei whose relaxation is measured by parametrically varying delay T. Insets A and B correspond to the measurement of RQ(D+) and RQ(Dz), respectively. The part of the scheme that is enclosed in a dashed rectangle should be modified as it is shown in the figure to measure the relaxation of the D+Dz+DzD+(3Dz2−2) elements in insets C(D). All narrow (wide) rectangular pulses are applied with the flip angles of 90°(180°) along the x-axis unless indicated otherwise. The 1H(2H; 15N) carriers are positioned at 4.7(4.5; 119) ppm. The 13C carrier is placed at 177 ppm, switched to 57 ppm before the first 90° 13Cα pulse (after the gradient g5), and switched back to 177 ppm after the last 90° 13Cα pulse (after the gradient g5). 15N WALTZ-1632 decoupling during acquisition is achieved using a 1.25 kHz field, while 2H GARP-133 decoupling uses a 0.9 kHz field. 2H decoupling is interrupted for the application of gradients g6 and g8 (insets A,B).34 SEDUCE35 13Cα decoupling is implemented with 300 μs seduce-shaped pulses applied at 13Cα frequency by phase-modulation of the carrier.36,37 1H WALTZ-1632 decoupling is applied with a 7 kHz field. All 1H, 2H and 15N pulses are applied with maximum possible power, while 90°(180°) 13C pulses shown with filled rectangles are applied with a field strength of Δ/√15(Δ/√3) where Δ is the difference in Hz between the 13Cα and 13CO chemical shifts.38 Vertical arrows at the beginning and the end of 2τc periods indicate the position of the 13CO Bloch-Siegert shift compensation pulses.38 13Cα shaped pulses marked with asterisks in the middle of 2τd periods are 350 μs RE-BURP39 pulses centered at 43 ppm by phase modulation of the carrier and cover the range of all 13C aliphatic chemical shifts. The 2H pulses shown with open rectangles in inset C have a flip angle of 45°. The 13Cα pulses shown with open dashed rectangles (insets A–C) are optional. All the experiments described in this work have been performed with these pulses included. The 1H pulse shown with an arc (preceding the gradient g3) is implemented as a water-selective 1.5 ms pulse of rectangular shape. Delays are: τa = 2.7 ms; τb = 12.5 ms; τc = 4.5 ms; τd = 14 ms; δ = 5.4 ms; ε = 11 ms; ζ = 7 ms; Δ = 0.4 ms. The phase-cycle is: φ1 = x,−x; φ2 = 2(x),2(−x) (insets A,B) and 4(x),4(−x) (insets C,D); φ3=x; φ4=8(x),8(−x); φ5=x; φ6=4(x),4(−x) (inset A,C) and 2(0°),2(45°),2(90°),2(135°) in inset D; φ7=2(x),2(y),2(−x),2(−y) (inset A) and 8(x),8(−x) (inset C); φ8=x,−x,y,−y (inset C); rec.=2(x,−x), 2(−x,x) (inset A), x,2(−x),x,−x,2(x),−x (inset B), x,2(−x),x,−x,2(x),−x,−x,2(x),−x,x,2(−x),x (inset C), x,2(−x),x,−x,2(x),−x (inset D). Quadrature detection in t1 is achieved via the Rance-Kay scheme: for each t1 value a pair of spectra is recorded with (φ5=x; g11) and (φ5=−x; −g11) and manipulated post-acquisition.40,41 The phase φ3 is inverted for each t1 point.42 Durations and strengths of pulsed-field gradients in units of (ms; G/cm) are: g1 = (1; 15); g2 = (0.25; 5); g3 = (1.2; 12); g4 = (0.5; 8); g5 = (0.6; 10); g6 = (0.3; 5); g7 = (0.7; 15); g8 = (0.35; 5); g9 = (0.5; 12); g10 = (0.4; 10); g11 = (1.25; 20); g12 = (0.25; 8); g13 = (0.3; 5); g14 = (0.0625; 20); g15 = (0.0625; −20); g7′ = (0.6; 10); g8′ = (0.8; 12).
Figure 1.
The HN(COCA)D pulse scheme for the measurement of relaxation rates of α-deuterons in proteins. See `Materials and Methods' for the pulse-sequence details.
Dα and 15N Relaxation Measurements
All 2H and 15N spin relaxation experiments were performed on a 600 MHz Bruker Avance III spectrometer equipped with a room temperature triple-resonance z-gradient probe. NMR data sets recorded with the pulse scheme of Figure 1 (Dα, [U-15N,13C,2H]-labeled samples) comprised [512, 40] complex points in the [1HN,15N] dimensions with corresponding acquisition times of [64 ms, 24 ms]. Typically, a recovery delay of 1.5 s was used along with 128 scans/FID giving rise to net acquisition times of ~4.8 hr./experiment. RQ(D+) rates in ubiquitin samples were recorded with parametrically varied delays T (inset A in Figure 1) of (0.02; 0.2; 0.4; 0.6; 0.8; 1.2; 1.6) ms, (0.02; 0.3; 0.6; 0.9; 1.2; 1.6; 2.0) ms, and (0.02; 0.2; 0.4; 0.6; 0.8; 1.2; 1.6) ms at 10°C, 27°C and 40°C, respectively, while RQ(Dz) rates (Figure 1, inset B) were recorded with parametrically varied delays T of (0.02; 2.0; 4.0; 6.0; 8.0; 10.0; 12.0; 14.0) ms, (0.02; 1.0; 2.0; 3.0; 4.0; 6.0; 8.0; 10.0) ms, and (0.02; 1.0; 2.0; 3.0; 4.0; 5.0; 6.0; 8.0) ms at 10°C, 27°C and 40°C. RQ(D+), RQ(Dz), RQ(D+Dz+DzD+), RQ(3Dz2−2) relaxation rates of α deuterons in GB1 have been measured at 22°C using the delays T of (0.02; 0.2; 0.4; 0.6; 0.8; 1.2; 1.6; 2.0) ms, (0.02; 2.0; 4.0; 6.0; 8.0; 10.0; 13.0) ms, (0.02; 0.2; 0.4; 0.6; 0.8; 1.2; 1.6; 2.0) ms, and (0.02; 1.0; 2.0; 3.0; 4.0; 6.0; 8.0; 10.0) ms, respectively. All NMR spectra were processed using the NMRPipe/NMRDraw suite of programs43 and associated software. Rates were obtained by fitting peak intensities to a single exponential function of the form I = I0 exp(−RT), where I is the measured intensity and R is the relaxation rate. Errors in peak intensities have been estimated from duplicate measurements or from the noise-floor level of the spectra, whichever was the highest, and subsequently propagated to the errors in the extracted rates using Monte-Carlo analysis.44 The estimated errors in RQ(D+)(RQ(Dz)) measurements are on the order of 2.0%(1.5%) on average in ubiquitin.
15N R1ρ, R and 1H-15N NOE measurements on [U-15N]-labeled samples of both proteins have been performed using standard procedures.45,46 Typically, NMR data sets comprised [512, 64] complex points in the [1HN,15N] dimensions with corresponding acquisition times of [64 ms, 38 ms]. Recovery delays of 1.0s and 4.3s (including a 2s presaturation period) for 15N R1ρ,R and 1H-15N NOE measurements respectively, along with 16 scans/FID gave rise to respective net acquisition times of ~0.7 and 2.5 hr./experiment. The spin-lock field strength of 1.9 kHz was used in 15N R1ρ measurements. R1ρ data have been subsequently corrected for resonance offset to obtain 15N R2 rates.5 Error analysis of peak intensities and the extracted relaxation rates closely followed the procedure used for 2H relaxation measurements at Dα positions.
The relaxation rates of NzC'zCαz 3-spin order, R(NzC'zCαz), have been measured using a pulse-scheme derived from the gradient sensitivity enhanced HN(COCA) experiment31 using the same acquisition parameters as for 2H relaxation measurements. A recovery delay of 1.0 s was used along with 16 scans/FID giving rise to net acquisition times of ~30 min./experiment. The relaxation delays T of (0.01; 50; 100; 150; 200; 300; 350; 400; 450; 500; 600) ms have been typically used for both proteins at all temperatures. The extracted R(NzC'zCαz) rates have been subsequently subtracted from the obtained Dα RQ[D] rates before analysis (see text).
Data Analysis
The relaxation rates of 2H transverse and longitudinal magnetization are given by19
| (1) |
| (2) |
where (e2qQ/h) is the quadrupolar coupling constant, QCC, and J(ωD) is the spectral density function evaluated at ωD frequency. A uniform value of QCC = 174 kHz has been used for α deuterons in this work (see text). It is usually assumed that the 2H electric field gradient tensor is axially symmetric with its principal axis parallel to the direction of the deuteron bond, so that only the anisotropy of the tensor, (e2qQ/h) = QCC, enters into eq 1–2. Indeed, the asymmetry values of the 2H tensor, η, in aliphatic deuterons are known to be <0.04.47,48 If the assumption of axial symmetry is dropped, the relaxation rates in eq 1–2 above should be multiplied by , that would contribute <0.06 % to R(D+) and R(Dz). Clearly, such small contributions are well within the errors of the relaxation rate measurements and can be safely neglected.
All 2H data have been analyzed using the following Lipari-Szabo model-free spectral density function for the axially symmetric molecular tumbling,15,16,49
| (3) |
where SCαDα is the generalized order parameter describing the fluctuations of Cα-Dα bond vectors, A1=(3/4)sin4(α), A2=3sin2(α)cos2(α), A3=[(3/2)cos2(α)−0.5]2, τ1=(4D||+2D⊥)−1, τ2=(D||+5D⊥)−1, τ3=(6D⊥)−1, D|| and D⊥ are the parallel and perpendicular components of the molecular diffusion tensor, α is the angle between the Cα-Dα bond vector (assumed collinear with Cα-Hα bond vector in protein structures) and the unique diffusion axis, and 1/τ' = 1/τf + 1/τc,eff with τc,eff = (2D|| + 4D⊥)−1 the effective correlation time of overall rotation and τf the correlation time of fast local motions. Direction cosines for the Cα-Hα vectors of ubiquitin and GB1 have been obtained from the x-ray structures with the respective PDB accession codes 1ubq50 and 2qmt51.
Diffusion tensors have been estimated by minimization of the error function χ2 expressed as,
| (4) |
where the summation extends over all sites included in analysis, and are the experimentally measured 2H/15N rates, and are the rates calculated using diffusion tensor parameters (eq 3) and the expressions for , , R1 rates, and σR2 / R1 is the uncertainty in the experimental R2/R1 ratios. A fit to a fully anisotropic diffusion tensor52 was not warranted for either protein because of relatively high errors in extracted Dα RQ[D] relaxation rates that preclude a statistically significant differentiation between the axially symmetric and fully anisotropic models. The diffusion tensor parameters obtained by minimization of χ2 (eq 4) are sensitive to the choice of residues whose dynamics is properly described by the first term of eq 3. Therefore, in both proteins only the residues in the secondary structure elements have been used. Likewise, the residues with missing coordinates (C-terminus of GB1), 1H-15N NOE<0.6 and the residues undergoing chemical exchange (15N data only) have been excluded from analysis. Errors in the fitted diffusion parameters (polar angles θ, φ describing the orientation of the unique axis of the diffusion tensor with respect to the inertial frame, and D||, D⊥) were estimated using 300 Monte-Carlo simulations44 with random additions of experimental errors to the measured rates. The standard deviations in the fitted parameters were used as uncertainties in diffusion parameters.
Dα(15N) relaxation rates have been interpreted in terms of motional parameters using their corresponding 2H-(15N)-derived diffusion tensor characteristics. Motional parameters of Dα sites, S2CαDα and the corresponding τf values, were obtained by fitting the 2H relaxation data to the corresponding expressions for relaxation rates (eq 1–2) using eq 3 for the spectral density function (see `Results and Discussion'), whereas the motional parameters of N-H bond vectors, S2 NH and τf, were obtained using the program Dynamics53,54 that models 15N relaxation data selecting for the appropriate motional model (that can be different from the simplest form of eq 3) based on statistical criteria. 15N relaxation data have been analyzed with standard expressions for 15N relaxation in 15N-1H spin pairs. 15N R2,R1 and 1H-15N NOE data were included in analysis that used the spectral density function of eq 3 where the squared order parameter describing the fluctuations of the backbone amide N-H bond vector, S2 NH, was used instead of S2 CαDα together with the corresponding N-H direction cosines. The N-H bond distance of 1.02Å and a uniform 15N CSA of −170 ppm were used in all calculations.
Dα quadrupolar splitting and 1DCα-Hα measurements in oriented GB1
Analysis of Dα QCC closely followed the work of Mittermaier and Kay where QCC values have been determined for methyl deuterons using the ratios of quadrupolar splittings, νQ, and 13Cmethyl-13C RDCs measured in an oriented protein.55 The same approach can be used for α deuterons provided that 1DCα-Hα RDCs are measured in the same sample. To enable the measurements of Dα splittings and 1DCα-Hα RDCs in the same protein sample, a mixture of [U-15N,13C,2H]-labeled and [U-15N,13C]-labeled GB1 was used (see `NMR samples' above). The use of the same sample with two different labeling schemes (one having 2H nuclei and the other 1H nuclei at α positions) ensures that the alignment characteristics and dynamical properties are exactly the same for the νQ and 1DCα-Hα measurements. The `mixed' GB1 sample was aligned in 18 mg/ml pf1 bacteriophage56 (quadrupolar D2O splitting of 24.7 Hz). 1DCα-Hα RDCs have been obtained using the HNCO-type experiment of Yang et al.57 modified to eliminate the resonances of 13Cα nuclei attached to deuterons arising from the (more concentrated) [U-15N,13C,2H]-labeled protein. This experiment allows for convenient measurements of 1DCα-Hα in H2O protein solutions by recording the modulation of carbonyl chemical shifts by (1JCα-Hα + 1DCα-Hα) couplings (see ref. 57). The quadrupolar splittings νQ in α deuterons have been obtained using the scheme of Figure 1 (inset A) with parametrically varied delays T of (0.02; 0.4; 1.0; 1.1; 1.6; 2.0; 2.3; 2.8; 3.1; 3.5; 4.0; 4.3; 4.8; 5.1; 5.5; 6.0; 6.3; 6.8; 7.1; 7.6; 8.0; 8.6) ms. The 1DCα-Hα and νQ measurements have been performed twice and the obtained νQ/1DCα-Hα ratios have been averaged.
Molecular dynamics simulations
A 1 μs molecular dynamics (MD) trajectory of ubiquitin was performed as described elsewhere.58 Briefly, the MD simulation was performed using the AMBER 9 package59 with the AMBER99SB force field,60 which was shown previously to accurately reproduce the native state dynamics of ubiquitin.59,61–63 The SHAKE algorithm64 was employed to constrain all bonds involving hydrogen atoms, and a time step of 2 fs was used. Non-deuterated ubiquitin was embedded in a cubic box with SPC/E water models and long-range electronic interactions were handled using the PME method65 with an 8 Å cutoff. The starting coordinates were taken from the crystal structure of ubiquitin (PDB entry 1ubq), and the simulation was run for 1000 ns at 300 K under NPT conditions after application of standard minimization and heating protocols. The values of S2 CαHα have been extracted using the iRED method66 averaged over time windows of 1 ns and 5 ns, i.e. on the order of the experimental global tumbling correlation time of ubiquitin.
Results and Discussion
NMR experiments for the measurement of 2H relaxation rates at Dα sites of proteins
Figure 1 shows the HN(COCA)D experiment used for the measurements of relaxation rates at Dα sites. The pulse scheme is derived from the gradient sensitivity-enhanced HNCOCA experiment31 with additional delays at 13Cα nuclei to allow the magnetization to evolve to and from Dα positions whose relaxation is measured during time period T (see `Materials and Methods' for the pulse-scheme details). The transfer of magnetization can be summarized by,
| (5) |
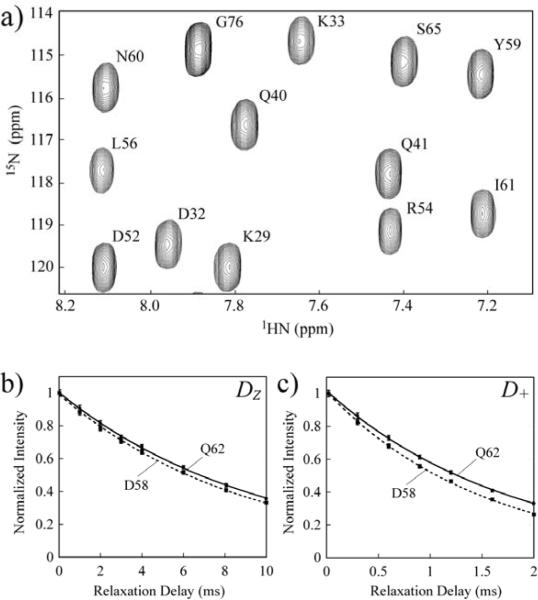
where the transfer from one spin to the next is achieved via one-bond scalar couplings and t1,t2 are acquisition times. A series of two-dimensional data sets is recorded as a function of T. The cross-peaks obtained at the frequencies (ωNi; ωHNi) decay with the relaxation rates of α-deuterons belonging to the previous residue, Dαi−1. A region of such a 2D spectrum recorded on ubiquitin at 27°C using the pulse scheme of Figure 1 (inset A, T = 0) is shown in Figure 2a. Relaxation rates can be extracted directly by fitting the intensity of each correlation to a single-exponential decay curve (Figures 2b–c). Since in glycines the magnetization is transferred from α carbons to both α-deuterons, the relaxation rates of the two (non-equivalent) Gly Dα positions can not be separated. Therefore, glycine residues (i.e. the amide correlations of the residues following glycines) have been excluded from analysis in this work. Likewise, Dα relaxation rates of residues preceding prolines can not be quantified using the experiment of Figure 1. The relaxation rates of proline Dα sites can be measured, however, through the amide correlation of the following (non-proline) residue. Although, as shown below, robust measures of backbone dynamics can be obtained from Dα relaxation rates, the Dα relaxation rate measurements using the scheme of Figure 1 are associated with very significant sensitivity losses compared to conventional 15N relaxation experiments. Taking into account different sample concentrations and acquisition times used for each time-point in the Dα/15N rate measurements (see `Materials and Methods'), we estimate that the scheme of Figure 1 is approximately 20 times less sensitive than 15N relaxation experiments necessitating the use of more concentrated protein samples and/or cryogenically cooled probes for data collection.
Figure 2.
a) A region of the 1HN-15N correlation map of the [U-15N,13C,2H]-labeled 3.2 mM ubiquitin (27°C; 600 MHz) acquired as the first measurement point using the experiment of Figure 1 (inset A, T = 0). Assignments of the cross-peaks are shown according to their 1HN-15N frequencies (located at position i if i−1 is the position of the decaying Dα nucleus). Typical decay curves of b) Dz and c) D+ magnetization are shown for Asp58 (dashed curves) and Gln62 (solid curves) of ubiquitin.
Dα relaxation rates
The R1 and R2 relaxation rates of Dα nuclei, RQ(D+) and RQ(Dz), have been measured using the experiments shown in insets A and B of Figure 1, respectively. Both experiments measure the relaxation rates of magnetization terms NzC'zCαz[D], where [D] is any deuterium spin operator and Az is a longitudinal spin operator of nucleus A (carbonyl/carbon-α of residue i−1 and nitrogen of residue i). As is the case in the previous deuterium relaxation studies,20,21,67 it can be shown that to a very good approximation R(NzC'zCαz[D]) = R(NzC'zCαz + R[D], and to obtain a `pure' deuterium relaxation rate it is sufficient to subtract R(NzC'zCαz) from the rates obtained in the experiments of Figure 1. In practice, however, the rates R(NzC'zCαz) are very small compared to R(NzC'zCαz[D]). For example, the R(NzC'zCαzD+) rates measured in ubiquitin vary between 372 and 1042(321 and 675; 370 and 569) s−1 at 10(27;40)°C, whereas R(NzC'zCαzDz) rates in ubiquitin at 10(27;40)°C vary between 62 and 115(90 and 129; 119 and 153)s−1. The rates R(NzC'zCαz) measured as described in `Materials and Methods' vary between 2.1 and 2.8(2.1 and 3.8; 1.9 and 4.0) s−1 at 10(27;40)°C. Clearly, these rates are within measurement errors of R(NzC'zCαzD+). This is, however, not necessarily the case for R(R(NzC'zCαzDz) measurements - although the corrections remain small. To avoid introduction of systematic errors to the quantified deuterium relaxation rates, the (R(NzC'zCαz) values have been subtracted on a residue-specific basis from all measured Dα rates in this work. It is important to emphasize that 2H relaxation of backbone Dα sites is completely dominated by the strong quadrupolar interaction, as is also the case in the previous 2H relaxation studies of 13CH2D20,21,27,68 and 13CHD227,28 methyl groups, 13CHD methylene sites in proteins23 as well as deuterated sugars and bases of RNA molecules.67 For example, calculations using typical sets of motional parameters obtained in this work for proteins tumbling with isotropic correlations times in the range between 2 and 10 ns show that the maximal contribution of the dipolar interaction of Dα deuterons with the directly bonded 13Cα spins to transverse(longitudinal) Dα relaxation rates D+(Dz) is 1.0(0.25) s−1. Evidently, such small contributions are within the errors of Dα relaxation rate measurements and can be safely ignored.
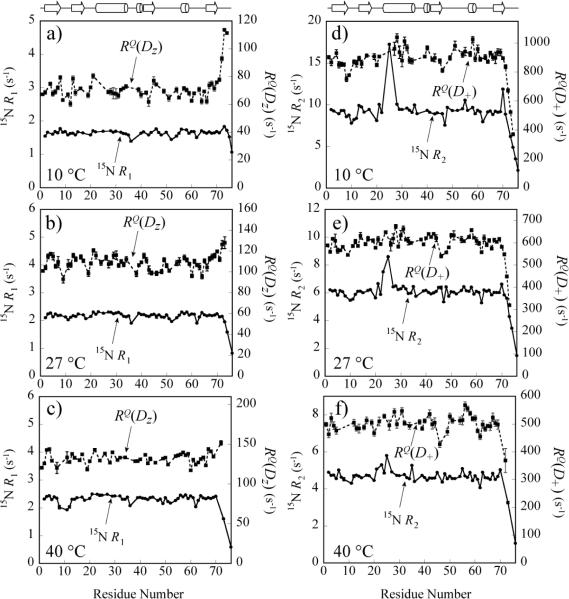
Figure 3 shows the profiles of experimental RQ(Dz) and RQ(D+) values obtained in ubiquitin at 10°C (Figure 3a,d), 27°C (Figure 3b,e) and 40°C (Figure 3c,f). For comparison, 15N R1 and R2 rate profiles are included in the same plots. The average RQ(D+) rates measured at 10(27;40)°C in ubiquitin are 880(597;500) s−1, whereas average RQ(Dz) rates are 72(107;132) s−1. Higher than average degree of backbone flexibility is manifested in decreased RQ(D+) values in (i) the loop between residues Thr7 and Lys11 with average RQ(D+) of 813(571)s−1 at 10(27)°C (Figures 3d and 3e; the residues in this region could not be reliably quantified at 40°C); (ii) near the Lys48 polymerization site (residues Ala46-Lys48) at all temperatures with average RQ(D+) values of 855(566;467)s−1 at 10(27;40)°C, and (iii) the C-terminus starting from Arg72 (Figures 3 d–f). These trends are largely mirrored by 15N R2 rates. Interestingly, RQ(Dz) profiles show that higher disorder at the C-terminus is accompanied by an increase in RQ(Dz) rates while 15 R1 rates decrease for the same residues (Figures 3a–c; some RQ(Dz) rates could not be quantified at the C-terminus at 40°C because of resonance overlap). Notably, the RQ(Dz) and RQ(D+) rates of Gly Dα positions have to be excluded from the plots in Figure 3 resulting in a loss of information as some of Gly residues in ubiquitin (e.g. Gly10 and Gly47) fall in the regions of increased backbone flexibility according to 15N data. It is apparent from Figures 3d–f that chemical exchange on the micro-to-millisecond time-scale - most notably affecting the amide of Asn25 with 15N R2 rate of 17.2(8.6;5.8)s−1, while the average 15N R2 rates in ubiquitin are 9.0(6.0;4.6)s−1 at 10(27;40)°C - does not affect the Dα rates to any significant extent. Large exchange contributions to R2 relaxation rates can significantly complicate 15N relaxation analysis, while Dα relaxation data (with the exception of double-quantum coherences, D2+, vide infra) remain unaffected by contributions from chemical exchange.
Figure 3.
Plots of Dα (shown with black rectangles and dashed lines) and 15N (black circles and solid lines) relaxation rates in ubiquitin as a function of the protein sequence. RQ(D) and 15N R1 rates are shown at a) 10°C, b) 27°C, c) 40°C, while RQ(D+) and 15N R2 rates are shown at d) 10°C, e) 27°C, f) 40°C. The lines connecting the symbols on the plots are intended solely to guide the eye. Schematic representation of the secondary structure of ubiquitin is shown on top: β-sheets are depicted with arrows, while α-helices are represented with cylinders.
Because the deuteron is a spin 1 nucleus, a total of five relaxation rates can be measured at Dα sites. As described by Millet et al.21 for the case of methyl groups, in addition to `rank-1' coherences D+ and Dz, the relaxation rates of `rank-2' elements (D+Dz+DzD+, 3Dz2 −2 and D+2) can be quantified in the same 2H site. Indeed, one of the principal advantages of 2H spin relaxation lies in the possibility to assess the self-consistency of the obtained rates prior to analysis in terms of motional parameters. Jacobsen and co-workers69 have shown that so long as J(0) ≥ J(ωD) ≥ J(2ωD), where J(ωD) is the spectral density function evaluated at the 2H Larmor frequency, ωD, (see `Materials and Methods') the following inequalities must hold: (5/3)RQ(D+Dz+DzD+) ≥ RQ(D) ≥ (5/3)RQ(3Dz2−2) ≥ RQ(Dz), where the relaxation rates of anti-phase 2H magnetization, (D+Dz+DzD+), and the quadrupolar order, (3Dz2−2), are given by,
| (6) |
| (7) |
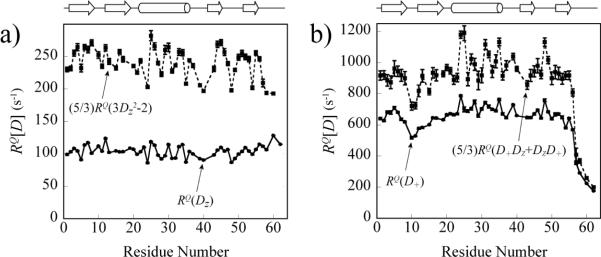
The pulse-scheme that can be used for RQ(D+Dz+DzD+) and RQ(3Dz2−2) measurements at Dα positions of proteins are shown in insets C and D of Figure 1, respectively. In contrast to 2H relaxation studies of methyl deuterons, however, the RQ(D+Dz+DzD+) and RQ(3Dz2−2) measurements at backbone Dα sites suffer from very poor sensitivity because of fast 2H spin-flips occurring during prolonged 13Cαi−1→D i−1(T)→13Cαi−1 magnetization transfer steps (two time periods τd+ζ in Figure 1, insets C–D). As a result, it was not possible to measure RQ(D+Dz+DzD+ and RQ(3Dz2−2) of Dα nuclei in ubiquitin within a reasonable time frame. Nevertheless, we have been able to quantify the RQ(D+Dz+DzD+) and RQ(3D2z−2) rates in a more concentrated sample of a smaller protein GB1. Figure 4 shows that the inequalities (5/3)RQ(3D2z−2)≥RQ(Dz) (Figure 4a) and (5/3)RQ(D+Dz+DzD+)≥RQ(D+) (Figure 4b) are indeed satisfied without a single exception in GB1 at 22°C representing a useful semi-quantitative consistency test of the experimental raw data. The profiles of RQ(D+),RQ(Dz) and 15N R2,R1 rates measured in GB1 are compared in Figure S1 of the Supporting Information. Notably, the flexibility of the backbone in the loop between Gly9 and Leu13 and the C-terminus of GB1 is `picked-up' by Dα relaxation data with decreased RQ(D+) and RQ(D+Dz+DzD+) rates in these regions (Figure 4b and Figure S1 of the Supporting Information). Unfortunately, the presence of two glycine residues (Gly38 and Gly41) prevents the quantification of Dα rates in another flexible loop of GB1 extending from Asn37 to Gly41 as it is apparent from 15N R1,R2 rate profiles (Figure S1b).
Figure 4.
Consistency plots of Dα relaxation rates. a) (5/3)RQ(3D 2z−2) (shown with black rectangles and dashed lines) and RQ(Dz) (black circles; solid lines); b) (5/3)RQ(D+Dz+DzD+) (black rectangles; dashed lines) and RQ(D+) (black circles; solid lines) rates measured in GB1 at 22°C (600 MHz) are plotted as a function of GB1 sequence. Schematic representation of the secondary structure of GB1 is shown on top.
As described above, fast 2H spin-flips lead to on average 4-to-5-fold sensitivity losses in the RQ(D+Dz+DzD+) and RQ(3D2z−2) experiments (Figure 1, insets C–D) compared to the RQ(D+) measurements (Figure 1, inset A) in GB1 at 22°C. This situation is similar to 2H relaxation measurements in the sugar and base moieties of RNA reported earlier.67 Because of low sensitivity of `rank−2' relaxation measurements and, as a result, substantial errors in the derived RQ(D+Dz+DzD+) and RQ(3D2z−2) rates, these data have not been used in further analysis. Mainly for the same reasons, no attempt has been undertaken to measure the relaxation rate of the fifth double-quantum 2H coherence, D+2, at Dα sites.
Dα relaxation derived diffusion tensor parameters
Prior to obtaining the 2H-derived measures of backbone order it is important to establish the diffusion parameters of the global molecular reorientation. In analogy to the case of 15N relaxation in protein backbones, 2H R2/R1 ratio, RQ(D+)/RQ (Dz), is, to a good approximation, independent of the amplitude and time-scale of rapid internal motions.13,52 It therefore serves as a good measure of the rate at which the Cα-Dα vector reorients with global tumbling.70 Table 1 compares the parameters of the (axially symmetric) diffusion tensors derived from Dα RQ(D+)/RQ(Dz) and 15N R2/R1 ratios for ubiquitin at three temperatures (see `Materials and Methods'). Since the diffusion tensor of ubiquitin has a relatively low diffusion anisotropy, we have chosen to test whether the RQ(D+)/RQ(Dz) ratios can reproduce a significantly more anisotropic reorientation on the sample of GB1 modified at the C-terminus (Table 1). Figure S2 of the Supporting Information shows the plots of RQ(D+)/RQ(Dz) as a function of the angle α that each of the Cα-Dα bond vectors subtends with respect to the unique axis of the diffusion tensor, along with the best fits of the data for GB1 (22°C) and ubiquitin (27°C). Although the Dα-derived orientations of the principal axes (polar angles θ and ϕ in the inertial coordinate frame) are less well defined in comparison to 15N-derived values, a good agreement between the 15N- and Dα-derived tensors is observed in all cases. The ratios of τc,eff = (2D∥ + 4D⊥)−1 values obtained at 10, 27 and 40°C in ubiquitin are very close to those expected based on the Stokes-Einstein relationship. Despite the fact that Dα relaxation rates in ubiquitin have been obtained using a 3-fold more concentrated protein sample than 15N rates, the Dα-derived values of τc,eff in ubiquitin are somewhat lower (3.6%, 5.6% and 2.8% at 10°C, 27°C and 40°C, respectively) than their 15N-derived counterparts at the same temperature (Table 1). Interestingly, in a recent study exchange-free, purely dipolar contributions to 15N relaxation rates, Rdd, in ubiquitin have been derived.17 These exchange-free rates indicated the presence of non-zero Rex contributions to 15N R1ρ rates for many residues in ubiquitin.17 This implies that Dα RQ(D+)/RQ(Dz) ratios that are not affected by chemical exchange to any significant degree might serve as more robust estimates of the global reorientation parameters in small proteins.
Table 1.
Comparison of Dα RQ(D+)/RQ(Dz)- and 15N R2/R1-derived Diffusion Tensor Parameters of Ubiquitin (10°C, 27°C, 40°C) and GB1 (22°C).a)
| τc,effb) | D||/D⊥ | θc) | φc) | |
|---|---|---|---|---|
| Ubiquitin (10 °C) | 6.68 ± 0.03 (6.92 ± 0.02) | 1.28 ± 0.04 (1.23 ± 0.02) | 12 ± 4 (6 ± 2) | −22 ± 12 (−19 ± 5) |
| Ubiquitin (27 °C) | 3.94 ± 0.03 (4.16 ± 0.01) | 1.22 ± 0.03 (1.18 ± 0.02) | 8 ± 3 (6 ± 2) | −8 ± 12 (−16 ± 4) |
| Ubiquitin (40 °C) | 2.90 ± 0.02 (2.98 ± 0.01) | 1.26 ± 0.03 (1.23 ± 0.01) | 16 ± 2 (6 ± 1) | −34 ± 14 (−48 ± 8) |
| GB1 (22 °C) | 4.43 ± 0.02 (4.42 ± 0.01) | 1.45 ± 0.03 (1.39 ± 0.02) | 20 ± 6 (24 ± 1) | −61 ± 26 (−99 ± 8) |
15N R2/R1-derived diffusion parameters are shown in parentheses and italics below the Dα RQ(D+)/RQ(Dz)-derived values. The orientation of the unique axis of the axially symmetric diffusion tensor is specified in the inertial frame for both proteins. The inertia tensors and direction cosine values for Cα-Hα and N-H bond vectors have been calculated using the coordinates of protonated x-ray structures of ubiquitin and GB1 with respective pdb accession codes 1ubq.pdb50 and 2qmt.pdb.51 Seven C-terminal residues of GB1 do not have crystallographic coordinates and have been excluded from the derivation of the diffusion tensor. See 'Materials and Methods' for the details of diffusion tensor determination.
τc,eff is given in units of nanoseconds (ns).
Angles are given in degrees. The angle γ between the Dα and 15N-derived diffusion axes can be estimated using the relationship cosγ = cosθ1cosθ2 + sinθ1sinθ2cosϕ1−ϕ2), where {θi,ϕi} are the polar angles that define the mean orientations of the unique axes of the two compared diffusion tensors. These angles are equal to 6(2,10)° for ubiquitin at 10(27,40)°C and 14.5° for GB1 (22°C).
The choice and estimation of Dα QCC values
Although the value of Dα QCC is not needed for determination of the diffusion tensor, the knowledge of its accurate value is of paramount importance for interpretation of Dα relaxation rates in terms of motional parameters. Several solid-state NMR studies have reported the values of QCC for aliphatic deuterons attached to sp3-hybridized carbons ranging from 168 ± 2 to 174 ± 2 kHz.71 Solid-state NMR measurements of Haeberlen and co-workers provided the QCC values of the two α-deuterons in zwitterionic glycine equal to 159.9 and 169.4 kHz.72 The authors explained the large difference between the two values by formation of weak C-H…O hydrogen bonds leading to a decrease of QCC in one of the two α-deuterons. Notably, oxygen acceptors are located in an adjacent layer of glycine molecules72 - a situation that cannot be encountered in solution. In another low-temperature liquid crystal NMR study, the QCC value obtained for deuterons in a CD3 methyl group of toluene (165 kHz) has been compared to the QCC of deuterons in cyclohexane-d12 (174 ± 2 kHz). The two values can be brought into exact agreement if the tetrahedral angle θ of the methyl group is assumed to be equal to 111° instead of 109.5°.73 Interestingly, using solution NMR techniques Mittermaier and Kay determined the QCC value of deuterons in 13CH2D methyl groups of proteins equal to 167 ± 1 kHz assuming θ = 109.5°.55 What is effectively determined in this study is the product P2(cosθ)QCC, where P2(x) = 0.5(3x2 − 1) is the second order Legendre polynomial. If the value of θ is increased by only 1°,74 the methyl QCC increases to 174 kHz. We note here that what is normally determined in single-crystal NMR measurements (unless they are performed at very low temperatures) is the product √S2QCC, where S is the order parameter of local motions. Here, local motions are assumed to be axially symmetric, and S includes the effects of slow motions and (potentially small) contributions from `rocking' motions of the molecule relative to the crystal lattice. If S2 is assumed to be equal to 0.95,75,76 then the measurements of Haeberlen and co-workers in α-glycine72 yield the value of QCC = 173.8 kHz for the non-hydrogen bonded deuteron.
To obtain an independent estimate of QCC of α-deuterons in proteins we followed the approach of Mittermaier and Kay.55 Briefly, in an oriented protein, during the period T in the pulse-scheme of Figure 1 (inset A) the 2H magnetization evolves according to55,77
| (8) |
, where the quadrupolar splitting , θ is the angle between the principal axis of the electric field gradient tensor and the magnetic field, and the brackets <> denote ensemble averaging. The relaxation rates of Dy and (DzDx+DxDz) coherences are described by eq 1 (the rate of in-phase 2H magnetization, RI) and eq 6 (the rate of anti-phase 2H magnetization, RA), respectively. Including relaxation during the period T, the evolution of the Dy magnetization (that is detected in the end of the experiment) is described by55
| (9) |
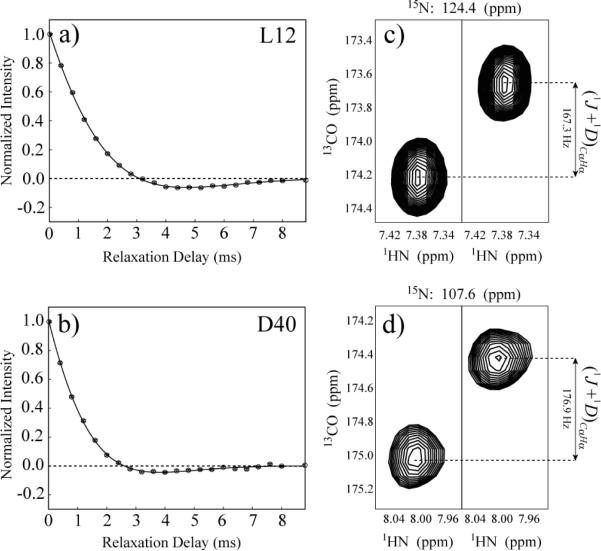
where and Δ = (RI − RA)/Ω. In contrast to the study of methyl groups,55 here, the average rate of magnetization decay, (RI + RA)/2, is 2-to-3 fold higher than the maximal achievable quadrupolar splitting νQ, making the analysis of the decay of Dy (eq 9) extremely unreliable except for a (small) subset of residues where νQ is close to its maximal value and the zero-crossing of the magnetization decay can be achieved experimentally. In pf1 phage-aligned, highly concentrated sample of GB1 (see `Materials and Methods'), a small subset of 11 peaks has been chosen where the zero-crossing of the Dy magnetization decay is apparent and where the extraction of a reliable albeit inexact value of νQ is still feasible. Although for this subset of residues the condition (2πνQ)2 >> (RI − RA)2 is always satisfied, simulations using synthetic data and average RI, RA rates and νQ values for GB1 showed that the fitting of the decay function Dy to a simpler 3-parameter expression with a single effective (RI + RA)/2 rate78 would produce errors in the derived νQ values of 5 to 8%. We have chosen therefore to fit the decay curves to the full expression in eq 9 above with four variable parameters (RI, RA, A and νQ). Two examples of such fits for Leu12 and Asp40 from the chosen subset of 11 peaks in GB1 are shown in Figures 5a–b.
Figure 5.
Examples of the decay curves are shown for a) for Leu12 and b) Asp40 of GB1(22°C) from the chosen subset of 11 peaks in GB1 that show clear-cut zero-crossing. The decay curves are fit to eq 9. Zero normalized intensity is shown with a dashed line. The 1HN-13CO correlations obtained in the experiment of Yang et al.56 that allows the measurement of 1DCα-Hα residual dipolar couplings for c) for Leu12 and d) Asp40. The measured frequency differences (1J+1DCα-Hα) are shown for each pair of peaks.
The value 1DCα-Hα RDC measured as described in `Materials and Methods' is expressed as, , where γi is the gyromagnetic ratio of nucleus i, μ0 is the vacuum permeability constant, and rCH is the distance between Cα and Hα nuclei. Figures 5c–d show the results of 1DCα-Hα measurements for the same pair of residues in GB1 as in Figures 5a and 5b, respectively. As shown by Mittermaier and Kay for methyl groups, the ratio of νQ/1DCα-Hα taken for the same α position, is independent of magnetic alignment (<3cos2θ −1>) and local motions.55 QCC value can then be obtained from the νQ/1DCα-Hα ratio following the relationship,
| (10) |
Note that unlike in the case of methyl groups,54 according to eq 10, Dα QCC does not depend on dihedral angles. The correlation of the 2H quadrupolar splitting νQ with the 1DCα-Hα dipolar coupling for the subset of 11 peaks in GB1 is shown in Figure S3 of the Supporting Information. Linear regression analysis of this correlation provided a slope of −5.66 ± 0.34 (Pearson R = 0.979) when the (statistically insignificant) intercept was fixed at zero. The sign of νQ can not be determined using this procedure, and νQ values have been assumed to have a sign opposite to that of the measured 1DCα-Hα. Using eq 10 and assuming a standard rCH distance of 1.095 Å79–81 we obtain the Dα QCC value of 173.7 kHz. Notably, any effects of local dynamics are cancelled out by taking the ratio of νQ and 1DCα-Hα allowing one to use the value of rCH distance `uncorrected' for any type of local motions.81
The procedure described above for the derivation of QCC values of Dα deuterons is only semi-quantitative due to large uncertainties associated with the derivation of νQ. From the variation of individual νQ/1DCα-Hα ratios for 11 peaks in GB1 and from propagated errors in (fitted) νQ and 1DCα-Hα values we estimate the uncertainty obtained in Dα QCC measurements on the order of 6–8% (~10–14 kHz). However, on average we have been able to obtain the value of Dα QCC that agrees quantitatively with the results of solid-state measurements in α-glycine if dynamics is taken into account (see above). In what follows, we therefore used a uniform value of Dα QCC equal to 174 kHz in all calculations. It is unlikely that the variation in individual νQ/1DCα-Hα ratios in GB1 reflects the actual variation in Dα QCC values in a protein rather than the uncertainties of the measurement. Although hydrogen bonding is known to significantly affect quadrupolar couplings of deuterons,76 α-deuterons in proteins are unlikely to participate in sufficiently strong hydrogen bonds. Of note, DFT calculations of QCC values of aliphatic deuterons bound to sp3-hybridized carbons show that QCC is a highly local parameter whose value is dependent almost exclusively on the choice of the rCD bond length (N.R. Skrynnikov, personal communication).
Comparison of 2H- and 15N-derived backbone order
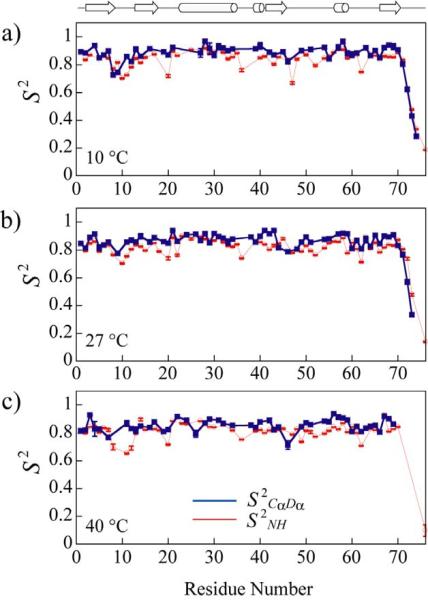
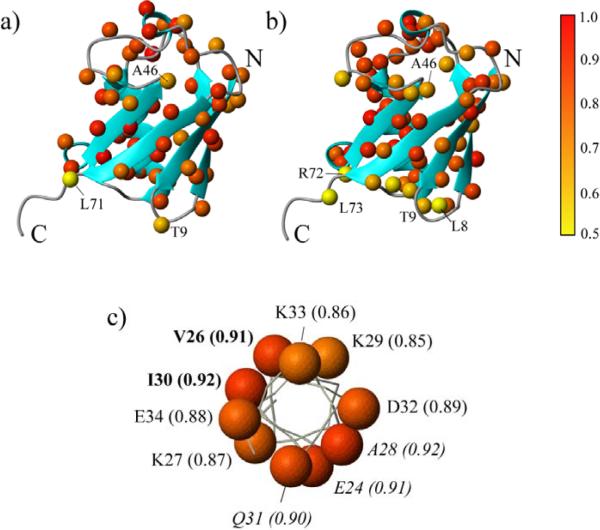
Since, commonly, only two rates, RQ(D+) and RQ(Dz), are available for the derivation of motional parameters of Cα-Dα vectors in proteins, caution must be exercised in a modelfree-type analysis of Dα relaxation data to avoid over-interpretation when the results are compared to 15N-derived dynamics parameters. Therefore, we have chosen to fit the RQ(D+) and RQ(Dz) rates first to the simplest possible motional model that excludes the term describing local motions in the spectral density function of eq 3 (τ' = 0). The majority of the residues in ubiquitin could be fit using such a single-parameter (S2 CαDα) spectral density function with 5% probability of exceeding χ2.82 If the χ2 of the fit exceeded this level of confidence, the RQ(D+) and RQ(Dz) rates have been fit to the full expression in eq 3 with 2 variable parameters (S2 CαDα; τf). The resulting values of S2 CαDα in ubiquitin at 10°C, 27°C and 40°C versus residue numbers are shown with blue rectangles in Figures 6a–c. For convenience of comparison we have included in the plots the values of S2 NH derived from 15N relaxation data (red circles in Figures 6a–c). Table S1 in the `Supporting Information' lists all the dynamics parameters obtained at Dα positions of ubiquitin at the three temperatures. Figure 7 shows the ribbon structure of ubiquitin where the Hα(Dα) atoms (Figure 7a) and HN atoms (Figure 7b) are color-coded according to the values of S2 CαDα and S2 NH, respectively. Overall, lower S2 CαDα and S2 NH values are observed in the loop region between residues Thr7 and Lys11, in the bend near the polyubiquitination site (residues Ala46-Lys48) and in several C-terminal residues.
Figure 6.
Dα-derived S2CαDα (blue rectangles and lines) and 15N-derived S2NH (red open circles and lines) in ubiquitin at a) 10°C, b) 27°C and c) 40°C plotted as a function of protein sequence. Schematic representation of the secondary structure of ubiquitin is shown on top: β-sheets are depicted with arrows, while α-helices are represented with cylinders.
Figure 7.
Ribbon diagrams of ubiquitin crystal structures with a) Dα and b) HN atoms represented as balls color-coded according to the values of S2CαDα and S2NH (27°C), respectively. The elements of the secondary structure are shown in blue. The placement of a number of residues discussed in the text is indicated with residue numbers. c) Schematic representation of the α-helical stretch of ubiquitin (residues Ile23-Glu34) viewed from the top along the helical axis. The color-coded balls represent Dα atoms. The values of S2CαDα are listed along with residue numbers.S2CαDα values of residues with Cα-Dα vectors directed towards a short 310-helical stretch (Pro38-Gln40) are shown in bold, whereas those directed towards the interior of the protein core on the other side of the α-helix are shown in italics. The color-coding scale is shown to the right of panel (b). The diagrams have been generated using the program Molmol.89
Cα-Dα bond vectors are motionally distinct from the N-H bond vectors, with 2H-derived S2 CαDα values on average slightly higher than their S2 NH counterparts in N-H amides in agreement with several earlier molecular dynamics simulations83,84 as well as NMR spin relaxation85,86 and liquid crystal studies.81 In particular, the average S2 CαDα values of 0.86(0.85;0.84) are obtained in ubiquitin at 10(27;40)°C for the full protein and 0.89(0.87;0.85) when the flexible C-terminal residues are excluded from analysis, while the respective average S2 NH values are 0.82(0.81;0.81) for the full protein and 0.84(0.83;0.82) when the C-terminus is excluded. For those residues where both S2 CαDα and S2 NH could be quantified, S2 CαDα values are higher than S2 NH on average, with their respective average values of 0.86(0.86;0.85) and 0.82(0.81;0.80) at 10(27;40)°C. The difference in order parameters is even more pronounced in GB1. The values of S2 CαDα and S2 NH in GB1 at 22°C are plotted as a function of the protein sequence in Figure S4 of the Supporting Information. The higher rigidity of the Cα-Hα (Cα-Dα) bond vectors in proteins is a consequence of the high correlation of their motions with those of the Cα-Cβ bond vector of the same amino acid.87 The latter anchors the side-chain to the backbone, and thereby any reorientational motion will need to involve the bulk of the side chain. By contrast, the N-HN amides are strongly affected by local crank-shaft-type motions of the peptide bond plane,84,88 which involve anti-correlated modulations of the associated backbone φi and ψi−1 dihedral angles. There are notable exceptions to this general trend, however. For example, in the C-terminal region of ubiquitin following Leu71, average S2 CαDα(S2 NH) of 0.61(0.63) have been obtained at 27°C, whereas in GB1 the average S2 CαDα(S2 NH) of the C-terminal residues are 0.22(0.24). Interestingly, the Dα rates of the C-terminal residues in both proteins can not be fit to the simplest (S2 CαDα only) Lipari-Szabo model because the increased RQ(Dz) rates at the C-terminus (Figure 3a–c) can not be explained without invocation of fast local motions. In principle, direct comparison of S2 CαDα and S2 NH on a per-residue basis can be ambiguous since higher S2 NH values may result from the use of different motional models for the derivation of S2 CαDα and S2 NH as well as significantly different time-scales of N-H and Cα-Dα bond vector fluctuations. Furthermore, since their respective diffusion tensor parameters have been used for the derivation of S2 CαDα and S2 NH, any small differences in these parameters (Table 1) can skew the differences between S2 CαDα and S2 NH (S2 CαDα - S2 NH) in favor of somewhat smaller values adding additional uncertainty to direct comparisons of backbone order at the amide and Dα sites (vide infra).
Since different motional processes are sampled by Dα and 15N relaxation rates, it would be of interest to compare the degree of backbone order in the elements of protein secondary structure where Cα-Hα(Dα) and N-H bond vectors are oriented in different directions. For example, 15N relaxation data do not sample fast local motions that occur around the helical axis, such as a rolling motion of an α-helical shaft,90 because in α-helices all N-H bonds lie approximately parallel to the helical axis forming hydrogen bonds with a carbonyl oxygen acceptor of residue i−4. In contrast, Cα-Hα(Dα) bond vectors are directed outward making angles of up to ~70° with the α-helical axis. Interestingly, in the α-helical segment of ubiquitin (residues Ile23-Glu34), S2 CαDα are noticeably higher for the residues whose Cα-Hα(Dα) bond vectors are directed towards a short 310-helical stretch the protein structure (Val26, Ile30 or oriented towards the interior of the protein at the other face of the α-helix (Glu24, Ala28, Gln31). Figure 7c shows a schematic representation of the α-helix in ubiquitin viewed from its N-terminal end approximately along the axis of the helix, with S2CαDα (27°C) shown for each Dα site. In GB1, the residues of the α-helix (Ala23-Asp36) facing the hydrophobic interior of the protein (Ala26, Phe30, Tyr33 and Ala34) also tend to have elevated S2CαDα. The resulting alternating patterns of RQ(D+) rates (Figures 3d–f and Figures S1 of the Supporting Information) and S2CαDα values (Figures 6a,b, Figure S4 of the Supporting Information) are apparent in the helical regions of both proteins indicating that the backbone order as probed by 2H spin relaxation at Dα positions is likely to be related to the tightness of hydrophobic packing in protein cores. Specifically, the values of S2CαDα in the α-helix of ubiquitin (Figure 7c) are weakly but statistically significantly correlated with the buried surface area and the hydrophobic contact potential91,92 at Cα positions (Pearson R > 0.5). We note that the `zigzag' patterns of RQ(D+) rates and the resulting S2CαDα values cannot be explained by the anisotropy of the global molecular tumbling, as the unique diffusion axis of ubiquitin subtends an angle of only ~10° relative to the α-helical axis.
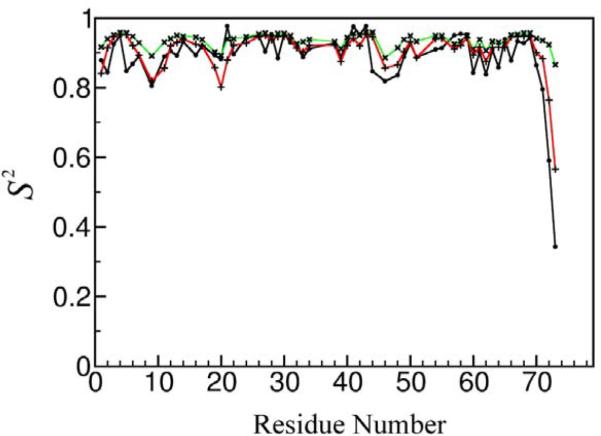
Molecular dynamics simulations and alternative analyses of Dα 2H rates
To gain more confidence in the 2H-derived measures of backbone order, we have performed molecular dynamics simulations for ubiquitin at 27°C (see `Materials and Methods'). Interestingly, the best agreement between MD-derived S2CαHα and experimental S2CαDα order parameters is achieved when the Dα QCC value is (slightly) lowered to 171 kHz. A comparison between experimental S2CαDα (QCC = 171 kHz) and MD-derived S2CαHα values obtained using a 1 μs MD trajectory of ubiquitin averaged over 1 ns and 5 ns time windows, is shown in Figure 8. A good agreement is found for the loop region of the N-terminal β-hairpin and the flexible C-terminus. The experimentally observed decrease in the order parameters of loop residues Ile44, Ala46, Lys48 and Glu49, whose side-chains point towards the solvent, is well reproduced by the MD simulation. Furthermore, the `zigzag' pattern displayed by the experimental S2CαDα values in the Tyr59-Lys63 loop is also clearly observable in the simulation profile (Figure 8). For this region, the order parameters directly reflect the orientation of the associated side-chain, with lower S2 for inward oriented side-chains and higher S2 for more solvent exposed ones. Lys63 is a notable exception with a relatively high S2CαHα despite its high solvent accessibility. The close relationship between S2CαDα and the associated side chain properties is corroborated by the very close agreement between S2CαDα and S2CαCβ values found in the MD simulation of ubiquitin (see Supporting Information, Figure S6).
Figure 8.
Experimental S2 CαDα order parameters of ubiquitin at 27°C (black line with closed circles) determined using a uniform QCC value of 171 kHz, in comparison with the MD-derived S2 CαHα values obtained from a 1 μs MD trajectory of ubiquitin averaged over 1 ns (green line with `x' symbols) and 5 ns (red line with `+' symbols) time windows. See `Materials and Methods' for the details of MD simulations.
The comparisons of 15N- and 2H-derived measures of backbone order described here have been performed using their respective (15N-derived or 2H-derived) overall diffusion tensor parameters (Table 1). Obviously, there is a unique diffusion tensor that characterizes the rotational reorientation of a molecule. Therefore, it would be of interest to ascertain that the relation between S2CαDα and S2NH noted above holds if analysis is performed using a common set of diffusion tensor parameters for both nuclei. We have repeated the analysis as described in the `Comparison of 2H- and 15N-derived backbone order' section above for ubiquitin at 27°C using common diffusion tensor parameters for 15N and 2H data with the averaged values of τc,eff = (2D|| + 4D⊥)−1 = 4.05 ns; D||/D⊥ = 1.20; θ = 7°; ϕ = −12°, and the Dα QCC value of 171 kHz as obtained from MD simulations. The results of this analysis are presented in Figure S5 of the Supporting Information. The main conclusions obtained in the case when separate diffusion tensors have been used, remain in force. In particular, the average S2 CαDα(S2 NH) values of 0.87(0.84) are obtained for all residues of ubiquitin, while S2 CαDα(S2 NH) values of 0.89(0.86) are obtained when the flexible C-terminal and loop regions are excluded from analysis. However, when the same analysis (common diffusion tensor, QCC = 171 kHz) is performed for GB1, a number of residues give S2 CαDα values higher than the theoretical limit of unity. When the Dα QCC value is `reset' to 174 kHz, the relationship between S2 CαDα and S2 NH still holds in both proteins although the average S2 CαDα values become only insignificantly higher than S2 NH in ubiquitin.
Concluding remarks
In summary, we have shown that deuterium relaxation rates measured at deuterated carbon-α positions (Dα) serve as robust measures of backbone order in proteins. Dα relaxation rates are straightforward to interpret in terms of motional parameters (S2 CαDα; τf) provided that a uniform quadrupolar coupling constant (QCC) is assumed for all Dα sites in the protein molecule. To the best of our knowledge, this is the first attempt to use 2H relaxation as a probe of backbone dynamics in proteins. Clearly, the experiments developed for Dα relaxation rate measurements are not sufficiently sensitive for routine applications requiring the use of concentrated [U-2H,13C,15N]-labeled protein samples. Most of the Dα relaxation measurements described in this work have been performed on a 3.2 mM [U-2H,13C,15N]-ubiquitin using a room-temperature probe. Obviously, at such high protein concentrations, potential aggregation of protein molecules in NMR samples is of concern. The data on diffusion tensor characteristics summarized in Table 1 show that this is apparently not the case for both proteins studied in this work. With the increased sensitivity of NMR measurements due to the continuing development of cryogenically-cooled detection devices and the availability of higher magnetic fields, we anticipate that RQ(D+), RQ(Dz) measurements would become feasible on protein samples with regular protein content (0.5–1.0 mM). Moreover, with the increasing molecular weight of a protein under study 2H spin-flipping rates would decrease (Figures 3a–c). Therefore, the methods described in this work may be applicable to well-behaved medium-sized proteins (up to ~200 residues), as the sensitivity of the experiment in Figure 1 is primarily determined by the rate of 2H spin-flips at the step when the magnetization is transferred from 13Cα spins to Dα and back.
For sensitivity reasons, because of the requirement for [U-2H,13C,15N] labeling, and because less data is available per nuclear probe in the case of Dα measurements at a single spectrometer field (RQ(D+), RQ(Dz) rates versus 15N R1, R2 and 1H-15N NOEs) the developed methodology is not meant to substitute for the commonly used 15N amide nuclei as NMR spin probes of backbone dynamics. Rather, it can be envisaged to serve as a useful complement to existing more sensitive techniques. Indeed, it should be kept in mind that the Dα relaxation rates measured in this work sample motions occurring in the protein backbone at positions that are distinct - chemically, structurally and motionally - from those normally sampled by conventional 15N-based techniques. This work represents an attempt to get an alternative view of dynamic processes in protein molecules and to establish the range of applicability and utility of the described NMR methodology. In this context, it is noteworthy that, in principle, the measurements of 13Cα relaxation in proteins93,94 would provide the same information about backbone dynamics in a protein molecule as Dα methodology described here. The use of (protonated) carbon-α probes would, however, suffer from the same set of shortcomings and uncertainties as 15N-based methods (the uncertainty in 13Cα-Hα distances; site-specific 13C CSA variation; contributions to 13C relaxation from dipolar interactions with 13Cβ and 13CO spins etc.). We have chosen to compare the Dα-derived motional parameters with more commonly used 15N spin probes. An NMR study that quantifies 13Cα relaxation rates in selectively 13Cα-enriched protein samples95 and compares the measures of backbone order thus obtained with the Dα-derived data reported here, is in progress.
Supplementary Material
Acknowledgments
This work has been supported in part by the General Research Board (GRB) Award to V.T. from the University of Maryland. The authors are grateful to Dr. Pramodh Vallurupalli and Prof. Lewis Kay (University of Toronto, Canada) for useful discussions, to Dr. Andy Byrd (NCI, Federick, Maryland) for the generous gift of [U-15N,13C,2H]-ubiquitin used in this work, Dr. Chenyun Guo (University of Maryland) for preparation of [U-15N,13C,2H]-GB1 and [U-15N]-GB1 samples, Prof. David Fushman (University of Maryland) for providing the sample of [U-15N]-ubiquitin and the Matlab-based software for 15N relaxation data analysis, and Prof. Nikolai Skrynnikov (Purdue University, West Lafayette, Indiana) for sharing with us some unpublished results of DFT calculations of quadrupolar coupling constants.
Footnotes
Supporting Information Available: One figure showing Dα RQ(D+), RQ(Dz) relaxation rate profiles along with 15N R1, R2 profiles in GB1 at 22°C as a function of the protein sequence (Figure S1). One figure showing the dependence of RQ(D+)/RQ(Dz) on the angle α formed by Cα-Dα bonds and the principal axis of the diffusion tensor in GB1 at 22°C and ubiquitin at 27°C (Figure S2). One figure showing the correlation plot of the Dα quadrupolar splittings, νQ, and 1DCα-Hα residual dipolar couplings measured for a subset of 11 peaks in the oriented sample of GB1 (Figure S3). One figure showing S2CαDα and S2NH as a function of sequence for GB1 at 22°C (Figure S4). One figure showing S2CαDα and S2NH for Ubiquitin at 27°C obtained using a common diffusion tensor and the QCC value of 171 kHz (Figure S5). One figure showing the agreement between S2CαHα and S2CαCβ values found in the 1-μs MD simulation of ubiquitin at 27°C (Figure S6). One Table listing S2CαDα and τf values obtained in ubiquitin at 10°C, 27°C and 40°C. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- (1).Fersht A. Structure and Mechanism in Protein Science. Freeman & Co.; New York: 2002. [Google Scholar]
- (2).Frauenfelder H, Sligar SG, Wolynes PG. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
- (3).Dobson CM, Karplus M. Curr. Opin. Struct. Biol. 1999;9:92–101. doi: 10.1016/s0959-440x(99)80012-8. [DOI] [PubMed] [Google Scholar]
- (4).Karplus M, Kuriyan J. Proc. Natl. Acad. Sci. USA. 2005;102:6679–6685. doi: 10.1073/pnas.0408930102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Peng JW, Wagner G. Methods Enzymol. 1994;239:563–596. doi: 10.1016/s0076-6879(94)39022-3. [DOI] [PubMed] [Google Scholar]
- (6).Palmer AG. Curr. Opin. Struc. Biol. 1997;7:732–737. doi: 10.1016/s0959-440x(97)80085-1. [DOI] [PubMed] [Google Scholar]
- (7).Ishima R, Torchia DA. Nat. Struct. Biol. 2000;7:740–743. doi: 10.1038/78963. [DOI] [PubMed] [Google Scholar]
- (8).Palmer AG, Kroenke CD, Loria JP. Methods Enzymol. 2001;339:204–238. doi: 10.1016/s0076-6879(01)39315-1. [DOI] [PubMed] [Google Scholar]
- (9).Kay LE. Nat. Struct. Biol. NMR Suppl. 1998;5:513–516. doi: 10.1038/755. [DOI] [PubMed] [Google Scholar]
- (10).Palmer AG. Annu. Rev. Biophys. Biomol. Struct. 2001;30:129–155. doi: 10.1146/annurev.biophys.30.1.129. [DOI] [PubMed] [Google Scholar]
- (11).Fushman D, Cowburn D. Methods Enzymol. 2001;339:109–26. doi: 10.1016/s0076-6879(01)39312-6. [DOI] [PubMed] [Google Scholar]
- (12).Korzhnev DM, Billeter M, Arseniev AS, Orekhov VY. Prog. Nucl. Magn. Reson. Spectrosc. 2001;38:197–266. [Google Scholar]
- (13).Kay LE, Torchia DA, Bax A. Biochemistry. 1989;28:8972–8979. doi: 10.1021/bi00449a003. [DOI] [PubMed] [Google Scholar]
- (14).Cavanagh J, Fairbrother WJ, Palmer AG, Rance M, Skelton NJ. Protein NMR Spectroscopy. Elsevier Academic Press; 2007. [Google Scholar]
- (15).Lipari G, Szabo A. J. Am. Chem. Soc. 1982;104:4559–4570. [Google Scholar]
- (16).Lipari G, Szabo A. J. Am. Chem. Soc. 1982;104:4546–4559. [Google Scholar]
- (17).Hansen DF, Yang D, Feng H, Zhou Z, Wiesner S, Bai Y, Kay LE. J. Am. Chem. Soc. 2007;129:11468–11479. doi: 10.1021/ja072717t. [DOI] [PubMed] [Google Scholar]
- (18).Xu J, Millet O, Kay LE, Skrynnikov NR. J. Am. Chem. Soc. 2005;127:3220–3229. doi: 10.1021/ja040215z. [DOI] [PubMed] [Google Scholar]
- (19).Abragam A. Principles of Nuclear Magnetism. Clarendon Press; Oxford: 1961. [Google Scholar]
- (20).Muhandiram DR, Yamazaki T, Sykes BD, Kay LE. J. Am. Chem. Soc. 1995;117:11536–11544. [Google Scholar]
- (21).Millet O, Muhandiram DR, Skrynnikov NR, Kay LE. J. Am. Chem. Soc. 2002;124:6439–6448. doi: 10.1021/ja012497y. [DOI] [PubMed] [Google Scholar]
- (22).Skrynnikov NR, Millet O, Kay LE. J. Am. Chem. Soc. 2002;124:6449–6460. doi: 10.1021/ja012498q. [DOI] [PubMed] [Google Scholar]
- (23).Yang D, Mittermaier A, Mok YK, Kay LE. J. Mol. Biol. 1998;276:939–954. doi: 10.1006/jmbi.1997.1588. [DOI] [PubMed] [Google Scholar]
- (24).Ishima R, Petkova AP, Louis JM, Torchia DA. J. Am. Chem. Soc. 2001;123:6164–6171. doi: 10.1021/ja0104711. [DOI] [PubMed] [Google Scholar]
- (25).Lee AL, Flynn PF, Wand AJ. J. Am. Chem. Soc. 1999;121:2891–2902. [Google Scholar]
- (26).Millet O, Mittermaier A, Baker D, Kay LE. J. Mol. Biol. 2003;329:551–563. doi: 10.1016/s0022-2836(03)00471-6. [DOI] [PubMed] [Google Scholar]
- (27).Tugarinov V, Ollerenshaw JE, Kay LE. J. Am. Chem. Soc. 2005;127:8214–8225. doi: 10.1021/ja0508830. [DOI] [PubMed] [Google Scholar]
- (28).Tugarinov V, Kay LE. J. Am. Chem. Soc. 2006;128:12484–12489. doi: 10.1021/ja063071s. [DOI] [PubMed] [Google Scholar]
- (29).Rosen MK, Gardner KH, Willis RC, Parris WE, Pawson T, Kay LE. J. Mol. Biol. 1996;263:627–636. doi: 10.1006/jmbi.1996.0603. [DOI] [PubMed] [Google Scholar]
- (30).Gardner KH, Rosen MK, Kay LE. Biochemistry. 1997;36:1389–1401. doi: 10.1021/bi9624806. [DOI] [PubMed] [Google Scholar]
- (31).Bax A, Ikura M. J. Biomol. NMR. 1991;1:99–104. doi: 10.1007/BF01874573. [DOI] [PubMed] [Google Scholar]
- (32).Shaka AJ, Keeler J, Frenkiel T, Freeman R. J. Magn. Reson. 1983;52:335–338. [Google Scholar]
- (33).Shaka AJ, Barker PB, Freeman R. J. Magn. Reson. 1985;64:547–552. [Google Scholar]
- (34).Kay LE. J. Am. Chem. Soc. 1993;115:2055–2057. [Google Scholar]
- (35).McCoy MA, Mueller L. J. Magn. Reson. 1992;98:674–679. [Google Scholar]
- (36).Patt SL. J. Magn. Reson. 1992;96:94–102. [Google Scholar]
- (37).Boyd J, Soffe N. J. Magn. Reson. 1989;85:406–413. [Google Scholar]
- (38).Kay LE, Ikura M, Tschudin R, Bax A. J. Magn. Reson. 1990;89:496–514. doi: 10.1016/j.jmr.2011.09.004. [DOI] [PubMed] [Google Scholar]
- (39).Geen H, Freeman R. J. Magn. Reson. 1991;93:93–141. [Google Scholar]
- (40).Kay LE, Keifer P, Saarinen T. J. Am. Chem. Soc. 1992;114:10663–10665. [Google Scholar]
- (41).Schleucher J, Sattler M, Griesinger C. Angew. Chem. Int. Ed. Engl. 1993;32:1489–1491. [Google Scholar]
- (42).Marion D, Ikura M, Tschudin R, Bax A. J. Magn. Reson. 1989;85:393. [Google Scholar]
- (43).Delaglio F, Grzesiek S, Vuister GW, Zhu G, Pfeifer J, Bax A. J. Biomol. NMR. 1995;6:277–293. doi: 10.1007/BF00197809. [DOI] [PubMed] [Google Scholar]
- (44).Kamith U, Shriver JW. J. Biol. Chem. 1989;264:5586–5592. [PubMed] [Google Scholar]
- (45).Farrow NA, Muhandiram R, Singer AU, Pascal SM, Kay CM, Gish G, Shoelson SE, Pawson T, Forman-Kay JD, Kay LE. Biochemistry. 1994;33:5984–6003. doi: 10.1021/bi00185a040. [DOI] [PubMed] [Google Scholar]
- (46).Ferrage F, Piserchio A, Cowburn D, Ghose R. J. Magn. Reson. 2008;192:302–313. doi: 10.1016/j.jmr.2008.03.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Wooten JB, Savitsky GB, Jacobus J, Beyerlein AL, Emsley JW. J. Chem. Phys. 1979;70:438–442. [Google Scholar]
- (48).Schramm S, Oldfield E. Biochemistry. 1983;22:2908–2913. doi: 10.1021/bi00281a020. [DOI] [PubMed] [Google Scholar]
- (49).Wöessner DE. J. Chem. Phys. 1962;37:647–654. [Google Scholar]
- (50).Vijay-Kumar S, Bugg CE, Cook WJ. J. Mol. Biol. 1987;194:531–544. doi: 10.1016/0022-2836(87)90679-6. [DOI] [PubMed] [Google Scholar]
- (51).Frericks-Schmidt HL, Sperling LJ, Gao YG, Wylie BJ, Boettcher JM, Wilson SR, Rienstra CM. J. Phys. Chem. B. 2007;111:14362–14369. doi: 10.1021/jp075531p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (52).Tjandra N, Feller SE, Pastor RW, Bax A. J. Am. Chem. Soc. 1995;117:12562–12566. [Google Scholar]
- (53).Fushman D, Cahill S, Cowburn D. J. Mol. Biol. 1997;266:173–194. doi: 10.1006/jmbi.1996.0771. [DOI] [PubMed] [Google Scholar]
- (54).Hall JB, Fushman D. J. Am. Chem. Soc. 2006;128:7855–7570. doi: 10.1021/ja060406x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Mittermaier A, Kay LE. J. Am. Chem. Soc. 1999;121:10608–10613. [Google Scholar]
- (56).Hansen MR, Mueller L, Pardi A. Nat. Struct. Biol. 1998;5:1065–1074. doi: 10.1038/4176. [DOI] [PubMed] [Google Scholar]
- (57).Yang D, Tolman JR, Goto NK, Kay LE. J. Biomol. NMR. 1998;12:325–332. doi: 10.1023/A:1008223017233. [DOI] [PubMed] [Google Scholar]
- (58).Showalter SA, Brüschweiler R. J. Chem. Theory Comput. 2007;3:961–975. doi: 10.1021/ct7000045. [DOI] [PubMed] [Google Scholar]
- (59).Case DA, Cheatham TE, Darden T, Gohlke H, Luo R, Merz KM, Onufriev A, Simmerling C, Wang B, Woods RJ. J. Comp. Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (60).Hornak V, Abel R, Okur A, Strockbine B, Roitberg A, Simmerling C. Proteins. 2006;65:712–725. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (61).Showalter SA, Brüschweiler R. J. Am. Chem. Soc. 2007;129:4158–4159. doi: 10.1021/ja070658d. [DOI] [PubMed] [Google Scholar]
- (62).Showalter SA, Johnson E, Rance M, Brüschweiler R. J. Am. Chem. Soc. 2007;29:14146–14147. doi: 10.1021/ja075976r. [DOI] [PubMed] [Google Scholar]
- (63).Maragakis P, Lindorff-Larsen K, Eastwood MP, Dror RO, Klepeis JL, Arkin IT, Jensen MO, Xu HF, Trbovic N, Friesner RA, Palmer AG, Shaw DE. J. Phys. Chem. B. 2008;112:6155–6158. doi: 10.1021/jp077018h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (64).Ryckaert JP, Ciccotti G, Berendsen HJC. J. Comput. Chem. 1977;23:327–341. [Google Scholar]
- (65).Darden T, York D, Pedersen L. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- (66).Prompers JJ, Brüschweiler R. J. Am. Chem. Soc. 2002;124:4522–4534. doi: 10.1021/ja012750u. [DOI] [PubMed] [Google Scholar]
- (67).Vallurupalli P, Kay LE. J. Am. Chem. Soc. 2005;127:6893–6901. doi: 10.1021/ja0427799. [DOI] [PubMed] [Google Scholar]
- (68).Yang D, Kay LE. J. Magn. Reson. Series B. 1996;110:213–218. [Google Scholar]
- (69).Jacobsen JP, Bildsöe HK, Schaumburg K. J. Magn. Reson. 1976;23:153–164. [Google Scholar]
- (70).Grzesiek S, Bax A. J. Am. Chem. Soc. 1994;116:10196–10201. [Google Scholar]
- (71).Burnett LH, Muller BH. J. Chem. Phys. 1971;55:5829–5831. [Google Scholar]
- (72).Muller C, Schajor W, Zimmermann H, Haeberlen U. J. Magn. Reson. 1984;56:235–346. [Google Scholar]
- (73).Rowell JC, Phillips WD, Melby LR, Panar M. J. Chem. Phys. 1965;43:3442–3454. [Google Scholar]
- (74).Ottiger M, Bax A. J. Am. Chem. Soc. 1999;121:4690–4695. [Google Scholar]
- (75).Henry ER, Szabo A. J. Chem. Phys. 1985;82:4753–4761. [Google Scholar]
- (76).LiWang AC, Bax A. J. Magn. Reson. 1997;127:54–64. doi: 10.1006/jmre.1997.1187. [DOI] [PubMed] [Google Scholar]
- (77).Sörensen OW, Eich GW, Levitt MH, Bodenhausen G, Ernst RR. Prog. Nucl. Magn. Reson. Spectrosc. 1983;16:163–192. [Google Scholar]
- (78).Kuboniwa H, Grzesiek S, Delaglio F, Bax A. J. Biomol. NMR. 1994;4:871–878. doi: 10.1007/BF00398416. [DOI] [PubMed] [Google Scholar]
- (79).Jeffrey G. Accurate molecular structures, their determination and importance. Oxford University Press; Oxford: 1992. [Google Scholar]
- (80).Demaison J, Wlodarczak G. Struct. Chem. 1994;5:57–66. [Google Scholar]
- (81).Ottiger M, Bax A. J. Am. Chem. Soc. 1998;120:12334–12341. [Google Scholar]
- (82).Bevington PR, Robinson DK. Data Reduction and Error Analysis for the Physical Sciences. WCB/McGraw-Hill; New York: 1992. [Google Scholar]
- (83).Palmer AG, Case DA. J. Am. Chem. Soc. 1992;114:9059–9067. [Google Scholar]
- (84).Fadel AR, Jin DQ, Montelione GT, Levy RM. J. Biomol. NMR. 1995;6:221–226. doi: 10.1007/BF00211787. [DOI] [PubMed] [Google Scholar]
- (85).Dellwo MJ, Wand AJ. J. Am. Chem. Soc. 1989;111:4571–4578. [Google Scholar]
- (86).LeMaster DM, Kushlan DM. J. Am. Chem. Soc. 1996;118:9255–9264. [Google Scholar]
- (87).Brüschweiler R. J. Chem. Phys. 1995;102:3396–3403. [Google Scholar]
- (88).Brüschweiler R, Wright PE. J. Am. Chem. Soc. 1994;116:8426–8427. [Google Scholar]
- (89).Koradi R, Billeter M, Wüthrich K. J. Mol. Graphics. 1996;14:51–55. doi: 10.1016/0263-7855(96)00009-4. [DOI] [PubMed] [Google Scholar]
- (90).Fischer MWF, Zeng L, Majumdar A, Zuiderweg ERP. Proc. Natl. Acad. Sci. USA. 1998;95:8016–8019. doi: 10.1073/pnas.95.14.8016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (91).Lee B, Richards FM. J. Mol. Biol. 1971;55:379–400. doi: 10.1016/0022-2836(71)90324-x. [DOI] [PubMed] [Google Scholar]
- (92).Kurochkina N, Lee B. Protein Eng. 1995;8:437–442. doi: 10.1093/protein/8.5.437. [DOI] [PubMed] [Google Scholar]
- (93).Lee LK, Rance M, Chazin WJ, Palmer AG. J. Biomol. NMR. 1997;9:287–298. doi: 10.1023/a:1018631009583. [DOI] [PubMed] [Google Scholar]
- (94).Idiyatullin D, Nesmelova I, Daragan V, Mayo KH. Protein Sci. 2003;12:914–922. doi: 10.1110/ps.0228703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (95).Lundström P, Teilum K, Carstensen T, Bezsonova I, Wiesner S, Hansen DF, Religa TL, Akke M, Kay LE. J. Biomol. NMR. 2007;38:199–212. doi: 10.1007/s10858-007-9158-6. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.