Why Do Phage Play Dice?

Abstract

Phage lambda is among the simplest organisms that make a developmental decision. An infected bacterium goes either into the lytic state, where the phage particles rapidly replicate and eventually lyse the cell, or into a lysogenic state, where the phage goes dormant and replicates along with the cell. Experimental observations by P. Kourilsky are consistent with a single phage infection deterministically choosing lysis and double infection resulting in a stochastic choice. We argue that the phage are playing a “game” of minimizing the chance of extinction and that the shift from determinism to stochasticity is due to a shift from a single-player to a multiplayer game. Crucial to the argument is the clonal identity of the phage.

Organisms typically use information from the environment to suitably modify their behavior. Some of these can be considered “strategic” decisions for maximizing the chances of success of the population. For example, many organisms are able to adjust their reproductive strategies according to environmental conditions. A typical signal that often triggers changes in the reproductive strategy is population density (1, 6). Temperate bacteriophages are among the simplest organisms that are able to sense population density and choose their reproductive strategy accordingly. In general, temperate phage choose to stay dormant and replicate along with the host (lysogeny) rather than making many virions and killing the host (lysis) when larger numbers of phage attack a bacterial population (4, 7, 10). Phage lambda's choice between lysis and lysogeny has become a paradigm for developmental decisions (12). For this lysis-lysogeny decision, we use game theory to understand under what conditions different strategies might be optimal. In particular, we focus on the determinism versus the stochasticity of the strategy. We show that deterministic strategies are best when the phage has minimal information and must consider itself as the only “player” in the game. In contrast, having multiple identical players can make a stochastic strategy the best.

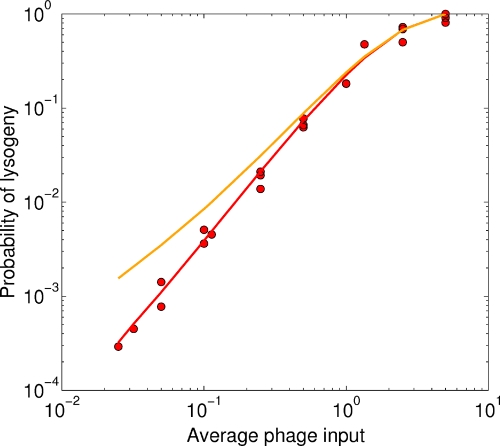
We consider the phage to be playing a game whose purpose is to minimize the chance of extinction. For single-player games of this kind, where the player has several options but limited information, the optimal strategies are typically deterministic (13). And it is indeed the case that the lysis-lysogeny decision is often deterministic. This statement is somewhat at odds with the general perception that stochasticity plays an important role in the decision, a view initiated by reference 2, which invoked stochasticity to explain Kourilsky's measurements (7) of the frequency of lysogenization in lambda. However, our analysis of Kourilsky's data (7, 8) (Fig. 1; see also Materials and Methods) shows that (i) when a single phage infects a bacterium (i.e., when the multiplicity of infection [MOI] is 1), it invariably goes lytic and (ii) when the MOI is 2, the decision is stochastic, with a slight preference toward lysogeny (this preference increases as the MOI increases).

FIG. 1.

Red circles show the fraction of bacteria that entered lysogeny as a function of the API (overall phage/bacterium ratio) in Kourilsky's experiments (7, 8, 9). Solid lines are theoretical estimates using different functions for Q(m), which is the probability of going lytic as a function of the MOI (m) (see Materials and Methods). As shown by the red curve, the best fits ± estimated 95% intervals (Table 1) for Q(m) are 0.004 ± 0.001, 0.70 ± 0.04, and 0.99 ± 0.08 for m values of 1, 2, and 3, respectively. Even a small amount of stochasticity in the decision for an MOI of 1 is inconsistent with the data: for the orange curve the Q(m) values are 0.05, 0.70, and 0.99 for m values of 1, 2, and 3, respectively.

The stochasticity in the strategy for an MOI of 2 refers to the fact that seemingly identical infection events lead to different developmental paths. This inhomogeneity in the decision could reflect either true randomness (for example, due to the stochasticity of individual molecular events) or inhomogeneity across different infected cells (for example, the cell size could affect the decision [14]).

The determinism in the phage decision for an MOI of 1 fits the game-theoretic expectation, as we will show, but then, the conundrum is this: why is the decision stochastic for an MOI of 2? In this paper, we argue that the shift from determinism at an MOI of 1 to stochasticity at an MOI of 2 is analogous to the shift from deterministic to stochastic strategies in single-player versus multiplayer games.

THEORY

Game theoretic view of the lysis-lysogeny decision.

We consider the set of all phages in an infected bacterium to be one player in a game where the choice is between lysis and lysogeny. Note that individual phage are not the players, as multiple phage inside the same bacterium cannot choose separately between lysis and lysogeny; it is the infected bacterium with all the phage that it contains that goes into one state or the other. From the point of view of a given player, one round of the game starts with the infection and the lysis-lysogeny decision and continues until one of the phage offspring released from the bacterium (either on immediate lysis or later, following prophage induction) subsequently infects another bacterium. The purpose of the game is to minimize the chance of extinction of the phage population. Whether this is best achieved by deterministically going lytic/lysogenic or making a stochastic decision may depend on the environmental conditions. How many bacteria are there? Do the phage outnumber the bacteria? Are the bacteria starving or growing well? The MOI provides some information about the first two questions, specifically, the relative numbers of phage to bacteria.

(i) MOI of 1.

Here, the phage in the bacterium has the least possible information about the surrounding environment. It does not know how many phage or bacteria are present or whether the phage outnumber the bacteria or not. In this situation of minimal information, we assume that the infected bacterium must play a solitary game, where it assumes it is the only player.

(ii) MOI of 2.

Now, the phage inside the bacterium do have some information about the environment. First, having two phage simultaneously infect the same bacterium means it is quite likely that the phage outnumber the bacteria. It is probable, in this case, that there are multiple infected bacteria. We assume that the strategy takes into account the presence of multiple players all playing the same game.

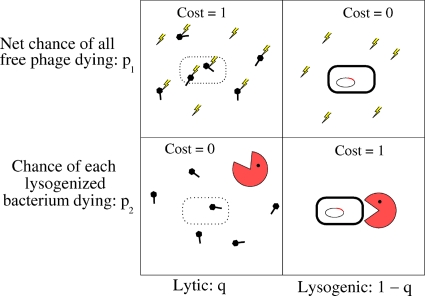
The game being played by the phage involves weighing the chance of extinction in lysogeny (the bacterium and its descendants may die before the phage escapes it by prophage induction) versus the chance of extinction if it goes lytic (for example, due to a toxic substance that kills phage before they find other bacteria to infect). We can set up a simple payoff matrix (Fig. 2) that reflects the consequences, for the phage population, of the different choices. We use p₁ to represent the net chance that all the free phage (the ones outside bacteria) die. We denote by p₂ the chance that each lysogenized bacterium and all its descendants die before the phage escape by prophage induction.

FIG. 2.

Phage game payoff matrix. p₁ is the probability that all free phage die, and p₂ is the probability that each lysogenized bacterium and all its descendants die before the phage escapes. q is the probability that the infected bacteria go lytic. “Cost” represents the probability of phage extinction in a given situation and, for simplicity, is set to either 1 or 0.

Throughout the rest of this paper, we assume that the two options are asymmetric in the sense that the lytic option exposes all phage to the current, possibly dangerous, conditions and that the lysogenic option initiates a lineage of lysogenized bacteria. As each such lineage could stretch far into the future, the fate of each lysogen is postponed to a later time and can be assumed to be independent of the fate of other lysogens.

MATERIALS AND METHODS

Interpreting Kourilsky's data.

Kourilsky measured the probability of lysogeny, P_lys, for different values of the average phage input (API) (a) for lambda phage infecting a population of Escherichia coli under conditions described in references 7 and 8. The API is simply the ratio of the total number of phage to the total number of bacteria. The API is thus the MOI averaged over the whole bacterial population. From the point of view of a given bacterium, the API reflects the probability of its being infected. The probability of lysogeny versus API curve, P_lys (a), shown in Fig. 1, is a combination of two probabilities: , where Q(m) is the probability of lysogeny at a given MOI (m) and P(m,a) is the probability that a bacterium will be infected by m phage at a given API (a). We assume, as is consistent with Kourilsky's data (see Fig. 4 in reference 7), that P(m,a) is Poissonian: , i.e., adsorption and injection of phage DNA are random, and the same is true for all bacteria in the population. The only unknown, then, is Q(m), and one can try different functions to fit the data. The best fits for Q(m) are shown in Table 1. Notice that the observed P_lys(a) (Fig. 1) scales as the second power of a for a small API. That is, P_lys(a) is ∼a² for small a. In words, the probability of lysogeny is proportional to the probability that two phage infect a bacterium (i.e., the chance of getting an MOI of 2). This is precisely what constrains Q(1) to be equal to zero. The orange curve in Fig. 1 shows that if Q(1) differs from zero by even a small amount (5%), the resultant P_lys(a) curve scales with the first power of a at a small API and therefore clearly deviates from the data. Even if the chance of lysogeny at an MOI of 1 were as low as 1%, the resultant P_lys value would be around a factor of 2 higher than what Kourilsky observed at the lowest API that he measured and is therefore clearly ruled out by his data.

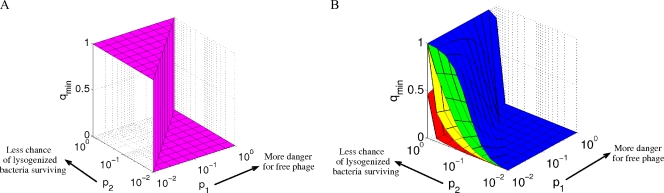
FIG. 4.

(A) Optimal strategies for the phage game for one player. The q_min strategy, which minimizes the chance of phage extinction, is deterministic: always go lytic (q_min = 1) when p₁ is <p₂, and always go lysogenic (q_min = 0) when p₁ is >p₂. All stochastic strategies result in a greater chance of extinction. (B) Optimal strategy for the phage game with n identical players. Blue, n = 2; green, n = 4; yellow, n = 10; red, n = 100. As there is a collective reward for going lytic, if the chance of free phage dying is low, the ideal situation is that in which one infected bacterium is lysed, leaving the rest to go lysogenic. This is possible only with the use of a stochastic strategy, because each player is using the same strategy. If the danger of going lytic is above a certain threshold (p₁ > p₂), however, then the best strategy is to deterministically go lysogenic.

TABLE 1.

Best fits for Q(m), found using the least-square fitting of log₁₀ P_lys^a

m	Q(m)
1	0.0038 ± 0.0012
2	0.6960 ± 0.0408
3	0.9886 ± 0.0769
4	0.9886 ± 0.0537
5	0.9886 ± 0.0487
6	0.9886 ± 0.0487
7	0.9886 ± 0.0487
8	0.9886 ± 0.0487
9	0.9886 ± 0.0487

^aThe Q(0) value of 0 and the Q(m≥10) value of 1 were kept fixed. There are no error bars for the data points in Kourilsky's paper, so we determined error bars (which indicate 95% intervals) for the Q(m) fit by redoing the fit 100 times, each time randomly perturbing the data points by up to ±10% (uniformly distributed).

RESULTS

Deterministic strategies are optimal for single players.

We denote the decision-strategy by q, the probability that the infected bacterium goes lytic. The probability that the phage population goes extinct when following this strategy in the model phage game defined in Fig. 2 is

(1)

What strategy, i.e., what value of q, will minimize this? Clearly, the best strategy is as follows: q is 0 if p₁ is >p₂, and q is 1 if p₁ is <p₂ (if p₁ equals p₂ exactly, it does not matter what the phage does) (see also Fig. 4A). Either way, the optimal strategy is deterministic. Note that changing the precise values of the costs in the payoff matrix will change only the threshold at which the best strategy shifts from that in which q is 0 to that in which q is 1. It will not change the fact that there exists a deterministic strategy that is at least as good as any stochastic one (see, for example, theorem 6.12 in reference 13).

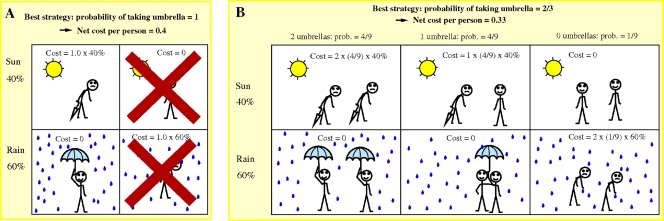
The underlying mathematical reason for this is that the net cost is a linear function of q (a function linear in q [in general, continuous and monotonic in q] necessarily has its minimum value at a boundary of the region under consideration, in this case representing a q value of 0 or 1). Intuitively, it may be easier to understand in the simpler, but analogous, game shown in Fig. 3A. This “umbrella game” involves trying to decide whether to carry an umbrella or not on the basis of the chance of rain. If the inconvenience of carrying an umbrella on a sunny day is the same as the unpleasantness of getting soaked by rain, then you should always carry an umbrella if the chance of rain is more than 50% [the net cost is p(1 − q) + (1 − p)q if p is the chance of rain and q is the chance of carrying an umbrella; if p is >0.5, the cost is minimized when q is 1]. Any stochastic strategy will be worse: the reduction in the number of times you carry an umbrella on sunny days will be outweighed by an increase in the number of days you get soaked. If you dislike getting wet more, a deterministic choice is still best; the threshold shifts just below 50%.

FIG. 3.

(A) Umbrella game for one person, with 60% chance of rain and 40% chance of sunshine. The best strategy is to always carry an umbrella; all stochastic strategies result in more mistakes. (B) Umbrella game for two people with identical strategies. As there is a collective reward for carrying an umbrella, if the chance of rain is significant, the ideal situation is that in which one person brings an umbrella, leaving the other person free from carrying one. This is possible only with the use of a stochastic strategy, because both individuals are using the same strategy. If the chance of rain is below a certain threshold (p < 1/3), however, then the deterministic strategy of never carrying an umbrella is best.

How do we then understand the stochastic decision when two phage infect a bacterium?

Stochastic strategies can be optimal for multiple players.

Let us now assume there are n infected bacteria. We will keep the costs the same as in Fig. 2 and assume that each of the n players follows the same strategy, represented by q. Further, for a clonal phage population, it is sufficient if at least one of the infected bacteria follows the “correct” developmental path so that the clone does not go extinct. That is, if free phage are not killed then even if only one of the n players chooses lysis, the cost is zero for all the players; this is a game with a “collective” reward. The chance of extinction is then

(2)

Each term in the above sum represents one extinction scenario: for instance, the first term is the probability that all infected bacteria lyse (qⁿ) and that all are killed (p₁), while the last term is the probability that all infected bacteria go lysogenic [(1 − q)ⁿ] and that all these lysogenized lineages die before the phage escape by prophage induction (p₂ⁿ). Notice how p₂ is raised to the power of n. This is because, as discussed earlier, we assume that the fate of each lysogenized lineage is independent of the others, whereas p₁ is not raised to a power because it represents the probability that all free phage die. That is, we assume that phage die together and that bacteria die independently of each other, an assumption that stems from the facts that bacterial lifetimes are much longer than those of phage and that therefore phage experience only the present environment whereas it is possible for bacteria to experience environments indefinitely far into the future.

Figure 4B shows the value of q that minimizes P for a range of p₁ and p₂ values at different values for n. Notice that the optimal strategy is now stochastic when p₁ is <p₂. Essentially, because there is a collective reward/punishment for going lytic, ideally in our model game, one infected bacterium should be lysed, leaving the rest to go lysogenic. With identical strategies, this is possible only with the use of a stochastic strategy.

Mathematically, a stochastic strategy can be optimal in this case because P is no longer linear in q, as there are n players. However, this is not enough. If the nonlinear function could be factorized into a product of identical linear functions, then, again, the optimal strategy would be deterministic. The reason this does not happen is that the collective rewards and punishments associated with free phage result in an asymmetry in the way in which p₁ and p₂ appear in equation 2. This becomes clear when we rewrite equation 2 as follows:

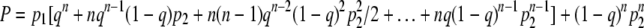(3)

The absence of p₁ in the last term is what makes this expression nonfactorizable. A more generic function could also include, for example, a collective probability that all lysogenized bacteria die. This would, in general, also be nonfactorizable. The existence of any collective rewards/punishments is enough to prevent factorization, and we have attempted to illustrate this more transparently by having such a collective cost only for the free phage. Adding a collective punishment for lysogenized bacteria would additionally favor stochastic strategies when p₁ is >p₂, a condition under which our simpler cost function always favors deterministic lysogeny (Fig. 4).

What makes a stochastic strategy optimal?.

Again, it is easier to understand what is going on by using a two-player version of the umbrella game (Fig. 3B), which is simpler than the phage game but illustrates the same point. As in the phage game, each player uses the same strategy, represented by q, and there is a collective reward because one umbrella is taken to be sufficient for both if it rains. The net cost is

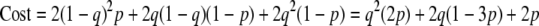(4)

To minimize this, one must choose the deterministic strategy in which q is 0 if p is <1/3 and the stochastic strategy in which q is (3p − 1)/2p otherwise. For the case considered in Fig. 3, where p is 0.6, the best strategy is therefore the stochastic one, wherein q is 2/3.

The umbrella game shows that the basic effect—the shift from determinism to stochasticity as one goes from single to multiple players—depends on (i) identical strategies and (ii) collective rewards/punishments. The collective reward—a single umbrella is sufficient to protect everyone—means that ideally one person would bring an umbrella, leaving the others free. Because everyone uses identical strategies, this is possible only with a stochastic strategy. The collective reward thus allows a population to hedge its bets and thereby do better than the sum of individuals. In a single-player game, there is no population, and therefore stochastic strategies simply result in more mistakes.

DISCUSSION

In this paper, we have attempted to connect two pieces of information: (i) under conditions explored by Kourilsky, an MOI of 1 deterministically leads to lysis, while the decision is stochastic for an MOI of 2, and (ii) in games involving a choice based on incomplete information, optimal single-player strategies are deterministic, while for multiple players they can be stochastic. Looking at the lysis-lysogeny decision from a game-theoretic point of view thus leads us to the conjecture that the shift from a deterministic strategy at an MOI of 1 to a stochastic one at an MOI of 2 arises from a shift from a single-player to a multiplayer game. Crucial to our argument is the clonal population of the phage, which results both in identical strategies among the multiple players and in collective rewards/punishments.

The game-theoretic framework used to describe the decision can be extended to incorporate elements that could be important under other conditions. For instance, the frequency of lysogenization may be influenced by properties of the bacterial cells, such as size (14) or starvation levels (5, 9). These properties are correlated with the growth rate of the cells, which in turn could affect the decision if some of the terms of the cost function depend on the growth rate. One reason for including such a dependence on growth rate is that extinction of the bacterial population will also lead to extinction of the phage. That is, under conditions where bacteria are starving badly, it might be important to take into account the fact that not only is the phage alone but possibly its host is also alone (15). In our game-theoretic framework we can do this by using a p₁ value that increases as the growth rate of the cells decreases. Because the terms in the cost function that involve p₁ are proportional to some power of q, a lower growth rate would then shift strategies toward more lysogenization. We would expect then that even at an MOI of 1, one could observe phage choosing lysogeny if p₁ were low enough. However, even in this case, the strategy would be deterministic, whereas it appears that, at least under conditions different from those used by Kourilsky, a stochastic strategy can be chosen at an MOI of 1 (9, 11, 14). Our considerations indicate that such stochasticity could survive only if the phage had evolved to use a multiplayer strategy even at an MOI of 1 under these conditions. That is, if phage lambda would have evolved to behave as if, when it infected a starved bacterium, it were not the only clonal phage infecting an E. coli bacterium in its vicinity.

We have concentrated here on why phage lambda might use different strategies for the lysis-lysogeny decision in different cases. We have not addressed the separate question of how the regulatory network of phage lambda is able to use the MOI to implement this shift in strategy. Clearly, gene copy number affects the behavior of genetic circuits; reference 16 shows how this is possible for lambda, and we are currently exploring this issue for a large class of simple regulatory motifs. St-Pierre and Endy (14) point out that the lambda circuitry may not be able to distinguish between infection of a large cell by two phages and infection of a small cell by a single phage. Thus, it is possible that the conditions used by Kourilsky produced a particularly homogeneous cell population, allowing observation of the deterministic lytic response at an MOI of 1.

On a more general note, the “collective reward games” that we have studied here differ in an interesting way from “cooperative games.” Collective rewards, as we have shown, favor strategies that use stochasticity to produce diversity of behavior in the population of players. In contrast, in cooperative games it is better for multiple players to follow the same cooperative strategy. This may have relevance for the phenomenon of bacterial persistence where occasionally bacteria that are resistant to antibiotics can arise in a clonal population, which allows the population to hedge its survival bets in case it encounters an antibiotic environment (3).

An amusing illustration of these ideas can be expressed within the context of human activity. Cooperative games, one can say, characterize the industrial age and favor mass production. Collective reward games, in contrast, characterize the information age; given our extensive ability to communicate, all members of a social group can gain from information obtained by one person. Basic research in science is an example of the latter type of game. Having too many scientists working on similar projects could result in a decrease of information gain per scientist. A more stochastic allocation of resources, on the other hand, could take better advantage of the collective-reward nature of research.